On the Laplace Transforms of the First Hitting Times for Drawdowns and Drawups of Diffusion-Type Processes
Abstract
1. Introduction
2. Preliminaries
2.1. Formulation of the Problem
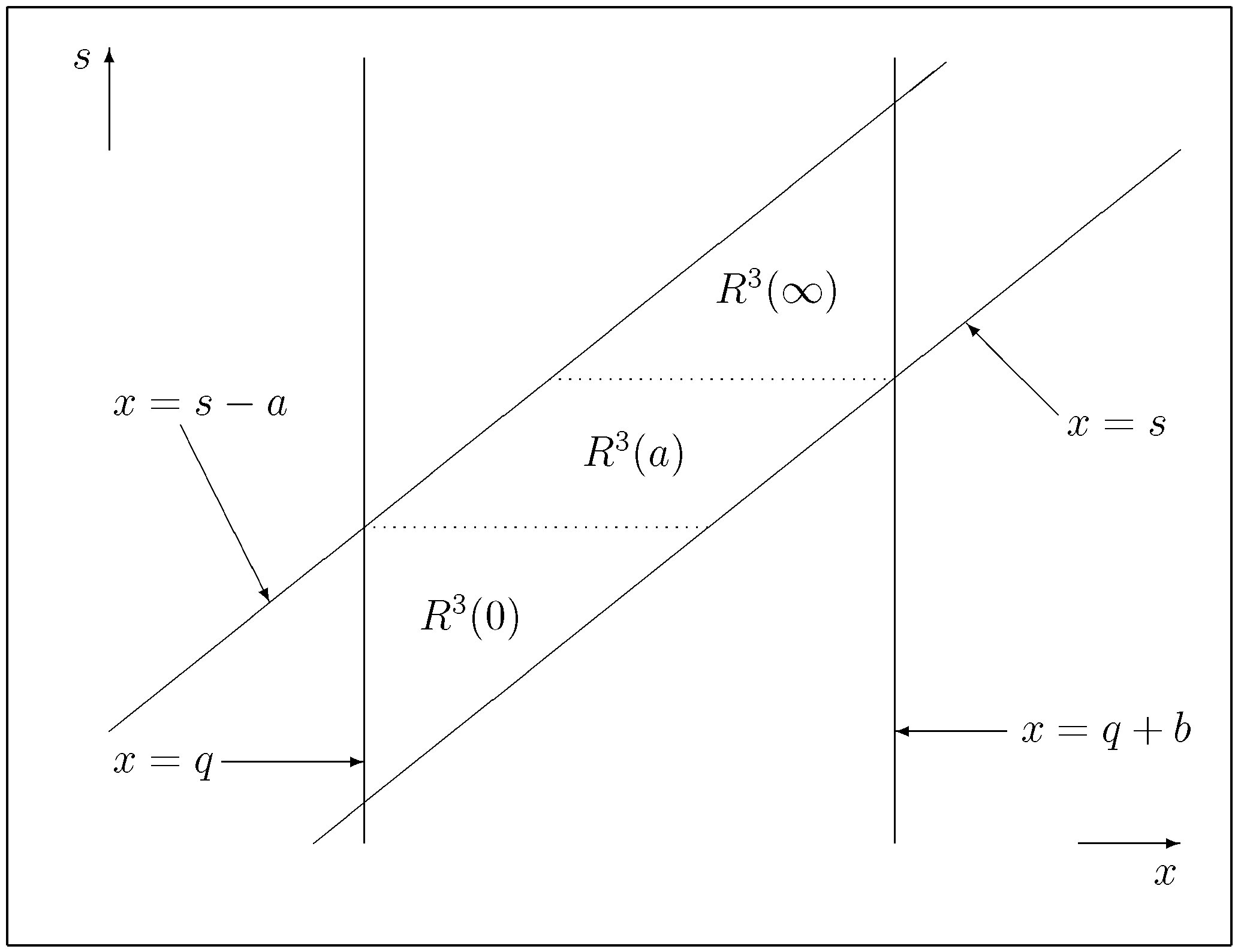
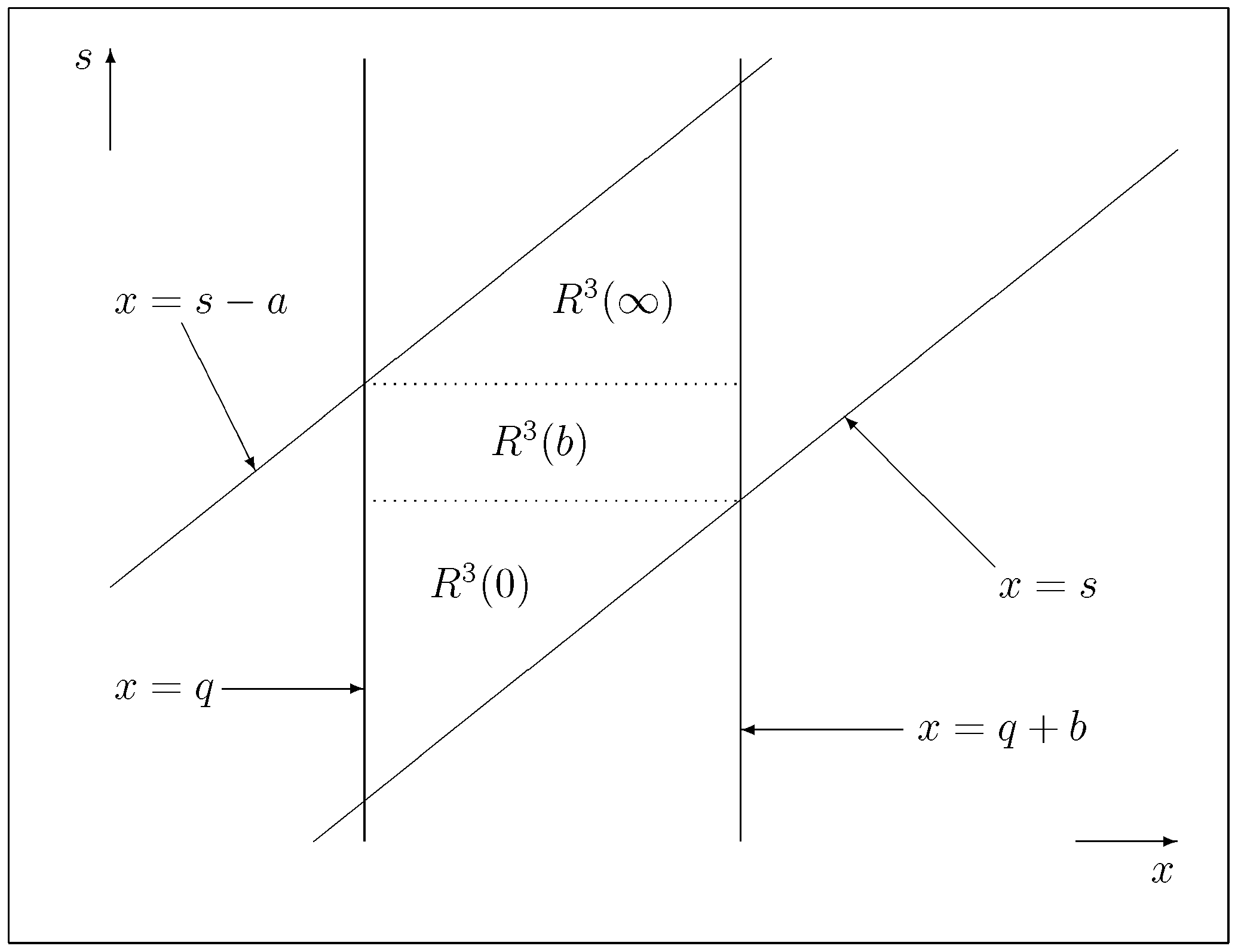
2.2. The Boundary-Value Problems
3. Solutions to the Boundary-Value Problem
3.1. The General Solution of the Ordinary Differential Equation
3.2. The Solution to the Boundary-Value Problem
3.3. Some Examples
4. The Result and Proof
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abramovitz, Milton, and Irene A. Stegun. 1972. National Bureau of Standards. In Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Wiley. [Google Scholar]
- Agarwal, Ankush, Sandeep Juneja, and Ronnie Sircar. 2016. American options under stochastic volatility: Control variates, maturity randomization and multiscale asymptotics. Quantitative Finance 16: 17–30. [Google Scholar] [CrossRef]
- Avram, Florin, A. E. Kyprianou, and M. Pistorius. 2004. Exit problems for spectrally negative Lévy processes and applications to (Canadized) Russian options. Annals of Applied Probability 14: 215–38. [Google Scholar]
- Bakhach, Amer, Venkata L. Raju Chinthalapati, Edward P. K. Tsang, and Abdul R. El Sayed. 2018. Intelligent dynamic backlash agent: A trading strategy based on the directional change framework. Algorithms 11: 171. [Google Scholar] [CrossRef]
- Bakhach, Amer, Edward P. K. Tsang, and Venkata L. Raju Chinthalapati. 2018. TSFDC: A trading strategy based on forecasting directional change. Intelligent Systems in Accounting, Finance and Management 25: 105–23. [Google Scholar] [CrossRef]
- Bateman, Harry, and Arthur Erdélyi. 1953. Higher Transcendental Functions. New York: Mc Graw-Hill. [Google Scholar]
- Borodin, Andrei N., and Paavo Salminen. 2002. Handbook of Brownian Motion, 2nd ed. Basel: Birkhäuser. [Google Scholar]
- Carr, Peter. 1998. Randomization and the American put. The Review of Financial Studies 11: 597–626. [Google Scholar] [CrossRef]
- Cont, Rama, and David-Antoine Fournié. 2013. Functional Itô calculus and stochastic integral representation of martingales. Annals of Probability 41: 109–33. [Google Scholar] [CrossRef]
- Douady, R., A. N. Shiryaev, and M. Yor. 2000. On the probability characteristics of downfalls in a standard Brownian motion. Theory of Probability and Its Applications 44: 29–38. [Google Scholar] [CrossRef]
- Dubins, Lester, Larry A. Shepp, and Albert Nikolaevich Shiryaev. 1993. Optimal stopping rules and maximal inequalities for Bessel processes. Theory of Probability and Its Applications 38: 226–61. [Google Scholar] [CrossRef]
- Dupire, Bruno. 1997. Pricing and hedging with smiles. In The Volume Mathematics of Derivative Securities. Edited by Dempster Michael A. H. and Pliska Stanley R. Cambridge: Cambridge University Press, pp. 103–11. [Google Scholar]
- Dynkin, Eugene B. 1965. Markov Processes. Volume I. Berlin: Springer. [Google Scholar]
- Forde, Martin. 2011. A diffusion-type process with a given joint law for the terminal level and supremum at an independent exponential time. Stochastic Processes and Their Applications 121: 2802–17. [Google Scholar] [CrossRef]
- Forde, Martin, Andrey Pogudin, and Hongzhong Zhang. 2013. Hitting times, occupation times, tri-variate laws and the forward Kolmogorov equation for a one-dimensional diffusion with memory. Advances in Applied Probability 45: 860–75. [Google Scholar] [CrossRef]
- Fournié, David-Antoine. 2010. Functional Itô Calculus and Applications. Ph.D. thesis, Columbia University, New York, NY, USA. [Google Scholar]
- Gapeev, Pavel V., and Neofytos Rodosthenous. 2014. Optimal stopping problems in diffusion-type models with running maxima and drawdowns. Journal of Applied Probability 51: 799–817. [Google Scholar] [CrossRef]
- Gapeev, Pavel V., and Neofytos Rodosthenous. 2015. On the drawdowns and drawups in diffusion-type models with running maxima and minima. Journal of Mathematical Analysis and Applications 434: 413–31. [Google Scholar] [CrossRef]
- Gapeev, Pavel V., and Neofytos Rodosthenous. 2016. Perpetual American options in diffusion-type models with running maxima and drawdowns. Stochastic Processes and their Applications 126: 2038–61. [Google Scholar] [CrossRef]
- Glattfelder, James, Alexandre Dupuis, and Richard Olsen. 2011. Patterns in high-frequency FX data: discovery of 12 empirical scaling laws. Quantitative Finance 11: 599–614. [Google Scholar] [CrossRef]
- Glover, Kristoffer, Hardy Hulley, and Goran Peskir. 2013. Three-dimensional Brownian motion and the golden ratio rule. Annals of Applied Probability 23: 895–922. [Google Scholar] [CrossRef]
- Guo, Xin, and Larry A. Shepp. 2001. Some optimal stopping problems with nontrivial boundaries for pricing exotic options. Journal of Applied Probability 38: 647–58. [Google Scholar] [CrossRef]
- Guo, Xin, and Mihail Zervos. 2010. π options. Stochastic Processes and their Applications 120: 1033–59. [Google Scholar] [CrossRef]
- Henry-Labordère, Pierre. 2009. Calibration of local stochastic volatility models to market smiles: A Monte-Carlo approach. Risk Magazine, September. [Google Scholar]
- Jacka, S. D. 1991. Optimal stopping and best constants for Doob-like inequalities I: The case p = 1. Annals of Probability 19: 1798–821. [Google Scholar] [CrossRef]
- Karatzas, Ioannis, and Steven E. Shreve. 1991. Brownian Motion and Stochastic Calculus, 2nd ed. New York: Springer. [Google Scholar]
- Lehoczky, John P. 1977. Formulas for stopped diffusion processes with stopping times based on the maximum. Annals of Probability 5: 601–7. [Google Scholar] [CrossRef]
- Liptser, Robert S., and Albert N. Shiryaev. 2001. Statistics of Random Processes I, 2nd ed. Berlin: Springer. First published 1977. [Google Scholar]
- Magdon-Ismail, Malik, Amir F. Atiya, Amrit Pratap, and Yaser S. Abu-Mostafa. 2004. On the maximum drawdown of a Brownian motion. Journal of Applied Probability 41: 147–61. [Google Scholar] [CrossRef]
- Mijatović, Aleksandar, and Martijn R. Pistorius. 2012. On the drawdown of completely asymmetric Lévy processes. Stochastic Processes and Their Applications 122: 3812–36. [Google Scholar] [CrossRef]
- Pedersen, Jesper Lund. 2000. Discounted optimal stopping problems for the maximum process. Journal of Applied Probability 37: 972–83. [Google Scholar] [CrossRef]
- Peskir, Goran. 1998. Optimal stopping of the maximum process: The maximality principle. Annals of Probability 26: 1614–40. [Google Scholar] [CrossRef]
- Peskir, Goran. 2007. A change-of-variable formula with local time on surfaces. Séminaire de Probabilité, Lecture Notes in Mathematics 1899: 69–96. [Google Scholar]
- Peskir, Goran. 2012. Optimal detection of a hidden target: The median rule. Stochastic Processes and Their Applications 122: 2249–63. [Google Scholar] [CrossRef][Green Version]
- Peskir, Goran. 2014. Quickest detection of a hidden target and extremal surfaces. Annals of Applied Probability 24: 2340–70. [Google Scholar] [CrossRef]
- Peskir, Goran, and Albert N. Shiryaev. 2006. Optimal Stopping and Free-Boundary Problems. Basel: Birkhäuser. [Google Scholar]
- Pospisil, Libor, Jan Vecer, and Olympia Hadjiliadis. 2009. Formulas for stopped diffusion processes with stopping times based on drawdowns and drawups. Stochastic Processes and their Applications 119: 2563–78. [Google Scholar] [CrossRef]
- Ren, Yong, Dilip Madan, and Michael Qian Qian. 2007. Calibrating and pricing with embedded local volatility models. Risk Magazine 20: 138. [Google Scholar]
- Rodosthenous, Neofytos, and Mihail Zervos. 2017. Watermark options. Finance and Stochastics 21: 157–86. [Google Scholar] [CrossRef]
- Rodosthenous, Neofytos, and Hongzhong Zhang. 2018. Beating the Omega clock: An optimal stopping problem with random time-horizon under spectrally negative Lévy models. Annals of Applied Probability 28: 2105–40. [Google Scholar] [CrossRef]
- Rogers, L. C. G., and David Williams. 1987. Diffusions, Markov Processes and Martingales II. Itô Calculus. New York: Wiley. [Google Scholar]
- Shepp, Larry A., and Albert N. Shiryaev. 1993. The Russian option: Reduced regret. Annals of Applied Probability 3: 631–40. [Google Scholar] [CrossRef]
- Shepp, Larry A., and Albert N. Shiryaev. 1994. A new look at the pricing of Russian options. Theory Probability and Applications 39: 103–19. [Google Scholar] [CrossRef]
- Taylor, Howard M. 1975. A stopped Brownian motion formula. Annals of Probability 3: 234–46. [Google Scholar] [CrossRef]
- Tsang, Edward P. K., Ran Tao, Antoaneta Serguieva, and Shuai Ma. 2017. Profiling high frequency equity price movements in directional changes. Quantitative Finance 17: 217–25. [Google Scholar] [CrossRef]
- Zhang, Hongzhong. 2014. Occupation times, drawdowns, and drawups for one-dimensional regular diffusions. Advances in Applied Probability 47: 210–30. [Google Scholar] [CrossRef]
- Zhang, Hongzhong. 2018. Stochastic Drawdowns. Singapore: World Scientific. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gapeev, P.V.; Rodosthenous, N.; Chinthalapati, V.L.R. On the Laplace Transforms of the First Hitting Times for Drawdowns and Drawups of Diffusion-Type Processes. Risks 2019, 7, 87. https://doi.org/10.3390/risks7030087
Gapeev PV, Rodosthenous N, Chinthalapati VLR. On the Laplace Transforms of the First Hitting Times for Drawdowns and Drawups of Diffusion-Type Processes. Risks. 2019; 7(3):87. https://doi.org/10.3390/risks7030087
Chicago/Turabian StyleGapeev, Pavel V., Neofytos Rodosthenous, and V. L. Raju Chinthalapati. 2019. "On the Laplace Transforms of the First Hitting Times for Drawdowns and Drawups of Diffusion-Type Processes" Risks 7, no. 3: 87. https://doi.org/10.3390/risks7030087
APA StyleGapeev, P. V., Rodosthenous, N., & Chinthalapati, V. L. R. (2019). On the Laplace Transforms of the First Hitting Times for Drawdowns and Drawups of Diffusion-Type Processes. Risks, 7(3), 87. https://doi.org/10.3390/risks7030087




