An Analysis and Implementation of the Hidden Markov Model to Technology Stock Prediction
Abstract
:1. Introduction
2. Hidden Markov Model and Its Algorithms
- Observation data, , where l is numbers of independent observation sequences and T is the length of each sequence,
- Hidden state sequence of O,
- Possible values of each state,
- Possible symbols per state,
- Transition matrix, , where
- Initial probability of being in state (regime) at time , , where ,
- Observation probability matrix, , where
- Given an observation data O and the model parameters , can we compute the probabilities of the observations ?
- Given the observation data O and the model parameters , can we find the best hidden state sequence of O?
- Given the observation O, can we find the model’s parameters ?
2.1. Forward Algorithm
| The forward algorithm |
|
2.2. Baum–Welch Algorithm
3. Model Selections and Data Collections
| Baum–Welch for L independent observations with the same length T |
|
3.1. Overview of Data Selections
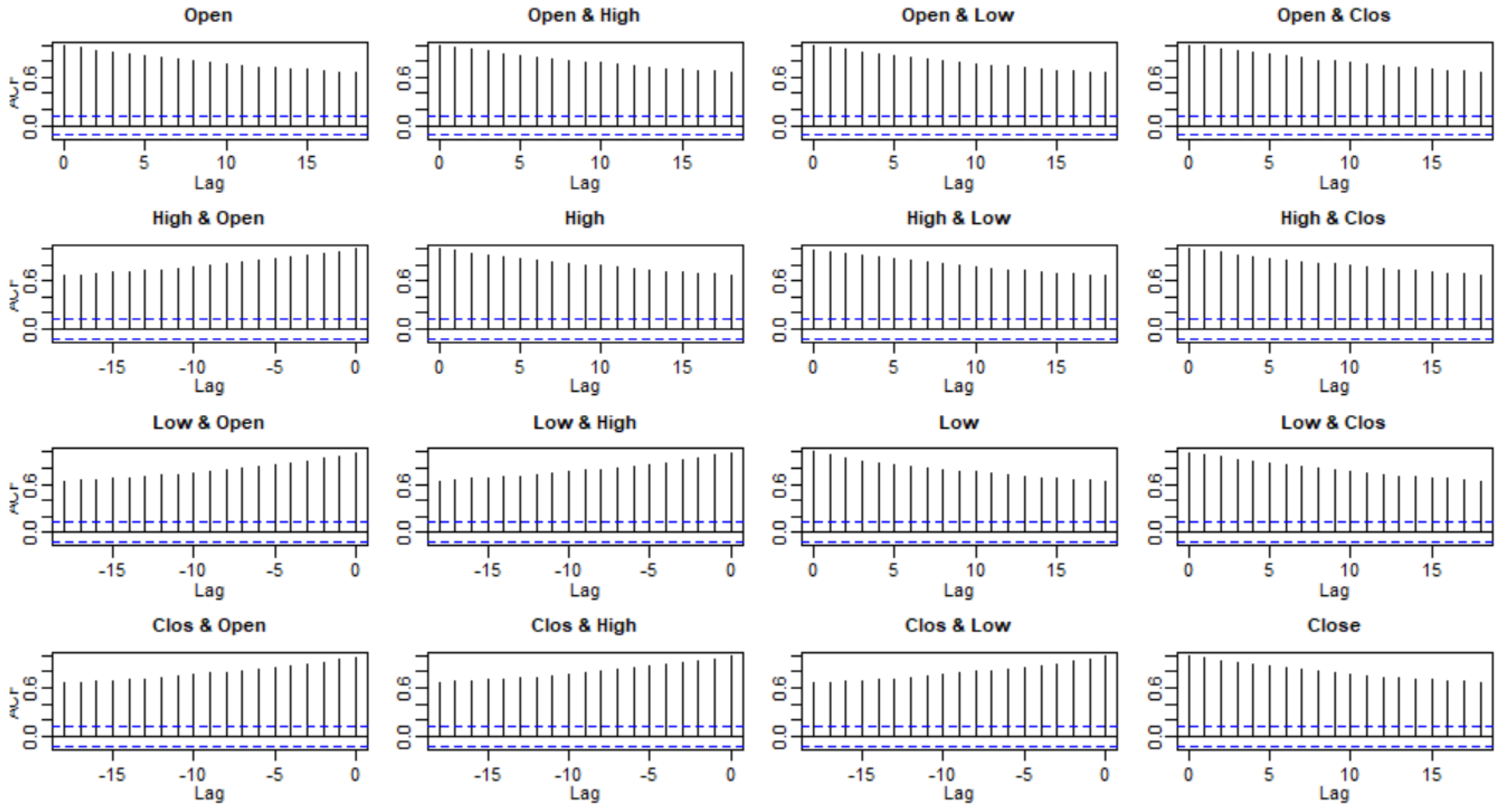
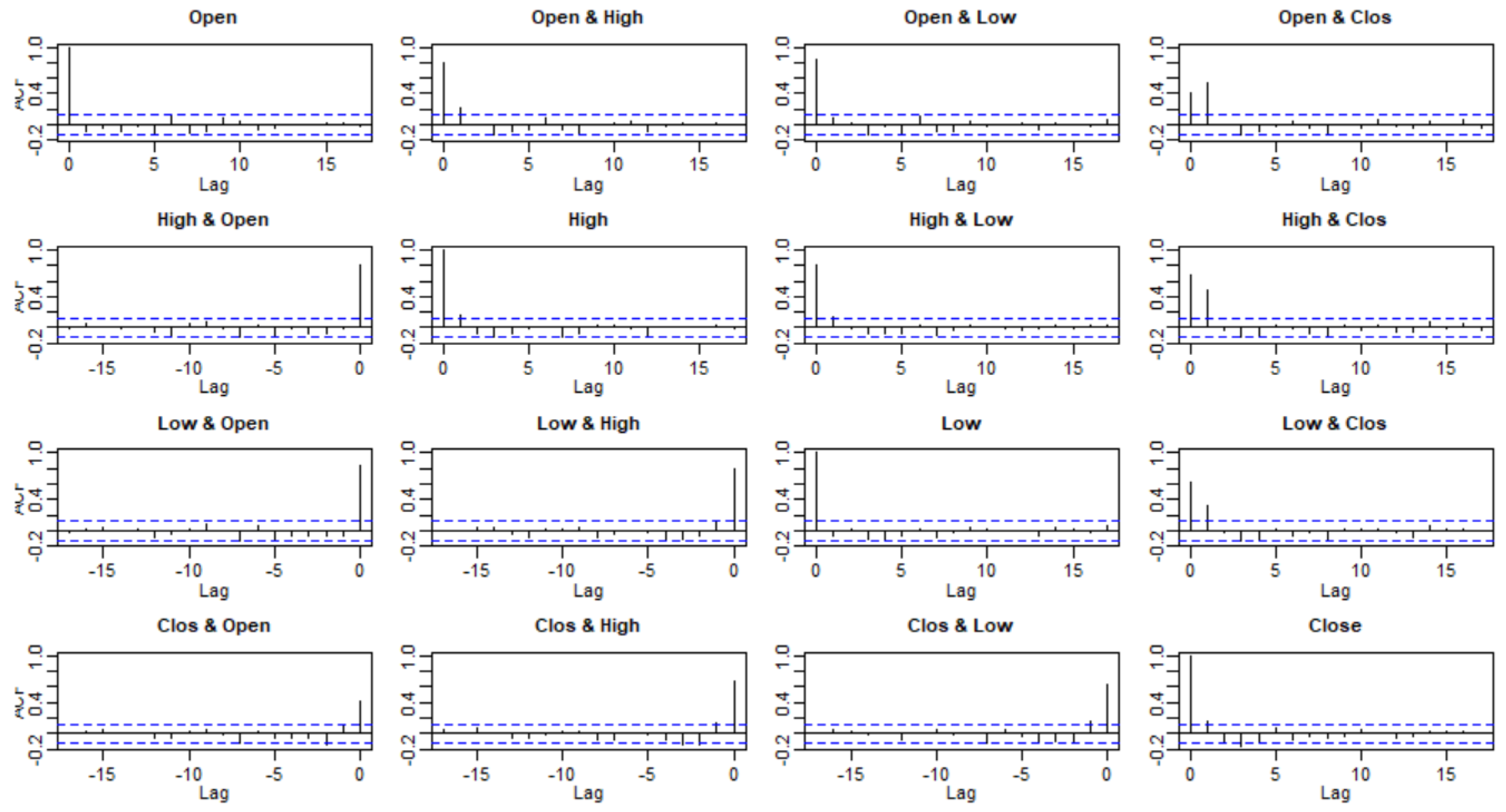
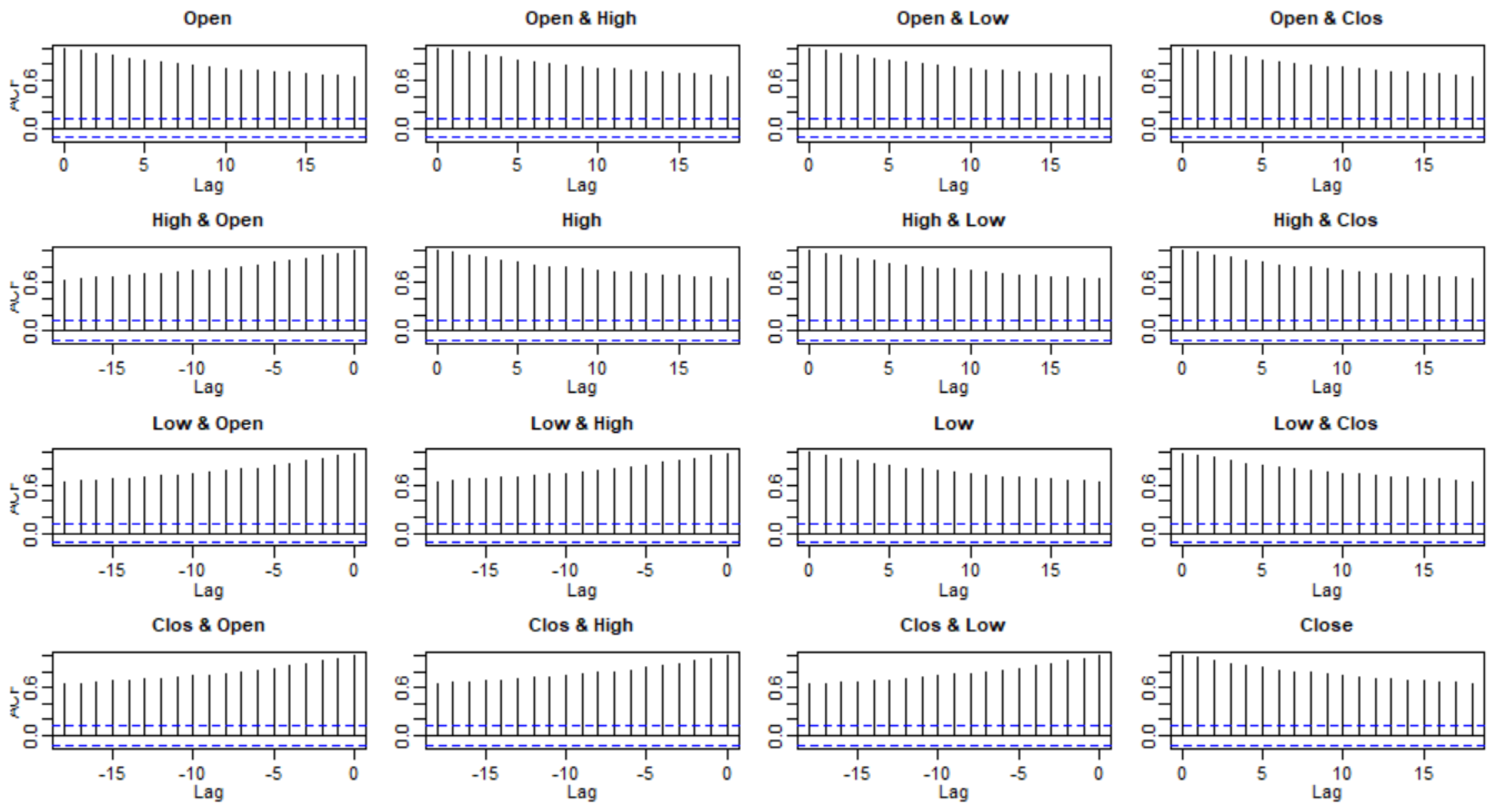
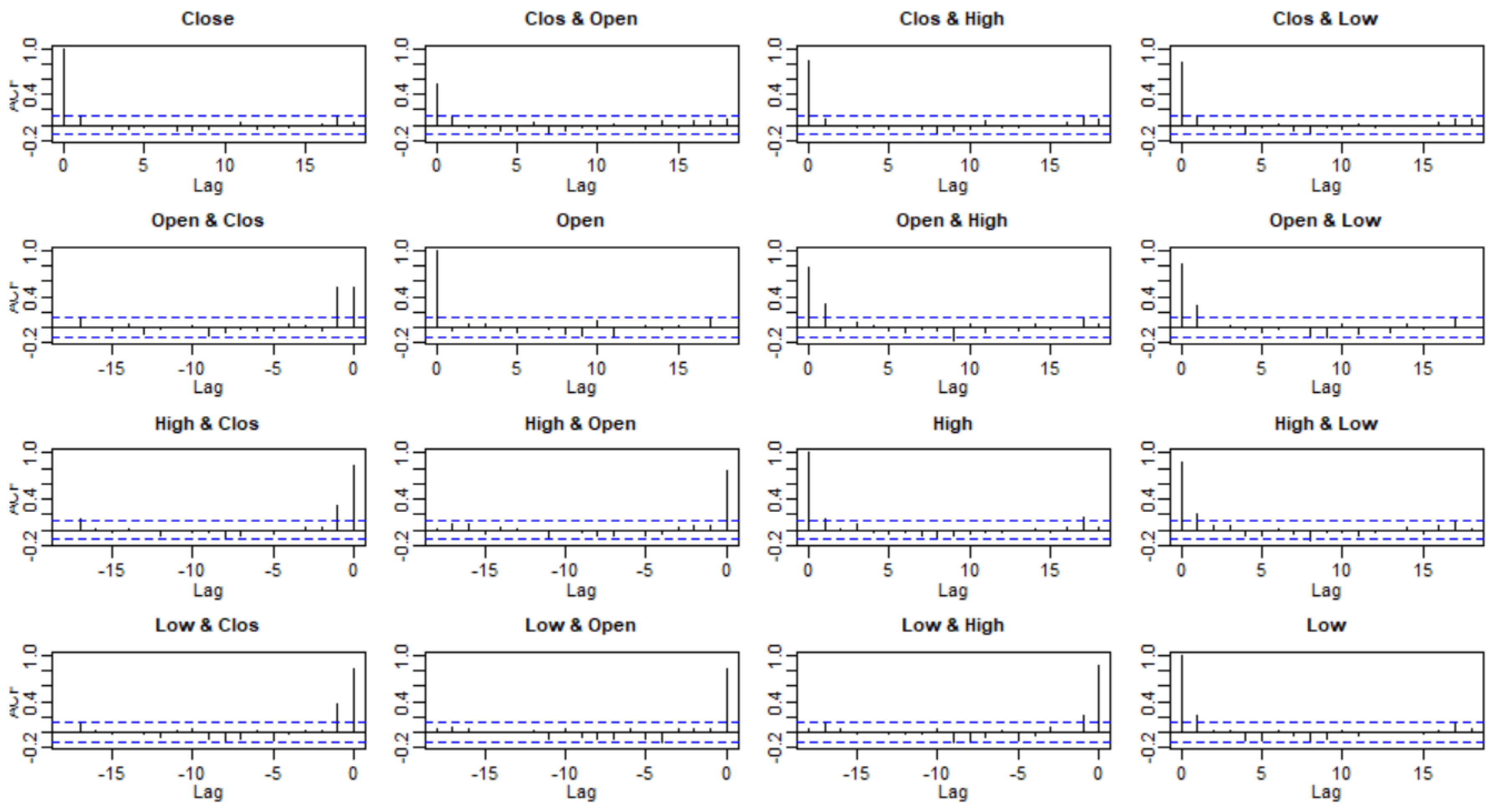
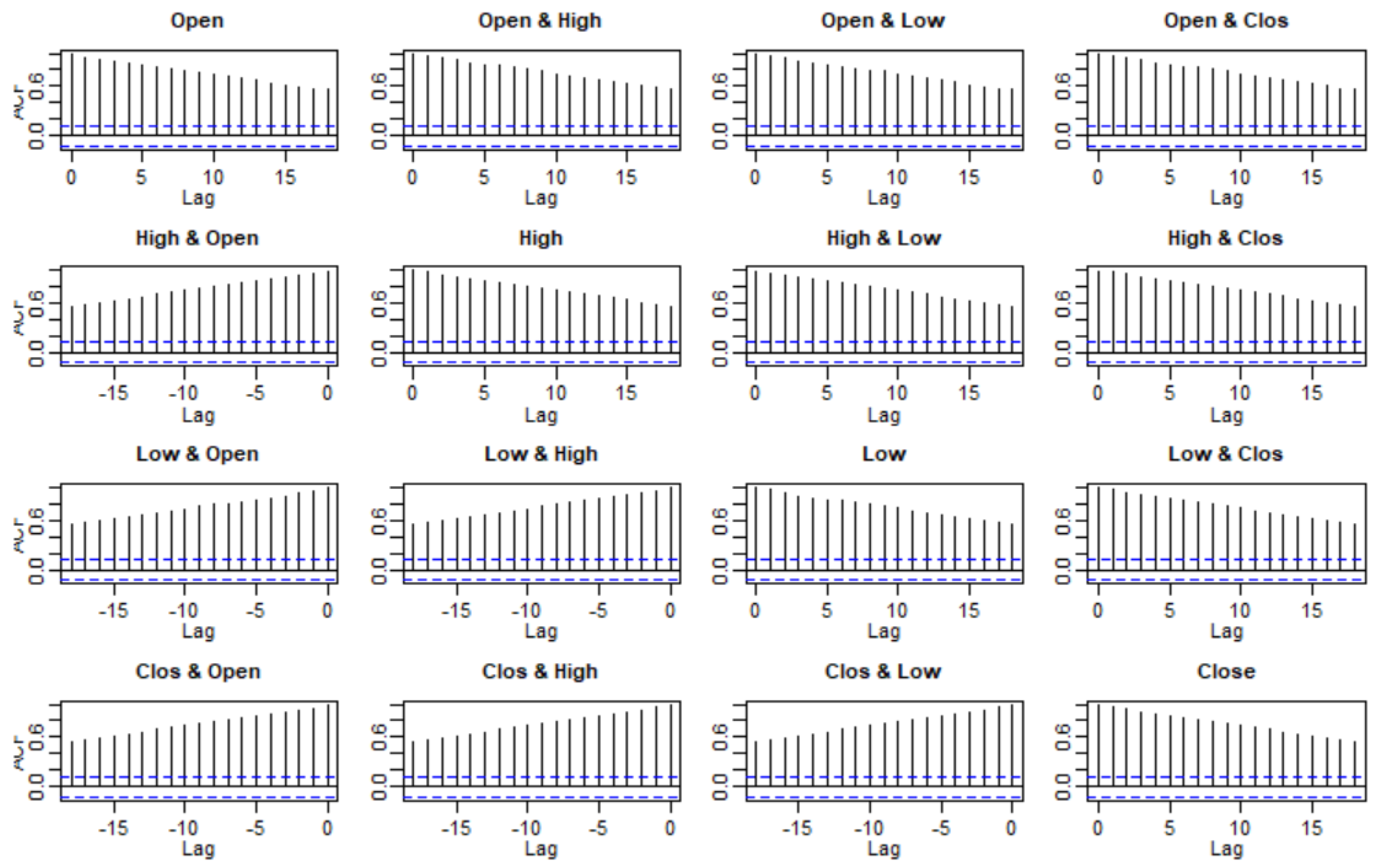
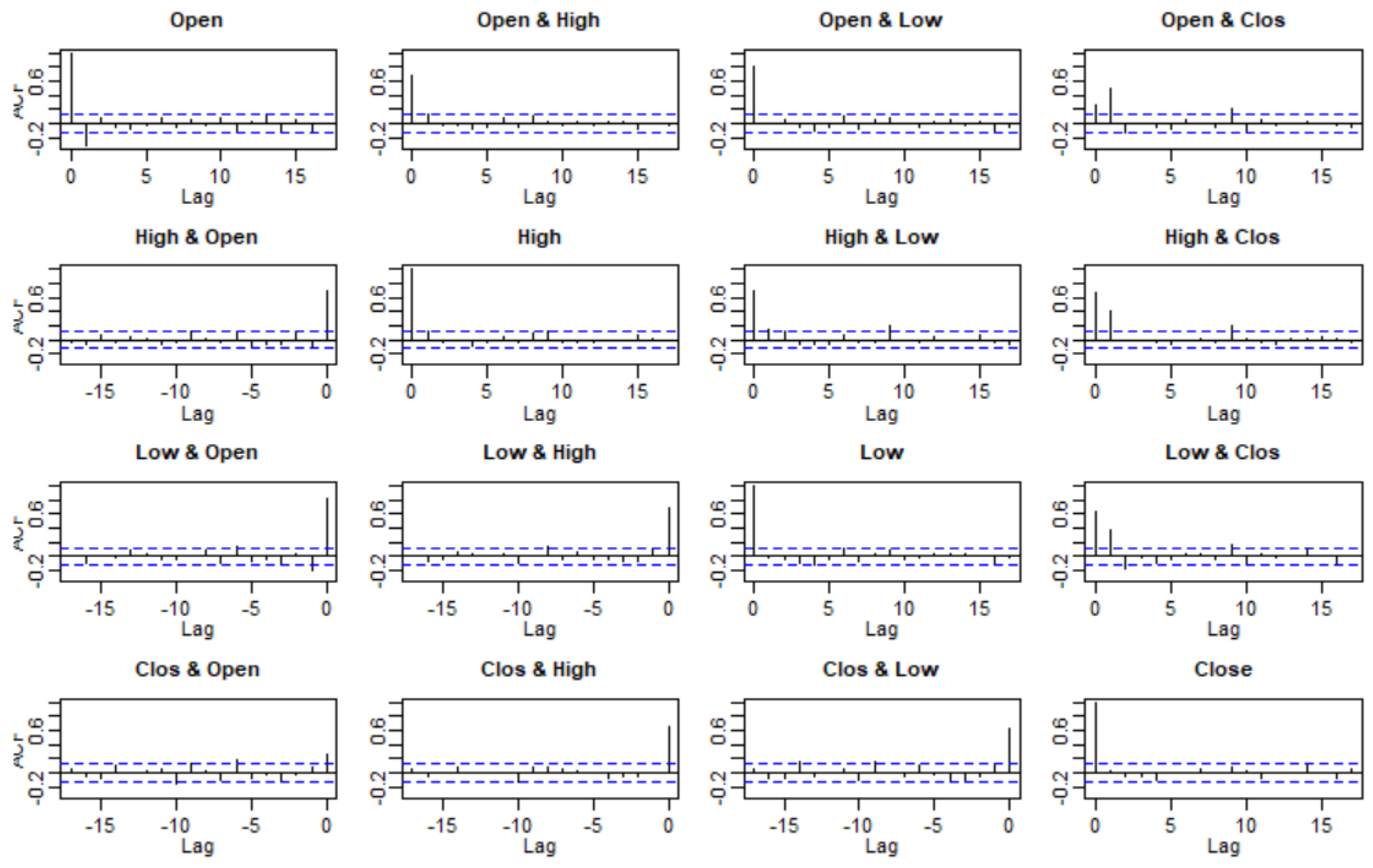
3.2. Checking Model Assumptions
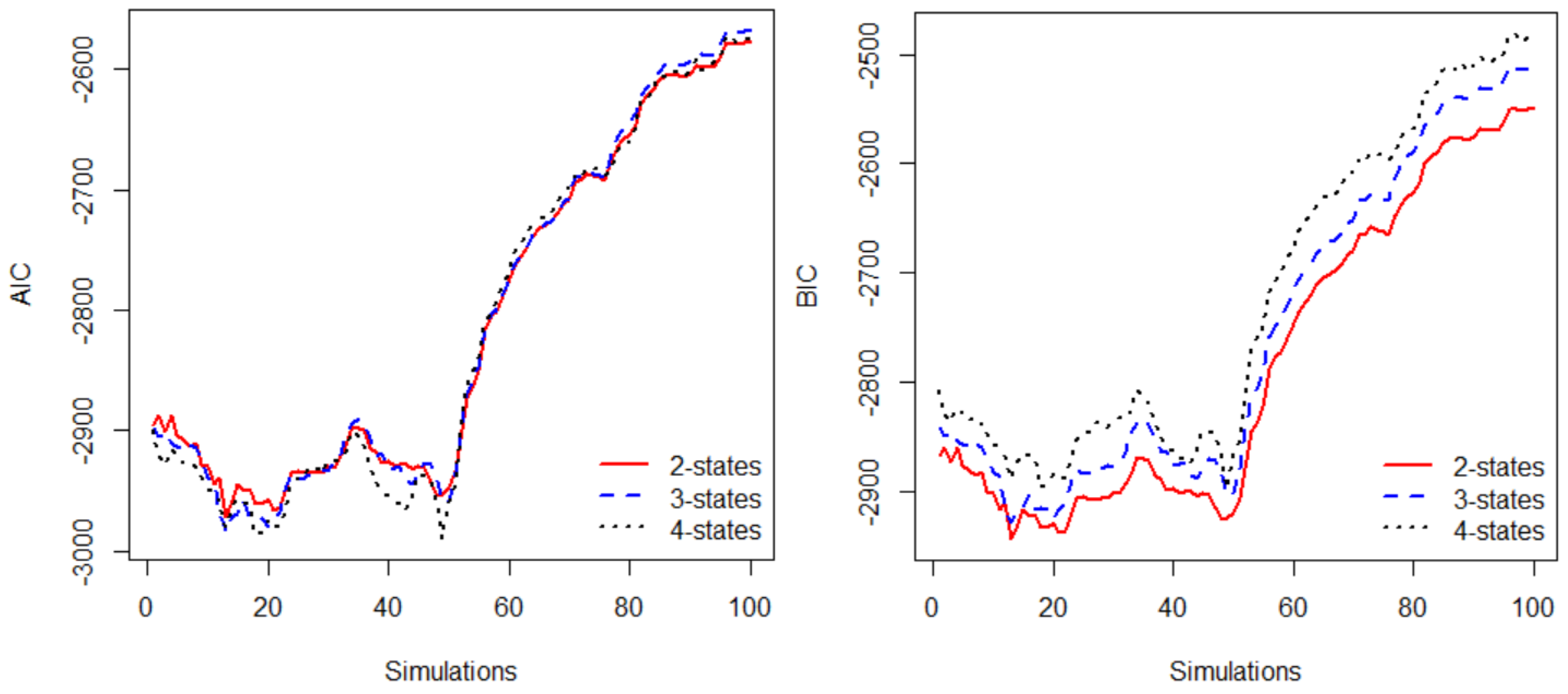
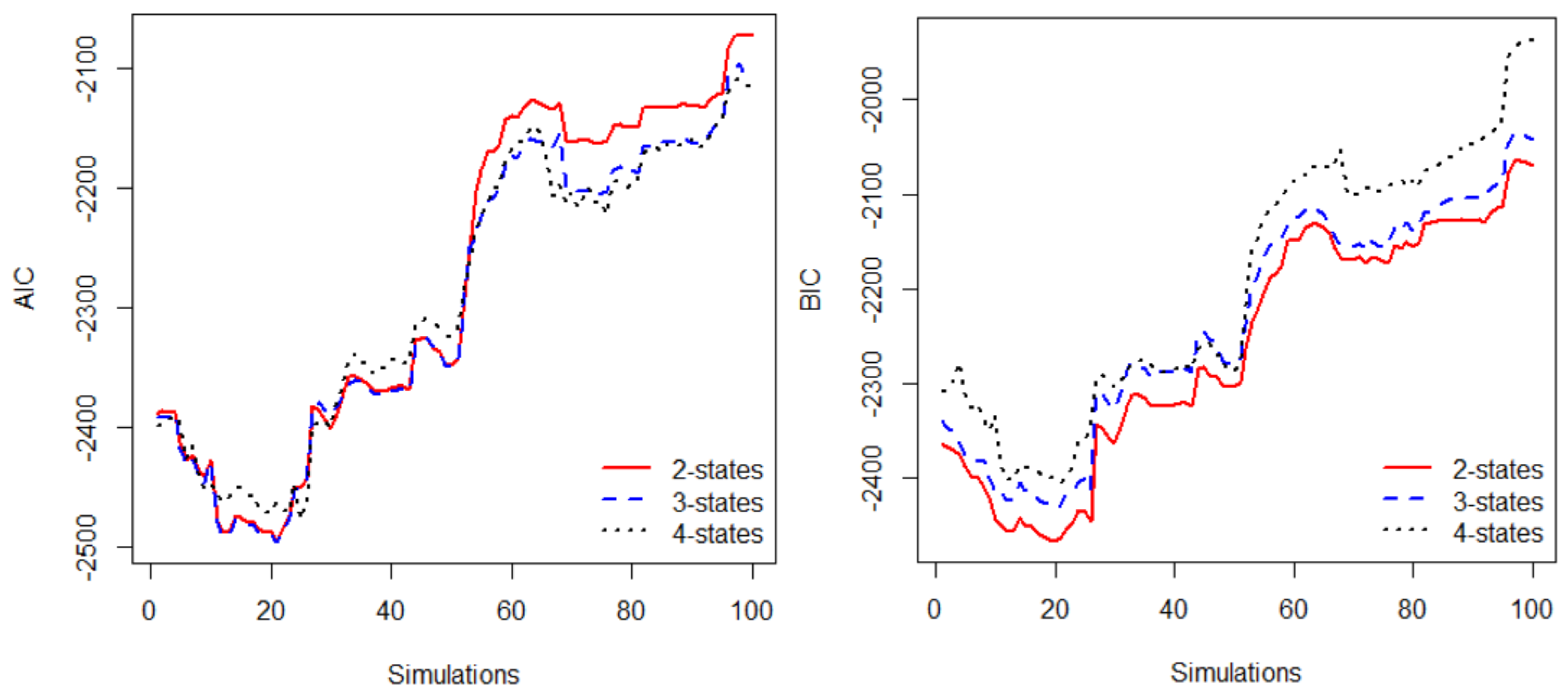
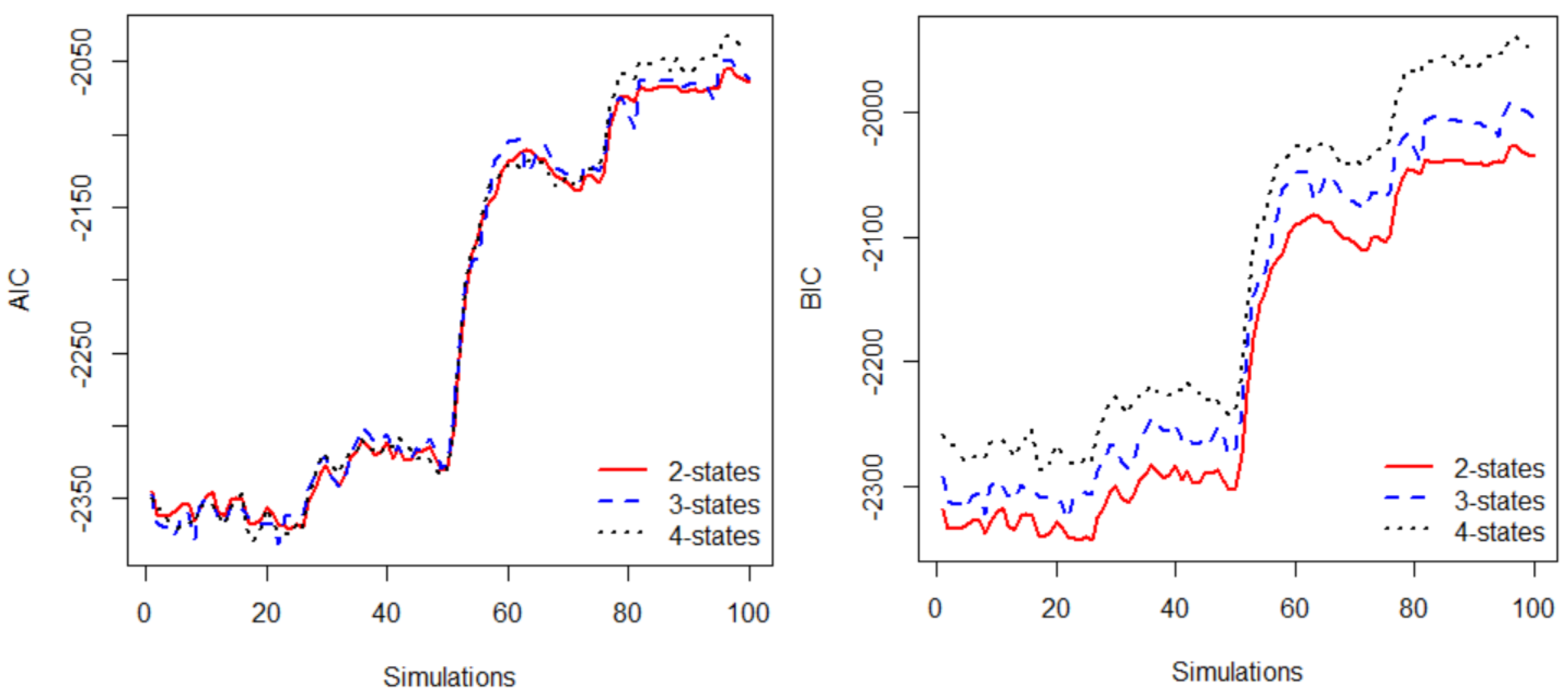
3.3. Model Selection
4. Stock Price Prediction and Stock Trading
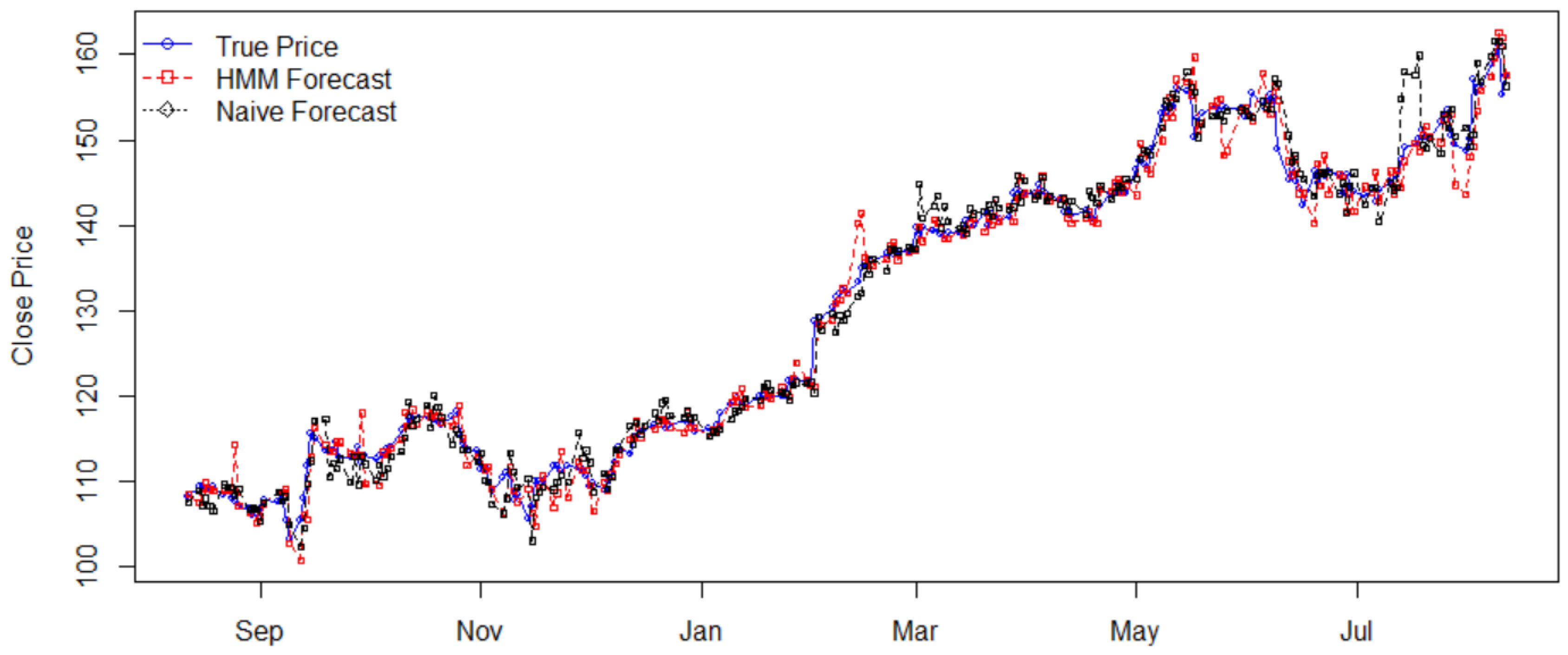
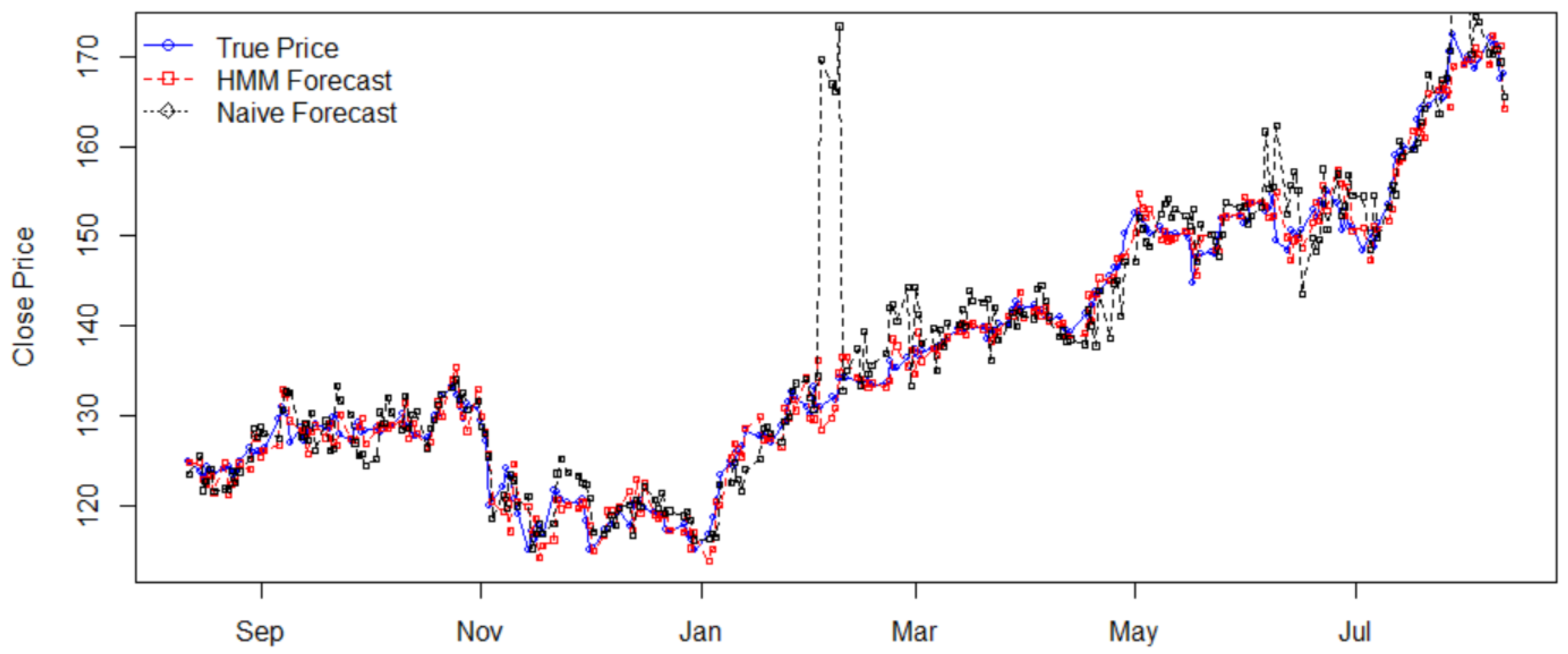
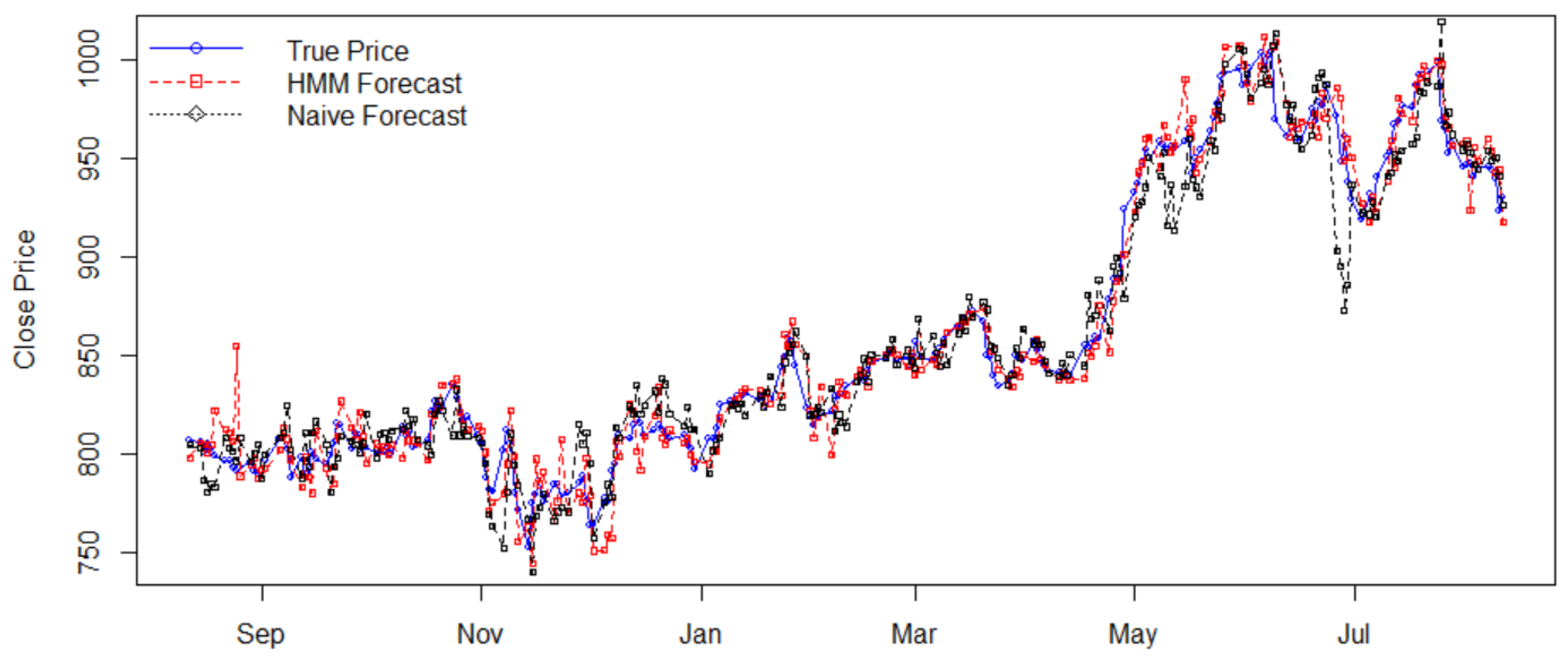
4.1. Stock Price Prediction
4.2. Stock Trading
5. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ang, Andrew, and Geert Bekaert. 2002. International Asset Allocaion with Regime Shifts. The Review of Financial Studies 15: 1137–87. [Google Scholar] [CrossRef]
- Baum, Leonard E., and John Alonzo Eagon. 1967. An inequality with applications to statistical estiation for probabilistic functions of Markov process and to a model for ecnogy. Bulletin of the American Mathematical Society 73: 360–63. [Google Scholar] [CrossRef]
- Baum, Leonard E., and Ted Petrie. 1966. Statistical Inference for Probabilistic Functions of Finite State Markov Chains. The Annals of Mathematical Statistics 37: 1554–63. [Google Scholar] [CrossRef]
- Baum, Leonard E., and George Roger Sell. 1968. Growth functions for transformations on manifolds. Pacific Journal of Mathematics 27: 211–27. [Google Scholar] [CrossRef]
- Baum, Leonard E., Ted Petrie, George Soules, and Norman Weiss. 1970. A maximization technique occurring in the statistical analysis of probabilistic functions of Markov chains. The Annals of Mathematical Statistics 41: 164–71. [Google Scholar] [CrossRef]
- Chen, Chunchih. 2005. How Well Can We Predict Currency Crises? Evidence from a Three-Regime Markov-Switching Model. Davis: Department of Economics, UC Davis. [Google Scholar]
- Forney, G. David. 1973. The Viterbi algorithm. Proceedings of the IEEE 61: 268–78. [Google Scholar] [CrossRef]
- Guidolin, Massimo, and Allan Timmermann. 2006. Asset Allocation under Multivariate Regime Switching. SSRN FRB of St. Louis Working Paper No. 2005-002C, FRB of St. Louis, MO, USA. [Google Scholar]
- Hassan, Md Rafiul, and Baikunth Nath. 2005. Stock Market Forecasting Using Hidden Markov Models: A New approach. Presented at the IEEE fifth International Conference on Intelligent Systems Design and Applications, Warsaw, Poland, September 8–10. [Google Scholar]
- Kritzman, Mark, Sebastien Page, and David Turkington. 2012. Regime Shifts: Implications for Dynamic Strategies. Financial Analysts Journal 68: 22–39. [Google Scholar] [CrossRef]
- Levinson, Stephen E., Lawrence R. Rabiner, and Man Mohan Sondhi. 1983. An introduction to the application of the theory of probabilistic functions of Markov process to automatic speech recognition. Bell System Technical Journal 62: 1035–74. [Google Scholar] [CrossRef]
- Li, Xiaolin, Marc Parizeau, and Réjean Plamondon. 2000. Training Hidden Markov Models with Multiple Observations—A Combinatorial Method. IEEE Transactions on PAMI 22: 371–77. [Google Scholar]
- Nguyen, Nguyet, and Dung Nguyen. 2015. Hidden Markov Model for Stock Selection. Journal of Risks in special issue: Recent Advances in Mathematical Modeling of the Financial Markets. Risks 3: 455–73. [Google Scholar] [CrossRef]
- Nguyen, Nguyet Thi. 2014. Probabilistic Methods in Estimation and Prediction of Financial Models. Electronic Theses, Treatises and Dissertations Ph.D. dissertation, The Florida State University, Tallahassee, FL, USA. [Google Scholar]
- Nobakht, B., C. E. Joseph, and B. Loni. 2012. Stock market analysis and prediction using hidden markov models. Presented at the 2012 Students Conference on IEEE Engineering and Systems (SCES), Allahabad, Uttar Pradesh, India, March 16–18; pp. 1–4. [Google Scholar]
- Petrushin, Valery A. 2000. Hidden Markov Models: Fundamentals and Applications (part 2-discrete and continuous hidden markov models). Online Symposium for Electronics Engineer. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.378.3099&rep=rep1&type=pdf (accessed on 23 November 2017).
- Rabiner, Lawrence R. 1989. A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition. Proceedings of the IEEE 77: 257–86. [Google Scholar] [CrossRef]
- Viterbi, Andrew J. 1967. Error bounds for convolutional codes and an asymptotically optimal decoding algorithm. IEEE Transactions on Information Theory IT-13: 260–69. [Google Scholar] [CrossRef]
| Stock | Open | High | Low | Close |
|---|---|---|---|---|
| AAPL | ||||
| FB | 0.2151 | |||
| GOOGL | 0.5378 | 0.0608 |
| Stock | Price Std. | Return Std. | HMM’s MAPE | Naïve’s MAPE | Efficiency |
|---|---|---|---|---|---|
| AAPL | 17.0934 | 0.0113 | 0.0113 | 0.0133 | 1.1770 |
| FB | 14.4879 | 0.0111 | 0.0116 | 0.0213 | 1.8362 |
| GOOGL | 69.9839 | 0.0098 | 0.0107 | 0.0137 | 1.2804 |
| Stock | Models | Investment $ | Earning $ | Profit % |
|---|---|---|---|---|
| AAPL | HMM | 10,908 | 3481 | 31.91 |
| Naïve | 10,818 | 3513 | 32.47 | |
| FB | HMM | 12,490 | 2939 | 23.53 |
| Naïve | 12,488 | 2565 | 20.54 | |
| GOOGL | HMM | 80,596 | 20,039 | 24.86 |
| Naïve | 79,965 | 2715 | 3.40 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, N. An Analysis and Implementation of the Hidden Markov Model to Technology Stock Prediction. Risks 2017, 5, 62. https://doi.org/10.3390/risks5040062
Nguyen N. An Analysis and Implementation of the Hidden Markov Model to Technology Stock Prediction. Risks. 2017; 5(4):62. https://doi.org/10.3390/risks5040062
Chicago/Turabian StyleNguyen, Nguyet. 2017. "An Analysis and Implementation of the Hidden Markov Model to Technology Stock Prediction" Risks 5, no. 4: 62. https://doi.org/10.3390/risks5040062
APA StyleNguyen, N. (2017). An Analysis and Implementation of the Hidden Markov Model to Technology Stock Prediction. Risks, 5(4), 62. https://doi.org/10.3390/risks5040062





