Frailty and Risk Classification for Life Annuity Portfolios

Abstract

Life annuities are attractive mainly for healthy people. In order to expand their business, in recent years, some insurers have started offering higher annuity rates to those whose health conditions are critical. Life annuity portfolios are then supposed to become larger and more heterogeneous. With respect to the insurer’s risk profile, there is a trade-off between portfolio size and heterogeneity that we intend to investigate. In performing this, there is a second and possibly more important issue that we address. In actuarial practice, the different mortality levels of the several risk classes are obtained by applying adjustment coefficients to population mortality rates. Such a choice is not supported by a rigorous model. On the other hand, the heterogeneity of a population with respect to mortality can formally be described with a frailty model. We suggest adopting a frailty model for risk classification. We identify risk groups (or classes) within the population by assigning specific ranges of values to the frailty within each group. The different levels of mortality of the various groups are based on the conditional probability distributions of the frailty. Annuity rates for each class then can be easily justified, and a comprehensive investigation of insurer’s liabilities can be performed.

1. Introduction

The largely unanticipated dynamics of mortality experienced in the latest decades suggests developing new mortality models and to further explore those already known. A critical aspect that we focus on in this paper is understanding how the heterogeneity of the population with respect to mortality does impact on the liabilities of a life annuity provider.

Heterogeneity with respect to mortality can result from observable or non-observable risk factors. While models accounting for observable risk factors generally adopt pragmatic solutions to represent differential mortality (namely, additive or multiplicative adjustments to the average mortality rate), the modeling of heterogeneity due to unobservable risk factors has found an elegant and rigorous solution in the concept of frailty, described already by [1], but formally defined by [2]. To some extent, also heterogeneity due to observable risk factors might be represented with a frailty model, via parameter calibration. This could be useful, for instance, when some observable risk factors cannot be adopted as rating factors, as is the case of gender in the EU. In this paper, heterogeneity is addressed via a frailty model. For a short review of models accounting for observable risk factors, see, for example, [3,4], as well as the references therein.

Apart from [1,2], the impact of heterogeneity on the age-pattern of mortality has been discussed through frailty models by [5,6,7,8,9,10] and many others.

The works in [1,2] express the non-observable heterogeneity in terms of a fixed individual frailty level, assuming that the individual frailty is due to genetic factors. Other assumptions have been discussed. The model proposed by [11] relies on the concept of a frailty that stochastically changes with age, that is throughout the individual life, viz. because of physiological changes and environmental influences. The two approaches are compared by [12]. Markov aging models, which generalize Le Bras’s assumption, have been adopted by [13,14,15,16].

The work in [17] shows that changing frailty models cannot be distinguished from a fixed frailty model. The fixed frailty model is more convenient, especially under the traditional Gompertz-Gamma assumption (see Section 2). Further, such a model fits satisfactorily a feature observed empirically, but hardly replicated by other models: it provides an analytical justification of the deceleration in the mortality increase at very old ages, observed in many populations.

While frailty models are well known in demography, their application to insurance risk management is not common. Significant research work in the actuarial field is anyhow available. The works in [18,19] calibrate (alternatively) two families of frailty models (namely, a Gompertz-Gamma and a Gompertz–Gaussian-inverse model) to insurance-based mortality data, finding evidence of frailty in insured populations. The work in [20] calibrates the Gompertz-Gamma model to Canadian pensioners’ mortality, finding strong support for the assumption. The work in [21] analyzes the impact of heterogeneity and frailty on the actuarial values of both standard life annuities and underwritten annuities (i.e., “special rate” life annuities). Conversely, the impact of heterogeneity on tail risk and solvency capital is investigated by [3,16].

In this paper, we focus on a potential application of the frailty model, which can be helpful to design a rating system for life annuities arranged in several risk classes.

Risk classification in the area of voluntary life annuities has recently been adopted to stimulate the demand. Indeed, the market is still underdeveloped, as the product is mainly underwritten by healthy people. In order to expand their portfolio, in recent years, some insurers have started offering special annuity rates to those whose health conditions are poor or critical; a useful description of the more common classes of special rate annuities is provided by [22]. Risk classes can then be identified within a life annuity portfolio, showing different levels of mortality. Adopting models used to represent differential mortality arising from observable risk factors, in common actuarial practice, the higher or lower mortality level of a risk group is represented by applying adjustment coefficients to the population mortality rates. Such coefficients are chosen empirically, calibrated on the average ratio (possibly measured for age groups) between the annuitants’ and the population mortality; conversely, a model formally justifying such a difference is not adopted.

Within a frailty model, lower or higher mortality rates can be explained by lower or higher frailty levels. We then suggest to adopt a frailty model for risk classification. We identify risk groups (or classes) within the population by assigning specific ranges of values to the frailty within each group. Conditional probability distributions for the frailty are obtained for each risk class, which allow us to describe the different levels of mortality of the various groups. Different values for the annuity rate then derive from the different assumptions about the frailty level of the specific risk class.

We also investigate the following issue. When accepting substandard risks, the insurer may increase its portfolio size, but also the heterogeneity of the portfolio. While a larger size implies an improved pooling effect, a higher risk profile follows from the increased heterogeneity. We investigate the result of this trade-off, by assessing the probability distribution of the present value of future benefits. Portfolios with only the standard risk class and with also special rate risk classes are compared, so to measure the trade-off between portfolio size and heterogeneity. We disregard systematic longevity risk, as heterogeneity mainly affects process risk (at least, so long as we can accept that the possible underlying mortality trend is common to all risk groups). We also disregard financial risk, as we mainly focus on the design of a risk classification structure with respect to mortality (and we can exclude a correlation between financial and mortality risk).

The remainder of the paper is arranged as follows. The main features of the traditional frailty model are recalled in Section 2. In Section 3, we design a risk classification arrangement for a life annuity portfolio based on a frailty model. In Section 4, we calibrate the model to Italian projected life tables. In Section 5, we investigate the probability distribution of the liabilities of life annuity portfolios with different compositions and sizes. Finally, Section 6 concludes with some further remarks.

2. Lifetime and Frailty: The Gompertz-Gamma Model

The heterogeneity of a population with respect to mortality arises from differences among the individuals. In their seminal paper, [2] define the frailty as a non-negative quantity whose level expresses the unobservable (and, possibly, some observable) risk factors affecting individual mortality. The underlying idea is that the expected lifetime of individuals with a higher frailty is lower than others. Several models can be developed in this framework; in what follows, we describe the traditional setting. All of the results that are commented on in this section are well known. We then skip the details, which can be found in the references already provided; see, for example, [2,19] or [3].

Refer to a heterogeneous cohort (defined at age 0 and closed to new entrants); in the following, we will use the term population, understanding that it consists of one cohort only. A non-negative, unknown variable called frailty is assigned to each individual, expressing mortality risk factors. The individual frailty level does not change in time, while keeping unknown. Conversely, because of deaths, the average frailty level in the whole population changes with age, and it is expected to decline, given that people with lower frailty are expected to live longer.

Let ${\mu }_x(z)$ denote the force of mortality for an individual current age x and frailty level z. The work in [2] suggests a multiplicative model:

$${\mu }_x(z)=z·{\mu }_x,$$

(1)

where ${\mu }_x$, namely the force of mortality for an individual with frailty level $z=1$, is called the standard force of mortality (note, however, that in the insurance application, ${\mu }_x$ does not necessarily represent the force of mortality of standard risks; indeed, the class of standard risks can be identified with a frailty interval $(0,z_1]$, where $z_1$ can be lower than one, as we discuss in Section 3.1 and Section 4). Since the frailty level z takes the value in $(0,\infty )$, for the individual force of mortality, we have ${\mu }_x(z)⋛{\mu }_x$. It is worth noting that in (1), the coefficient z could be interpreted as a multiplicative adjustment coefficient (with respect to the standard force of mortality), and then, ${\mu }_x(z)$ would represent an adjusted force of mortality. This is to say that Model (1) resembles the pragmatic approach to differential mortality. However, z is unknown in (1), while fixed (and known) adjustment coefficients are adopted in the pragmatic approach. See also the end of Section 3.1 for a further comment with respect to this comparison.

Denote with $H(x)$ the cumulative standard force of mortality in the age-interval $(0,x)$, i.e.:

$$H\left(x\right)={\int }_0^x{\mu }_t\mathrm{d}t.$$

(2)

The survival function for an individual (newborn) with frailty z is:

$$S\left(x\right|z)={\mathrm{e}}^{-{\int }_0^x{\mu }_t\left(z\right)\mathrm{d}t}={\mathrm{e}}^{-z·H\left(x\right)}.$$

(3)

Let $Z_x$ denote the random value of the frailty, whose probability distribution is assessed on the population at age x and $g_x(z)$ its probability density function. The average frailty level in the population at age x is:

$$\mathbb{E}\left[Z_x\right]={\overline{z}}_x={\int }_0^{\infty }z·g_x\left(z\right)\mathrm{d}z,$$

(4)

while the expected force of mortality of the population at age x and frailty level $Z_x$ is:

$${\overline{\mu }}_x=\mathbb{E}\left[{\mu }_x\left(Z_x\right)\right]={\mu }_x·{\int }_0^{\infty }z·g_x\left(z\right)\mathrm{d}z={\mu }_x·{\overline{z}}_x.$$

(5)

Thanks to the multiplicative assumption (1), the probability density function of $g_x(z)$ can easily be derived from $g_0(z)$. We find:

$$g_x\left(z\right)=\frac{g_0\left(z\right)·S\left(x\right|z)}{\overline{S}\left(x\right)},$$

(6)

where $\overline{S}\left(x\right)$ is the average survival function of the population or the expected share of individuals alive at age x out of the initial newborns, which can be assessed as follows:

$$\overline{S}\left(x\right)={\int }_0^{\infty }S\left(x\right|z)·g_0\left(z\right)\mathrm{d}z.$$

(7)

It is interesting to note that ${\overline{\mu }}_x={\mu }_x$ only if ${\overline{z}}_x=1$, and that $\frac{\mathrm{d}}{\mathrm{d}x}{\overline{z}}_x<0$; then, the average force of mortality increases less rapidly than the standard one. This is why heterogeneity could explain why the age-pattern of mortality rates shows a deceleration in the increase at the highest ages.

The work in [2] suggests a Gamma distribution for $Z_0$, due to its nice features. Then, let $Z_0\sim \mathrm{Gamma}(\delta ,\theta )$. It can be shown that also $Z_x$, $x>0$, holds a Gamma distribution, with updated parameters; in particular, $Z_x\sim \mathrm{Gamma}(\delta ,\theta +H\left(x\right))$. To shorten the notation, we set $\theta \left(x\right)=\theta +H\left(x\right)$, with $\theta \left(0\right)=\theta$; then $Z_x\sim \mathrm{Gamma}(\delta ,\theta \left(x\right))$ for $x\ge 0$.

For the average frailty level in the population, we find:

$${\overline{z}}_x=\frac{\delta }{\theta \left(x\right)},$$

(8)

while the variance of $Z_x$ is given by:

$$\mathbb{V}\mathrm{ar}\left[Z_x\right]=\frac{\delta }{{\left(\theta \left(x\right)\right)}^2}.$$

(9)

Parameters are commonly chosen so that ${\overline{z}}_0=1$; thus, $\theta =\delta$. After noting that the coefficient of variation of $Z_x$ is given by:

$$\mathbb{CV}\left[Z_x\right]=\frac{\sqrt{\mathbb{V}\mathrm{ar}\left[Z_x\right]}}{\mathbb{E}\left[Z_x\right]}=\frac{1}{\sqrt{\delta }},$$

(10)

we understand that the parameter δ is chosen considering the degree of heterogeneity of the population. Higher values of δ corresponds to lower levels of heterogeneity; in particular, the population can be considered (almost) homogeneous when $\delta \to \infty$. Note that, in this model, whilst the expected value of the frailty reduces with age, its relative variability keeps constant.

For the average survival function of the population, we find:

$$\overline{S}\left(x\right)={\left(\frac{\theta }{\theta \left(x\right)}\right)}^{\delta }={\left(\frac{{\overline{z}}_x}{{\overline{z}}_0}\right)}^{\delta }.$$

(11)

Now, still following [2], we assume a Gompertz law for the standard force of mortality, namely:

$${\mu }_x=\alpha ·{\mathrm{e}}^{\beta ·x}.$$

(12)

Plugging (12) and (8) into (1), we find the following expression for the average force of mortality of the population:

$${\overline{\mu }}_x=\frac{{\alpha }^{\prime }·{\mathrm{e}}^{\beta ·x}}{1+{\delta }^{\prime }·{\mathrm{e}}^{\beta ·x}},$$

(13)

where: ${\alpha }^{\prime }=\frac{\alpha ·\delta }{\theta -\frac{\alpha }{\beta }}$ and ${\delta }^{\prime }=\frac{\alpha }{\beta ·\theta -\alpha }$. Equation (13) shows that the average force of mortality in the population is Perks-type, namely the first Perks law with parameter $\gamma =0$; see [23]. The law (13) has been proposed also by [1]; in (13), the parameters ${\alpha }^{\prime }$ and ${\delta }^{\prime }$ depend on the parameters $\delta ,\theta$ of the frailty distribution. We note that (13) is in the logistic class; such models imply a deceleration in the increasing age-pattern of mortality, which in the current setting is a consequence of the presence of frailty in the population. For a formal approach and more details, see, for example, [3,24].

3. Risk Classification Based on a Frailty Model

3.1. Identification of the Risk Classes

A heterogeneous population can be arranged in classes that group individuals with a similar risk profile. While we cannot expect that risk classes are fully homogeneous, each of them will show a reduced heterogeneity, provided that the underwriting process is appropriate. When heterogeneity is with respect to mortality, risk classes group people with a similar health status and then with a similar life expectancy. Risk classification in insurance is mainly aimed at the differentiation of premium rates; more generally, it can be part of the risk management process, in particular in face of strongly heterogeneous portfolios. When the risk classification is adopted for rating purposes, which is the case that we are addressing, the choice of the number of classes and their features depends not only on the nature of the causes of heterogeneity, but also on market issues. As a result of the underwriting process, an individual is placed in a specific risk class depending on his/her health status and is charged a specific premium rate.

When compared to the general population, higher or lower values for the life expectancy within each risk group can be obtained by adopting appropriate adjustment coefficients for the mortality rates. On the other hand, different values for the life expectancy can also be justified by assuming different frailty levels. As already mentioned earlier, the latter is the approach that we develop in this paper.

We then design a risk classification arrangement based on a frailty model. We assume to hold the probability distribution of the frailty, as described in Section 2, for the general population. Based on such a probability distribution, the insurer identifies risk classes, each characterized by a given range of values of the frailty. Since the reference population for the frailty model is the general population, not all of the risk groups will be present in the portfolio, and if they are, the proportions among them are not necessarily those observed in the general population. Indeed, as a result of a self-selection process, also driven by the premium rates set by the insurer for the various risk groups, not all individuals will be interested in purchasing the insurance product.

Let $(z_{j-1},z_j]$ be the range of values of the frailty for a given risk group, say $G_j$. At age x, the group is defined as follows:

$$G_j=\{i:z_{j-1}<Z_x^{\left(i\right)}\le z_j\},$$

(14)

where $Z_x^{\left(i\right)}$ is the frailty of individual i. Let J be the number of groups that we identify; we assume $z_0=0$ and $z_J\to \infty$; thus, the set $\{G_j;j=1,\dots ,J\}$ constitutes a partition of the sample space of the frailty. Note that we assume that the lower the index j of the risk group, the lower is the expected frailty level in such a group; group $G_1$, in particular, is the class of standard risks. Referring to a cohort closed to new entries, the size and composition of each group change with age, due to deaths; anyhow, the limiting values for the frailty in each group keep the same.

Before moving forward with further assessment, and with the model implementation, we think it is useful to highlight a significant difference between the pragmatic approach to differential mortality, based on the adjustment of mortality rates, and the approach we are discussing.

In the prevailing practice, a time-discrete mortality model is adopted. To simplify the comparison, let us refer to a time-continuous mortality model. Following the pragmatic approach, the adjusted force of mortality would be defined as follows:

$${\mu }_x^{\left[a\right]}=a·{\mu }_x,$$

(15)

where a, $a>0$, is a fixed parameter. A risk group consists of those with the same value for parameter a. Since a is assumed to be known, the residual heterogeneity within each risk group is disregarded.

Under the frailty model, the individual force of mortality ${\mu }_x\left(z\right)$ has the same structure as (15); see (1). However, the parameter z is unknown in this case. A risk group is defined by the interval $(z_{j-1},z_j]$. The residual heterogeneity within the group can be assessed, as we suggest below.

3.2. Lifetime and Frailty for the Risk Classes

As mentioned in Section 3.1, we work within the Gompertz-Gamma model described in Section 2. In particular, we assume that the frailty $Z_x$ at age x in the general population (to which individuals underwriting an insurance contract belong) has a $\mathrm{Gamma}(\delta ,\theta (x\left)\right)$ distribution. We denote with $F(z;\delta ,\theta (x\left)\right)$ the probability distribution function of a $\mathrm{Gamma}(\delta ,\theta (x\left)\right)$-distributed random variable.

In what follows, we derive the probability distribution of the frailty for each group $G_j$ and the main summary statistics. Results are referred to the partition $\{G_j;j=1,\dots ,J\}$ for the frailty in the general population. The probability distribution of the frailty for group $G_j$ can be assessed as a conditional distribution of the frailty for the whole population; some simplifications are obtained thanks to the properties of Gamma distributions. Computation details are omitted here, as they are only based on standard results for Gamma distributions; for completeness, they are sketched in Appendix A, Appendix B, Appendix C and Appendix D.

The relative size of group $G_j$ at age x in the general population is given by:

$${\rho }_{j;x}=\mathbb{P}[z_{j-1}<Z_x\le z_j]=F(z_j;\delta ,\theta \left(x\right))-F(z_{j-1};\delta ,\theta \left(x\right)).$$

(16)

Clearly, at any age x, we have ${\sum }_{j=1}^J{\rho }_{j;x}=1$.

The probability distribution function of the frailty in group $G_j$ at age x can be assessed as follows:

$$F(z;\delta ,\theta \left(x\right)|G_j)=\left\{\begin{array}{ccc}0\hfill & & \mathrm{if}z\le z_{j-1};\hfill \\ \frac{F(z;\delta ,\theta \left(x\right))-F(z_{j-1};\delta ,\theta \left(x\right))}{{\rho }_{j;x}}\hfill & & \mathrm{if}{z}_{j-1}<z\le z_j;\hfill \\ 1\hfill & & \mathrm{if}z>z_j.\hfill \end{array}\right.$$

(17)

The expected value and variance of the frailty in group $G_j$ at age x can, respectively, be expressed as follows (after some rearrangements; see Appendix A and Appendix B):

$$\mathbb{E}\left[Z_x\right|G_j]=\mathbb{E}\left[Z_x\right]·\frac{F(z_j;\delta +1,\theta \left(x\right))-F(z_{j-1};\delta +1,\theta \left(x\right))}{{\rho }_{j;x}};$$

(18)

$$\begin{array}{cc}\hfill \mathbb{V}\mathrm{ar}\left[Z_x\right|G_j]=\mathbb{V}\mathrm{ar}\left[Z_x\right]·& \left((\delta +1)·\frac{F(z_j;\delta +2,\theta \left(x\right))-F(z_{j-1};\delta +2,\theta \left(x\right))}{{\rho }_{j;x}}\right.\hfill \\ & -\left.\delta ·\frac{F(z_j;\delta +1,\theta \left(x\right))-F(z_{j-1};\delta +1,\theta \left(x\right))}{{\rho }_{j;x}}\right).\hfill \end{array}$$

(19)

We further note that the expected value and variance of the frailty for the general population, defined respectively by (8) and (9), can be expressed in terms of the corresponding conditional values, as follows:

$$\mathbb{E}\left[Z_x\right]=\sum _j\mathbb{E}\left[Z_x\right|G_j]·{\rho }_{j;x};$$

(20)

$$\mathbb{V}\mathrm{ar}\left[Z_x\right]=\sum _j\mathbb{V}\mathrm{ar}\left[Z_x\right|G_j]·{\rho }_{j;x}+\sum _j\sum _{k:k>j}{(\mathbb{E}\left[Z_x\right|G_j]-\mathbb{E}\left[Z_x\right|G_k])}^2·{\rho }_{j;x}·{\rho }_{k;x}.$$

(21)

While (20) is straightforward, details for (21) are given in Appendix C. Note that the second sum in (21) expresses the correlation among the frailty groups, while the first sum measures the residual heterogeneity within the groups.

For the average survival function in group $G_j$ at age x, we find (after some rearrangements; see Appendix D):

$$\overline{S}\left(x\right|G_j)=\overline{S}\left(x\right)·\frac{{\rho }_{j;x}}{{\rho }_{j;0}}.$$

(22)

After having set the frailty limits $z_{j-1},z_j$, it is then (relatively) simple to make an assessment of the probability distribution of the lifetime in risk group $G_j$.

4. Model Calibration

The model described in Section 3 is general, as it can be applied to any type of life insurance business. In this paper, we discuss the case of immediate life annuities. We refer to a (closed) cohort of males initial age $x_0=65$. We assume that, while group $G_1$ collects standard risks, higher groups collect preferred risks, i.e. risks with a lower expected lifetime.

The Gompertz-Gamma model is calibrated on Italian projected life tables. In particular, we address the life table TG62, which refers to the general population, and the life table A62I, which is adopted for voluntary immediate life annuities. The projection producing the life table TG62 is performed with the standard Lee–Carter model (see [25,26,27]). Mortality rates for the highest ages (precisely, ages higher than 95) are not based on observed data, but on a parametric model (see [28]). The life table A62I is obtained by applying reduction coefficients to the mortality rates of the life table TG62. Such coefficients are chosen according to U.K. data and express the self-selection observed in pools of voluntary immediate life annuities (see [27]). The maximum attainable age in such life tables is $\omega =120$, which we assume also for the Gompertz-Gamma model.

A comparison between the life tables TG62 and A62I is performed in Figure 1, where the force of mortality, the probability density function of $T_{65}$ (i.e., the remaining lifetime at age 65) and the survival function are plotted (the life tables TG62 and A62I list mortality rates and the survival function for integer ages; the force of mortality and the probability density function $f_{65}\left(t\right)$ have been obtained through standard numerical approximations). The assumed impact of the self-selection of those underwriting a voluntary annuity emerges.

Parameters for the Gompertz-Gamma model are assessed considering only the range of ages $[65,95]$. Higher ages have been disregarded in order to avoid the smoothing effects embedded in the data used for the projection (see above). We perform the following steps.

• We first calibrate the mortality model for the general population, based on the life table TG62. As it is common in the literature, we set $\theta =\delta$; then, we need to set three parameters (namely, $\alpha ,\beta ,\delta$), and we assume the following requirements:

  • The expected value and variance of the lifetime in the range of ages $[65,95]$ under the Gompertz-Gamma model is the same as in the life table TG62;
  • The mean squared error (MSE) between the force of mortality in the range of ages $[65,95]$ under the Gompertz-Gamma model and the life table TG62 is minimum. While the analytical expression for the force of mortality is available for the Gompertz-Gamma model (see (13)), as already noted for the life table TG62, a standard numerical approximation has been used.
• Then, we calibrate the lifetime for standard risks, i.e., individuals in group $G_1$. We now need to set one parameter (namely, $z_1$), and we choose it so to minimize the MSE between the force of mortality under the Gompertz-Gamma model for individuals in group $G_1$ and the table A62I, in the range of ages $[65,95]$. Similarly to the life table TG62, the force of mortality for the life table A62I has been approximated numerically. For the Gompertz-Gamma model, the force of mortality for group $G_1$ can be obtained through its definition, as ${\overline{\mu }}_x\left(G_1\right)=-\frac{{\overline{S}}^{\prime }\left(x\right|G_1)}{\overline{S}\left(x\right|G_1)}$. For simplicity, we omit writing its expression, which cannot be simplified nicely.
• Finally, we calibrate the probability distribution of the lifetime for two additional groups, $G_2$ and $G_3$, characterized by higher average frailty levels; we set a (reasonable) benchmark for the reduced expected lifetime in these groups, with respect to the value for standard risks. Such benchmarks are commented on below.

Table 1. Parameters for the Gompertz-Gamma model. General population. Initial age $x_0=65$.

Parameters
α	$4.88661\times {10}^{-06}$
β	0.111902
δ	18.408049
θ	18.408049
${\alpha }^{\prime }$	$4.886619\times {10}^{-06}$
${\delta }^{\prime }$	$2.372256\times {10}^{-06}$

quotes the parameters of the Gompertz-Gamma model for the general population, initial age $x_0=65$. We recall that, since $\theta =\delta$, we have $\mathbb{E}\left[Z_0\right]=1$, and then, $\mathbb{E}\left[Z_x\right]<1$ for $x>0$. We note that the heterogeneity measured in the general population is expressed by $\mathbb{CV}\left[Z_{65}\right]=\frac{1}{\sqrt{\delta }}=23.308\%$. This outcome, which clearly drives the risk classification that we perform, could partially be affected by the modeling assumptions underlying the life table TG62. On the other hand, TG62 is the starting point of the rating of voluntary life annuities in the Italian insurance industry, so we prefer this reference to other choices of the dataset.

Table 2. Summary statistics of the probability distribution of the lifetime $T_{65}$. General population.

	TG62	Gompertz-Gamma (Population)
$\mathbb{E}\left[T_{65}\right]$	21.70	21.67
$\mathbb{CV}\left[T_{65}\right]$	41.93%	41.73%
$\mathrm{Mo}\left[T_{65}\right]$	25	24.71
$T_{65[0.25]}$	15.57	15.43
$T_{65[0.75]}$	28.12	28.38
$\mathrm{IQR}=T_{65[0.75]}-T_{65[0.25]}$	12.55	12.95
$T_{65[0.95]}$	35.92	35.45
$T_{65[0.99]}$	40.25	39.64

quotes the summary statistics of the probability distribution of the lifetime $T_{65}$ at age 65 for the life table TG62 and for the Gompertz-Gamma model with parameters as in Table 1. With $T_{65\left[\epsilon \right]}$, we denote the ε-percentile of the probability distribution of the lifetime, defined in the usual way; $\mathrm{IQR}$ then denotes the interquartile range, usually meant as a measure of dispersion. There are only small differences between the summary statistics of the probability distribution of $T_{65}$ under the life table TG62 and the Gompertz-Gamma model.

Table 3. Gompertz-Gamma model: expected value and coefficient of variation of the frailty at age x. General population.

	$\mathbb{E}\left[{\mathit{Z}}_{\mathit{x}}\right]$
65	0.996594
70	0.994053
75	0.989638
80	0.982007
85	0.968933
90	0.946874
95	0.910599
100	0.853391
105	0.768868
110	0.655299
115	0.520714
$\mathbb{CV}\left[Z_x\right]$	23.308%

lists the expected value of the frailty at various ages, as well as the coefficient of variation of the frailty at age x, which is constant with respect to age (see (10)).

Figure 2 shows the force of mortality, the probability density function of $T_{65}$ and the survival function of life table TG62 compared to the Gompertz-Gamma model applied to the general population. The differences between the forces of mortality at the highest ages are due to the different modeling assumptions for this range of ages. Some differences emerge also in the probability density function $f_{65}\left(t\right)$; however, when considering the scale of the y-axis of this plot with respect to the other two, these differences look small.

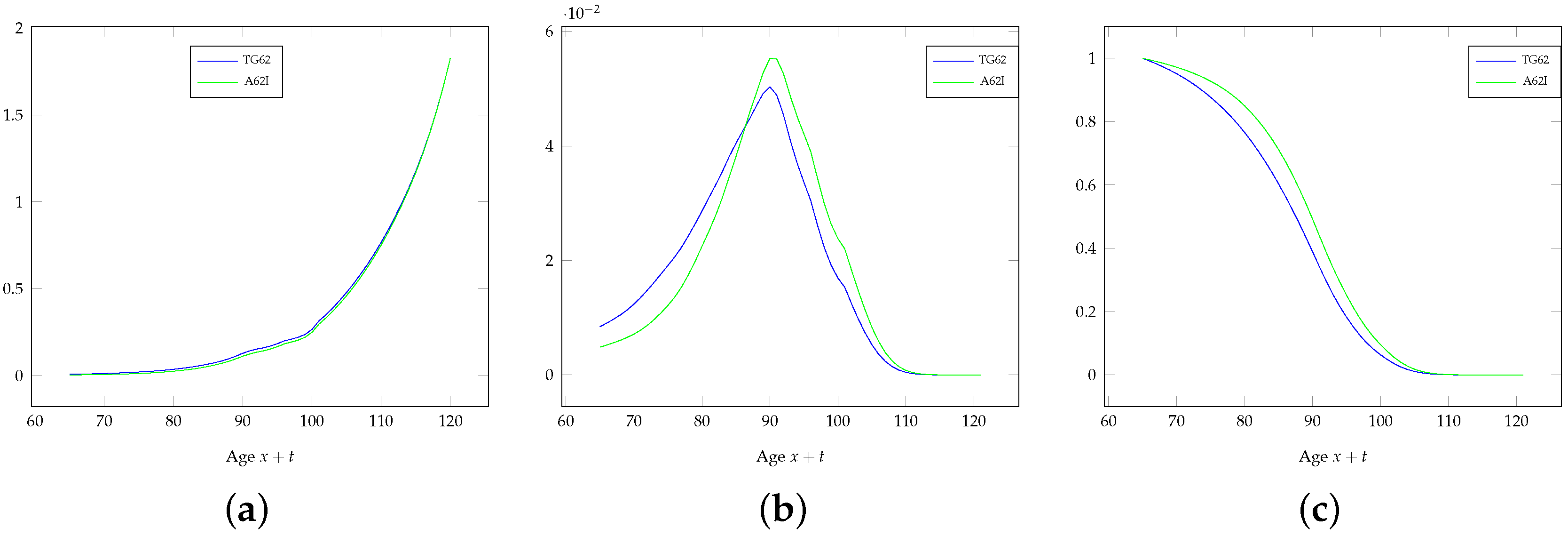
Figure 3 shows the force of mortality, the probability density function of $T_{65}$ and the survival function of the life table A62I compared to the Gompertz-Gamma model referring to group $G_1$. In this case, some differences are visible also in the survival function; this is due to the very different modeling assumptions about the self-selection backing the life table A62I and the Gompertz-Gamma model. This is confirmed by the comparison between the summary statistics of the probability distribution of $T_{65}$ for the life table A62I and the Gompertz-Gamma model for group $G_1$, which are quoted in

Table 4. Summary statistics of the probability distribution of the lifetime $T_{65}$. Risk group $G_1$.

	A62I	Gompertz-Gamma (Group ${\mathit{G}}_1$)
$\mathbb{E}\left[T_{65}\right]$	24.08	22.81
$\mathbb{CV}\left[T_{65}\right]$	59.92%	40.13%
$\mathrm{Mo}\left[T_{65}\right]$	25	26
$T_{65[0.25]}$	18.85	16.61
$T_{65[0.75]}$	30.05	29.62
$\mathrm{IQR}=T_{65[0.75]}-T_{65[0.25]}$	11.19	13.01
$T_{65[0.95]}$	37.34	36.55
$T_{65[0.99]}$	41.32	40.60

. While the method adopted in practice is very pragmatic, the Gompertz-Gamma model leads to a rigorous analytical solution. It is in particular interesting to note that the coefficient of variation of $T_{65}$ suggests a wider dispersion of the lifetime for life table A62I than TG62. This is against the idea that the mortality described by A62I refers to a group less heterogeneous than for TG62.

We note here that for setting the parameter $z_1$, rather than minimizing the MSE between the forces of mortality, we could adopt a requirement involving the expected lifetime (for instance: the same value under A62I and the Gompertz-Gamma model). However, this would lead to unconvincing results about the composition of the population. On the other hand, the life table A62I has been derived from TG62 adjusting the mortality rates; this is also why we set a requirement with respect to the force of mortality.

Table 5. Risk classes.

Group	Frailty Interval $({\mathit{z}}_{\mathit{j}-1},{\mathit{z}}_{\mathit{j}}]$	Relative Size at Age 65 of Group ${\mathit{G}}_{\mathit{j}}$ in the General Population ${\mathit{\rho }}_{\mathit{j};65}$	Expected Value of the Frailty $\mathbb{E}\left[{\mathit{Z}}_{65}\right|{\mathit{G}}_{\mathit{j}}]$	Coefficient of Variation $\mathbb{CV}\left[{\mathit{Z}}_{65}\right|{\mathit{G}}_{\mathit{j}}]$	Expected Lifetime $\mathbb{E}\left[{\mathit{T}}_{65}\right|{\mathit{G}}_{\mathit{j}}]$
$G_1$	$(\phantom{0.00000}0,1.038741]$	60.121%	0.845593	15.243%	22.81
$G_2$	$(1.038741,1.307144]$	30.111%	1.152338	6.479%	20.36
$G_3$	$(1.307144,\infty \phantom{.00000})$	9.769%	1.445866	8.736%	18.71
Population	$(\phantom{0.00000}0,\infty \phantom{.00000})$	100%	0.996594	23.308%	21.67

quotes the summary statistics of the frailty at age 65 for the three groups that we identify. The relative size of each group at age 65 refers to the general population; the real composition of the insurer’s portfolio depends on the number of people actually underwriting the contract. Note that each risk class shows a reduced coefficient of variation of the frailty (and then, less heterogeneity) with respect to the general population, as well as a lower (namely, group $G_1$) or higher (namely, groups $G_2$ and $G_3$) average frailty level. Note also that we have assumed that the expected lifetime of those in group $G_1$ is 12% higher than those in group $G_2$ and roughly 22% higher than those in group $G_3$. We think that these assumptions are reasonable with respect to the available data. Of course, different choices are possible. One could decide to set just one additional risk class for special rate annuities or more than two classes; further, different values for the lower expected lifetime for those in higher classes could be set. The final choice depends on what is classified as a critical health condition, how the health status can be ascertained, as well as on market issues.

5. The Value of the Liabilities of a Life Annuity Portfolio

5.1. The Present Value of Future Benefits

We address a portfolio consisting of one cohort of immediate life annuities in arrears, issued at time $t=0$, age $x_0$, and we investigate the present value at time $t\ge 0$ of future benefits.

In principle, the portfolio is arranged into risk classes ($G_1,G_2,G_3$, in our implementation). However, some risk classes could be empty, because the insurer could decide not to offer differentiated annuity rates, or to offer just some annuity rates, or individuals in critical health conditions could decide not to underwrite the contract. The number of individuals in class j at time $t=0$ is $n_{0;j}$, known, whereas at time $t>0$ it is $N_{t;j}$, random. The total portfolio size at time $t=0$ is $n_0={\sum }_j{n}_{0;j}$, while at time $t>0$, it is $N_t={\sum }_j{N}_{t;j}$.

For each risk class, the annuity rate is assessed adopting the traditional equivalence principle. Setting to S the initial amount paid (as the single premium) by each individual at time $t=0$, the benefit amount $b_j$ for group $G_j$ is assessed as follows:

$$b_j=S·\frac{1}{a_{x_0;j}},$$

(23)

where:

$$a_{x_0;j}=\sum _{s=1}^{\infty }{(1+r)}^{-s}·\frac{\overline{S}(x_0+s|G_j)}{\overline{S}\left(x_0\right|G_j)},$$

(24)

and r is the discount rate, which is assumed to be deterministic (and constant).

The present value at time t, $t\ge 0$, of future benefits for group $G_j$ is defined as follows:

$$P{V}_{t;j}=\sum _{s=t+1}^{\infty }{b}_j·N_{s;j}·v(t,s),$$

(25)

where $v(t,s)$ is the discount factor, which is assumed to be deterministic. In particular, we set the discount rate to r, the same that is used for pricing. Then: $v(t,s)={(1+r)}^{-(s-t)}$.

The present value at time t, $t\ge 0$, of future benefits for the whole portfolio is given by:

$$P{V}_t=\sum _{j}P{V}_{t;j}.$$

(26)

Our aim is to analyze the magnitude and risk profile of the value of the liabilities of a portfolio, depending on its composition and size. In order to perform the comparisons, we will refer to a portfolio only consisting of standard risks, i.e., only consisting of group $G_1$, as the base case. We assess:

• The expected value $\mathbb{E}\left[P{V}_t\right]$,
• The coefficient of variation, $\mathbb{CV}\left[P{V}_t\right]$,
• The right tail, measured through the ε-percentiles $P{V}_{t\left[\epsilon \right]}$

of the present value at time t of future benefits for the whole portfolio. The quantities $\mathbb{E}\left[P{V}_t\right]$, $\mathbb{CV}\left[P{V}_t\right]$, $P{V}_{t\left[\epsilon \right]}$ are based on standard definitions and are assessed through stochastic simulation.

5.2. Numerical Investigation

The portfolio is arranged into three groups, identified as described in Section 4. We set to $n_{0;1}=1000$ the maximum number of standard risks that can be interested into the insurer’s product. The total portfolio size anyhow can be larger, if risk classes $G_2$ and $G_3$ are non-empty. According to the frailty model, the maximum size of the portfolio at time 0 is $\frac{1000}{{\rho }_{1;65}}=1663$, while the maximum size at time 0 of classes $G_2$ and $G_3$ is, respectively, $1663·{\rho }_{2;65}=501$ and $1663·{\rho }_{3;65}=162$.

Table 6. Alternative portfolios.

Groups	Portfolio
	A	B	C	D	E	F
$G_1$	1 000	1 000	1 000	1 000	1 000	500
$G_2$	0	200	250	200	501	500
$G_3$	0	0	0	50	162	0
All	1 000	1 200	1 250	1 250	1 663	1 000

lists the six alternative portfolios that we test. In Portfolios A–E, $n_{0;1}=1000$, i.e., we assume that the initial size of group $G_1$ takes the maximum possible value. The five portfolios A–E, then, differ for the size of the other two groups. Conversely, Portfolio F has the same size as Portfolio A, but a different composition.

In detail:

• Portfolio A is the base case; it only consists of standard risks;
• Portfolio E has the largest possible size, including policies in groups $G_2$ and $G_3$;
• Portfolio B and C include some policies in group $G_2$, where C has a larger size;
• Portfolio D has the same size as portfolio C, but with some policies also in group $G_3$;
• Portfolio F shows adverse-selection: the number of standard risks is lower than in the other cases, but the size is the same as Portfolio A, due to risks in class $G_2$.

This way, we address various portfolio sizes and degrees of heterogeneity.

Setting the discount rate $r=0\%$,

Table 7. Individual benefit amount for the three risk classes.

	Group ${\mathit{G}}_1$	Group ${\mathit{G}}_2$	Group ${\mathit{G}}_3$
Benefit amount $b_j$	4.483	5.034	5.492
$\frac{b_j}{b_1}-1$	0%	12.302%	22.515%

lists the benefits obtained for an initial amount $S=100$.

In

Table 8. Average benefit amount for the portfolio: additional amount with respect to the base case, $\frac{{\overline{b}}_t}{b_1}-1$.

Time t	Portfolio A	Portfolio B	Portfolio C	Portfolio D	Portfolio E	Portfolio F
0	0%	2.050%	2.460%	2.869%	5.899%	6.151%
5	0%	2.022%	2.434%	2.826%	5.820%	6.112%
10	0%	1.981%	2.381%	2.740%	5.694%	6.032%
15	0%	1.913%	2.296%	2.633%	5.481%	5.893%
20	0%	1.786%	2.150%	2.402%	5.116%	5.654%
25	0%	1.592%	1.918%	2.073%	4.503%	5.227%
30	0%	1.268%	1.555%	1.587%	3.574%	4.522%
35	0%	0.868%	1.001%	1.120%	2.287%	3.189%
40	0%	0.000%	0.000%	0.000%	0.879%	1.757%
45	0%	0.000%	0.000%	0.000%	0.000%

, we quote the average benefit amount for the portfolio, assessed as:

$${\overline{b}}_t=\frac{{\sum }_j{b}_j·N_{t;j}}{{\sum }_j{N}_{t;j}}.$$

(27)

Such an average depends on the portfolio composition, which changes in time, as is illustrated in

Table 9. Portfolio size and composition.

Time t	Portfolio A					Portfolio B
	Total Size		Relative Group Size			Total Size		Relative Group Size
	${\mathit{n}}_{\mathit{t}}$	$\frac{{\mathit{n}}_{\mathit{t}}}{{\mathit{n}}_0}$	Group ${\mathit{G}}_1$	Group ${\mathit{G}}_2$	Group ${\mathit{G}}_3$	${\mathit{n}}_{\mathit{t}}$	$\frac{{\mathit{n}}_{\mathit{t}}}{{\mathit{n}}_0}$	Group ${\mathit{G}}_1$	Group ${\mathit{G}}_2$	Group ${\mathit{G}}_3$
0	1 000	100.00%	100%	0%	0%	1 200	100.00%	83.333%	16.667%	0.000%
5	961	96.10%	100%	0%	0%	1 150	95.83%	83.565%	16.435%	0.000%
10	896	89.60%	100%	0%	0%	1 068	89.00%	83.895%	16.105%	0.000%
15	793	79.30%	100%	0%	0%	939	78.25%	84.452%	15.548%	0.000%
20	642	64.20%	100%	0%	0%	751	62.58%	85.486%	14.514%	0.000%
25	444	44.40%	100%	0%	0%	510	42.50%	87.059%	12.941%	0.000%
30	235	23.50%	100%	0%	0%	262	21.83%	89.695%	10.305%	0.000%
35	79	7.90%	100%	0%	0%	85	7.08%	92.941%	7.059%	0.000%
40	13	1.30%	100%	0%	0%	13	1.08%	100.000%	0.000%	0.000%
45	1	0.10%	100%	0%	0%	1	0.08%	100.000%	0.000%	0.000%
50	0	0.00%				0	0.00%
Time t	Portfolio C					Portfolio D
	Total Size		Relative Group Size			Total Size		Relative Group Size
	${\mathit{n}}_{\mathit{t}}$	$\frac{{\mathit{n}}_{\mathit{t}}}{{\mathit{n}}_0}$	Group ${\mathit{G}}_1$	Group ${\mathit{G}}_2$	Group ${\mathit{G}}_3$	${\mathit{n}}_{\mathit{t}}$	$\frac{{\mathit{n}}_{\mathit{t}}}{{\mathit{n}}_0}$	Group ${\mathit{G}}_1$	Group ${\mathit{G}}_2$	Group ${\mathit{G}}_3$
0	1 250	100.00%	80.000%	20.000%	0.000%	1 250	100.00%	80.000%	16.000%	4.000%
5	1 198	95.84%	80.217%	19.783%	0.000%	1 197	95.76%	80.284%	15.789%	3.926%
10	1 111	88.88%	80.648%	19.352%	0.000%	1 109	88.72%	80.794%	15.509%	3.697%
15	975	78.00%	81.333%	18.667%	0.000%	973	77.84%	81.501%	15.005%	3.494%
20	778	62.24%	82.519%	17.481%	0.000%	774	61.92%	82.946%	14.083%	2.972%
25	526	42.08%	84.411%	15.589%	0.000%	522	41.76%	85.057%	12.644%	2.299%
30	269	21.52%	87.361%	12.639%	0.000%	266	21.28%	88.346%	10.150%	1.504%
35	86	6.88%	91.860%	8.140%	0.000%	86	6.88%	91.860%	6.977%	1.163%
40	13	1.04%	100.000%	0.000%	0.000%	13	1.04%	100.000%	0.000%	0.000%
45	1	0.08%	100.000%	0.000%	0.000%	1	0.08%	100.000%	0.000%	0.000%
50	0	0.00%				0	0.00%
Time t	Portfolio E					Portfolio F
	Total Size		Relative Group Size			Total Size		Relative Group Size
	${\mathit{n}}_{\mathit{t}}$	$\frac{{\mathit{n}}_{\mathit{t}}}{{\mathit{n}}_0}$	Group ${\mathit{G}}_1$	Group ${\mathit{G}}_2$	Group ${\mathit{G}}_3$	${\mathit{n}}_{\mathit{t}}$	$\frac{{\mathit{n}}_{\mathit{t}}}{{\mathit{n}}_0}$	Group ${\mathit{G}}_1$	Group ${\mathit{G}}_2$	Group ${\mathit{G}}_3$
0	1 663	100.00%	60.132%	30.126%	9.741%	1 000	100.00%	50.00%	50.00%	0.00%
5	1 586	95.37%	60.593%	29.887%	9.521%	954	95.40%	50.31%	49.69%	0.00%
10	1 461	87.85%	61.328%	29.500%	9.172%	879	87.90%	50.97%	49.03%	0.00%
15	1 267	76.19%	62.589%	28.808%	8.603%	762	76.20%	52.10%	47.90%	0.00%
20	991	59.59%	64.783%	27.548%	7.669%	594	59.40%	54.04%	45.96%	0.00%
25	648	38.97%	68.519%	25.309%	6.173%	386	38.60%	57.51%	42.49%	0.00%
30	316	19.00%	74.367%	21.519%	4.114%	185	18.50%	63.24%	36.76%	0.00%
35	95	5.71%	83.158%	14.737%	2.105%	54	5.40%	74.07%	25.93%	0.00%
40	14	0.84%	92.857%	7.143%	0.000%	7	0.70%	85.71%	14.29%	0.00%
45	1	0.06%	100.000%	0.000%	0.000%	0	0.06%
50	0	0.00%					0.00%

. In such a table, and in the following as well, we assume that at any valuation time t, the observed number $n_t$ of survivors is as expected (while, clearly, at any valuation time t, the future numbers of survivors keep random). When classes $G_2$ and $G_3$ are non-empty, since those with a higher frailty are expected to die earlier, the relative size of group $G_1$ increases in time, and then, the average benefit amount decreases. Trivially, the initial average benefit amount is higher the larger is the (relative) size of groups $G_2$ and $G_3$. The column $\frac{n_t}{n_0}$ in Table 9 shows the average survival rate in the portfolio, i.e., the average number of survivors out of the initial $n_0$. Note that the average survival rate is lower in the presence of preferred risks (for the same reason that we have commented on above); this has an impact on the expected value of liabilities, as we show in

Table 10. Expected present value of future benefits, per policy in-force: $\frac{\mathbb{E}\left[P{V}_t\right]}{n_t}$.

Time t	Portfolio A	Portfolio B	Portfolio C	Portfolio D	Portfolio E	Portfolio F
	Abs.Value	% of the Value Obtained for Portfolio A
0	100.00	100.00%	100.00%	100.00%	100.01%	100.01%
5	81.26	99.71%	99.65%	99.60%	99.18%	99.13%
10	64.00	99.37%	99.24%	99.15%	98.24%	98.10%
15	48.62	99.00%	98.80%	98.66%	97.24%	96.94%
20	35.44	98.63%	98.35%	98.22%	96.25%	95.67%
25	24.66	98.32%	97.98%	97.89%	95.45%	94.47%
30	16.35	98.18%	97.77%	97.82%	95.13%	93.55%
35	10.34	98.31%	98.04%	97.94%	95.72%	93.71%
40	6.32	100.00%	100.00%	100.00%	97.63%	95.54%
45	3.93	100.00%	100.00%	100.00%	100.00%

. We also note that no survivor is expected at time $t=45$ (i.e., age 110) for Portfolio F (while the other portfolios are still expected to be in-force, although with a negligible size); this explains why in Table 8, Table 9, Table 10,

Table 11. Coefficient of variation of the present value of future benefits: $\mathbb{CV}\left[P{V}_t\right]$.

Time t	Portfolio A	Portfolio B	Portfolio C	Portfolio D	Portfolio E	Portfolio F
0	1.30%	1.20%	1.17%	1.18%	1.04%	1.87%
5	1.48%	1.37%	1.34%	1.35%	1.19%	1.55%
10	1.75%	1.62%	1.60%	1.60%	1.39%	1.80%
15	2.10%	1.96%	1.91%	1.93%	1.70%	2.19%
20	2.64%	2.45%	2.41%	2.43%	2.17%	2.80%
25	3.55%	3.34%	3.31%	3.31%	3.04%	3.97%
30	5.62%	5.38%	5.32%	5.35%	4.96%	6.54%
35	11.10%	10.78%	10.78%	10.73%	10.28%	13.82%
40	32.19%	32.19%	32.19%	32.19%	31.40%	44.42%
45	136.25%	136.25%	136.25%	136.25%	136.25%

,

Table 12. Ninety-fifth percentile of $P{V}_t$, as a % of $\mathbb{E}\left[P{V}_t\right]$.

Time t	Portfolio A	Portfolio B	Portfolio C	Portfolio D	Portfolio E	Portfolio F
0	102.11%	101.96%	101.90%	101.94%	101.72%	103.06%
5	102.43%	102.25%	102.21%	102.22%	101.94%	102.52%
10	102.86%	102.69%	102.63%	102.64%	102.30%	102.99%
15	103.43%	103.24%	103.13%	103.23%	102.80%	103.61%
20	104.43%	104.04%	103.98%	104.00%	103.57%	104.67%
25	105.86%	105.53%	105.54%	105.43%	105.08%	106.55%
30	109.34%	109.04%	108.82%	108.93%	108.27%	110.73%
35	118.51%	118.05%	117.97%	117.83%	116.92%	123.53%
40	158.21%	158.21%	158.21%	158.21%	155.67%	180.28%
45	342.00%	342.00%	342.00%	342.00%	342.00%

and

Table 13. Ninety-ninth percentile of $P{V}_t$, as a % of $\mathbb{E}\left[P{V}_t\right]$.

Time t	Portfolio A	Portfolio B	Portfolio C	Portfolio D	Portfolio E	Portfolio F
0	103.07%	102.81%	102.70%	102.76%	102.44%	104.35%
5	103.46%	103.18%	103.06%	103.13%	102.73%	103.63%
10	104.12%	103.70%	103.77%	103.73%	103.22%	104.17%
15	104.98%	104.58%	104.48%	104.58%	104.00%	105.08%
20	106.36%	105.90%	105.73%	105.79%	105.15%	106.59%
25	108.28%	107.88%	107.78%	107.83%	106.98%	109.49%
30	113.66%	112.77%	112.77%	112.75%	111.91%	115.31%
35	126.74%	125.91%	125.69%	125.67%	124.79%	133.88%
40	185.49%	185.49%	185.49%	185.49%	181.62%	222.70%
45	570.00%	570.00%	570.00%	570.00%	570.00%

, no quantity is listed for Portfolio F at time $t=45$.

Table 10, Table 11, Table 12 and Table 13 report the findings of the numerical investigation about the present value of future benefits. To ease comparisons, all results are expressed per policy in-force at the valuation time t, i.e., $n_t$.

Table 10 quotes the expected value of the present value of future benefits at time t (per policy in-force at time t). To ease comparisons, values for Portfolios B–F are expressed per unit of the expected value obtained for Portfolio A. The value per capita of $\mathbb{E}\left[P{V}_0\right]$ is the same in all of the portfolios, as at time 0, it is simply the total amount cashed as the single premium (which we have assumed to be the same for all of the annuitants). Then, it obviously decreases in time for all of the portfolios; however, the value at times $t>0$ is smaller in Portfolios B–F, which consist of several risk groups, than Portfolio A, which consists of one risk group only. This is due to the lower average survival rate, as well as to the changing composition of the portfolios: as those with higher frailty are supposed to die earlier, the relative size of group $G_1$ increases in time, and these are the annuitants cashing the lowest benefit amount.

Table 11 lists the coefficient of variation of $P{V}_t$ (per capita). When comparing the results for the alternative portfolios, we should keep in mind that the volatility is affected by the portfolio size, but also by its heterogeneity with respect to the frailty. From the results in Table 11, it seems that in the trade-off between size and heterogeneity, the former prevails. Indeed, larger portfolios show a lower coefficient of variation at any time t; thus, Portfolio A, only consisting of standard risks, shows the highest volatility when compared to Portfolios B–E, and the difference between such volatility and that of the other portfolios increases in time. On the other hand, if adverse-selection emerges after the introduction of special rate annuities, then the insurer’s risk profile could get worse. This is shown by Portfolio F with respect to Portfolio A. Portfolios C and D have the same initial size (and roughly the same size at times $t>0$), Portfolio D showing a greater heterogeneity; this is why $\mathbb{CV}\left[P{V}_t\right]$ takes higher values in the case of Portfolio D (but the difference is very small). Note that the difference between the percentiles of Portfolio A and Portfolios B–E increases in time both in absolute and relative terms, showing that a stronger heterogeneity can be accepted if matched by a larger portfolio size. Portfolio F, on the other hand, shows the possible consequence of adverse selection.

Table 12 and Table 13 quote, respectively, the 95th and 99th percentile of the probability distribution of $P{V}_t$, listed as a % of $\mathbb{E}\left[P{V}_t\right]$. Comments are similar to those discussed for the coefficient of variation of $P{V}_t$.

5.3. Sensitivity Analysis

As we have mentioned, the choice of the rating structure depends on the level of heterogeneity of the population, on how critical health conditions are classified and on market issues, as well. In this section, we investigate the insurer’s liabilities in situations or choices for the risk classes alternative with respect to what we have previously considered. In particular:

• Assuming the same parameters for the Gompertz-Gamma model referring to the general population as in Table 1, we consider a rating structure arranged on a higher number of risk classes (precisely, four or five);
• We assume a higher degree of heterogeneity in the general population, and we identify three risk classes, assuming the same composition of the general population as in Table 5.

We want to investigate what differences emerge with respect to the value of liabilities. To allow some comparisons with the discussion in Section 5.2, we set the portfolio size to 1 663, i.e., the same as Portfolio E. Differences in the distribution of insurer’s liabilities then can be assumed to arise from either the different risk classification or the degree of heterogeneity.

We consider three additional portfolios, namely Portfolios G, H and I.

• For Portfolio G, the rating structure is arranged into four classes; details are quoted in

  Table 14. Portfolio G: tariff structure and benefit amounts.

  	Group ${\mathit{G}}_1$	Group ${\mathit{G}}_2$	Group ${\mathit{G}}_3$	Group ${\mathit{G}}_4$	Population
  Frailty interval $({\mathit{z}}_{\mathit{j}\mathbf{-}\mathbf{1}}\mathbf{,}{\mathit{z}}_{\mathit{j}}]$	$(0,1.038741]$	$(1.038741,1.186127]$	$(1.186127,1.410339]$	$(1.410339,\infty )$	$(0,\infty )$
  Relative size in the population ${\mathit{\rho }}_{\mathit{j};\mathbf{65}}$	60.121%	20.000%	15.000%	4.879%	100%
  Expected value of the frailty $\mathbb{E}\left[{\mathit{Z}}_{\mathbf{65}}\right|{\mathit{G}}_{\mathit{j}}]$	0.845593	1.107415	1.277892	1.538161	0.996594
  Coefficient of variation $\mathbb{CV}\left[{\mathit{Z}}_{\mathbf{65}}\right|{\mathit{G}}_{\mathit{j}}]$	15.243%	3.806%	4.871%	7.706%	23.308%
  Expected lifetime $\mathbb{E}\left[{\mathit{T}}_{\mathbf{65}}\right|{\mathit{G}}_{\mathit{j}}]$	22.81	20.65	19.59	18.26	21.67
  Benefit amount ${\mathit{b}}_{\mathit{j}}$	4.483	4.963	5.238	5.632
  as a % of the standard benefit, $\frac{{\mathit{b}}_{\mathit{j}}}{{\mathit{b}}_{\mathbf{1}}}\mathbf{-}\mathbf{1}$	0%	10.708%	16.855%	25.6347%

  . Note that we keep the same definition for the standard risk class, i.e., class $G_1$, as for Portfolios A–F, while we arrange preferred risk classes into four groups.
• For Portfolio H, the rating structure is arranged into five classes, with a reduced frailty interval for standard risks. This means that in this case, the definition of what is considered to be a standard risk is more restrictive than in the previous cases. Details are listed in

  Table 15. Portfolio H: tariff structure and benefit amounts.

  	Group ${\mathit{G}}_1$	Group ${\mathit{G}}_2$	Group ${\mathit{G}}_3$	Group ${\mathit{G}}_4$	Group ${\mathit{G}}_5$	Population
  Frailty interval $({\mathit{z}}_{\mathit{j}\mathbf{-}\mathbf{1}}\mathbf{,}{\mathit{z}}_{\mathit{j}}]$	$(0,0.921533]$	$(0.921533,1.038742]$	$(1.038742,1.186128]$	$(1.186128,1.307152]$	$(1.307152,\infty )$	$(0,\infty )$
  Relative size in the population ${\mathit{\rho }}_{\mathit{j};\mathbf{65}}$	40.000%	20.121%	20.000%	10.111%	9.768%	100%
  Expected value of the frailty $\mathbb{E}\left[{\mathit{Z}}_{\mathbf{65}}\right|{\mathit{G}}_{\mathit{j}}]$	0.778312	979346	1.107417	1.241204	1.445874	0.996594
  Coefficient of variation $\mathbb{CV}\left[{\mathit{Z}}_{\mathbf{65}}\right|{\mathit{G}}_{\mathit{j}}]$	13.398%	3.440%	3.806%	2.787%	8.736%	23.308%
  Expected lifetime $\mathbb{E}\left[{\mathit{T}}_{\mathbf{65}}\right|{\mathit{G}}_{\mathit{j}}]$	23.43	21.58	20.65	19.80	18.71	21.67
  Benefit amount ${\mathit{b}}_{\mathit{j}}$	4.362	4.744	4.963	5.182	5.492
  as a % of the standard benefit, $\frac{{\mathit{b}}_{\mathit{j}}}{{\mathit{b}}_{\mathbf{1}}}\mathbf{-}\mathbf{1}$	0%	8.776%	13.781%	18.802%	25.915%
  as a % of the standard benefit in Portfolio A, $\frac{{\mathit{b}}_{\mathit{j}}}{{\mathit{b}}_{\mathbf{1}}[\mathbf{Ptf}\mathbf{.}\mathbf{A}]}\mathbf{-}\mathbf{1}$	$-2.700\%$	5.839%	10.708%	15.594%	22.515%

  .
• While Portfolios G and H are based on the same assessment of the heterogeneity of the population as for Portfolios A–F, Portfolio I is designed assuming a stronger degree of heterogeneity of the general population. We identify three risk classes, whose initial relative size in the population is the same as for Portfolios A–F. See

  Table 16. Portfolio I: tariff structure and benefit amounts.

  	Group ${\mathit{G}}_1$	Group ${\mathit{G}}_2$	Group ${\mathit{G}}_3$	Population
  Frailty interval $({\mathit{z}}_{\mathit{j}-\mathbf{1}},{\mathit{z}}_{\mathit{j}}]$	$(0,1.04219]$	$(1.04219,1.41721]$	$(1.41721,\infty )$	$(0,\infty )$
  Relative size in the population ${\mathit{\rho }}_{\mathit{j};\mathbf{65}}$	60.121%	30.111%	9.768%	100%
  Expected value of the frailty $\mathbb{E}\left[{\mathit{Z}}_{\mathbf{65}}\right|{\mathit{G}}_{\mathit{j}}]$	0.789420	1.199340	1.619084	0.993896
  Coefficient of variation $\mathbb{CV}\left[{\mathit{Z}}_{\mathbf{65}}\right|{\mathit{G}}_{\mathit{j}}]$	20.728%	8.686%	11.507%	31.623%
  Expected lifetime $\mathbb{E}\left[{\mathit{T}}_{\mathbf{65}}\right|{\mathit{G}}_{\mathit{j}}]$	23.25	19.93	17.79	21.71
  Benefit amount ${\mathit{b}}_{\mathit{j}}$	4.397	5.147	5.783
  as a % of the standard benefit, $\frac{{\mathit{b}}_{\mathit{j}}}{{\mathit{b}}_{\mathbf{1}}}-\mathbf{1}$	0%	17.071%	31.531%
  as a % of the standard benefit in Portfolio A, $\frac{{\mathit{b}}_{\mathit{j}}}{{\mathit{b}}_{\mathbf{1}}[\mathbf{Ptf}\mathbf{.}\mathbf{A}]}\mathbf{-}\mathbf{1}$	$-1.920\%$	14.824%	29.006%

  for details.

Table 14, Table 15, Table 16,

Table 17. Portfolio G: portfolio size and composition.

Time t	Portfolio G
	Total Size		Relative Group Size
	${\mathit{n}}_{\mathit{t}}$	$\frac{{\mathit{n}}_{\mathit{t}}}{{\mathit{n}}_0}$	Group ${\mathit{G}}_1$	Group ${\mathit{G}}_2$	Group ${\mathit{G}}_3$	Group ${\mathit{G}}_4$
0	1 663	100.000%	60.132%	20.024%	14.973%	4.871%
5	1 586	95.370%	60.593%	19.924%	14.754%	4.729%
10	1 461	87.853%	61.328%	19.713%	14.442%	4.517%
15	1 267	76.188%	62.589%	19.416%	13.812%	4.183%
20	991	59.591%	64.783%	18.769%	12.815%	3.633%
25	648	38.966%	68.519%	17.593%	11.111%	2.778%
30	316	19.002%	74.367%	15.190%	8.544%	1.899%
35	96	5.773%	82.292%	11.458%	5.208%	1.042%
40	14	0.842%	92.857%	7.143%	0.000%	0.000%
45	1	0.060%	100.000%	0.000%	0.000%	0.000%
50	0	0.000%

,

Table 18. Portfolio G: portfolio average benefit amount (additional amount with respect to the standard benefit for Portfolio A, $\frac{{\overline{b}}_t}{b_1[\mathrm{Ptf}.\mathrm{A}]}-1$) and summary statistics of the probability distribution of insurer’s liabilities.

Time t	$\frac{{\overline{\mathit{b}}}_{\mathit{t}}}{{\mathit{b}}_1[\mathbf{Ptf}.\mathbf{A}]}-1$	$\frac{\mathbb{E}\left[{\mathit{PV}}_{\mathit{t}}\right]}{{\mathit{n}}_{\mathit{t}}}$	$\mathbb{CV}\left[{\mathit{PV}}_{\mathit{t}}\right]$	95th perc.of ${\mathit{PV}}_{\mathit{t}}$	99th perc. of ${\mathit{PV}}_{\mathit{t}}$
		as a % of the Value		as a % of $\mathbb{E}\left[{\mathit{PV}}_{\mathit{t}}\right]$	as a % of $\mathbb{E}\left[{\mathit{PV}}_{\mathit{t}}\right]$
		for Ptf.A
0	5.917%	100.01%	1.04%	101.68%	102.48%
5	5.833%	99.17%	1.18%	101.94%	102.71%
10	5.703%	98.23%	1.41%	102.32%	103.31%
15	5.480%	97.22%	1.69%	102.77%	103.81%
20	5.101%	96.22%	2.19%	103.63%	105.19%
25	4.469%	95.42%	3.05%	105.01%	107.18%
30	3.553%	95.05%	4.96%	108.27%	111.75%
35	2.372%	95.42%	10.28%	117.02%	124.71%
40	0.765%	97.69%	31.38%	155.57%	182.05%
45	0.000%	100.00%	136.25%	342.00%	570.00%

,

Table 19. Portfolio H: portfolio size and composition.

Time t	Portfolio H
	Total Size		Relative Group Size
	${\mathit{n}}_{\mathit{t}}$	$\frac{{\mathit{n}}_{\mathit{t}}}{{\mathit{n}}_0}$	Group ${\mathit{G}}_1$	Group ${\mathit{G}}_2$	Group ${\mathit{G}}_3$	Group ${\mathit{G}}_4$	Group ${\mathit{G}}_5$
0	1 663	100.000%	39.99%	20.14%	20.02%	10.10%	9.74%
5	1 586	95.370%	40.42%	20.18%	19.92%	9.96%	9.52%
10	1 461	87.853%	41.14%	20.19%	19.71%	9.79%	9.17%
15	1 268	76.248%	42.35%	20.19%	19.40%	9.46%	8.60%
20	991	59.591%	44.60%	20.18%	18.77%	8.78%	7.67%
25	648	38.966%	48.46%	20.06%	17.59%	7.72%	6.17%
30	315	18.942%	55.24%	19.37%	15.24%	6.03%	4.13%
35	96	5.773%	65.63%	16.67%	11.46%	4.17%	2.08%
40	14	0.842%	78.57%	14.29%	7.14%	0.00%	0.00%
45	1	0.060%	100.00%	0.00%	0.00%	0.00%	0.00%
50	0	0.000%

,

Table 20. Portfolio H: portfolio average benefit amount (additional amount with respect to the standard benefit for Portfolio A, $\frac{{\overline{b}}_t}{b_1[\mathrm{Ptf}.\mathrm{A}]}-1$) and summary statistics of the probability distribution of insurer’s liabilities.

Time t	$\frac{{\overline{\mathit{b}}}_{\mathit{t}}}{{\mathit{b}}_1[\mathbf{Ptf}.\mathbf{A}]}-1$	$\frac{\mathbb{E}\left[{\mathit{PV}}_{\mathit{t}}\right]}{{\mathit{n}}_{\mathit{t}}}$	$\mathbb{CV}\left[{\mathit{PV}}_{\mathit{t}}\right]$	95th perc. of ${\mathit{PV}}_{\mathit{t}}$	99th perc. of ${\mathit{PV}}_{\mathit{t}}$
		as a % of the Value		as a % of $\mathbb{E}\left[{\mathit{PV}}_{\mathit{t}}\right]$	as a % of $\mathbb{E}\left[{\mathit{PV}}_{\mathit{t}}\right]$
		for Ptf. A
0	6.009%	100.01%	1.03%	101.70%	102.38%
5	5.918%	99.16%	1.20%	101.98%	102.82%
10	5.771%	98.19%	1.39%	102.29%	103.20%
15	5.524%	97.10%	1.70%	102.81%	103.94%
20	5.080%	95.99%	2.18%	103.58%	105.22%
25	4.340%	95.04%	3.05%	105.02%	107.21%
30	3.141%	94.48%	4.94%	108.26%	111.58%
35	1.547%	94.36%	10.06%	116.76%	124.25%
40	−0.523%	95.00%	31.01%	152.56%	179.67%
45	−2.700%	99.35%	134.82%	334.93%	558.22%

,

Table 21. Portfolio I: portfolio size and composition.

Time t	Portfolio I
	Total Size		Relative Group Size
	${\mathit{n}}_{\mathit{t}}$	$\frac{{\mathit{n}}_{\mathit{t}}}{{\mathit{n}}_0}$	Group ${\mathit{G}}_1$	Group ${\mathit{G}}_2$	Group ${\mathit{G}}_3$
0	1 663	100.000%	60.132%	30.126%	9.741%
5	1 587	95.430%	60.744%	29.805%	9.452%
10	1 462	87.913%	61.696%	29.343%	8.960%
15	1 267	76.188%	63.457%	28.335%	8.208%
20	989	59.471%	66.431%	26.694%	6.876%
25	648	38.966%	71.296%	23.611%	5.093%
30	320	19.242%	78.750%	18.438%	2.813%
35	103	6.194%	88.350%	10.680%	0.971%
40	18	1.082%	94.444%	5.556%	0.000%
45	1	0.060%	100.000%	0.000%	0.000%
50	0	0.000%

and

Table 22. Portfolio I: portfolio average benefit amount (additional amount with respect to the standard benefit for Portfolio A, $\frac{{\overline{b}}_t}{b_1[\mathrm{Ptf}.\mathrm{A}]}-1$) and summary statistics of the probability distribution of insurer’s liabilities.

Time t	$\frac{{\overline{\mathit{b}}}_{\mathit{t}}}{{\mathit{b}}_1[\mathbf{Ptf}.\mathbf{A}]}-1$	$\frac{\mathbb{E}\left[{\mathit{PV}}_{\mathit{t}}\right]}{{\mathit{n}}_{\mathit{t}}}$	$\mathbb{CV}\left[{\mathit{PV}}_{\mathit{t}}\right]$	95th perc. of ${\mathit{PV}}_{\mathit{t}}$	99th perc. of ${\mathit{PV}}_{\mathit{t}}$
		as a % of the Value		as a % of $\mathbb{E}\left[{\mathit{PV}}_{\mathit{t}}\right]$	as a % of $\mathbb{E}\left[{\mathit{PV}}_{\mathit{t}}\right]$
		for Ptf. A
0	6.472%	100.01%	1.03%	101.71%	102.44%
5	6.304%	99.09%	1.19%	101.97%	102.73%
10	6.013%	98.07%	1.40%	102.29%	103.16%
15	5.500%	97.07%	1.69%	102.78%	103.86%
20	4.673%	96.32%	2.18%	103.57%	105.13%
25	3.422%	96.31%	3.04%	104.99%	107.14%
30	1.641%	98.01%	4.89%	108.16%	111.53%
35	−0.129%	102.99%	9.85%	116.45%	124.06%
40	−1.920%	112.69%	26.89%	147.46%	168.03%
45	−1.920%	131.86%	127.36%	339.18%	508.78%

quote the numerical assessment of the benefit amounts, portfolio composition and summary statistics of the present value of future benefits for the three portfolios. The values obtained for the several quantities are expressed in a way similar to what was performed in Section 5.2, and they can be compared to the corresponding values obtained for Portfolio E. We note:

• The average survival rate for Portfolios G and H is (almost) the same as for Portfolio E (apart from some rounding in the number of survivors, which must be integer).
• Portfolio G, which has the same class of standard risks, shows a profile of the value of the liabilities that is similar to Portfolio E. Conversely, Portfolio H, which has a reduced class of standard risks, shows a similar dispersion, but a lower expected value of future benefits.
• Portfolio I shows a slightly higher average survival rate, especially at the highest ages (which is due to the lower frailty level for standard risks). From this, it follows a higher expected value of the liabilities, in particular at high ages; conversely, differences in the dispersion are not significant.

Overall, the sensitivity analysis suggests that different rating structures can have an impact in particular on the magnitude of insurer’s liabilities, rather than on its dispersion.

6. Some Remarks to Conclude

This paper is mainly motivated by the need to model differential mortality for life annuities, following the introduction of special rate annuities. The solution adopted in current actuarial practice is pragmatic and straightforward to implement, but is not completely satisfactory, as it is not backed by a rigorous model. The Gompertz-Gamma model that we adopt in this paper is simple, but is convenient, in particular in view of practical applications. We show how it could be implemented to realize a rigorous rating system arranged in risk classes. In any case, it can be adopted for estimating the potential composition of a heterogeneous portfolio.

Further, we investigate the impact on the insurer’s liabilities of the increased portfolio heterogeneity following the introduction of special rate annuities. As is known, higher degrees of heterogeneity imply a higher risk profile for the provider. However, if matched by a larger portfolio size, the risk profile of the insurer can benefit from a portfolio diversification (clearly, if appropriate annuity rates are adopted). Indeed, the higher volatility incurred because of the portfolio heterogeneity is more than compensated by the stronger pooling effect resulting from the larger size. The specific choice of the rating structure seems to have a significant impact on the expected value of insurer’s liabilities, rather than on its risk profile.

Various directions for future research can be conceived. First, we note that adverse-selection could emerge as a result of the rating structure, and its possible impact should be addressed, possibly through a modeling of the demand, which represents a possible topic for future research.

A further aspect that is interesting to investigate is the impact on insurer’s liabilities of an incorrect allocation of risks to the various risk classes. Since the frailty is unobservable and the risk classification is based on observable proxies, a misspecification of the risk class is always possible. This would result in an unfair annuity rate applied to some individuals and then in an increased (or reduced) probability of loss for the insurer. In this regard, the research task concerns in particular the modeling of the incorrect specification of the risk class.

In the paper, we have assumed that insurer’s liabilities are only affected by the volatility caused by random fluctuations in mortality and frailty. However, a major risk for a life annuity provider is the aggregate longevity risk, namely the risk of unanticipated mortality improvements. It is reasonable, in particular, to assume that the several risk groups follow different mortality trends, anyhow correlated (in particular because of the underlying frailty distribution). While the joint modeling of the frailty and the stochastic mortality dynamics is controversial, this is a research topic that should be further developed.