Combining Alphas via Bounded Regression
Abstract
:1. Introduction
2. Bounded Regression
2.1. Notations
2.2. Weighted Regression
2.3. Bounds
2.4. Running a Bounded Regression
2.5. Application to Stock Portfolios
2.5.1. Establishing Trades
2.5.2. Rebalancing Trades
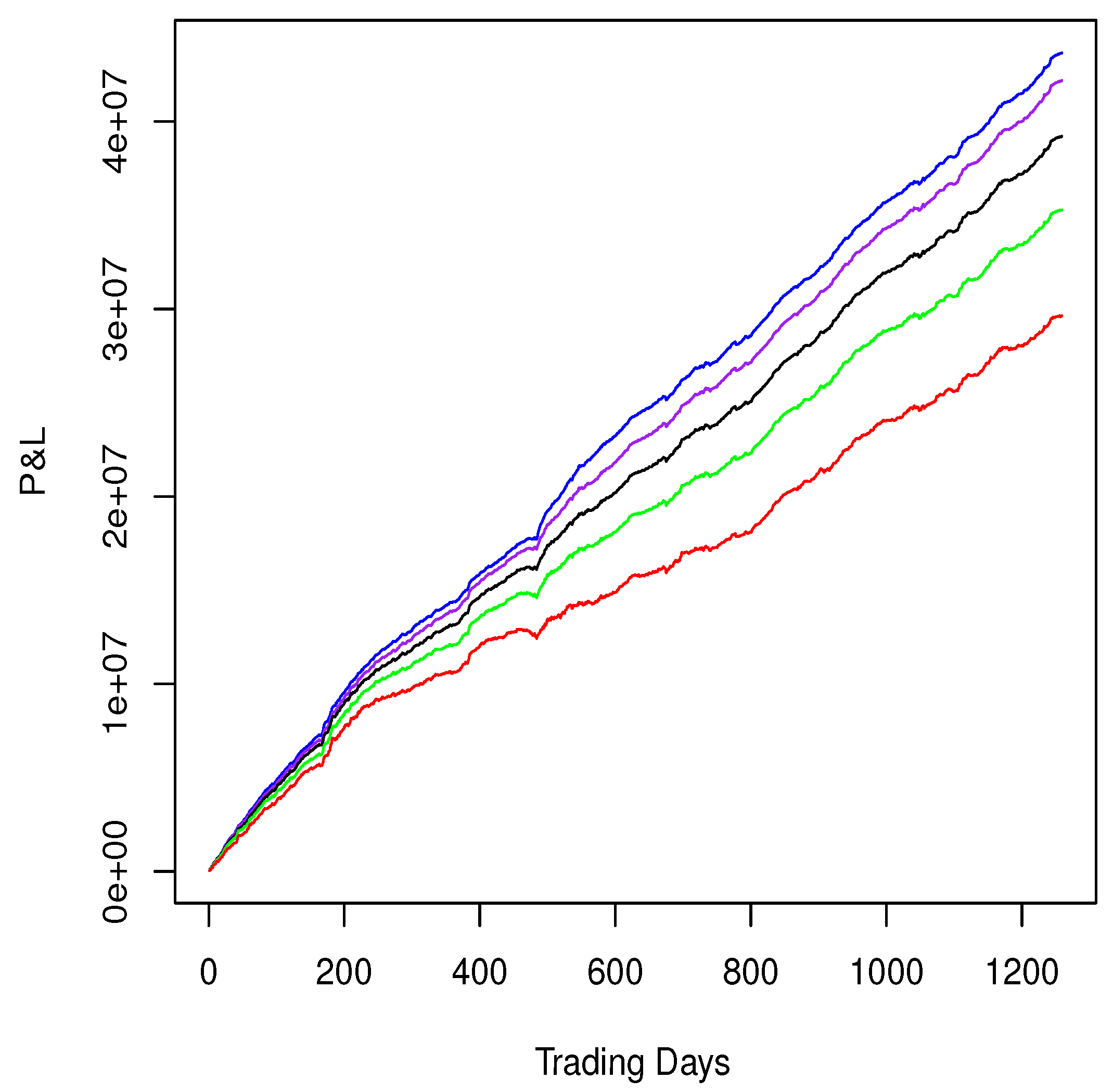
2.5.3. Examples: Intraday Mean Reversion Alphas
| Alpha | ROC | SR | CPS |
|---|---|---|---|
| Regression: Intercept only | 33.59% | 5.59 | 1.38 |
| Regression: BICS sectors | 39.28% | 7.05 | 1.61 |
| Regression: BICS industries | 42.66% | 8.19 | 1.75 |
| Regression: BICS sub-industries | 45.25% | 9.22 | 1.84 |
| Regression: 4 style factors plus BICS sub-industries | 46.60% | 9.85 | 1.90 |
| Alpha | ROC | SR | CPS |
|---|---|---|---|
| Regression: Intercept only | 29.66% | 7.36 | 1.25 |
| Regression: BICS sectors | 35.32% | 9.89 | 1.48 |
| Regression: BICS industries | 39.25% | 12.00 | 1.65 |
| Regression: BICS sub-industries | 42.23% | 14.13 | 1.75 |
| Regression: 4 style factors plus BICS sub-industries | 43.70% | 15.54 | 1.82 |
3. Concluding Remarks
Conflicts of Interest
Appendix
A. The R Code
calc.bounded.lm <- function(ret, load, weights, upper, lower, prec = 1e-5)
{
reg <- lm(ret ∼ -1 + load, weights = weights)
x <- weights * residuals(reg)
ret <- ret / sum(abs(x))
repeat{
x <- bounded.lm(ret, load, weights, upper, lower)
if(abs(sum(abs(x)) - 1) < prec)
break
ret <- ret / sum(abs(x))
}
return(x)
}
bounded.lm <- function(ret, load, weights, upper, lower, tol = 1e-6)
{
calc.bounds <- function(z, x)
{
q <- x - z
p <- rep(NA, length(x))
pp <- pmin(x, upper)
pm <- pmax(x, lower)
p[q > 0] <- pp[q > 0]
p[q < 0] <- pm[q < 0]
t <- (p - z)/q
t <- min(t, na.rm = T)
z <- z + t * q
return(z)
}
if(!is.matrix(load))
load <- matrix(load, length(load), 1)
n <- nrow(load)
k <- ncol(load)
ret <- matrix(ret, n, 1)
upper <- matrix(upper, n, 1)
lower <- matrix(lower, n, 1)
z <- diag(weights)
w.load <- z %*% load
w.ret <- z %*% ret
J <- rep(T, n)
Jp <- rep(F, n)
Jm <- rep(F, n)
z <- rep(0, n)
repeat{
Jt <- J & !Jp & !Jm
y <- t(w.load[Jt, ]) %*% ret[Jt, ]
if(sum(Jp) > 1)
y <- y + t(load[Jp, ]) %*% upper[Jp, ]
else if(sum(Jp) == 1)
y <- y + upper[Jp, ] * matrix(load[Jp, ], k, 1)
if(sum(Jm) > 1)
y <- y + t(load[Jm, ]) %*% lower[Jm, ]
else if(sum(Jm) == 1)
y <- y + lower[Jm, ] * matrix(load[Jm, ], k, 1)
if(k > 1)
take <- colSums(abs(load[Jt, ])) > 0
else
take <- T
Q <- t(load[Jt, take]) %*% w.load[Jt, take]
Q <- solve(Q)
v <- Q %*% y[take]
xJp <- Jp
xJm <- Jm
x <- w.ret - w.load[, take] %*% v
x[Jp, ] <- upper[Jp, ]
x[Jm, ] <- lower[Jm, ]
z <- calc.bounds(z, x)
Jp <- abs(z - upper) < tol
Jm <- abs(z - lower) < tol
if(all(Jp == xJp) & all(Jm == xJm))
break
}
return(z)
}
B. Disclaimers
References
- Z. Kakushadze. “Factor Models for Alpha Streams.” J. Invest. Strategies 4 (2014): 83–109. [Google Scholar]
- Z. Kakushadze. “Mean-Reversion and Optimization.” J. Asset Manag. 16 (2015): 14–40. [Google Scholar] [CrossRef]
- Z. Kakushadze. “Combining Alpha Streams with Costs.” J. Risk 17 (2015): 57–78. [Google Scholar] [CrossRef]
- T. Schneeweis, R. Spurgin, and D. McCarthy. “Survivor Bias in Commodity Trading Advisor Performance.” J. Futures Markets 16 (1996): 757–772. [Google Scholar] [CrossRef]
- C. Ackerman, R. McEnally, and D. Revenscraft. “The Performance of Hedge Funds: Risk, Return and Incentives.” J. Financ. 54 (1999): 833–874. [Google Scholar] [CrossRef]
- S.J. Brown, W. Goetzmann, and R.G. Ibbotson. “Offshore Hedge Funds: Survival and Performance, 1989–1995.” J. Bus. 72 (1999): 91–117. [Google Scholar] [CrossRef]
- F.R. Edwards, and J. Liew. “Managed Commodity Funds.” J. Futures Markets 19 (1999): 377–411. [Google Scholar] [CrossRef]
- F.R. Edwards, and J. Liew. “Hedge Funds versus Managed Futures as Asset Classes.” J. Deriv. 6 (1999): 45–64. [Google Scholar] [CrossRef]
- W. Fung, and D. Hsieh. “A Primer on Hedge Funds.” J. Empir. Financ. 6 (1999): 309–331. [Google Scholar] [CrossRef]
- B. Liang. “On the Performance of Hedge Funds.” Financ. Anal. J. 55 (1999): 72–85. [Google Scholar] [CrossRef]
- V. Agarwal, and N.Y. Naik. “On Taking the “Alternative” Route: The Risks, Rewards, and Performance Persistence of Hedge Funds.” J. Altern. Invest. 2 (2000): 6–23. [Google Scholar] [CrossRef]
- V. Agarwal, and N.Y. Naik. “Multi-Period Performance Persistence Analysis of Hedge Funds Source.” J. Financ. Quant. Anal. 35 (2000): 327–342. [Google Scholar] [CrossRef]
- W. Fung, and D. Hsieh. “Performance Characteristics of Hedge Funds and Commodity Funds: Natural vs. Spurious Biases.” J. Financ. Quant. Anal. 35 (2000): 291–307. [Google Scholar] [CrossRef]
- B. Liang. “Hedge Funds: The Living and the Dead.” J. Financ. Quant. Anal. 35 (2000): 309–326. [Google Scholar] [CrossRef]
- C.S. Asness, R.J. Krail, and J.M. Liew. “Do Hedge Funds Hedge? ” J. Portf. Manag. 28 (2001): 6–19. [Google Scholar] [CrossRef]
- F.R. Edwards, and M.O. Caglayan. “Hedge Fund and Commodity Fund Investments in Bull and Bear Markets.” J. Portf. Manag. 27 (2001): 97–108. [Google Scholar] [CrossRef]
- W. Fung, and D. Hsieh. “The Risk in Hedge Fund Strategies: Theory and Evidence from Trend Followers.” Rev. Financ. Stud. 14 (2001): 313–341. [Google Scholar] [CrossRef]
- B. Liang. “Hedge Fund Performance: 1990–1999.” Financ. Anal. J. 57 (2001): 11–18. [Google Scholar] [CrossRef]
- A.W. Lo. “Risk Management For Hedge Funds: Introduction and Overview.” Financ. Anal. J. 57 (2001): 16–33. [Google Scholar] [CrossRef]
- C. Brooks, and H.M. Kat. “The Statistical Properties of Hedge Fund Index Returns and Their Implications for Investors.” J. Altern. Invest. 5 (2002): 26–44. [Google Scholar] [CrossRef]
- D.-L. Kao. “Battle for Alphas: Hedge Funds versus Long-Only Portfolios.” Financ. Anal. J. 58 (2002): 16–36. [Google Scholar] [CrossRef]
- G. Amin, and H. Kat. “Stocks, Bonds and Hedge Funds: Not a Free Lunch! ” J. Portf. Manag. 29 (2003): 113–120. [Google Scholar] [CrossRef]
- N. Chan, M. Getmansky, S.M. Haas, and A.W. Lo. “Systemic Risk and Hedge Funds.” In The Risks of Financial Institutions. Edited by M. Carey and R.M. Stulz. Chicago, IL, USA: University of Chicago Press, 2006, Chapter 6; pp. 235–338. [Google Scholar]
- H. Markowitz. “Portfolio selection.” J. Financ. 7 (1952): 77–91. [Google Scholar]
- A. Charnes, and W.W. Cooper. “Programming with linear fractional functionals.” Nav. Res. Logist. Q. 9 (1962): 181–186. [Google Scholar] [CrossRef]
- W.F. Sharpe. “Mutual fund performance.” J. Bus. 39 (1966): 119–138. [Google Scholar] [CrossRef]
- R.C. Merton. “Lifetime portfolio selection under uncertainty: The continuous time case.” Rev. Econ. Stat. 51 (1969): 247–257. [Google Scholar] [CrossRef]
- S. Schaible. “Parameter-free convex equivalent and dual programs of fractional programming problems.” Z. Oper. Res. 18 (1974): 187–196. [Google Scholar] [CrossRef]
- M. Magill, and G. Constantinides. “Portfolio selection with transactions costs.” J. Econ. Theory 13 (1976): 245–263. [Google Scholar] [CrossRef]
- A.F. Perold. “Large-scale portfolio optimization.” Manag. Sci. 30 (1984): 1143–1160. [Google Scholar] [CrossRef]
- M. Davis, and A. Norman. “Portfolio selection with transaction costs.” Math. Oper. Res. 15 (1990): 676–713. [Google Scholar] [CrossRef]
- B. Dumas, and E. Luciano. “An exact solution to a dynamic portfolio choice problem under transaction costs.” J. Financ. 46 (1991): 577–595. [Google Scholar] [CrossRef]
- C.J. Adcock, and N. Meade. “A simple algorithm to incorporate transactions costs in quadratic optimization.” Eur. J. Oper. Res. 79 (1994): 85–94. [Google Scholar] [CrossRef]
- S. Shreve, and H.M. Soner. “Optimal investment and consumption with transaction costs.” Ann. Appl. Probab. 4 (1994): 609–692. [Google Scholar] [CrossRef]
- D. Bienstock. “Computational study of a family of mixed-integer quadratic programming problems.” Math. Program. 74 (1996): 121–140. [Google Scholar] [CrossRef]
- J. Cvitanić, and I. Karatzas. “Hedging and portfolio optimization under transaction costs: A martingale approach.” Math. Financ. 6 (1996): 133–165. [Google Scholar] [CrossRef]
- A. Yoshimoto. “The mean-variance approach to portfolio optimization subject to transaction costs.” J. Oper. Res. Soc. Jpn. 39 (1996): 99–117. [Google Scholar]
- C. Atkinson, S.R. Pliska, and P. Wilmott. “Portfolio management with transaction costs.” Proc. R. Soc. Lond. Ser. A 453 (1997): 551–562. [Google Scholar] [CrossRef]
- D. Bertsimas, C. Darnell, and R. Soucy. “Portfolio construction through mixed-integer programming at Grantham, Mayo, Van Otterloo and Company.” Interfaces 29 (1999): 49–66. [Google Scholar] [CrossRef]
- A. Cadenillas, and S.R. Pliska. “Optimal trading of a security when there are taxes and transaction costs.” Financ. Stoch. 3 (1999): 137–165. [Google Scholar] [CrossRef]
- T.-J. Chang, N. Meade, J.E. Beasley, and Y.M. Sharaiha. “Heuristics for cardinality constrained portfolio optimisation.” Comput. Oper. Res. 27 (2000): 1271–1302. [Google Scholar]
- H. Kellerer, R. Mansini, and M.G. Speranza. “Selecting portfolios with fixed costs and minimum transaction lots.” Ann. Oper. Res. 99 (2000): 287–304. [Google Scholar] [CrossRef]
- R.T. Rockafellar, and S. Uryasev. “Optimization of conditional value-at-risk.” J. Risk 2 (2000): 21–41. [Google Scholar]
- J. Gondzio, and R. Kouwenberg. “High-performance computing for asset-liability management.” Oper. Res. 49 (2001): 879–891. [Google Scholar]
- H. Konno, and A. Wijayanayake. “Portfolio optimization problem under concave transaction costs and minimal transaction unit constraints.” Math. Program. 89 (2001): 233–250. [Google Scholar] [CrossRef]
- S. Mokkhavesa, and C. Atkinson. “Perturbation solution of optimal portfolio theory with transaction costs for any utility function.” IMA J. Manag. Math. 13 (2002): 131–151. [Google Scholar] [CrossRef]
- O.L.V. Costa, and A.C. Paiva. “Robust portfolio selection using linear-matrix inequalities.” J. Econ. Dyn. Control 26 (2002): 889–909. [Google Scholar]
- F. Alizadeh, and D. Goldfarb. “Second-order cone programming.” Math. Program. 95 (2003): 3–51. [Google Scholar] [CrossRef]
- M.J. Best, and J. Hlouskova. “Portfolio selection and transactions costs.” Comput. Optim. Appl. 24 (2003): 95–116. [Google Scholar] [CrossRef]
- K. Janeček, and S. Shreve. “Asymptotic analysis for optimal investment and consumption with transaction costs.” Financ. Stoch. 8 (2004): 181–206. [Google Scholar] [CrossRef]
- M.S. Lobo, M. Fazel, and S. Boyd. “Portfolio optimization with linear and fixed transaction costs.” Ann. Oper. Res. 152 (2007): 341–365. [Google Scholar] [CrossRef]
- R. Zagst, and D. Kalin. “Portfolio optimization under liquidity costs.” Int. J. Pure Appl. Math. 39 (2007): 217–233. [Google Scholar]
- M. Potaptchik, L. Tunçel, and H. Wolkowicz. “Large scale portfolio optimization with piecewise linear transaction costs.” Optim. Methods Softw. 23 (2008): 929–952. [Google Scholar] [CrossRef]
- E. Moro, J. Vicente, L.G. Moyano, A. Gerig, J.D. Farmer, G. Vaglica, F. Lillo, and R.N. Mantegna. “Market impact and trading profile of hidden orders in stock markets.” Phys. Rev. E 80 (2009): 066102. [Google Scholar] [CrossRef]
- J. Goodman, and D.N. Ostrov. “Balancing small transaction costs with loss of optimal allocation in dynamic stock trading strategies.” SIAM J. Appl. Math. 70 (2010): 1977–1998. [Google Scholar] [CrossRef]
- M. Bichuch. “Asymptotic analysis for optimal investment in finite time with transaction costs.” SIAM J. Financ. Math. 3 (2012): 433–458. [Google Scholar] [CrossRef]
- J.E. Mitchell, and S. Braun. “Rebalancing an investment portfolio in the presence of convex transaction costs, including market impact costs.” Optim. Methods Softw. 28 (2013): 523–542. [Google Scholar] [CrossRef]
- H. Soner, and N. Touzi. “Homogenization and asymptotics for small transaction costs.” SIAM J. Control Optim. 51 (2013): 2893–2921. [Google Scholar] [CrossRef]
- Z. Kakushadze, and J.K.-S. Liew. “Is It Possible to OD on Alpha? ” J. Altern. Invest. 18 (2015): 39–49. [Google Scholar] [CrossRef]
- Z. Kakushadze. “4-Factor Model for Overnight Returns.” Wilmott Mag. 2015 (2015): 56–62. [Google Scholar] [CrossRef]
- Z. Kakushadze. “Russian-Doll Risk Models.” J. Asset Manag. 16 (2015): 170–185. [Google Scholar] [CrossRef]
- Z. Kakushadze. “A Spectral Model of Turnover Reduction.” Econometrics 3 (2015): 577–589. [Google Scholar] [CrossRef]
- 1Here “alpha”, following the common trader lingo, generally means any reasonable “expected return” that one may wish to trade on and is not necessarily the same as the “academic” alpha. In practice, often, the detailed information about how alphas are constructed may not be available, e.g., the only data available could be the position data, so “alpha” then is a set of instructions to achieve certain stock holdings by some times
- 2For a partial list of hedge fund literature, see, e.g., [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23] and the references therein. For a partial list of portfolio optimization and related literature, see, e.g., [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58] and the references therein.
- 3One approach to rectify this is to add a turnover-based factor to the loadings matrix [1].
- 4For a recent discussion, see [59].
- 5Actually, this assumes that there are no N/Asin any of the alpha time series. If some or all alpha time series contain N/As in a non-uniform manner and the correlation matrix is computed by omitting such pair-wise N/As, then the resulting correlation matrix may have negative eigenvalues that are not zeros distorted by computational rounding.
- 6Here, the turnover (over a given period, e.g., daily turnover) is defined as the ratio of total dollars (long plus short) traded by the alpha labeled by i over the corresponding total dollar holdings (long plus short).
- 7By capacity for a given alpha, we mean the value of the investment level for which the P&L is maximized (considering nonlinear effects of impact).
- 8Since the regression we consider here is weighted with the regression weights , this already controls exposure to alpha volatility, so imposing bounds based on volatility would make a difference only if one wishes to further suppress volatile alphas.
- 9The regression limit of optimization essentially amounts to the limit , , , where is the specific (idiosyncratic) risk in the factor model with the factor loadings matrix identified with the regression loadings matrix (and the factor covariance matrix becomes immaterial in the regression limit); see [2] for details.
- 10This is the case if the columns of are comprised of the first K principal components of SCM corresponding to its positive eigenvalues. However, as mentioned above, here, we keep the loadings matrix general.
- 11Various generalizations are possible, some more straightforward than others.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kakushadze, Z. Combining Alphas via Bounded Regression. Risks 2015, 3, 474-490. https://doi.org/10.3390/risks3040474
Kakushadze Z. Combining Alphas via Bounded Regression. Risks. 2015; 3(4):474-490. https://doi.org/10.3390/risks3040474
Chicago/Turabian StyleKakushadze, Zura. 2015. "Combining Alphas via Bounded Regression" Risks 3, no. 4: 474-490. https://doi.org/10.3390/risks3040474
APA StyleKakushadze, Z. (2015). Combining Alphas via Bounded Regression. Risks, 3(4), 474-490. https://doi.org/10.3390/risks3040474





