Effectively Tackling Reinsurance Problems by Using Evolutionary and Swarm Intelligence Algorithms
Abstract
:1. Introduction
2. Black-Box Optimization Problems in Reinsurance
- is a search space, formed by feasible elements .
- is an objective function , to be optimized (maximized or minimized).
2.1. Problem 1: Excess of Loss Reinsurance
2.2. Problem 2: Stop-Loss Reinsurance
2.3. Problem 3: Threshold Proportional Reinsurance
3. Evolutionary-Based Algorithms
3.1. Evolutionary Algorithms: Evolutionary Programming
- Generate an initial population of μ individuals (solutions). Let t be a counter for the number of generations; set it to . Each individual is taken as a pair of real-valued vectors, , , where ’s are objective variables and ’s are standard deviations forGaussian mutations.
- Evaluate the fitness value for each individual (, ) (using the problem’s objective function).
- Each parent (, ), , then creates a single offspring (, ) as follows (j denotes components of the i-th vector):where denotes a normally distributed one-dimensional random number with mean zero and standard deviation one, and and are random numbers of mean zero and standard deviation one, generated anew for each value of i or j, respectively. The parameters, τ and , are commonly set to and , respectively [19], where n is the length ofthe individuals.
- If , then , and if , then .
- Calculate the fitness values associated with each offspring (,.
- Conduct pairwise comparison over the union of parents and offspring: for each individual, p opponents are chosen uniformly at random from all the parents and offspring. For each comparison, if the individual’s fitness is better than the opponent’s, it receives a “win”.
- Select the μ individuals out of the union of parents and offspring that have the most “wins” to be parents of the next generation.
- Stop if the halting criterion is satisfied, and if not, set and go to Step 3.
3.2. Particle Swarm Optimization
4. Numerical Results

4.1. Results in Problem 1
| Algorithm | Computation time (s) | ||
|---|---|---|---|
| EP | 0.57372111552 | 0.1200013 | 3.5 |
| PSO | 0.5737211153 | 0.1200014 | 2.2 |
4.2. Results in Problem 2
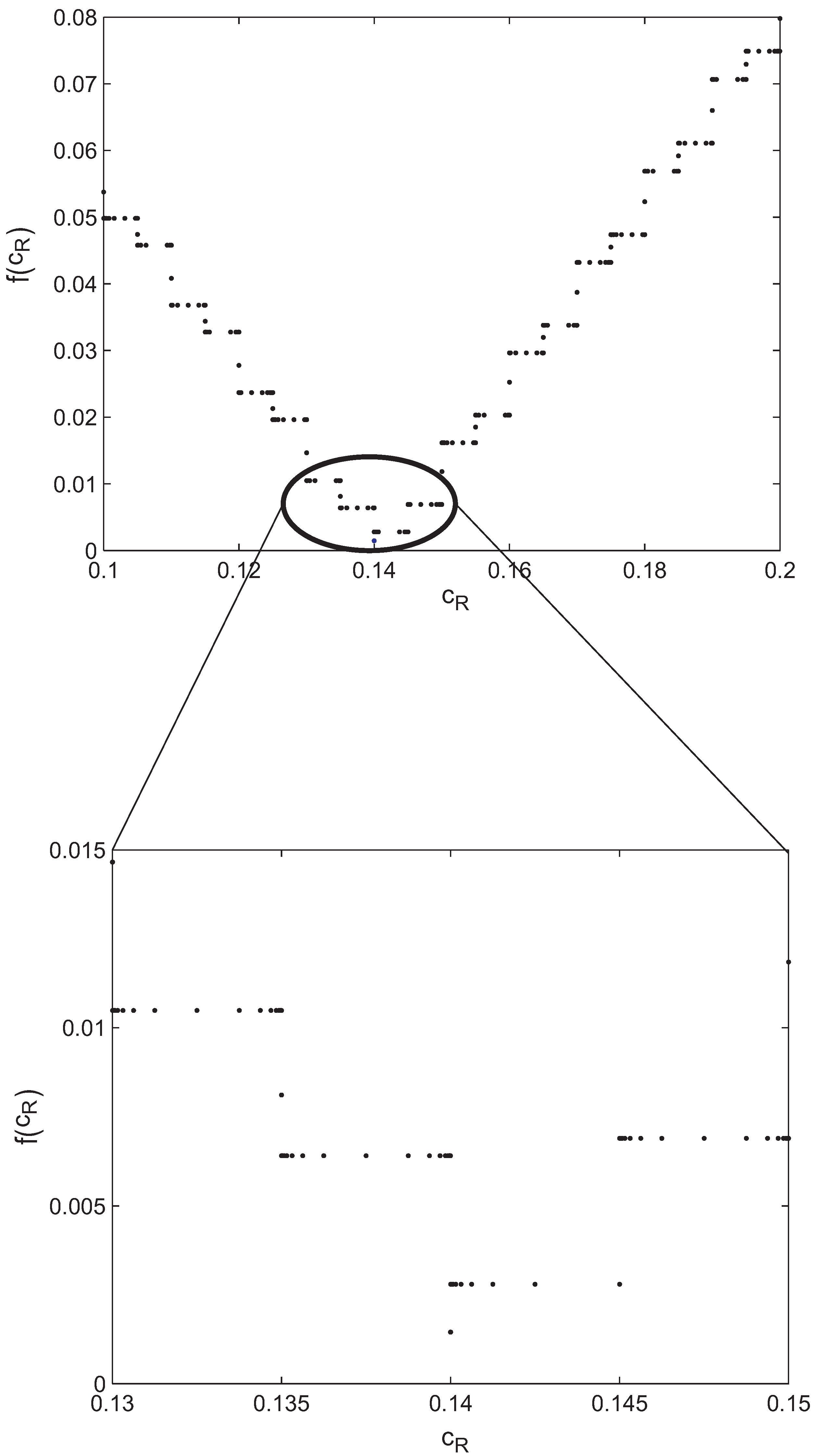
| Algorithm | Computation time (s) | ||
|---|---|---|---|
| EP | 0.0014486748 | 0.14 | 2.9 |
| PSO | 0.0014486748 | 0.14 | 2.4 |
4.3. Results in Problem 3
| Algorithm | b | Computation time (s) | |||
|---|---|---|---|---|---|
| Exponential | |||||
| EP | 0.4980669653 | 1.0 | 0.7596477801 | 3.2688654179 | 9.6 |
| PSO | 0.4980669664 | 1.0 | 0.7596477914 | 3.2688441178 | 8.5 |
| Erlang(2,2) | |||||
| EP | 0.415635 | 1.0 | 0.761572 | 1.9871 | 9.5 |
| PSO | 0.415641 | 1.0 | 0.761564 | 1.9866 | 8.5 |
4.4. Discussion
| Problem # | Optimal solution | Computation time (s) |
|---|---|---|
| Problem 1 | ; | 2100 |
| Problem 2 | ; | 2840 |
| Problem 3 (Exponential) | ; ; | 3700 |
| Problem 3 (Erlang) | ; ; ; | 3850 |
5. Concluding Remarks
Acknowledgments
Conflicts of Interest
References
- R. Kaas, M.J. Goovaerts, J. Dhaene, and M. Denuit. Modern Actuarial Risk Theory: Using R. New York, NY, USA: Springer, 2008. [Google Scholar]
- A. Balbas, B. Balbas, and R. Balbas. “Optimal reinsurance: A risk sharing approach.” Risks 1 (2013): 45–56. [Google Scholar] [CrossRef] [Green Version]
- D. Li, X. Rong, and H. Zhao. “Optimal reinsurance-investment problem for maximizing the product of the insurer’s and the reinsurer’s utilities under a CEV model.” J. Comput. Appl. Math. 255 (2014): 671–683. [Google Scholar] [CrossRef]
- Y. Zhu, L. Zhang, and Y. Zhang. “Optimal reinsurance under the Haezendonck risk measure.” Insur.: Math. Econ. 83 (2013): 1111–1116. [Google Scholar] [CrossRef]
- G. Carlier, and A. Lachapelle. “A numerical approach for a class of risk-sharing problems.” J. Math. Econ. 47 (2011): 1–13. [Google Scholar] [CrossRef]
- M.L. Centeno, and O. Simões. “Optimal reinsurance.” Revista de la Real Academia de Ciencias Exactas Fisicas y Naturales Serie A-Matematicas 103 (2009): 387–404. [Google Scholar] [CrossRef]
- H. Meng, and T.K. Siu. “On optimal reinsurance, dividend and reinvestment strategies.” Econ. Model. 28 (2011): 211–218. [Google Scholar] [CrossRef]
- M. Zhou, and K.C. Yuen. “Optimal reinsurance and dividend for a diffusion model with capital injection: Variance premium principle.” Econ. Model. 29 (2012): 198–207. [Google Scholar] [CrossRef] [Green Version]
- A. Castañer, M.M. Claramunt, and M. Mármol. “Ruin probability and time of ruin with a proportional reinsurance.” TOP J. 20 (2012): 614–638. [Google Scholar] [CrossRef]
- J. Müller, C.A. Shoemaker, and R. Piché. “SO-MI: A surrogate model algorithm for computationally expensive nonlinear mixed-integer black-box global optimization problems.” Comp. Oper. Res. 40 (2013): 1383–1400. [Google Scholar] [CrossRef]
- P. Pos̆ík, W. Huyer, and L. Pál. “A comparison of global search algorithms for continuous black box optimization.” Evol. Comput. 20 (2012): 509–541. [Google Scholar] [CrossRef] [PubMed]
- W.F. Abd-El-Wahed, A.A. Mousa, and M.A. El-Shorbagy. “Integrating particle swarm optimization with genetic algorithms for solving nonlinear optimization problems.” J. Comput. Appl. Math. 235 (2011): 1446–1453. [Google Scholar] [CrossRef]
- M.M. Rytgaard. “Stop-Loss Reinsurance.” In Encyclopedia of Actuarial Science. Edited by J.L. Teugels and B. Sunt. Hoboken, NJ, USA: Wiley, 2011, Volume 3, pp. 1620–1625. [Google Scholar]
- A. Castañer, M.M. Claramunt, and C. Lefèvre. “Survival probabilities in bivariate risk models, with application to reinsurance.” Insur. Math. Econ. 53 (2013): 632–642. [Google Scholar] [CrossRef]
- A. Castañer, M.M. Claramunt, M. Gathy, C. Lefèvre, and M. Mármol. “Ruin problems for a discrete time risk model with non-homogeneous conditions.” Scand. Actuar. J. 2013 (2013): 83–102. [Google Scholar] [CrossRef]
- T. Bäck, and H.P. Schwefel. “An overview of evolutionary algorithms for parameter optimization.” Evol. Comput. 1 (1993): 1–23. [Google Scholar] [CrossRef]
- D.B. Fogel. “An introduction to simulated evolution.” IEEE Trans. Neur. Netw. 5 (1994): 3–14. [Google Scholar] [CrossRef] [PubMed]
- D.E. Goldberg. Genetic Algorithms in Search, Optimization and Machine Learning. Reading, MA, USA: Addison-Wesley, 1989. [Google Scholar]
- X.Y. Yao, Y. Liu, and G. Lin. “Evolutionary programming made faster.” IEEE Trans. Evol. Comput. 3 (1999): 82–102. [Google Scholar] [CrossRef]
- T. Lux, and S. Schornstein. “Genetic learning as an explanation of stylized facts of foreign exchange markets.” J. Math. Econ. 41 (2005): 169–196. [Google Scholar] [CrossRef]
- M.G. Castillo-Tapia, and C. Coello-Coello. “Applications of multi-objective evolutionary algorithms in economics and finance: A survey.” In Proceedings of the IEEE Conference on Evolutionary Computation, September 2007; pp. 532–539.
- F. Scholottmann, and D. Seese. “Financial Applications of Multi-Objective Evolutionary Algorithms: Recent Developments and Future Research Directions.” In Applications of Multi-Objective Evolutionary Algorithms. Edited by C.A. Coello Coello and G.B. Lamont. 2004, pp. 627–652. [Google Scholar]
- A.F. Shapiro. “The merging of neural networks, fuzzy logic, and genetic algorithms.” Insur.: Math. Econ. 31 (2002): 111–115. [Google Scholar] [CrossRef]
- O.A. Cortés, A. Rau-Chaplin, D. Wilson, I. Cook, and J. Gaiser-Porter. “Efficient optimization of reinsurance contracts using discretized PBIL.” In Proceedings of the 2nd International Conference on Data Analytics, Porto, Portugal, September–October 2013; pp. 18–24.
- I. Oesterreicher, A. Mitschele, and F. Schlottmann. “Comparison of multi-objective evolutionary algorithms in optimizing combinations of reinsurance contracts.” In Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation; 2006, pp. 1–9. [Google Scholar]
- C.Y. Lee, and X. Yao. “Evolutionary programming using mutations based on the Levy Probability distribution.” IEEE Trans. Evol. Comput. 8 (2004): 1–13. [Google Scholar] [CrossRef]
- R. Eberhart, and Y. Shi. “Particle swarm optimization: Developments, applications and resources.” In Proceedings of the IEEE Congress on Evolutionary Computation, May 2001; pp. 81–86.
- D.R. Jones, C.D. Perttunen, and B.E. Stuckman. “Lipschitzian optimization without the Lipschitz constant.” J. Optim. Theory Appl. 19 (1993): 157–181. [Google Scholar] [CrossRef]
- M. Denuit. “A new distribution of Poisson-type for the number of claims.” Astin Bull. 27 (1997): 229–242. [Google Scholar] [CrossRef]
- Y. Chi. “Optimal reinsurance under variance related premium principles.” Insur.: Math. Econ. 51 (2012): 310–321. [Google Scholar] [CrossRef]
- D.C. Dickson, and H.R. Waters. “Reinsurance and ruin.” Insur.: Math. Econ. 19 (1996): 61–80. [Google Scholar] [CrossRef]
- P. Gupta, G. Mittal, and M.K. Mehlawat. “Expected value multiobjective portfolio rebalancing model with fuzzy parameters.” Insur.: Math. Econ. 52 (2013): 190–203. [Google Scholar] [CrossRef]
- V.K. Kaishev. “Optimal retention levels, given the joint survival of cedent and reinsurer.” Scand. Actuar. J. 2004 (2004): 401–430. [Google Scholar] [CrossRef]
- M. Laguna, F. Gortázar, M. Gallego, A. Duarte, and R. Martí. “A black-box scatter search for optimization problems with integer variables.” J. Glob. Optim., 2013, in press. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Salcedo-Sanz, S.; Carro-Calvo, L.; Claramunt, M.; Castañer, A.; Mármol, M. Effectively Tackling Reinsurance Problems by Using Evolutionary and Swarm Intelligence Algorithms. Risks 2014, 2, 132-145. https://doi.org/10.3390/risks2020132
Salcedo-Sanz S, Carro-Calvo L, Claramunt M, Castañer A, Mármol M. Effectively Tackling Reinsurance Problems by Using Evolutionary and Swarm Intelligence Algorithms. Risks. 2014; 2(2):132-145. https://doi.org/10.3390/risks2020132
Chicago/Turabian StyleSalcedo-Sanz, Sancho, Leo Carro-Calvo, Mercè Claramunt, Ana Castañer, and Maite Mármol. 2014. "Effectively Tackling Reinsurance Problems by Using Evolutionary and Swarm Intelligence Algorithms" Risks 2, no. 2: 132-145. https://doi.org/10.3390/risks2020132
APA StyleSalcedo-Sanz, S., Carro-Calvo, L., Claramunt, M., Castañer, A., & Mármol, M. (2014). Effectively Tackling Reinsurance Problems by Using Evolutionary and Swarm Intelligence Algorithms. Risks, 2(2), 132-145. https://doi.org/10.3390/risks2020132





