Estimating Policy Impact in a Difference-in-Differences Hazard Model: A Simulation Study

Abstract

This article estimates the impact of a policy change on an event probability in a difference-in-differences hazard model using four estimators. We examine the error distributions of the estimators via a simulation experiment with twelve different scenarios. In four simulation scenarios when all relevant variables are known, three of the four methods yield accurate estimates of the policy impact. In eight simulation scenarios when an individual characteristic is unobservable to the researcher, only one method (nonparametric maximum likelihood) achieves accurate estimates of the policy change. The other three methods (standard Cox, three-step Cox, and linear probability) are severely biased.

1. Introduction

An important question in financial risk management concerns the impact of a policy change on the probability of an event. As an example, a financial institution owned a pool of loans from two neighboring states. Initially, both states had the same legal protection for borrowers, and default rates of loans were similar in both states. At a later date, the first state reduced the legal protection for borrowers while the second state did not. Subsequent to this policy change, the default rates of loans diverged between the two states. The financial institution wants to estimate the impact of the policy change on default rates from this episode, in order to predict changes in default rates in anticipation of additional states making the same policy change.

As a general rule, a researcher will find a statistical model to explain the observed data, estimate the parameters of that model, and use the model and the estimated parameters for prediction. A popular model to study the impact of a policy change applies the “difference-in-differences” (DiD) approach, designed to estimate causal impact in economic data without random assignment. In the standard DiD setting, a regression model is used to calculate the causal impact of an event (“treatment”) on a group of subjects (“treated group”), by comparing the change in the variable of interest in the treated group to the change in the same variable in subjects that did not receive the treatment (“control group”). The difference between these two changes (“differences”) is attributed to the policy change. The underlying assumption is that the treated group and the control group follow a parallel trend over time, and the treatment shifts the trend of the treated group but not the trend of the control group.

The standard DiD model uses a linear regression to estimate the policy impact on the observed variable of interest. When the variable of interest is not observed, as in the case of the probability of loan default, the regression model cannot be implemented. Instead, researchers often turn to the branch of statistics known as “time-to-event” models that study event probability over time. The Cox (1972) proportional hazard is one of the most popular versions, as it allows for observed characteristics as part of the hazard function. To calculate the policy impact, a natural approach is to add a policy change variable in the hazard function, as in Conti et al. (2013) in biostatistics, Mastrobuoni and Pinotti (2015) in criminology, and Feng and Sass (2018) in education. They apply the extension of the Cox (1972) partial likelihood method to time-varying covariates, as in Therneau and Grambsch (2000), to estimate the parameters of the hazard function using pre- and post- policy change data for a treated group and a control group. Along similar lines, Wu and Wen (2022) in demography proposed a three-step estimator based on the standard Cox (1972) partial likelihood method.

A key assumption in the Cox (1972) model is that all relevant variables are observed and included in the hazard function. In the context of loan defaults, it is likely that some borrower characteristics (e.g., financial sophistication, behavioral biases) are not observed by the researcher. It is well known that omitted variables (usually known as “unobserved heterogeneity”) can result in biased parameter estimates of the hazard function. In this article, we propose a nonparametric maximum likelihood estimator of the hazard function that allows for unobserved borrower characteristics as in Heckman and Singer (1984). We use a simulation experiment, which is an extension of the one in Wu and Wen (2022), to demonstrate the unbiasedness of the Cox (1972) estimator in the absence of unobserved heterogeneity, and its bias in the presence of unobserved heterogeneity. In addition, the simulation experiment shows that the nonparametric maximum likelihood estimator is mostly unbiased in the presence of unobserved heterogeneity.

Lastly, the simulation experiment shows that the linear probability estimator, which applies a linear regression after replacing the unobserved default probability with the observed binary outcome as proposed by Angrist and Pischke (2009), is severely biased with or without unobserved heterogeneity. See O’Malley (2021) and Ashin (2021) for implementing this approach in mortgage loan defaults.

This article proceeds as follows. Section 2 describes the regression version and the hazard version of the difference-in-differences (DiD) model, and the four estimators of the policy impact in the hazard version. Section 3 details a more general version of the simulation used in Wu and Wen (2022) that includes additional explanatory variables, non-horizontal baseline hazards, and unobserved heterogeneity. Section 4 gives the simulation result of the four different estimators on the impact of the treatment. Section 5 and Section 6 contain additional discussion and conclusions.

2. The Difference-in-Differences Hazard Model

2.1. The Difference-in-Differences Regression Model

To understand the difference-in-differences hazard model, it is useful to start with the standard difference-in-differences (DiD) setting, where a linear regression is used to calculate the causal impact of an event (“treatment”) on a group of subjects (“treated group”), by comparing the change in the variable of interest in the treated group to the change in the same variable in subjects that did not receive the treatment (“control group”). The underlying assumption is that the treated group and the control group follow a parallel trend over time, and the treatment shifts the trend of the treated group but not the trend of the control group.

In a classic study, Card and Kreuger (1994) estimated the impact of a change in the minimum wage on labor employment in New Jersey, by comparing the employment in New Jersey before and after the minimum wage change, to the employment in Pennsylvania over the same time periods. The assumption is that, absent the change in minimum wage, the employment growth in New Jersey would parallel the employment growth in Pennsylvania, as they are neighboring states subject to similar macroeconomic conditions as well as local conditions (such as weather). Therefore, the differential employment growth in New Jersey around the minimum wage change, over and above the employment growth in Pennsylvania, is attributed to the impact of the minimum wage change in New Jersey.

In the most basic form, the DiD model can be represented in the following linear regression:

$$y_{it}={\beta }_0+{\beta }_1 T_t+{\beta }_2 G_i+{\beta }_3 \left(T_t\times G_i\right)+{\epsilon }_{it}$$

(1)

In Card and Kreuger (1994), the index i represents a “group” (i.e., New Jersey or Pennsylvania) and the index t represents time. The explanatory variable $T_t$ is the treatment timing variable, which is 0 for the periods before the minimum wage change in New Jersey, and 1 for the periods after the minimum wage change. The indicator variable $G_i$ is set to be 1 for the treated group (i.e., New Jersey), and 0 for the control group (i.e., Pennsylvania). The dependent variable, $y_{it}$, is the employment in group i at time t. The treatment effect is captured by the regression coefficient ${\beta }_3$, which is the change in the dependent variable in the treatment group after the treatment is applied. In empirical applications, Equation (1) is generalized to include additional control variables for observed group characteristics in the form of vector $X_i$ with coefficient vector $\gamma$.

$$y_{it}={\beta }_0+{\beta }_1 T_t+{\beta }_2 G_i+{\beta }_3 \left(T_t\times G_i\right)+X_i^{\prime }\gamma +{\epsilon }_{it}$$

(2)

The error term, ${\epsilon }_{it}$, is assumed to be orthogonal to all the other variables in (2). For simplicity, we will refer to this as the “DiD regression” model.

2.2. The Difference-in-Differences Hazard Model

In the context of loan defaults, the variable of interest is the probability of default, which is not directly observed. Instead, we can only observe a binary outcome: “default” or “no default”. In statistics, hazard models are often used to study the probability of events over time. An example of the use of hazard models to study loan defaults is Deng et al. (2000). In this article, we use the highly popular Cox (1972) proportional hazard model with the following specification to capture the policy impact:

$$h\left(t|i\right)=\lambda \left(t\right)exp\left(x_{1i}{\beta }_1+x_{2i}{\beta }_2+G_i{\beta }_3+G_i\times d_{ti}{\beta }_4+u_i\right)$$

(3)

For simplicity, we will refer to Equation (3) as the “DiD hazard” model. Here, $h\left(t\right|i)$ is the hazard function for subject i at time t, where t = 0 denotes the start of the observation time for subject i. A subject could be the issuer of a defaultable bond in a credit risk study. Here $h\left(t\right|i)$ is the probability of borrower i defaulting at time t, conditional on not having defaulted previously. $\lambda \left(t\right)$ is the baseline hazard common for all borrowers; the assumption that the baseline hazard is the same for the treated group and the control group is the analog of the “parallel trend” assumption in the DiD regression setup. The baseline hazard is shifted up or down by a number of variables specific to each subject i. For simplicity of illustration, we use two explanatory variables (“covariates”) $x_{1i}$ and $x_{2i}$ that are time-invariant observable characteristics of borrower i; for example, these could be a borrower’s credit score and the loan-to-value ratio.

To examine the impact of a policy change (“treatment”) on a group of borrowers (“treated group”), the covariate $G_i$ is an indicator variable which is set to 1 for the affected loans in the treated group and set to 0 for the unaffected loans in the “control” group. For each loan i, the treatment timing variable, $d_{ti}$, is set to 0 before the policy change, and set to 1 after the policy change. This treatment timing variable in the DiD hazard model, $d_{ti}$, is different from the treatment timing variable in the DiD regression model, $T_t$, in a subtle manner. Suppose there is a policy change in January 2025. In the DiD regression model, the treatment timing variable is 0 before this month, and switches to 1 on and after January 2025. In the DiD hazard model, loans that were initiated in July 2024 will have a treatment timing variable equal to 0 for t = 1 to 6, and 1 for t ≥ 7. Loans initiated in September 2024 will have a treatment timing variable equal to 0 for t = 1 to 4, and 1 for t ≥ 5. This subtle difference arises because “t” is an index for calendar time in the DiD regression model, while “t” is an index for event time in the DiD hazard model. The parameter, ${\beta }_4$, is the key variable of interest, as exp(${\beta }_4$) is the proportional change in the hazard function for the treated group after the treatment is applied.

The DiD hazard model in Equation (3) is a generalization of the models in Mastrobuoni and Pinotti (2015) in criminology, Feng and Sass (2018) in education, and Wu and Wen (2022) in demography. All of these researchers assume the absence of unobserved heterogeneity, $u_i$ in Equation (3). Our rationale for the inclusion of $u_i$ is that the researcher is unlikely to observe all individual characteristics relevant in the hazard function. In the case of loan defaults, omitted variables could be behavioral biases or prior default history of borrowers that are not available to the researcher. We refer to the x variables as “observed heterogeneity” and the u variable as “unobserved heterogeneity”. This specification is analogous to “frailty” models in the biostatistics literature, where relevant patient characteristics are not observed by the researcher.

2.3. Estimators of the Policy Impact Parameter ${\beta }_4$

In this article, we consider four different estimates of the policy impact parameter, ${\beta }_4$. First, take the natural logarithms of both sides of Equation (3). We will obtain an equation that resembles the DiD regression model:

$$\log \left(h\left(t|i\right)\right)={\alpha }_t+x_{1i}{\beta }_1+x_{2i}{\beta }_2+G_i{\beta }_3+G_i\times d_{ti}{\beta }_4+u_i$$

(4)

where ${\alpha }_t=\mathrm{l}\mathrm{o}\mathrm{g}\left(\lambda \left(t\right)\right)$ are constants for event month t. If we observe the dependent variable, $\log \left(h\left(t|i\right)\right)$, we can run the DiD regression model, treating $u_i$ as the (unobserved) error term, to obtain an estimate for ${\beta }_4$. Unfortunately, in the DiD hazard setting, we only observe events occurring in a given observation month t, but not the hazard rate in that month. It is tempting to replace the dependent variable in Equation (4) with “1” when an event is observed, and “0” otherwise. Indeed, this is advocated in Angrist and Pischke (2009), and implemented in O’Malley (2021) and Ashin (2021) for mortgage loans. Wu and Wen (2022) refer to this as the “linear probability” (LinProb) estimator, and demonstrate analytically that the linear probability estimator may not provide an accurate estimate of ${\beta }_4$.

Returning to Equation (3), in the absence of unobserved heterogeneity, previous research has estimated Equation (3) in two ways. Mastrobuoni and Pinotti (2015) and Feng and Sass (2018) use the Cox (1972) partial likelihood estimator extended to time-varying covariates, as in Therneau and Grambsch (2000). We will refer to the estimate of ${\beta }_4$ as the “Cox_TV” estimator of the policy impact.

Wu and Wen (2022) proposed a three-step Cox estimator of ${\beta }_4$. In step 1, estimate the Cox proportional hazard model in (3) using only the data after the treatment is applied, i.e., when $d_{ti}=1$. Since $G_i\times d_{ti}=G_i$, this term is excluded in the Cox estimation and the coefficient of $G_i$ will be the sum (${\beta }_3+{\beta }_4)$. In step 2, estimate the Cox proportional hazard model in (3) using only the data before the treatment is applied, i.e., when $d_{ti}=0$. Since $G_i\times d_{ti}=0$, this term is again excluded from the Cox estimation and the coefficient of $G_i$ will be ${\beta }_3$. In step 3, the estimate of ${\beta }_4$ is the estimated coefficient of $G_i$ in step 1 minus the estimated coefficient of $G_i$ in step 2. Wu and Wen (2022) used a simulation experiment, setting $\lambda \left(t\right)=0.008$ and ${\beta }_4=0.10$, in the absence of unobserved heterogeneity $u_i$, to show that the three-step Cox estimator is unbiased. We will refer to this estimate of ${\beta }_4$ as the “Cox_3S” estimator.

In both Cox_TV and Cox_3S, the Cox partial likelihood method is used to estimate the $\beta$ parameters, while the baseline hazard $\lambda \left(t\right)$ is estimated non-parametrically. This approach assumes that events are recorded in continuous time. Unfortunately, most economic data are recorded at fixed time intervals (typically a month), which implies that $\lambda \left(t\right)$ within each observation month t cannot be identified from the data. It is well known that the application of the Cox partial likelihood to fixed interval data can lead to biased estimates of the $\beta s$ in the hazard function. In this article, we propose a third estimator. To accommodate fixed interval sampling, we will specify $\lambda \left(t\right)$ to be a non-negative step-wise function which is constant within each observation month t, as in Han and Hausman (1990), Sueyoshi (1992), and An and Qi (2012) in the econometrics literature. The steps of $\lambda \left(t\right)$ are treated as nuisance parameters to be estimated jointly with the $\beta$ parameters of the hazard function. To accommodate for unobserved heterogeneity, we will use a discrete distribution to approximate the unknown distribution of $u_i$, following Heckman and Singer (1984). We will estimate the $\beta$ parameters, the steps of the baseline hazard, and the discrete distribution jointly via maximum likelihood. The resulting estimate of ${\beta }_4$ will be known as the nonparametric maximum likelihood estimator (NPMLE).

Detailed implementation of NPMLE and simulations are in Baker and Melino (2000) for a single hazard, and Gaure et al. (2007) and Hsieh (2025) for two competing hazards. We will provide a brief discussion, as follows.

In the absence of unobserved heterogeneity, it is straight forward to write down the log likelihood function of (3), and its maximization over the parameters $\beta$ = (${\beta }_1, {\beta }_2, {\beta }_3, {\beta }_4)$ and $\alpha =({\alpha }_1,\dots ,{\alpha }_T)$ is also straight forward. In the presence of unobserved heterogeneity, NPMLE approximates the unknown distribution of $u_i$ with a discrete distribution consisting of N mass points: ($a_n,p_n:n=1,\dots ,N)$, where the $a_n$ are the locations of mass points with corresponding probabilities $p_n$. The discrete distribution must obey the following four restrictions:

$$a_n>0, p_n>0,\hspace{1em}\hspace{1em}{\sum }_{n=1}^N{p}_n=1,\hspace{1em}\hspace{1em}{\sum }_{n=1}^N{a_{n}p}_n=1$$

(5)

The first three restrictions ensure that we have a valid probability distribution. The fourth restriction is an identification condition, which is needed for the following reason. In Equation (3), we have the same numerical hazard function if we add a constant c > 0 to all the ${\alpha }_t$s and subtract c from all the $a_n$s. The fourth restriction means that, on average, the unobserved heterogeneity does not shift the hazard function. This normalization is frequently used in the “frailty” literature in biostatistics.

The discrete distribution adds 2N parameters to the likelihood function: N locations ($a_{n}s$), N−1 probabilities ($p_{n}s$), plus the number of mass points (N). The NPMLE is found by maximizing the likelihood function with respect to the parameter space $\mathsf{\Gamma }$, which consists of the ${\beta }_i$s and ${\alpha }_{t}s$, plus 2N mass points: $a_{n}s$, $p_{n}s$, and N. Since N is an integer, the maximization problem is non-trivial. The recommended procedure in Heckman and Singer (1984) is to start with N = 1. Maximize the likelihood function with respect to all other parameters. Then increase N to 2. Again maximize the likelihood function with respect to all remaining parameters. Continue with this process of increasing N until we cannot increase the likelihood function. For each N, we carry out the numerical optimization using the maxLik package in R (version 1.5-2.1) as described in Henningsen and Toomet (2011).

A natural concern regards overfitting the discrete distribution with too many mass points, which also arises in cluster analysis. However, unlike cluster analysis, our objective is not to recover the unobserved heterogeneity distribution accurately, but to estimate ${\beta }_4$ accurately, using the discrete distribution to avoid misspecification of the unobserved heterogeneity distribution. Here, we follow the recommendation in Gaure et al. (2007) to stop increasing N when the improvement of the log likelihood is less than 0.01. Simulations in Gaure et al. (2007) and Hsieh (2025) show that this method to select the optimal number of mass points yields the least biased estimators of the $\beta$ parameters in the hazard function over methods that impose a penalty on the number of mass points, such as the Akaike information criterion or the Bayesian/Schwarz information criterion.

3. Simulation Setup

To simulate the occurrence of an event (e.g., default), we generate data from the DiD hazard model:

$$h\left(t|i\right)=exp\left({\alpha }_t+x_{1i}{\beta }_1+x_{2i}{\beta }_2+G_i{\beta }_3+G_i\times d_{ti}{\beta }_4+u_i\right)$$

(6)

This specification expands the simulation in Wu and Wen (2022) in several aspects. First, we add two explanatory variables to control for observed heterogeneity across subjects, as is often performed in empirical studies. The two observed heterogeneity variables, $x_{1i}$ and $x_{2i}$, are generated as bivariate normal with mean 0, variance 1, and correlation −0.2, based on Sueyoshi (1992). In a credit risk study, these observed heterogeneity could be credit scores, loan-to-value ratios, loan amounts, loan rates, etc. The indicator variable, $G_i$, assigns a subject (“loan”) to the treated group or the control group. In a credit risk study of a policy impact on defaults, loans with $G_i$ = 1 belong to the “treated” group; they are the loans affected by the policy change. Loans with $G_i$ = 0 are in the “control” group; they are unaffected by the policy change. $G_i$ is created by drawing from a normal distribution (independent of $x_{1i}$ and $x_{2i}$) with mean 0 and variance 1; if positive, $G_i$ is set to 1, otherwise 0. This procedure yields roughly the same number of loans in the treated group and the control group, as done in Wu and Wen (2022). For each loan, we assume that the policy change occurs sometime between event time t = 6 and t = 12 drawn from a uniform distribution.

Second, there is no obvious theoretical reason to assume a constant baseline hazard, as is the case in Wu and Wen (2022). We use four different baseline hazards for $\lambda \left(t\right)=exp\left({\alpha }_t\right)$: (a) downward sloping, using a Weibull function with shape 1; (b) upward sloping, using a Weibull function with shape 1.5; (c) horizontal, using a constant function, and (d) hump shaped, using a Weibull function with shape 5.0.

Third, we assume that the researcher is not likely to observe all relevant variables in the hazard function. We simulate this phenomenon by adding “random individual effects” or “unobserved heterogeneity” ($u_i$). For each baseline hazard, we perform three versions of the unobserved heterogeneity, $u_i$: (0) none; (n) the exponential of a normal random variable with mean −0.5 and variance 1; (g) gamma random variable with shape 1 and scale 1. Note that the normal and gamma distributions are often used in the frailty literature in biostatistics. This combination results in twelve scenarios, denoted as {0a, 0b, 0c, 0d, na, nb, nc, nd, ga, gb, gc, gd}, where the first letter refers to the heterogeneity distribution (0, n, and g) and the second letter refers to the baseline shapes (a, b, c, and d).

Fourth, while we simulate events occurring in continuous time, we will record events in monthly intervals, as in the case for most economic data. The parameters $\beta =$ (${\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4$) are arbitrarily set to (1.0, 0.5, −0.5, −0.1). These parameter values are within the range of −1.0 to 1.0 used in the simulation experiments in Han and Hausman (1990), Sueyoshi (1992), Baker and Melino (2000), Gaure et al. (2007), An and Qi (2012), and Wu and Wen (2022). Specifically, the key policy change parameter ${\beta }_4=-0.1$ means that the treatment (i.e., policy change) shifts the hazard rate for the treated loans down by exp(−0.1) or roughly 10% downward following the policy change. We follow each loan up to event time t = 24; if a loan defaults at event time $T_i$ < 24, it will have observations in t = 1, …, $T_i$, with a status of “default” at t = $T_i$. If the loan has not experienced the default event by t = 24, it will have observations in t = 1, …, 24 with a status of “censored” at t = 24.

For each of the 12 scenarios, we perform 100 trials. We redraw all random variables in each trial. For each trial, we compute four estimators of ${\beta }_4$, the treatment effect: NMPLE, Cox_TV, Cox_3S, and LinProb.

4. Simulation Results

Our simulation covers two sample sizes of 25,000, and 5000 subjects for the twelve scenarios (three heterogeneity distributions by four baseline hazards). The higher sample size is comparable to the simulations in Wu and Wen (2022) and Gaure et al. (2007). The lower sample size is commonly used in the other simulation studies. Figure 1 displays the error distribution of the four estimators of the policy impact parameter, ${\beta }_4$, for the simulation experiment with 25,000 subjects in the twelve scenarios. In the upper left panel labeled “NMPLE”, the horizontal axis represents the twelve scenarios. The first four scenarios (“0a”, “0b”, “0c”, “0d”) have contain only observed heterogeneity (i.e., $x_{1i} \mathrm{and} x_{2i}$) in the four baselines (upward sloping, downward sloping, horizontal, and humped). The middle four scenarios (“na”, “nb”, “nc”, “nd”) add the normal heterogeneity with the four baselines, and the last four scenarios (“ga”, “gb”, “gc”, “gd”) add the gamma heterogeneity with the four baselines. The “0c” scenario is the version closest to the simulation experiment in Wu and Wen (2022): without unobserved heterogeneity and a horizontal baseline. The vertical color bars represent the error distribution at each scenario (i.e., the estimator of ${\beta }_4$ minus the true value of −0.1). The bottom of the vertical bar is the first quartile, the short horizontal segment is the median, and the top of the vertical bar is the third quartile. Across all twelve scenarios, the NPMLE error bars include the horizontal axis, indicating that 50% of the NMPLE estimates are close to the true parameter.

The upper right panel labeled “Cox_3S” contains the error distribution for the three-step Cox estimator of Wu and Wen (2022). The error bar for the “0c” scenario (i.e., observed heterogeneity and horizontal baseline) confirms the simulation result in Wu and Wen (2022) for a horizontal baseline. In addition, the three other scenarios with observed heterogeneity (“0a”, “0b”, and “0d”) show that the three-step Wu and Wen (2022) estimator performs equally well in upward sloping, downward sloping, and hump shaped baselines. However, the three-step Cox estimator is biased upwards in the remaining eight scenarios with the addition of unobserved heterogeneity.

The lower left panel labeled “Cox_TV” contains the error distribution of the extended Cox estimator using the “coxph” function in the survival package in R (version 3.5-8) by Therneau (2022) applied to the data formatted according to Therneau and Grambsch (2000). This error distribution of this estimator is very similar to that of the three-step Cox estimator.

The lower right panel labeled “LinProb” is the linear probability estimator, using the “lm” function in the base R software (version 4.3.3). This estimator is severely biased upwards in all twelve scenarios.

Figure 2 provides the error distribution of the four estimators in sample size of 5000. The vertical bars are wider, indicating that the estimators are less accurate at the smaller sample size. While the two Cox estimators perform well in the four scenarios absent unobserved heterogeneity, the NPMLE is the more accurate estimator in the eight scenarios with unobserved heterogeneity. The linear probability estimator continues to be severely biased in all twelve scenarios.

5. Discussion

Table 1. Distribution of Estimators in 12 Scenarios for Sample Size of 25,000.

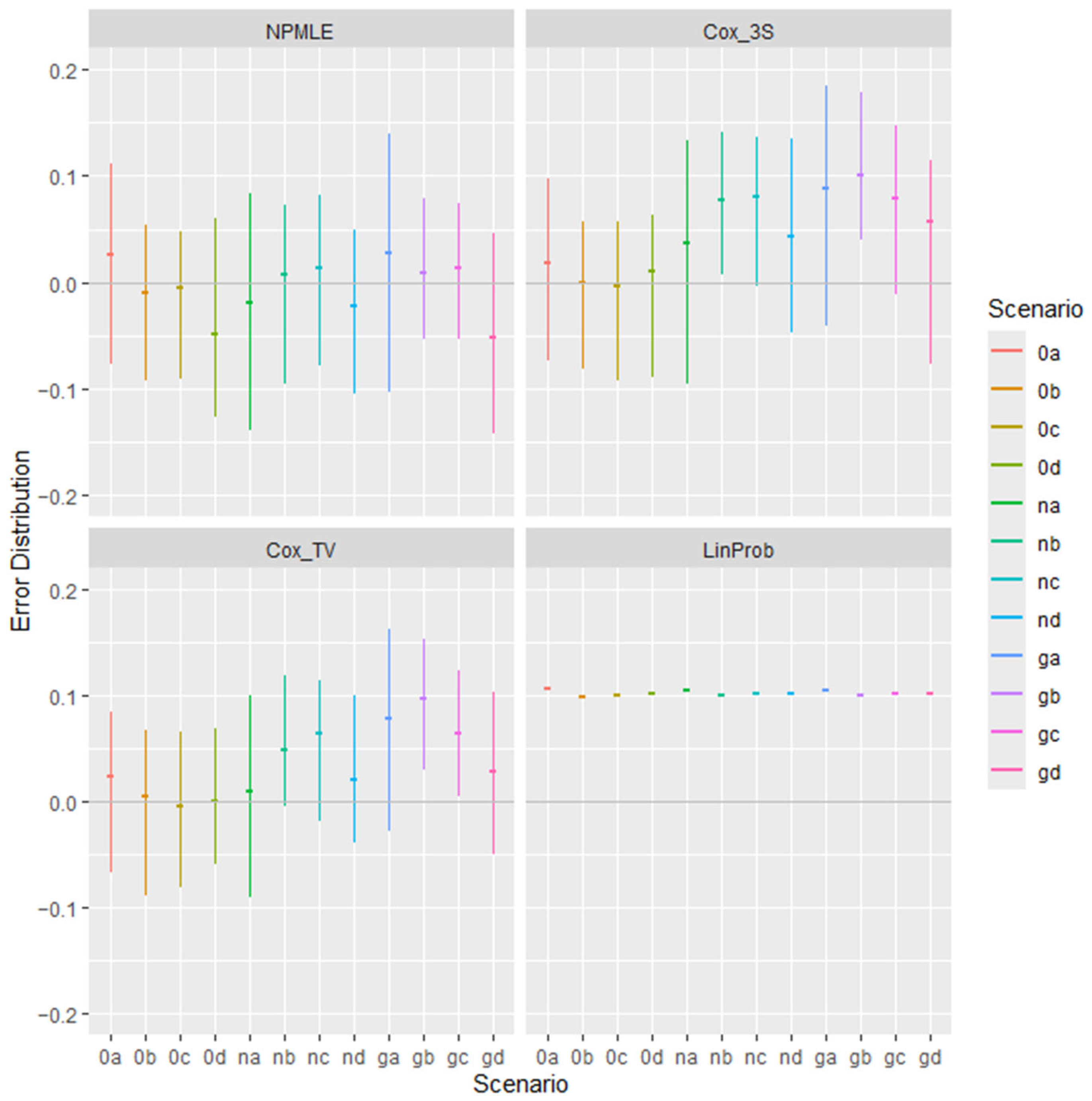
Panel A. Mean Error of Estimators in 100 Trials
Scenario	NPMLE	Cox_3S	Cox_TV	LinProb
0a	0.00414	−0.00914	−0.00862	0.10492
0b	−0.01072	−0.00587	−0.00237	0.09741
0c	−0.00592	−0.00103	0.00071	0.10014
0d	−0.03560	−0.00198	0.00183	0.10064
na	0.00283	0.03994	0.02711	0.10424
nb	−0.01157	0.07143	0.05451	0.09928
nc	0.00585	0.06379	0.05306	0.10091
nd	−0.02241	0.04902	0.03624	0.10134
ga	0.02163	0.06390	0.05120	0.10454
gb	−0.00340	0.09586	0.07646	0.09950
gc	−0.00574	0.06923	0.05134	0.10089
gd	−0.02193	0.05632	0.03678	0.10132
The mean error is the average estimate minus the true parameter (−0.1) in the 100 trials of each of the twelve simulation scenarios. Green denotes the estimator with the lowest absolute mean error in each row.
Panel B. Standard Deviation of Estimators in 100 Trials
Scenario	NPMLE	Cox_3S	Cox_TV	LinProb
0a	0.06954	0.05480	0.05158	0.00063
0b	0.04197	0.04236	0.03891	0.00061
0c	0.05240	0.05354	0.04744	0.00057
0d	0.08727	0.05163	0.04341	0.00072
na	0.08643	0.06542	0.06267	0.00062
nb	0.05970	0.04780	0.04806	0.00059
nc	0.05015	0.05217	0.04375	0.00045
nd	0.08124	0.05798	0.04675	0.00061
ga	0.07356	0.06755	0.06122	0.00062
gb	0.05481	0.05081	0.04701	0.00059
gc	0.05684	0.05138	0.05148	0.00055
gd	0.07883	0.05210	0.03823	0.00053
The standard deviation is the sample standard deviation of the estimator in the 100 trials of each of the twelve simulation scenarios. Green denotes the estimator with the smallest standard deviation in each row.
Panel C. Root Mean Squared Error of Estimators in 100 Trials
Scenario	NPMLE	Cox_3S	Cox_TV	LinProb
0a	0.06931	0.05529	0.05204	0.10492
0b	0.04312	0.04255	0.03878	0.09741
0c	0.05247	0.05328	0.04721	0.10014
0d	0.09385	0.05141	0.04323	0.10064
na	0.08604	0.07637	0.06800	0.10424
nb	0.06052	0.08582	0.07251	0.09928
nc	0.05024	0.08224	0.06863	0.10091
nd	0.08388	0.07571	0.05897	0.10134
ga	0.07632	0.09274	0.07957	0.10454
gb	0.05465	0.10837	0.08963	0.09950
gc	0.05684	0.08606	0.07252	0.10089
gd	0.08145	0.07654	0.05291	0.10132
Root mean square error (RMSE) is the square root of the mean squared estimation error in the 100 trials of each of the twelve scenarios. Green denotes the estimator with the lowest RMSE in each row.

provides numerical information on the distribution of these estimators for the sample size of 25,000. Panel A has the mean errors of the four estimators in 100 trials across the twelve simulated scenarios. Panel B provides the standard deviations of the four estimators, and Panel C has their root mean squared errors (RMSE).

For the linear probability (LinProb) estimator, these panels confirm the graphical information in Figure 1. Basically, the LinProb estimator is unable to pick up useful information from the data. Its bias is typically 100% away from the true parameter value of −0.1, with virtually no deviation around the mean. For the discussion of Panels B and C, we will focus on the remaining three estimators: NPMLE, Cox_3S and Cox_TV.

In terms of estimator bias across all twelve simulated scenarios (see Panel A), the largest bias of the NPMLE (in absolute value) is −0.02241, nearly 23% away from the true parameter value of −0.1. For the two Cox estimators, the largest bias of Cox_3S is 0.09586, almost 100% away from the true parameter, and the largest bias of Cox_TV is 0.05451, close to 55% away from the true parameter. Across the twelve simulated scenarios, NPMLE is the least biased estimator in nine scenarios, including all eight scenarios with unobserved heterogeneity. Cox_TV is the least biased in the remaining three scenarios, all of which exclude unobserved heterogeneity.

In terms of standard deviation, Panel B indicates that the Cox_TV estimator has the lowest standard deviation in nine of twelve simulated scenarios. The Cox_3S estimator has the lowest standard deviation in the remaining three scenarios. NPMLE is never the estimator with the lowest standard deviation across all twelve scenarios. If we use root mean squared error (RMSE) as the metric to weigh bias versus variance, then Panel C tells us that NPMLE has the lowest RMSE in five simulated scenarios with unobserved heterogeneity, and Cox_TV has the lowest RMSE in the remaining seven simulated scenarios.

Table 2. Error Distribution of Estimators in 12 Scenarios for Sample Size of 5000.

Panel A. Mean Error in 100 Trials
Scenario	NPMLE	Cox_3S	Cox_TV	LinProb
0a	0.02510	0.01567	0.01672	0.10520
0b	−0.01995	−0.01315	−0.00993	0.09729
0c	−0.01204	−0.00897	−0.00286	0.10003
0d	−0.05055	−0.00339	0.00181	0.10062
na	−0.02932	0.01975	0.00624	0.10415
nb	−0.00785	0.07007	0.05705	0.09933
nc	0.00691	0.06818	0.05481	0.10092
nd	−0.02222	0.03725	0.02986	0.10128
ga	0.00968	0.07392	0.06150	0.10470
gb	0.00919	0.10213	0.08737	0.09965
gc	0.00547	0.07514	0.06582	0.10107
gd	−0.06225	0.05472	0.02338	0.10113
The mean error is the average estimate minus the true parameter (−0.1) in the 100 trials of each of the twelve simulation scenarios. Green denotes the estimator with the lowest ab-solute mean error in each row.
Panel B. Standard Deviation of Error in 100 Trials
Scenario	NPMLE	Cox_3S	Cox_TV	LinProb
0a	0.15775	0.13639	0.12467	0.00148
0b	0.10634	0.09910	0.09921	0.00152
0c	0.12082	0.12639	0.11766	0.00140
0d	0.17306	0.12399	0.09874	0.00155
na	0.17562	0.16060	0.14456	0.00140
nb	0.12324	0.11617	0.10972	0.00138
nc	0.11187	0.11295	0.10568	0.00110
nd	0.15796	0.13624	0.10838	0.00136
ga	0.17670	0.15347	0.14843	0.00142
gb	0.10789	0.10845	0.10097	0.00134
gc	0.11071	0.11851	0.10296	0.00112
gd	0.17668	0.12664	0.10759	0.00145
The standard deviation is the sample standard deviation of the estimator in the 100 trials of each of the twelve simulation scenarios. Green denotes the estimator with the smallest standard deviation in each row.
Panel C. Root Mean Squared Error in 100 Trials
Scenario	NPMLE	Cox_3S	Cox_TV	LinProb
0a	0.15896	0.13660	0.12517	0.10492
0b	0.10767	0.09948	0.09921	0.09741
0c	0.12081	0.12608	0.11711	0.10014
0d	0.17946	0.12342	0.09827	0.10064
na	0.17719	0.16102	0.14397	0.10424
nb	0.12287	0.13517	0.12317	0.09928
nc	0.11153	0.13145	0.11858	0.10091
nd	0.15873	0.14058	0.11190	0.10134
ga	0.17608	0.16965	0.15998	0.10454
gb	0.10774	0.14858	0.13314	0.09950
gc	0.11029	0.13983	0.12177	0.10089
gd	0.18649	0.13091	0.10957	0.10132
Root mean square error (RMSE) is the square root of the mean squared estimation error in the 100 trials of each of the twelve scenarios. Green denotes the estimator with the lowest RMSE in each row.

provides the distribution of the four estimators for the sample size of 5000. The linear probability (LinProb) estimator remains uninformative, being roughly 100% biased with very low standard deviations. In the remaining three estimators, Panel A indicates that NPMLE is the least biased in six of the eight simulated scenarios in the presence of unobserved heterogeneity, while Cox_TV (Cox_3S) is the least biased in five (one) remaining cases. In terms of standard deviation, Cox_TV has the lowest standard deviation in eleven of the twelve simulated scenarios, and Cox_3S has the lowest standard deviation in the remaining case. It is useful to note that the standard deviations of the estimators in the smaller 5000 sample size are roughly 2.25 times larger than their corresponding standard deviations in the larger 25,000 sample size. This is in line with the prediction from asymptotic theory that the standard deviation of estimators decreases at the rate of the square root of the sample size. In terms of RMSE, Cox_TV has the lowest RMSE among the three estimators in all twelve simulated scenarios, after excluding the severely biased LinProb estimator.

Given these four estimators, how should a researcher proceed? In the first place, we note that the Cox_3S and Cox_TV estimators should be close to each other. The reason is as follows. In the dataset, each loan is represented by two observation periods: pre-treatment and post-treatment. In Cox_3S, the two observation periods are split into two subsamples, and the standard Cox estimator is applied to each subsample separately. Since the treatment dummy, $d_{ti}$, is 0 in the pre-treatment period, the cross-product term $G_i\times d_{ti}$ = 0, so Equation (3), without the unobserved heterogeneity, is reduced to

$$h\left(t|i\right)=\lambda \left(t\right)exp\left(x_{1i}{\beta }_1+x_{2i}{\beta }_2+G_i{\beta }_3\right)$$

(7)

in the pre-treatment subsample. Similarly, the treatment dummy, $d_{ti}$, is 1 in the post-treatment period, the cross-product term $G_i\times d_{ti}$= $G_i$, therefore Equation (3), without the unobserved heterogeneity, is reduced to:

$$h\left(t|i\right)=\lambda \left(t\right)exp\left(x_{1i}{\beta }_1+x_{2i}{\beta }_2+G_i\left({\beta }_3+{\beta }_4\right)\right)$$

(8)

in the post-treatment subsample. The difference between the estimates of the parameter for $G_i$ in the two subsamples is the “three-step” Cox estimator, “Cox_3S”.

In comparison, the Cox (1972) estimator as extended by Therneau and Grambsch (2000) for time-varying covariates, Cox_TV, combines the pre-treatment and post-treatment subsamples into a single dataset. Now Equation (3), without the unobserved heterogeneity, becomes:

$$h\left(t|i\right)=\lambda \left(t\right)exp\left(x_{1i}{\beta }_1+x_{2i}{\beta }_2+G_i{\beta }_3+G_i\times d_{ti}{\beta }_4\right)$$

(9)

In the combined dataset, the cross-term, $G_i\times d_{ti}$, is time-varying; its value is 0 in the pre-treatment subsample and $G_i$ in the post-treatment subsample. When we apply the standard Cox estimator to the combined dataset, the parameter for the cross-product term is the estimate of ${\beta }_4$.

Given that the standard Cox estimator is used to obtain Cox_3S and Cox_TV, the difference between them arises as follows. The Cox_3S estimator allows ${\beta }_1$ and ${\beta }_2$ to be different across the pre- and post-treatment subsamples, while the Cox_TV estimator imposes the restriction that ${\beta }_1$ and ${\beta }_2$ are the same across the two subsamples. Since the assumed model specifies ${\beta }_1$ and ${\beta }_2$ to be unchanged between the pre- and post- treatment periods, the Cox_TV is a more efficient estimator than Cox_3S. On the other hand, if ${\beta }_1$ and ${\beta }_2$ are different between the pre- and post- treatment periods, then Cox_3S may be more robust than Cox_TV.

Another difference between Cox_TV and Cox_3S is that Cox_TV uses the standard Cox estimator available in most statistical software, which provides the estimate of the standard error of ${\beta }_4$. In contrast, Wu and Wen (2022) did not provide an estimate of the standard error of Cox_3S. One suggestion is to favor Cox_TV when the standard error of the estimator is required.

Next, we turn to the use of the NPMLE. Based on the simulation results, this estimator should give the least biased estimate in the presence of unobserved heterogeneity. Since it is not possible to test for the presence of unobserved heterogeneity, one suggestion is to calculate the NPMLE and Cox_TV. If these two estimators are close (e.g., within one standard error of each other), then either one is acceptable. However, if they are very different, then NPMLE is preferred. It would be interesting to compare NPMLE to the Cox_3S/Cox_TV estimates in Conti et al. (2013), Mastrobuoni and Pinotti (2015), Feng and Sass (2018), and Wu and Wen (2022).

Lastly, we turn to the LinProb estimator. Given the severe bias of this estimator in the simulation, we caution its use to estimate the policy impact on event probabilities. It would be interesting to compare NPMLE to the LinProb estimates in O’Malley (2021) and Ashin (2021).

6. Conclusions

Unlike many of the physical sciences, fiancé and economic researchers do not have the luxury of controlled experiments to test our models. Also, unlike medical researchers, we are not able to utilize randomized experiments to test the efficacy of a treatment or policy change. The best we can do is to assume a model for our observed data from a policy change, estimate the parameters of the assumed model, and use the assumed model and estimated parameters to predict the outcomes of a future policy change. The quality of the prediction depends on the correctness of the assumed model and the accuracy of the estimation method. In this article, we study the impact of a policy change on the probability of an event (e.g., loan default) by assuming that the data generating mechanism is a Cox (1972) proportional hazard model, where the policy impact takes place via the parameter associated with a time-varying policy change variable. We focus on the accuracy of four estimators. We use a simulation to confirm a number of known theoretical results about these estimators: (a) when all relevant characters in the hazard function are observed, three estimators (three-step Cox, time-varying Cox, and nonparametric maximum likelihood) are unbiased; (b) when a characteristic in the hazard function is not observed, the nonparametric maximum likelihood estimator is unbiased while the two Cox estimators are typically biased; and (c) the linear probability estimator, which can be thought of as a linearization of the nonlinear hazard function, is severely biased in all simulated scenarios.

We acknowledge that a simulation is not a proof. It is meant to validate that the predictions of asymptotic theory are achievable at some finite sample size. We also caution that the analysis in this article applies to a specific assumed difference-in-differences hazard model. To the extent that we do not know the true data generating mechanism of any set of observed data in economics and finance, it is prudent to try other statistical models that may generate the observed data, and to study the accuracy of the estimators of the parameters of these alternative models via simulation.