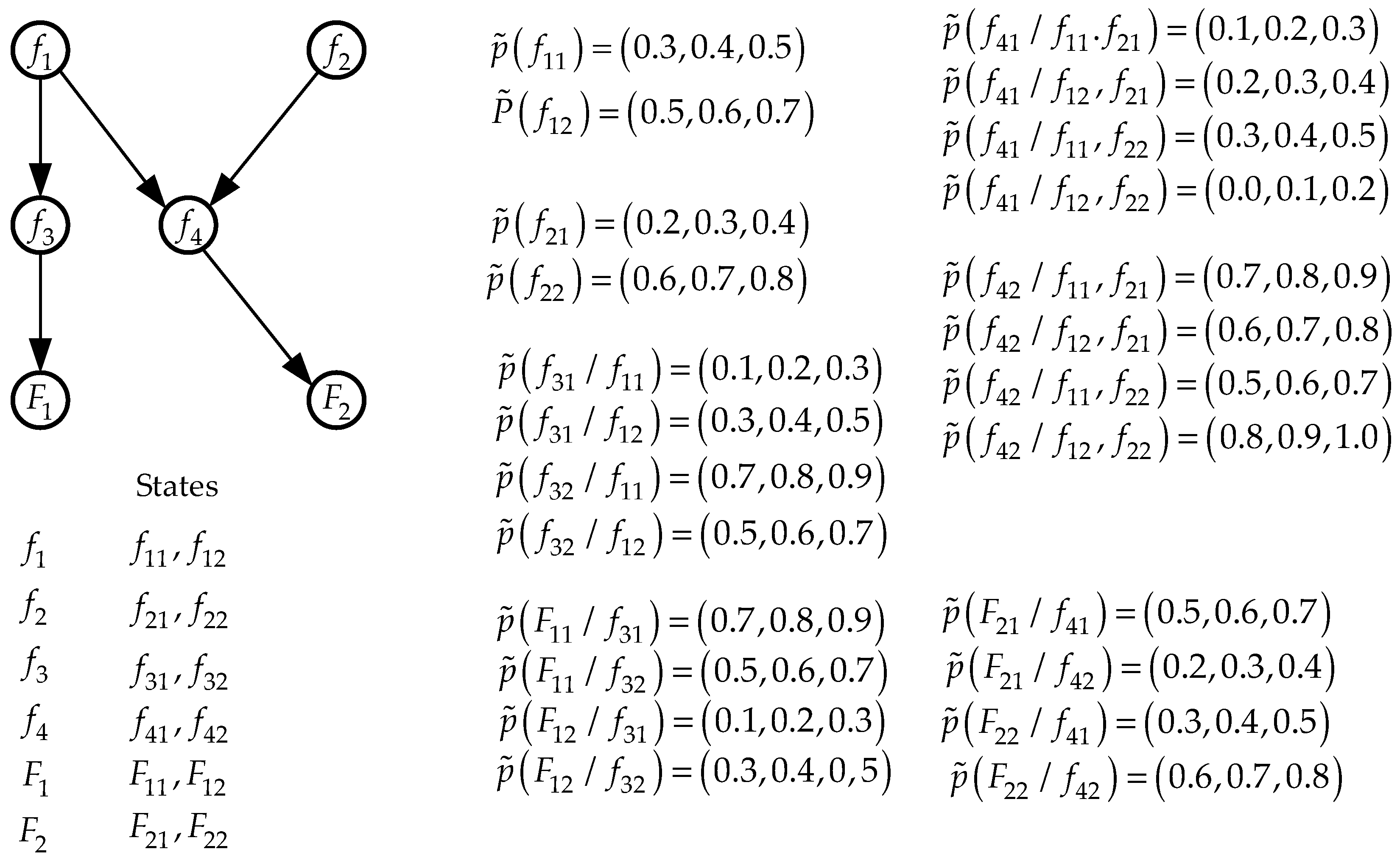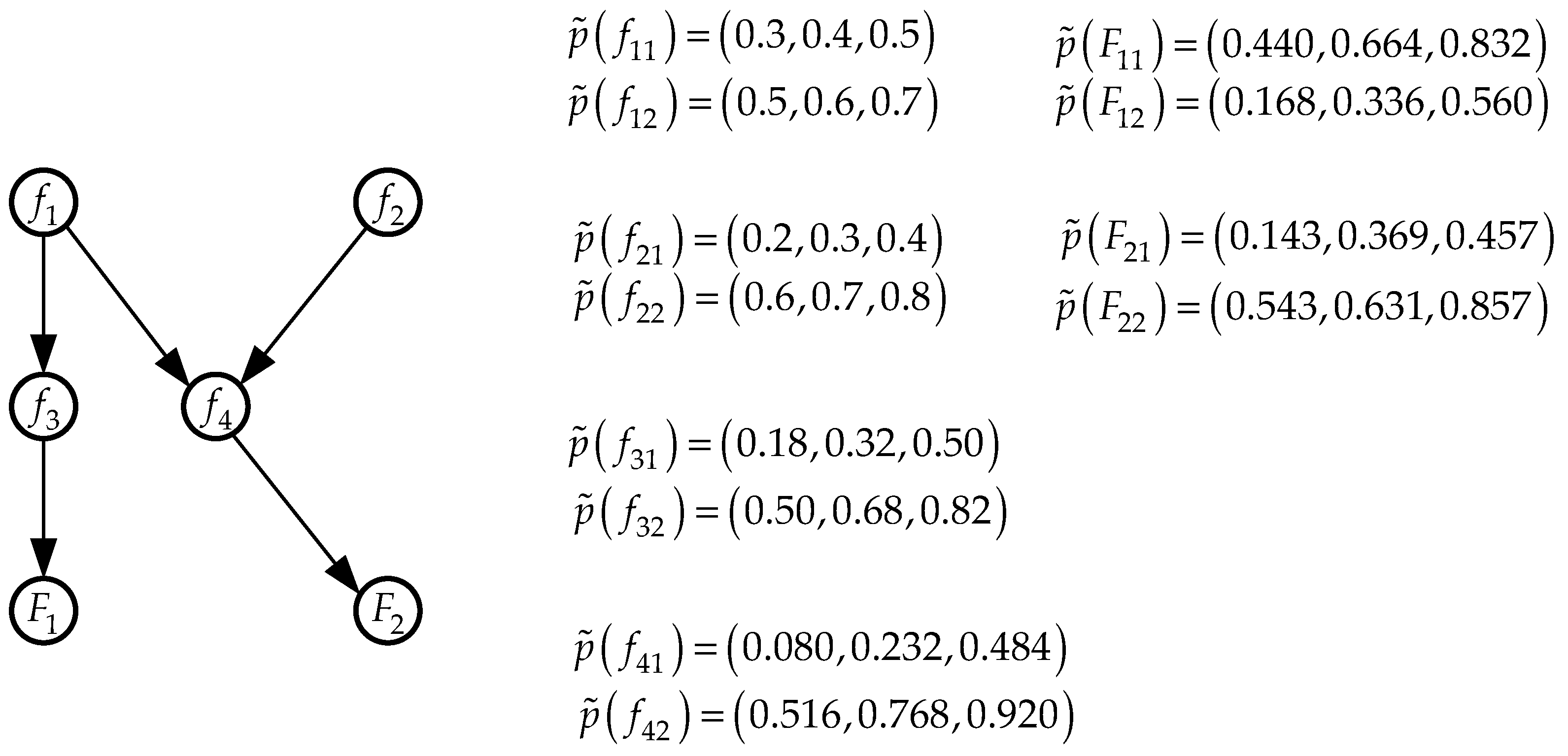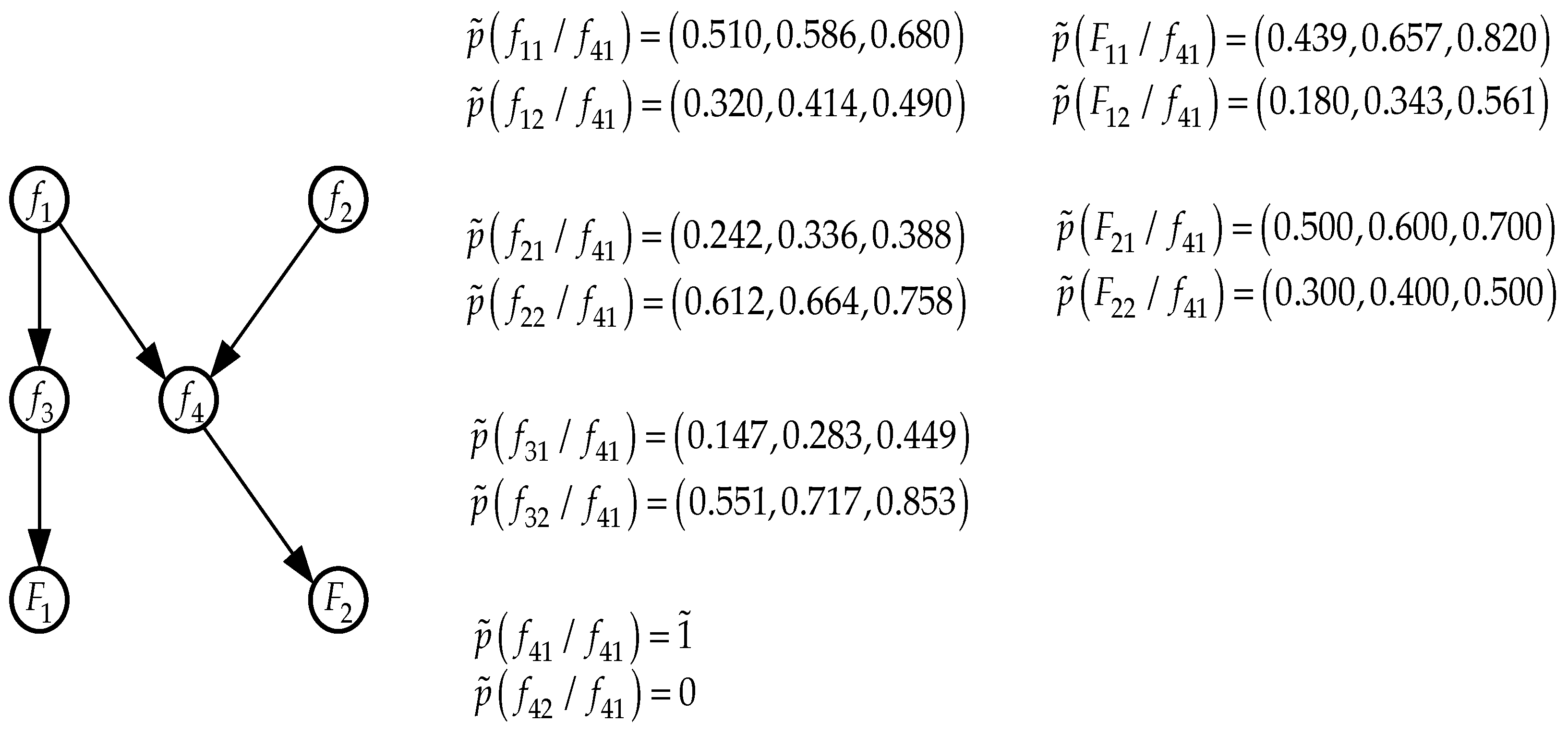1. Introduction
Assigning any environmental risk is a complex computational task. The degree of its complexity is determined by the number of common factors, the states of which determine various adverse consequences. To probabilistically assign an identified risk, two parameters must be assessed: (1) the probabilities of all possible states for each of the major risk factors; (2) adverse consequences associated with all possible combinations of underlying factor.
The probabilities of the states of the main factors are influenced by the states of multiple subfactors. For a compact and visual representation of many subfactors and factors, their states and the probabilities of these states, mutual connections between factors, graphical modeling based on Bayesian networks is widely used. Each node of such a network displays a subfactor or factor, the set of its possible states, and the unconditional or conditional probabilities of the implementation of each of the states. An arc connecting two nodes indicates that the probabilities of states in the node into which the arc enters depend on the states in the node from which the arc originates. In other words, the probabilities of the states in the node in which that the arc enters are conditional probabilities.
Using information about the initial values of unconditional and conditional probabilities in network nodes and information about the network structure, the full conditional probabilities at all network nodes can be calculated. Such a problem is called a probabilistic inference problem.
In problems of assigning environmental risks, there is usually many subfactors and factors with complex connections between them. External risk factors for people’s activities and health include pollution, radiation, noise, long use patterns, work environment, and climate change (
Rojas-Rueda et al. 2021;
Booth et al. 2021;
Prűss-Ustűn et al. 2016). The effects of invasive species include extinction of native plants and animals, reducing biodiversity, competing with native organisms for limited resource, and altering habitats (
Linders et al. 2019). For such situations, Bayesian networks seem to be most suitable for modeling the current situation.
The second problem associated with assigning environmental risks is estimating the required unconditional and conditional probabilities. Since, as a rule, there are no statistical data in such tasks, the necessary assessments are carried out by experts using their knowledge and experience. Unfortunately, the confidence of such estimates may be low. Therefore, it seems logical to introduce some degree of uncertainty for the estimated probability values. These degrees of uncertainty can be introduced in various ways. In this article, we use probabilistic estimates in the form of triangular normal fuzzy numbers.
To solve probabilistic inference problems on Bayesian networks, the probability propagation algorithm is widely used (
Pearl 1988). The essence of this algorithm is to spread special estimates in the direction and against the direction of network arcs and to calculate special values at network nodes. Based on these values, the full conditional probabilities of the states of the subfactor or factor in the corresponding network node are calculated. The values of these overall conditional probabilities are based on all the information accumulated on the network.
The original version of the algorithm is intended for point-based probability estimates. The advantages of the original version of the algorithm are as follows:
- -
complex sequential calculations are not required, as with direct use of the Bayes formula;
- -
based on the initial probabilities, special estimates and values are introduced. These estimates and values are handled using an algorithm that requires only simple and formal calculations.
The disadvantage of the original version of the algorithm is the limited scope of its use, which includes only Bayesian networks with point probability estimates. To expand the scope of the algorithm to specific cases of uncertain data sources, in this paper, we extend the original version of the algorithm to the case of probability estimates, given in the form of triangular normal fuzzy numbers.
The article has the following structure.
Section 2 reviews the literature on environmental risks and widely known approaches to assigning them.
Section 3 presents the theoretical foundations of Bayesian networks.
Section 4 presents the proposed fuzzy version of Pearl’s algorithm.
Section 5 demonstrates the operation of this fuzzy version of the algorithm on a simple Bayesian network.
Section 6 discusses the results obtained.
Section 7 provides a brief overview of the materials and methods used.
Section 8 presents concluding remarks and directions for future research.
2. Literature Review
According to the nature of the manifestation, environmental risks can be classified into the following large groups.
Risks associated with negative impacts on the external environment, which are consequences of humanity’s technogenic activities (
Rhind 2009;
Ansari and Matondkar 2014;
Arihilam and Arihilam 2019). Pollution of the earth’s surface, water, and air due to the use of coal, oil, and gas products as fuel. The widespread uncontrolled use of plastic products leads to the penetration of their waste into the external environment, which leads to extremely negative impacts on ecosystems. Uncontrolled deforestation and the increasing involvement of natural areas in economic activities lead to the degradation of existing ecosystems. Potential accidents at nuclear power plants can lead to catastrophic impacts on the external environment. A consistent increase in the average temperature on the Earth’s surface can lead to global catastrophic consequences: melting glaciers, rising sea levels, and destruction of permafrost.
Internal risks associated with changes in the conditions of existence and interaction of ecosystems at regional levels. These risks are mainly due to the above-mentioned external negative impacts on the external environment. Reducing the areas occupied by plant and animal populations leads to serious negative effects. Interruption of existing food chains leads to additional competition between populations, and the spread of populations into regions less suitable for them, which leads to additional pressure on local populations (
Reynolds and Aldridge 2021;
Kumar and Singh 2020;
Dickey et al. 2018). Huge amounts of money are spent to reduce the negative impacts of invasive populations on native populations. According to media reports, 0.5 trillion dollars has already been spent on a global scale for these purposes.
Environmental risks are characterized by many determining factors and many associated subfactors. In addition, the necessary estimates are highly uncertain. All this requires the use of complex initial models and the use of mathematical methods with the help of which relevant risks can be assigned in the presence of uncertainty and variability in the external environment.
To assign a variety of risks, including environmental risks, two main conceptual approaches can be distinguished.
The first approach is based on the use of fuzzy logic. The essence of this approach is as follows. The input of the fuzzy logical inference system receives the values of the parameters of the controlled system (object). These crisp parameter values are fuzzified. Using a set of fuzzy rules, the fuzzy input values are transformed into an integrated fuzzy output value, which is defuzzified. The resulting crisp value characterizes the current state of the controlled system (object).
The fuzzy logic approach is widely used to control various types of technical systems and devices. If the monitored parameters of the system exceed critical values, this indicates a risk of unintended operation of the system or its damage. This serves as the basis for developing control actions that transfer the system to normal operation mode.
A characteristic feature of fuzzy inference systems is that they can successfully estimate existing or potential adverse consequences for risky situations, but they cannot say anything about the likelihood of these adverse consequences in the future.
The traditional approach to assigning environmental risks is to assess the uncertainties regarding the occurrence of adverse consequences using probabilistic estimates. The problem of such assessments is greatly complicated by the fact that the probabilities of adverse consequences can be influenced by the states of multiple subfactors that are interconnected in a complex way.
If the unconditional and conditional probabilities of the states of all relevant subfactors are known, then, using a suitable method of probabilistic inference, the probabilities of the states of the main factors (which are expressions of adverse consequences) can be calculated for all possible scenarios.
A characteristic feature of this approach is that, on its basis, the likelihood of adverse consequences occurring can be assessed, but not the consequences themselves, therefore the assessment of these adverse consequences is a separate task.
3. Theoretical Foundations of Bayesian Networks
Let two complete groups of random events be given: , . It is assumed that the events are mutually exclusive and exhaustive in these groups. This means that all possible events are included in the group, only one event can occur, and the sum of the probabilities of all events is equal to 1. In the literature, such complete groups of random events are often called variables, the components of which are the relevant random events.
Probabilistic inference is the determination of the probabilities of random events of interest to us based on information about the probabilities of other events associated with them.
Let the following probability distributions be given:
—probability distribution of the variable ;
—joint probability distribution of variables and ;
—distribution of conditional probabilities of a variable depending on the values of the variable .
Expression (1) symbolically represents the potential possibility of mutual transformation of distributions.
From this expression, it follows that knowing the probability distributions and , the probability distribution can be determined. On the other hand, knowing the probability distributions and , the probability distribution can be determined. Such simple procedures of probabilistic inference are called elementary probability calculus.
If there are many variables (groups of random events) with many connections between variables, the problem arises of correct modeling of such initial data. This problem can be solved using a graphical model—a Bayesian network.
Formally, any Bayesian network (alternative names—causal network, belief network) can be defined as a directed acyclic graph , where is a set of nodes; is a set of arcs; and is a set of probability distributions.
Each network node represents a complete group of random events (variable) with which the probability distribution of these events is associated. An arc between nodes indicates that the probabilities of events in the node into which the arc enters depend on events in the node from which the arc emerges. For any Bayesian network, the following concepts can be defined (
Korb and Nicholson 2011):
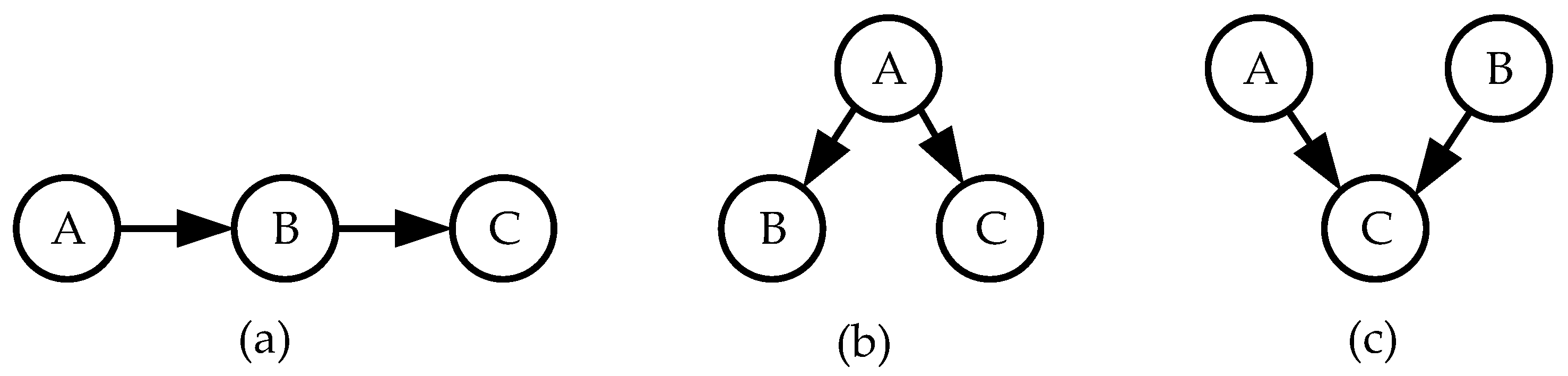
Let us present several provisions related to the syntax of Bayesian networks. The following characteristic types of connections between nodes in any Bayesian network can be defined (see
Figure 1) (
Korb and Nicholson 2011).
In
Figure 1a, nodes
,
,
are connected in a series (chain connection). This type of relationship indicates that the probabilities of events in node
depend on events in node
, and the probabilities of events in node
depend on events in node
. It can be argued that the probabilities of events in node
depend on events in node
, but not directly, but only through events in node
.
Figure 1b shows the divergent type of connections. The probabilities of events at nodes
and
depend on events in node
. In this sense, we can say that nodes
and
have a common cause, node
. Naturally, the concept of a common cause can be extended to several nodes greater than two.
Figure 1c shows the convergent type of connections. The probabilities of events at node
depend on both events at node
and events at node
. Here we can say that variable
has two causes. Naturally, the number of causes may be more than two.
The following terminology is used for Bayesian network structures. If nodes
and
are connected by an arc emanating from node
, then node
is called the direct predecessor (parent) of node
, and node
is called the direct successor (child) of node
.
Figure 1b shows a situation where node
has two children: nodes
and
.
Figure 1c shows the situation when node
has two parents: nodes
and
.
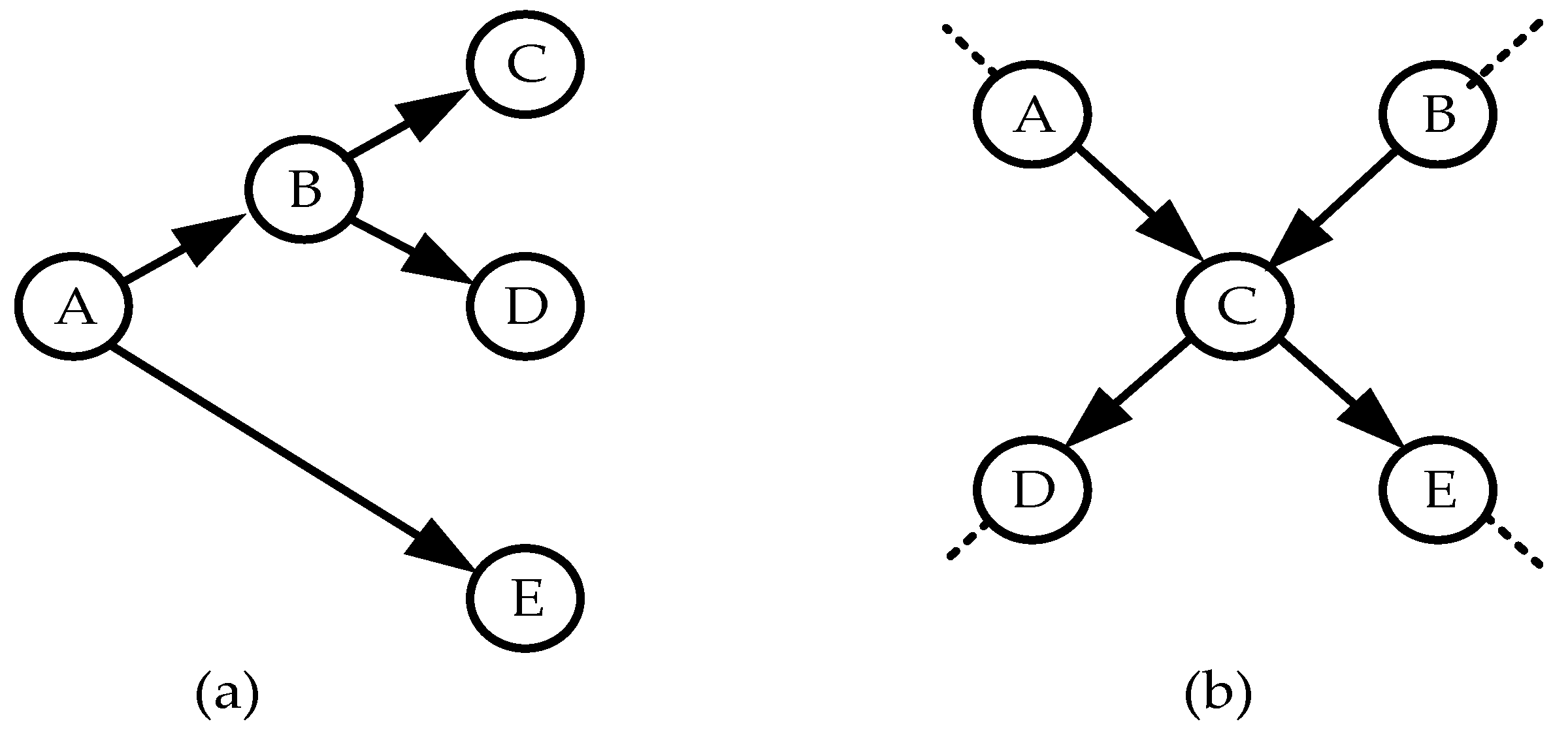
Based on the shapes of their structure, the following types of Bayesian networks can be distinguished (see
Figure 2).
Figure 2a shows an example of a tree-like Bayesian network. The characteristic features of the structures of such networks are: (1) each network’s node has only one parent; (2) there is only one path between the starting node (the root of the tree) and any terminal node (the leaf of the tree).
Figure 2b shows a fragment of a conditional simply connected Bayesian network. In this type of network, some intermediate or terminal node may have more than one parent (nodes
and
are the parents of node
).
Let us present the main provisions of the semantics of Bayesian networks. The probabilities of events represented by the initial nodes of the network are unconditionally independent. Otherwise, the probabilities of these events do not depend on any events in other network nodes. But if an event occurs in a certain parent node, then the events in the nodes that are children of this node become conditionally independent. Thus, if in node
in
Figure 2b some event occurred, then the events in nodes
and
become conditionally independent. If in node
in
Figure 2b some event occurred, then the probabilities of events in node
no longer are dependent on events in node
, but remain dependent on events in node
.
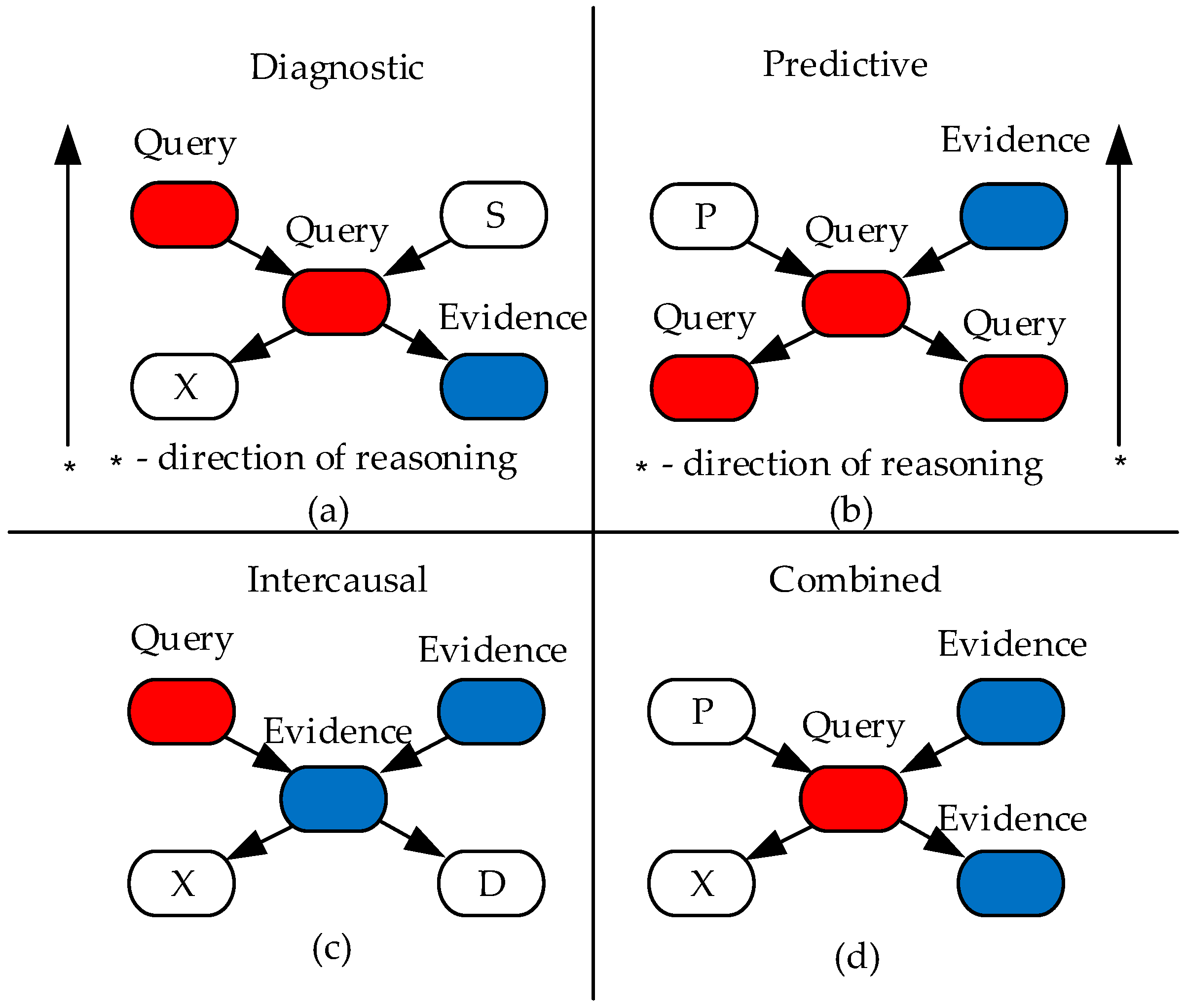
On a fully formed Bayesian network, the probabilistic inference problem of interest to us can be solved (alternatively, the type of reasoning can be implemented). Common types of probabilistic inference (reasoning) are schematically presented in
Figure 3 (
Korb and Nicholson 2011).
Figure 3a presents diagnostic inference. An example of such an inference would be re-estimating the probabilities of the causes of some disease if a patient is diagnosed with that disease. A characteristic feature of this type of inference is that the inference is made in the direction opposite to the direction of the arcs on the network.
Figure 3a presents diagnostic inference.
Figure 3b presents predictive inference. An example of such an inference would be a re-estimation of the probabilities of possible diseases in a patient when certain symptoms appear. A characteristic feature of this type of inference is that the inference is made in the direction of the network arcs.
Intercausal inference (
Figure 3c) is used to re-estimate the probabilities of causes in the corresponding network nodes if some cause event occurred in one of the network nodes. An example of this type of inference would be a re-estimating the probabilities of possible causes of a patient’s illness if one of the causes is confidently established.
Combined inference (
Figure 3d) is a combination of some of the above types of probabilistic inference.
How can probabilistic inference be analytically performed on some Bayesian network? Let some path from the initial to the terminal node of the network include
variables (nodes)
. Then the general probability distribution for this path can be represented as:
Considering that the probabilities of events in an intermediate or terminal node of the network depend only on events in the parent node (nodes) of this node, expression (2) can be presented in the following generalized form:
where
is the set of parent nodes of node
.
It must be kept in mind that the probabilities of events at some intermediate or terminal node on a selected path may be dependent on events in other nodes that are the parents of this node but are not included in the selected path. Therefore, conditional probabilities of events in this node must be assigned over the entire set of its parents. If there are many such nodes with multiple parent nodes on the network, this greatly increases the number of required assignments and calculations.
It follows that direct calculations to determine the general probability distribution on the network using expression (2) are computationally expensive. To simplify and unify the required calculations, the probability propagation algorithm (
Pearl 1988;
Neapolitan 1990,
2004) is widely used. We will present a fuzzy version of this algorithm in the next section.
4. Fuzzy Version of the Pearl’s Algorithm
In a classical version of Pearl’s algorithm, calculations of a priori and posteriori probabilities of events in network nodes are performed by spreading of -estimates and -estimates vectors throughout the network. It is assumed that all initial and calculated probability values in networks nodes are deterministic values and -estimates and -estimates are also uniquely determined.
In essence, the concepts -estimates, -estimates, -values, and -values are artificial entities. They are introduced for the purpose of formally using the Pearl algorithm. These estimates and values are established, calculated distributed according to the rules of the algorithm. The transition from -values and -values to real estimates of probabilities in the relevant nodes of the network is also carried out according to the rules of the algorithm.
In this section we present a fuzzy version of the Pearl’s algorithm. The values of the relevant probabilities are represented in the form of triangular normal fuzzy numbers. The values of estimates distributed over the network are also represented in the form of triangular normal fuzzy numbers. Since, when performing calculation procedures, the values of some estimates and values are set equal to 1, we use a conditional fuzzy value to unify definitions and calculation procedures.
When applying the proposed fuzzy version of this algorithm, the problem of normalizing the resulting fuzzy probability values arises. To normalize the crisp resulting probability values, each of the probability values from the set of calculated probabilities in some network node is simply divided by the sum of these probabilities. Thus, the initial probability values are normalized.
The conditions for normalizing fuzzy probability values are formulated in a more complex way. Let there be a complete group of n random events. The values of these probabilities are given in the form of triangular normal fuzzy numbers , , where is the lower bound of the fuzzy number basis, is the probability value for which , and is the upper bound of the fuzzy number basis.
Let us formulate the conditions under which the values are normalized fuzzy values.
The sum of the central values of m fuzzy numbers must be equal to 1:
If condition (4) is not satisfied for the set of fuzzy probabilities
under consideration, then new values
are calculated using the expression
Let us denote the bases boundaries of fuzzy probability values by , . These intervals are equal in size to the original intervals , but are shifted along the axis according to the changed values .
If conditions (5), (6) are not met for the transformed set of fuzzy probability values
, then the new values of the bases’ boundaries of the relevant fuzzy probability values are recalculated using the expressions (
De Campos et al. 1994)
In a general sense, normalization of fuzzy probabilities means that it is always possible to choose such crisp values of probabilities on the bases of the corresponding fuzzy numbers that will be normalized, that is, their sum is equal to 1. From expressions (8) and (9) it immediately follows that this condition is satisfied for the boundary values of the bases of the relevant fuzzy numbers. From expression (7), it directly follows that this condition is satisfied for the central values of the relevant fuzzy values. It follows from this that, on the bases of the corresponding fuzzy numbers, a set of normalized clear probability values can always be formed. To simplify the problem of selecting the crisp probability values that interest us, the algorithm proposed in (
Uzhga-Rebrov 2019) can be used. Using this algorithm, a set of normalized crisp probability values of interest to us can be selected for cases of three and four fuzzy probability values.
To avoid potential normalization of the original fuzzy probability values, it may be recommended to assign these estimates in the form of consistent fuzzy values (
Uzhga-Rebrov 2016): (1)
; (2) all the bases of the corresponding fuzzy numbers are the same.
There is another method for normalizing fuzzy probability values:
However, this method gives wider intervals for the bases of fuzzy normalized probability values. Therefore, normalization by expressions (7)–(9) seems to be preferable, and it will be used in this work.
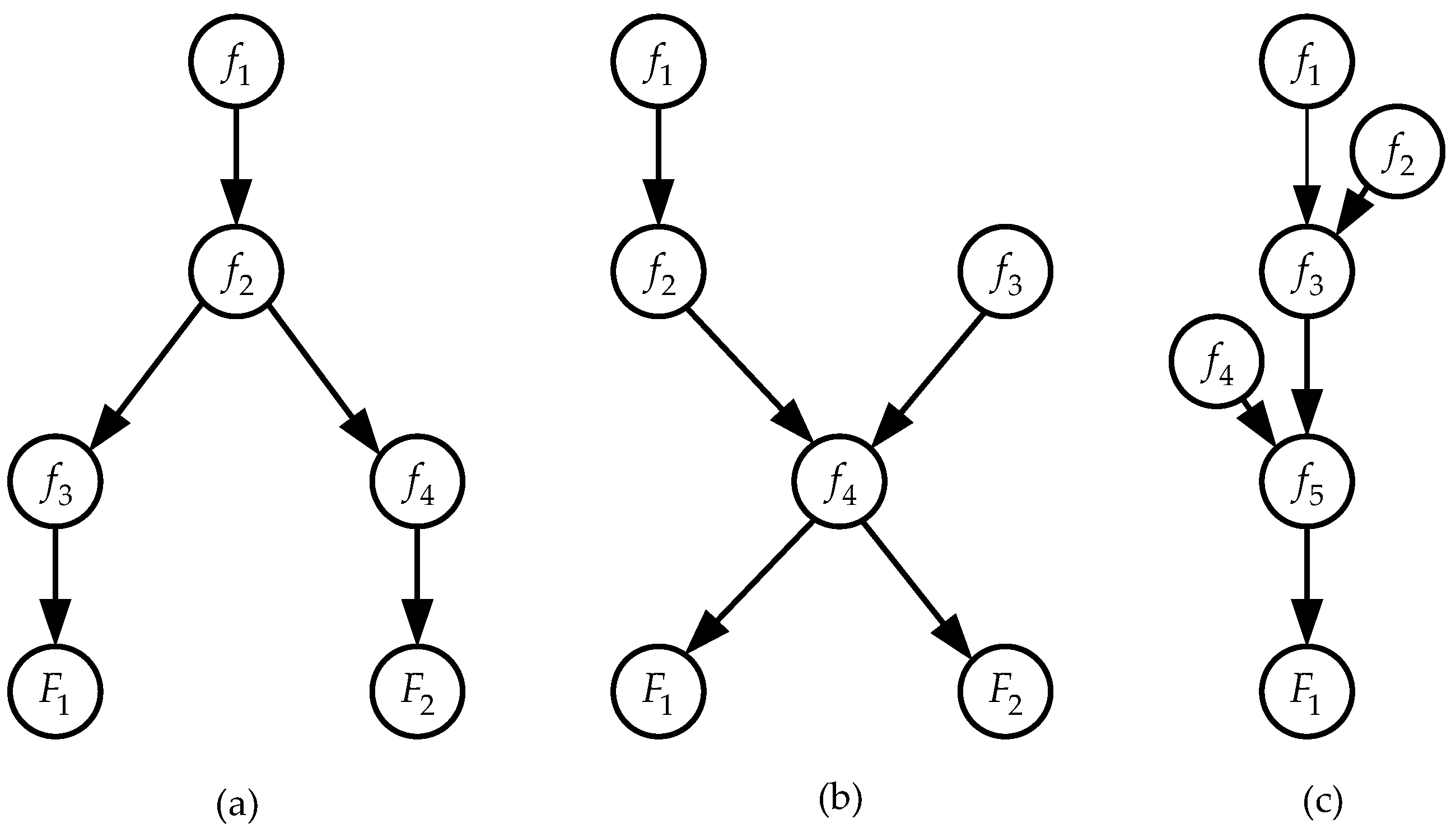
Let us present characteristic types of simply connected Bayesian networks that can represent connections between subfactors and factors in problems of probabilistic risk assignment (
Figure 4).
Figure 4a shows a tree-like Bayesian network. Subfactor
states influence the probabilities of subfactor
states. Subfactor
states influence the probabilities of subfactor
states. In turn, the states of the subfactor
influence the probabilities of the states of the factor
, and the states of the subfactor
influence the probabilities of the states of the factor
. This type of connection between subfactors and factors is quite rare in problems of probabilistic assignment of environmental risks.
Figure 4b shows the convergent-divergent type of connections between subfactors and factors. The probabilities of the subfactor
states depend on the subfactor
states. The probabilities of subfactor
states depend on the states of subfactors
. The probabilities of the states of the factors
and
depend on the states of the subfactor
.
In
Figure 4c, the subfactors
and factor
nodes are connected in a chain manner. Additionally, the probabilities of subfactor
states are influenced by subfactor
states, and the probabilities of subfactor
states are influenced by subfactor
states. The structure of this network may be called a “reverse tree”, but this network is a typical example of a simply connected network. Note that this type of network structure is the most common in problems of probabilistic assignment of environmental risks.
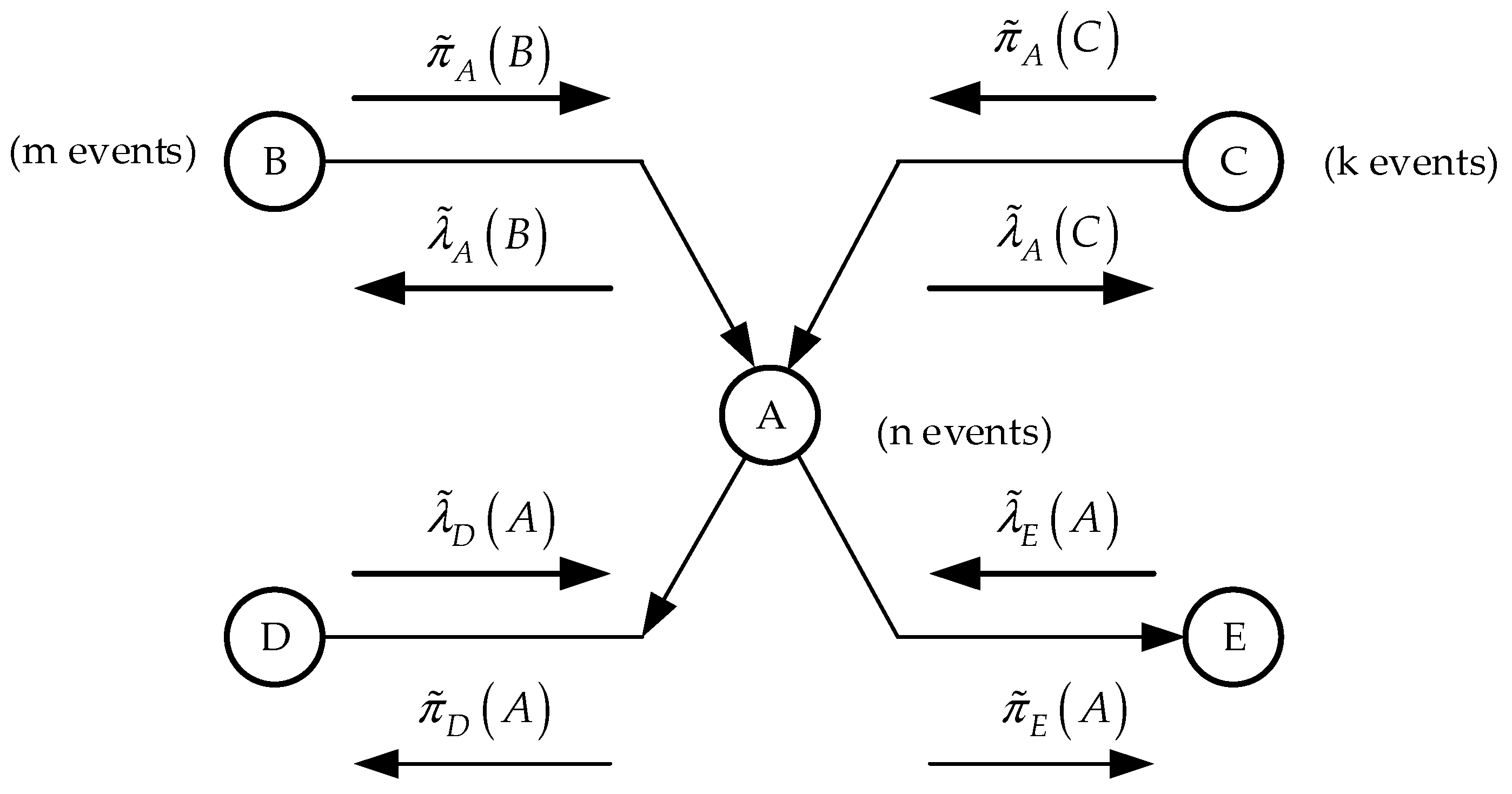
We will present a fuzzy version of Pearl’s probability propagation algorithm on a Bayesian network, taking as a basis the network fragment in
Figure 5.
The choice of this structure is because this structure simultaneously reflects both the convergent and divergent type of connections between nodes. The inference algorithm presented below for this network fragment is applicable to any other types of Bayesian networks. To calculate all fuzzy values of total probabilities in some intermediate network node (node
in
Figure 5), this node must receive a vector of fuzzy
-estimates
from its direct successors (children)—nodes
and
—and vectors of fuzzy
-estimates,
, from their direct predecessors (parents)—nodes
and
. After performing the necessary calculations in node
, vectors of fuzzy
-estimates
can be sent to nodes
and
and a vector of fuzzy
-estimates
to nodes
and
. The necessary calculation expressions will be presented in subsequent definitions. We combine algorithms for propagating fuzzy prior and posterior probabilities over the network. To do this, let
denote the set of nodes in which events occurred.
Definition 1 (fuzzy estimates). Let node , displaying events, have two direct predecessors (parents): node , displaying events, and node , displaying events (see Figure 5). Then for where is the fuzzy conditional probability of an event occurring, subject to the simultaneous occurrence of events and ; is given in Definition 3; is given in Definition 2. If node has only one parent, node , then the value is calculated by the expression: The complete vector of estimates for everyone is called a fuzzy -estimate from to and is denoted by .
Definition 2 (fuzzy -values). Let be a subset of nodes in which events occurred, be a node displaying events, and , be the direct successors (children) of node . Then:
If and is also a terminal node, then If and is also an intermediate or initial node, then If and is an arbitrary network node, then The complete vector of values is called the fuzzy -value and is denoted by .
Definition 3 (fuzzy -estimates). Let be a subset of nodes in which events occurred, be an arbitrary initial or intermediate network node reflecting events, and be a direct successor (child) of node . Then:
If , thenwhere is the current fuzzy value of the probability of the event occurring; —is given in Definition 1. If node has a set of nodes as direct successors (children), , then -estimates are calculated for each node either by expression (15) or by expression (16).
The complete vector of fuzzy estimates for is called a fuzzy -estimate from to and is denoted by .
Definition 4 (fuzzy -values). Let be an arbitrary network node containing events. Then:
If node is an arbitrary intermediate or terminal node of the network, and it has direct predecessors (parents) node , displaying events, and node , having events (see Figure 5), then forwhere is the fuzzy conditional probability of an event occurring, subject to the simultaneous occurrence of events and ; , are given in Definition 3. If node has only one direct predecessor (parent), node , then expression (12a) takes the form If node is the initial node of the network, then for where is the fuzzy value of the unconditional probability of the event occurring. The complete vector of values is called the fuzzy -value and is denoted by .
Definition 5 (fuzzy complete conditional probabilities). Let be a subset of nodes where events occurred and be an arbitrary network node containing events. Then for where the symbol denotes the procedures for normalizing the calculated fuzzy values using expressions (7)–(9). Note that normalization procedures are performed only in those cases when the calculated fuzzy values are not normalized.
Let us present the steps and procedures of the fuzzy probability propagation algorithm on simply connected Bayesian networks. Let all initial unconditional and conditional fuzzy probability values be specified in all network nodes. First, without considering whether certain events occurred or did not occur in individual nodes of the network, a priori fuzzy conditional probabilities are propagated throughout the network. To do this, the following steps of the algorithm are performed.
Step S.1. For -values, -estimates, and -estimates, set the values equal to .
Step S.2. For events in all the initial nodes of the network, -values are set equal to the fuzzy values of the a priori unconditional probabilities of these events: where is the node number and is the event number in the -th node.
If no event occurs in any network node, then the following steps of the algorithm are performed:
Step S.3. New -estimates are sent to all direct successors (children) of the initial nodes according to expression (15).
Step S.4. Fuzzy -values are calculated for events in nodes that are direct successors (children) of the initial nodes using expressions (17) or (18).
Step S.5. Fuzzy a priori conditional probabilities of events in nodes that are direct successors (children) of the initial nodes are calculated using expression (20).
Steps S.3, S.4, and S.5 are sequentially repeated for all nodes in the direction of the network arcs until all terminal nodes are reached.
If an event occurred at some node , or node received new -estimates, or new -estimates provided that , then one of the following procedures is performed:
Procedure A. If an event occurs in node , then:
Step A.1. Set and , .
Step A.2. Set the value according to the expression (13).
Step A.3. Send new -estimates to all direct predecessors (parents) of node according to expression (11) in the case of one parent node and according to expression (10) for the case of multiple parents of node .
Step A.4. Send new -estimates to all direct successors (children) of node using expression (16).
Procedure B. If (no event occurred at node ) and node received new -estimates from all its direct successors (children), then:
Step B.1. Calculate new values using the expression (13).
Step B.2. If new values are known, calculate the value of the vector using expression (20).
Step B.3. Send new -estimates to all direct predecessors (parents) of node using expressions (10) or (11), respectively.
Step B.4. Send new -estimates to all direct successors (children) of node using expression (16).
Procedure C. (no event occurred at node ) and node received new -estimates from all its direct predecessors (parents), then:
Step C.1. Calculate new values using expressions (17) or (18), respectively.
Step C.2. If the value is known, calculate the values of the vector using expression (20).
Step C.3. Send new -estimates to all direct successors (children) of node using expression (15).
Step C.4. If , send new -estimates to all direct predecessors (parents) of node using expressions (10) or (11).
5. Illustrative Example
We will demonstrate the use of a fuzzy version of the Pearl’s probability propagation algorithm on the simple Bayesian network shown in
Figure 6. In this figure, the nodes
display the states of relevant factors and the nodes
display the states of the subfactors associated with them. All assigned probability values for the states of factors and subfactors are consistent fuzzy values. Therefore, by definition, they are normalized fuzzy values.
Note that the requirement of consistency of initial fuzzy probability values is not a mandatory requirement. The consistency condition means that the fuzzy probabilities of the states of factors and subfactors are assigned with the same degrees of uncertainty. If the initial fuzzy probability values are not consistent, a check for normalization conditions (4), (5) is required and, if necessary, these values must be normalized using expressions (6), (8) (9).
Let us carry out the initial steps of assignments, provided that no event has occurred in any network node (the state of the corresponding factor has not changed) .
- S.1.
, , , , , , , , , , , , , , , .
- S.2.
- S.3.
For the node steps S.4, S.5, S.3 can now be performed:
- S.4.
- S.5.
For the calculated fuzzy probability values, the normalization condition (4) is satisfied. Let us check the fulfilment of the normalization condition (5).
The normalization condition (5) is not satisfied. Let us check whether the normalization condition (6) is satisfied.
The normalization condition (6) is not satisfied. Let us transform the boundaries of the bases of fuzzy numbers
,
according to the expressions (8), (9).
- S.3.
Node F1.
- S.4.
- S.5.
The normalization condition (4) for fuzzy estimates
is satisfied, but the normalization conditions (5), (6) are not satisfied. Using expressions (8), (9), we transform the boundaries of the bases of these fuzzy estimates.
Node .
This node is a direct successor (child) of nodes and . Let us perform the necessary steps of the algorithm for this node.
- S.4.
- S.5.
Performing normalization of the obtained values according to the expression (8), (9), we finally have:
- S.3.
Node .
- S.4.
- S.5.
Performing normalization of the obtained fuzzy estimates by expressions (8), (9), we finally have:
The propagation of prior probabilities is complete. Re-estimated probabilities of subfactor and factor states from the Bayesian network in
Figure 6 are shown in
Figure 7.
Let us assume that an event occurred in the node (the state of the factor was realized). Now the sequence of A algorithm procedures can be applied to this node.
Node .
- A.1.
; .
- A.2.
; .
- A.3.
- A.4.
Since the node has received new -estimates, the sequence of B algorithm procedures can be applied to this node.
Node .
- B.1.
- B.2.
(We write the values , in the form of conditional probabilities in order to explicitly show that these values are calculated under the condition of the implementation of the state at the node . These notations are only illustrative, and nothing more. We will use a similar notation system for the resulting fuzzy probabilities of the states of subfactors and factors and further in this section).
Performing normalization of the calculated fuzzy probability values according to expressions (7), (8), (9), we finally have:
Step B.3 fails because the node has no direct predecessors.
- B.4.
Node .
- B.1.
; .
- B.2.
Applying normalization procedures (7)–(9) to the obtained fuzzy values, we have:
Steps B.3 and B.4 fails because the node has no direct predecessors (parents) and no other direct successors (children).
Node .
- C.1.
- C.2.
Normalizing the obtained fuzzy values by expressions (8), (9), we have:
- C.3.
Node .
- C.1.
- C.2.
Normalizing the obtained fuzzy values according by the expressions (8), (9), we have:
Node .
- C.1.
- C.3.
Normalization of the obtained fuzzy probability values is not required.
The reassigned fuzzy probability values are presented in
Figure 8.
If the states of subfactors are realized sequentially in time in other nodes of the network, calculations of the full conditional probabilities are made by analogy, taking as the initial information obtained at the previous stage of the process and the fact of the implementation of a new state of one of the subfactors.
Based on the illustrative example presented above, the following scheme of algorithm actions can be established when propagating fuzzy posterior probabilities. When an event occurs in some intermediate node of the network (a specific state of the corresponding subfactor is realized), changes in the a priori fuzzy probabilities in the nodes of the branch (branches) from this node to the terminal node (to the terminal nodes) are happening due to changes in
-estimates. In
Figure 8 this applies to nodes
and
. Changes in fuzzy prior probabilities in the branch (branches) to the initial node (to the initial nodes) of the network are happening due to changes in
-estimates. In
Figure 8 the change
-estimates occur in the direction of the initial nodes
and
. In the branch (branches) from the initial node (nodes), in which no events occurred, the propagation of the influences of the event are happening due to changes in
-estimates (branch
in
Figure 8).
If an event (realization of a certain state of a specific subfactor) occurs at the initial node of the network, influences in the direction of terminal nodes are spread due to -estimates. These influences propagate in the direction of other initial nodes due to changes in estimates. If there are other branches from other initial nodes, then in these branches the influences spread due to changes in -estimates.