Abstract
Insurance pricing is the process of determining the premiums that policyholders pay in exchange for insurance coverage. In order to estimate premiums, actuaries use statistical based methods, assessing various factors such as the probability of certain events occurring (like accidents or damages), where the Generalized Linear Models (GLMs) are the industry standard method. Traditional GLM approaches face limitations due to non-differentiable loss functions and expansive variable spaces, including both main and interaction terms. In this study, we address the challenge of selecting relevant variables for GLMs used in non-life insurance pricing both for frequency or severity analyses, amidst an increasing volume of data and variables. We propose a novel application of the Genetic Algorithm (GA) to efficiently identify pertinent main and interaction effects in GLMs, even in scenarios with a high variable count and diverse loss functions. Our approach uniquely aligns GLM predictions with those of black box machine learning models, enhancing their interpretability and reliability. Using a publicly available non-life motor data set, we demonstrate the GA’s effectiveness by comparing its selected GLM with a Gradient Boosted Machine (GBM) model. The results show a strong consistency between the main and interaction terms identified by GA for the GLM and those revealed in the GBM analysis, highlighting the potential of our method to refine and improve pricing models in the insurance sector.
1. Introduction
The objective in pricing a non-life insurance product is to establish the premium for the insurance policy. Accurate premiums ensure that individuals pay premiums that reflect their actual level of risk and ensure that the insurance company covers its expected losses and operating expenses. Typically, the final premium offered to the client is determined in two consecutive phases: initially, a technical or pure premium is calculated, representing the expected loss for the specific contract. This phase often employs a substantial set of predictors to assess the contract’s risk. In the second phase, insurance company professionals adjust this technical premium for marketing and sales objectives. This article, however, focuses solely on the first phase of pricing, particularly on identifying the key variables that contribute to a more accurate technical premium.
Over time, depending on the type of non-life insurance product, certain variables have become recognized in actuarial practice as essential for calculating the technical premium. In motor insurance, for example, the driver’s experience and age, along with the car’s characteristics (such as power and safety equipment), are considered fundamental. Conversely, in property insurance, the location of the insured property and the value of the building and its contents are deemed crucial. A robust variable selection technique can challenge these established beliefs and reveal additional, potentially less obvious variables that are significant in modeling the technical premium. In 2019, the European Insurance and Occupational Pensions Authority (EIOPA) presented a study over 200 insurance undertakings and intermediaries from 28 jurisdictions (European Insurance and Occupational Pensions Authority (EIOPA) (2019)). The study reports an increased appetite for better risk assessment with more rating factors, enabled by an increased data availability.
The Generalized Linear Model (GLM) is the predominant model in the insurance industry for setting technical premiums, mainly due the good interpretability of GLMs (Frees et al. 2014; Ohlsson and Johansson 2010). The dominance of the GLM framework remains notable though, given that the predictive quality of most black-box machine learning (ML) models (such as bagging and boosting-based models and deep learning models) typically surpasses the predictive quality of GLMs (Wuthrich and Buser 2021). Moreover, black-box ML models automatically detect complex, non-linear patterns in input variables regarding the outcome of interest (Ke et al. 2017), while this is often a labor-intensive process within the GLM framework Blier-Wong et al. (2020).
In this article, we address this gap in automated discovery on non-linear effects. To this end, we demonstrate a non-standard adaptation of the Genetic Algorithm (GA) to identify relevant main and interaction effects from a given set of variables, strictly within the GLM framework. This approach will also allow us to step away from just using significance as a variable selection criterion and using the predictive ability of the covariate effect instead. Since distinguishing risky clients from less risky clients is of primordial importance for most insurance models, discriminatory measures such as the concordance probability are particularly well tailored to this task. The work of Ponnet et al. (2021) shows the non-trivial adaptation of the widely popular concordance probability to the context of non-life pricing models.
Finally, we also show how the GA approach can be adapted to find a GLM that most closely correlates with the predictions of a given black-box ML model. This development aims to help practitioners to better understand the predictions made by black-box ML models, or to even replace a black-box model by the GLM that resembles it the most from a predictive point of view.
This article is structured as follows: Section 2.1 briefly describes existing methods and related work. Section 3 introduces the GA for variable selection problems. In Section 4, we present two applications in motor insurance. The first application utilizes GA to determine the main effects and interaction effects to be included in the final model. The second application employs GA to identify the GLM that most strongly correlates with a given GBM model, considering only first-order interactions in the GLMs. We conclude the article in Section 5, discussing our results and conclusions.
2. Interaction Term and Variable Selection
2.1. Statistical Interaction
Statistical interaction refers to the presence of non-additive effects between at least two variables of a set of p variables when modeling some function . Hence, in the presence of statistical interaction, a pure additive model for will be extended by adding terms to the former sum such as second-order effects , third-order effects or more. Note that functions and are not constrained to linear forms.
In this article, the function of interest corresponds to , or a transformation hereof, with Y being the outcome variable that we want to predict. Furthermore, we will focus on first-order interactions only, allowing us to construct rich yet interpretable models, as higher-order interactions often lead to a complexity that challenges practical interpretation.
For Generalized Linear Models (GLMs) in particular, the model that will be considered corresponds to
where is the link function, is the intercept, is the main effects of variable i, and is the first-order interaction effect between variables and . Note that in the GLM framework, typically only interaction terms of the type are considered, i.e., multiplicative interaction terms with a linear covariate effect.
Hence, in the context of the GLM framework, variable selection does not just operate on the level of the main effect, but also on the level of the first-order interaction effects. Moreover, since the inclusion of a first-order interaction effect is hard to interpret without the presence both corresponding main effects, a main effect can only be removed from a GLM during the variable selection procedure if no first-order interaction terms of that variable are present in the model. Furthermore, the number of first-order interaction terms that need to be estimated in the function of the number of parameters is equal to . This exponential growth in model parameters with increasing p underscores the need for an effective variable selection method, particularly one adept at identifying relevant interaction effects in high-dimensional settings.
2.2. Related Work on Variable Selection Methods
In this subsection, we review prevalent methods for detecting first-order interaction effects, particularly within the GLM framework used in technical pricing. Moreover, we focus on variable selection methods that allow the user to choose the loss function, allowing users to customize the model to specific use-case requirements.
Existing approaches for detecting statistical interactions can be divided into two classes: Direct Modeling and Performance Comparison Methods.
- Direct Modeling: This class includes methods that model both interaction and main effects directly. Techniques such as tree-based models can split using different predictors at various nodes, thus accommodating non-linear, non-additive terms. Examples include
- Regression trees and Random Forests capable of modeling complex interaction structures (Friedman and Popescu 2008; Ke et al. 2017).
- Generalized Additive Models (GAMs) and their extensions that incorporate interaction terms (Hastie et al. 2009; Wood 2006).
- Performance Comparison Methods: This class involves comparing the performance of models with and without certain interactions (referred to as restricted and unrestricted models). Techniques include
- The all-possible-regression method, where all combinations of main effects and interactions are fitted separately. This becomes computationally intensive for large p (Wood 2006).
- H-statistics using partial dependence plots to assess pairwise interactions (Hastie et al. 2009).
- Feature importance metrics from tree-based models, though these may suffer from issues like collinearity (Lundberg et al. 2020).
- Tree-based extended GAMs () that detect interactions but often have limited loss function choices (Lou et al. 2013).
Within the context of GLMs, the Least Absolute Shrinkage and Selection Operator (LASSO) is a popular method for variable selection. When the number of variables p is manageable, one can fit a full model, including all main effects and interaction terms, and retain non-zero s. However, as p increases, the number of parameters can become too large and computationally impractical. Additionally, LASSO’s loss function, the penalized log-likelihood, is fixed, potentially limiting its utility in diverse scenarios.
2.3. Genetic Algorithm
The Genetic Algorithm (GA) has been a popular method for variable selection for several decades (Broadhurst et al. 1997; Gayou et al. 2008; Stefansson et al. 2020). GA functions as an optimization algorithm over a discrete candidate space, which, in our case, encompasses all possible combinations of main and interaction effects. A distinctive feature of GA, setting it apart from many optimization algorithms like gradient descent, is its independence from the gradient of the loss function. This allows users to freely choose the loss function, offering the flexibility to employ measures such as the area under the Receiver Operating Characteristic curve (ROC-AUC), or a generalization thereof like the concordance probability. These measures are often not directly available for most variable selection methods due to their non-differentiable nature, unless approximations of the AUC, from which gradients can be derived, are used (Mingote et al. 2020).
Additionally, GA can be considered a highly flexible meta-learning algorithm, adaptable to the specific requirements of various applications. In our context, this includes the selection of interaction terms and identifying the GLM that most strongly correlates with the predictions of a black-box ML model. Given these advantages, we have selected GA as our preferred method for variable selection. It is worth noting that other swarming algorithms, like Particle Swarm Optimization (PSO), also present valid alternatives (Qasim and Algamal 2018).
3. Methodology
3.1. GA for Variable Selection
The Genetic Algorithm (GA) is an optimization algorithm inspired by the biological process of evolution. It begins with an initialization step, or initial population, and then iterates through a series of predefined “evolutionary” steps over multiple cycles, or generations. This process continues until convergence or a predetermined number of generations has been reached. With proper tuning, the quality of this model population, as evaluated by a chosen fit criterion, is expected to improve progressively with each generation. The fundamental workings of a standard GA are detailed in Mitchell (1997) and depicted in Figure 1.
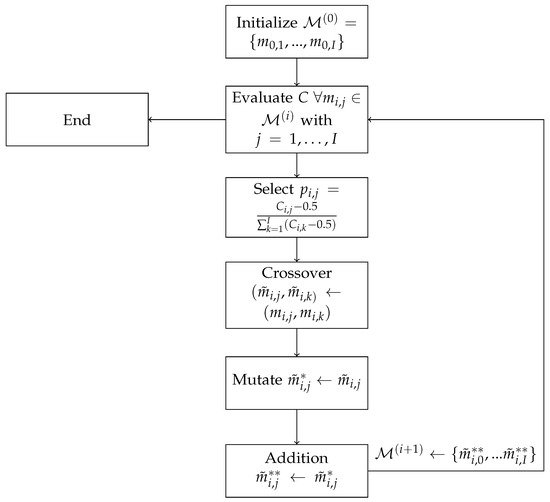
Figure 1.
Overview of the different steps of a vanilla GA, augmented with an addition step.
Within the framework of the GA, main and interaction effects are represented as a bit or ‘0/1’ vector string. The length of this vector corresponds to the total possible number of main and interaction effects. Each bit in the string represents a specific effect; ‘1’ indicates the presence of that effect in the model, while ‘0’ signifies its absence.
We make an important modification of the vanilla GA: any variable that is part of an interaction term is automatically included as a main effect in the model. This inclusion is represented in the bit string notation. This modification is vital for interpretability: interaction terms without their corresponding main effects can be challenging to interpret meaningfully. Given that one of the primary reasons for choosing Generalized Linear Models (GLMs) in technical pricing is their interpretability, ensuring that all necessary main effects are included to contextualize interaction terms becomes a crucial aspect of the model design.
We introduce the basic building blocks of the GA as follows:
- 0
- Initialization step: I different models are generated at random, with the jth model of the ith generation. corresponds to the population of models that will serve as an input to generate the population of models of the first generation (see the selection step below).
- 1
- Evaluation step: Each model of is evaluated against a fitting criterion. In this article, we use the concordance probability C as this criterion Ponnet et al. (2021).
- 2
- Selection step: The estimates of the fitting criterion, concordance probability C in our case, of each model of the current generation are transformed into sampling probabilities. Given that the C of the null model equals 0.5, an intuitive way of constructing these probabilities corresponds to , where and are the sampling probability and C, respectively, of model j of generation i. These sampling probabilities are used to sample a new population of size I of models for generation , randomly (with replacement) from the population of models of generation i.
- 3
- Crossover step: At random, two models are selected (without replacement) from the current population. Next, both strings are aligned, a random position is chosen in the string, beyond which the strings are interchanged between both models. The reasoning is that this operation introduces some randomness to prevent premature convergence of the GA. However, the resulting models are still quite familiar to the pre-crossover models, since a lot of features are still shared over both sets of models. An example of such a crossover step is shown in Figure 2.
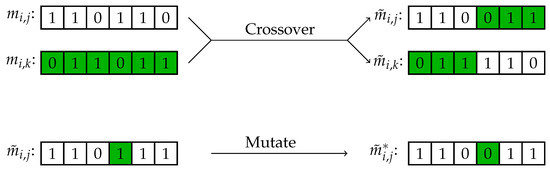 Figure 2. Crossover and mutate steps in GA applied to a variable selection problem with six possible variables. The bits in this example represent whether the main effect of the variable is selected or not in the j-th model () of generation i.
Figure 2. Crossover and mutate steps in GA applied to a variable selection problem with six possible variables. The bits in this example represent whether the main effect of the variable is selected or not in the j-th model () of generation i. - 4
- Mutation step: At random, one digit in the bit string of each model is switched to its opposite value, hence from 0 to 1 or from 1 to 0. See Figure 2 for a visual display of the mutation step.
- 5
- Addition step: For every model, it is verified that every variable involved in at least one interaction term also contains its corresponding main effect. This step is typically not present in most GAs.
In this article, we limited both the number of crossovers per pair of models and the number of mutations per model to one. This restriction aims to prevent excessive randomness from generation to generation, which could otherwise impede the convergence of the GA framework. The crossover and mutation steps are primary sources of variability within the GA that are not directly driven by the fitting criterion. Therefore, it is crucial to control their impact to ensure that progress made over successive generations is not negated by an inopportune crossover split or mutation.
This procedure is repeated for Q generations or until convergence is achieved. Convergence can be determined through various methods, such as monitoring the stabilization of the mean concordance probability across the entire population, or observing the consistency in the number of variables retained in the models of a given generation, among other criteria.
3.2. Concordance Probability C
As mentioned in Section 3, the GA does not require the objective loss function to be differentiable, unlike many other optimization-based algorithms. This desirable feature enables the use of a rank-based loss function. The concordance probability is a popular choice for this class of loss functions (Hastie et al. 2009). In this subsection, we will review some of the desirable properties of the concordance probability, after which we will discuss how this concept can be adapted to the special needs of frequency and severity data of a non-life insurance product, as presented in Ponnet et al. (2021).
The concordance probability C is commonly used for evaluating the quality of a binary classification problem. In this context, represents the binary outcome for observation i, and is the predicted probability of some model with input variables , or . Note that in the case that a GLM was used to generate the predictions, . The concordance probability C then equals the probability that a randomly selected observation with outcome has a lower predicted probability than a randomly selected observation with outcome (Pencina and D’Agostino (2004)), or
In the absence of ties in the predictions, it can be shown that the C corresponds to the Area Under the Receiver Operating Characteristic Curve (ROC-AUC) (Bamber 1975). In the context of frequency data, the definition (2) of C needs to be extended in order to meet its unique data structure (see Ponnet et al. (2021) for more details). In short, three groups of policies are defined: policies that experienced zero events, one event and two events or more, respectively, during the exposure period. The following different definitions of the concordance probability have been proposed:
where and are the observed number of events and input variables, respectively, for observation i during the exposure period . is a tuning parameter representing the maximal difference in exposure between both members of a randomly selected pair. In our application, is set to a small value (0.05), meaning that only pairs are considered of which the exposure is very similar. Informal check indicated that slight changes in value of did not influence results in a significant manner. In the remainder of the article, the above definitions will therefore not be considered as a function depending on . Interestingly, local versions, albeit not considered in this manuscript, of the above set of (global) concordance probabilities are available as well.
In the context of severity data, the following modification of definition (2) has been proposed Ponnet et al. (2021):
where is the predicted claim size of the severity model and the observed claim size. Note that the above definition only considers pairs of observations where the difference in claim size is at least value (with ). Hence, this enables the practitioner to remove claims with a very similar claim cost from the evaluation of the predictive quality of the model, since it is of limited practical importance to distinguish claims with a very similar claim cost from one another. By constructing a (,) plot, the effect of on can be investigated and a good value for can be chosen for the data at hand.
4. Application
In this section, we introduce the motor insurance data set used in this study, followed by an application of optimizing a Generalized Linear Model (GLM) incorporating first-order interaction effects, aimed at maximizing the Concordance Probability in relation to the frequency as the chosen loss function through a genetic algorithm approach. Then, we extend our methodology by adapting the optimization of the Concordance Probability to the predictions derived from a Gradient Boosting Model. Finally, we illustrate a brief application of this optimization strategy to enhance the Concordance Probability with severity considered as the loss function.
4.1. Data Set Description
The data set used in this study, object of the CASdatasets R package, originates from the 2015 pricing game organized by the French Institute of Actuaries on 5 November 2015. It comprises data on hundred thousands Third Party Liability policies for private motor insurance. Each record in the data set corresponds to a distinct policy and includes a set of 12 variables that we have renamed as follows:
- uwYear: called CalYear in the original dataset, it refers to the underwriting/renewal year we are looking at (2009 or 2010);
- gender: called Gender in the original dataset, it refers to the gender (male or female) of the policyholder—assumed to be the insured person;
- carType: called Type in the original dataset, it refers to the type of car the insured person is driving (6 different types are defined);
- carCat: called Category in the original dataset, it refers to category of the car that the policyholder is driving (Small, Medium or Large);
- job: called Occupation in the original dataset, it refers to the type of occupation of the policyholder (5 categories are defined: Employed, Housewife, Retired, Self-employed and Unemployed);
- age: called Age in the original dataset, it refers to the age of the policyholder (not binned a priori—see below);
- group1: called Group1 in the original dataset, it splits the dataset in 20 different groups;
- bm: called Bonus in the original dataset, it refers to the bonus-malus level of the policyholder; this is a scale from −50 to 150 assumed to reflect the driver quality (in terms of past claims);
- nYears: called PolDur in the original dataset, it refers to the duration of the policyholder contract (it goes from 0 for new business to 15);
- carVal: called Value in the original dataset, it provides the value of the car in the range between EUR 1.000 and EUR 49.995 (a priori, this variable is not binned—see below);
- cover: called Adind in the original dataset, it is binary information of whether or not the policyholder is subscribing ancillaries;
- density: called Density in the original dataset, it provides information on the average density where the policyholder is driving (this is a number between 14.37 and 297.38); this variable is a priori not binned (see below).
Therefore, these variables represent various attributes of the policyholder and the insured vehicle and serve as explanatory variables in our analyses.
The continuous variables age, carVal, and density were categorized using a tree-based binning strategy introduced by Menvouta et al. (2022), resulting in ageGrouped, carValGrouped and densityGrouped, respectively. We followed the preprocessing and renaming steps detailed in Ponnet et al. (2021) for consistency.
Figure 3 explores the univariate effects of these twelve explanatory variables on the incidence of bodily injury claims. This analysis was conducted by calculating the ratio of bodily injury claims to the total exposure period for each variable category. The findings indicate that most categories across the variables are sufficiently populated and that none of the explanatory variables have more than six levels. Approximately 75% of the policyholders had full-year insurance coverage, and less than 5% reported at least one claim. Notably, only 0.17% of policyholders filed two or more claims during their policy period. Among those who filed a claim, over a third had costs of EUR 1000 or less, with the highest claim cost nearing EUR 70,000.
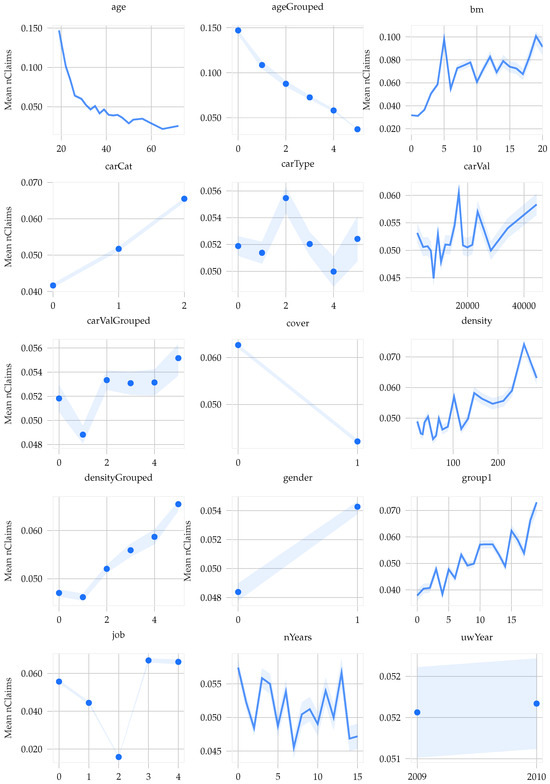
Figure 3.
Univariate analysis of 12 independent variables on bodily injury claims: This figure visualizes the effect of each variable on bodily injury claims by displaying the mean number of claims (‘MeannClaims’) relative to the total exposure period for each categorical level. For the variables age, carVal and density, we show the effects in both their continuous and categorized (binned) forms. The confidence intervals are calculated under the assumption that claim occurrences follow a Poisson distribution.
In addition, it was investigated whether each of the 15 presented variables of Figure 3 have a significant correlation with the outcome variable. To this end, the -test was used for the categorical variables and the Wilcoxon rank-sum test for the continuous variables. It was found that all but the variables uwYear, carType and carValGrouped showed a significant correlation with the number of bodily injury claims. Interestingly, patterns also emerged when investigating the correlation among these 15 variables. Since we are dealing with mixed types, it was chosen to just check whether the pairwise correlation was significant or not, in order to make comparisons of the different type combinations comparable. Interestingly, the same three variables (uwYear, carType and carValGrouped) together with the three variables carVal, density and densityGrouped showed little correlation with any other variable, while the remaining nine variables generally showed a significant correlation with any other variable of this set of nine variables (see Figure 4).
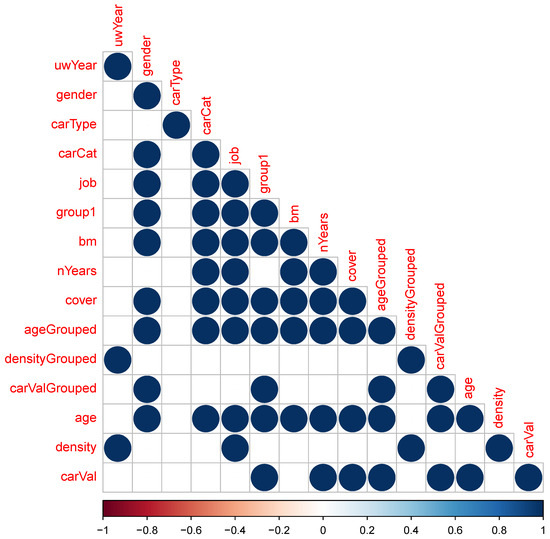
Figure 4.
Significance of pairwise correlations of the 12 independent variables: For both the continuous and categorized (binned) form of each of the variables, the significance of any other variable is determined. When both variables are categorical, the -test is used, and if one variable is continuous and the other is categorical, the Kruskal–Wallis test is selected and finally when both variables are continuous, the test of zero correlation of the Spearman correlation coefficient is used.
In the following analysis, we will focus on bodily injury claims. Three Genetic Algorithms will be presented: one to identify key main and interaction effects for the final model and another to find the GLM that best correlates with the predictions of a machine learning model, specifically a Gradient Boosted Machines (GBM) model. Both GAs will be applied to frequency data. We present last a separate attempt at modeling severity data.
Note that Poisson regression models are used to fit the frequency data, using as a fitting criterion of the GA, since this definition contains much more comparable pairs than or , such that it can be estimated with a much higher precision. is estimated using the marginal approximation (with 1000 boundary values), which strongly reduces the computational burden in exchange of a negligible approximation error (Van Oirbeek et al. 2023). In case of severity data, Gamma regression was chosen as a model, and is estimated using the k-means approximation (with 1000 clusters), again leading to minimal approximation error and very fast computational times (Van Oirbeek et al. 2023).
4.2. Parameter Tuning in Genetic Algorithms
Applying the GA in its standard form, as detailed in Section 3, often results in challenges regarding convergence to a stable solution. To address this, we introduced additional tuning parameters, which significantly improved the algorithm’s effectiveness. The complete list of these nine parameters is available in Appendix A. Here, we focus on the three most influential parameters for achieving convergence:
- nTimesInMods: the minimal number of times a variable should appear over the different interaction terms over all models at the end of a generation;
- nKeptBestMods: the number of top performers of the current generation that are retained at the end of a generation;
- nMods: the population size of each generation.
A GA was executed with varying values of these parameters. The remaining six parameters are presented in Appendix A. A critical decision in this process is selecting the final model upon GA termination. To mitigate the risk of overfitting, the GA was run on a training set (80% of the original dataset), and the final model selection was based on a validation set (the remaining 20%). This approach significantly reduces overfitting risks.
The final model was chosen using a 5-fold cross-validation on the validation set. To minimize computational demands, we limited candidate models to three options: the best or second-best model from the training set, or a model composed of the main and interaction effects most commonly found in the top four models. Table 1 displays the outcomes of this tuning process. Note that the table does not specify which of the three model types was selected as the final model in each scenario. The best-tuned GA yielded a significantly higher validated concordance probability (67%) compared to the worst-performing model (63%), which is a substantial improvement.

Table 1.
Overview of the tuning process of the GA with respect to nTimesInMods, nKeptBestMods, nMods and the concordance probability observed on a validation set, using a 5-fold cross-validation. The tested values for the nTimesInMods correspond to value ‘1’, or value 1 for all (20) generations, and value ‘1–3’, or value 1 for the first 3 generations and value 3 for the remaining 17 generations. The tested values for the nKeptBestMods correspond to value ‘2’, ‘3’ and ‘5’, or value 2, 3 or 5, respectively, for all (20) generations, and value ‘3–5’, or value 3 for the 5 first generations and value 5 for the remaining 15 generations. The tested values for the nMods correspond to value ‘10’, ‘15’ and ‘30’, or value 10, 15 or 30, respectively, for all (20) generations.
- nTimesInMods should not be set excessively high, as this could prematurely limit the exploration of the search space by reducing randomness.
- nKeptBestMods needs to be set to a reasonably high value. The standard GA can sometimes overlook promising models; therefore, it is advantageous to fine-tune these models over successive generations by ensuring that some are consistently retained in the model population.
- nMods should also be reasonably high, allowing the GA to explore a broader range of possibilities within the search space. However, a very high nMods value increases the GA’s runtime and can introduce excessive randomness. Therefore, while it should not be set too high, a substantial number is recommended. This parameter is particularly crucial for tuning.
In essence, proper tuning of the GA is crucial; otherwise, it may yield suboptimal results.
In Table 2, the characteristics of the final model of each scenario is investigated, from which we can conclude that

Table 2.
Comparison of the final models of the tuning process of the GA. The selection method that has indicated which of the candidate models of the GA turned out to be the best performing model on the validation set can be found in the ‘Selection’ column. The column ‘nVars’ refers to the number of main and interaction effects that were selected for the given final model. ‘Shared’ refers to the number of main and interaction effects of the given final model that is shared with the one of the best final model.
- All final models included at least twelve main and interaction effects. Notably, the worst-performing model contained the maximum of twenty main and interaction effects. This suggests that a well-tuned GA tends to produce models with fewer main and interaction effects than the maximum possible number.
- The best final model shared a significant number of main and interaction effects with the other final models. In every case, at least 50% of the main and interaction effects in a final model overlapped with those in the best final model. Interestingly, the degree of overlap in main and interaction effects tended to increase with better model tuning.
- Throughout our tuning process, the best-performing model in the GA was never selected as the final model upon validation. This highlights the importance of using both training and validation sets to mitigate the risk of overfitting.
Additionally, it is important to note that, beyond these tuning parameters, the rule used in the selection step for constructing probabilities based on the estimated Cs was also modified. Furthermore, the order of main and interaction effects within the bit string representation was reshuffled after each generation. Detailed explanations of these adjustments are available in Appendix B.
In Figure 5, we present the evolution of the unique number of variables and the mean, the maximum and the standard deviation of the whole set of estimated Cs of a given generation. The unique number of variables over the complete generation seems to stabilize around 17 generations and the evolution of the maximum and the mean around generation 10 and the evolution of the standard deviation stabilizes around generation 15, as presented by the dotted line on Figure 5. These patterns seem to indicate that 20 generations is reasonably large enough to converge given the selected values for the tuning parameters.
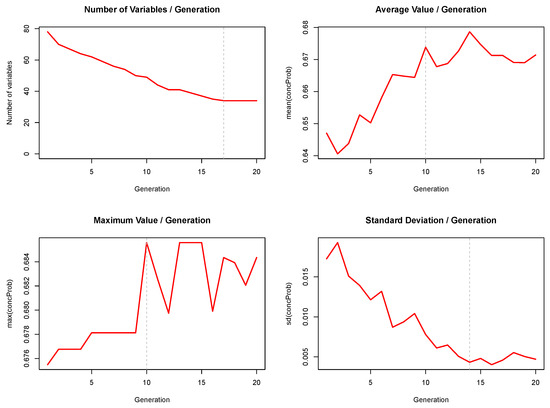
Figure 5.
Visualization of the evolution of the unique number of variables and the mean, the maximum and the standard deviation of the whole set of estimated Cs of a given generation. The dashed vertical lines indicate for each plot at which generation the pattern seems to have stabilized.
In the initial 10 generations, there is a significant rise in the mean concordance probability per generation (advancing from approximately 0.64 to 0.67), coupled with a marked reduction in the standard deviation (decreasing from around 0.015 to 0.005). These trends reflect the Genetic Algorithm’s (GA’s) efficacy in progressively eliminating inferior models, thereby reducing variability in subsequent generations. However, a baseline level of variability is maintained, indicating an optimal balance between exploitation of promising models and exploration of the solution space.
The maximum values of the concordance probabilities also exhibit interesting fluctuations across generations, with gains not as pronounced over time (increasing from around 0.674 to 0.686) and showing non-monotonic progress, suggesting occasional losses and recoveries of superior models by the GA.
The most effective model identified for the validation set comprises eight interaction terms and ten primary effects, with notable inclusions and exclusions among the variables and certain variables participating in multiple interaction terms.
- Main effects: age, gender, carCat, bm, carVal, job, density, cover, uwYear, group1.
- Interaction effects: age*gender, carCat*bm, carVal*job, density*gender, gender*job, job*cover, uwYear*gender, uwYear*group1.
Noteworthy is the prevalence of the ’gender’ variable in several interaction terms, indicating its significance in the model.
The estimates for and are presented in Table 3, with both demonstrating significantly higher values compared to . This suggests a clear distinction between the 2+ group and the other groups, delineating the unique characteristics of clients within the 2+ group. Conversely, the 0 and 1+ groups, while distinct, share closer similarities.

Table 3.
, and of the final model (selection of the main and interaction effects).
4.3. Identifying the Strongest Correlating GLM
In this section, we shift the focus of optimization. Rather than directly modeling the frequency data, our objective is to approximate a complex “black box” machine learning model using a simpler Generalized Linear Model (GLM). Utilizing a Genetic Algorithm (GA), we aim to identify a GLM that most closely correlates with the predictions of a given, potentially intricate, model (specifically, a Gradient-Boosting Model (GBM)) while exclusively addressing frequency data. This approach bears resemblance to a variable selection task (see Section 4.2); however, it necessitates the application of a modified version of Equation (4) as the fitting criterion for the GA.
where () are the predictions of the GLM (GBM model) and () the set of independent variables that were included in both models, and which do not necessarily need to be the same set. In short, the above equation measures the rank-correlation between the predictions of the GLM and the GBM model.
Our analyses yield insights into the GA’s performance over various generations, as depicted in Figure 6. We observe stabilization in the mean and standard deviation by generations 12 and 10, respectively, alongside notable initial fluctuations. The maximum value demonstrates slight oscillations, with a notable peak at generation 18. The variable count tends to stabilize around the 17th generation after significant initial changes, indicating a refinement in the model’s complexity.
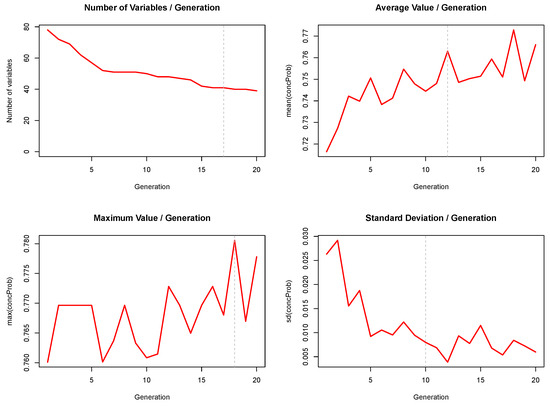
Figure 6.
Visualization of the evolution of the unique number of variables and the mean, the maximum and the standard deviation of the estimated Cs of a given generation, in the selection of the strongest correlating GLM model with the GBM model. The dashed vertical lines indicate for each plot at which generation the pattern seems to have stabilized.
The best final model, in this case, the second best model on the validation set, consists of eight interaction terms and eleven main effects:
- Main effects: age, gender, bm, job, density, cover, uwYear, nYears, group1, carVal and carType.
- Interaction effects: uwYear*bm, age*cover, nYears*cover, uwYear*gender, density*uwYear, density*job, age*uwYear and carVal*carType.
Of all the 12 variables, only carCat was not involved in the above list. The variable carType was selected for the first time, and group1 is only included as a main effect. UwYear was involved in four of the eight interaction terms, and age, cover and density in two distinct interaction terms. Note that the interaction term uwYear*gender is also present in the model of the previous section. The selected main and interaction terms correspond to the ones of the second best model.
The optimal model, ranking second best in our validation set, comprises eight interaction terms and eleven main effects, with a notable exclusion of the ‘carCat’ variable. ‘UwYear’ dominates the interaction terms, appearing in four, while ‘age’, ‘cover’ and ‘density’ feature in two each. Noteworthy is the inclusion of ‘carType’ for the first time and ‘group1’ solely as a main effect. This selection reflects the model’s nuanced interplay between variables to best approximate the GBM.
Further investigation into both models’ performance, as shown in Table 4, reveals a consistent pattern in their pairwise differences across the values, indicating a generalizable feature of predictive ability difference across the considered groups. Notably, the GBM model surpasses a 90% predictive ability for both and , underscoring its robustness.

Table 4.
, and of the final model of the GA (strongest correlater with the GBM model).
4.4. Claim Size Analysis
In this subsection, we apply the final model, composed of 10 main effects and 8 interaction effects, to the severity data, utilizing claimCharge as the target variable. The concordance statistic, , for this model is 0.565. This modest value is not entirely surprising; it is a well-established fact in actuarial science that constructing a predictive model for severity is more challenging than for frequency, a notion corroborated by our findings. Furthermore, developing a robust model for severity data is inherently difficult due to its generally smaller dataset size compared to frequency data.
Figure 7 illustrates how the model’s discriminatory ability evolves concerning the threshold parameter . It is evident that significantly influences the model’s predictive performance, with the concordance probability increasing monotonically with . The range of concordance probability spans from 0.565 to an impressive 0.90. This implies that claims with markedly different observed costs are easily distinguishable by the model; notably, small claims can be effectively differentiated from large ones. This finding is particularly significant, leading to the consideration of whether the model’s capability to discriminate between closely valued claims is even necessary for assessing a severity model’s predictive performance. Setting to zero seems impractical in any real-world scenario. The observed trend suggests that in the context of technical pricing severity analysis, it might be beneficial to consider the integration of the value of over a selected range of interest, , determined by either actuarial expertise or specific commercial objectives of the insurance firm.
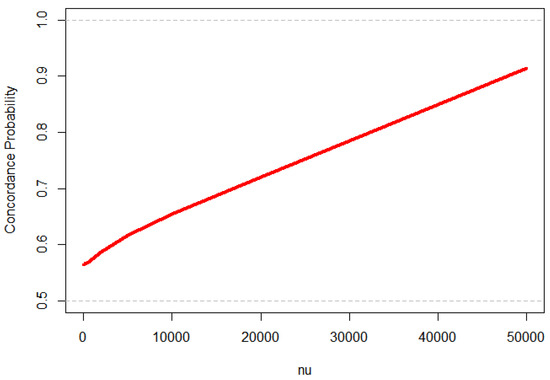
Figure 7.
Depicting the progression of discriminatory ability of the final optimal model, applied to the complete severity dataset across varying values.
5. Discussion and Conclusions
The objective of this article was the introduction of a Genetic Algorithm (GA) approach for optimizing a non-differentiable loss function. The concordance probability was chosen to this end, since it is a very popular measure of the predictive ability that is very well suited to the setting of insurance. The standard GA framework was adapted to even better identify crucial main and interaction effects of Generalized Linear Models (GLMs).
Our key result is that we have proven on a real-life example that our methodology provides a robust framework for, on the one hand, navigating the complex and high-dimensional search space inherent in such optimization problems and for, on the other hand, adapting effectively to both discrete and continuous target variables. Therefore, our approach is suitable for both frequency and severity modeling. Moreover, our novel approach uniquely aligns GLM predictions with those of machine learning models (especially GBMs), enhancing interpretability and reliability. The challenge lies in adapting and even tuning key steps of the GA framework which provides additional insights into the parameter selection process and convergence of the GA.
Additionally, we proposed a method within the GA framework to uncover the GLM with the strongest correlation to a black-box machine learning model. This approach aids in identifying non-linear patterns for inclusion in a GLM, enhancing its overall accuracy. This can help pricing actuaries to discover and exploit non-linear patterns from Machine Learning models, when using a GLM as a final model is a constraint.
Future research directions could explore the following:
- Higher-Order Interaction Effects: While this study focused on first-order interaction effects, further exploration could investigate strategies to adapt the GA for exploring higher-order interaction effects. Given the exponential search space associated with higher-order interactions, strategies may involve constraints on their inclusion in a generation based on the selection of a (m − 1)th interaction effect in the preceding generation.
- Connection with Shapley Values: The connection between Genetic Algorithms for variable selection, including interaction effects, and popular variable importance methods like Shapley values could be investigated. Although GAs and Shapley values are distinct optimization concepts, they can be related in the context of measuring the contribution of individual variables in different generations (GA) or coalitions (Shapley).
- Consideration of Protected Attributes: In our application, we observed a notable contribution of the gender feature in multiple interaction terms. As gender is often considered a protected attribute, particularly in the insurance pricing literature (e.g., Lindholm et al. (2022)), the approach presented could be adapted to focus specifically on one or multiple protected variables. This adaptation could reveal interaction effects with non-protected variables and contribute to discussions on fairness and discrimination in modeling practices.
Author Contributions
Conceptualization, R.V.O.; Methodology, R.V.O., F.V., T.B., G.W. and C.G.; Software, G.W. and R.V.O.; Validation, F.V., T.B. and R.V.O.; Formal analysis, R.V.O.; Writing—original draft, R.V.O.; Writing—review and editing, F.V., T.B., C.G. and T.V.; Supervision, T.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data set used for the analysis corresponds to the object of the CASdatasets R package.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Complete List Tuning Parameters
Below, the complete list of nine tuning parameters can be found, together with the value that was used in our application. These values were set after a long series of informal investigations and they can be used as a starting point when applying our proposed methodology to a new data source.
- nVarInit: the number of the interaction terms that are selected at random during the initialization phase. In our application this was set to 10.
- nGens: the number of generations. In our application this was set to 20, as we frequently observed that convergence according the above explained rule was almost always reached by 20 generations.
- nCrossOver: the number of cross-overs. In our application this was set to one for all generations. Note that one could make an nCrossOver change over the different generations.
- nMuts: the number of mutations. In our application this was set to one for all generations. Note that one could make an nMuts change over the different generations.
- nVarMax: the maximum number of interaction terms of a model by the end of the generation. In our application this was set to 20. Note that one could make an nVarMax change over the different generations.
- nRedMods: For models with more than nVarMax variables, the pruning step is repeated nRedModels times. In our application this was set to five. Note that one could make an nRedMods change over the different generations.
- nTimesInMods: the minimal number of times a variable should appear over the different interaction terms over all models at the end of a generation. Note that one could make an nTimesInMods change over the different generations.
- nKeptBestMods: the number of top performers of the current generation that are retained at the end of a generation. Note that one could make an nKeptBestMods change over the different generations.
- nMods: the population size of each generation. Note that one could make an nMods change over the different generations.
Appendix B. Additional Changes to the Vanilla GA
Both the selection and the crossover step were mildly adapted in our application to facilitate convergence of the GA even more. We will start with the adaptation of the selection step: in Section 3, the vanilla method for computing the sampling probabilities of the selection step, when using C as a fitting criterion, is shown:
In our application, we could see that even the rather bad performing (random) models of the first generation generally obtained reasonably large values for C, i.e., around 0.60. This is a problem, since the above equation will still give a lot of weight to the worst performing models of the population of the current generation, hereby unnecessarily slowing down convergence of the GA. Therefore, the following modification was proposed:
where corresponds to the entire set of C estimates of all models of the current generation i. Note that the correction term was added to ensure that the poorest performing model of the current generation still has a non-zero probability of being selected during the selection phase of the GA. One just needs to ensure that is not lower than the difference between the worst model of the given generation and 0.5. In Table A1, the effect choosing both types of sampling probabilities is shown.

Table A1.
Comparison of applying the vanilla sampling probabilities versus applying the corrected sampling probabilities during the selection phase of the GA. The population size of the considered generation equals five and .
Table A1.
Comparison of applying the vanilla sampling probabilities versus applying the corrected sampling probabilities during the selection phase of the GA. The population size of the considered generation equals five and .
| 0.58 | 0.16 | 0.04 |
| 0.59 | 0.18 | 0.12 |
| 0.60 | 0.20 | 0.20 |
| 0.62 | 0.24 | 0.36 |
The vanilla sampling probabilities are all quite close to one another, while the modified sampling probabilities are more spread out. Needless to say that, by applying equation instead of equation equation , the GA requires fewer generations to convergence.
The cross-over step of the vanilla GA was also adapted in our application: the main or interaction effect that are attached to each position of the bit string are reshuffled after each generation, as to remove as many systematic biases as possible. As such, we prevent the same interaction terms from systematically experiencing a move in the same direction during a crossover step (i.e., are in the same part after the split of the string). Indeed, imagine that the position of two effects are right next to each other in the model string. Since we have 12 independent variables in our application, there are 66 first-order interaction terms and 12 main effects, meaning that the probability is rather small (1/77) that both interaction terms move in an opposite direction during a cross-over step. However, if one term is at the first position and the second term at the last position, both will always move in the opposite direction during a cross-over step. In order to avoid these kind of systematic patterns due to merely the position in which terms are placed in the model string, these positions need to be reshuffled systematically at the beginning of each generation (or at least at the beginning of each cross-over step).
References
- Bamber, Donald. 1975. The area above the ordinal dominance graph and the area under the receiver operating characteristic graph. Journal of Mathematical Psychology 12: 387–415. [Google Scholar] [CrossRef]
- Blier-Wong, Christopher, Hélène Cossette, Luc Lamontagne, and Etienne Marceau. 2020. Machine learning in P&C insurance: A review for pricing and reserving. Risks 9: 4. [Google Scholar] [CrossRef]
- Broadhurst, David, Royston Goodacre, Alun Jones, Jem J. Rowland, and Douglas B. Kell. 1997. Genetic algorithms as a method for variable selection in multiple linear regression and partial least squares regression, with applications to pyrolysis mass spectrometry. Analytica Chimica Acta 348: 71–86. [Google Scholar] [CrossRef]
- European Insurance and Occupational Pensions Authority (EIOPA). 2019. Big Data Analytics in Motor and Health Insurance: A Thematic Review. Luxembourg: Publications Office of the European Union. [Google Scholar]
- Frees, Edward W., Richard A. Derrig, and Glenn Meyers. 2014. Predictive Modeling Applications in Actuarial Science. Cambridge: Cambridge University Press, vol. 1. [Google Scholar]
- Friedman, Jerome H., and Bogdan E. Popescu. 2008. Predictive learning via rule ensembles. The Annals of Applied Statistics 2: 916–54. [Google Scholar] [CrossRef]
- Gayou, Olivier, Shiva K. Das, Su-Min Zhou, Lawrence B. Marks, David S. Parda, and Moyed Miften. 2008. A genetic algorithm for variable selection in logistic regression analysis of radiotherapy treatment outcomes. Medical Physics 35: 5426–33. [Google Scholar] [CrossRef]
- Hastie, Trevor, Robert Tibshirani, and Jerome Friedman. 2009. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Berlin: Springer, Heidelberg: Springer, vol. 2. [Google Scholar]
- Ke, Guolin, Qi Meng, Thomas Finley, Taifeng Wang, Wei Chen, Weidong Ma, Qiwei Ye, and Tie-Yan Liu. 2017. Lightgbm: A highly efficient gradient boosting decision tree. Advances in Neural Information Processing Systems 30: 3146–54. [Google Scholar]
- Lindholm, Mathias, Ronald Richman, Andreas Tsanakas, and Mario V. Wüthrich. 2022. Discrimination-free insurance pricing. ASTIN Bulletin: The Journal of the IAA 52: 55–89. [Google Scholar] [CrossRef]
- Lou, Yin, Rich Caruana, Johannes Gehrke, and Giles Hooker. 2013. Accurate intelligible models with pairwise interactions. Paper presented at 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, August 24–27; pp. 623–31. [Google Scholar]
- Lundberg, Scott M., Gabriel Erion, Hugh Chen, Alex DeGrave, Jordan M. Prutkin, Bala Nair, Ronit Katz, Jonathan Himmelfarb, Nisha Bansal, and Su-In Lee. 2020. From local explanations to global understanding with explainable AI for trees. Nature Machine Intelligence 2: 56–67. [Google Scholar] [CrossRef] [PubMed]
- Menvouta, Emmanuel Jordy, Jolien Ponnet, Robin Van Oirbeek, and Tim Verdonck. 2022. mCube: A Multinomial Micro-level reserving Model. arXiv arXiv:2212.00101. [Google Scholar]
- Mingote, Victoria, Antonio Miguel, Alfonso Ortega, and Eduardo Lleida. 2020. Optimization of the area under the ROC curve using neural network supervectors for text-dependent speaker verification. Computer Speech Furthermore, Language 63: 101078. [Google Scholar] [CrossRef]
- Mitchell, Tom M. 1997. Machine Learning. Burr Ridge: McGraw Hill, vol. 45, pp. 870–77. [Google Scholar]
- Ohlsson, Esbjörn, and Björn Johansson. 2010. Non-life Insurance Pricing with Generalized Linear Models. Berlin: Springer, Heidelberg: Springer, vol. 174. [Google Scholar]
- Pencina, Michael J., and Ralph B. D’Agostino. 2004. Overall C as a measure of discrimination in survival analysis: Model specific population value and confidence interval estimation. Statistics in Medicine 23: 2109–23. [Google Scholar] [CrossRef] [PubMed]
- Ponnet, Jolien, Robin Van Oirbeek, and Tim Verdonck. 2021. Concordance Probability for Insurance Pricing Models. Risks 9: 178. [Google Scholar] [CrossRef]
- Qasim, Omar Saber, and Zakariya Yahya Algamal. 2018. Feature selection using particle swarm optimization-based logistic regression model. Chemometrics and Intelligent Laboratory Systems 182: 41–6. [Google Scholar] [CrossRef]
- Stefansson, Petter, Kristian H. Liland, Thomas Thiis, and Ingunn Burud. 2020. Fast method for GA-PLS with simultaneous feature selection and identification of optimal preprocessing technique for datasets with many observations. Journal of Chemometrics 34: e3195. [Google Scholar] [CrossRef]
- Van Oirbeek, Robin, Jolien Ponnet, Bart Baesens, and Tim Verdonck. 2023. Computational Efficient Approximations of the Concordance Probability in a Big Data Setting. Big Data. [Google Scholar] [CrossRef]
- Wood, Simon N. 2006. Generalized Additive Models: An Introduction with R. London: Chapman and Hall. Boca Raton: CRC. [Google Scholar]
- Wuthrich, Mario V., and Christoph Buser. 2021. Data Analytics for Non-Life Insurance Pricing. Swiss Finance Institute Research Paper. Zürich: Swiss Finance Institute. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).