Discrete-Time Survival Models with Neural Networks for Age–Period–Cohort Analysis of Credit Risk

Abstract

Survival models have become popular for credit risk estimation. Most current credit risk survival models use an underlying linear model. This is beneficial in terms of interpretability but is restrictive for real-life applications since it cannot discover hidden nonlinearities and interactions within the data. This study uses discrete-time survival models with embedded neural networks as estimators of time to default. This provides flexibility to express nonlinearities and interactions between variables and hence allows for models with better overall model fit. Additionally, the neural networks are used to estimate age–period–cohort (APC) models so that default risk can be decomposed into time components for loan age (maturity), origination (vintage), and environment (e.g., economic, operational, and social effects). These can be built as general models or as local APC models for specific customer segments. The local APC models reveal special conditions for different customer groups. The corresponding APC identification problem is solved by a combination of regularization and fitting the decomposed environment time risk component to macroeconomic data since the environmental risk is expected to have a strong relationship with macroeconomic conditions. Our approach is shown to be effective when tested on a large publicly available US mortgage dataset. This novel framework can be adapted by practitioners in the financial industry to improve modeling, estimation, and assessment of credit risk.

1. Introduction

Credit risk is a critical problem in the financial industry and remains an active topic of academic research. Credit risk indicates the risk of a loss caused by a borrower’s default, referring to its failure to repay a loan or fulfill contractual obligations. The credit score, which is calculated based on financial data, personal (or company) details, and credit history, is a quantification of this risk. It can distinguish good customers from high risk ones when making a decision on loan applications. Banks and other financial institutions are most interested in evaluating credit risk. Traditionally, banks used linear model such as discriminate analysis and logistic regression. Nowadays, they are exploring survival models and some non-linear methods, e.g., machine learning (ML), especially deep neural network (DNN). For example, Hussin Adam Khatir and Bee (2022) explored several machine learning algorithms with different data balancing methods and concluded that random forest with random oversampling works well. Jha and Cucculelli (2021) showed that an ensemble of diverse non-linear models is able to provide improved and robust performance. However, Blumenstock et al. (2022) showed that there has been limited work on ML/DNN models specifically for survival analysis in credit scoring due to the concern about the use of black-box models in the finance community and their paper is the first to apply DNN in the credit risk context. In this paper, we propose machine learning-based survival models with interpretability mechanisms to enable complex interaction terms between features and representations of non-linear relationships between variables and output. We construct the neural networks at the vintage level, which contains a suite of subnetworks, one for each origination period. Traditional DNN lacks the ability to provide an interpretation of its predictions, which cannot convince the banks and financial companies. In our study, we want to make the neural network more explainable by visualizing and interpreting the predictions and the risk behavior from the model. To realize this, Lexis graphs are employed to record the information from the neural network. Then, ridge regression is used to decompose the probability of default (PD) estimation by the neural network in the Lexis graph into three age–period–cohort (APC) timelines. Our model, the neural network for the discrete-time survival model (NN-DTSM), is capable of extracting different kinds of customer risk behaviors from the datasets, which cannot be realized by survival analysis methods in previous studies. Meanwhile, the three time functions decomposed by the APC modeling method can be used to interpret the black box of the neural network in this credit risk application.

The remainder of this article is divided into the following sections: Section 2 introduces the background with the literature review, Section 3 describes the DTSM, neural network, and APC methodologies used, Section 4 describes the US mortgage datasets that are used, along with the experimental results, Section 5 presents results and discussions, and, finally, Section 6 provides conclusions.

2. Background and Literature Review

Over the past 50 years, much impressive research has been performed to better predict default risk. Among those studies, the first, and one of the most seminal, works is the Z-score model (Altman 1968). Altman used multivariate discriminant analysis (MDA) to investigate bankruptcy prediction in companies. MDA is a linear and statistical technique that can classify observations into different groups based on predictive variables. The discriminant function of MDA is

$$Z=v_1{x}_1+v_2{x}_2+\cdots +v_n{x}_n$$

(1)

where $x_1, x_2, \cdots , x_n$ are observation values of n features used in the model and $v_1, v_2,\cdots ,v_n$ are the discriminant coefficient computed by the MDA method. For the Z-score model, the typical features used are financial ratios from company accounts. This model can then transform an individual company’s features into a one-dimensional discriminant score, or Z, which can be used to classify companies by risk of bankruptcy. For consumer credit, MDA and other linear models such as logistic regression have traditionally been used for credit scoring (Khemais et al. 2016; Sohn et al. 2016; Thomas et al. 2017).

Although this kind of traditional linear method can determine whether an applicant is in a good or bad financial situation, it cannot deal with dynamic aspects of credit risk, in particular, time to default. Therefore, survival analysis has been proposed as an alternative credit risk modeling approach default time prediction. Banasik et al. (1999) pointed out that the use of survival analysis facilitates the prediction of when a borrower is likely to default, not merely a binary forecast of whether or not a default would occur in a fixed time period. This is because survival analysis models permit the inclusion of dynamic behavioral and environmental risk factors in a way that regression models cannot perform.

One of the early popular multivariate survival models is the Cox proportional hazard (PH) model (Cox 1972). Unlike regression models, Cox’s PH model can include variables that affect survival time. The semiparametric nature of the model means that a general non-linear effect is included. The Cox PH model is composed of a linear component, the parametric form, and a baseline hazard part in non-parametric form as follows:

$$h\left(t|x_1, x_2, \cdots , x_n\right)=h_0\left(t\right)\mathrm{e}\mathrm{x}\mathrm{p}\left({\mathsf{\alpha }}_1{x}_1+{\mathsf{\alpha }}_2{x}_2+\cdots +{\mathsf{\alpha }}_n{x}_n\right).$$

(2)

This function assumes the risk for a particular individual at time t is the product of a non-specified baseline hazard function of time $h_0\left(t\right)$ and an exponential term of linear series of variables. The coefficients, ${\mathsf{\alpha }}_i$, are estimated using maximum partial likelihood estimation without needing to specify the hazard function $h_0\left(t\right)$. Therefore, the Cox PH model is called a semiparametric model. One advantage of the Cox PH model is that it can estimate the hazard rate (the probability that the event occurs per unit of time conditioning on no prior event happened before) for each variable separately, without needing to estimate the baseline hazard function $h_0\left(t\right)$. However, for predictive models, as would typically be required in credit risk modeling, the baseline hazard will need to be estimated post hoc.

Thomas (2000) and Stepanova and Thomas (2001) developed survival models for behavioral scoring for credit and showed how these could be used for profit estimation over a portfolio of loans. Bellotti and Crook (2009) developed a Cox PH model for credit risk for a large portfolio of credit cards and showed it provided benefits beyond a standard logistic regression model, including improved model fit and forecasting performance. They showed that credit status is influenced by the economic environment represented through time-varying covariates in the survival model. Dirick et al. (2017) provided a benchmark of various survival analysis technologies including the Cox PH model, with and without splines, accelerated failure time models, and mixture cure models. They considered multiple evaluation techniques such as the receiver operating characteristic (ROC) curve, the area under the ROC curve (AUC), and deviation from time to default, across multiple datasets. They found that no particular variant strictly outperforms all others, although Cox PH with splines was best overall. In their notes, they mentioned the challenges of choosing the correct performance measure for this problem, when using survival models for prediction. This remains an open problem.

Traditional survival models are continuous time survival models. However, discrete-time survival models (DTSM) have received great attention in recent years. For credit risk, where data are collected at discrete time points, typically monthly or quarterly repayment periods, a discrete time approach matches the application problem better than continuous time modeling; furthermore, for prediction, using discrete time is computationally more efficient (Bellotti and Crook 2013). Gourieroux et al. (2006) pointed out that the continuous time affine model often has a poor model fit due to a lack of flexibility. They developed a discrete-time survival affine analysis for credit risk which allows dynamic factors to be less constrained. De Leonardis and Rocci (2008) adapted the Cox PH model to predict the firm default at discrete time points. Although time is viewed as a continuous variable, companies’ datasets are constructed on a monthly or yearly discrete-time basis. Companies’ survival or default is measured within a specific time interval, which means the Cox PH model needs to be adapted so that the time will be grouped into discrete time intervals. The adapted model not only produces a sequence of each firm’s hazard rates at discrete time points but also provides an improvement in default prediction accuracy. Bellotti and Crook (2013) used a DTSM framework to model default on a dataset of UK credit cards. They used credit card behavioral data and macroeconomic variables to improve model fit and better predict the time to default. In their paper, time is treated monthly and the model is trained using three large datasets from UK credit card data, including over 750,000 accounts from 1999 to mid-2006. The model is more flexible than the traditional one. Bellotti and Crook (2014) followed up by building a DTSM for credit risk and showed how it can be used for stress testing. Both papers treat the credit data as a panel dataset indexed by both account number and loan age (in months), with one observation being a repayment statement for the account at a particular loan age. Unlike previous studies, they used models to measure the risk, forecasting, and stress testing and pointed out that including statistically explanatory behavioral variables can improve model fit and predictive performance.

Even though the Cox model is a popular approach for survival analysis, it still suffers from a number of drawbacks. Firstly, the baseline hazard function is assumed to be the same across all observations but this may not be realistic in many applications, such as credit risk, where we may expect that different population segments may have different default behavior. Furthermore, since the parametric component of the Cox PH model is linear, non-linear effects of variables must be included by transformations or by including explicit interaction terms. But it can be difficult to identify these by manual processes. These difficulties, however, can be handled automatically using some other non-linear methods, such as an underlying machine learning algorithm like the random survival forest (RSF), support vector machine (SVM), and different kinds of artificial neural networks (ANN), which can also potentially improve the model fit.

The random survival forest (Ptak-Chmielewska and Matuszyk 2020) evolved from random forests and inherited many of its characteristics. Only three hyperparameters need to be specified in a random survival forest (RSF): the number of predictors, which are randomly selected, the number of trees, and the splitting rules. Also, unlike the Cox PH model, RSF is essentially assumption-free, although the downside of this is that it does not (directly) provide statistical inference. However, this is a very useful property in survival modeling in the context of credit risk, where the value of a model is in prediction, rather than inference. Ptak-Chmielewska and Matuszyk (2020) showed that RSF has a lower concordance error when compared with the Cox PH model. Therefore, RSF is a promising approach to predict account default.

To further improve the model fit and the model prediction of credit risk, ANN has received increased attention in credit risk, known as a more powerful and complex non-linear method with improved performance in other areas such as computer vision (Lu and Zhang 2016). Faraggi and Simon (1995) upgraded the Cox proportional hazards model with a neural network estimator. The linear term ${\mathsf{\alpha }}_1{x}_1+{\mathsf{\alpha }}_2{x}_2+\cdots +{\mathsf{\alpha }}_n{x}_n$ in Equation (2) is replaced by the output of a neural network $g(x_1,x_2,\cdots ,x_n)$. This neural network model incorporates all the benefits of the standard Cox PH model and retains the proportional hazard assumption but allows for non-linearity amongst the risk factors. Ohno-Machado (1996) tackled the survival analysis problem utilizing multiple neural networks. The model is composed of a collection of subnetworks and each of them corresponds to a certain discrete time point, such as a month, quarter, or year. Each subnetwork has a single output forecasting survival probability at its corresponding time period. The datasets are also divided into discrete subsets consisting of cases at specific time points in the same way and assigned to each subnetwork for training. The paper also describes that the learning performance of the neural network can be enhanced by combining the subnetworks, such as using outputs of some subnetworks as inputs for another subnetwork. But the issue of how to configure an optimal architecture of neural networks (i.e., how to combine the neural networks) remains an open research problem. Gensheimer and Narasimhan (2019) proposed a scalable DTSM using neural networks that can deal with non-proportional hazards, trained using mini-batch gradient descent. This approach can be especially useful when there are non-proportional hazard effects on observations for large datasets with large numbers of features. Time is divided into multiple intervals dependent on the length of the timelines. Each observation is transformed into a vector format to be used in the model, where one vector represents the survival indicator and another represents the event or default indicator, if it happened. The results show that this discrete-time survival neural network model can speed up the training time and can produce good discrimination and calibration performance.

Many studies using machine learning with survival models are in the medical domain. Ryu et al. (2020) utilized a deep learning approach to survival analysis with competing risk called DeepHit, which uses a deep learning neural network in a medical setting to learn individual’s behavior and allow for the dynamic risk effect of time-varying covariates. The architecture of DeepHit consists of a shared network and a group of sub-networks and both are composed of a series of fully connected layers. The output layer uses the SoftMax activation function, which produces the probability of events for different discrete time points.

There are few papers studying the application of neural networks for DTSM specifically in the context of credit risk models. Practitioners and researchers in credit risk have begun to explore machine learning (ML) and deep learning (DL) in application to survival analysis, see, e.g., Breeden (2021) for an overview. Blumenstock et al. (2022) explored ML/DL models for survival analysis, comparing them with traditional statistical models such as the Cox PH model motivated by the results in previous work on ML/DL credit risk models. They found that the performance of the DL method DeepHit (Lee et al. 2018) outperforms the statistical survival model and RSF. Another contribution of their paper is introducing an approach to extract feature importance scores from DeepHit, which is a first step to building trust in black box models among practitioners in industry. However, this approach cannot reveal a clear picture of the mechanism and prediction behavior of DL models for analysts. As we describe later, one of our contributions is using local APC models as a means to interpret the black box of the DL model across different segments of the population. Dendramis et al. (2020) also proposed a deep learning multilayer artificial neural network method for survival analysis. The complex interactions of the neural network structures can capture the non-linear risk factors causing loan default among the behavioral variables and other institutional factors. These factors play more important roles in predicting default than the frequently used traditional fundamental variables in statistical models. They also showed that their neural network outperforms alternative logistic regression models. Their experimental results are based on a portfolio of 11,522 Greek business loans during the severe recession period, March 2014 to June 2017, with a relatively high default rate.

In this article, we report the results of a study using neural networks for DTSM on a large portfolio of US mortgage data over a long period, from 2004 to 2013, which covers the global financial crisis and its aftermath. This long period of data allows us to explore and decompose the maturation, vintage, behavioral, and environmental risk factors more clearly. We show that these models are more flexible than the standard linear models and provide an improved predictive performance overall.

Studies in credit risk modeling with machine learning typically focus on predictive performance, which is indeed the primary goal in this application context. However, there is an increasing concern in the financial industry that credit risk models are not interpretable or explainable. Banks and companies do not trust the black box of complex neural network architectures or other machine learning algorithms that lack transparency and interpretability (Quell et al. 2021; Breeden 2021). To address this concern, in this paper, we use the output of the DTSM neural network as an input to local linear models that can provide an interpretation of risk behavior for individuals or population segments in terms of the different risk timelines related to loan age (maturity), origination cohort (vintage), and environmental and economic effect over calendar time. These types of models are known as age–period–cohort (APC) models and are well-known outside credit risk (see, e.g., Fosse and Winship 2019), but their use as a method to decompose the timeline of credit risk was pioneered by Breeden (e.g., see Breeden 2016). There remains an identification problem with APC models and in this study, we address this problem using a combination of regularization and fitting the environmental timeline to known macroeconomic data. To the best of our knowledge, this is the first use of APC models in the context of neural networks for credit risk modeling.

3. Research Methodology

In this section, we describe the algorithms and approaches used in our method, including the DTSM, neural network, lexis graph, APC effect, and time-series linear regression model. All of these methods helped predict the time-to-default event and solve the APC identification problem.

3.1. Discrete-Time Survival Model

Even though time-to-default events can be viewed as occurring in continuous time, credit portfolios are typically represented as panel data, which record account usage and repayment in discrete time (typically monthly or quarterly records). Therefore, it is more natural to treat time as a discrete point for a credit risk model (Bellotti and Crook 2013). If we use discrete time, the data are presented as a panel data indexed on both account i and discrete time t. We provided the following concepts, notations, and functions for a credit risk DTSM.

• The variable $t$ was used as the primary time-to-event variable and indicated the loan age of a credit account. Loan age is the span of the time since a loan account was created. It is also called loan maturity. For this study, data were provided monthly so $t$ is the number of months but the period could be different, e.g., quarterly;
• The variable $m$ represents the number of loan accounts in the dataset, so $i\in \left\{1,\cdots ,m\right\}$;
• We let $t_i^{*}$ be the loan age time index of the last observation recorded for account $i$, so that for each account $i$, records only exist for loan age $t\in \left\{1,\cdots ,t_i^{*}\right\}$;
• The binary variable $d_{it}$ represents whether account $i$ defaults or not (1 denotes default and 0 denotes non-default) at a certain loan age t. The precise definition of default can vary by application but for this study, three months’ consecutive missed payments were used, which is an industry-standard following the Basel II convention of 90 days of missed payments (BCBS 2006);
• Notably, in the survival analysis context, the default must be the last event in a series; hence, for $t<t_i^{*}$, $d_{it}=0$ and for $t=t_i^{*}$, $d_{it}=0$, which indicates a censored account (i.e., event time, such as death time in medical or default time in credit risk, is unknown during the whole observation period), and $d_{it}=1$ indicates the default event;
• The variable ${\mathbf{w}}_i$ is a vector of static application variables collected at the time when the customer applies for a loan (e.g., credit score, interest rate, debt-to-income ratio, and loan-to-value);
• We let $v_i$ be the origination period, or vintage, of account i. Normally, the period is the quarter or year when the account was originated. This is actually just one of the features in the vector ${\mathbf{w}}_i$. We let $N_v$ be the total number of vintages (the time when an individual customer open the account) in the dataset;
• Meanwhile, we denoted time-varying variables (e.g., behavioral, repayment history, and macroeconomic data) by vector ${\mathbf{x}}_{it}$, which is collected across the lifetime of the account;
• We let $c_{it}$ be the calendar time of account i at loan age t, with $N_c$ being the total number of calendar time periods. The measurement of calendar time is typically monthly, quarterly, or annually. Notably, $c_{it}$ is actually just one of the features in the vector ${\mathbf{x}}_{\mathit{i}\mathit{t}}$.

Notably, loan age, vintage, and calendar time are related additively: $c_{it}=v_i+t$. For example, suppose an account originated ($v_i$) in June 2009 and we consider repayment at loan age (t) of 10 months, then this repayment observation must then have a calendar time ($c_{it}$) of April 2010.

The DTSM model’s probability of default (PD) for each account $i$ at time $t$ is given as

$$P_{it}=P\left(d_{it}=1\right|d_{is}=0 \forall s<t; {\mathbf{w}}_i, {\mathbf{x}}_{it})$$

(3)

PD at time t is dependent on the account not defaulting prior to t, i.e., the account has survived up to time $t-1$. A further constraint on the model is that we did not consider further defaults after the default was first observed. It is these conditions that make such a model a survival model. The linear DTSM was built using the following model structure:

$$P_{it}=F({\beta }_0+\alpha \phi \left(t\right)+{\mathsf{\beta }}_1{\mathbf{w}}_i+{\mathsf{\beta }}_2{\mathbf{x}}_{it})$$

(4)

where F is an appropriate link function, such as logit, $\phi$ is some transformation of t, ${\beta }_0$ is the intercept term, and ${\mathsf{\beta }}_1$ and ${\mathsf{\beta }}_2$ are vectors of coefficients. Even though this model was across observations indexed by both account i and time t and we could not assume independence between each time $t$ and $t-1$ within the same account i, by applying the chain rule for conditional probabilities, the likelihood function could be expressed as

$$L\left(D\right)=\prod _{i=1}^m\prod _{s=1}^{t_i^{*}}{P_{is}}^{d_{is}}{(1-P_{is})}^{(1-d_{is})}$$

(5)

where D refers to the panel data, which records accounts behavior at consecutive time points. With F as the logit link function, it is the same form as logistic regression and hence the intercept, coefficients, and parameters in $\phi$ can be estimated using a maximum likelihood estimator for logistic regression. Details can be found in Allison (1982).

3.2. Vintage Model

In the financial industry, analysis is often performed and models are built at the vintage level (Siarka 2011). That is, separate models are built on accounts that originate within the same time period, e.g., in the same quarter or same year. The parallel is with wine production where wines produced in the same year generally share the same quality and is referred to as vintage. A similar phenomenon is recognized in credit due to lenders’ different risk appetites and different borrower demographics, at different times (Breeden 2016). Using the notation above, it means they all have the same value of $v_i$. Vintage modeling leads to a suite of models, one for each origination period. This is a useful practice since it may be expected that different vintages will behave in different ways and hence require separate models. The DTSM can be built as a vintage model for a fixed origination date, in which case loan age t also corresponds to calendar time, in the context of each separate vintage model.

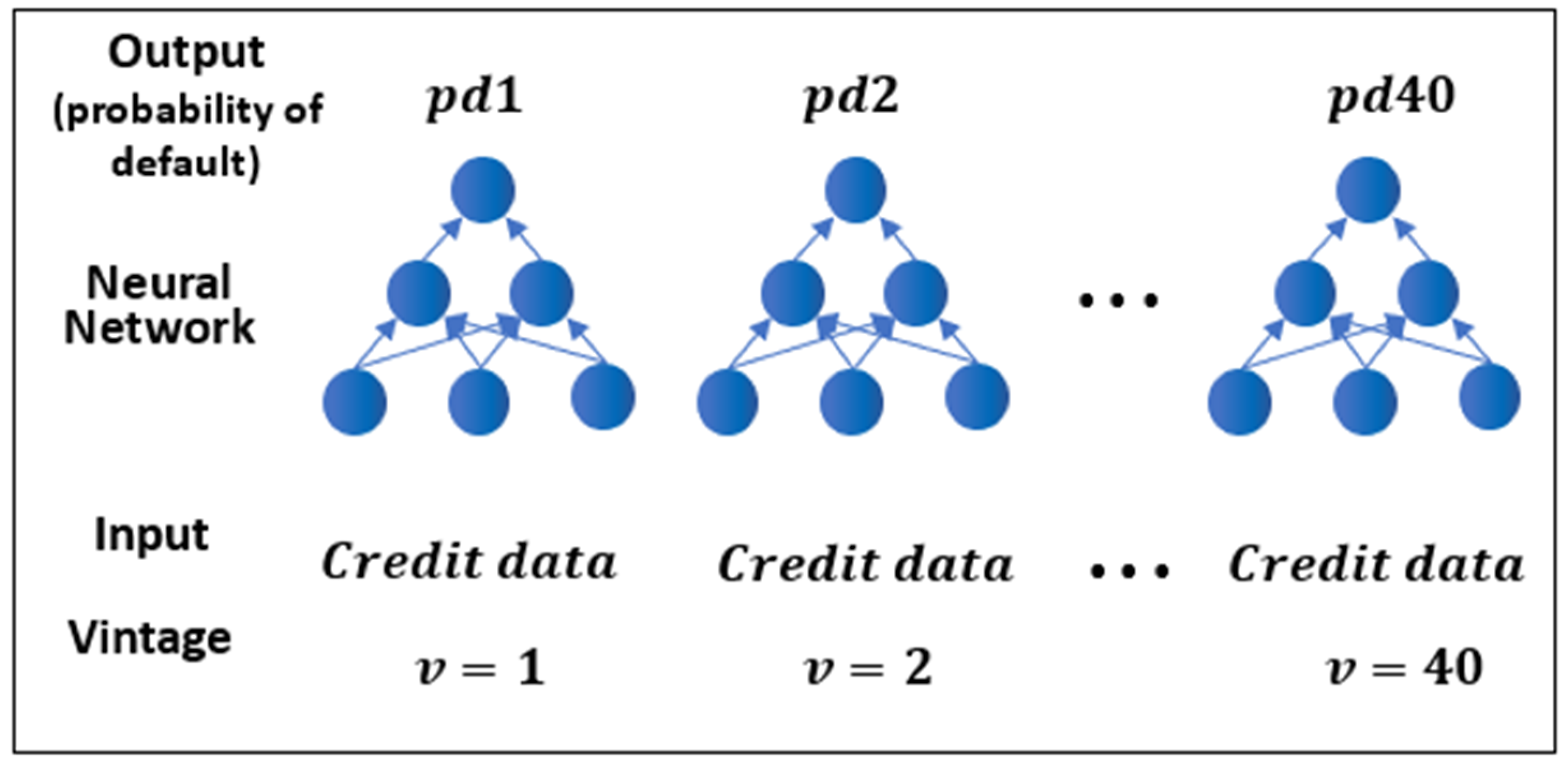
3.3. Neural Network with DTSM (NN-DTSM) for Credit Risk

The model structure in Equation (4) is constrained as a linear model. We hypothesize that a better model can be built with a non-linear model structure since introducing non-linearity enables interaction terms between features, automated segmentation between population subgroups, and representation of non-linear relationships between features and outcome variables. Equation (4) can be extended by changing the linear term into a nonlinear equation. For this, we replaced Equation (4) with a neural network structure. The log of the likelihood function in Equation (5) could be taken as the objective function for the neural network and this corresponds to the usual cross-entropy loss.

The neural networks are built as vintage models, i.e., a suite of neural networks, one for each origination period, following Ohno-Machado (1996). This is to match standard industry practice for vintage models and also to make estimations of neural networks less computationally expensive. Each subnetwork of this architecture is a multilayer perceptron (MLP) neural network (Correa et al. 2011), which consists of a dropout layer (to moderate overfitting), an input layer, several hidden layers, and an output layer. The dropout was proposed by Dahl et al. (2013) who pointed out that the overfitting can be prevented by randomly deleting part of the neurons in hidden layers and repeating this process in different small data samples to reduce the interaction between feature detectors (neurons). Each neuron in the hidden layer receives input from the former layer, computes its corresponding value with a specific activation function, and transfers the output to the next layer. The output of the neuron calculated with the activation function represents the status. In each neural subnetwork, we applied the RELU activation function to each hidden layer, $y=\max (0,x)$, and applied the sigmoid activation function to the output layer which corresponds to a logit link function:

$$y=\frac{1}{1+e^{-x}}$$

(6)

The overall architecture of the multiple neural networks with discrete-time survival analysis is shown in Figure 1.

Each neural network has a single unit in the output layer predicting an estimation of PD (with value 0 to 1) at a certain discrete time point. In our study, we combined 40 neural networks which were constructed at the vintage level based on the datasets covering the period from 2004 to 2013 (i.e., from v = 1 to v = 40), which was divided into quarterly subsets (the input of each separate model) and assigned to the subnetworks for training and testing. Each subnetwork predicted the default event at its corresponding quarter and the overall output function for the DTSM with neural network is

$$P_{it}=F\left(s_j\left({\mathbf{w}}_i, {\mathbf{x}}_{it}\right)\right) \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} {j=v}_i$$

(7)

where $s_j$ is the subnetwork in each vintage j and $F$ is the logit function.

In machine learning frameworks, it is important to tune hyperparameters for optimal performance. Unsuitable selection of hyperparameters can lead to problems of underfitting or overfitting. However, the process of selecting appropriate hyperparameters is time-consuming. Manually combining different hyperparameters in neural networks is tedious. Meanwhile, it is impossible to explore many multiple combinations in a limited time. As a result, grid search is a compromise between exhaustive search and manual selection. Grid search tries all possible combinations of hyperparameters from a given candidate pool and chooses the best set of parameters according to prediction performance. Typically, grid search calculates loss (e.g., mean square error or cross-entropy) for each set of possible values from the pool by using cross-validation (Huang et al. 2012). The use of cross-validation is intended to reduce overfitting and selection bias (Pang et al. 2011). In our study, we combined grid search with cross-validation with specified parameter ranges for the number of hidden layers, the number of neurons in each layer, and the control parameter for regularization.

3.4. Age–Period–Cohort Effects and Lexis Graph

In the context of better analyzing time-ordered datasets, age–period–cohort (APC) analysis is proposed to estimate and interpret the contribution of three kinds of time-related changes to social phenomena (Yang and Land 2013). APC analysis is composed of three time components, age effects, period effect, and cohort effect, where each one plays a different role, see (Glenn 2005; Yang et al. 2008; Kupper et al. 1985).

• The age effect reflects effects relating to the aging and developmental changes to individuals across their lifecycle;
• The period effect represents an equal environmental effect on all individuals over a specific calendar time period simultaneously, since systematic changes in social events, such as a financial crisis or COVID-19, may cause similar effects on individuals across all ages at the same time;
• The cohort effect is the influence on groups of observations that originate at the same time, depending on the context of the problem. For example, it could be people born at the same time or cars manufactured in the same batch.

In the context of credit risk, loan performance can be decomposed by an APC model into loan age performance, period effect through calendar time of loan repayment schedule, and cohort effect through origination date (vintage) of the loan (Breeden 2016; Breeden and Crook 2022). In credit risk, the calendar time effect reflects macroeconomic, environmental, and societal effects that impact borrowers at the same time, along with changes in legislation. Operational changes in the lender’s organization, such as changes in risk appetite, can affect vintage (cohort) or environmental (period) timelines.

The Lexis graph is a useful tool to represent and visualize APC in data. We describe it in the context of credit risk here to show default intensities in different timelines. In the Lexis graph, the x-axis represents the calendar time and the y-axis represents the loan age effect. Each square in the graph represents a specific PD modeled by the DTSM based on the account panel data corresponding to that time point. The shade (or color) of each square thus indicates the degree of the probability of default of each account at the corresponding time point, the darker, and the higher. For examples of Lexis graphs, see the figures following experimental results in Section 5.2.

Although a Lexis graph can be produced for the whole loan population, it is useful to produce Lexis graphs and, consequently, APC analysis by different subpopulations or population segments. If linear survival models are used to construct the Lexis graph, this is not possible, since the time variables are not linked to other variables that could differ between segments. However, the use of NN-DTSM will enable segment-specific Lexis graphs as a natural consequence of the non-linearity in the model structure and it is one of the key contributions of this study.

3.5. Age Period Cohort Model

We considered APC models built on aggregations of accounts using the prediction output of the DTSMs as training data. These data are essentially the points given in the Lexis graph and the APC model could be seen as a way to decompose the three time components in the Lexis graph.

Firstly, it is notable that calendar time c can be given as the sum of origination date v and loan age t: $c=v+t$. Therefore, the outcome of the APC model could be expressed and indexed on any two of these and we used loan age (t) and vintage (v). For this study, the outcome variable was the average default rate predicted by the DTSM at this particular time point computed as

$$D_{vt}=\frac{1}{\left|S\right|}\sum _{i\in S}{P}_{it} \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} S=\left\{i:t\le t_i^{*}, v=v_i\right\}$$

(8)

where $S$ is the index set of observations to include in the analysis. This may be the whole test set or some segment that we wish to examine. To represent the APC model, we used the following notation for three sets of indicator variables corresponding to each timeline at the time point given by $v,t,\mathrm{a}\mathrm{n}\mathrm{d} c$

• For all t such that $1\le t\le N_T$, where $N_T=\max \left(t_i^{*}\right)$

  $${\delta }_t^{\left[T\right]}(x)=\left\{\begin{array}{l}1, \mathrm{if} x=t\\ 0, \mathrm{otherwise}\end{array}\right.$$

  (9)
• For all v such that $1\le v\le N_v$

  $${\delta }_v^{\left[V\right]}(x)=\left\{\begin{array}{l}1, \mathrm{if} x=v\\ 0, \mathrm{otherwise}\end{array}\right.$$

  (10)
• For all c such that $1\le c\le N_c$

  $${\delta }_c^{\left[C\right]}(x)=\left\{\begin{array}{l}1, \mathrm{if} x=c\\ 0, \mathrm{otherwise}\end{array}\right.$$

  (11)

These represent the one-hot encoding of the time variables. Then, the general APC model in discrete time is

$$D_{vt}=\sum _{s=1}^{N_T}{\alpha }_s{\delta }_t^{\left[T\right]}(s)+\sum _{u=1}^{N_v}{\beta }_u{\delta }_v^{\left[V\right]}(u)+\sum _{b=1}^{N_c}{\gamma }_b{\delta }_c^{\left[C\right]}(b)+{\epsilon }_{vt}$$

(12)

where ${\alpha }_s$, ${\beta }_u$, and ${\gamma }_b$ represent the coefficients on the timeline indicator variables and ${\epsilon }_{vt}$ is an error term given from a known distribution, typically normal. This is a general model in discrete time since it allows the estimation of a separate coefficient for each value in each timeline. Once the data points $D_{vt}$ were generated from the model using (8), the APC model (12) could be estimated using linear regression.

However, the APC identification problem needed to be solved. This was due to the linear relationship between the three timelines, i.e., $c=v+t$. The identification problem in APC analysis cannot be automatically, perfectly, or mechanically solved without making further restrictions and assumptions on the model to find a plausible combination of APC, ensuring those assumptions are validated across the whole lifecycle of analysis (Bell 2020). The identification problem was derived as follows to show there was not a unique set of solutions to Equation (12); rather, there were different sets of solutions controlled by an arbitrary slope term $\sigma$.

Firstly, $c=v+t$ was combined with Equation (12) for some arbitrary scalar $\sigma$,

$$D_{vt}=\sum _{s=1}^{N_T}{\alpha }_s{\delta }_t^{\left[T\right]}(s)+\sigma t+\sum _{u=1}^{N_v}{\beta }_u{\delta }_v^{\left[V\right]}(u)+\sigma v+\sum _{b=1}^{N_c}{\gamma }_b{\delta }_c^{\left[C\right]}(b)-\sigma c+{\epsilon }_{vt}$$

(13)

Then, it was noticed from the definition of the indicator variables that

$$t=\sum _{s=1}^{N_T}s{\delta }_t^{\left[T\right]}(s),v=\sum _{u=1}^{N_v}u{\delta }_v^{\left[V\right]}(u),c=\sum _{b=1}^{N_c}b{\delta }_c^{\left[C\right]}(b),$$

(14)

this gave

$$D_{vt}=\sum _{s=1}^{N_T}\left({\alpha }_s+\sigma s\right){\delta }_t^{\left[T\right]}(s)+\sum _{u=1}^{N_v}\left({\beta }_u+\sigma u\right){\delta }_v^{\left[V\right]}(u)+\sum _{b=1}^{N_c}\left({\gamma }_b-\sigma b\right){\delta }_c^{\left[C\right]}(b)+{\epsilon }_{vt}$$

(15)

New coefficients are thus constructed as follows:

$${\alpha }_s^{\prime }={\alpha }_s+\sigma s,{\beta }_u^{\prime }={\beta }_u+\sigma u,{{\gamma }_b^{\prime }=\gamma }_b-\sigma b$$

(16)

to form

$$D_{vt}=\sum _{s=1}^{N_T}{\alpha }_s^{\prime }{\delta }_t^{\left[T\right]}(s)+\sum _{u=1}^{N_v}{\beta }_u^{\prime }{\delta }_v^{\left[V\right]}(u)+\sum _{b=1}^{N_c}{\gamma }_b^{\prime }{\delta }_c^{\left[C\right]}(b)+{\epsilon }_{vt}$$

(17)

which is another solution to the exact same regression problem. Therefore, we showed that Equation (12) has no unique solution and, indeed, there are infinite solutions, one for each choice of $\sigma$. We called $\sigma$ a slope since it alters each collection of indicator variable coefficients by a linear term scaled by $\sigma$. The identification problem is to identify the correct value of slope $\sigma$.

To resolve this problem, there were several approaches which involved placing constraints on the model, such as removing some variables (essentially setting them to zero) or arbitrarily setting one set of the coefficients to a fixed value (i.e., no effect), see, e.g., Fosse and Winship (2019). However, these solutions can be arbitrary. Therefore, in this study, two approaches were considered: (1) regularization and (2) constraining the calendar time effect in relation to observed macroeconomic effects. The first approach includes regularization penalties on the coefficients in the loss function that can be implemented in Ridge regression expressed by the loss function,

$$L=\left(\frac{1}{N_v{N}_t}\sum _{v=1,t=1}^{N_v, N_t}{\epsilon }_{vt}^2\right)+\lambda \left(\sum _{s=1}^{N_T}{\alpha }_s^2+\sum _{u=1}^{N_v}{\beta }_u^2+\sum _{b=1}^{N_c}{\gamma }_b^2\right)$$

(18)

which minimizes mean squared error plus the regularization term, where $\lambda$ is the strength of the regularization penalty. This loss function provides a unique solution in the coefficients for (12). The second approach is discussed in detail in the next section.

3.6. Linear Regression and Fitting Macroeconomic Variables

In the initial APC model, $\sigma$ was unknown. A common and recommended solution to the identification problem is to use additional domain knowledge (Fosse and Winship 2019). In this case, we supposed that the calendar-time effect would be caused by macroeconomic conditions, at least partly. Therefore, by treating the APC model calendar-time coefficients $\gamma$ as outcomes, these could be regressed from observed macroeconomic data. As part of this process, the slope $\sigma$ could be estimated to optimize the fit. Therefore, we used the term $\sigma$, which relates to the time trend of the calendar to adjust the shape of the calendar time function. Once the calendar time function was fitted, the vintage function and loan age function were also determined. The time-series regression was defined as

$$\left({\gamma }_c-\sigma c \right)={{\beta }_0}^{\prime }+\sum _{j=1}^M{{\beta }_j}^{\prime }{m}_{j(c-l_j)}+{\epsilon }_c$$

(19)

where ${\gamma }_c$ represents the raw coefficients of the calendar time function from the APC model regression, $M$ is the number of macroeconomic variables (MEVs), $m_{j(c-l_j)}$ indicates the $j\mathrm{t}\mathrm{h}$ MEV, with a particular time lag $l_j$ and ${\epsilon }_c$ is an error term, normally distributed as usual. This can be rewritten as

$${\gamma }_c={{\beta }_0}^{\prime }+\sum _{j=1}^M{{\beta }_j}^{\prime }{m}_{j(c-l_j)}+\sigma c+{\epsilon }_c$$

(20)

and it can be seen as a linear regression with $\sigma$ a coefficient on variable c, which can then be estimated with the intercept ${{\beta }_0}^{\prime }$ and other coefficients ${{\beta }_j}^{\prime }$. Typical MEVs for credit risk are gross domestic product (GDP), house price index (HPI), and national unemployment rate (see, e.g., Bellotti and Crook 2009). This solution, to fit estimated coefficients against economic conditions, is similar to that used by Breeden (2016) who solves the identification problem by retrending the calendar-time effect to zero. However, in that research, the retrending is against a long series of economic data, whereas we used time series regression against a shorter span of data. This is because for shorter periods of time (less than 5 years), the calendar-time effect may have a genuine trend that can be observed in macroeconomic data over that time but retrending over long periods would remove that.

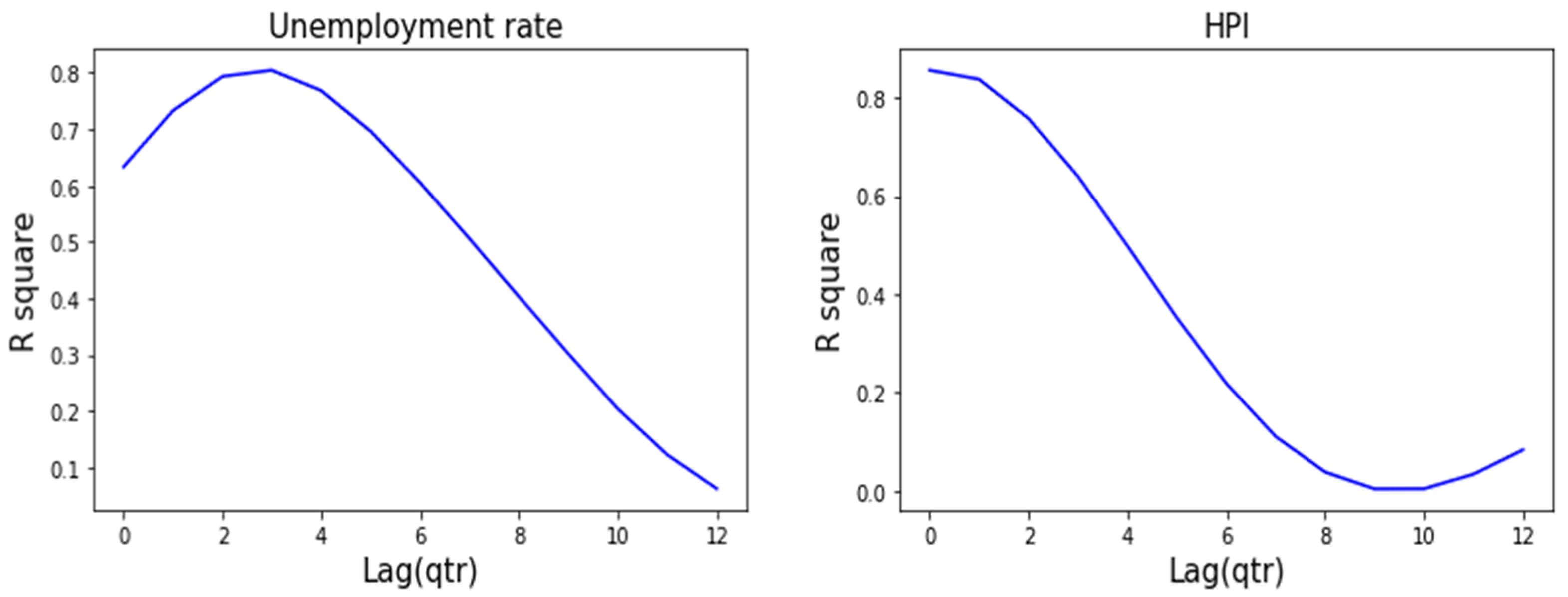
3.7. Lagged Macroeconomic Model

Some MEVs might have a lagged effect in the model. For example, the fluctuation in the house price will not have an immediate effect on people’s behavior but people will change their consumer behavior after a few months. To find the best fit between dynamic economic variables and customer behaviors, a lagged univariate model was used for each MEV:

$$y_c={{\beta }_0}^{\prime }+{{\beta }_1}^{\prime }{m}_{j(c-l_j)}+{\eta }_c$$

(21)

Formula (21) is in the form of time series regression, where $y_c$ indicates the customer behavioral variables, $m_j$ denotes the $j\mathrm{t}\mathrm{h}$ macroeconomic time series variable, $l_j$ is the lagged offset, and ${\eta }_c$ is a normally distributed error term. Univariate regression of $y_c$ on the MEV was repeated for different plausible values of $l_j$ and the best value of $l_j$ was chosen based on maximizing $R^2$. Once $l_j$ was selected for each MEV $j$, Equation (20) could then be estimated.

3.8. Overall Framework of the Proposed Method

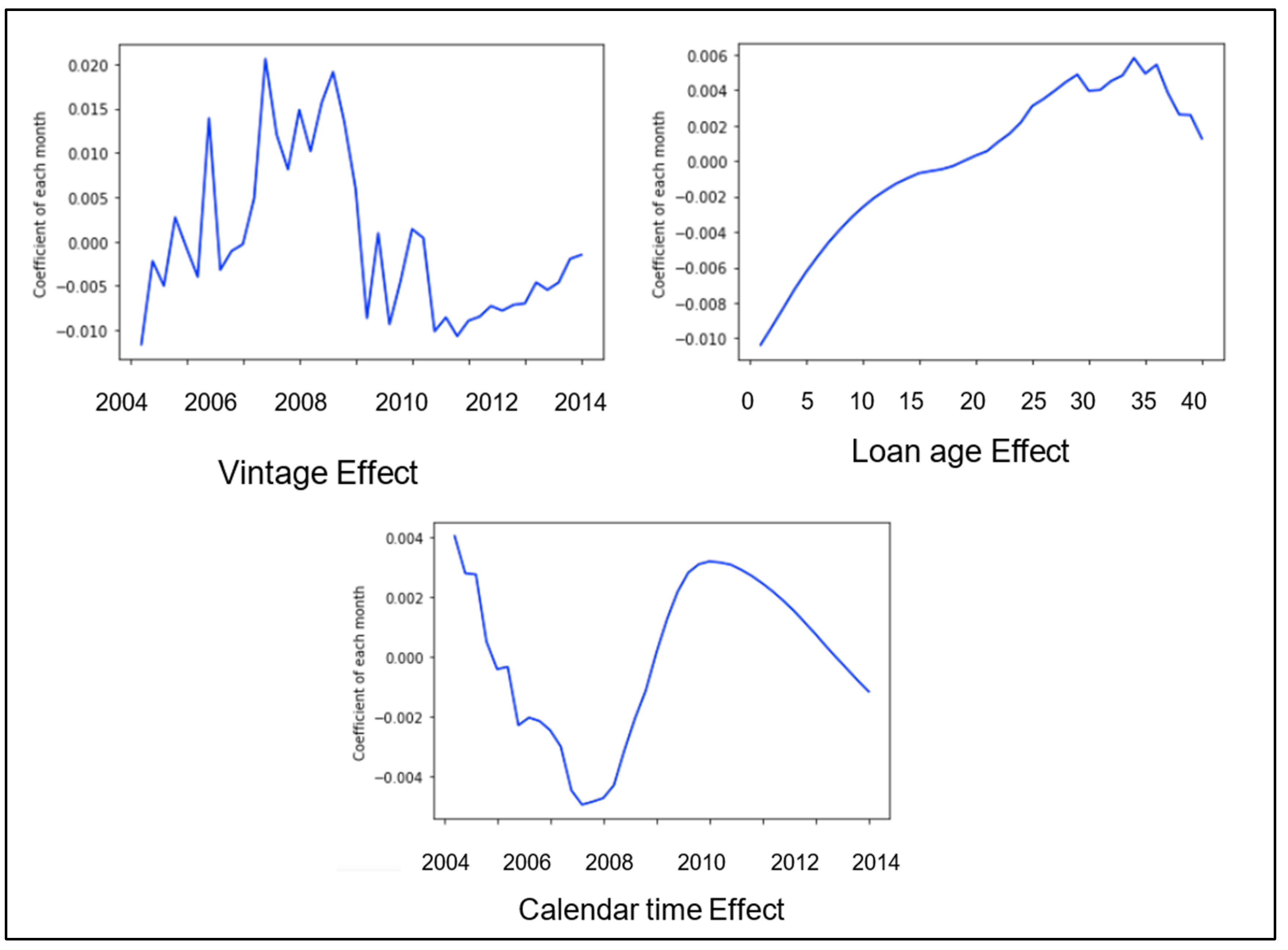
The overall flowchart for our method is shown in Figure 2. The neural network in this study consisted of multiple vintage-level sub-networks. After the model was trained, the next step was to extract and analyze different kinds of customer behaviors from the model by inputting different data segments, which might show varied characteristics (e.g., low-interest rate customer groups). These data segments helped to construct Lexis graphs from the model which can visualize the characteristics of different data groups. To better capture and analyze the risk from the model, we used APC ridge regression to decompose the default rate modeled by the neural network in the Lexis graph into the three APC timelines: age, vintage, and calendar time. These can finally be expressed as three APC graphs that can help experts to better understand and explain the behavior of different loan types.

The coefficients of calendar dates extracted from the neural network represented the size and direction of the relationship between the specific calendar date and loan performance. Matching these coefficients with the macroeconomic data revealed the relationship between the macroeconomic effect in the model and its impact on loans. This helped to solve the APC identification problem. It is possible that the regularized APC model already provided the correct slope $\sigma$ and that a statistical test on the time-series macroeconomic model was used to test this.

4. Data and Experimental Design

4.1. Mortgage Data

We used a dataset of over 1 million mortgage loan-level credit performance data originating in the USA from 2004 to 2013, publicly available from Freddie Mac1. Freddie Mac is a government-sponsored enterprise which plays an important role in the US housing finance system. It buys loans from approved lenders and sells the securitized mortgage loans to investors, which helps to improve the liquidity and stability of the US secondary mortgage market and promote access to mortgage credit, particularly among low- and moderate-income households (Frame et al. 2015). These characteristics of Freddie Mac facilitate us to gain access to a large number of publicly available data covering various kinds of accounts which are representative of the US mortgage market.

The quarterly datasets contain one file of loan origination data and one file of monthly performance data covering each loan in the origination file. The origination data file includes variables that are static and collected at the time of application from the customers, while the monthly performance data files contain dynamic variables which record customers’ monthly repayment behavior. See the general user guide and summary statistics from the Freddie Mac single family loan level dataset web site2 for further information about the variables available in the dataset. Loan sequence number is a unique identifier assigned to each loan. These two data files contain the same sequence number for each loan, which is used to join the two files together to form the training datasets. The credit score, UPB (unpaid balance), LTV (loan-to-value percentage), DTI (debt-to-income percentage), and r (interest rate) are five core variables used in the default model. A credit score is a number that represents an assessment of the creditworthiness of a customer, in other words, credit score is the likelihood that the customer will repay the money (Arya et al. 2013). UPB is the portion of a loan that has not been repaid to the lenders. LTV is the mortgage amount borrowed divided by the appraised value of the property, where applications with high LTV ratios are generally considered high risk loans. DTI is calculated by dividing monthly debt payment by monthly income. If the status of these variables is not so good, the application will be rejected, or possibly approved with a higher interest rate to cover the additional risk. Apart from these variables, there are other categorical variables, which may represent risk factors and are preprocessed before being included into the model. For example, there are five categories in the loan purpose variable: P (purchase), C (refinance—cash out), N (refinance—no cash out), R (refinance—not defined), and 9 (not available), which cannot be included directly in the model. Therefore, one-hot encoding is used to transform the categorical variable into numeric indicator variables.

We defined an account status as default based on the failure event that minimum expected repayment was not received for three consecutive months or more. This definition is common in the industry and follows the Basel II convention (BCBS 2006). Notably, a loan extension or repayment holiday, which enables the borrower to skip repayments with agreement from the lender, would not be recorded as a missed repayment and would not trigger a default event. Since we used a survival model where default was recorded at a particular loan age, there was no need to measure default in an observation window following origination, as would be required for static credit risk models (Bellotti and Crook 2009).

Default rates in the dataset are shown in Figure 3. The default event is rare, which leads to an unbalanced dataset. This may affect the performance of the machine learning classification algorithm. The model would, in theory, have been dominated by the majority class (i.e., non-default) and thus may not have made accurate predictions for the minority class, while in many contexts like credit risk, we were more interested in discovering patterns for the rare class. To address this problem, the non-defaults in the dataset were under sampled at the account level, so that only 10% of the non-default accounts were reserved by random selection. In the original dataset, the proportion of default data was only 0.1% and after under sampling, the default rate in the modified dataset rose to around 1%.

4.2. Macroeconomic Data

Survival analysis provides a framework for introducing MEVs, which in turn can influence the prediction of default. Bellotti and Crook (2009) explored the hypothesis that macroeconomic variables such as unemployment index, house price index, production index can affect the probability of default. For instance, an increase in unemployment rate is expected to cause a higher risk since individuals who lost their job may not be able to make their repayments. Experiments were conducted to test the relationship between MEVs and PD. The results showed that unemployment index, house price index, and production index (proxy for GDP) have a statistically significant explanation of default. Following this study, we included these variables in our experiments for APC modeling as described in Section 3.6. Real GDP was used instead of nominal GDP because the nominal GDP was calculated based on current prices, whereas the real GDP was adjusted by a GDP deflator, which is a measurement of inflation since a base year. In the previous work, MEVs were included directly in the DTSM (Bellotti and Crook 2013) but, in this study, we did not take this approach for the following reasons:

• We devised APC to capture the whole calendar-time effect. If MEVs were included directly into the model, this most important part of the calendar-time effect would be missing;
• We did not assume MEVs represent all calendar time effects, because some effects such as legislation, environmental or social changes would also influence the calendar time function and these should also be included as part of the calendar-time effect;
• Some previous papers were looking to build explanatory models but, in this study, we developed predictive models. MEVs in our study will be used later as criteria to assess the accuracy of the model and directly including them in the model would reduce the reliability of this testing process.

All of the macroeconomic datasets covering the period of 2001 to 2013 show moderate changes over time. Figure 4 shows each of the MEV time series. The GDP growth dropped sharply in 2008, after which it went down to a trough (−3.99%), then quickly rose back and fluctuated slightly (ranging from 0.9% to 2.9%). The house price index gradually rose from 247.88 in 2001 to 380.9 in 2007, before falling to 308.79 in 2012, after which it slightly rose to 329.2 in 2013. As for the growth of the unemployment rate, it rose in a very short time within 2001 (by 35.9%) and fell until 2006, after which it sharply rose by 80% in 2009, before falling again steadily over the remaining period.

4.3. Evaluation Methods

Since we modeled time-to-default events, this meant the outcomes were binary (0 or 1), so the usual performance measures such as mean squared error and R-squared did not apply. The ROC curve is one of the ubiquitous methods to show the performance of a binary classifier at all classification thresholds in machine learning. The ROC curve is a graph showing the true positive rate against the false positive rate at each set of the decision threshold from 0 to 1 (on probability) and the area under this curve (AUC) was used to indicate the overall goodness of fit of the binary classifier. AUC can also be used in the context of survival analysis. However, it cannot fully estimate the performance of the survival model since AUC does not fully take time aspects into account (Dirick et al. 2017). Also, the dataset in our study was extremely imbalanced, which limits the power of AUC. Therefore, to better measure and validate the goodness of model fit with the data, we used McFadden’s pseudo-R-squared to compare between our proposed NN-DTSM and linear DTSM:

$${pseudo-R}^2=1-\frac{\log L\left(M_{target}\right)}{\log L\left(M_{baseline}\right)}$$

(22)

where $L\left(M_{target}\right)$ and $L\left(M_{baseline}\right)$ indicate the likelihood of the target prediction model and baseline model (null model), respectively. Similar to R-squared used in linear regression to calculate the proportion of explained variance, pseudo-R-squared measures the degree of improvement in the model likelihood over a null model, which is a simple baseline model containing no predictor variables (Hemmert et al. 2018).

5. Results

5.1. Neural Network versus Linear DTSM

5.1.1. Experimental Setup

The mortgage dataset is divided into 40 subsets corresponding to each quarter of the origination data from 2004 to 2013. Each of these data subsets is then randomly split into 75% training data for model build and 25% independent test data. Each DTSM and NN-DTSM is trained on only the training data and is labeled with its corresponding time period, e.g., model07_4 represents the model for the fourth quarter of 2007. The underlying neural network is initially fully connected between layers, although dropout is used during training to regularize the network and avoid overfitting.

5.1.2. Hyperparameter Selection Using Grid Search

The performance of the neural network is dependent on tuned hyperparameters. The structure of the neural network (e.g., the number of neurons and the number of layers) and the training approach (e.g., training iteration for the neural network) will affect the model accuracy. Additionally, the dropout layer embedded in the neural network will prevent the model from overfitting and potentially improve performance too. Hence, different combinations of values of these parameters are explored to find the optimal performance of the model. Formally, we express this as an optimization problem,

$$\min l(d,nn,nl,ti)$$

where $l$ is the measurement of the goodness of fit of the neural network built with hyperparameters, $d$ id the percentage of dropout in the hidden layers, $nn$ is the number of neurons in each hidden layer, $nl$ is the number of hidden layers, and $ti$ is the number of training iterations. For this study,$l$ is the minus log-likelihood function (a lower value indicates better performance; the likelihood function is Equation (5)).

Grid search with cross-validation is used to find a solution to this optimization problem. The grid search algorithm is commonly used for hyperparameter tuning (see, e.g., Radzi et al. (2021) and Alfonso Perez and Castillo (2023)). Grid search works by building the neural network across all combinations of plausible sets of candidate values for each hyperparameter. The combination of values that achieves the minimum value of $l(d,nn,nl,ti)$ is selected as the solution for building the final model for independent testing. To avoid overfitting, only training data are used during the grid search process and $k$-fold cross-validation is used to measure performance within each iteration of grid search. This means that the training data are randomly split into $k$ approximately equal sized partitions and the model is built on $k-1$ of these partitions and tested on the remaining $k$th. There are $k$ ways to do this, so the final performance is then given as the average,

$$l\left(d,nn,nl,ti\right)=\frac{1}{k}\sum _{s=1}^k{l}_s\left(d,nn,nl,ti\right)$$

where $l_s(d,nn,nl,ti)$ is the minus log-likelihood measured on partition $s$, of the neural network built on all partitions of the training data except the $s$th, with hyperparameters $d,nn,nl, \mathrm{a}\mathrm{n}\mathrm{d} ti$.

Candidate sets for hyperparameters are given in

Table 1. Candidate sets of possible values of the hyperparameters for a grid search.

	Hyperparameter	Values
$d$	Percentage of dropout (regularization):	0, 0.1, 0.2, 0.3, 0.4, 0.5
$nn$	Number of hidden layers:	2, 4, 6, 8
$nl$	Number of neurons in each layer:	2, 4, 6, 8
$ti$	Training iteration for the network:	5, 10, 15, 20, 25, 30

and 5-fold cross-validation is used. Overall, with these settings, the grid search requires $6\times 4\times 4\times 6\times 5=2880$ builds of NN-DTSM. Other hyperparameters were not included where reasonable default values were available, in order to manage the computational time of the grid search. In particular, a batch size of 32 was used as the default setting for Keras’ Model.fit method. The result of the grid search gives values of minus log-likelihood (the target loss function) ranging from 0.07681 to 0.08257, with the best value 0.07681 when using the following hyperparameters of the neural network: no dropout, 4 hidden layers, 8 neurons in each layer, and 20 epochs for training.

5.1.3. Comparison between NN-DTSM and Linear DTSM

The vintage-level neural networks are compared against vintage-level linear DTSM and aggregate linear DTSM, which is built across training data from all vintages together. Pseudo-R-Square was calculated for each model in quarterly test sets from 2004 to 2013 and the results are shown in Figure 5. We used L2 regularization to stabilize the linear DTSM estimations. Figure 5 shows that the neural network outperforms the vintage-level linear DTSMs most of the time. The aggregate linear DTSM performs better but, on average, the neural network outperforms it, especially after 2009.

5.2. Lexis Graphs

Based on the predictions from the NN-DTSM, several Lexis graphs are produced for the whole population (the general case) and for different segments of the population: broadly, low risk (LTV < 50% and r < 4%), and high risk (r > 7.5%). Since the neural network is non-linear we can expect it to generate Lexis graphs that are sensitive to population segment characteristics. Since the underlying DTSM models include origination variables such as credit score and LTV, it should be noted when interpreting these Lexis curves that the vintage effect is the remaining vintage effect controlling for these measurable risk factors, or, in other words, the vintage effect shown is the “unknown” vintage effect that is not directly measurable in the given risk variables, such as underwriting rules, risk appetite, unobserved borrower characteristics, and so on. This is somewhat different to vintage effects reported by Breeden (2016), e.g., which represent the whole vintage effect (including possibly measurable risk factors). Results are shown in Figure 6, Figure 7 and Figure 8.

For the Lexis graph for the whole population, Figure 6, we can see the financial crisis emerging after 2008 with a dark cloud of defaults from 2009 to 2013. But, interestingly, the Lexis graph shows that these defaults are along diagonal bands, corresponding to different account vintages; thus, each band indicates the risk associated with some vintage. In particular, if we trace the dark diagonals back to the horizontal axis (loan age = 0) we see that the riskiest origination periods were between 2006 and 2008. On the vertical axis, we can see that defaults are rarer within the first year of a loan.

The Lexis graphs for especially low and high risks accounts reveal two different kinds of customer behavior patterns. For high risk, high default rates emerge earlier and PD is much higher. For high risk customers, PD is as high as 0.05, whereas for low risk groups, PD is only as high as 0.0035. We see that in both groups, the most vulnerable cohorts begin in 2006 but end sharply in 2010 for high risk groups, whereas a tail of further defaults are found for low risk groups into 2012 although with much lower PDs.

5.3. APC Model

We use the Lexis graph and local APC linear models to interpret the black box of neural network. The relationship between the three time components: loan age, calendar time and vintage, and the PD outputs of the neural network are modeled using ridge regression. The ridge coefficient is chosen to maximize model fit on an independent hold-out dataset. APC effects are decomposed using this approach, as described in Section 3.5, and different risk patterns for different customers are analyzed. Different groups of mortgage applicants are illustrated in this section.

Figure 9 shows time components for the general population. Higher values relate to higher risk of default on a PD scale. This vintage curve clearly shows that the risk reached a peak before 2008, remained at a high level for around two quarters, and then dropped rapidly in 2009, indicating the time the banks became more risk adverse facing the unfolding mortgage crisis. For the loan age effect of the general case, the risk steadily increased to around 30 quarters and then maintained at a stable level, before dropped slightly at 40 quarters. For the calendar time effect, the risk actually went down until 2008, which indicates that the operating environment and US economy were performing well at that time, just before the financial crisis. However, the risk increased sharply in 2009 and 2010 as the financial crisis took hold.

Figure 10 shows the results for the segment of relatively low LTV (<50%) and low r (<4%), corresponding to the Lexis graph in Figure 7. All APC effects are much smaller than that of the general case, which makes sense since this is expected to be a low risk group. In particular, the vintage effect is flatter, with noise, and has one peak in risk during 2006. Also, the calendar time effect peaked much later: 2013 compared to 2011 in the general case.

Figure 11 shows the results for a segment of accounts with exceptionally high interest rates, corresponding to the Lexis graph in Figure 8. All APC effects are much larger than in the general case; the vintage effect is shaped differently with a sharper rise and peak from 2007 to 2008. Noticeably, the calendar time effect became apparent about two to three quarters before the general case (i.e., it is already quite high in 2009).

5.4. Macroeconomic Data Fitting

5.4.1. Choose Time Lag for Macroeconomic Data

We suppose the MEVs have a lagged effect on default risk and we use univariate linear regression models to fit the calendar time effect decomposed by the model with each MEV with different time lags of the variables to discover the best lag, using the method discussed in Section 3.7 and Equation (21). Each linear model is trained using the macroeconomic data ranging from 2000 to 2013 and the calendar time coefficient ranging from 2004 to 2013 (we define the range of potential lag time as up to 3 years). The results are shown in Figure 12.

For every MEV, the $R^2$ peaks within 12 quarters, which means the best fitting of time lags for those variables are all within 3 years. The highest $R^2$ value for GDP growth and growth of unemployment rate are still very low (around 40%), which shows that they do not fit well with the calendar time effect. So, these two variables are excluded from our experiments. Only unemployment rate and HPI are reserved for further studies.

After the MEVs used for fitting are determined, the next step is to find the time lag with the best fits (highest $R^2$) for each variable. We select different data segments representing different customer profiles and use NN-DTSM to construct APC graphs. The calendar time effect of each APC model is then fitted against unemployment rate and HPI to find particular time lags using the method described in Section 3.6. The results are shown in Figure 12 (lower graphs) and Figure 13 and Figure 14. For the unemployment rate, low-risk customers have the longest time lag with a peak of $R^2$ (R square) at 5 quarters, followed by the general customer group of 4 quarters and the high-risk group of 3 quarters; while for HPI, only low-risk group have time lag of 1 quarter, which indicates that HPI affects the low-risk customer a quarter behind but has an immediate impact on the general and high-risk customer groups.

5.4.2. Multivariate Fit of MEVs with a Calendar Time Effect Component

To handle the APC identification problem, we use the time trend of calendar dates and MEVs to fit with the APC calendar time effect, using Equation (20). Lags on MEVs are chosen based on the results of univariate analysis in Section 5.4.1. The results are shown in

Table 2. Result of macroeconomic time series regression (adjusted R-squared = 0.938).

Variable	Coefficient Estimate	p-Value
X1 (coefficient of unemployment rate, lag 4 months)	$+4.000\times {10}^{-4}$	<0.0001
X2 (coefficient of HPI, lag 1 month)	$-3.118\times {10}^{-5}$	<0.0001
X3 (coefficient of the time trend)	$-5.309\times {10}^{-6}$	0.522

for the general case.

The results show that the adjusted $R^2$ exceeds 0.9, meaning the time trend together with the two MEVs with different best-fit time lag can fit well with the calendar time effect. Adjusted $R^2$ is used since sample size for this regression is low (40 observations). The coefficient on time trend is very small and the p-value is large (>0.5), which indicates that time trend is not an important variable for this regression and it is reasonable to suppose the slope $\sigma =0$. The consequence is that the regularization in the APC ridge regression is sufficient to solve the APC identification problem for this particular dataset and there is no need to adjust the slope post hoc.

6. Discussion

This new framework will benefit practitioners and supervisors in the financial services industry.

Firstly, many may not have already adopted panel models and DTSM in their credit risk modeling, but this paper may inspire them to do so and provide background on how to do it.

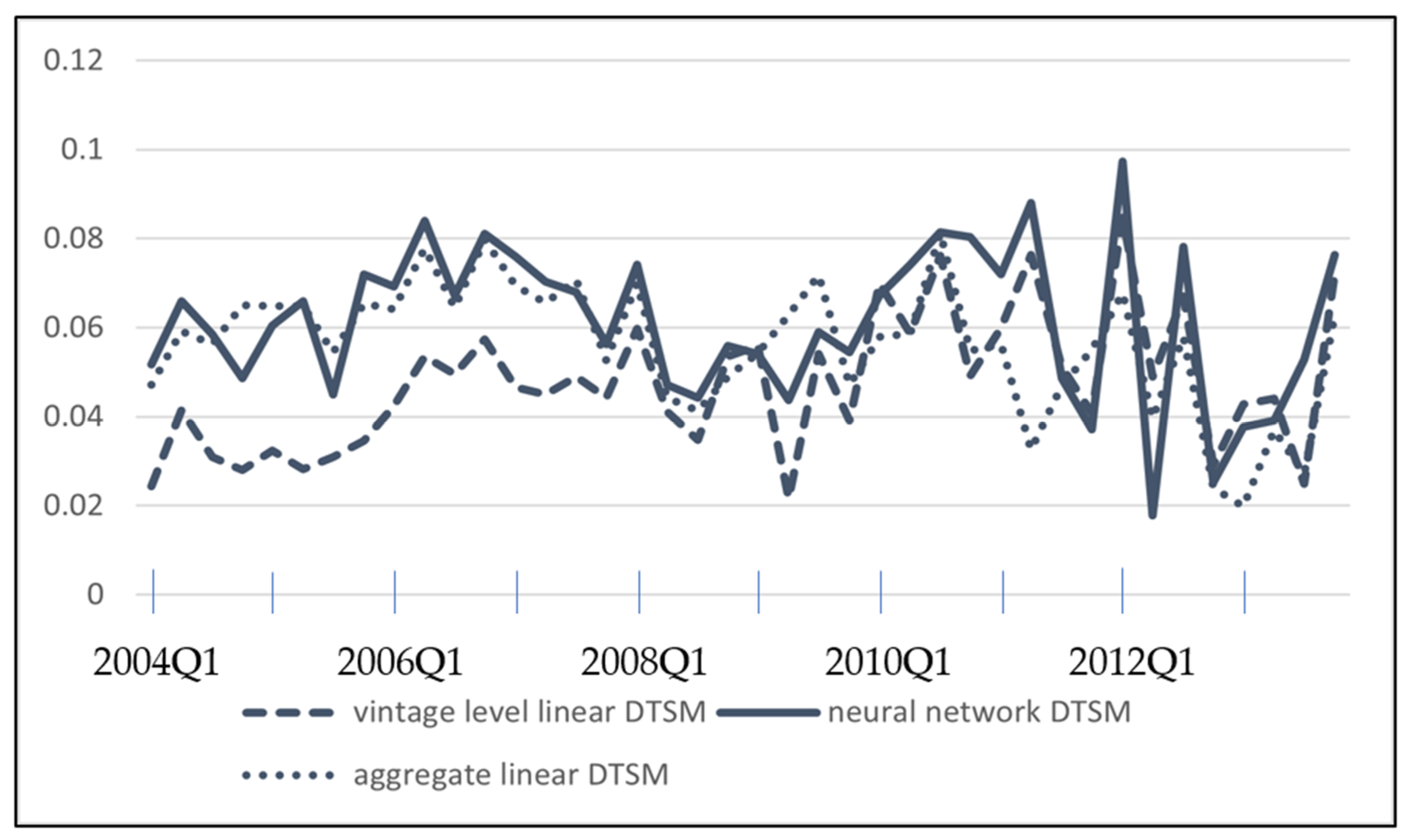
Secondly, machine learning is currently of great interest in industry and wider society and many financial institutions are considering how to leverage this technology in their business, especially neural networks. For those who already use linear DTSM based on existing approaches (e.g., Bellotti and Crook 2013; Breeden and Crook 2022) but who may wonder how to incorporate non-linear machine learning algorithms, this study provides a blueprint that can be used directly or as the basis for their own custom approaches. Our experiments on real-world mortgage data also demonstrate the potential benefit when adopting NN-DTSM for credit risk modeling, in terms of improved model fit and accuracy.

A key challenge for deploying machine learning in financial services is opacity and lack of explainability (Breeden 2021). The approach in this article addresses this concern by showing how the output of NN-DTSM can be interpreted using APC analysis, which will already be familiar with many practitioners, and can be conducted at the global level (i.e., across the whole population) or local level (i.e., for different segments), thus enabling trust in the model. Some practitioners have recently wondered how generative AI can be used in financial services to gain value (Kielstra 2023). Interestingly, the explanatory approach taken in this study is an example of generative AI since the Lexis graph is generated from the trained NN-DTSM.

Thirdly, this approach will also be valuable for supervisors as a methodological framework to test bank’s dynamic model development or be recommended for use. It can also be implemented as a benchmark model to check the performance of bank’s models. Finally, it could be extended to support stress tests, e.g., following a similar approach to Bellotti and Crook (2014).

The models in this study were implemented using Python 3.5 and Keras 2.4.3. Running on a conventional laptop (CPU:Intel(R) Core(TM) i7-10750H CPU @ 2.60 GHz, memory: 16 GB), it took less than 20 min to train NN-DTSM for all 40 vintages. Therefore, this model development is within the technological capacity of all financial institutions.

7. Conclusions

In this paper, the vintage-level neural networks were built for DTSM and evaluated on a large US mortgage dataset over a long period of time covering the 2009 financial crisis. The results show that the neural network is competitive with the vintage level and aggregate DTSMs. Furthermore, to improve the explainability of the black-box neural networks, we introduce Lexis graphs and local APC modeling. The Lexis graph shows the PD estimate from NN-DTSM decomposed into the three timelines using APC analysis: loan age, vintage, and calendar time, which allow us to visualize the change in the model behavior with the different time components. This approach helps to construct customer segment-specific APC graphs from the neural networks, which can better estimate, decompose, and interpret the contribution and risk pattern of the three time-related risks on the accounts due to loan age, calendar time, and vintage. Instead of just looking at the performance and estimates from NN-DTSM without understanding the mechanism and the reliability of the models, these APC graphs can help practitioners and researchers to build trust in the neural networks and better understand the story of the loan portfolio over time for specific datasets and customer segments. In contrast, the linear survival model can only provide PD estimate APC graphs for the entire population. To solve the APC identification problem due to the linear relationship between the three timelines (calendar time = loan age + vintage), we make further restrictions and assumptions on the model functions to find a reliable set of APC parameters. In this study, we use two approaches: (1) add regularization term into the loss function to control the complexity of the APC model and (2) control the parameters of APC timelines by an arbitrary slope term σ and correlate the calendar time effect with observed macroeconomic effects to calculate a unique solution, using time-series regression. We find a strong correlation between MEVs and the environmental risk time component estimated using our methodology.

This study was based on building separate NN-DTSMs at the vintage level. This is computationally convenient but it is worth considering that NN-DTSM is built on all data together, utilizing recurrent neural networks to leverage the time-series aspect of the data and allow the feedforward of information from one vintage to another. This will require more computational power to train the single large model but could yield benefits in terms of overall model performance. Additionally, this study includes only application and macroeconomic variables, since we specifically wish to explore the link between default and economic conditions. However, a further development would be to include lagged behavioral data such as past delinquency data or records of communication with borrowers. However, this will require special treatment of the behavioral variables since they are likely to be correlated over time to economic conditions themselves. Both of these would be interesting directions for future research.