Abstract
Wind-power generators around the world face two risks, one due to changes in wind intensity impacting energy production, and the second due to changes in electricity retail prices. To hedge these risks simultaneously, the quanto option is an ideal financial tool. The natural logarithm of electricity prices of the study will be modeled with a variance gamma (VG) and normal inverse Gaussian (NIG) processes, while wind speed and power series will be modeled with an Ornstein–Uhlenbeck (OU) process. Since the risk from changing wind-power production and spot prices is highly correlated, we must model this correlation as well. This is reproduced by replacing the small jumps of the Lévy process with a Brownian component and correlating it with wind power and speed OU processes. Then, we will study the income of the wind-energy company from a stochastic point of view, and finally, we will price the quanto option of European put style for the wind-energy producer. We will compare quanto option prices obtained from the VG process and NIG process. The novelty brought into this study is the use of a new dataset in a new geographic location and a new Lévy process, VG, apart from NIG.
1. Introduction
To achieve the ambitious goal of a world having net carbon zero emissions by 2050, renewable energy sources such as wind and solar are essential for power generation. In 2022, the contribution of wind energy increased beyond 2100 TWh in global energy production, which is an increase of 14% compared to the previous year, according to the International Energy Agency (IEA n.d.). Although on the world stage, wind-power production is increasing, the same movement can be seen in Alberta, Canada as well. According to the Alberta Electric System Operator (AESO), 1349 Mw capacity of wind-power generation was added to the grid in 2022 and has provided 12% of total electricity needs in Alberta (AESO n.d.a). Although there is clear popularity for wind energy, there are limitations to when wind can be utilized for energy production. For instance, wind turbines require a minimum wind speed to start rotating the blades, and the operation can be done only up to a certain maximum wind speed. This is because of concerns over wind-related structural damage to the turbines, which is explained in detail in Burton (2011). This illustrates that wind-energy producers are facing a risk due to variations in the wind speed, which directly affects wind-power production.
Weather derivatives were introduced to the finance world in 1996, and demand for these has been growing ever since (Benth and Šaltytė Benth 2013). These derivatives are financial contracts that provide a mechanism to protect industries from weather variables such as temperature, wind, and precipitation. A subclass of these derivatives is called wind derivatives. Wind derivatives hedge the risk against wind-related weather events for the buyers. As mentioned above, wind-power production needs favorable wind conditions to generate electricity and meet its planned production. Due to these variations in the weather, wind-power producers face risks to their revenue streams. Thus, wind derivatives or, generally, weather derivatives based on weather index are crucial for hedging the risk against weather events. One might think that insurance provides a similar financial contract as weather derivatives, i.e., hedging its risk against the weather event. The distinction between these two contracts comes into play in the process of obtaining the claim. In the case of insurance, the insurance agent must quantify the damages due to weather events before claims are paid. In general, assessing the damage is a tedious and difficult process. For example, let us take a paddy farmer who has taken insurance against drought in the cultivating season. If there is a drought, insurance agents must assess the damages to the paddy crops, and only then can claims be paid. On the other hand, let us say the same farmer bought a weather derivative based on temperature during the cultivating season. If there was a drought in that season, the temperature should be higher than a specific threshold. Once the temperature goes beyond this threshold, and if the contract is designed to this threshold, the farmer will obtain a fixed amount of money according to the contract instantly. This is regardless of the damages the farmer faced due to drought. This is the main advantage regarding the weather derivative compared to insurance (Benth and Šaltytė Benth 2013). Currently, the Chicago Mercantile Market is the only financial market that offers weather derivatives (Benth and Šaltytė Benth 2013). Meanwhile, wind-energy companies operating in deregulated electricity markets face the risk of not only a change in production but also a risk of price change.
The deregulation of the electricity market in Alberta began in 1996, intending to increase competition among power generators through the establishment of the Power Pool of Alberta. This is a non-profit organization that was the operating body of the wholesale electricity market. By 2001, Alberta’s electricity market had become fully deregulated, and in 2003, AESO was established as the transmission administrator of the electricity grid system (AESO n.d.b). In general, electricity prices will have a limited price variation prior to deregulation, and after deregulation, volatility increases significantly in the market (Cartea and Figueroa 2006). Due to this, new financial contracts were developed to hedge the risk of volatility of electricity prices.
Wind-energy companies do not only face the above risks separately but also their correlated risk. As an example, when wind-energy companies generate a surplus of energy due to unexpectedly high wind intensity, they will have to increase the supply to the electricity grid. Thus, this excess energy must now be sold at a price below the market rate. As a result, the company would incur a loss against the planned revenue of, the product of excess energy produced and the price gap between the sold and retail prices. This indicates that the wind-energy company faces not only risk due to an increase in wind speed and high-power generation but also an indirect risk caused by the drop in selling price. To hedge this correlated risk, a traditional weather derivative based only on wind speed is not sufficient as these derivatives only compensate for the change in demand for electricity and do not account for the change in price (Benth et al. 2014). Due to this, a tailor-made contract that accounts for changes in both volume and price is required for the energy producer to hedge its risk perfectly against weather conditions. This type of contract is known as “Quanto Options”. A quanto option has the property of double hedging; thus, it is advantageous to hedge the risk of wind-power stations. More details of the quanto option are discussed in Section 3.1.
The objectives of this study are twofold. The first is to identify a suitable Lévy process for the electricity price process for the Alberta wind-energy market, and the second is to price the quanto option for the Alberta wind-energy market. We follow Benth et al. (2018) notations through the paper, and the process of pricing the quanto option is as follows: first, in Section 3 we convert the spot prices to logarithm values and use the converted values to model the spot prices with a non-Gaussian Ornstein–Uhlenbeck (OU) process with a suitable Lévy process. Then, the wind speed and power process are modeled by a Gaussian OU process, and historical data is used to calibrate the model parameters. Following that, we studied the income of the wind-power generation plant and modeled the correlation between the two processes, the spot-price process and the wind processes, in Section 4. This was possible by approximating the Lévy process by continuous process and jump process. Finally, in Section 5, we price the quanto option using the models we developed for both the spot-price process and the wind processes. All the parameter estimations and numerical results are presented in Section 6.
2. Literature Review
Electricity is traditionally defined as a commodity similar to oil and natural gas (Benth et al. 2008). Nevertheless, there are key distinctions in electricity markets compared to other commodity markets. One of the key differences is that electricity is nearly impossible to store or highly expensive to store compared to other commodities (Cartea and Figueroa 2006). Another distinctive feature is the mean-reverting properties of spot prices and the existence of jumps (Cartea and Figueroa 2006). After studying six different electricity markets by Meyer-Brandis and Tankov (2009), authors have discussed six distinctive features of electricity spot prices. These are differences in distribution during the weekends compared to weekdays, the presence of annual seasonality in data, stationary behavior of data, mean-reversion, presence of spikes, and multi-scale autocorrelation in different markets. The classical model for commodity prices was introduced by Schwartz, which is an exponential mean-reverting OU process (Schwartz 1997). As an extension for the above, Lucia and Schwartz (2002) modeled the electricity spot prices for Nordic Power exchange using a one-factor model and a two-factor model incorporating deterministic component. The one-factor base spot-price model considers spot price as a sum of deterministic components, which has trend and seasonal variations, and the stochastic process , where is an OU process. Similarly, Lucia and Schwartz (2002) also considered the natural log of spot prices as a sum of deterministic components and the stochastic process . An extension of the one-factor model can be obtained by adding the stochastic component to capture the short-term mean-reverting and Xt to capture the long-term equilibrium price level. Here, follows an arithmetic Brownian motion, which is a separate Brownian component compared to the process, and two Brownian motions are correlated. Representing logarithmic spot prices as an OU process allows the researcher to model the different mean-reversions in the data, and it is possible to incorporate jumps to the models as well (Benth et al. 2008). A similar approach has been taken by Pilipović (1998). The author compared three models: the well-known geometric Brownian motion model, log price mean-reverting model, and price mean-reverting models for different energy markets along with the Standard and Poor 500 stock index and concluded that the mean-reverting models perform better compared to geometric Brownian motion model (Pilipović 1998). When jumps are incorporated into Schwartz’s model, the model becomes a jump-diffusion model where drift or mean-reversion is from both the jump component and the diffusion component. The objective of the model is that the Brownian motion will be responsible for small variations in spot prices while the jump component is responsible for larger variations due to changes in supply and/or demand. Thus, this is ideal for leptokurtic data (Benth et al. 2008). This model was utilized by Benth and Šaltytė Benth (2004) to model the natural gas and oil by making the diffusion component zero and taking normal inverse Gaussian (NIG) process as the jump component of the above. Eberlein and Stahl (2003) use an even simpler model by removing the mean-reversion component and using Generalized Hyperbolic (GH) distribution as the jump component, which was carried out on Nordic Electricity spot prices. Cartea and Figueroa (2006) extended the Schwartz model by adding a compound Poisson process as the jump component of the spot prices of England and Wales. As with Lucia and Schwartz (2002), Cartea and Figueroa (2006) took the natural log of spot prices as the sum of the natural log of deterministic seasonal function and the stochastic process . The stochastic process has the dynamics of a mean-reverting jump-diffusion process, which has a mean-reverting component, volatility of diffusion component, and random jump component. Benth et al. (2018) followed the same model for European Power Exchange spot-price data which was proposed by Benth and Šaltytė Benth (2004) for Oil and Gas energy markets.
There is extensive literature on the modeling and analysis of wind-speed data. The popular approach to characterize wind speed is through a Probability Density function (PDF) (Arenas-López and Badaoui 2020). The most common PDF for the wind speed among scholars is the Weibull distribution, see (Carta et al. 2009). Nevertheless, Weibull distribution cannot be generalized for some wind regimes and for shorter time scales like daily, hourly, or less than 10 min as it is not effective, refer (Jaramillo and Borja 2004; Zárate-Miñano et al. 2013) for details. The reason for this is that the Weibull PDF is not a time-dependent distribution but rather a static distribution (Johnson et al. 2017). Another approach to model wind speed is to use autoregressive moving average (ARMA) time-series models. Hill et al. (2012) used the ARMA model to model the wind speeds in the U.K. for hourly data to identify the impact of wind power on the electric power system. Karki et al. (2006) used the ARMA model to study wind speeds for hourly data in three different locations in Canada, which are Swift Current, North Battleford, and Toronto for reliability studies in power systems. Going beyond ARMA models, Rodríguez et al. (2021) used the autoregressive fractionally integrated moving average (ARFIMA) model to model and forecast wind speed for Colombian data. The ARMA model with the combination of artificial neural networks is also proposed in the literature for forecasting wind speeds, and it is rising in popularity among scholars. The reason behind this is that it allows more accurate wind-speed forecasting. Li et al. (2018) introduced a novel combined forecasting model for 10-min wind speeds data in Penglai, China and Wang et al. (2017) introduce a novel hybrid model called MOWOA for forecasting wind speeds using 10-min wind speeds data from six different sites and 30-min wind-speed data in China. There have been recent developments in the application of stochastic differential equations (SDE), especially in modeling short-term fluctuations of wind speeds. A Langevin equation-based model was proposed by Calif (2012) for three different PDFs to model the fluctuation of wind speeds. Calif (2012) proposed this model for a time scale of less than 10 min. To model wind speed in the time scale of hours, Zárate-Miñano et al. (2013) used two models, one is an OU process, and the second is a memoryless transformation of the previous OU process into a Weibull SDE. Arenas-López and Badaoui (2020) proposed modeling wind speed based on OU process while Loukatou et al. (2018) proposed to model the wind speed by decomposing wind speed into deterministic and stochastic components and used OU process to model the stochastic component. Furthermore, the authors used the Fokker–Planck equation to compute the PDF of wind speed. A similar approach is taken by Benth et al. (2018) to model the stochastic component of the wind speeds for European data.
There is literature available on studying different types of wind derivatives for wind-energy markets (Yamada and Matsumoto 2023), e.g., using collar options by Masala et al. (2022) for France’s electricity market, using barrier options by authors Xiao et al. (2016) for electricity market of Iberian and by Rodríguez et al. (2021) to price the put-type barrier option as the wind derivative for Columbia wind-energy market based on Nordix index. Moreover, Kanamura et al. (2021) used call options as the wind derivatives for European data and Benth and Pircalabu (2017) used futures as the wind derivative for German data. In the above, the authors only discuss the volumetric risk faced by the wind-power generator or only use a wind-related index as the underlying assets in the wind derivatives. However, we are interested in hedging both volumetric risk and price risk, and thus, in this study, we are using the quanto options as our wind derivative. There is only a limited amount of literature available on its application in energy markets. As described in Section 1, the quanto option provides the hedging for both volumetric change in demand and change in spot prices due to weather effects simultaneously. One can argue that this can be obtained by combining two simple plain vanilla options, but it has been shown that it is too expensive and not efficient compared to the quanto option by Ho et al. (2006). Caporin et al. (2012) proposed quanto option pricing based on Monte Carlo simulations where the joint dynamics of temperature and energy prices are captured by a bivariate time-series model. The underlying assets were a log of energy prices and average temperature. The drawback of Caporin et al. (2012) is that there is no closed-form analytical solution for the option pricing problem. This was addressed by Benth et al. (2014) where researchers use Heath–Jarrow–Morton (HJM) to model the future price dynamics and derive the option prices. The researcher replaced the underlying assets, the log of energy price, and average temperature by trading futures contracts on the same indexes and considered that these are log-normally distributed. The replacement of underlying assets by futures was possible because the energy quanto option payoff has an “Asian” structure on temperature and spot index. Meanwhile, the markets price the futures such that the value of futures at the end of the delivery period becomes equal to the average energy price and temperature index. Thus, “Asian” payoff on the above two assets will be similar to the “European” payoff of futures of the same assets (Benth et al. 2014). This is a key distinction from the Caporin et al. (2012), and this allows hedging the quanto option by futures contract of the same assets. Using the same closed-form analytical solution for quanto option price, researchers Benth et al. (2018) price the quanto option price for wind derivative using European data. The researchers used a non-Gaussian OU process with NIG process as the dynamics of the stochastic component of spot prices while using a Gaussian OU process to model the dynamics of the stochastic component of the wind process.
Even though there are research studies on pricing the quanto option, we identified a research gap in quanto option pricing for the Alberta energy market. The available studies in the literature have used European data to price the quanto option. We identified another research gap in modeling the electricity process, i.e., most of the studies have used NIG process as the Lévy process to model the electricity price process in the literature. In this study, we are researching other Lévy processes that can be used to model the electricity price process specifically for the Alberta energy market other than NIG process.
3. Electricity, Wind-Speed, and Power Models
3.1. Basic Definition and Notions
In this session, we will introduce the basic definitions and notations that are used throughout this paper.
Futures contracts are financial contracts entered into by two parties, a buyer and a seller. In a futures contract, buyers must buy the underlying asset on the future date mentioned in the contract at the mentioned prices, while the seller must sell the underlying asset on the future date at the mentioned price. This is the main difference between the call–put option and a futures contract, where in call–put options, the buyer only has a right, not an obligation, to buy the underlying asset at the set price at the expiry of the contract. These financial contracts are standard contracts that are available to buy and sell in exchanges like the Chicago Mercantile Market. These contracts allow the buyers and sellers to protect themselves from price movements of the underlying asset in the market. For example, if an oil producer speculates that future oil prices will decline or that current oil prices are profitable, then the oil producer will sell futures contracts to an oil buyer. This allows the oil producer to fix the future income and sales. If a manufacturer is required to hedge its risk to oil price movement and to have guaranteed delivery in the future, buying a futures contract is the way to hedge manufacturer risk. These particular futures contracts are known as oil futures.
Wind derivatives are sub-categories of weather derivatives. Weather derivatives are financial tools that allow organizations (buyers) to hedge their risk against weather effects on their revenue stream. There are standard weather derivatives as well as trailer-made weather derivatives available to purchase. A key feature of weather derivatives is that these have underlying weather indexes such as rainfall, temperature, wind speed, etc. Similar to traditional call–put options on specific stocks or stock indexes, the payoff of weather derivatives is based on the movement of their underlying index with the respective strike. When a weather derivative is based on the wind-speed or wind-related index, we identify these derivatives as wind derivatives. Usually, wind derivatives have buyers and sellers; the buyer is the wind-power producer who is a risk hedger, and the seller is a financial institute that is a risk taker (Kanamura et al. 2021).
A quanto option is a type of financial tool like call–put options or barrier options that can be used to hedge the risk faced by energy producers. The differentiation between a traditional weather derivative and the quanto option is that in a weather derivative, you can only have one underlying asset, for this case, it will be either wind energy or electricity price; but in a quanto option, we can have two underlying assets, in this case, it can be both wind energy and electricity prices. Thus, this gives an advantage where the buyer can hedge its risk from two risk factors and their correlated risk. This is an essential feature for wind-energy producers, as explained in the example in Section 1. However, the term “Quanto Option” is frequently used to describe a class of derivatives that function as a hedge against the risk of a currency exchange when the value is stated in one currency but settled in a different one. This option is different compared to the quanto option in energy markets. A currency quanto option has a payoff function of a traditional call–put option while the energy quanto option we refer to in this paper has a payoff function of a product of two call–put options (Benth et al. 2014). The mechanism of the quanto option is as follows; for example, assume the wind-energy producer needs to hedge its risk from lower wind-energy production and lower electricity prices, then the energy producer should purchase the European put-type quanto option, where the payoff function is a product of two put options on wind energy and electricity prices. By purchasing this type of quanto option, if the wind-energy production is below the respective strike, then the buyer will be compensated accordingly. If the market spot rate for electricity is lower than the respective strike, then the buyer will be compensated accordingly. More details of the contract structure are discussed in Section 5.
Throughout this paper, we use the Ornstein–Uhlenbeck (OU) process to model electricity, wind-speed, and power processes. OU process is a mean-reverting stochastic process. The term mean-reverting emphasizes that a process will always come back to its mean level in the long term, even though there are upward and downward movements in the process in the short term. Below is the SDE of the OU process:
The first term of the above SDE is known as the drift term, and the second term is known as the diffusion term. The drift term is responsible for the overall direction of the process, and is known as the mean-reverting constant. The diffusion term is responsible for the volatility of the process, is the volatility constant, and is the Brownian motion. This process is also known as the Gaussian OU process since is a Gaussian term, and when is replaced by non-Gaussian processes such as a NIG process, then this process is known as a non-Gaussian OU process.
In Section 4, we are discussing the income of the wind-energy company. This is defined as the operating revenue obtained by the wind-power station by selling its produced electricity to the wholesale market in Alberta. Thus, revenue is calculated by the product of the spot price of electricity (CAD/MWh) and the number of units (MWh) of electricity sold to the market.
3.2. Electricity Model
In a probability space with filtration , the class of Lévy processes can be considered a most suitable solution compared to diffusion model due to presence of spikes in the data. From Benth and Šaltytė Benth (2013) electricity spot prices are modeled by:
Here represents the deterministic component of the process. By considering the natural logarithm of gives:
where equates to the sum of seasonal and trend components of the natural logarithm of spot prices, and represents the stochastic component price process. The is said to follow a mean-reverting non-Gaussian OU process as below:
where a constant parameter and L is a Lévy process with the triplet (Applebaum 2009) and (Schoutens 2003). To solve this differential equation, we consider the Ito–Doeblin formula, and below is the solution for Equation (4):
By replacing , , substituting and considering using Equation (5), we can rearrange Equation (5) as follows:
The process is discrete and in the form of an autoregressive model of order one (AR (1)) with parameter and random noise . We can observe that and and the random noise is a Lévy process. The estimated value for is displayed in Table 1 of Section 6.1.
Even though, in Benth and Šaltytė Benth (2004), where the researchers analyzed energy markets (oil and natural gas) and showed that the NIG is suitable to model the stochastic component of the natural logarithm of spot prices and Benth et al. (2018) used the same process to model the European Power Exchange (EPEX) electricity prices, we will be using below list of Lévy process and identify the most suited process for Alberta data:
- Normal Compound Poisson Process with Diffusion
- Normal Compound Poisson Process
- Gamma Compound Poisson Process
- Exponential Compound Poisson Process
- Stable Process
- Cauchy process
- Normal Inverse Gaussian Process
- Variance Gamma Process
3.2.1. Normal Compound Poisson Process with Diffusion (n.c.p.d)
The residuals of the AR(1) model, is considered to follow a compound Poisson process where jump size, is normally distributed with and jump intensity, is Poisson distributed with . Meanwhile, is normally distributed with . Below is the list of the first four cumulants:
3.2.2. Normal Compound Poisson Process (n.c.p)
Here we consider the residuals of the AR (1) model, follows a compound Poisson process, where jump sizes, is normally distributed with and number of jumps, is Poisson distributed with . Below is the list of the first four cumulants:
3.2.3. Gamma Compound Poisson Process (g.c.p)
We consider follows a compound Poisson process where jump size, is a gamma process with shape and scale while jump intensity, is Poisson distributed with . Below is a list of the first three cumulants of the above process:
3.2.4. Exponential Compound Poisson Process (e.c.p)
The residuals of the AR(1) model, is considered to follow the compound Poisson process where is exponentially distributed with and is Poisson distributed with . A list of the first two cumulants of the above process is below:
3.2.5. Stable Process
A stable process is an infinitely divisible Lévy process. The parameter in the stable process is known as the “index of stability”. The definitions of other parameters are: is the asymmetry parameter, is the scale parameter, and is the location parameter. The density are generally expressed in series form; see (Applebaum 2009, pp. 33–35) and below are three instances where close-form density is available.
- Normal distribution when
- Cauchy distribution when and
- Lévy distribution when and
3.2.6. Cauchy Process
The Cauchy process is a pure-jump Lévy process and a special case of a stable process, as mentioned above. Although when one-dimensional Brownian motion is subordinated with Lévy subordinator, the resulting process becomes a symmetric Cauchy process with location parameter () equal to zero and scale parameter () equals to 1 (Applebaum 2009). The density of the Cauchy distribution is defined as:
3.2.7. NIG Process
Using the intuition from Benth and Šaltytė Benth (2004), a NIG process characterized by a Lévy measure with parameters is given by:
where and is the modified Bessel function of the third kind and Index 1 (Jørgensen 1982). Furthermore, these parameters are described as follows: represents the steepness. represents the asymmetry, therefore when we obtain symmetric density. represents the scale parameter and represents location parameter.
3.2.8. Variance Gamma Process
From Salem et al. (2020), a Variance Gamma (VG) process characterized by a Lévy measure with parameters :
These parameters are described as follows: is the location parameter or the mean rate. is the spread parameter or volatility of the Brownian motion. is the asymmetry parameter or drift in the Brownian motion. Therefore, when , we obtain symmetric density. is a shape parameter or variance rate of gamma time change.
3.2.9. Goodness of Fit Test
To choose the most suitable Lévy process from the above, we used the chi-squared test as the goodness of fit test similar to Madan and Seneta (1987). We use the real data and the simulated data from estimated parameters mentioned in Table 2 of Section 6.1 to identify whether two distributions are from the same distribution. We divided the real data and simulated data into seven intervals of which is similarly done by Madan and Seneta (1987), and carried out the chi-squared test. Hence, for each model, the degree of freedom will be six. Below are the hypothesis and test statistics of the chi-squared test:
H0:
The data follows a specific distribution.
H1:
The data do not follow a specific distribution.
From the goodness of fit test, we will be choosing VG and NIG processes as the suitable Lévy processes out of the above processes to model the electricity price process. This is discussed in detail in Section 6.1.
3.3. Wind-Speed and Power Models
Similar to Benth et al. (2018), Betz’s law will be used as the main framework in this study to model wind speed to wind power. According to Betz’s law, power production obtained through a wind-power station is directly proportional to wind speed by the power of three (Betz 1966). Furthermore, according to Burton (2011), a wind-power plant needs a cut-in speed: to begin power production and has a cut-out speed: to stop power production and avoid the risk of damaging infrastructure. Whenever the wind speed goes below m or goes beyond M, there will be no power generation. Thus, the expression for the power series P to wind speed W is given as below:
In the above equation, is known as the heat rate, and it reflects the effectiveness and capability of the power plant. This value depends on factors such as the number of wind turbines, area of the rotor blade, humidity, etc.; (Burton 2011).
Using the relation in Equation (22), we can analyze the power series of our study in two different approaches. The first approach is to analyze the real power series , and the second approach is to use the wind speed to analyze the power series. We follow the initiative by Benth et al. (2008), where an OU process is considered to be the dynamics for the stochastic component of both the wind and power series.
The stochastic processes for W and P are modeled by the following equations:
where . Applying natural logarithm for wind-speed and power series in Equation (23) produces:
Similar to the spot-price model, and are deterministic functions, and their logarithm represents the sum of seasonal and trend components of the logarithm of W and P, respectively. , are the random or stochastic component of wind and power processes and have dynamic of:
here, , , , are constant parameters and B Brownian motion. The Brownian motion B is considered the same for both wind-power production and wind speed as both are related by Betz law. Thus, W and P can be considered to be governed by common law. Again, using the Ito–Doeblin formula, it can obtain the following solutions for the above SDEs:
Since processes and are Gaussian, their conditional mean and variance are given by:
From here onward, we replace the terms and with Y to represent either or and set , . For and Equation (25) becomes:
here and . Next we set , and we can rewrite in the form of autoregressive model of order one (AR(1)):
The residual of AR (1) component is distributed as Gaussian random variables with mean zero variance given by:
by subjecting from Equation (29) we obtain the following estimate for :
4. Income of Wind-Energy Company
The main intention of this section is twofold. The first is to incorporate the correlation between the two processes, electricity and wind power, and the second is to observe the income of the wind-power station.
The said income at time until time , for , is given by:
where P is the power series, S is the spot price and for a constant risk-free rate . These incomes are priced under the real-world probability . Using the Betz law in Equation (22), we can redefine the in terms of the wind speed W instead of wind-power P as follows:
where . Hence, we can redefine and using Equations (2) and (23) as:
where and , for .
4.1. Lévy Process Approximation
The processes VG and NIG are pure-jump processes since in their Lévy–Khintchine formula, the continuous martingale part is zero (Tankov 2003). Thus, the two processes cannot be correlated with continuous processes such as Brownian motion. However, the correlation is vital for quanto pricing, as spot prices and the power process are two correlated processes. To develop the correlation, we will follow the footsteps of Benth et al. (2018) and approximate VG and NIG processes by two additive components. The first component is driven by a scaled Brownian motion, which represents the small jumps of L, and the second component is Lévy driven compound Poisson process for bigger jumps. A similar approximation is suggested by Asmussen and Rosiński (2001) for NIG process. Thus, the Lévy measure of VG and NIG Lévy processes L in Equations (16) and (20) can be approximated by sum of scaled Brownian motion and the compound Poisson process for ; where is the approximated Lévy processes:
and the variance of small jump of L, is given by:
Meanwhile, with Lévy measure , which is independent of , is defined by:
Using the estimated parameters of VG and NIG Lévy processes from Table 2 in Section 6.1 and by Equations (16)–(20) in Section 3.2 we can approximate from below expressions for respective Lévy processes.
For VG process, is:
for NIG Process, is:
4.2. Models for Income
In this section, we will introduce two new processes and :
By setting , the sum of G and H can be replaced by the OU Process K in Equation (5) as a result of Section 4.1:
Since and are independent, the terms G and H are independent as well. The process G follows a Gaussian distribution, which is defined in Equation (39). Thus, its conditional mean and variance are given by:
Next, we will consider the correlation between the Brownian motion B in the OU process of wind and power dynamics and the Brownian motion in the process G. The function for correlation between G and Y (either W or P) is in below expression:
where is the constant correlation. Finally, we can redefine the and using the relation in Equation (33), Equation (34) and the independence of H with both Y and G, as follows:
We can again rewrite the above two functions into three new functions by defining as a new function. These three functions, their analytical expression, and proofs are available in (Benth et al. 2018, eqs. 34–42).
5. Quanto Option Pricing
In this section, we focus on constructing a quanto option of the style European put. Pricing of derivative contracts is carried out under a probability measure , which is considered risk-neutral. This will consider the risk premium when pricing the option, thus guaranteeing no arbitrage opportunities are present. However, in energy markets, electricity cannot be traded or stored like other assets. It must be utilized as soon as it is produced. Thus, electricity cannot be held as an asset in a portfolio. Due to this, the electricity price is not considered when selecting the pricing measure. Hence, any probability measure equivalent to the real-world probability measure can be used as the pricing measure in this scenario. In futures markets, futures are liquid, and it is necessary for futures contracts to have arbitrage-free pricing (Benth et al. 2008). Due to the above reasons and following Benth et al. (2018), we chose the pricing measures as to reduce the complexity.
5.1. Contract Structure
Quanto options have a double-hedging characteristic when compared to other options. This implies that the payoff of the option is dependent on two underlying assets. The payoff function is denoted by , where E represents the index of energy price, and I represents the power production index. The underlying assets are defined by following the Benth et al. (2018). The contract period of the option is considered to start at and ends at . The average spot price during this period is defined as E. The index I represents the cumulative difference between the theoretical power production (power production based on the Betz law using the recorded wind speed W), and the actual power production P that is recorded:
The reason for taking the modulus in index I is that our theoretical power production is lower compared to the actual power production, which can be seen in Section 6.2. Hence, we must take the absolute value of the difference.
According to the definition given in Benth and Šaltytė Benth (2013), the price of the quanto option without any arbitrage opportunity at the time where expiry is at time , is equal to the discounted expected value of the payoff function:
where is the risk-free interest rate. According to the Benth et al. (2014), futures contracts can be related to quanto option price where the underlying assets of both are the same. Specifically, the future contracts based on indices E and I, their price at for the contract period is shown by below expression:
Furthermore, the future can be viewed as the difference between two different futures contracts as below:
As per the Lemma 1 of (Benth et al. 2018, p. 14), we can equate the quanto option price in Equation (49) to another quanto option where underlying is replaced by two futures contracts with same indices at expiry, with the same contract period as below expression:
Therefore, we can state that the quanto option with underlying E and I is equal to a quanto option of underlying futures contracts of E and I at the expiry. Furthermore, We can define payoff function as product of two put options:
where strike values , . If we required quanto options of European call type or European call–put type, the above payoff function should be adjusted accordingly.
5.2. Models of Futures Contracts
Consider the futures contracts introduced in Equation (50), Equation (51) and models introduced for spot price and wind dynamics in Section 3.2, Section 3.3 and Section 4.
By Lemma 2 from (Benth et al. 2018, p. 15), For , the value of the futures of Equation (50) is as below:
meanwhile, for , futures values of Equation (50) becomes:
and are the mean and variance of G process given in Equations (42) and (43), respectively. is the function defined on the Benth et al. (2018, eq. 41).
5.3. Contract Details
The contract drafts on the date , and the contract period is , with a fixed annual risk-free interest rate of . As explained in Benth et al. (2018), usually given this nature of the contract, the measurement period is divided into sub-intervals with different strike prices for each interval, based on seasonal behavior. However, in this case, the option is considered to be at-the-money with strikes and set to be equal to and , respectively.
The futures and were modeled using two log-normal distributed processes. This assumption was taken for the purpose of reducing the complexity of calibration of price; see (Benth et al. 2018) for more details. Thus, for , futures prices follow the below dynamics:
We define and such that they are two Gaussian random variables, independent of such that has zero mean and variance defined by and . The correlation is defined as .
5.4. Option Pricing
By the Theorem 1 of the (Benth et al. 2018, p. 16), we can define the payoff of the quanto option by:
The variables are defined in (Benth et al. 2018, eq. 56). The denoted the standard bivariate Gaussian cumulative distribution function with correlation . We can calculate values for using Equations (52) and (54).
When we consider the option is at-the-money, we can modify the above equation as below:
6. Empirical Analysis
Parameter estimations and numerical analysis discussed in previous sections are presented in this section. For the analysis of the study, we used Alberta, Canada data from the period 1st January 2019 to 31st December 2022. There were a total of 1460 daily observations for spot price, wind-power, and wind-speed data after removing 29th February 2020. For all datasets, no negative values were observed. The open-source software R (www.R-project.org) (accessed on 9 August 2023) is used for the analysis and creation of plots in the study. The relevant R packages utilized for the analysis are mentioned in each step.
6.1. Spot-Price Process Calibration
We examined the spot prices for electricity using data provided by www.nrgstream.com (accessed on 9 August 2023) for Alberta using spot daily indices (CAD/MWh). We begin our analysis by taking the natural logarithm of the time series. Using the function “stl” from the package “stats” in R, we decompose the time series of our spot-price data considering into seasonal, trend, and the remainder components as presented in Equation (3) in Section 3.2. The deterministic part is considered to be the sum of trend and seasonal components. Therefore, the remainder component of the decomposition is used for further analysis. Figure 1 displays the decomposition of and was produced from R functions “stl” and “plot”.
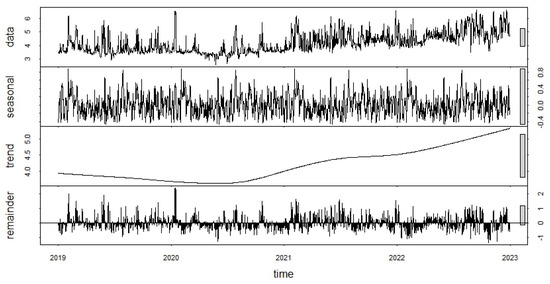
Figure 1.
Electricity price process decomposition.
Using Equation (6) in Section 3.2, we model the above remainder using the AR (1) model and estimated the value for and then for . This is carried out by deploying the R function “arima” from the package “stats”. To calculate the confidence interval (C.I.) for 95% significance, the R function “arima.boot” of the package “Pracma” was used. Estimated parameters and are displayed in Table 1.

Table 1.
Parameter estimations for the electricity price process.
Table 1.
Parameter estimations for the electricity price process.
| Estimated Value | 95% C.I. | Estimated Value | 95% C.I. | ||
|---|---|---|---|---|---|
Since it was assumed that the is driven by the Lévy process, using a chi-squared goodness of fit test, we choose a suitable Lévy process as mentioned in Section 3.2. For the Lévy processes with compound Poisson process, the parameters were estimated using the cumulant matching method in the spirit of Grubbström and Tang (2006) and Press (1967). For the stable, Cauchy, NIG, and VG processes, parameter estimation was carried out using the maximum likelihood estimation (MLE) method. Stable process parameters were estimated using the R function “stableFit” from the package “fBasics”. For the Cauchy process, parameters estimation was conducted using the R function “fitdist”; for the NIG process, we deployed the R function “nigFit” of the package “fBasics”. Parameters of VG were estimated using the R function “vgFit” from the package “VarianceGamma”. The table below displays the parameter estimates for the Lévy processes mentioned in Section 3.2 for Alberta data.
We deployed a chi-squared test for the above Lévy processes to identify the best-suited Lévy process for our data. We conducted 1000 simulations for each model and took the average chi-squared value and p-value. These values are displayed in the Table 3. It can be observed that all compound Poisson processes have high chi-squared values, thus indicating that the distance between the real data and the simulated data is high. We can also observe that there is a significant difference between Cauchy and stable processes. The reason for this is, “index of stability” is estimated as 1.566 for the stable process, and in the Cauchy process, we assume this is equal to 1. We can identify that NIG and VG processes have very low chi-squared values, thus indicating they are better at modeling the stochastic process of the electricity spot prices. This can also be seen visually by the quantile-quantile (Q-Q) plot of the two processes compared with the Gaussian distribution. The below Q-Q plot is produced from the functions “qqnorm”, “qqnig” and “qqvg” of packages “stats”, “fBasics” and “Variance Gamma”, respectively.

Table 2.
Estimated parameters of Lévy processes for electricity spot-price process.
Table 2.
Estimated parameters of Lévy processes for electricity spot-price process.
| Parameters | n.c.p.d | n.c.p | g.c.p | e.c.p | Stable | Cauchy | nig | vg |
|---|---|---|---|---|---|---|---|---|
| - | - | - | - | - | - | |||
| - | - | - | - | - | - | - | ||
| 0 | - | - | - | - | - | - | ||
| - | - | - | - | - | - | - | ||
| - | - | - | - | - | - | - | ||
| - | - | - | - | - | - | - | ||
| 0.002 | - | - | - | - | ||||
| - | - | - | - | - | - | - | ||
| - | - | - | - | - | - | - | ||
| - | - | - | - | - | - | - | ||
| - | - | - | - | - | - | - | ||
| - | - | - | - | - | - | - | ||
| - | - | - | - | - | - | - | ||
| - | - | - | - | - | - | - | ||
| - | - | - | - | - | - | - | ||
| - | - | - | - | - | - | - | ||
| - | - | - | - | - | - | - | ||
| - | - | - | - | - | - | - | ||
| - | - | - | - | - | - | - | ||
| - | - | - | - | - | - | - | ||
| - | - | - | - | - | - | - |

Table 3.
Chi-squared value and p-value for Lévy processes.
Table 3.
Chi-squared value and p-value for Lévy processes.
| Model | Chi-Squared | p-Value |
|---|---|---|
| Normal Compound Poisson with Diffusion | 224.376 | 0 |
| Normal Compound Poisson | 888.895 | 0 |
| Gamma Compound Poisson | 886.944 | 0 |
| Exponential Compound Poisson | 1587.365 | 0 |
| Stable Process | 13.894 | 0.088 |
| Cauchy Process | 142.548 | 0 |
| Normal Inverse Gaussian Process | 5.430 | 0.537 |
| Variance Gamma Process | 4.080 | 0.675 |
When comparing the plots in Figure 2, we can be observed that the Q-Q plot for NIG and VG is better than the Gaussian Q-Q plot. From the chi-squared test statistics and Q-Q plot, we can observe that both NIG and VG processes are suitable fits as the Lévy process of the spot prices, but VG is slightly better compared to NIG in the goodness of fit test. Thus, we will be using both processes going forward, as the Lévy processes, and compare the results.
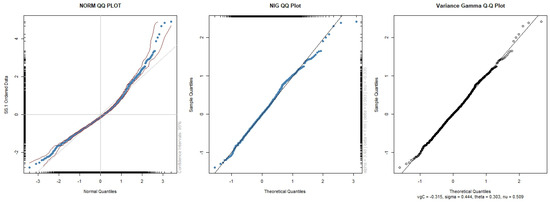
Figure 2.
Q-Q plot for different distributions (left) Gaussian distribution; (middle) NIG distribution; (right) VG distribution.
6.2. Wind Process Calibration
To model the wind, we used the data from the Summerview wind-power plant in Alberta from www.nrgstream.com (accessed on 24 July 2023).
Hourly power production of the power plant was obtained in MW and converted to daily observations in MWh. Next, the wind speed (m/s) data were collected from www.acis.alberta.ca (accessed on 30 October 2023) for the region of Brocket, Alberta, measured at 10 m above the ground.
To estimate wind-power production using wind speed by Equation (22), we require the value for h, which is defined as the heat rate in Section 3.3. The heat rate h is dependent on factors mentioned in Section 3.3, and this information is not available to us. Thus, similar to Benth et al. (2018), we used a linear regression model to calibrate h for Betz law. For this, we consider the time series, production of power, and cubic wind speed as dependent and independent variables, respectively. We set the cut-in wind speed and cut-out wind speed similar to Benth et al. (2018), hence the Indicator function will always be one. To model Betz law using the regression model, we used the R function “lm” of the package “stats”. The estimated value for the heat rate h is displayed in Table 4.

Table 4.
Estimated heat rate parameter for Betz’s law.
Figure 3 represents the actual power series (bold line) versus the power series obtained from the Betz law (dash line) for the data. The plot is limited to only the first 100 days and was generated from the function “plot.ts” of package “stats”. It can be observed that the real power series is higher than the estimated power series most of the time. We believe this difference would have been minimized if the wind speed data were collected from 100 m above the ground rather than 10m above the ground. The impact of height is as follows: the wind has a higher wind speed when the elevation from the ground is higher (Wasiati et al. 2020). Hence, the wind speed measured at 10m is significantly lower compared to the wind speed measured at 100 m. When we measure wind speed at 10 m height and calculate wind power using Betz law (Equation (22)) we do obtain a lower wind power compared to the actual wind power. This is because wind turbines usually have a height of approximately 120 m (Hartman 2023).
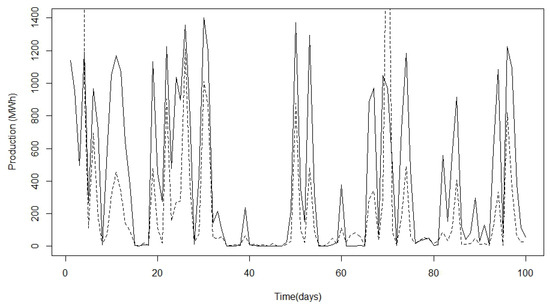
Figure 3.
Power process (bold line) and power process obtained by the Betz law (dash line) for first one hundred days.
By following the same methodology used in spot-price calibration, we decompose logarithmic wind speed and power process data and set , as the sum of the seasonal and trend components. We then model the logarithmic residuals of two processes as AR(1) model following Equation (28) in Section 3.3. Thus, similar to spot-price calibration, we estimate and then we estimate for and use Equation (30) to estimate . The values obtained for these estimates, along with their 95% confidence intervals, are given in the Table 5. The confidence interval was obtained by the method of bootstrapping in R.

Table 5.
Estimated parameters for the wind-speed and power processes.
6.3. Income of Wind-Energy Company
From the above calibrations, we have the estimated values for the parameters required to observe the income of the wind-energy company. We can look at the income of the wind-energy company from wind speed as well as from the wind-power perspective using Equations (45) and (46), respectively. This can be done using the analytical expression for Equations (45) and (46) in (Benth et al. 2018, eqs. 34–42). It must be noted that when approximating the value for Equation (42) in Benth et al. (2018) for the VG process, the integration was considered only for the positive real line. Otherwise, the value for and becomes zero. For the NIG process, this is not the case.
Next, we plot the estimated income from the above series, (bold line) and (dash line) of the first 100 days to observe the difference between the two income curves. The plots were produced from the function “ggplot” of package “ggplot2”.
According to Figure 4 and Figure 5, we observe that is higher than in most instances. Therefore, we can conclude that it is possible to obtain a higher forecast for income when considering the wind-power production process rather than considering the wind-speed process. Here, it should be noted that wind-speed data used for this study was measured 10 m above the ground. We believe the results could be improved when considering wind speeds of 100 m above the ground since the average height of a wind turbine is approximately 120 m above the ground.
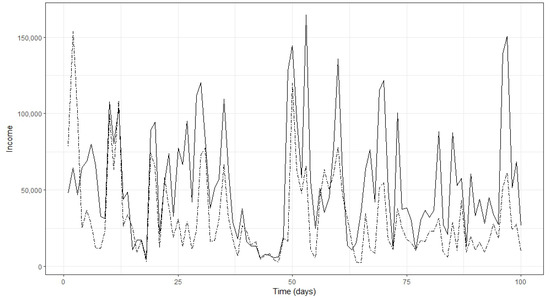
Figure 4.
(bold line) and (dash line) using the VG process for the first one hundred days.
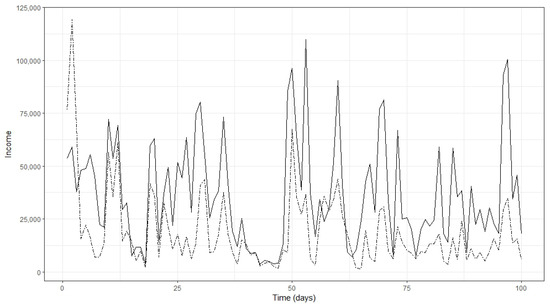
Figure 5.
(bold line) and (dash line) using NIG process for the first one hundred days.
6.4. Quanto Option Price
Using the theorems and methodology discussed in Section 5, the quanto option was calibrated for three separate periods, first from 1st January 2019 to 31st December 2021, second from 1st January 2020 to 31st December 2021, and third from 1st January 2021 to 31st December 2021. This exercise aims to observe whether there are any differences in the price values with respect to the different lengths of the historical data sets used. The correlation values, were used to see whether the correlation between futures contracts affects the option price. To obtain the option price value for three different calibrations, the steps in Section 5 need to be repeated three times for three different periods.
Table 6 displays the quanto option prices for three different calibrations when the VG process is used as the stochastic process. Table 7 provides the same when NIG process is used as the stochastic process. The percentage change in option price corresponds to , is mentioned in the parenthesis.

Table 6.
Quanto option prices for Alberta using VG process.

Table 7.
Quanto option prices for Alberta using NIG process.
As per the results, we can see for both VG and NIG-based prices for the quanto option, the three-year calibration has the lowest values compared to the other two calibration periods. It is very clear from the option price values that the calibration period does affect the price of the quanto option. It is also noticeable that option price values obtained from VG and NIG processes are different, and this difference increases when calibration time decreases. This price difference comes from the Lévy measure of the two different processes. Apart from that, we can also observe the effect of correlation on the price of the quanto option, but the correlation has the same effect for all three calibrations. We can observe that when correlation increases, the price of the quanto option also increases. As per the explanation given by Benth et al. (2018), we can say that the definition given for the payoff function agrees with the prices we obtain, i.e., the payoff function has higher returns when both and are well below the strike and and less otherwise. When the correlation is negative, it indicates that only one of the futures contract values is decreasing. This leads to low option prices, and a positive correlation indicates that both futures contracts go in the same direction. This result proves that futures contracts are correlated, and it is important for the option pricing; see (Benth et al. 2018).
We now compare our results with the results of (Benth et al. 2018, p. 17), where authors conducted their study on the European market for the period 2012 to 2015. Even though the numerical values of quanto option prices are not the same, there are similarities in the quanto option prices. Similar to the results in Table 6 and Table 7, in Benth et al. (2018), three-year calibration has the lowest quanto option price while the one-year calibration has the highest quanto option price. Furthermore, in Benth et al. (2018), quanto option prices increase when correlation moves from to , similar to the results in this study. In addition, the effect of correlation is similar in all three calibrations in the Benth et al. (2018) results, similar to Table 6 and Table 7, thus indicating that the length of the historical data and the correlation play a role in the quanto option pricing regardless of the geographical location or time period considered.
Table 8 reports the measured correlation for three separate calibration settings. It can be seen that the correlation value is similar from three-year calibration to one-year calibration for both processes except for the one-year calibration of NIG process. It can also be seen that all correlation values are positive. Even though correlation values obtained by (Benth et al. 2018, p. 18) are also positive, its correlation for three-year calibration is significantly less compared to two-year and one-year calibration. As explained by Benth et al. (2018), the reason for the positive correlation is due to the definition of E and I in our option pricing. When the difference between theoretical power and actual power decreases, it implies that the power plant has utilized the wind speed to its maximum, which results in the overproduction of electricity. This results in lower electricity spot prices, i.e., lower E values. Thus, lower I results in lower E, and higher I results in higher E.

Table 8.
Correlations estimated for three different calibrations.
7. Conclusions
The objectives of this study are to identify a suitable Lévy process for the Alberta electricity market and to price the quanto option for wind-power producers in the Alberta wind-energy market. We achieved these objectives by following the techniques of Benth et al. (2018) in this study. First, we used eight different Lévy processes and estimated their parameters using historical data on electricity prices in the Alberta market. Then we simulated their paths and identified the best fit Lévy process for the stochastic component of the spot prices are VG and NIG processes. This was identified by the goodness of fit test using chi-squared statistics as similarly done by Madan and Seneta (1987). Thus, we decided to use both Lévy processes for the spot-price modeling. We modeled the wind-speed and wind-power process using two OU processes following the intuition of Benth et al. (2008). Next, we explore two possible approaches to model the wind process using the relationship between wind-speed and wind-power production, as described by the Betz law. We then observed the wind-power station income and identified that considering wind speed as the wind variable results in lower income compared to directly modeling wind-power production. This result contrasts with Benth et al. (2018) research for European data. We suggest that this difference may be because data obtained for wind speeds is only 10 m above the ground, while, in reality, we require wind speeds 100 m above the ground. To model the correlation between the electricity spot price and the wind power and speed processes, an approximation of the chosen Lévy process involving a sum of a scaled Brownian motion and a compound Poisson process was used. This enables us to model the correlation between the chosen Lévy process and the OU process. The approach is based on the work of Asmussen and Rosiński (2001). Finally, we construct a European put-type quanto option that allows wind-energy producers to hedge against both volume risk (i.e., reduced production) and price risk. Using the closed-form solution for the quanto option of Benth et al. (2014), we priced the quanto option for Alberta. We observed similar patterns in the price values obtained in this study and the study conducted by Benth et al. (2018). The similarities are that, in both studies, three-year calibration has the lowest quanto option price compared to the other two calibration periods. The option prices increase when the correlation between futures contracts increases. The effect of correlation to the option price in all three calibration periods is similar, and the correlation of the two futures is positive in both studies. Yet, three-year calibration correlation values obtained in Benth et al. (2018) are significantly lower compared to the other two calibration periods, while this is not the case in our study.
The limitations and future works of this study are as follows: In this study, we only focused on the stochastic component of the data, and we can improve our results by modeling the deterministic components as well. As mentioned several times in this paper, wind-speed data used in this study was only 10 m above the ground, and better results can be obtained by measuring the wind speeds at the same height of the wind turbine and the same location where wind turbines are located. More information about the wind-power station would reduce the gap between the real power series and the power series obtained by Betz law. Instead of using linear regression to model the wind speed to wind power, more complex parametric and non-parametric models can be introduced to model the wind speed to wind power; see Sohoni et al. (2016) for details. As suggested by Benth et al. (2018), more complex models can be taken to model the futures dynamics instead of assuming they are log-normally distributed. Finally, the quanto option is priced by taking the assumption that the market is complete, but the reality might be different, and markets are low on liquidity; thus, markets are incomplete; see Kanamura et al. (2021).
Author Contributions
Conceptualization, A.S.; methodology, S.W. and A.S.; formal analysis, S.W. and A.S.; investigation, S.W. and A.S.; data curation, S.W.; resources, A.S.; writing—original draft, S.W.; writing—review & editing, S.W. and A.S.; visualization, S.W.; supervision, project administration and funding acquisition, A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by NSERC grant number RT732266.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Nrgstream https://www.nrgstream.com/ (accessed on 9 August 2023) and Alberta.ca https://acis.alberta.ca/weather-data-viewer.jsp (accessed on 30 October 2023).
Acknowledgments
Authors thank NSERC for continuing support.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AESO | Alberta Electric System Operator |
| ARMA | Autoregressive Moving Average |
| AFRIMA | Autoregressive Fractionally Integrated Moving Average |
| C.I. | Confidence Interval |
| e.c.p | Exponential Compound Poisson |
| EPEX | European Power Exchange |
| g.c.p | Gamma Compound Poisson |
| GH | Generalized Hyperbolic |
| HJM | Heath–Jarrow–Morton |
| IEA | International Energy Agency |
| MLE | Maximum Likelihood Estimation |
| n.c.p.d | Normal Compound Poisson Process with Diffusion |
| n.c.p | Normal Compound Poisson |
| NIG | Normal Inverse Gaussian |
| OU | Ornstein–Uhlenbeck |
| Probability Density Function | |
| SDE | Stochastic Differential Equations |
| VG | Variance Gamma |
References
- Alberta Electric System Operator (AESO). n.d.a Alberta’s Power System in Transition. Available online: https://www.aeso.ca/future-of-electricity/albertas-power-system-in-transition/ (accessed on 30 October 2023).
- Alberta Electric System Operator (AESO). n.d.b Guide to Understanding Alberta’s Electricity Market. Available online: https://www.aeso.ca/aeso/understanding-electricity-in-alberta/continuing-education/guide-to-understanding-albertas-electricity-market/ (accessed on 30 October 2023).
- Applebaum, David. 2009. Lévy Processes and Stochastic Calculus, 2nd ed. Cambridge: Cambridge University Press. [Google Scholar] [CrossRef]
- Arenas-López, Jonatan Pablo, and Mohamed Badaoui. 2020. Stochastic modelling of wind speeds based on turbulence intensity. Renewable Energy 155: 10–22. [Google Scholar] [CrossRef]
- Asmussen, Søren, and Jan Rosiński. 2001. Approximations of small jumps of Lévy processes with a view towards simulation. Journal of Applied Probability 38: 482–93. [Google Scholar] [CrossRef]
- Betz, Albert. 1966. Introduction to the theory of flow machines. Pergamon. [Google Scholar] [CrossRef]
- Benth, Fred Espen, and Anca Pircalabu. 2017. A Non-Gaussian Ornstein-Uhlenbeck Model for Pricing Wind Power Futures. Applied Mathematical Finance 25: 36–65. [Google Scholar] [CrossRef]
- Benth, Fred Espen, and Jūratė Šaltytė Benth. 2004. The Normal Inverse Gaussian Distribution and Spot Price Modelling in Energy Markets. International Journal of Theoretical and Applied Finance 7: 177–92. [Google Scholar] [CrossRef]
- Benth, Fred Espen, and Jūratė Šaltytė Benth. 2013. Modeling and Pricing in Financial Markets for Weather Derivatives. Number Volume 17 in Advanced Series on Statistical Science and Applied Probability. Singapore: World Scientific. [Google Scholar]
- Benth, Fred Espen, Jūratė Šaltytė Benth, and Steen Koekebakker. 2008. Stochastic Modeling of Electricity and Related Markets. Volume 11 of Advanced Series on Statistical Science & Applied Probability. Singapore: World Scientific. [Google Scholar] [CrossRef]
- Benth, Fred Espen, Luca Di Persio, and Silvia Lavagnini. 2018. Stochastic Modeling of Wind Derivatives in Energy Markets. Risks 6: 56. [Google Scholar] [CrossRef]
- Benth, Fred Espen, Nina Lange, and Tor Age Myklebust. 2014. Pricing and Hedging Quanto Options in Energy Markets. Journal of Energy Markets 8: 1–35. [Google Scholar] [CrossRef]
- Burton, Tony, ed. 2011. Wind Energy: Handbook. Hoboken: J. Wiley. [Google Scholar]
- Calif, Rudy. 2012. PDF models and synthetic model for the wind speed fluctuations based on the resolution of Langevin equation. Applied Energy 99: 173–82. [Google Scholar] [CrossRef]
- Caporin, Massimiliano, Juliusz Preś, and Hipolit Torro. 2012. Model based Monte Carlo pricing of energy and temperature Quanto options. Energy Economics 34: 1700–12. [Google Scholar] [CrossRef]
- Carta, José A., Penélope Ramírez, and Sergio Velázquez. 2009. A review of wind speed probability distributions used in wind energy analysis. Renewable and Sustainable Energy Reviews 13: 933–55. [Google Scholar] [CrossRef]
- Cartea, Álvaro, and Marcelo G. Figueroa. 2006. Pricing in Electricity Markets: A Mean Reverting Jump Diffusion Model with Seasonality. Applied Mathematical Finance 12: 313–35. [Google Scholar] [CrossRef]
- Eberlein, Ernst, and Gerhard Stahl. 2003. Both sides of the fence: A statistical and regulatory view of electricity risk. Energy and Power Risk Management 8: 32–6. [Google Scholar]
- Grubbström, Robert W., and Ou Tang. 2006. The moments and central moments of a compound distribution. European Journal of Operational Research 170: 106–19. [Google Scholar] [CrossRef]
- Hartman, Liz. 2023. Wind Turbines: The Bigger, the Better; Washington, DC: U.S. Department of Energy. Available online: https://www.energy.gov/eere/articles/wind-turbines-bigger-better (accessed on 25 August 2023).
- Hill, David, David McMillan, Keith Bell, and David Infield. 2012. Application of Auto-Regressive Models to U.K. Wind Speed Data for Power System Impact Studies. IEEE Transactions on Sustainable Energy 3: 134–41. [Google Scholar] [CrossRef]
- Ho, Teng Suan, Richard C. Stapleton, and Marti Gurunath Subrahmanyam. 2006. Correlation risk, cross-market derivative products and portfolio performance. European Financial Management 1: 105–24. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). n.d. Wind. Available online: https://www.iea.org/energy-system/renewables/wind (accessed on 30 October 2023).
- Jaramillo, Oscar A., and Marco Antonio Borja. 2004. Wind speed analysis in la ventosa, mexico: A bimodal probability distribution case. Renewable energy 29: 1613–30. [Google Scholar] [CrossRef]
- Johnson, Paul, Sydney Howell, and Peter Duck. 2017. Partial differential equation methods for stochastic dynamic optimization: An application to wind power generation with energy storage. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences.London: The Royal Society. [Google Scholar] [CrossRef]
- Jørgensen, Bent. 1982. Statistical Properties of the Generalized Inverse Gaussian Distribution. Volume 9 of Lecture Notes in Statistics. New York: Springer. [Google Scholar] [CrossRef]
- Kanamura, Takashi, Lasse Homann, and Marcel Prokopczuk. 2021. Pricing analysis of wind power derivatives for renewable energy risk management. Applied Energy 304: 117827. [Google Scholar] [CrossRef]
- Karki, Rajesh, Po Hu, and Roy Billinton. 2006. A Simplified Wind Power Generation Model for Reliability Evaluation. IEEE Transactions on Energy Conversion 21: 533–40. [Google Scholar] [CrossRef]
- Li, Hongmin, Jianzhou Wang, Haiyan Lu, and Zhenhai Guo. 2018. Research and application of a combined model based on variable weight for short term wind speed forecasting. Renewable Energy 116: 669–84. [Google Scholar] [CrossRef]
- Loukatou, Angeliki, Sydney Howell, Paul Johnson, and Peter Duck. 2018. Stochastic wind speed modelling for estimation of expected wind power output. Applied Energy 228: 1328–40. [Google Scholar] [CrossRef]
- Lucia, Julio J., and Eduardo S. Schwartz. 2002. Electricity prices and power derivatives—Evidence from the Nordic Power Exchange. Review of Derivatives Research 5: 5–50. [Google Scholar] [CrossRef]
- Madan, Dilip B., and Eugene Seneta. 1987. Chebyshev Polynomial Approximations and Characteristic Function Estimation. Journal of the Royal Statistical Society: Series B (Methodological) 49: 163–69. [Google Scholar] [CrossRef]
- Masala, Giovanni, Marco Micocci, and Andrea Rizk. 2022. Hedging Wind Power Risk Exposure through Weather Derivatives. Energies 15: 1343. [Google Scholar] [CrossRef]
- Meyer-Brandis, Thilo, and Peter Tankov. 2009. Multi-Factor Jump-Diffusion Models of Electricity Prices. International Journal of Theoretical and Applied Finance 11: 503–28. [Google Scholar] [CrossRef]
- Pilipović, Dragana. 1998. Energy Risk: Valuing and Managing Energy Derivatives. New York: McGraw-Hill. [Google Scholar]
- Press, S. James. 1967. A Compound Events Model for Security Prices. The Journal of Business 40: 317–35. [Google Scholar] [CrossRef]
- Rodríguez, Yeny E., Miguel A. Pérez-Uribe, and Javier Contreras. 2021. Wind Put Barrier Options Pricing Based on the Nordix Index. Energies 4: 1177. [Google Scholar] [CrossRef]
- Salem, Marwa Belhaj, Estelle Deloux, and Mitra Fouladirad. 2020. Modelling and Prognostics of System Degradation using Variance Gamma Process. Paper present at the 30th European Safety and Reliability Conference and 15th Probabilistic Safety Assessment and Management Conference, Venice, Italy, November 1–5; Singapore: Research Publishing Services, pp. 2886–93. [Google Scholar] [CrossRef]
- Schoutens, Wim. 2003. Lévy Processes in Finance: Pricing Financial Derivatives. Wiley Series in Probability and Statistics; Chichester: J. Wiley. [Google Scholar]
- Schwartz, Eduardo S. 1997. The Stochastic Behavior of Commodity Prices: Implications for Valuation and Hedging. The Journal of Finance 52: 923–73. [Google Scholar] [CrossRef]
- Sohoni, Vaishali, S. C. Gupta, and Rajesh K. Nema. 2016. A Critical Review on Wind Turbine Power Curve Modelling Techniques and Their Applications in Wind Based Energy Systems. Journal of Energy 2016: e8519785. [Google Scholar] [CrossRef]
- Tankov, Peter. 2003. Financial Modelling with Jump Processes. Boca Raton: Chapman and Hall/CRC. [Google Scholar] [CrossRef]
- Wang, Jianzhou, Pei Du, Tong Niu, and Wendong Yang. 2017. A novel hybrid system based on a new proposed algorithm—Multi-Objective Whale Optimization Algorithm for wind speed forecasting. Applied Energy 208: 344–60. [Google Scholar] [CrossRef]
- Wasiati, S., F. Augusta, V. Purwanto, Putri Wulandari, and A. Syahrirar. 2020. Darrieus type vertical axis wind turbine (VAWT) design. Journal of Physics: Conference Series 1517: 012064. [Google Scholar] [CrossRef]
- Xiao, Yunpeng, Xifan Wang, Xiuli Wang, and Zechen Wu. 2016. Trading wind power with barrier option. Applied Energy 182: 232–42. [Google Scholar] [CrossRef]
- Yamada, Yuji, and Takuji Matsumoto. 2023. Construction of Mixed Derivatives Strategy for Wind Power Producers. Energies 16: 3809. [Google Scholar] [CrossRef]
- Zárate-Miñano, Rafael, Marian Anghel, and Federico Milano. 2013. Continuous wind speed models based on stochastic differential equations. Applied Energy 104: 42–49. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).