The Cost of Borrowing as a Limiting Factor of Non-Life Insurance Development: The Italian Case

Abstract

We address the effect of local financial conditions on the demand for non-life insurance. We consider the spread between the interest rates faced by the insured on the local credit market and the return rates earned by the insurer on national or international financial markets, sketching how it influences the present value of an insurance policy; we then use the local invariance of the insurer’s returns to identify the effect on demand. Drawing on a panel of Italian provinces with ample variability in insurance density as well as borrowing conditions, we show that the demand for non-life insurance decreases with the borrowing rate. We separate between different non-life insurance lines, finding a stronger effect for the lines prevailing in advanced economic systems. Credit conditions turn out to be an important factor of non-life insurance development, and they help to explain the underdevelopment of insurance markets in Southern Italy.

1. Introduction

With an insurance contract, one exchanges a fixed payment today against a contingent claim in the future; thus, the insured incurs an opportunity cost from not investing, while the insurer obtains investment revenue from the reserves. For this reason, as far as demand is concerned, the so-called ‘inverted economic cycle’ of insurance, in which one pays first, then, in the event of loss, receives their dues, suggests that the financial rate of return, seen as an opportunity cost for those who allocate funds in an insurance policy, should be inversely related to demand. That is, self-insuring gives one an opportunity gain to invest the spared amount of the premium on financial markets, which increases alongside the prevailing rate of return. Beenstock et al. (1988) formalize the inverse relationship between the rate of return and the demand for insurance. The effect of interest rates on insurance supply can be supposed to go in the opposite direction. The supply of insurance will depend on the return on underwriting capital, which is determined mainly by the premium rate (the unit price of coverage), the probability of loss and the interest rate. Insurance supply can be hypothesized to depend positively on the interest rate, because of the gains from investing the premiums on financial markets in the time between premium collection and claims settling. In a nutshell, higher investment revenues allow insurers to compensate for technical losses, so they can set lower tariffs. Therefore, interest rates should belong to the drivers of insurance development, but the a priori sign of the effect is unclear.

Millo and Carmeci (2011), in their sub-regional analysis of the drivers of Non-Life insurance consumption in Italy, find a negative association with the real interest rate on borrowing (see also Millo and Millossovich 2015). Our goal in the present paper is more ambitious: identifying the effect on insurance demand. Moreover, we set out to identify the effect of borrowing rates on different lines of Non-Life insurance. In fact, Non-Life is a mixed bag, putting together mandatory insurance like Motor Third Party Liability (MTPL) with non-mandatory insurance, and lines covering very basic needs of an economy (Fire and Other Damage To Property) with lines typical of the more advanced stages of economic development, like Professional Liability, Credit and Cautions or Nuclear Risks and the like. Our idea is, given that a well-functioning insurance market is generally considered a key ingredient of economic development (one for all, Arena 2008), then, if local credit conditions have a negative effect on some insurance lines, this will be all the more detrimental to economic development if they affect the insurance lines most crucial for a developed economy. In the following, we check whether credit conditions do explain regional differences in Italian Non-Life insurance consumption. Following Millo and Carmeci (2011), we elaborate on their findings that the total consumption of non-mandatory Non-Life insurance is negatively related to real interest rates, separating insurance lines by the type of risk insured.

Our identification strategy is based on the observational context. At the province level, consumers and firms—with the exclusion of the largest ones—face the local borrowing conditions. On the contrary, the financial returns of insurers are determined by international financial markets and, thus, independently from the spatial location of the insured. For all the above, observing a panel of provincial data allows us to separate the effect of interest rates on insurance demand. The financial returns for the insured (the opportunity cost of insurance) can in turn reasonably be assumed to be cross-sectionally invariant, as they depend on investment opportunities at the national scale (i.e., treasuries, bank products and listed shares). For all of the above, it will be sufficient to control for time shifts in order to isolate the effect of interest.

Sample, Scope and Relevance

Drawing on a panel database of 103 Italian provinces over the years of 1998–2007, constructed by extending the original database of Millo and Carmeci (2011) both in time and in scope, we provide evidence that the demand for some important lines of Non-Life insurance is in fact decreasing with the interest rate on borrowing, while that of others is not. Most notably, among non-mandatory insurance lines (i.e., not considering Motor TPL), the standard and “commoditized” Property lines such as Motor Hull, Fire and Other Damage To Property do not correlate with the interest rates. Conversely, the lines most sensitive to borrowing cost are in the “others” category, which includes the most innovative forms of insurance typical of an advanced economy, as follows: Liability, Credit, Caution, Workers Compensation, and the like. This suggests that the effect of bad credit conditions is particularly detrimental to the most advanced sectors of the economy.

Unfortunately, insurance data are seldom very detailed, and it has already been quite a busy job to assemble the present dataset. A more detailed assessment will have to wait for more detailed provincial data: this is unlikely to happen in Italy, where the publication of provincial premium revenue has been reduced to Total Non-Life and Motor TPL since 2003. On the plus side, the variance in insurance, income and other demographic data over Italian provinces is high enough to span very diverse development levels, from some of the most advanced regions in Europe to well below the European average. Therefore, while a similar analysis on different countries would be welcome, our results can be taken as representative of a rather general population of regions.

Lastly, our choice of the observation period is, of course, due to the aforementioned issues with data availability; however, it is also underpinned by the need to observe sufficient variability in the borrowing rate. In fact, during the long phase of depressed nominal yields—often leading to negative real rates—that followed the 2008 crisis, the economic mechanism we try to identify in this paper is likely to have been muted. In fact, nominal rates are effectively bounded to be non-negative. Therefore, in a liquidity trap-like situation, such as that experienced after 2008, the borrowing–lending spread will be compressed towards zero (see, e.g., Eggertsson and Woodford 2003). Near-zero spreads will become negligible in the insured’s decision process and invalidate our identification strategy; just like near-zero fixed-income returns become less relevant in the tariffication process of the insurers, financial returns on invested reserves are being dominated by technical profitability (see the formalization in Equation (1) below).

One could surmise that borrowing costs have probably been superseded by outright rationing during the “liquidity years” after 2008, so that the analysis of the period from 2009 to 2020 does perhaps call for a different theoretical and empirical framework. However, this is speculation. It can instead be confidently said that our findings are relevant again in the present, with inflation rising and the interest rate structure again similar to that of our observation period.

2. Materials and Methods

2.1. Literature Review

Economic theory states that insurance improves welfare by shifting risk from risk-averse people to risk-neutral parties, the insurers, who efficiently pool and handle a large number of risks (Mossin 1968). In an intertemporal framework, it serves a similar purpose of stabilizing consumption pathways (for a survey, see Esho et al. 2004). From an industrial perspective, the Modigliani–Miller theorem states that insurers would not have a comparative advantage in diversifying risks compared to other corporations on a frictionless capital market. However, in the real world, insurance companies are able to efficiently manage a variety of low-probability risks for which contingent claim contracts would be unavailable or prohibitively expensive; as a result, the big firms’ motivation to purchase insurance is their desire to reduce transaction and bankruptcy costs (see MacMinn and Garven 2000; Skogh 1989).

The financial justification for acquiring Non-Life insurance is to shift future wealth from an uncertain to a certain state by receiving an indemnity for future losses in exchange for paying a fixed price, the premium, today. Based on theoretical models of Non-Life insurance demand, which date back to the seminal papers of Pratt (1964), Arrow (1978) and Mossin (1968), insurance demand is predicted to increase with risk aversion, the probability of loss and total wealth for a given level of risk exposure and price (see also Sweeney and Beard 1992; Szpiro 1985).

The concept of the “inverted economic cycle” in insurance, which refers to the payment of premiums upfront, followed by reimbursement in the case of a loss, implies that the financial rate of return—which is viewed as either an opportunity cost (from not investing) or a financing cost (from borrowing) for people who invest money in insurance policies—should be inversely correlated with demand. Though these conditions seem reasonable, Falciglia (1980) demonstrates that higher market interest rates should only reduce insurance demand if consumers have a declining risk aversion and are net savers.

The supply of insurance can be thought to depend on the return on insuring capital, which is primarily influenced by the premium rate (the unit price of coverage), the chance of loss and the interest rate, as addressed by Beenstock et al. (1988). It is conceivable that the supply of insurance will be positively impacted by the interest rate and premium rates (the latter, symmetrically to what was previously observed, due to gains from investing premiums on financial markets during the interim between premium collection and claims settlement), and negatively impacted by the likelihood of loss.

According to Beenstock et al. (1988), the equilibrium quantity of insurance traded on the market should be positively correlated with income and negatively correlated with interest rates and accident probability. Similarly, the equilibrium price should be positively correlated with income and loss probability and negatively correlated with interest rate. Therefore, total premiums should be positively correlated with income, and correlated to an undetermined degree with interest rates and loss likelihood. In the following, in line with most of the literature, we proxy for loss likelihood through population density.

2.2. The Economic Model

In the following section, we sketch the economic model underlying our identification strategy. We consider the decision faced by an individual whether to insure an asset at risk (a car, a home or any kind of personal belonging) or any other financial loss in general (financial liabilities arising from personal responsibility, financial losses from an inability to work or any other insurable financial loss).

Consider two periods, 0 (when the insurance decision is made) and 1 (when the result is observed and the loss indemnified, if any). Let s be the insured amount (potential loss) and, for simplicity, consider only total losses, so that the loss S is either 0 or s; this is incurred with probability $\pi$. Let r be the return on the investments for the insurer, earned on the national/international financial markets, and let i be the lending rate (the time cost of borrowing money) incurred, or gained, by borrowing/lending money on the local market, so that i is either an opportunity cost—if the insured foresakes lending opportunities to pay the insurance premium—or an incurred cost—if the insured has to finance the premium through borrowing.

The fair insurance premium is then as follows:

$$p={\displaystyle \frac{\pi S}{1+r}}$$

The insurer expects to pay $E\left[S\right]=\pi S$ in 1, but, after collecting p in 0, they can invest these proceedings for the period on financial markets. In other words, the fair premium is the current value of the expected loss, discounted at the rate relevant to the insurer.1

In turn, the present value of the indemnity in 1 is just the expectation of the loss, as follows: $E\left[S\right]=\pi S$. Hence, the present value of the insurance operation is as follows:

$$V(S,\pi ,r,i)=-p+{\displaystyle \frac{\pi S}{1+i}}$$

where the expectation of the future indemnity is discounted at the relevant rate for the insured, i. By substituting p and rearranging the equation, we get the value per unit of insured loss, as below:

$$V/S=\pi {\displaystyle \frac{r-i}{(1+r)(1+i)}}$$

(1)

which is decreasing in i: so that the insurer’s fair premium is more or less convenient to the insured, depending on the time cost/value of money he/she faces.

All this being said, and all other things being equal—in our case, insurers facing a common rate of return, regardless of the insured’s location, and tariffication being set at the national level, conditional on personal characteristics of the insured and local risk conditions—the insurance contract can be expected to be more advantageous in local economies where borrowing is cheaper. This leads us to formulating our research hypothesis in the following form:

 H₀:

Demand for Non-Life insurance is higher, ceteris paribus, where borrowing rates are lower.

Conditional on the above-mentioned determinants of insurance demand and supply, we therefore translate testing $H_0$ into obtaining a significant and negative coefficient for the borrowing rate in the regression of insurance consumption on it and controls.

2.3. The Data

Italy has already been chosen as an ideal sample for assessing the scope of given local differences in an otherwise homogeneous national environment; in fact, besides common laws, a common language and one and a half centuries of unitary history, wide regional differences persist which allow us to identify the net effects of institutional heterogeneity (see the discussion in Zingales 2003, see also Guiso et al. 2004, p. 2).

Both from a strictly economic perspective and from a social, cultural and demographic one, the Italian territory is immensely differentiated. The population’s age distribution demonstrates that elder people tend to live in the north-west and the center–north regions, while the youngest people tend to live in the central north and the south regions. Families vary greatly in their structures as well; the average number of people in a family consistently declines with latitude. Per capita income varies greatly by region, with the capital and the north having the highest and the south having the lowest. Economic growth indicators, such as the number of registered automobiles per capita, are distributed similarly, although they are more concentrated in the north-west and the center–north region than in the north-east. While unemployment is relatively low in much of the north and a small portion of the central region, it is quite high in the south. Though industry’s proportion of the land’s production is high in the central region as well, with the notable exception of Rome and its environs, the north is the most industrialized. Services, particularly those related to tourism, are crucial across the south and predominate in the Islands. Our main explanatory variable, the effect of the interest rate on borrowing, is no exception, in that it shows surprisingly high variance across the Italian territory.

Insurance penetration (premiums/GDP) and insurance density (premiums per capita) are the two standard normalized measurements used by practitioners and in the literature. Hereafter, we concentrate on the latter, not least to facilitate the comparison with the relevant previous literature. Notice, though, that despite much of the literature considering these two measures separately, linear models in logs of, respectively, insurance penetration or density end up being reparameterizations of each other, as long as income is included in the specification. In fact, consider an empirical log-log specification with per capita income as the only regressor; let $GWP$ be the total insurance premium revenue of a region, $INC$ some measure of total income, $POP$ the population and Z some control variable, so that the log-log model of insurance density is as follows:

$$log(GWP/POP)={\alpha }_{!}+{\beta }_{1}log(INC/POP)+{\gamma }_{1}Z+u$$

(2)

while that of insurance penetration is as follows:

$$log(GWP/INC)={\alpha }_2+{\beta }_{2}log(INC/POP){\gamma }_{2}Z+u$$

(3)

With simple manipulations, either (2) and (3) can be expressed as

$$log\left(GWP\right)={\delta }_0+{\delta }_{1}log\left(INC\right)+{\delta }_{2}log\left(POP\right)+{\delta }_{3}Z+u$$

s.t. ${\delta }_1+{\delta }_2=1$; however, from a practical estimation viewpoint, the scaled specifications in either penetration or density will be conveniently free from spurious size effects.

The Italian Insurance Authority (ISVAP, now superseded by IVASS) used to gather information on insurance premiums at the provincial level. This are still available for total Non-Life insurance and is split into the macrocategories MTPL and Non-MTPL. Since 1998 and up to the year 2002, by-province data on premium income for the lines MTPL, Motor Hull, Fire and Other Damage To Property are available from the ISVAP survey on insurance fraud. In turn, our comparable measure of borrowing rates comes from the National Observatory on Credit by Unioncamere and the Tagliacarne Institute (Capuano 2003). These data have been published and only the data from between 1998 and 2005 are available to us (see Supplementary Materials), effectively limiting the overall scope of our analysis to the latter period. However, please see the argument in the Introduction on how the structure of rates has flattened pathologically in subsequent years, leading to a sort of liquidity trap, which is likely to have temporarily invalidated the economic reasoning underpinning our analysis by reducing the time value of money to zero.

A description of the variables considered can be found in

Table 1. Data description and sources.

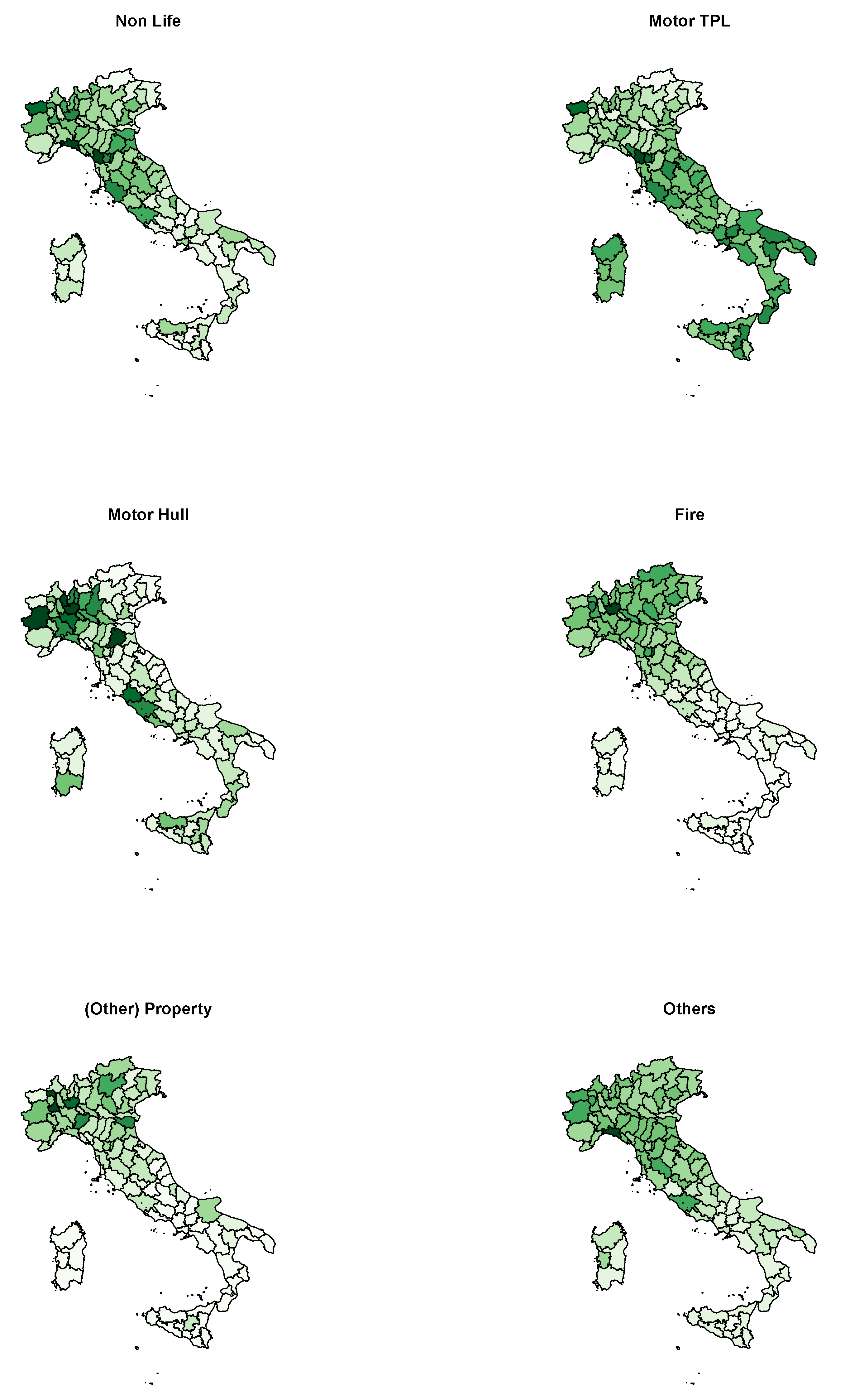
	Description	Source	Sample
RGDP	Real Gross Domestic Product per capita	Tagliacarne Inst.	1998–2007
POP	Total population	Istat	1998–2007
POPD	Population density per square km	Istat	1998–2007
RIRS	Real short-term interest rate on borrowing	Tagliacarne Inst.	1998–2005
AGRI	Share of value added, agricultural sector	Tagliacarne Inst.	1998–2007
FAM	Average number of family members	Istat	1998–2007
GWP	Gross written premiums (Non-Life)	ISVAP Yearbook	1998–2007
	Gross written premiums (MTPL)	ISVAP Yearbook	1998–2007
	Gross written premiums (Other lines)	ISVAP Crime Survey	1998–2002

; summary statistics by macroregion are reported in

Table 2. Macroregional averages from the year 2000.

	N-W	N-E	Center	South	Islands
RGDP	20,475.58	21,815.82	18,354.19	12,677.81	12,368.46
POPD	301.84	250.97	204.35	270.67	149.61
RIRS	4.47	4.43	4.60	6.01	5.76
AGRI	3.07	3.38	3.01	5.36	5.84
FAM	2.39	2.48	2.58	2.85	2.79

.

As is apparent from

Table 3. Matrix of pairwise correlations between RIRS and insurance density per capita in the various premium lines.

	RIRS	Non-Mt	MTPL	MH	Fire	Prop	Oth
RIRS	1.00	−0.81	−0.75	−0.69	−0.76	−0.70	−0.77
Non-Motor	−0.81	1.00	0.77	0.77	0.93	0.90	0.96
MTPL	−0.75	0.77	1.00	0.55	0.72	0.62	0.78
Motor Hull	−0.69	0.77	0.55	1.00	0.66	0.68	0.62
Fire	−0.76	0.93	0.72	0.66	1.00	0.89	0.85
Property	−0.70	0.90	0.62	0.68	0.89	1.00	0.79
Other	−0.77	0.96	0.78	0.62	0.85	0.79	1.00

, the real borrowing cost is strongly and negatively correlated with premium revenue across all lines.

The spatial distribution of insurance density (premiums per capita) across lines of business is depicted in Figure 1; while total Non-Life has a clear geographic gradient from the north-west to the south-east, lines are distributed heterogeneously, as follows: Motor TPL is distributed very evenly, in line with the high and homogeneous density of cars on the road throughout the country; Motor Hull, on the contrary, is very concentrated in the north-west and around Rome; the presence of Fire insurance is strongest in the industrialized north (including Emilia-Romagna and northern Tuscany), similarly to Other Damage To Property, which is nevertheless more heterogeneous and less diffused in the central region. Lastly, Other lines have a more even penetration across the country, with a bigger presence in the central region and some regions in the south.

2.4. The Empirical Model

A fixed effects analysis is not an option because our study primarily aims to explain provincial differences; therefore, we want to preserve some cross-sectional variability to be used in estimation. Conversely, if there is any unobservable heterogeneity connected with the regressors, which is quite plausible in our case, then a pure random effects model is inconsistent. Adding subgroup dummies, typically on a geographic- or development-level basis, is a workable strategy that falls somewhere between fixed and random effects (see Wooldridge 2010, p. 288). We incorporate subgroup dummies at two different, alternative levels, namely macroregional (5) in the maintained model, or regional (20, minus two regions containing a single province) as a robustness check. We assume that the residual individual impact is uncorrelated with the regressors due to the inclusion of (macro)-regional and time effects, so that, under the above conditions, we can treat the individual heterogeneity as random. The time dummies are intended to capture the effects of global shocks in general, which may cause a non-spatial type of cross-sectional dependence, as noted, for example, by Elhorst (2010), and the so-called “insurance cycle”, a long-term swing in prices and profitability that has been empirically established (see the seminal paper of Cummins and Outreville 1987).

Our empirical model links insurance expenditure (INS) to real borrowing rates (RIRS), i.e., observed nominal rates deflated by the national consumer price index (CPI), as a provincial CPI has never been available in Italy. Following Millo and Carmeci (2011), we control for real GDP per capita (RGDP/POP), which takes into account both income and the overall level of economic activity; the average number of family members (FAM), which takes into account the composition of the family; population density per square kilometer (POPD), serving as a stand-in for risk factors; and the proportion of value added by the agricultural sector (AGRI) to account for the composition of the productive sector.

$$\begin{array}{cc}\hfill log{(INS/POP)}_{it}& =\beta RIR{S}_{it}+{\gamma }_{1}log{(RGDP/POP)}_{it}+{\gamma }_{2}log{\left(FAM\right)}_{it}\hfill \\ \hfill & +{\gamma }_{3}log{\left(POPD\right)}_{it}+{\gamma }_{4}AGR{I}_{it}\hfill \\ \hfill & +\sum _{j=1}^J{\delta }_j{D}_j^{\left(M\right)}+\sum _{t=1}^T{\tau }_t{D}_t^{\left(T\right)}+{\mu }_i+u_{it}\hfill \end{array}$$

(4)

where $D^{\left(M\right)}$ are 5 macroregional dummies (of which the central region is taken as the baseline); $D^{\left(T\right)}$ are T yearly dummies; and $\mu$ is a random effect, assumed iid and uncorrelated with both the regressors and the idiosyncratic error u. All variables are expressed as logs exception made for rates and ratios in general. All monetary variables are deflated through the CPI. We employ the standard FGLS-RE estimator in the Swamy and Arora (1972) version.

2.5. Diagnostic Tests

Panel data analysts usually consider two possible kinds of temporal correlation in the errors. Next to that due to the presence of a random component, which induces a non-decaying persistence in composite errors and is well modeled in a RE framework, there is also the possibility of time-decaying correlation, due to the persistence of shocks. This second form of dependence can be accounted for through the popular heteroskedasticity- and autocorrelation-robust (HC) standard errors of Arellano (1987). In the output, we report robust standard errors, and also the p-values of the Breusch–Godfrey–Wooldridge diagnostic test for AR(1) serial correlation (Wooldridge 2010).2

A panel analysis on regional or subregional data always raises the issue of spatial correlation. Since this aspect is both more problematic in our context—HC standard errors being inconsistent under spatial error correlation—and less known, we dedicate the next paragraph to a description of the diagnostic employed; moreover, in the Appendix A, we estimate a full spatio-temporal model in the framework of Baltagi et al. (2007).

Spatial Permutation Test

In order to check for spatial dependence in regression residuals, we employ the permutation test of Millo (2017) ($RW$), which is based on the distribution of Pesaran (2004)’s $CD\left(p\right)$ statistic under permutations of the proximity matrix W. The general $CD$ test for cross-sectional dependence is based on averages of pairwise correlation coefficients between cross-sectional units, as follows:

$$CD=\sqrt{{\displaystyle \frac{2T}{N(N-1)}}}\left(\sum _{i=1}^{N-1}\sum _{j=i+1}^N{\widehat{\rho }}_{ij}\right);\phantom{pi}{\widehat{\rho }}_{ij}={\displaystyle \frac{{\sum }_t{e}_{it}{e}_{jt}}{{\left({\sum }_t{e}_{it}^2\right)}^{1/2}{\left({\sum }_t{e}_{jt}^2\right)}^{1/2}}}.$$

The $CD\left(p\right)$ (Pesaran 2004, sct. 7) is a “spatial” variant, testing the null of no cross-sectional dependence against the alternative of spatial dependence by appropriately subsetting the sample into neighboring cross-sectional units. The pairs of neighboring units can be selected according to a binary proximity matrix W. The test becomes the following:

$$C{D}_p=\sqrt{{\displaystyle \frac{T}{{\sum }_{i=1}^{N-1}{\sum }_{j=i+1}^{N}w{\left(p\right)}_{ij}}}}\left(\sum _{i=1}^{N-1}\sum _{j=i+1}^N{\left[w\left(p\right)\right]}_{ij}{\widehat{\rho }}_{ij}\right)$$

where ${\left[w\left(p\right)\right]}_{ij}$ is the $(i,j)$-th element of the p-th order proximity matrix, so that, if $h,k$ are not neighbors, ${\left[w\left(p\right)\right]}_{hk}=0$.

However, both versions of the $CD$ test are inappropriate under serial correlation (which would violate Assumption 1 in Pesaran 2004). Moreover, the spatial $CD\left(p\right)$ test has power against the false positive of non-spatial cross-sectional dependence (see Millo 2017). The $RW$ test is instead robust to general cross-sectional dependence, serial correlation or any other cause of non-centrality in the $CD\left(p\right)$ statistic, as long as it is independent from the spatial position of the observations. Hence, it will only detect spatial dependence. We employ the asymmetric two-tailed version, defined as follows:

$${\widehat{p}}^{*}\left(R{W}_p\right)=2\times min\left({\displaystyle \frac{{\sum }_{h=1}^{M}I[{\tau }_h^{*}\le \widehat{\tau }]}{M+1}},{\displaystyle \frac{{\sum }_{h=1}^{M}I[{\tau }_h^{*}>\widehat{\tau }]}{M+1}}\right).$$

(5)

where I is the indicator function; ${\tau }_h^{*}$ is the randomized $CD\left(p\right)$ statistic from the h-th draw, with $h=1\dots M$; and $\widehat{\tau }$ is the one under the “true” spatial ordering.

3. Results

The main results of the estimation of the RE, plus the macroregional dummies specification, are presented in

Table 4. By-line models: RE plus macroregional dummies. MTPL is Motor Third Party Liability; MH is Motor Hull (own damage). Heteroskedasticity- and autocorrelation-robust standard errors (Arellano) are reported in brackets. BG is the Breusch–Godfrey–Wooldridge test for serial error correlation (p-values reported); RW is the randomization test for error spatial correlation (pseudo-p-values reported). All models contain a full set of time dummies.

	NonLife	NonMTPL	MTPL	MH	Fire	Property	Other
RIRS	−1.89 **	−2.42 **	−1.44	−0.03	−2.67 *	2.05	−5.40 **
	(0.66)	(0.90)	(0.86)	(2.04)	(1.28)	(1.63)	(1.82)
RGDP	0.35 ***	0.18 *	0.39 ***	0.31	0.67 ***	0.76 ***	1.13 ***
	(0.07)	(0.09)	(0.07)	(0.17)	(0.16)	(0.23)	(0.18)
POPD	0.04 *	0.07 *	0.02	0.19 ***	0.07 *	0.10 *	0.02
	(0.02)	(0.03)	(0.01)	(0.04)	(0.03)	(0.05)	(0.03)
AGRI	−0.00	−0.00	−0.00	0.00	−0.00	0.00	0.00
	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.01)	(0.01)
FAM	−0.03	−0.07	−0.01	−0.69	0.01	−0.66	−0.05
	(0.08)	(0.10)	(0.10)	(0.48)	(0.24)	(0.48)	(0.33)
BG test	0.00	0.00	0.00	0.00	0.00	0.00	0.26
RW test	0.00	0.91	0.00	0.00	0.79	0.00	0.09
s_idios	0.04	0.06	0.05	0.09	0.06	0.10	0.10
s_id	0.10	0.15	0.10	0.27	0.21	0.28	0.19
$R^2$	0.80	0.66	0.78	0.26	0.71	0.60	0.68
Adj. $R^2$	0.79	0.66	0.78	0.24	0.70	0.59	0.67
Num. obs.	824	824	824	515	515	515	515

*** p < 0.001; ** p < 0.01; * p < 0.05.

, with standard errors robust to heteroskedasticity and autocorrelation (Arellano 1987). The effect of RIRS is consistently negative across all models, significant for the aggregate Non-Life, the aggregate non-mandatory Non-MTPL, and for the following lines of business: Fire and Other lines. The by-line results are also less sharp than those of the aggregates, because they are drawing on smaller samples; nevertheless, in particular, the results of the Other lines—including General and Professional Liability, Industrial Risks, Transport, Credit, Caution and so forth—point at a strong negative influence of borrowing costs on insurance turnover in those lines which are characteristic of a developed economy. From this last viewpoint, it is worth noting that only for the Other lines is the coefficient of income in the regression larger than one in magnitude (although it is not significantly larger than one); this is further evidence that the importance (measured as the share over GDP) of these insurance lines is increasing with the rise of GDP per capita.

Diagnostic tests point at a strong serial correlation for the errors of all models in all lines except for Other; therefore, the use of HC standard errors is justified. Nevertheless, as can be seen from the RE-AR(1) models reported in the Appendix A, AR(1) coefficients never approach unity, so nonstationarity is not a concern3. Moreover, the substantive conclusions remain unchanged.

Spatial permutation tests also find spatial dependence in the residuals of some lines (the Motor pair and Property). For this reason, in the Appendix A, we report a spatiotemporal model estimated by maximum likelihood, assessing the importance of this aspect and the consequences on parameter estimates. Again, the qualitative conclusions from this more sophisticated specification are unchanged, with respect to the main results described above.

4. Conclusions

Interest rates affect both Non-Life insurance supply and demand, possibly in opposite directions. Insurers issue contingent debt contracts and invest the funds until they are needed to pay the claims, so interest rates are a source of revenue for the insurers and a cost for the insured. More in particular, they are an opportunity cost for the net lenders, and a financing cost for the net borrowers. Therefore, a negative effect of local interest rates on demand should be expected.

Prices and quantities are generally unobservable in insurance data, forbidding the estimation of a demand and supply system. In order to isolate the effect of interest rates on demand, we observed a panel of Italian provinces. At this level, most of the insured—except for the bigger firms and corporations—face local borrowing conditions, while financial returns from the national and international financial markets are uniform.

Interest rates on short-term borrowing vary within a range of almost 400 bp across Italian provinces, and in a range of over 150 bp across macroregions, over our sample period. At the same time, yearly per-capita expenditure on Non-Life insurance varies between 50 and over 500 euros. Such large variance in the phenomena of interest, together with the relative institutional, cultural and legal uniformity within a single country, provided an ideal testbed for identifying their contributions, free from the confounding effect of country heterogeneity, as already observed in the literature.

Controlling for all possible other influences, we provide regression evidence that the demand for Non-Life insurance is in fact decreasing with the interest rate on borrowing. This result is robust across a number of specifications.

Why do the different Non-Life lines have varying degrees of sensitivity to interest rates?4 The varying sensitivity of different lines to interest rates is an empirical discovery for which we do not really have an explanation. Tentatively, it might well be that the insured in more “advanced” lines are financially more sophisticated (in particular, lines like Third Party Liability, Credit and Suretyship, and even Accidents will cater mainly to small firms and individual professionals). We present this as an empirical fact, worthy of further investigation, perhaps with more disaggregated data.

We conclude that, consistent with our expectations, credit conditions are a significant driver of Non-Life insurance development; additionally, according to the results of our empirical exercise, they have also been an important limiting factor in the development of the insurance market in the particular case of Southern Italy.