The Effect of Risk Management on Direct and Indirect Capital Structure Deviations

Abstract

This study explores the effect of risk management on capital structure deviations. Specifically, we innovatively classify capital structure deviations into direct and indirect deviations, with our classification being based on deviations resulting mainly from changes in either actual or target leverage. Thus, if the variation in the actual leverage exceeds the variation in the target leverage, this deviation is considered direct. Conversely, if the target leverage varies more than the actual leverage, it is considered an indirect deviation. Our results reveal that risk management can help reduce these deviations, which mainly result from changes in actual leverage. We further demonstrate that insurers with direct deviations adjust their capital structure approximately 29.2% faster than insurers with indirect deviations.

1. Introduction

Trade-off theory suggests that convergence toward target capital structures represents the optimal capital structure decision for effectively balancing the costs and benefits of debt (Fischer et al. 1989). The capital structure adjustment process, which exploits the tax benefits of debt and does not lead to financial distress, is a type of risk exposure adjustment. Thus, risk management is related to capital structure adjustments.

Previous studies have investigated capital structure adjustment, focusing only on the difference between actual and target leverage to measure the outcome of such adjustments (e.g., Uysal 2011; Oztekin and Flannery 2012; Hovakimian and Hovakimian 2019; Wang et al. 2024). However, variations in both actual and target leverage can lead to variations in deviations from the target leverage. For example, an increase in capital structure deviations (actual leverage minus target leverage) can reflect either an increase in actual leverage or a reduction in target leverage, each of which involves different mechanisms. We argue that capital structure deviations can be categorized as direct or indirect.

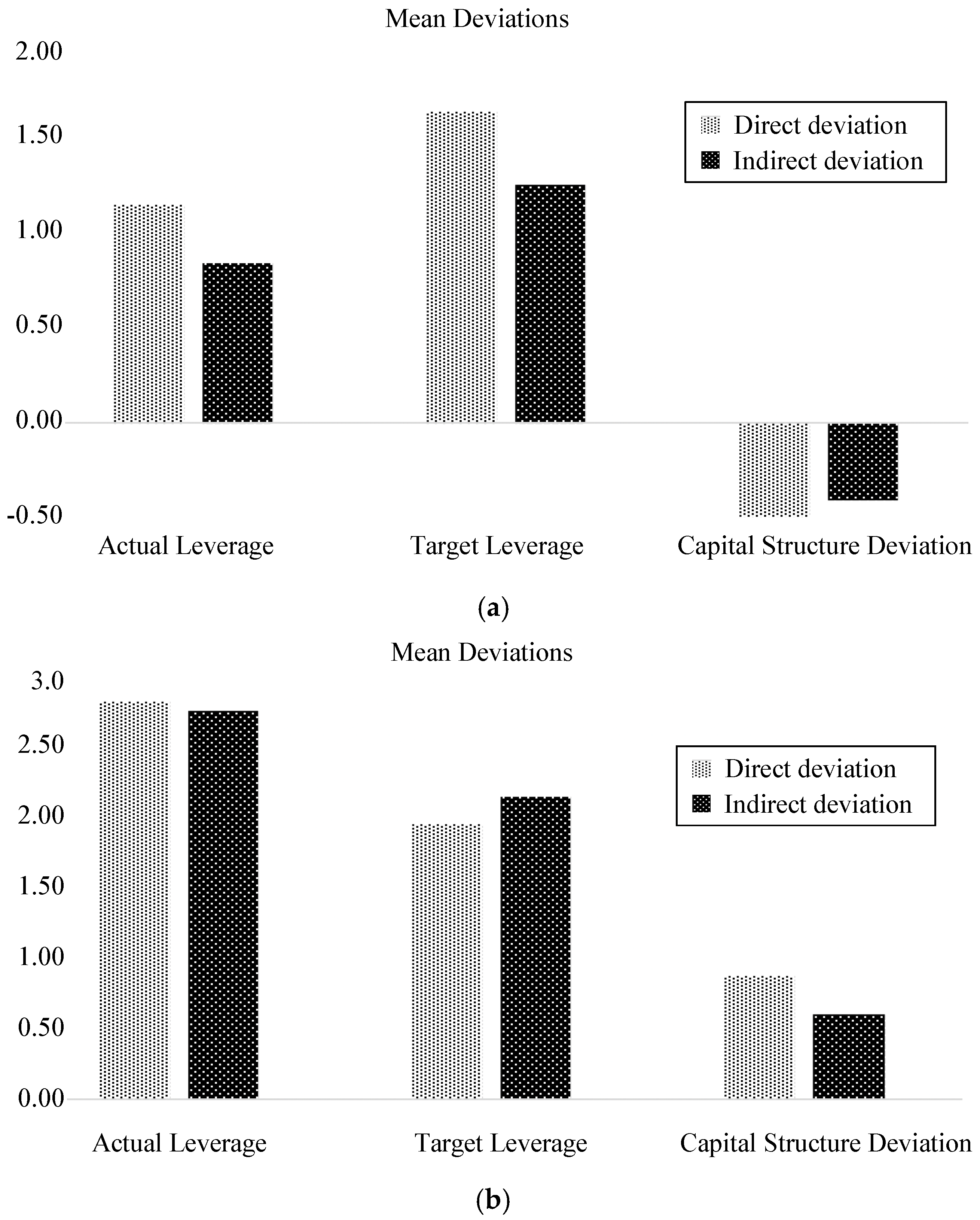
To some extent, this situation is similar to the direct and indirect interventions employed by a country’s central bank in the foreign exchange market. A country’s central bank can directly intervene by influencing the demand or supply of its currency; however, this can also affect other factors, such as interest rates and government controls, which will affect the value of the currency; this is an example of indirect intervention. Although direct and indirect interventions can have the same effect on currency value, their mechanisms are different. Inspired by the direct and indirect interventions noted above, we argue that a firm can deliberately cause capital structure deviations by directly changing actual leverage or indirectly changing factors that can subsequently affect target leverage. Therefore, in this study, we identify different types of capital structure deviations based on changes in actual or target leverage. If | ΔLev_act | > | ΔLev_tgt |, the deviation is regarded as a direct deviation, while the reverse is regarded as an indirect deviation. | ΔLev_act | represents the absolute value of the difference between time t and time t − 1 for actual leverage, and | ΔLev_tgt | represents that for target leverage.

In contrast to actual leverage, target leverage is unobservable and can therefore only be estimated (e.g., Hovakimian et al. 2004; Flannery and Rangan 2006; Cook et al. 2016; Yin and Ritter 2020; Kumar 2024). Several related studies have noted that target leverage varies with the stock price, firm profitability (Hovakimian et al. 2001), and asset restructuring (Cook et al. 2016). Variations in firm characteristics lead to changes in target leverage.

The categorization of capital structure deviations into direct and indirect forms builds on the theoretical understanding that deviations can stem from different adjustment mechanisms—either through active changes in actual leverage or passive fluctuations in target leverage due to external factors. Direct deviations occur when actual leverage diverges more significantly than target leverage, reflecting an active management response where firms can promptly adjust leverage levels. Conversely, indirect deviations result from greater variation in target leverage due to external factors like market conditions or asset price fluctuations, which are harder to manage directly.

Reinsurance impacts these deviation types through distinct mechanisms. For direct deviations, reinsurance allows insurers to offload risk and free up capital, which can be used to actively recalibrate their leverage ratios. However, for indirect deviations, reinsurance is less effective in influencing target leverage, as it does not directly address the factors (e.g., profitability and stock prices) that affect target levels. This theoretical distinction highlights how reinsurance aligns more with active adjustments, making it more relevant for managing direct deviations.

Variations that are generally discernible in firm characteristics are not normally regarded as a means of adjusting target leverage; therefore, any changes in target leverage are likely to be passively influenced by firm characteristics. We define capital structure deviations as indirect deviations when they are primarily the result of variations in target leverage, indicating a situation in which capital structure deviations are primarily the result of other factors affecting target leverage. Conversely, because actual leverage is observable, direct adjustment is possible. As such, an insurer can actively and directly manage its actual leverage toward its target leverage by changing the amount of debt or assets that it holds. When capital structure deviation is primarily the result of a change in actual leverage, such capital structure movements are regarded as direct deviations.

Risk management, and particularly reinsurance, is a critical consideration for insurance companies. Reinsurance allows insurers to mitigate risk by transferring a portion of their liabilities to other parties (Mayers and Smith 1990). This practice provides financial stability and enables insurers to underwrite more policies, increasing their capacity to generate revenue. Effective risk-management strategies are essential for maintaining solvency, especially in the face of catastrophic events that can lead to considerable financial losses. Therefore, reinsurance has a dramatic effect on capital structure deviations (Li and Shiu 2023).

Understanding how property casualty insurers adjust their capital structures in response to deviations from target levels is critical. It sheds light on the strategic financial decisions made by insurers and their approaches to risk management through reinsurance. The regulatory environment in the US further underscores the importance of studying this sector. Insurers are subject to stringent capital requirements and oversight by regulatory bodies, such as the National Association of Insurance Commissioners (NAIC). These regulations aim to ensure that insurers maintain adequate capital reserves to meet policyholders’ obligations, thereby protecting consumers and maintaining market stability.

We aim to fill a gap in the literature by providing empirical evidence on the dynamic relationship between capital structure deviations and risk-management practices in the US property casualty insurance industry. We also innovatively identify different types of capital structure deviations based on those resulting mainly from changes in either actual or target leverage, thereby providing deeper insights into the different types of capital structure deviations.

This study contributes to the literature in two ways. First, our findings contribute to the growing literature on capital structure deviations in financial decisions (e.g., Harford et al. 2009; Cook and Tang 2010; Uysal 2011; Faulkender et al. 2012; Zhou et al. 2016). Previous studies on capital structure deviation usually focused on the relative position between actual and target leverage (over-leveraged or under-leveraged status). A firm with higher actual leverage than the target leverage is regarded as over-leveraged. Conversely, a firm with actual leverage lower than the target leverage is under-leveraged. However, none of these studies identified the types of capital structure deviation based on channels, resulting in variations. Variations in both the actual and target leverage can lead to variations in deviations toward the target leverage. Therefore, our study innovatively identifies direct and indirect capital structure deviations, rather than positive and negative deviations.

Second, this study contributes to the literature on risk management and capital structure. Most studies investigated the effects of risk management and capital structure (e.g., Zou and Adams 2008; Pérez-González and Yun 2013; Shiu 2016; Li and Shiu 2021). We focus on the effect of risk management on capital structure deviations rather than capital structure. Insurers are subject to stringent regulatory requirements to ensure that they have sufficient capital to cover policyholder liabilities. Deviations from a target capital structure can lead to regulatory noncompliance, risking fines or sanctions. Leverage increases the risk of financial distress, potentially leading to bankruptcy or restructuring. Therefore, insurers’ capital structures are a critical aspect of their financial management and have key implications for regulatory compliance, risk management, financial stability, and market competitiveness. Capital structure deviations can have severe consequences, making it crucial for insurers to carefully manage their mix of debt and equity.

As risk management is related to capital structure adjustment, this study investigates whether risk management plays different roles across direct and indirect deviations. The main results are summarized as follows: First, our empirical analyses reveal that both under-leveraged and over-leveraged insurers with direct deviations tend to actively adjust their leverage levels to converge with their target leverage by adopting risk-management methods, whereas this is not indicated for insurers with indirect deviations. We also find that risk management both helps reduce deviations toward the target leverage and makes these adjustments more efficient. Insurers with direct deviations adjust their capital structure approximately 29.2% faster than insurers with indirect deviations.

The remainder of this paper is organized as follows: Section 2 describes the data and methodology, including the research design, data sources, and sample selection used in the analysis. Section 3 presents the findings. Finally, Section 4 presents the conclusions of this study.

2. Data and Methodology

We use annual statement data obtained from the NAIC from 2001 to 2016. We exclude insurers with negative assets and those with missing reinsurance data from the sample. Our final sample contained 2829 insurers, providing an unbalanced panel of 29,549 firm-year observations. To eliminate outliers, all variables are winsorized at the top and bottom 1% levels (Che and Liebenberg 2017).

We first follow these studies to estimate the target capital structures of our sample of insurers using the two-way fixed effects method (e.g., Flannery and Rangan 2006; Zhou et al. 2016). Target leverage is defined as follows:

$$L_{i,t}^{*}=\beta X_{i,t-1}$$

where $L_{i,t}^{*}$ refers to the target leverage of firm i at time t; β is a vector of coefficients; and $X_{i,t-1}$ is a vector of target leverage determinants.1 Second, we measure capital structure deviations based on the target capital structure. Capital structure deviation is defined as actual leverage minus target leverage. Notably, both actual and target leverage can lead to variations in capital structure deviations from targets; for example, an increase in capital structure deviations can be the result of either an increase in actual leverage, a reduction in target leverage, or both. Moreover, actual leverage can be directly observed and adjusted, whereas target leverage is unobservable and, therefore, only estimated. Inspired by the idea of central banks’ direct and indirect interventions, we classify capital structure deviations into direct and indirect. We identify different deviations based upon deviations primarily resulting from actual or target leverage, such that | ΔLev_act | > | ΔLev_tgt | is regarded as a direct deviation, while | ΔLev_act | < | ΔLev_tgt | is regarded as an indirect deviation. For convenience, the definitions of | ΔLev_act | and | ΔLev_tgt | are restated here. | ΔLev_act | represents the absolute value of the difference between time t and time t − 1 for actual leverage, and | ΔLev_tgt | represents that for target leverage. To test the effect of reinsurance on capital structure deviation, we include several control variables: Size, defined as the natural logarithm of total assets (Powell and Sommer 2007); Prof, profitability, the ratio of net income to assets (De Haan and Kakes 2010); GrOpp, growth opportunities, defined as changes in net premiums written (Myers 1984); and HHIBus (HHIGeo), the Herfindahl–Hirschman Index based upon lines of business concentration (geographical concentration) (Berry-Stölzle et al. 2012; Che and Liebenberg 2017). Derivatives are calculated as the fair value of derivative transactions divided by total assets (Leland 1998; Guay 1999; Cummins et al. 2001).

Table 1. Variable definitions.

Variable	Definition
Dev	Capital structure deviations, calculated as the actual leverage minus the target leverage.
Rein	Reinsurance, calculated as the ratio of premiums ceded to total premium written.
Lev	Leverage, calculated as the ratio of liabilities to surplus.
Size	Firm size, calculated as the natural logarithm of total assets.
Prof	Profitability, calculated as the ratio of net income to total assets.
GrOpp	Growth opportunities, calculated as the ratio of changes in net premiums written to total assets.
HHIBus	Herfindahl–Hirschman Index of lines of business concentration.
HHIGeo	Herfindahl–Hirschman Index of geographical concentration.
Longtail	Long-tailed line, calculated as the ratio of insurance reserves to losses incurred.
Deriv	Derivatives, calculated as the fair value of derivatives transactions divided by total assets.

provides the definitions of the variables.

To mitigate the potential endogeneity between reinsurance and deviations from target capital structures, we use a simultaneous equation model with the three-stage least squares (3SLS) method. We use a simultaneous equation model to test the effect of reinsurance on capital structure deviations. This is a type of statistical model used in econometrics and other fields to describe multiple interdependent relationships between variables. Unlike single-equation models, in which each equation stands alone, simultaneous equation models comprise multiple equations that are estimated together because the dependent variables in these equations are determined jointly. The dependent variables are the capital structure deviation and reinsurance. Regarding the estimation method, following Shim (2010) and Mankai and Belgacem (2016), we employ 3SLS. 3SLS is an advanced estimation technique that improves upon the two-stage least squares method by accounting for the correlations between error terms across equations in a simultaneous system. This leads to more efficient and robust estimates, making the 3SLS particularly valuable for complex economic models and other applications involving interdependent relationships among variables.

3. Empirical Results

3.1. The Effects of Reinsurance on Direct and Indirect Deviations

This study proposes a novel classification of capital structure deviations based on deviations primarily resulting from actual or target leverage, defining a capital structure deviation primarily resulting from a change in actual (target) leverage as a direct (indirect) deviation. The means of the actual leverage, target leverage, and capital structure deviations for direct and indirect deviations are illustrated in Figure 1, with Figure 1a revealing that under-leveraged insurers with direct deviations generally have higher actual and target leverage than those with indirect deviations. Insurers with direct deviations exhibit higher actual and target leverage than those with indirect deviations, suggesting that they may actively adjust their capital structure by increasing actual leverage to align more closely with target levels. In sharp contrast, as Figure 1b shows, over-leveraged insurers with direct deviations have lower target leverage levels than insurers with indirect deviations.

Figure 1 reveals considerable heterogeneity in the direct and indirect deviations across the under-leveraged and over-leveraged insurers; however, concerning capital structure deviations, the same feature is discernible for both groups of insurers; that is, more capital structure deviations involve direct deviations than indirect deviations. Overall, direct deviations are more prevalent in both under- and over-leveraged insurers, suggesting a stronger tendency toward active rebalancing among insurers facing direct deviations compared to those with indirect deviations.

Table 2. Summary statistics.

Panel A: Direct Deviations
	No. of Obs.	Mean	SD	P25	Median	P75
Dev	14,947	0.065	1.204	−0.439	−0.125	0.298
Rein	14,947	0.398	0.327	0.107	0.332	0.654
Size	14,947	18.500	1.846	17.170	18.410	19.700
Prof	14,947	0.022	0.059	0.002	0.025	0.048
GrOpp	14,947	0.002	0.141	−0.016	0.007	0.040
Longtail	14,733	1.163	2.363	0.469	0.810	1.172
HHIBUS	14,947	0.344	0.239	0.164	0.288	0.500
HHIGEO	14,947	0.535	0.393	0.127	0.486	1.000
Deriv	14,947	−0.048	2.816	0.000	0.000	0.000
Panel B: Indirect Deviations
	No. of Obs.	Mean	SD	P25	Median	P75
Dev	11,523	−0.090	0.764	−0.471	−0.210	0.103
Rein	11,523	0.386	0.328	0.092	0.313	0.650
Size	11,523	18.320	1.910	16.940	18.190	19.540
Prof	11,523	0.026	0.044	0.009	0.026	0.045
GrOpp	11,523	0.009	0.094	−0.009	0.006	0.032
Longtail	11,394	1.167	2.456	0.448	0.824	1.194
HHIBUS	11,394	0.346	0.244	0.165	0.286	0.500
HHIGEO	11,523	0.560	0.395	0.145	0.544	1.000
Deriv	11,523	−0.038	6.808	0.000	0.000	0.000

This table presents the descriptive statistics of all the variables in our regression analysis. Direct (indirect) deviations are capital structure deviations that mainly result from actual (target) leverage. | ΔLev_act | > | ΔLev_tgt | is regarded as a direct deviation, while | ΔLev_act | < | ΔLev_tgt | is regarded as an indirect deviation. Dev (target leverage deviation): actual leverage minus target leverage; Rein: ratio of premiums ceded to total premiums written; Size: ln (total assets); Prof: ratio of net income to assets; GrOpp: ratio of changes in net premiums written to total assets; Deriv: volume of derivative transactions divided by total assets; HHIBus: Herfindahl–Hirschman Index of line of business; HHIGeo: geographical Herfindahl–Hirschman Index.

presents the summary statistics of our sample. Regarding capital structure deviation types, more than half of the observations were direct. In Panel A (B), the mean capital structure deviation is 0.065 (−0.090), indicating that insurers with direct deviations tend to have positive deviations, whereas those with indirect deviations tend to have negative deviations. The mean reinsurance ratio was nearly 0.4, with a standard deviation of 0.3. This suggests that both insurer groups use reinsurance at similar levels but might apply it differently depending on their deviation type. Firm size has a mean of 18.500 and 18.320 in Panels A and B, respectively, indicating that insurers with direct or indirect capital structure deviations have similar firm sizes, on average. Additionally, profitability has a mean of about 0.020 and a standard deviation of no more than 0.06 for both direct and indirect capital structure deviations, suggesting a non-significant variation among insurers. This reflects a stable profitability trend among insurers regardless of deviation type, possibly affecting how insurers with indirect deviations passively adjust capital structure.

Table 3. Pearson correlation matrix.

Variable	Dev	Rein	Size	Prof	GrOpp	Longtail	HHIBUS	HHIGEO	Deriv
Dev	1.000
Rein	−0.001	1.000
Size	−0.094 ***	0.016 ***	1.000
Prof	−0.264 ***	−0.051 ***	0.089 ***	1.000
GrOpp	0.119 ***	−0.162 ***	0.022 ***	−0.067 ***	1.000
Longtail	−0.020 ***	−0.043 ***	−0.066 ***	0.085 ***	0.052 ***	1.000
HHIBUS	0.058 ***	−0.072 ***	−0.271 ***	0.013	0.052 ***	0.074 ***	1.000
HHIGEO	0.121 ***	−0.128 ***	−0.411 ***	−0.049 ***	0.012	−0.009	0.282 ***	1.000
Deriv	0.007	0.008	−0.024 ***	0.003	0.000	0.001	0.017 ***	0.001	1.000

This table presents the Pearson correlation coefficients for all the variables. Dev (target leverage deviation): actual leverage minus target leverage; Rein: ratio of premiums ceded to total premiums written; Size: ln(total assets); Prof: ratio of net income to assets; GrOpp: ratio of changes in net premiums written to total assets; Deriv: volume of derivative transactions divided by total assets; HHIBus: Herfindahl–Hirschman Index of line of business; HHIGeo: geographical Herfindahl–Hirschman Index. *** p < 0.01.

presents Pearson’s correlation coefficients for the key variables. The correlation between reinsurance and capital structure deviation is −0.001, which is non-significant (p < 0.01). This implies that the effect of reinsurance on different types of deviation may be opposite and thus offset. Notably, profitability and capital structure deviations exhibit a relatively significant negative correlation (p < 0.01), suggesting that as profitability increases, capital structure deviations tend to decrease. Additionally, firm size and capital structure deviation have a weak negative correlation, implying that an increase in firm size is associated with a slight decrease in capital structure deviation. Overall, the absolute value of the Pearson correlation coefficient was no greater than 0.3, indicating that there was no multicollinearity among the variables used in the regression analysis.

Table 4. Direct and indirect deviations.

Variable	Direct Deviations			Indirect Deviations
	No. of Obs.	Mean	SD	No. of Obs.	Mean	SD
Dev	15,241	0.066	1.235	12,035	−0.096	0.788
| ΔLevact |	15,241	0.597	1.146	12,035	0.121	0.241
| ΔLevtgt |	15,241	0.174	0.343	12,035	0.312	0.529

This table provides the mean and standard deviations of the capital structure deviations, Dev, and the actual and target leverage variations for both direct and indirect deviations, with | ΔLev_act | reporting the absolute value of the difference the between time t and time t − 1 for actual leverage and | ΔLev_tgt | reporting that for target leverage. Direct (indirect) deviations are capital structure deviations that mainly result from actual (target) leverage. | ΔLev_act | > | ΔLev_tgt | is regarded as a direct deviation, while | ΔLev_act | < | ΔLev_tgt | is regarded as an indirect deviation.

provides evidence of broad-based propensities for direct and indirect deviations. Direct deviations primarily result from greater fluctuations in actual leverage, while indirect deviations reflect greater variation in target leverage. This distinction underlines that direct deviations are driven by active leverage adjustments, whereas indirect deviations stem from changes in target leverage due to external factors. Regardless of whether the focus is on the number of observations, the mean, or the standard deviation, the capital structure deviations involving direct deviations are greater than those involving indirect deviations, implying that direct deviations are more volatile and capital structure adjustments are more pronounced. Further, when attempting to identify the factors driving such deviations, it is not surprising to find greater volatility in actual leverage for direct deviations and in target leverage for indirect deviations, as actual leverage is the main driver of direct deviations and target leverage is the main driver of indirect deviations.

In this section, we test the effects of risk management on direct and indirect capital structure deviations. For direct deviations, the coefficient on Rein is significantly positive (negative) for under-leveraged (over-leveraged) insurers, thereby clearly implying that actual and target leverage levels begin to converge for both under-leveraged and over-leveraged insurers in Panel A (

Table 5. The effects of reinsurance on direct and indirect deviations.

Variables	Under-Leveraged			Over-Leveraged
	Coeff.		SE	Coeff.		SE
Panel A: Direct Deviations
Constant	−0.155	**	0.07	1.272	***	0.24
Rein	0.384	***	0.02	−0.430	***	0.06
Size	−0.028	***	0.00	−0.021	*	0.01
Prof	2.456	***	0.12	−5.709	***	0.38
GrOpp	0.359	***	0.06	−0.450	***	0.16
Longtail	0.004	*	0.00	−0.006		0.01
HHIBus	−0.262	***	0.02	0.628	***	0.08
HHIGeo	0.167	***	0.02	0.020		0.05
Deriv	−0.000		0.00	−0.008		0.02
R2	0.002			0.041
No. of obs.	8777			6126
Panel B: Indirect Deviations
Constant	0.268	***	0.03	−0.856	***	0.25
Rein	0.142	***	0.01	2.329	***	0.04
Size	−0.041	***	0.00	0.003		0.01
Prof	0.682	***	0.05	−3.137	***	0.35
GrOpp	0.318	***	0.02	0.397	***	0.14
Longtail	0.002		0.00	−0.004		0.01
HHIBus	−0.212	***	0.01	0.772	***	0.08
HHIGeo	0.139	***	0.01	0.307	***	0.06
Deriv	0.000		0.00	−0.001		0.00
R2	0.132			−0.332
No. of obs.	7834			3663

This table provides the effects of reinsurance on direct and indirect capital structure deviations in direct (indirect) deviation based on simultaneous equations using three-stage least squares estimations. The dependent variable for all observations is capital structure deviation Dev, which is defined as the actual leverage minus the target leverage. Under-leveraged (over-leveraged) insurers are defined as those whose actual leverage is lower (higher) than their target leverage, whereas direct (indirect) deviations are defined as capital structure deviations that mainly result from actual (target) leverage. | ΔLev_act | > | ΔLev_tgt | is regarded as a direct deviation, while | ΔLev_act | < | ΔLev_tgt | is regarded as an indirect deviation. Rein denotes the ratio of premiums ceded to total premiums written; Size is defined as ln(total assets); Prof is the ratio of net income to assets; GrOpp denotes the change in net premiums written; Longtail is the ratio of insurance reserves to losses incurred; Deriv is the volume of derivatives transactions divided by total assets; HHIBus is the Herfindahl–Hirschman index of the line of business; and HHIGeo is the geographical Herfindahl–Hirschman index. * p < 0.1, ** p < 0.05, *** p < 0.01.

). Consistent with prior studies (e.g., Leary and Roberts 2005; Flannery and Rangan 2006; Byoun 2008; Zhou and Li 2024), this finding provides support for trade-off theory, which posits that firms usually tend to converge toward their targets once their leverage levels deviate from their target levels.

Regarding indirect deviations, capital structure deviations primarily result from target leverage; significantly positive coefficients on Rein are discernible for both under-leveraged and over-leveraged insurers. Because target leverage is influenced by asset shocks (Cook et al. 2016), variations in target leverage are passive and, therefore, are more uncertain and unpredictable. Insurers with larger changes in target leverage than in actual leverage may be exposed to greater uncertainty. Overall, our results indicate that reinsurance plays a key role in reducing the deviation between the actual and target leverage for insurers with direct deviations. However, when the capital structure deviation is indirect, insurers with more reinsurance tend to deviate further from their target leverage. These results are consistent with our expectation that the effects of reinsurance differ for direct and indirect capital structure deviations. From a policy perspective, these findings highlight the strategic importance of differentiating between direct and indirect deviations when designing risk management frameworks. Insurers may benefit from regulatory guidance that encourages reinsurance strategies tailored to specific deviation types, ensuring more targeted capital structure stabilization.

3.2. The Speed of Capital Structure Adjustment

We follow Flannery and Rangan (2006) and Lian et al. (2024) to estimate the partial adjustment model in this study. The results of the partial adjustment model on the following equation:

$${Lev}_{{act}_{i,t}}=\left(\lambda \beta \right)X_{i,t-1}+\left(1-\lambda \right){Lev}_{{act}_{i,t-1}}+{\epsilon }_{i,t}$$

Table 6. Partial adjustment model results.

Variable	Coeff.		SE	Coeff.		SE
	Direct Deviations			Indirect Deviations
Constant	0.152		0.12	0.022		0.03
Levacti,t−1	0.671	***	0.02	0.963	***	0.01
Size	0.021	***	0.01	0.001		0.00
Prof	−1.396	***	0.39	0.051		0.09
GrOpp	0.546	***	0.13	0.091	***	0.03
Longtail	−0.001		0.00	0.001	*	0.00
HHIBus	0.129	***	0.05	−0.034	***	0.01
HHIGeo	0.024		0.02	−0.014	**	0.01
Deriv	−0.003		0.00	0.000		0.00
R2	0.441			0.972
No. of obs.	14,903			11,497

This table provides the results of the partial adjustment model. The dependent variable is the actual leverage Lev, which is defined as the ratio of liabilities to surplus. Direct (indirect) deviations are capital structure deviations that mainly result from actual (target) leverage. | ΔLev_act | > | ΔLev_tgt | is regarded as a direct deviation, while | ΔLev_act | < | ΔLev_tgt | is regarded as an indirect deviation. The X (lagged) variables comprise the following: Size, defined as ln(total assets); Prof, the ratio of net income to assets; GrOpp, the change in net premiums written; Longtail, the ratio of insurance reserves to losses incurred; Deriv, the fair value of derivatives transactions divided by assets; HHIBus, the Herfindahl–Hirschman Index of the line of business; and HHIGeo, the geographical Herfindahl–Hirschman Index. * p < 0.1, ** p < 0.05, *** p < 0.01.

shows the results on the speed of adjustment for direct and indirect deviations. Regarding direct deviations, the coefficient on Lev_act, 0.671, implies that the adjustment speed is 32.9% (=1 − 0.671) per year, which is much more rapid than that for indirect deviations (adjustment speed 3.7% (=1 − 0.963) per year); thus, direct deviations are, to some extent, more active than their indirect counterparts. This result is not surprising because indirect deviations, similar to the indirect interventions of a central bank in the foreign exchange market, are relatively time-consuming and ineffective. Variations in firm characteristics are generally not a method for adjusting target leverage; therefore, any changes in target leverage are likely to be passively influenced by these characteristics. Conversely, because actual leverage is observable, direct adjustment is possible, allowing an insurer to actively manage its actual leverage toward its target; thus, it is more effective. Economically, this disparity suggests that firms with indirect deviations may face higher costs of misalignment and greater exposure to systemic risks.

3.3. Subsamples with Different Levels of Reinsurance

Table 7. Subsamples with different levels of reinsurance.

Variable	Less Reinsurance		More Reinsurance
	Coeff.	SE	Coeff.	SE
Panel A: Direct Deviations
Constant	1.518 ***	0.16	0.292	0.20
Rein	−0.033	0.09	0.461 ***	0.06
Size	−0.085 ***	0.01	−0.037 ***	0.01
Prof	−1.987 ***	0.28	−1.211 ***	0.30
GrOpp	0.423 ***	0.14	0.569 ***	0.12
Longtail	0.002	0.01	−0.005	0.01
HHIBus	0.035	0.05	0.044	0.06
HHIGeo	0.202 ***	0.04	0.370 ***	0.04
Deriv	0.001	0.01	−0.008	0.01
R2	0.041		0.023
No. of obs.	7320		7583
Panel B: Indirect Deviations
Constant	0.537 ***	0.10	−1.565 ***	0.15
Rein	0.634 ***	0.06	1.289 ***	0.04
Size	−0.046 ***	0.01	0.026 ***	0.01
Prof	−1.287 ***	0.17	−1.602 ***	0.21
GrOpp	0.206 **	0.09	0.570 ***	0.08
Longtail	−0.003	0.00	−0.001	0.00
HHIBus	0.054	0.04	0.103 **	0.05
HHIGeo	0.184 ***	0.03	0.388 ***	0.03
Deriv	0.003	0.00	0.001	0.00
R2	0.049		−0.124
No. of obs.	5845		5652

This table provides the effects of reinsurance on direct and indirect capital structure deviations in direct (indirect) deviation based on simultaneous equations using three-stage least squares estimations. The dependent variable for all observations is capital structure deviation Dev, which is defined as the actual leverage minus the target leverage. Less (more) reinsurance is defined as a median reinsurance level below (above). Direct (indirect) deviations are capital structure deviations that mainly result from actual (target) leverage. | ΔLev_act | > | ΔLev_tgt | is regarded as a direct deviation, while | ΔLev_act | < | ΔLev_tgt | is regarded as an indirect deviation. Rein denotes the ratio of premiums ceded to total premiums written; Size is defined as ln(total assets); Prof is the ratio of net income to assets; GrOpp denotes the change in net premiums written; Longtail is the ratio of insurance reserves to losses incurred; Deriv is the volume of derivatives transactions divided by total assets; HHIBus is the Herfindahl–Hirschman index of the line of business; and HHIGeo is the geographical Herfindahl–Hirschman index. ** p < 0.05, *** p < 0.01.

presents an analysis of the effect of reinsurance on the direct and indirect capital structure deviations among insurers. For insurers experiencing direct deviations, higher reinsurance levels appear to significantly influence capital structure deviations. Conversely, reinsurance has a non-significant effect on direct capital structure deviations for insurers with lower reinsurance levels. This reflects the role of reinsurance as a stabilizing tool, offering financial flexibility that facilitates faster and more effective adjustments to actual leverage. However, insurers with lower reinsurance levels do not experience significant effects on their direct deviations, suggesting that insufficient risk transfer mechanisms can impair their ability to realign capital structures. By contrast, the impact of reinsurance on indirect deviations presents a different perspective. For insurers whose indirect capital structure deviations result primarily from changes in target leverage, both lower and higher levels of reinsurance have similar positive effects on capital structure deviations. It suggests that reinsurance level plays a critical role in how insurers manage capital structure deviations. Insurers with high reinsurance levels can affect their capital structure deviations more effectively, whether direct or indirect. This finding underscores the strategic importance of reinsurance as a tool for managing capital structures and highlights the inherent difficulty in addressing indirect deviations through reinsurance alone, as these are more influenced by exogenous factors than by risk management strategies.

3.4. Regulatory Intervention

Regulatory requirements significantly influence insurer behavior, especially when solvency is a concern. We examine the relationship between reinsurance and direct/indirect deviations for insurers under regulatory intervention. Under the RBC system, regulators have the legal authority to take preventive and corrective measures if the RBC ratio is below 200%. In

Table 8. The effects of reinsurance on direct and indirect deviations under regulatory intervention.

Variables	Under-Leveraged			Over-Leveraged
	Coeff.		SE	Coeff.		SE
Panel A: Direct Deviations
Constant	1.407		1.51	0.064		1.94
Rein	1.355	***	0.33	−1.027	**	0.47
Size	−0.156	*	0.08	0.144		0.10
Prof	9.625	***	1.64	−9.843	***	2.35
GrOpp	−0.183		0.97	0.413		1.16
Longtail	0.020		0.05	−0.090	*	0.05
HHIBus	−0.528		0.50	1.944	***	0.63
HHIGeo	−0.507		0.34	0.537		0.48
Deriv	0.122		0.18	−0.816		0.55
R2	0.174			0.078
No. of obs.	207			436
Panel B: Indirect Deviations
Constant	0.366		0.03	−5.517	***	1.60
Rein	0.318	***	0.01	2.358	***	0.30
Size	−0.050	***	0.00	0.378		0.08
Prof	1.589	***	0.05	−4.125	**	1.92
GrOpp	0.505	***	0.02	−0.731		0.88
Longtail	0.005		0.00	0.039		0.10
HHIBus	−0.437	***	0.01	0.626		0.55
HHIGeo	0.150	**	0.01	−0.073		0.42
Deriv	--	--	0.00	−0.297		0.33
R2	0.471			−0.021
No. of obs.	135			278

This table provides the effects of reinsurance on direct and indirect capital structure deviations in direct (indirect) deviation based on simultaneous equations using three-stage least squares estimations for the insurers with an RBC ratio below 200%. The dependent variable for all observations is capital structure deviation Dev, which is defined as the actual leverage minus the target leverage. Under-leveraged (over-leveraged) insurers are defined as those whose actual leverage is lower (higher) than their target leverage, whereas direct (indirect) deviations are defined as capital structure deviations that mainly result from actual (target) leverage. | ΔLev_act | > | ΔLev_tgt | is regarded as a direct deviation, while | ΔLev_act | < | ΔLev_tgt | is regarded as an indirect deviation. Rein denotes the ratio of premiums ceded to total premiums written; Size is defined as ln(total assets); Prof is the ratio of net income to assets; GrOpp denotes the change in net premiums written; Longtail is the ratio of insurance reserves to losses incurred; Deriv is the volume of derivatives transactions divided by total assets; HHIBus is the Herfindahl–Hirschman index of the line of business; and HHIGeo is the geographical Herfindahl–Hirschman index. * p < 0.1, ** p < 0.05, *** p < 0.01.

, we focus on the insurers with an RBC ratio below 200%.

For under-leveraged insurers with direct deviations, reinsurance exhibits a significant positive effect, suggesting that reinsurance helps these insurers reduce deviations and move closer to their desired capital structures. Conversely, for over-leveraged insurers with direct deviations, reinsurance has a significant negative effect. This outcome suggests that for insurers above their target leverage, reinsurance is a tool to manage excess leverage by shifting risk and potentially reducing liabilities.

For under-leveraged insurers with indirect deviations, reinsurance still demonstrates a significant positive relationship with capital structure deviation. Similarly, for over-leveraged insurers with indirect deviations, reinsurance positively impacts capital structure deviation (coefficient = 2.358, p < 0.01), suggesting that reinsurance leads these insurers to further distance themselves from target leverage levels.

Overall, these findings reveal that under regulatory intervention, reinsurance has divergent effects on direct versus indirect deviations for both under- and over-leveraged insurers. The results align with our main findings, confirming that our conclusions are robust even after controlling for regulatory intervention.

4. Conclusions

Previous studies usually investigate capital structure adjustments based on the difference between actual and target leverage. However, both actual and target leverage can lead to variations in capital structure deviations from targets; for example, an increase in capital structure deviations can be the result of either an increase in actual leverage, a reduction in target leverage, or both. The variation in capital structure deviation, stemming from different components, indicates distinct types of deviations.

We identify an important connection between risk management and capital structure deviations. In particular, we innovatively classify capital structure deviations into direct deviations and indirect deviations, resulting primarily from changes in actual leverage (direct capital structure deviations). That is, reinsurance plays a key role in mitigating capital structure deviations, particularly for direct deviations. Insurers that adopt reinsurance can align their actual leverage with target levels, thereby enhancing financial stability and regulatory compliance. Further, our empirical analysis reveals that insurers experiencing direct deviations adjust their leverage levels more rapidly and converge toward their target leverage. By contrast, insurers with indirect deviations exhibit slower adjustment speeds, indicating that these deviations are more passive and influenced by external factors. Specifically, insurers with direct deviations adjust their capital structure approximately 29.2% faster than insurers with indirect deviations. This insight challenges and refines the existing financial theories, offering a new lens through which to view the strategic role of reinsurance in managing financial risk and stability.

These findings have two key implications. First, for insurance practitioners, this study underscores the strategic importance of reinsurance in managing capital structure. Insurers with significant direct deviations can leverage reinsurance to more effectively reduce deviations, enhancing their ability to meet regulatory requirements and improving financial resilience. By aligning actual leverage with target levels, insurers reduce the risk of over- or under-leverage, thus fostering a more stable and competitive market position. This strategic use of reinsurance both helps manage day-to-day operational risks and strengthens the insurer’s overall financial health and competitive positioning within the industry.

Second, for regulatory bodies, our findings provide insights into how insurers use reinsurance as a tool for capital structure optimization. Recognizing the differing impacts of reinsurance on direct and indirect deviations, regulators might consider tailored guidelines that encourage effective reinsurance practices, particularly for insurers managing high direct deviations, which are more responsive to reinsurance adjustments.

Our study focuses exclusively on the insurance sector, which operates under specific regulatory and financial conditions, such as risk-based capital requirements and stringent solvency standards. This unique regulatory environment may limit the generalizability of our findings to other industries in which capital structure management and reinsurance function differently or are less regulated. Additionally, while reinsurance is a primary risk management tool in insurance, other sectors rely on a broader range of risk mitigation strategies, such as derivatives, hedging, and diversification. Future studies could explore how these tools impact capital structure deviations across different sectors.

To expand these insights, future research could explore cross-industry comparisons to determine if direct and indirect deviation classifications hold in sectors beyond insurance, where risk management tools and leverage adjustments differ. Additionally, examining how economic cycles or regulatory changes impact insurers’ responses to capital structure deviations could deepen the theoretical framework, especially regarding adaptation under financial stress or regulatory shifts.