Abstract
Managing a portfolio whose value closely tracks an index by trading only in a subset of the index constituents involves an NP-hard optimisation problem. In the prior literature, it has been suggested that this problem be solved using sequential Monte Carlo (SMC, also known as particle filter) methods. However, this literature does not take transaction costs into account, although transaction costs are the primary motivation for attempting to replicate the index by trading in a subset, rather than the full set of index constituents. This paper modifies the SMC approach to index tracking to allow for proportional transaction costs and implements this extended method on empirical data for a variety stock indices. In addition to providing a more practically useful tracking strategy by allowing for transaction costs, we find that including a penalty for transaction costs in the optimisation objective can actually lead to better tracking performance.
1. Introduction
Index tracking, also known as index replication, is a passive investment strategy that has gained popularity due to the higher costs associated with active investing and scepticism regarding the ability of active funds to outperform the market (see e.g., Rompotis (2013), Barber and Odean (2000)). Financial indices track the performance of a collection of financial assets or an overall market. Indices are not tradable instruments themselves; however, replication can be achieved by creating a portfolio of assets that closely match the performance of an index. To perfectly replicate the performance of an index, one would need to invest in all its constituent stocks in the appropriate proportions. This may require continuously trading in hundreds of assets, which is both costly and often infeasible. More specifically, index replication’s effectiveness can be influenced by the constituent assets’ liquidity. Furthermore, continuous trading can lead to high transaction costs due to the costs incurred with each trade and the adjustments made during the rebalancing of the portfolio’s composition. The goal of sparse index tracking is to create a portfolio that closely replicates the performance of a benchmark index while avoiding the need to invest in all its constituent assets. The desired solution is a portfolio of a relatively small subset of assets that replicates an index at a lower cost.
Satpathy and Shah (2022) proposed a Sequential Monte Carlo (SMC) algorithm to address the sparse index tracking problem. The key idea is to interpret the index-tracking problem as a maximisation problem over the set of all possible (fixed-size) subsets of stocks composing some index and then using SMC as a global optimisation technique. Despite the novelty and the success of this approach when compared to other methods, such as Tibshirani (1996), Xu et al. (2015), Benidis et al. (2018), it is not clear whether this technique is an optimal index-tracking strategy, as it falls short in addressing the equally significant objective of reducing transaction costs. Indeed, when rebalancing the tracking portfolio, the algorithm does not explicitly minimise transaction costs. It focuses solely on minimising the tracking error between the portfolio and the index returns. This approach may lead to marginal improvements in the tracking error, but the cost associated with the portfolio rebalancing could outweigh any benefit gained.
The purpose of this work is to improve the Sequential Monte Carlo algorithm proposed by Satpathy and Shah (2022) by accounting for transaction costs in portfolio rebalancing. To this end, we redefine the dynamics of the index-tracking portfolio in such a way as to account for (proportional) transaction costs. Relying on this, we first reformulate the problem by adding a penalisation term to the objective function of the index-tracking problem and then study this modified problem by adopting similar techniques.
The remainder of the report is structured as follows. The general formulation of the index tracking problem, as proposed by Satpathy and Shah (2022), is presented in Section 2. In Section 3, a description of how to adjust the index tracking problem for transaction costs is given. Section 4 details the methods used for model implementation and testing, followed by the results in Section 5. Finally, the report concludes in Section 6 with a brief summary of the outcomes as well as a short description of possible further studies.
2. Preliminaries
2.1. The Index Tracking Problem
In this section, we recall the general formulation of the index–tracking problem. Let us consider an index I comprising n stocks. Denote by the column vector of daily returns of the index over a period of T days before day t. For each constituent stock i, let be the corresponding returns and set . The index tracking problem at time t consists of finding , where , such that
Here, time t is the rebalancing point. The composition of the tracking portfolio is based on market data up until time t, with a predefined lookback period. Thus, the optimisation problem (1) uses only the subset of the data specific to that lookback period. Constraint (3) represents a full budget constraint, while (2) imposes a constraint on that limits investors to taking only long positions. The cardinality constraint (4) restricts the number of stocks used to track the index to a fixed number . An increase in p might lead to a reduction in tracking errors, but possibly incurring larger transaction costs. Thus, p allows us to control the trade-off between tracking error and trading costs.
The cardinality constraint for is non-convex and gives rise to an NP-hard problem. A wealth of methods exist in the literature to solve this. Popular methods include applying regularisation, using a Lagrangian version with an approximated -norm, replacing the -norm with an -norm (the LASSO technique), employing Mixed-Integer Quadratic optimisation and various genetic algorithm methods. We refer to Satpathy and Shah (2022) and the references therein for a more general discussion on this problem as well as an overview of these methods.
Optimisation Problem as Sampling Problem
In Satpathy and Shah (2022), a Sequential Monte Carlo (SMC) sampler is used to solve the optimisation problem (1). There, the key idea is to interpret the optimisation problem as a maximisation problem over the set of all possible (fixed-size) permutations of stocks composing some index and then using SMC sampling as a global optimisation technique. Hereafter, we briefly recall the main idea in Satpathy and Shah (2022); see also Duan (2019).
The index tracking problem with a -norm penalty is a regression problem where the objective function in Equation (1) is minimised. Similarly, one can consider the following maximisation problem:
Introducing the -norm penalty translates to finding the optimal permutation of p stocks (a fixed number of regressors) that solves
where is the submatrix of corresponding to columns in for p regressors and is given via1
Moreover, since for every fixed permutation , and bounded above by 1, if a normalisation constant is introduced, we can interpret this as a discrete probability distribution function over the permutation space. The target distribution to be maximised is then expressed as
The optimal composition of p stocks is then the permutation that maximises this .
2.2. Sequential Monte Carlo Sampling
A naive approach to solve problem (6) would comprise drawing samples from and choosing the optimal that maximises it. However, it is not easy to sample from . For such a case, can be empirically approximated via SMC methods. SMC methods sample particles2 from an initial proposal distribution, after which a sequence of (sequential) importance sampling, resampling, and support boosting steps are employed. A collection of weighted particles is then obtained, which then represents the approximation of the target distribution. In what follows, we describe in more detail the steps within the SMC algorithm as employed in Satpathy and Shah (2022). See also Del Moral et al. (2006) for a more general discussion of the SMC method.
2.2.1. Sequential Importance Sampling
The first step in an SMC algorithm is importance sampling. It can be described as follows: N particles, denoted by , are sampled from an easy-to-sample distribution , also called proposal distribution. Then, for each , normalised importance weights are computed:
The pair completely characterises the target distribution approximation, and all quantities of interest from the distribution can be computed.
The quality of the sample drawn depends on the choice of , in particular on its closeness to the target distribution. Moreover, a necessary condition for to be a good initial choice is that its support includes the support of .
A tool to gauge the quality of the sample (and thus of the proposal distribution) is given by the computation of its Effective Sample Size defined by
Since the weights are normalised, the ESS value will range from 1 to N, where we remember that N is the number of samples drawn from the proposal distribution. An ESS value of 1 indicates a poor choice of , contrary to a value equal to N, which stands for a good choice of . Indeed, this happens if, for instance, each importance weight is equal to .
However, when approximating a target distribution that is high-dimensional and complex, the simple importance sampling method tends to yield poor approximations (Satpathy and Shah (2022)). To account for this, Sequential Importance Sampling (SIS) methods are used. They aim to gradually approximate the target distribution with a sequence of approximating distributions.
SIS methods are commonly employed in filtering problems, where a sequence of new information arrives sequentially. However, in the context of this report, a sequence of new information used to approximate does not occur in the same manner. To account for this, density tempering is introduced.
Density tempering is a process proposed by Del Moral et al. (2006) which allows for sampling from target distributions with higher dimensions.
Its main ideas can be summarised as follows: a collection of synthetic, intermediate target distributions are introduced, where for all , with . The sequence of -modulated distribution is computed as follows:
Notice that and , corresponding to the proposal and (true) target distribution. Similarly, the importance weights between each intermediate step are calculated according to the following formula:
The initial proposal distribution suggested by Satpathy and Shah (2022) is described as follows. Consider the regression coefficient of determination for the jth stock returns (vis-à-vis the index to be replicated). A high would imply that stock j is more likely to appear in the final that maximises . A sampling strategy without replacement is considered, and the probability of the first jth stock to be chosen is described as
Similarly, the probability of choosing the next mth stock in a set of stocks is . Following this logic, for a given permutation of p stocks is computed as follows:
Notice that described above is sequence-dependent. The order in which stocks are chosen to compute matters. However, this is not the case for the regression solution that we consider. Indeed, the value of is the same for each combination of p stocks despite the order in which they appear within the permutation. We are only concerned with the choice of stocks used to track the index and their proportion of the current portfolio wealth (their respective weights).
2.2.2. Resampling
As evolves, and with each re-weighting process, more variability is introduced, and fewer samples retain significant weights. This causes weight degeneracy and consequently a low ESS value. To overcome this phenomenon, one gets rid of samples with low-importance weights and repeatedly samples those with high-importance weights. This is in practice carried out by applying some resampling methods (see e.g., Chen (2003), Speekenbrink (2016), Gellert and Schlögl (2021)) whenever the ESS value falls below a certain threshold (commonly set to N/2). In Satpathy and Shah (2022), a multinomial resampling technique is implemented. Here, we instead consider the systematic resampling technique,3 which can be described as follows. Fix the number of particles to be resampled to . For , and let
Consider the m-th resampling in the algorithm. Replace particle k with particle i satisfying the following condition:
where denotes the weight corresponding to the particle j on the m-th resampling.
2.2.3. Support Boosting and Metropolis–Hastings Algorithm
Since, in the resampling step, samples with high weights are repeatedly resampled, this method leads to a loss in particle diversity, causing the support of the sequence of distributions represented by the particles and their weights to shrink. To account for this problem, an additional step is added with the intention of boosting the support. To this end, several moves of the Metropolis–Hastings (MH) algorithm are performed in Satpathy and Shah (2022). We do not employ the support-boosting step, since it results in a prohibitive and stochastic run time; however, we briefly describe the method as follows: after each resampling step, the MH algorithm is used for sampling from the current intermediate target distribution by using a new distribution for proposing a new sample and then accepting or rejecting the new sample with some probability.
The MH probability of acceptance, that is, the probability of replacing the current particle with the new sample , is computed as follows:
where denotes the proposal density. Notice that if the ratio is high, there is a greater chance of moving from to .
The acceptance or rejection step in the MH algorithm is applied until the accumulative acceptance rate reaches 500% to ensure the support of the distribution is sufficiently boosted.
The choice of the proposal distribution4 h is performed as follows. Initially, a count-based probability is considered, meaning that the probability of choosing a stock to be sampled in a permutation is proportional to the number of times the stock appears in the current sample of permutations. Notice that this choice reflects the relative importance of particles after the SMC algorithm has reached the stage indicated by the current . Then, the proposal distribution h is defined as a weighted sum of , the initial proposal distribution described in Section 2.2.1, and :
where . Moreover, the distribution employed in Satpathy and Shah (2022) h is defined in such a way that only a given subset A of the permutation is replaced. More precisely, to describe the computation of and as in Satpathy and Shah (2022), consider a subset A of the permutation that we wish to replace in order to transform to . Since only a subset of is replaced, for every , it holds that . Thus, we sample A from the set of stocks that exclude stocks in . In particular, if the set of all stocks is , we sample A from . We then define as the probability of sampling A from given the count-based probability described above. Similarly, can be computed based on applied to the set of stocks.
Finally, Satpathy and Shah (2022) set the number of stocks for constructing an index tracking portfolio as a constant, p, representing 20% of the total number of stocks in the index. We instead use Principal Component Analysis (PCA) to set the number of stocks chosen for the index tracking portfolio. The variance explained by the principal components is set to 95%. The variable p is then assigned a value equal to the number of principal components computed under this constraint. The heuristic (which of course represents an approximation in our context) behind this approach is that indices are linear combinations of stock prices, and if stock price dynamics were fully spanned by p linear factors, p stocks would be sufficient to replicate the index (assuming constant index weights).
Summary of SMC Algorithm
- Fix the number of stocks used to replicate the index to p (using PCA).
- Draw n permutations of size p from , for computed as in Equation (9). Set the importance weights for each permutation to .
- Choose and increment such that .
- At , compute the importance weights for each permutation using recursive formulas in Section 2.2.1.
- Compute ESS
- While ,
- (a)
- If ESS proceed to Step 3.
- (b)
- If ESS . Resample the particles (Satpathy and Shah (2022)) suggest that if support boosting is applied, initialise MH with an accumulative acceptance rate of 500%).
- (c)
- Set the weights of new samples computed in MH to and proceed to Step 3.
- At , samples from are obtained, represented as pairs of permutations and their respective weights.
- Resample once more to obtain new permutations with equal weights.
- Compute for the new sample of permutations to obtain the optimal that maximises the given by Equation (8).
3. Transaction Costs
As briefly mentioned in Section 1, in Satpathy and Shah (2022), transaction costs have not been considered when rebalancing the index tracking portfolio. This can potentially cause stocks to enter and exit the tracking portfolio with minimal benefit but at an increased cost. In order to consider this aspect, in this section, we reformulate the index-tracking problem by adding an additional term to the objective function, which results in a more gradual rebalancing of the index-tracking portfolio.
3.1. Dynamics of the Wealth Process Given Proportional Transaction Costs
We start by describing the evolution of the value of the index-tracking portfolio over rebalancing times. Consider the rebalancing time point t. Let us also denote the money invested in the j-th stock at time t as . If transaction costs are not considered, the value of the index tracking (self-financing) portfolio X, for an index comprising n stocks, is given by
where stands for the moment just before the rebalancing.
If transaction costs are instead allowed, we model the evolution of as follows:
where is the proportion of our wealth spent on the transaction costs at t. Since the portfolio wealth is lower due to transaction costs, we take into account that there is now less money to invest in each stock. Here, the portfolio is constructed in such a way that after paying the transaction costs, the portfolio weights are strictly equal to the target portfolio weights: . Thus, the following equation represents the value of the portfolio after rebalancing:
Recall that only the p of all ’s are not zero. Now recall that we pay a transaction cost for each unit of money we buy or sell. Let be the percentage we pay per unit of money we buy or sell, i.e., the rate of transaction costs. We assume here that the transaction costs for buying and selling are the same. We will incur a transaction cost of enforced on the difference in the amount of money invested in each stock before and after the rebalancing. In some sense, it means that instead of buying a stock for USD 1, we buy it for USD (1 + ).
It was demonstrated in Ruf and Xie (2019) that knowing the target portfolio weights, , and the amount of money invested in each stock prior to rebalancing, , is sufficient to compute C. Refer to Ruf and Xie (2019) for a detailed approach on the computation of C. Here, we introduce notations and ideas from Ruf and Xie (2019) necessary to present the exact formula for C.
Recall that the portfolio is self-financing; that is, the amount of currency used to buy extra stocks should be exactly the amount of currency obtained from selling redundant stocks, and hence, the following should be satisfied:
where dividends are not taken into account. We introduce and as follows:
If we now divide both parts of (12) by we will obtain the following equation:
where the LHS of (15) is a continuous function of C and strictly increasing from 0 to 1, as C changes from to ∞. Conversely, the RHS of (15) is a continuous function of C strictly decreasing from ∞ to , as C changes from to , and equals to as C changes from to ∞. Therefore, both sides of Equation (15), treated as functions of C, must intersect at a unique point, indicating the existence of a unique solution for Equation (15).
Given the above, an expression for C now follows:
Here, , where with defined as follows:
Using these formulas, we will be able to update the wealth process after each rebalancing step. The formula was given in (11).
3.2. Index Tracking Problem with Proportional Transaction Costs
Our goal is to minimise the transaction costs incurred at each rebalancing step, i.e., to minimise the money lost due to transaction costs, . In order to do that, we will introduce the updated version of the regression problem from Satpathy and Shah (2022). The objective function is the following:
where is a flexible parameter needed to model the sensitivity of the algorithm to transaction costs. The intuition behind this formula is that we do not want to change the weights too abruptly or quickly as it implies higher transaction costs.
Given all these considerations, we introduce the (simplified) index tracking problem (allowing for transaction costs) as follows:
Similarly to the approach in Satpathy and Shah (2022), we introduce distribution on the space of permutations as a means to solve this problem
Then, applying similar reasoning as in the case of the optimisation problem without transaction costs, in order to find the optimal permutation at time t, is approximated via SMC methods using density tempering.
4. Methodology and Data
The index-tracking algorithm utilised in this study builds upon the framework introduced in Section 2, with further details provided in Section 3. Here, we delve into the methodological framework used for implementing index-tracking strategies, emphasising their reliance solely on historical data. To clarify, at each rebalancing point (t), the composition of the tracking portfolio is determined based solely on market data available up to time t, within a predefined lookback period of 30 trading days. This approach ensures that no future data beyond time t influence our backtesting methodology. Furthermore, we have defined the temporal scope to encompass 20 portfolio rebalancing instances for each strategy under investigation. The rebalancing frequency is set to every 60 observations, corresponding to a span of 60 trading days.
4.1. Model Cases
The model cases examined in this analysis primarily differ in their hyperparameter settings. To provide a concise overview of the diverse models formulated, Table 1 summarises the hyperparameters employed for each case.

Table 1.
Hyperparameters chosen for implementation and comparison of model cases on real-world data.
In order to assess the performance of the updated model that incorporates transaction costs compared to the initial model, we maintain the hyperparameters of both models at the values specified in Table 1. When , this corresponds to the initial model without accounting for transaction costs.
Following an initial examination of the efficacy of the proposal distribution in identifying accurate stock selections, it became evident that its capacity to accurately pinpoint assets relevant to the experimental framework was inadequate. Consequently, an alternative proposal distribution rooted in multiple linear regression was employed. Specifically, this approach entails evaluating all assets within the designated universe at a given time point and computing the coefficients of multiple linear regression for these stock prices relative to index prices. Subsequently, the absolute values of these regression coefficients are obtained, normalised to ensure their cumulative sum equals one, thereby constituting the basis of our prior/proposal distribution. An exploratory analysis unveiled the superiority of this proposal distribution over the variant originally posited by Satpathy and Shah (2022).
The enhanced efficacy of the revised proposal distribution, coupled with considerations regarding numerical efficiency, culminated in the decision to forgo the Metropolis–Hastings support boosting step. The proposal distribution gives a good sampling of the state space and is close enough to the posterior distribution to make additional steps such as support boosting redundant or even counterproductive. Due to this, we have chosen to not use the support boosting step in our version of the particle filter algorithm.
4.2. Constraints and Optimisation
In our numerical experiments, we implemented the index-tracking algorithm with the inclusion of no-short-selling constraints and full-budget constraints. It is worth noting the implications of introducing these constraints. When incorporating no-short-selling and full-budget constraints, an explicit solution of the parameters cannot be obtained, necessitating the use of numerical optimisation techniques. This introduces a critical consideration, as the numerical optimisation algorithm needs to be run multiple times during the execution of the index-tracking algorithm, particularly when the Effective Sample Size (ESS) falls below the threshold, requiring Metropolis–Hastings steps. Consequently, this can significantly increase the overall runtime and potentially limit the algorithm’s performance and efficiency.
Fortunately, the problem at hand benefits from the presence of a closed-form expression for the Jacobian, which provides valuable gradient information. The closed-form expression for the Jacobian, obtained by simply differentiating Equation (19), is given by
Numerical optimisers that utilise this gradient information can leverage it to enhance the convergence speed and improve overall efficiency. In our study, we employed the Sequential Least Squares Quadratic Programming (SLSQP) algorithm while incorporating the provided Jacobian. This approach allowed us to reduce the computation time by a substantial factor of approximately 7 (compared to algorithms not using gradient information).
4.3. Data
4.3.1. Simulated Data
In the process of algorithm development, we employed simulated index and stock data where the true parameters were known. To generate the stock price paths for N stocks up to some future time , we employed the Standard Geometric Brownian Motion (GBM) model. Each stock price path follows the process
where and denote the drift and volatility of the i-th stock, respectively, and denotes a standard Brownian Motion process. The Brownian Motion processes are correlated such that and . This leads to an explicit form to determine the stock price paths for each stock using
with time points and time increments . corresponds to the i-th element in a multivariate normal vector , where denotes the correlation matrix. The multivariate normal random vectors can be calculated as where and denotes the Cholesky decomposition of the correlation matrix .
To account for the dynamic nature of index constituents, we established a fixed maximum number of stocks (n) in the asset universe and a maximum number of stocks that could compose the index (). From the asset universe , a random selection of stocks was made to form the index, along with random time points indicating when these stocks entered or exited the index. This gives the set of stocks that the index comprises at each time point as . This simulation setup mirrors the dynamic nature of real-world indices, where stocks are added or removed based on specific criteria and timing.
In order to construct the simulated index time series, we take the weighted average of stock returns in the index at each time point, i.e.,
where at each time point, we have that
The simulated data spanned a predetermined temporal window, with a daily frequency. The parameters for drift, volatility, and initial stock prices for the constituent stocks in the index were uniformly sampled within appropriate ranges. The rationale behind uniformly sampling GBM parameters was primarily to introduce random variation among the simulated stocks. By incorporating this variation, we aimed to capture the inherent diversity and unpredictability observed in real-world stock markets. This approach ensured that the simulated data reflected a realistic scenario, allowing us to evaluate the algorithm’s performance under more representative conditions.
To evaluate the accuracy and effectiveness of the index-tracking algorithm, we calculated index returns as the average of the individual stock returns that constituted it (i.e., ). By aggregating these returns, we obtained the index value, which served as a benchmark for evaluating the algorithm’s ability to accurately select the constituent stocks and their weights in the tracking portfolio.
Throughout the simulation experiments, the index-tracking algorithm consistently demonstrated the capability to effectively identify the stocks forming the index and their constituent weights. This successful performance suggests that the algorithm holds promise in real-world scenarios, where the true underlying stock dynamics are not known. The key test, however, is the algorithm’s performance on such real-world data, which will be considered next.
4.3.2. Empirical Data
Daily data for various indices were obtained from Bloomberg for an empirical study. This resulted in a diverse set of empirical datasets, encompassing the number of constituent stocks and economy sectors. Additionally, data points were excluded from the analysis when the timelines for the indices did not align with those of the individual stocks. The results presented in this paper are based on the indices from Table 2 and the period spanning 18 October 2018 to 5 July 2023. The presented number of stocks in each index is approximate as stocks enter and exit the indices from time to time.

Table 2.
Equity indices used to test the performance of the algorithm, ordered by the number of stocks.
4.4. Metrics
In this section, we outline the metrics of interest. These metrics fall into two categories: “Performance metrics,” which directly impact the decision-making process for selecting investment strategies and parameters, and “Research metrics,” which we explore in order to understand the nature of the algorithms more deeply.
4.4.1. Tracking Error
The primary performance measure we utilise is the tracking error, as defined in Satpathy and Shah (2022). For actual index returns and tracking portfolio returns at times , the tracking error can be calculated as
The tracking error quantifies the level of deviation between the returns of the index tracking portfolio and the target index. It can be calculated as the standard deviation of the return residuals, which are the differences between the returns of the index and the returns of the index tracking portfolio.
4.4.2. Total Transaction Costs
The second performance metric we looked at was the total transaction costs. In the context of transaction cost-conscious investing, monitoring the evolution of the wealth process over time becomes crucial. If transaction costs are defined as in Section 3, then the total transaction costs can be calculated as
Recall that is the moment just before the rebalancing at t. Tracking the total transaction costs allows us to assess the overall cost-effectiveness of the tracking strategy. These costs are calculated at the end of each rebalancing period, representing the expenses incurred during the adjustment of the portfolio’s composition.
The interpretation of the results regarding transaction costs should take into account the specific investment objectives and constraints of the investor. Lower total transaction costs are generally desired, as they indicate a more efficient allocation of resources. However, it is important to balance these cost considerations with the tracking error. Intuitively, there is often a trade-off between minimising the tracking error and minimising transaction costs. Achieving a lower tracking error may require more frequent portfolio rebalancing, leading to higher transaction costs. Conversely, reducing transaction costs may involve a less frequent rebalancing strategy, potentially resulting in a higher tracking error.
4.4.3. Wealth Error
The assessment of tracking error conventionally involves the examination of the standard deviation of error terms derived from the difference between the simple returns of an index and those of a tracking portfolio. While this method provides valuable insights into tracking performance, we sought to devise a composite metric that not only evaluates tracking accuracy but also integrates considerations of cost efficiency inherent to a tracking strategy. To this end, we have opted to employ a metric that combines both aspects by computing the average absolute differences between the cumulative returns of the portfolio wealth and the benchmark returns. Formally, our proposed metric, denoted as the Wealth Error (WE), is defined as:
where T represents the total number of observations, denotes the return of the index at time u, and represents the portfolio wealth at time t. Furthermore, represents the cumulative return of the index, whereas represents the cumulative return of the portfolio. This formulation encapsulates both the magnitude and direction of disparities between the portfolio’s cumulative returns and those of the benchmark index, thereby providing a comprehensive measure of tracking performance while considering the cost efficiency of the tracking strategy.
By evaluating both the tracking error and the total transaction costs, we can comprehensively assess the performance of the index tracking strategy. It allows us to understand the trade-offs between achieving accurate index replication and managing transaction costs, enabling investors to make informed decisions based on their specific investment goals and preferences.
The following metrics relates to the “Research metrics” category.
4.4.4. Other Cost Metrics
To better understand the interplay and distribution of costs in a tracking strategy, we additionally investigate the minimum, mean and maximum transaction costs associated with a rebalancing over the investment horizon.
4.4.5. Retention
This metric indicates the proportion of stocks retained in the tracking portfolio after each rebalancing. For instance, if initially there are 20 stocks in the portfolio and after rebalancing 12 of them are replaced with others from the index, the retention is 40%.
We aggregate the values of Min, Mean, and Max Retention over all the rebalancing time points in the experiment.
4.4.6. Maximum Weight
Lastly, in order to assess the effect that our objective function has on portfolio concentration, we will look at the maximum weight metric, which is defined as the overall maximum weight achieved by a single asset in the tracking portfolio, over the entire investment horizon.
5. Results and Discussion
In this section, we present an analysis of the experimental results. Our primary objective is to investigate the various patterns exhibited by the metrics concerning changes in the number of particles, denoted as N, and the cost aversion parameter, represented by . The stochastic nature of the optimisation algorithm means that there is some random variation in the outcomes, which we also need to quantify. Thus, we consider each of these metrics for different choices of N and , where for each pair, we run 40 (independent) replications of the algorithm. The averages for each metric and choice are reported in Table 3, Table 4, Table 5, Table 6 and Table 7, along with a plus/minus value of 1.96 standard deviations of these averages (i.e., corresponding to the upper and lower bounds of a 95% confidence interval).

Table 3.
Tracking error, Wealth Error, and transaction costs observed for 10 particles (N) and all cost aversions () for each index observed. Values are averages based on 40 independent runs of the algorithm, along with a plus/minus value of 1.96 standard deviations of these averages (i.e., corresponding to the upper and lower bounds of a 95% confidence interval).

Table 4.
Tracking error, Wealth Error and transaction costs observed for 100 particles (N) and all cost aversions () for each index observed. Values are averages based on 40 independent runs of the algorithm, along with a plus/minus value of 1.96 standard deviations of these averages (i.e., corresponding to the upper and lower bounds of a 95% confidence interval).

Table 5.
Tracking error, Wealth Error and transaction costs observed for 1000 particles (N) and all cost aversions () for each index observed. Values are averages based on 40 independent runs of the algorithm, along with a plus/minus value of 1.96 standard deviations of these averages (i.e., corresponding to the upper and lower bounds of a 95% confidence interval).

Table 6.
Minimum and maximum portfolio retention under varying levels of the transaction cost penalty and number of particles (N). Values are averages based on 40 independent runs of the algorithm, along with a plus/minus value of 1.96 standard deviations of these averages (i.e., corresponding to the upper and lower bounds of a 95% confidence interval).

Table 7.
Max weight and mean portfolio retention under varying levels of the transaction cost penalty and number of particles (N). Values are averages based on 40 independent runs of the algorithm, along with a plus/minus value of 1.96 standard deviations of these averages (i.e., corresponding to the upper and lower bounds of a 95% confidence interval).
5.1. Tracking Error
Ex ante, one would intuitively expect there to be a trade–off between transaction costs and tracking error, as including transaction costs in the optimisation objective reduces the amount of rebalancing in the tracking portfolio, therefore leading one to expect tracking performance to be worse. However, the tracking errors reported in Table 3, Table 4 and Table 5 do not bear this out. The performance of the tracking strategy, in terms of tracking error, remains largely unaffected by the size of the cost aversion parameter . Plotting the tracking portfolio performance against the target indices (see Appendix A.1 for graphs of the 40 tracking portfolio runs against the target index in each scenario) illustrates that the introduction of cost aversion has minimal impact on tracking performance and in some cases even improves this performance. Consequently, it is possible to reduce total transaction costs without significantly affecting tracking performance.
In the tracking plots in Appendix A.1, one does observe a few instances where increased cost aversion leads to poor tracking performance in some portfolio wealth trajectories. This is a consequence of the random element in the optimisation algorithm, it can be avoided by conducting multiple runs of the algorithm and eliminating “outlier” results. However, an interesting observation is that for some indices, when cost aversion increases and tracking performance deteriorates, the tracking portfolio actually tends to outperform the index: This is evident in Figure A2, Figure A6, Figure A7, Figure A8, Figure A10, Figure A11 and Figure A14.
While it might seem counterintuitive that a larger transaction cost weighting does not imply a larger tracking error, this may be because the future return behaviour of real-world data may differ from past behaviour, and in particular, correlations can change. Thus, the optimal tracking portfolio based on past returns is not necessarily optimal going forward. As including transaction costs tends to stabilise the tracking portfolio weights, this may result in better tracking performance, compared to ignoring transaction costs and rebalancing fully to reflect any change in return correlations in the lookback estimation window, which may be partly due to random noise.
Similarly, one might expect that increasing the number of particles would improve tracking error, given that a larger particle set should enable the particle filter algorithm to achieve more accurate index tracking. However, the results presented in Table 3, Table 4 and Table 5 show that the increase in particle numbers has minimal impact on tracking error. In some instances, employing only ten particles results in better tracking performance compared to a higher number of particles.
From a computational efficiency perspective, using fewer particles significantly reduces the execution time of the particle filter algorithm. This highlights the potential for optimising particle numbers to balance between computational demands and tracking performance.
5.2. Total Cost
The investigation into total cost (Figure 1) shows that increasing the weighting of transaction costs in the optimisation has the desired effect of reducing the cumulative transaction costs. Unlike when considering tracking performance, the number of particles used in the algorithm does have a substantial impact here: The variability of cumulative transaction costs across the 40 runs of the algorithm is reduced as the number of particles increases, and cumulative transaction costs are substantially reduced when this is part of the optimisation objective (i.e., for and = 10,000).
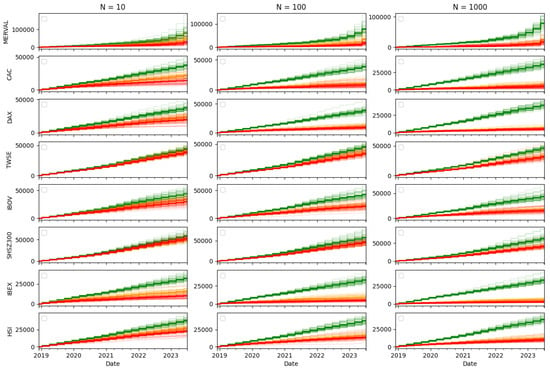
Figure 1.
Total cost for each index and all cases of . Here, the green line represents , the orange line represents and the red line represents 10,000. Each line corresponds to one independent run of the algorithm.
5.3. Retention
Table 6 and Table 7 offer insights into the behaviour of portfolio retention under varying levels of , representing transaction cost sensitivity. When is set to 0, indicating no consideration for transaction costs, there are notable instances where the entire portfolio experiences complete turnover during rebalancing.
However, as increases, reaching values as high as 10,000, the frequency of rebalancing events resulting in no stock replacements becomes more pronounced. This trend suggests a shift towards a conservative approach, where transaction costs heavily influence decision-making processes, leading to fewer adjustments in the portfolio composition.
Further examination of the mean retention reveals additional nuances. On average across all indices, around 25% of stocks persist in the portfolio post-rebalancing when . This relatively low retention rate underscores the high level of churn as a consequence of ignoring transaction costs.
In contrast, with increasing sets, the average retention rate increases, signifying a more stable portfolio composition. This implies that higher values effectively curb the turnover of stocks, promoting greater stability.
For an exemplary run of the algorithm on DAX data, this is visualised in Figure 2 (additional examples are given in Appendix A.3). This chart vividly showcases the dynamic evolution of the tracking portfolio’s composition, illustrating how larger values of lead to a more stable portfolio, whereas smaller values of permit frequent changes in the portfolio composition at each rebalancing step.
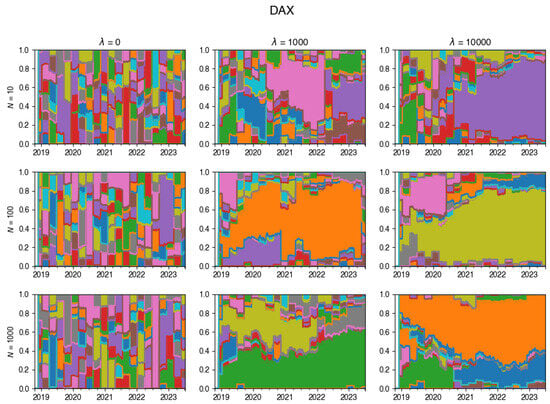
Figure 2.
Changes in the composition of the tracking portfolio for the DAX index.
Overall, the observed patterns suggest that the adjustment of plays a crucial role in determining the level of portfolio turnover, and thus including transaction costs in the index tracking algorithm acts as a deterrent to excessive stock hopping and fosters a more stable investment strategy.
This is also reflected by the maximum weight that the algorithm assigns to any single asset over the life of the tracking strategy, as reported in Table 7: Increasing the aversion to transaction costs reduces this maximum weight, while ignoring transaction costs allows the algorithm to “hop” frequently between large allocations to individual assets in an inherently unstable manner, exposing the tracking portfolio to potentially large idiosyncratic risk.
Unlike tracking performance (but like transaction costs), the number of particles used in the algorithm does impact the asset retention results: The algorithm achieves the objective of minimising transaction costs better when a larger number of particles is used, and this is reflected by higher rates of asset retention. This can also be seen in the distribution of mean asset retention rates across the 40 runs in each scenario for each index, as represented by the histograms in Appendix A.4: Increasing the number of particles tends to shift the distribution of asset retention to the right. This shift suggests that a higher number of particles results in portfolios where dominant assets are retained for longer periods over the tracking strategy’s time horizon. This observation aligns with the expectation that more particles enhance the exploration of possible subsets of assets used to track the index, thereby allowing the algorithm to find better solutions in terms of the objective of minimising transaction costs.
6. Conclusions
Overall, the incorporation of the cost aversion parameter into the algorithm serves as a mechanism for managing transaction costs by enhancing asset retention across rebalancing periods. This mitigates excessive rebalancing due to estimation noise. Increased asset retention leads to portfolio strategies characterised by not only greater stability but also more appropriate diversification. Notably, including transaction costs in the tracking objective has little impact on tracking performance, suggesting that the benefit of cost control and portfolio stability can be achieved without any substantial performance trade–off.
However, it is important to recognise that the nature and intrinsic properties of the index being analysed, such as its size and the maturity of the market that it represents, can also influence the outcomes of the strategy. For instance, an analysis of the S&P 500 index reveals that the strategy consistently performs better compared to other indices, especially those representing emerging markets. This indicates that the algorithm may be more effective in more liquid markets.
These conclusions emphasise the complex interplay between tracking error minimisation and the incorporation of transaction costs into the objective function. The study reveals that there are additional factors at play beyond the straightforward trade-off between minimising tracking error and integrating transaction costs. This highlights the need for a deeper understanding of the underlying mechanisms that govern the relationship between these variables.
Opportunities for Further Study
Future research to be explored could include the following:
- Considering the market impact, as it can also lead to additional losses when working with large volumes. Hence, investors should come up with smart order routing algorithms to optimise trade execution and reduce market impact. These algorithms can help split large orders into smaller ones and execute them in a way that minimises the price impact.
- Considering liquidity screening to avoid investing in assets that may have high transaction costs or are illiquid, as these can significantly impact the performance of your tracking strategy.
- Considering short sales so one can also track “short” indices, as well as considering the short position, i.e., negative ’s, which will relax the constraints in the proposed method.
- Considering other types of transaction costs: tiered commissions, fixed-plus-percentage commissions, flat-fee commissions.
Author Contributions
Conceptualisation, E.S.; Formal analysis, T.M.O., L.H.-R. and D.S.; Investigation, T.M.O., L.H.-R. and D.S.; Methodology, T.M.O., L.H.-R., D.S. and E.S.; Software, T.M.O., L.H.-R. and D.S.; Supervision, E.S.; Visualisation, T.M.O., L.H.-R. and D.S.; Writing—original draft, T.M.O., L.H.-R. and D.S.; Writing—review and editing, T.M.O., L.H.-R., D.S. and E.S. Authors are listed in alphabetical order in the article citation. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Market data (history of closing prices for indices and component stocks) that support the findings of this study are available from Bloomberg. Commercial restrictions apply to the availability of this data, which were used under license for this study.
Acknowledgments
The initial research for this paper was conducted as part of the Financial Mathematics Team Challenge (FMTC) at AIFMRM, University of Cape Town. The authors thank Francesca Primavera for her contributions to this work as Team Leader at the FMTC and for subsequent helpful discussions about the formulation of the index tracking problem under transaction costs in Section 2.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
This part provides additional plots obtained during the experiments.
Appendix A.1. Tracking Performance
In this subsection, you will find plots that illustrate the returns of the constructed portfolio compared to the real index returns across various values of -s and numbers of particles. The red line indicates the index returns and the blue indicates the tracking portfolio’s returns, with one blue line for each of the 40 independent runs of the algorithm.
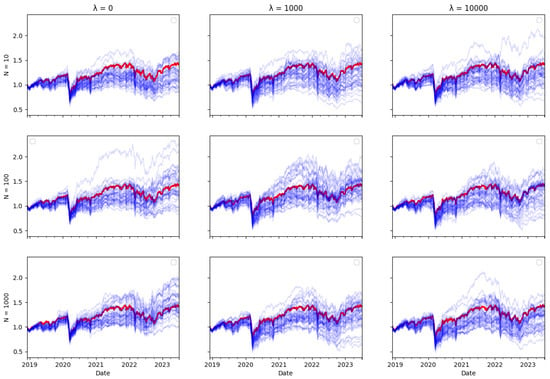
Figure A1.
DAX Tracking portfolio return (blue) versus actual index returns (red).
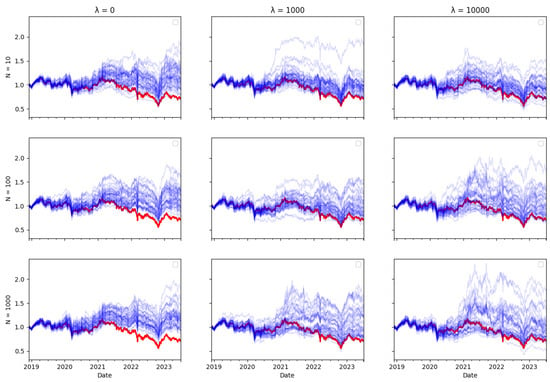
Figure A2.
HSI Tracking portfolio return (blue) versus actual index returns (red).
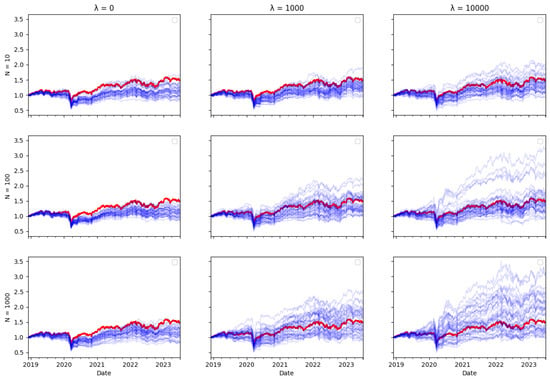
Figure A3.
JALSH Tracking portfolio return (blue) versus actual index returns (red).
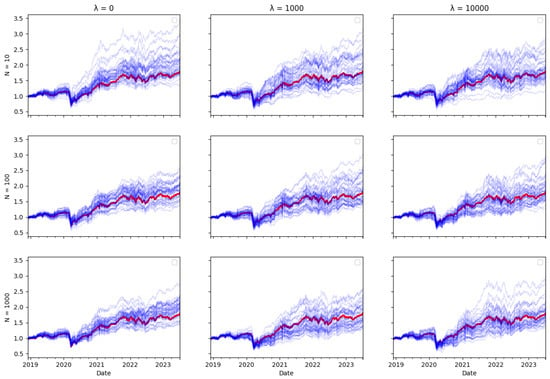
Figure A4.
SENSEX Tracking portfolio return (blue) versus actual index returns (red).
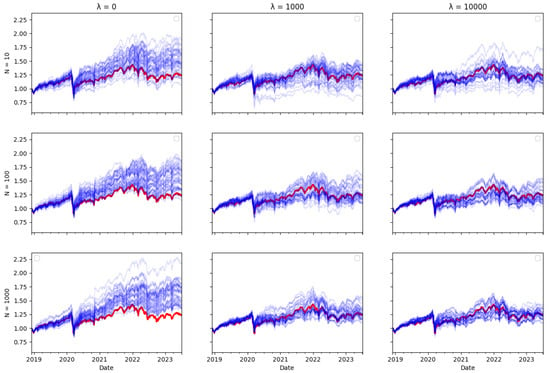
Figure A5.
SMI Tracking portfolio return (blue) versus actual index returns (red).
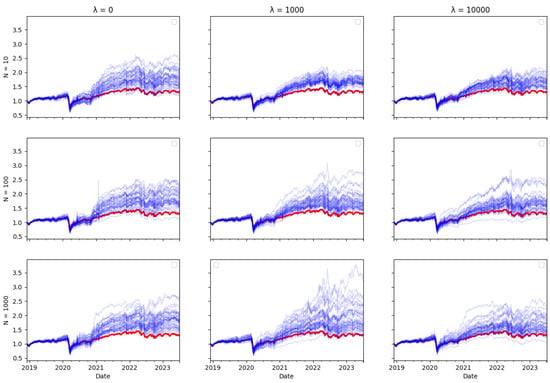
Figure A6.
SPTSX Tracking portfolio return (blue) versus actual index returns (red).
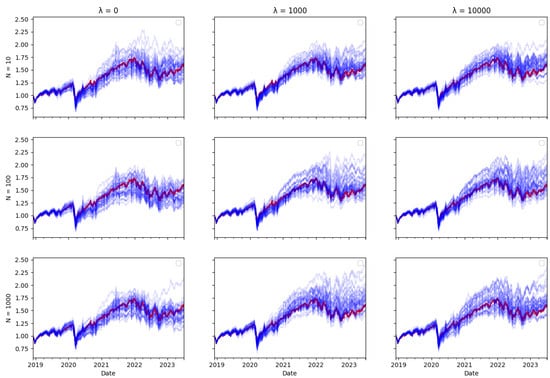
Figure A7.
SPX Tracking portfolio return (blue) versus actual index returns (red).
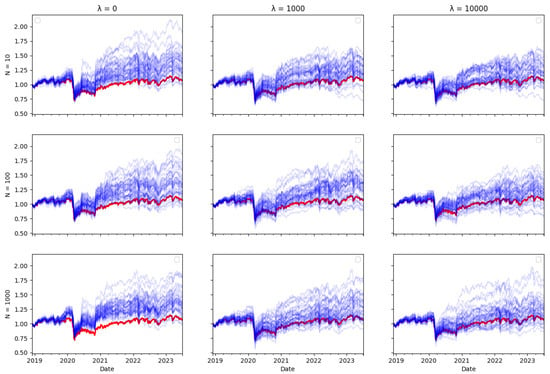
Figure A8.
UKX Tracking portfolio return (blue) versus actual index returns (red).
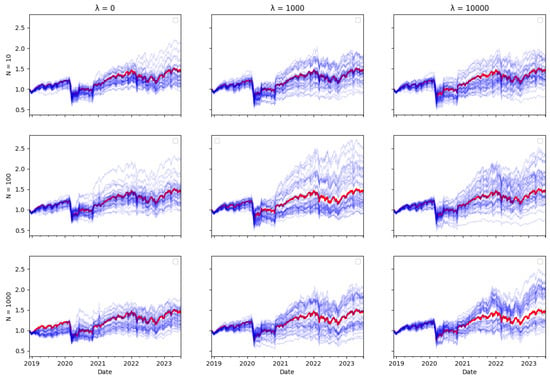
Figure A9.
CAC Tracking portfolio return (blue) versus actual index returns (red).
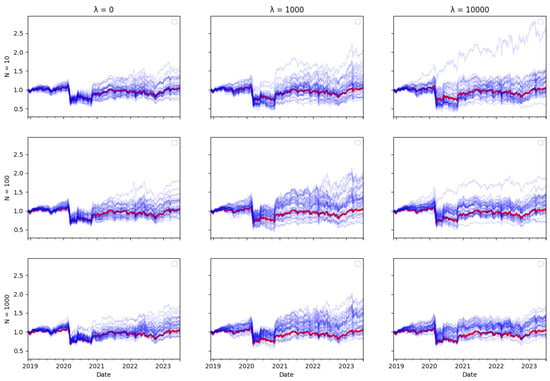
Figure A10.
IBEX Tracking portfolio return (blue) versus actual index returns (red).
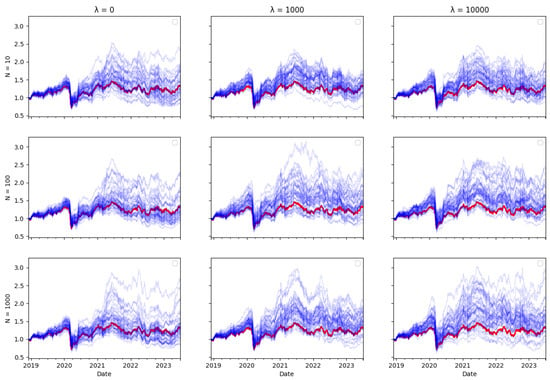
Figure A11.
IBOV Tracking portfolio return (blue) versus actual index returns (red).
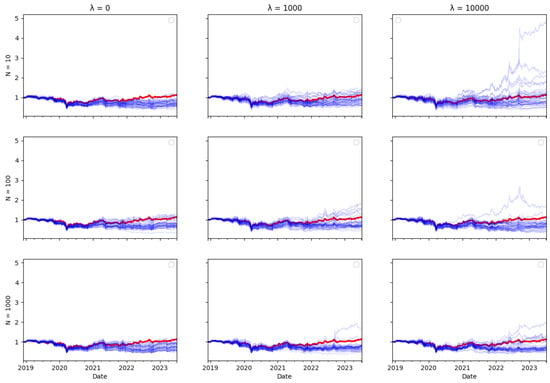
Figure A12.
IPSA Tracking portfolio return (blue) versus actual index returns (red).
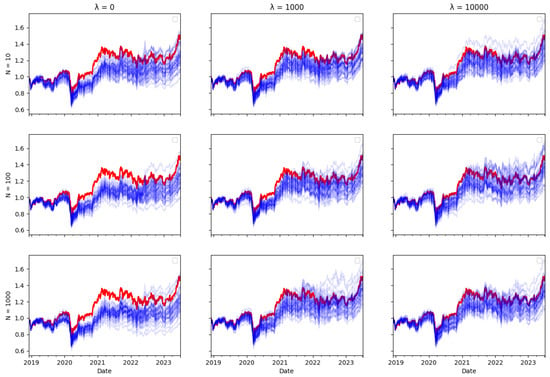
Figure A13.
NKY Tracking portfolio return (blue) versus actual index returns (red).
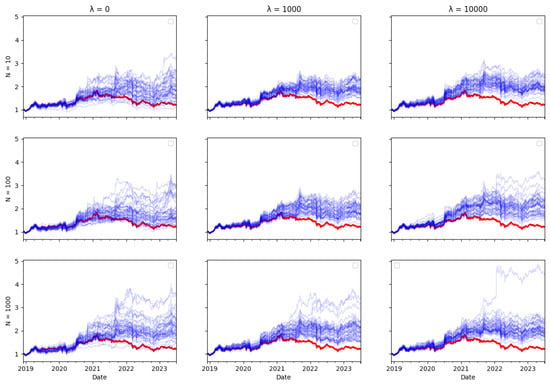
Figure A14.
SHSZ300 Tracking portfolio return (blue) versus actual index returns (red).
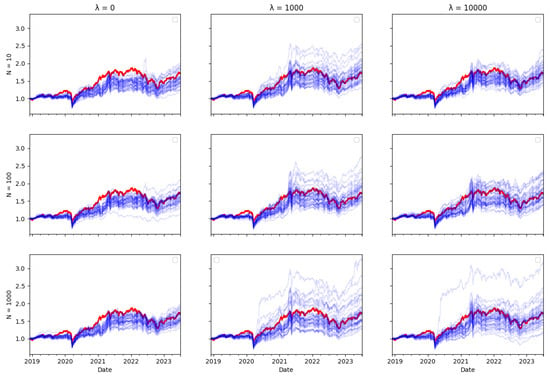
Figure A15.
TWSE Tracking portfolio return (blue) versus actual index returns (red).
Appendix A.2. Transaction Costs
The plots below illustrate the cumulative transaction costs resulting from running the algorithm various numbers of particles.
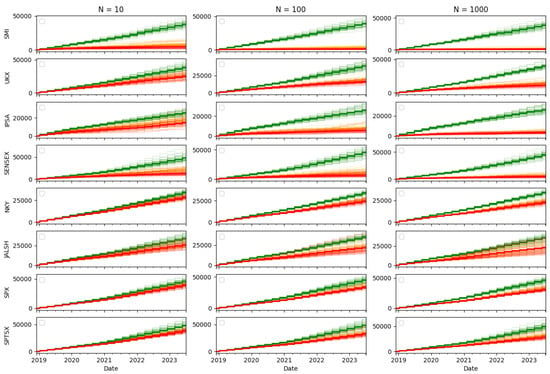
Figure A16.
Cumulative transaction costs paid. Here, green is for , orange is and red is 10,000.
Appendix A.3. Composition Plots
These plots illustrate how the composition of the tracking portfolio was changing during the experiments for various values of .
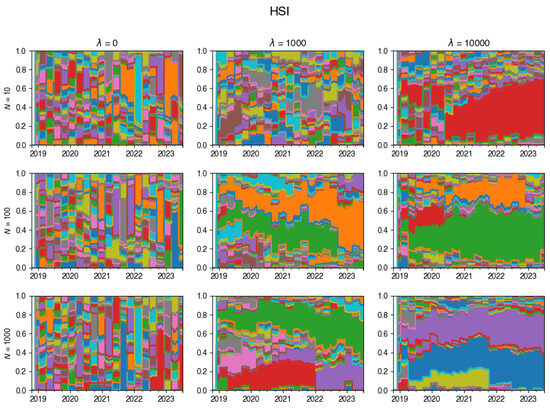
Figure A17.
Changes in the composition of the tracking portfolio for the HSI index.
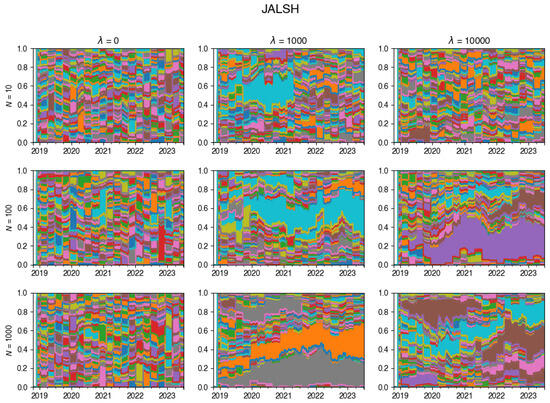
Figure A18.
Changes in the composition of the tracking portfolio for the JALSH index.
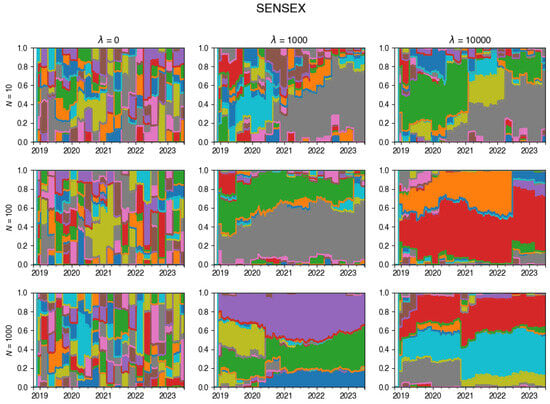
Figure A19.
Changes in the composition of the tracking portfolio for the SENSEX index.
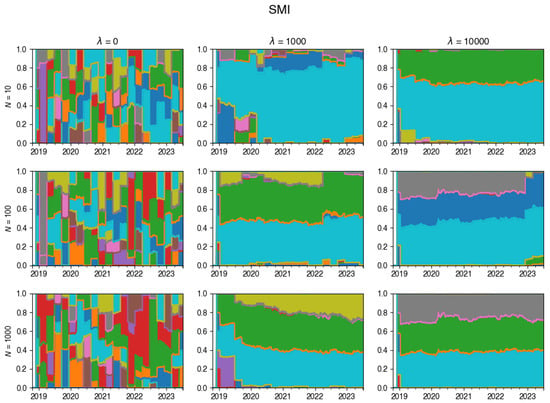
Figure A20.
Changes in the composition of the tracking portfolio for the SMI index.
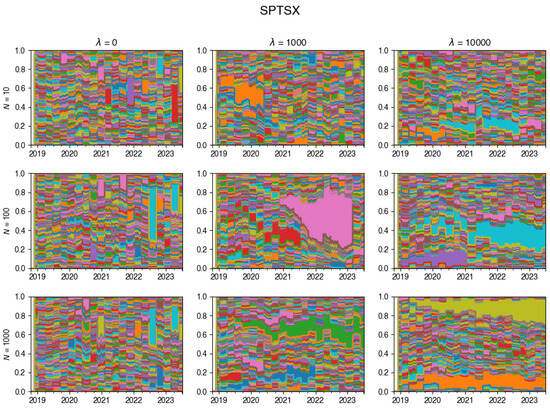
Figure A21.
Changes in the composition of the tracking portfolio for the SPTSX index.
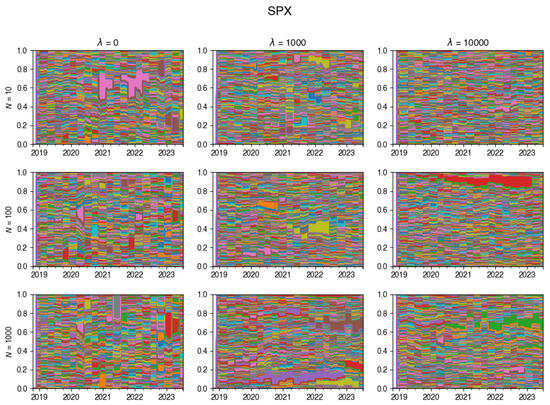
Figure A22.
Changes in the composition of the tracking portfolio for the SPX index.
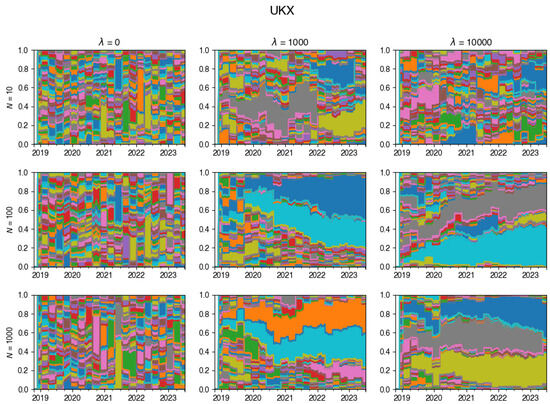
Figure A23.
Changes in the composition of the tracking portfolio for the UKX index.
Appendix A.4. Mean Assets Retention
The plots below show the distribution (across 40 independent runs of the algorithm) of the average (over the life of the strategy) proportion of the portfolio that was maintained between rebalancing periods for various values of the number of particles N and the cost aversion coefficient . The red line indicates the mean of the distribution.
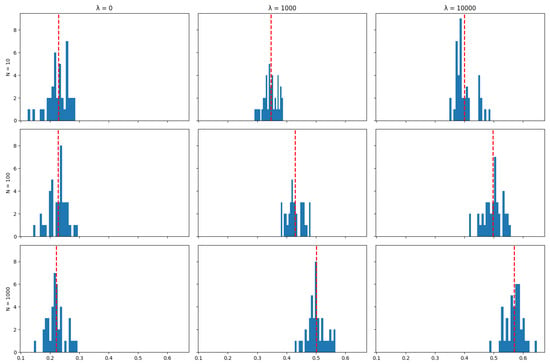
Figure A24.
CAC Mean Assets retention.
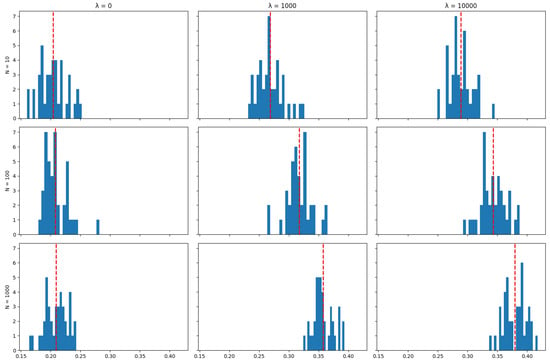
Figure A25.
HSI Mean Assets retention.
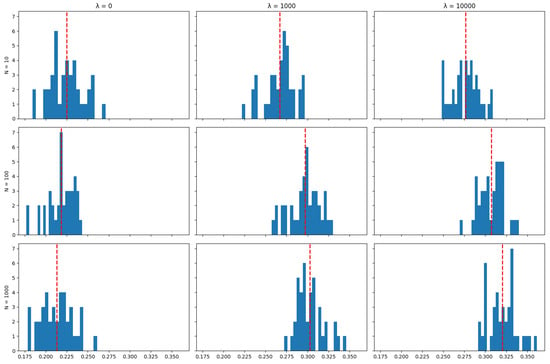
Figure A26.
JALSH Mean Assets retention.
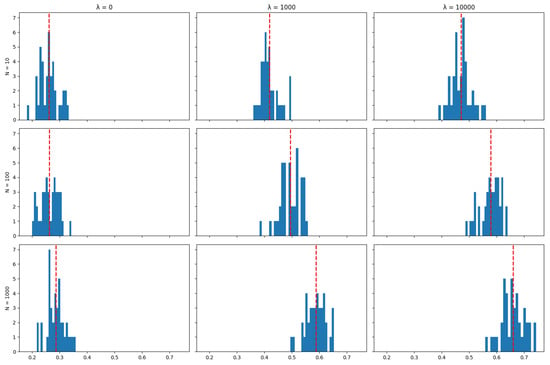
Figure A27.
SENSEX Mean Assets retention.
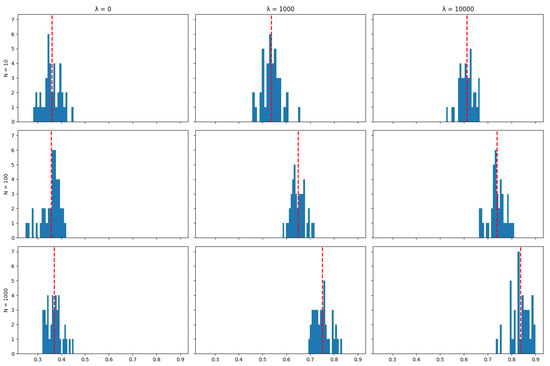
Figure A28.
SMI Mean Assets retention.
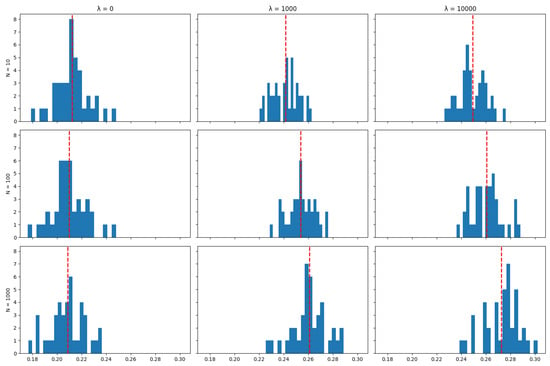
Figure A29.
SPTSX Mean Assets retention.
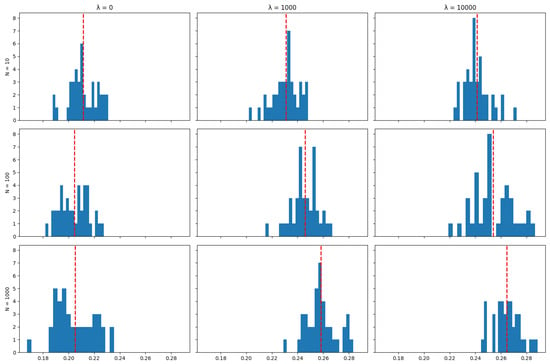
Figure A30.
SPX Mean Assets retention.
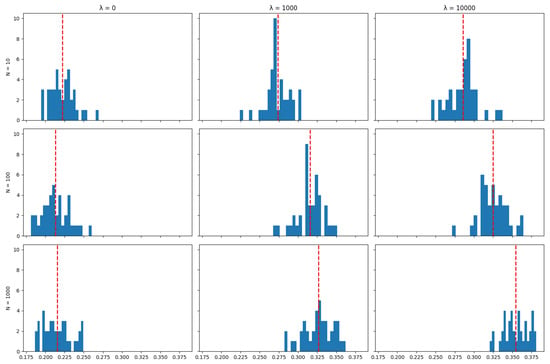
Figure A31.
UKX Mean Assets retention.
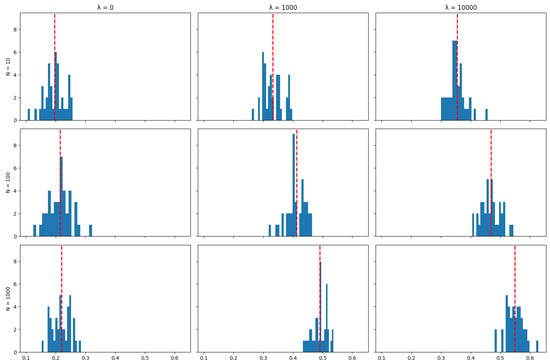
Figure A32.
DAX Mean Assets retention.
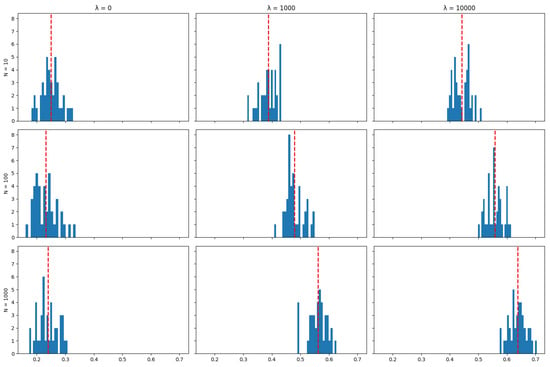
Figure A33.
IBEX Mean Assets retention.
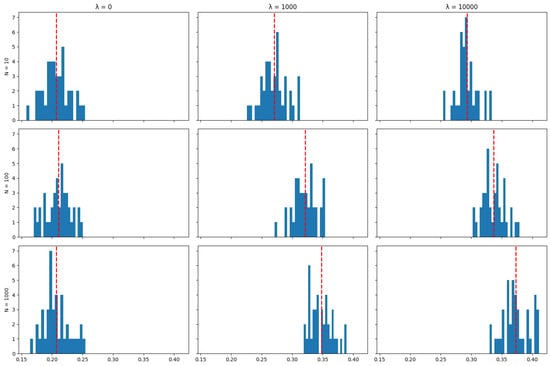
Figure A34.
IBOV Mean Assets retention.
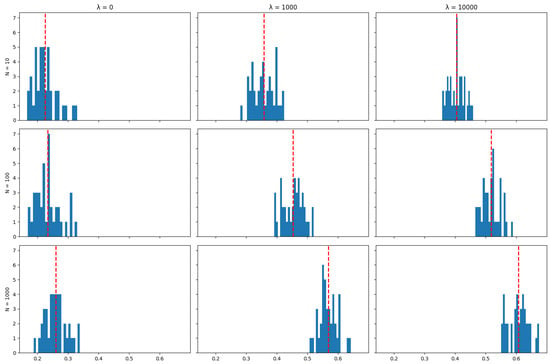
Figure A35.
IPSA Mean Assets retention.
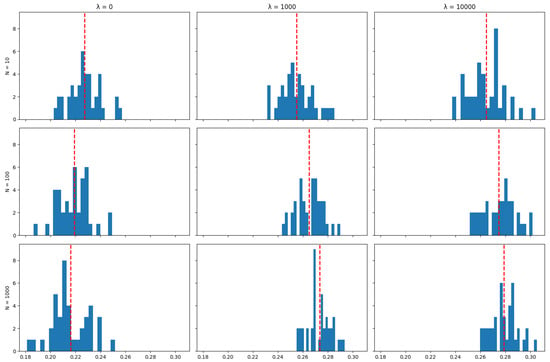
Figure A36.
NKY Mean Assets retention.
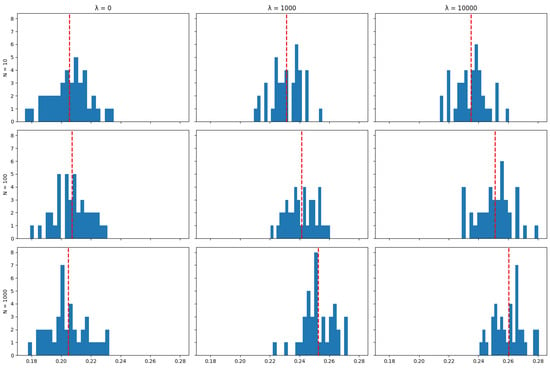
Figure A37.
SHSZ300 Mean Assets retention.
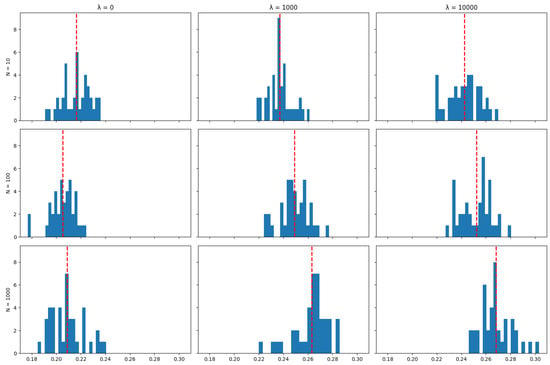
Figure A38.
TWSE Mean Assets retention.
Notes
| 1 | In Satpathy and Shah (2022) the sparse index problem is solved without considering any constraints on the . In such a case the optimal solution admits an explicit form. |
| 2 | Going forward particles, samples and permutations will be used interchangeably, i.e., each particle represents a particular subset of p of the n stocks comprising the index. |
| 3 | Results in the literature suggest that multinomial resampling is not a good choice in this context. For example, Hol et al. (2006) note that “theoretical analysis shows that the resampling quality can be improved by using a different algorithm than multinomial resampling.” In particular, residual and stratified resampling have lower variances, and Hol et al. (2006) advocate systematic resampling over stratified resampling as it has the lowest discrepancy. |
| 4 | The proposal in MH algorithm has no relation to the proposal in the Importance Sampling step. |
References
- Barber, Brad, and Terrance Odean. 2000. Trading is hazardous to your wealth: The common stock investment performance of individual investors. Journal of Finance 55: 773–806. [Google Scholar] [CrossRef]
- Benidis, Konstantinos, Yiyong Feng, and Daniel P. Palomar. 2018. Optimization methods for financial index tracking: From theory to practice. Foundations and Trends® in Optimization 3: 171–279. [Google Scholar] [CrossRef]
- Chen, Zhe. 2003. Bayesian filtering: From Kalman filters to particle filters, and beyond. Statistics 182: 1–69. [Google Scholar] [CrossRef]
- Del Moral, Pierre, Arnaud Doucet, and Ajay Jasra. 2006. Sequential Monte Carlo Samplers. Journal of the Royal Statistical Society Series B: Statistical Methodology 68: 411–36. [Google Scholar] [CrossRef]
- Duan, Jin-Chuan. 2019. Variable selection with big data based on zero norm and via sequential Monte Carlo. SSRN. [Google Scholar] [CrossRef]
- Gellert, Karol, and Erik Schlögl. 2021. Parameter Learning and Change Detection Using a Particle Filter with Accelerated Adaptation. Risks 9: 228. [Google Scholar] [CrossRef]
- Hol, Jeroen D., Thomas B. Schon, and Fredrik Gustafsson. 2006. On resampling algorithms for particle filters. Paper presented at the 2006 IEEE Nonlinear Statistical Signal Processing Workshop, Cambridge, UK, September 13–15; pp. 79–82. [Google Scholar]
- Rompotis, Gerasimos G. 2013. Actively vs. passively managed exchange traded funds. Aestimatio 6: 116–35. [Google Scholar]
- Ruf, Johannes, and Kangjianan Xie. 2019. The impact of proportional transaction costs on systematically generated portfolios. SIAM Journal on Financial Mathematics 11: 881–96. [Google Scholar] [CrossRef]
- Satpathy, Tanmay, and Rushabh Shah. 2022. Sparse index tracking using sequential Monte Carlo. Quantitative Finance 22: 1579–92. [Google Scholar] [CrossRef]
- Speekenbrink, Maarten. 2016. A tutorial on particle filters. Journal of Mathematical Psychology 73: 140–52. [Google Scholar] [CrossRef]
- Tibshirani, Robert. 1996. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society Series B: Statistical Methodology 58: 267–88. [Google Scholar] [CrossRef]
- Xu, Kelvin, Jimmy Ba, Ryan Kiros, Kyunghyun Cho, Aaron Courville, Ruslan Salakhudinov, Rich Zemel, and Yoshua Bengio. 2015. Show, attend and tell: Neural image caption generation with visual attention. In International Conference on Machine Learning. Birmingham: PMLR, pp. 2048–57. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).