Analyzing the Impact of Carbon Risk on Firms’ Creditworthiness in the Context of Rising Interest Rates
Abstract
1. Introduction
2. Literature Review
3. Data and Methodology
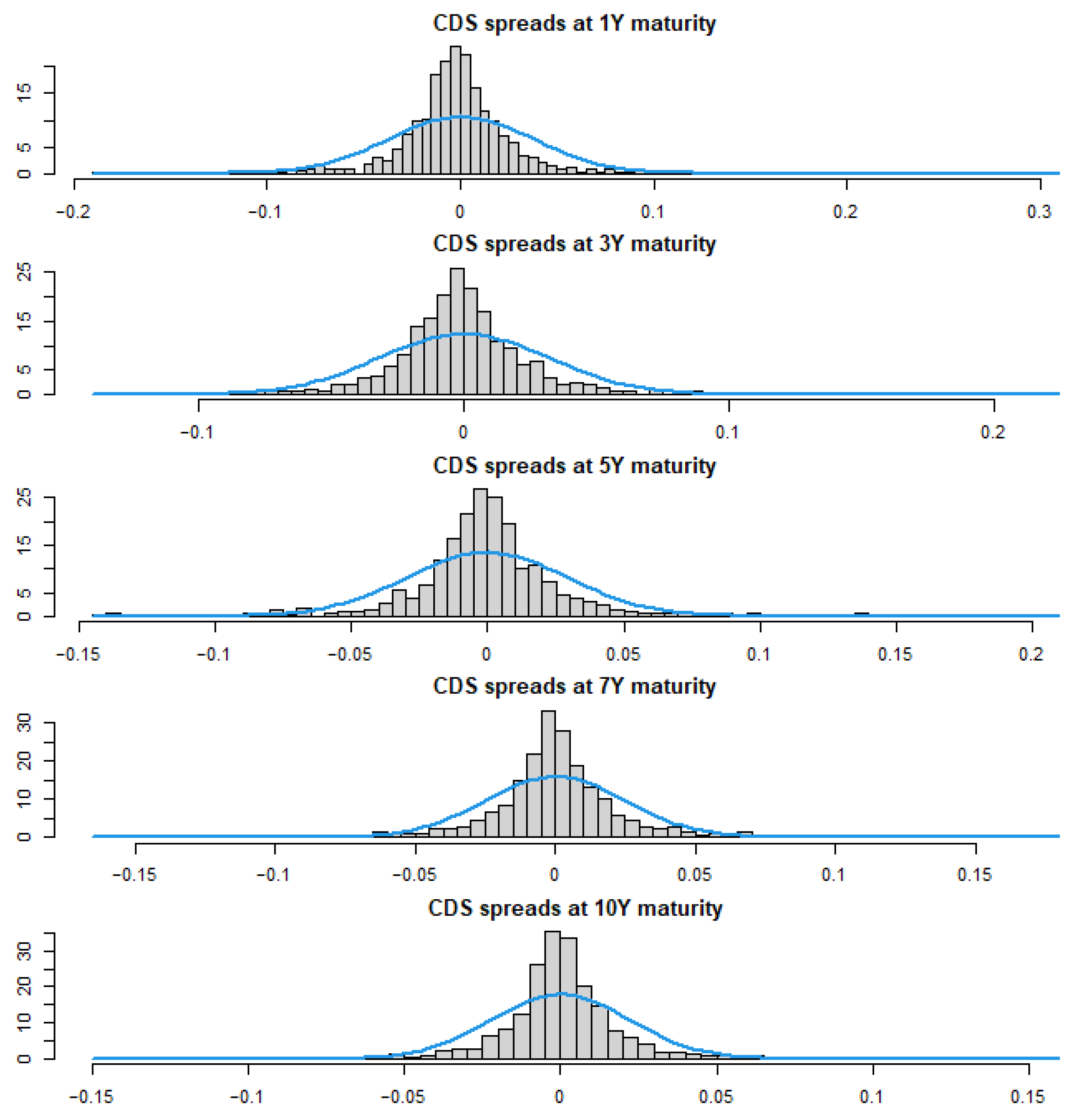
3.1. Data
- Stock returns: , where is the stock price of the firm at time t. This variable is determined by subtracting of the natural log of daily stock prices retrieved from Bloomberg. Higher stock returns boost the value of a company, which reduces its corresponding CDS spreads. As proven in previous research, for example, Blasberg et al. (2022); Zhang et al. (2023); Galil et al. (2014), a negative relationship between CDS spreads and stock returns is expected.
- Stock volatility: , where is the time interval considered in which every observation is made, in this case 180 days, and is the annualization factor considered. This component is gathered from Bloomberg as the annualized historical 180-day window standard deviation of firms’ daily excess return. According to empirical evidence, there is a direct relationship between stock return volatility and default probability. In other words, increased stock volatility implies greater uncertainty for the firm, which results in higher corresponding CDS spreads.
3.2. Quantile Regression
4. Results
4.1. Descriptive Statistics
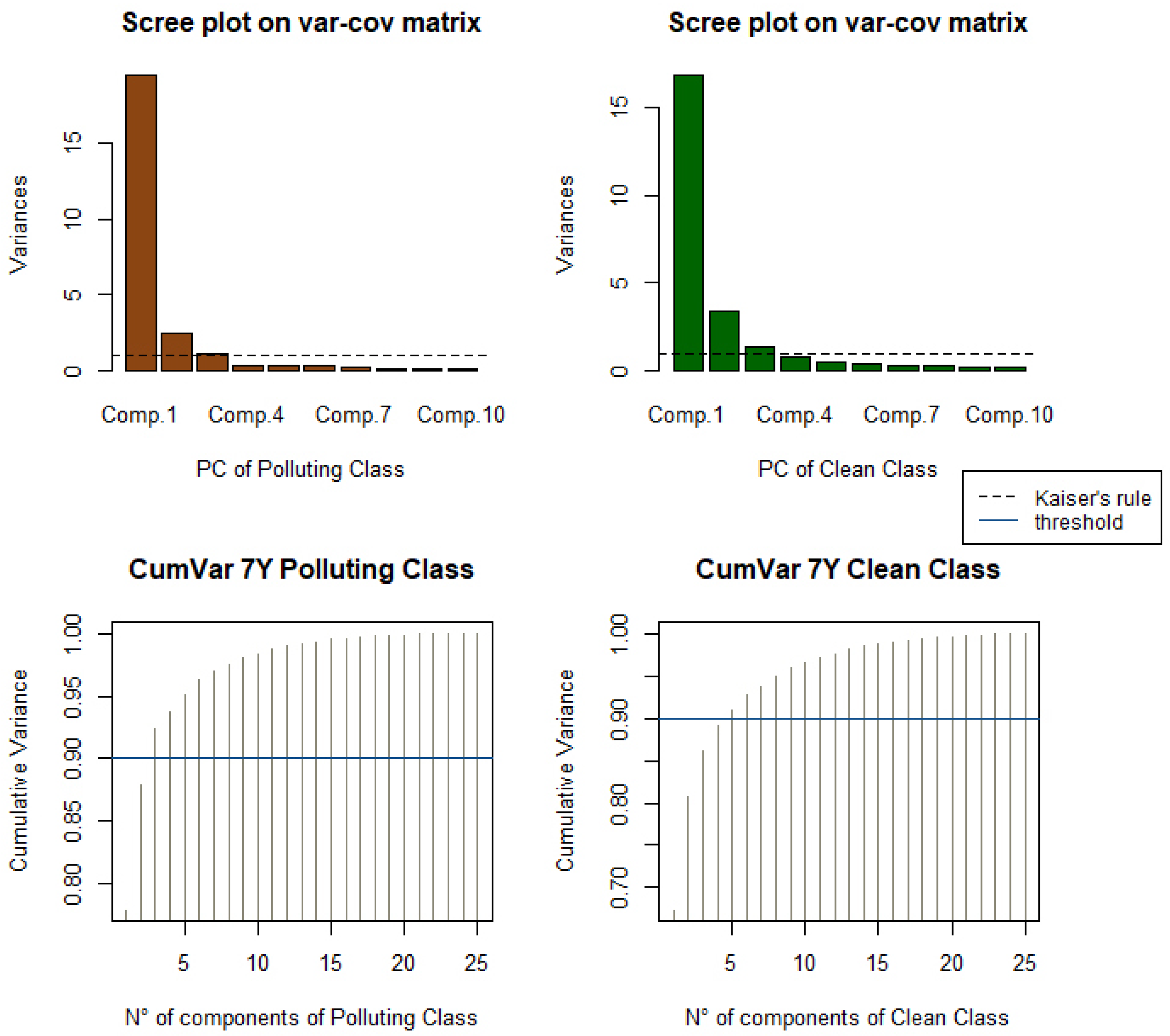
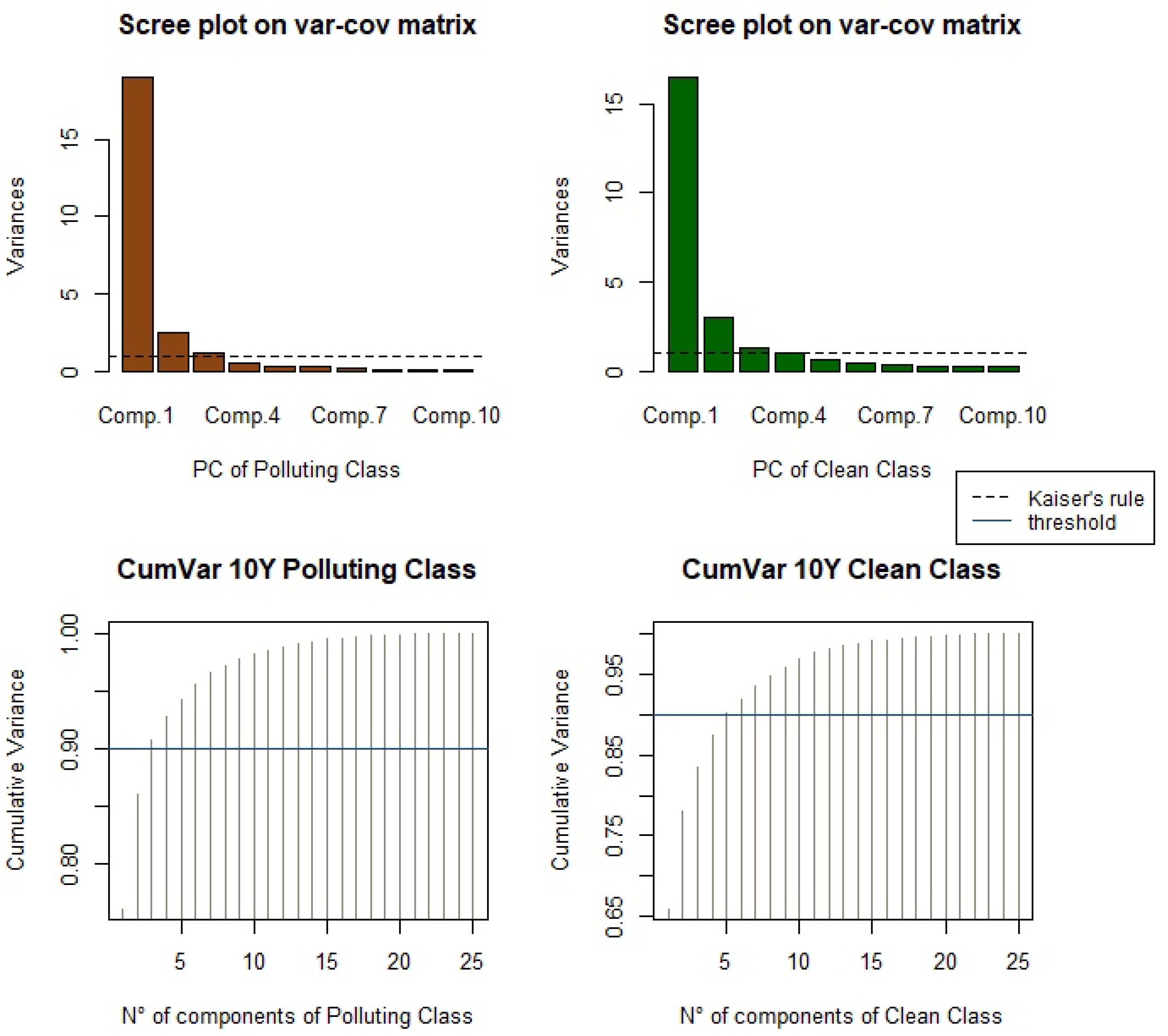
4.2. Preliminary Analysis through PCA
- (i)
- A scree plot (top), which illustrates the eigenvalue of each principal component, typically paired up with Kaiser’s rule, depicted by the straight black line. The eigenvectors represent the principal components of the data, and the corresponding eigenvalues indicate the amount of variance explained by each component.
- (ii)
- A histogram-like plot (bottom), which illustrates the cumulative variance explained by each principal component, given as the cumulative sum of the eigenvalues divided by the total sum of these eigenvalues. For this study, a cumulative variance explained by a threshold equal to 90%, indicated by the dark blue dashed line, was adopted.
4.3. Hypothesis Validation
- (i)
- An increase in the CDS spread, which is for , indicates a deterioration in a firm’s creditworthiness;
- (ii)
- A decrease in the CDS spread, which is for , indicates an improvement in a firm’s creditworthiness;
- (iii)
- The median, , corresponds to an unchanged CDS spread.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Sector | Industry | Firm | Country |
|---|---|---|---|
| Consumer Discretionary | Leisure Facilities | Accor SA | France |
| Consumer Staples | Food Products | Tate & Lyle PLC | United Kingdom |
| Energy | Oil and Gas Producers | Eni SpA | Italy |
| Repsol SA | Spain | ||
| Industrial Products | Transportation and Logistics | Deutsche Lufthansa AG | Germany |
| Materials | Chemicals | Air Liquide SA | France |
| Koninklijke DSM NV | Netherlands | ||
| Lanxess AG | Germany | ||
| Linde AG | Germany | ||
| Solvay SA | Belgium | ||
| Construction Materials | HeidelbergCement AG | Germany | |
| Holcim AG | Switzerland | ||
| Lafarge SA | France | ||
| Forestry, Paper and Wood Products | UPMJmmene Oyj | Finland | |
| Metals and Mining | AngloAmerican PLC | United Kingdom | |
| Steel | ArcelorMittal SA | Luxembourg | |
| Thyssenkrupp AG | Germany | ||
| Utilities | Electric Utilities | E.ON SE | Germany |
| EDP Energias de Portugal SA | Portugal | ||
| Engie SA | France | ||
| Fortum Oyj | Finland | ||
| Iberdrola SA | Spain | ||
| National Grid PLC | United Kingdom | ||
| SSE PLC | United Kingdom | ||
| Gas Utilities | Naturgy Energy Group SA | Spain | |
| Integrated Electric Utilities | Electricite de France SA | France | |
| Enel SpA | Italy | ||
| Water Utilities | Veolia Environnement SA | France |
| Sector | Industry | Firm | Country |
|---|---|---|---|
| Communications | Telecommunications | SES SA | France |
| Telecommunications and Media | ITV PLC | United Kingdom | |
| Koninklijke KPN NV | Netherlands | ||
| Pearson PLC | United Kingdom | ||
| Publicis Group SA | France | ||
| Swisscom AG | Switzerland | ||
| Telecom Italia SpA | Italy | ||
| Television Francaise 1 SA | France | ||
| Telia Co AB | Sweden | ||
| Vivendi SE | France | ||
| Consumer Discretionary | Apparel and Textile | Kering SA | France |
| LVMH Moet Hennesy Louis Vuitton SE | France | ||
| Automotive | Bayerische Motoren Werke AG | Germany | |
| Leisure Facilities and Services | Compass Group PLC | United Kingdom | |
| Sodexo SA | France | ||
| Consumer Staples | Tobacco and Cannabis | Imperial Brands PLC | United Kingdom |
| Healthcare | Medical Equipment and Devices | Koninklijke Philips NV | Netherlands |
| Industrial Products | Aerospace and Defence | Airbus SE | France |
| Thales SA | France | ||
| Commercial Support Services | Adecco Group AG | Switzerland | |
| Diversified Industrials | Siemens AG | Germany | |
| Electrical Equipment | Schneider Electric SE | France | |
| Machinery and Transportation Equipment | Alstom SA | France | |
| VOLVO AB | Sweden | ||
| Transportation and Logistics | PostNL NV | Netherlands | |
| Technology | Software and Tech Services | Wolters Kluwer NV | Netherlands |
| Technology Hardware and EMS/ODM | Nokia Oyj | Finland | |
| Telefonakitiebolaget LM Ericsson | Sweden |
Appendix B
| Variable | 0.01 | 0.05 | 0.1 | 0.5 | 0.9 | 0.95 | 0.99 |
|---|---|---|---|---|---|---|---|
| 1Y | |||||||
| Consumer Discretionary | −2.32 | −1.15 | −0.30 | 1.54 | −1.24 | −0.18 | 19.42 |
| (5.60) | (3.10) | (2.48) | (1.13) | (2.84) | (5.00) | (20.72) | |
| Materials | −6.18 | 2.63 | 1.97 | 2.05 | 3.97 | 5.17 | 32.48 |
| (9.60) | (2.57) | (2.10) | (0.78) | (1.35) | (2.39) | (14.14) | |
| Industrial Products | −18.62 | −3.00 | −2.14 | −0.09 | −0.44 | −0.78 | −2.76 |
| (17.39) | (4.79) | (2.13) | (1.55) | (1.83) | (3.13) | (22.32) | |
| Utilities | 8.63 | 5.52 | 3.52 | 5.02 | 4.78 | 6.56 | 9.85 |
| (6.71) | (2.08) | (1.77) | (1.04) | (2.76) | (2.96) | (11.46) | |
| Energy | 9.09 | 6.97 | 5.09 | 5.09 | 5.42 | 5.50 | 21.54 |
| (6.63) | (6.03) | (4.65) | (1.16) | (3.68) | (4.34) | (14.48) | |
| Consumer Staples | 9.62 | −3.33 | −1.90 | 1.15 | −0.44 | 2.15 | 17.32 |
| (9.82) | (3.00) | (2.03) | (0.88) | (1.98) | (3.40) | (13.78) | |
| Communications | −6.81 | −0.38 | 0.76 | 2.62 | −0.60 | −2.09 | 20.90 |
| (7.63) | (2.30) | (1.32) | (1.05) | (1.91) | (2.98) | (11.86) | |
| Healthcare | 8.35 | −6.67 | −4.02 | 0.86 | 3.98 | −3.33 | 28.84 |
| (17.72) | (6.19) | (3.39) | (0.77) | (3.94) | (9.61) | (17.66) | |
| Technology | −8.76 | −3.60 | 0.43 | −0.26 | −0.08 | −1.16 | 21.06 |
| (11.82) | (4.48) | (2.55) | (1.30) | (2.08) | (5.30) | (17.23) | |
| 3Y | |||||||
| Consumer Discretionary | 4.03 | 2.82 | 4.07 | 2.30 | 3.38 | 4.28 | −1.05 |
| (4.75) | (2.70) | (1.61) | (1.13) | (2.36) | (2.80) | (8.08) | |
| Materials | 12.07 | 8.75 | 6.72 | 5.03 | 3.54 | 5.10 | 18.17 |
| (5.61) | (3.51) | (2.09) | (0.93) | (1.93) | (3.27) | (11.88) | |
| Industrial Products | 6.77 | 3.64 | 1.77 | 1.39 | −0.29 | −0.78 | −5.60 |
| (14.30) | (3.27) | (2.54) | (0.83) | (1.07) | (2.41) | (13.51) | |
| Utilities | 9.36 | 6.82 | 7.15 | 6.72 | 7.65 | 6.60 | 10.57 |
| (6.90) | (3.19) | (1.77) | (1.18) | (2.20) | (1.88) | (10.09) | |
| Energy | 11.65 | 7.28 | 7.27 | 7.71 | 6.62 | 9.28 | −9.23 |
| (6.34) | (2.52) | (2.25) | (2.16) | (3.01) | (3.47) | (12.12) | |
| Consumer Staples | 4.42 | 0.24 | 2.13 | 2.41 | 2.52 | 2.17 | 10.86 |
| (3.97) | (1.35) | (1.69) | (1.10) | (1.38) | (1.94) | (7.70) | |
| Communications | 1.02 | 1.88 | 3.43 | 2.05 | 2.55 | 3.22 | 10.27 |
| (4.83) | (2.09) | (1.90) | (1.21) | (1.75) | (1.73) | (5.63) | |
| Healthcare | −4.39 | −0.43 | 3.16 | 2.03 | −0.64 | 1.93 | −0.89 |
| (7.13) | (3.49) | (2.61) | (1.28) | (3.16) | (7.12) | (9.27) | |
| Technology | −0.88 | 4.82 | 3.82 | 3.13 | 3.51 | 5.35 | −2.53 |
| (5.07) | (3.16) | (1.49) | (1.84) | (1.89) | (2.21) | (13.00) | |
| 7Y | |||||||
| Consumer Discretionary | 1.89 | −0.53 | 1.51 | 1.04 | 1.03 | −1.24 | 1.17 |
| (2.74) | (1.32) | (1.05) | (0.97) | (1.32) | (1.60) | (2.14) | |
| Materials | 12.47 | 4.05 | 2.63 | 2.45 | 3.07 | 5.50 | 14.47 |
| (7.19) | (2.28) | (1.72) | (0.93) | (1.04) | (1.42) | (5.96) | |
| Industrial Products | −13.94 | −3.63 | −1.07 | 0.52 | −0.15 | −1.65 | −5.12 |
| (18.44) | (2.27) | (1.48) | (0.94) | (1.51) | (1.90) | (13.44) | |
| Utilities | 8.63 | 2.59 | 4.00 | 1.96 | 4.20 | 5.10 | 6.46 |
| (5.79) | (1.77) | (1.39) | (1.01) | (0.73) | (0.98) | (2.69) | |
| Energy | 6.43 | 1.93 | 3.41 | 1.74 | 2.76 | 4.95 | 2.37 |
| (7.66) | (3.06) | (1.97) | (0.87) | (1.24) | (1.50) | (3.62) | |
| Consumer Staples | 0.43 | 2.29 | 2.54 | 0.37 | 0.08 | −0.30 | 5.76 |
| (15.33) | (1.64) | (1.37) | (0.79) | (1.22) | (2.06) | (11.54) | |
| Communications | −7.19 | −0.68 | 0.39 | 0.79 | −0.83 | −2.77 | −8.80 |
| (6.78) | (2.11) | (1.05) | (0.90) | (1.90) | (1.74) | (7.27) | |
| Healthcare | −2.50 | −2.04 | −1.51 | −0.18 | −0.33 | −1.28 | −7.34 |
| (6.22) | (2.48) | (2.26) | (0.59) | (1.43) | (3.07) | (7.08) | |
| Technology | 6.78 | 1.43 | 2.91 | 0.96 | 1.51 | 1.34 | 3.67 |
| (4.83) | (2.12) | (1.76) | (0.97) | (1.65) | (1.47) | (4.12) | |
| 10Y | |||||||
| Consumer Discretionary | 1.53 | 0.89 | 1.37 | 1.83 | 1.62 | 1.78 | −0.01 |
| (2.32) | (1.04) | (0.89) | (0.82) | (1.64) | (2.06) | (2.38) | |
| Materials | 7.46 | 3.17 | 2.40 | 2.30 | 1.85 | 3.16 | 8.23 |
| (9.29) | (1.39) | (1.39) | (0.77) | (1.14) | (1.44) | (5.90) | |
| Industrial Products | −0.92 | −0.91 | 0.57 | 0.27 | −1.07 | −0.56 | −4.24 |
| (5.70) | (2.07) | (1.57) | (0.82) | (1.31) | (1.20) | (18.34) | |
| Utilities | 3.14 | 4.27 | 3.87 | 3.59 | 3.13 | 3.81 | 5.69 |
| (4.21) | (1.46) | (0.91) | (0.92) | (0.76) | (1.17) | (1.63) | |
| Energy | 1.71 | 4.13 | 4.57 | 2.23 | 3.74 | 4.43 | −0.27 |
| (4.94) | (2.18) | (0.93) | (1.08) | (1.79) | (1.42) | (3.19) | |
| Consumer Staples | 2.16 | −0.68 | 1.47 | 1.02 | −0.76 | −0.50 | 0.88 |
| (3.69) | (1.37) | (0.85) | (0.70) | (1.21) | (1.68) | (1.64) | |
| Communications | 4.44 | 1.02 | 1.13 | 1.56 | 0.40 | 1.19 | −0.07 |
| (4.06) | (1.31) | (1.02) | (0.68) | (1.05) | (1.41) | (4.72) | |
| Healthcare | −0.76 | 0.56 | 1.86 | 1.47 | 1.34 | 3.18 | 2.38 |
| (5.22) | (2.15) | (1.78) | (0.88) | (1.42) | (3.98) | (7.51) | |
| Technology | 3.88 | 2.54 | 2.03 | 1.78 | 1.04 | 0.56 | 2.70 |
| (4.44) | (1.88) | (1.82) | (1.07) | (1.24) | (2.43) | (3.40) | |
Appendix C
| Polluting Class | Clean Class | |||
|---|---|---|---|---|
| No. | Eigenvalue | Cumulative Variance (%) | Eigenvalue | Cumulative Variance (%) |
| 1Y | ||||
| 1 | 17.72 | 70.88 | 15.82 | 63.28 |
| 2 | 4.42 | 88.59 | 3.79 | 78.42 |
| 3 | 0.72 | 91.47 | 2.04 | 86.58 |
| 4 | - | - | 0.78 | 89.70 |
| 5 | - | - | 0.44 | 91.46 |
| 3Y | ||||
| 1 | 19.02 | 76.01 | 16.72 | 66.89 |
| 2 | 3.59 | 90.37 | 3.85 | 82.29 |
| 3 | - | - | 1.29 | 87.45 |
| 4 | - | - | 0.92 | 91.15 |
| 7Y | ||||
| 1 | 19.47 | 77.87 | 16.83 | 67.33 |
| 2 | 2.49 | 87.85 | 3.34 | 80.70 |
| 3 | 1.12 | 92.33 | 1.35 | 86.10 |
| 4 | - | - | 0.75 | 89.08 |
| 5 | - | - | 0.47 | 90.96 |
| 10Y | ||||
| 1 | 16.49 | 74.98 | 16.49 | 65.95 |
| 2 | 3.02 | 86.83 | 3.02 | 78.02 |
| 3 | 0.97 | 90.71 | 1.34 | 83.38 |
| 4 | - | - | 1.00 | 87.40 |
| 5 | - | - | 0.67 | 90.07 |


| 1 | This refers to the fact that bondholders are willing to accept a lower yield in order to invest in green securities compared to conventional securities with similar characteristics. |
| 2 | This is a heuristic rule that suggests only retaining components with an eigenvalue greater than 1. |
| 3 | The results obtained referring to other tenors are available in Appendix B. |
References
- Bachelet, Maria J., Leonardo Becchetti, and Stefano Manfredonia. 2019. The green bonds premium puzzle: The role of issuer characteristics and third-party verification. Sustainability 11: 1098. [Google Scholar] [CrossRef]
- Benz, Lukas, Stefan Paulus, Julia Scherer, Julia Syryca, and Stefan Trück. 2021. Investors’ carbon risk exposure and their potential for shareholder engagement. Business Strategy and the Environment 30: 282–301. [Google Scholar] [CrossRef]
- Blasberg, Alexander, Ruediger Kiesel, and Luca Taschini. 2022. Carbon Default Swap-Disentangling the Exposure to Carbon Risk through CDS. CESifo Working Paper. Munich: CESifo. [Google Scholar]
- Bolton, Patrick, and Marcin Kacperczyk. 2020. Do Investors Care about Carbon Risk? NBER Working Paper Series; Cambridge, MA: NBER. [Google Scholar]
- Bro, Rasmus, and Age K. Smilde. 2014. Principal component analysis. Analytical Methods 6: 2812–31. [Google Scholar] [CrossRef]
- Carbone, Sante, Margherita Giuzio, Sujit Kapadia, Johannes Krämer, Kwn Nyholm, and Katia Vozian. 2021. The Low-Carbon Transition, Climate Commitments and Firm Credit Risk. Frankfurt: European Central Bank. [Google Scholar]
- Cheema-Fox, Alexander, Bridger LaPerla, George Serafeim, David Turkington, and Hui Wang. 2021. Decarbonizing Everything. Financial Analysts Journal 77: 93–108. [Google Scholar] [CrossRef]
- European Central Bank. 2022. ECB Takes Further Steps to Incorporate Climate Change into Its Monetary Policy Operations. Frankfurt: ECB. [Google Scholar]
- Flammer, Caroline, Michael Toffel, and Kala Viswanathan. 2021. Shareholder activism and firms’ voluntary disclosure of climate change risks. Strategic Management Journal 42: 1850–79. [Google Scholar] [CrossRef]
- Galil, Koresh, Offer Mashe Shapir, Dan Amiram, and Uri Ben-Zion. 2014. The determinants of CDS spreads. Journal of Banking and Finance 41: 271–82. [Google Scholar] [CrossRef]
- Hachenberg, Britta, and Dirk Schiereck. 2018. Are green bonds priced differently from conventional bonds? Journal of Asset Management 19: 371–83. [Google Scholar] [CrossRef]
- Han, Bing, and Yi Zhou. 2015. Understanding the term structure of credit default swap spreads. Journal of Empirical Finance 31: 18–35. [Google Scholar] [CrossRef]
- Jung, Juhyun, Kathleen Herbohn, and Peter Clarkson. 2018. Carbon risk, carbon risk awareness and the cost of debt financing. Journal of Business Ethics 150: 1151–71. [Google Scholar] [CrossRef]
- Kleimeier, Stefanie, and Michael Viehs. 2021. Pricing carbon risk: Investor preferences or risk mitigation? Economics Letters 205: 109936. [Google Scholar] [CrossRef]
- Koenker, Roger, and Gilbert Bassett. 1978. Regression Quantiles. Econometrica 46: 33–50. [Google Scholar] [CrossRef]
- Mercuri, Lorenzo, Andrea Perchiazzo, and Edit Rroji. 2023. Investigating Short-Term Dynamics in Green Bond Markets. arXiv arXiv:2308.12179. [Google Scholar]
- Merton, Robert. 1974. On the Pricing of Corporate Debt: The Risk Structure of Interest Rates. The Journal of Finance 29: 449–70. [Google Scholar]
- Nguyen, Justin, and Hieu Phan. 2020. Carbon risk and corporate capital structure. Journal of Corporate Finance 64: 101713. [Google Scholar] [CrossRef]
- Reboredo, Juan Carlos. 2018. Green bond and financial markets: Co-movement, diversification and price spillover effects. Energy Economics 74: 38–50. [Google Scholar] [CrossRef]
- Sohag, Kazi, M. Kabir Hassan, Stepan Bakhteyev, and Oleg Mariev. 2023. Do green and dirty investments hedge each other? Energy Economics 120: 106573. [Google Scholar] [CrossRef]
- Zhang, Yuqi, Yaorong Liu, and Haisen Wang. 2023. How credit default swap market measures carbon risk. Environmental Science and Pollution Research 30: 82696–716. [Google Scholar] [CrossRef] [PubMed]



| Variable | Min | Median | Mean | Max | Std Dev | Skew | Kurt |
|---|---|---|---|---|---|---|---|
| Dependent Variables | |||||||
| −0.18909 | −0.00197 | 0.00034 | 0.30857 | 0.03745 | 2.74890 | 24.55104 | |
| −0.13967 | −0.00179 | 0.00008 | 0.22051 | 0.03223 | 1.01756 | 11.03029 | |
| −0.14008 | −0.00073 | −0.00012 | 0.20845 | 0.02962 | 0.43911 | 11.14989 | |
| −0.16462 | −0.00059 | −0.00010 | 0.17804 | 0.02507 | 0.31751 | 11.72097 | |
| −0.14785 | −0.00031 | −0.00009 | 0.15558 | 0.02238 | 0.26230 | 14.58722 | |
| Independent Variables | |||||||
| −0.13622 | 0.00106 | 0.00028 | 0.08224 | 0.00020 | −1.16196 | 17.36467 | |
| −0.02344 | −0.00007 | −0.00004 | 0.04415 | −0.00001 | 5.76883 | 129.96059 | |
| −5.51113 | 0.00411 | 0.00896 | 5.17267 | 0.73276 | −0.36153 | 12.13311 | |
| −6.87281 | 0.02468 | 0.00823 | 8.03090 | 2.02136 | 0.31258 | 9.38611 | |
| −10.62168 | −0.01062 | 0.01387 | 12.04706 | 4.05895 | 0.50074 | 12.19177 | |
| −9.90050 | 0.00158 | −0.00788 | 11.00020 | 4.53931 | 0.13575 | 8.84092 | |
| −17.75170 | 0.02416 | −0.01912 | 20.21900 | 6.50648 | −0.03539 | 16.51952 | |
| 1.00000 | −0.26280 | −0.05081 | |
| −0.26280 | 1.00000 | 0.04705 | |
| −0.05081 | 0.04705 | 1.00000 |
| Polluting Class | Clean Class | |||
|---|---|---|---|---|
| No. | Eigenvalue | Cumulative Variance (%) | Eigenvalue | Cumulative Variance (%) |
| 1 | 18.74 | 74.98 | 14.87 | 59.50 |
| 2 | 2.96 | 86.83 | 3.48 | 73.41 |
| 3 | 0.97 | 90.71 | 1.57 | 79.70 |
| 4 | - | - | 0.98 | 83.63 |
| 5 | - | - | 0.89 | 87.20 |
| 6 | - | - | 0.67 | 89.87 |
| 7 | - | - | 0.61 | 92.30 |
| Variable | 0.01 | 0.05 | 0.1 | 0.5 | 0.9 | 0.95 | 0.99 |
|---|---|---|---|---|---|---|---|
| Consumer Discretionary | 0.80 | 3.68 | 3.45 | 1.92 | 0.42 | −1.86 | 1.21 |
| (2.91) | (1.52) | (1.20) | (1.27) | (1.75) | (1.72) | (3.78) | |
| Materials | 11.85 | 5.08 | 4.87 | 3.93 | 2.36 | 3.28 | 0.33 |
| (15.41) | (2.15) | (1.21) | (0.93) | (1.86) | (2.65) | (10.96) | |
| Industrial Products | −2.75 | 1.49 | 1.92 | 1.75 | 0.92 | 0.03 | −3.92 |
| (5.96) | (3.00) | (1.73) | (1.10) | (1.61) | (1.95) | (4.85) | |
| Utilities | 9.76 | 5.15 | 3.97 | 4.44 | 3.05 | 3.21 | 1.17 |
| (5.44) | (1.69) | (1.68) | (1.09) | (1.39) | (1.56) | (2.35) | |
| Energy | 7.99 | 4.88 | 5.67 | 4.45 | 5.42 | 6.95 | 3.57 |
| (5.18) | (2.82) | (1.73) | (0.86) | (2.69) | (3.45) | (4.11) | |
| Consumer Staples | 4.21 | 3.32 | 3.67 | 3.11 | 3.21 | 3.18 | −6.14 |
| (3.02) | (1.70) | (1.19) | (1.45) | (1.42) | (1.76) | (7.02) | |
| Communications | 2.56 | 1.47 | 1.33 | 1.56 | −0.37 | 0.13 | −4.70 |
| (4.53) | (2.14) | (1.42) | (0.78) | (1.35) | (1.96) | (7.34) | |
| Healthcare | 7.79 | 6.16 | 5.16 | 2.14 | 1.30 | −0.49 | 6.29 |
| (3.74) | (2.20) | (1.78) | (1.00) | (2.70) | (3.60) | (6.92) | |
| Technology | 6.70 | 7.41 | 4.13 | 1.25 | 0.88 | −1.56 | −10.37 |
| (5.04) | (1.82) | (1.33) | (0.98) | (2.17) | (3.06) | (6.80) | |
| Materials (2022) | 15.63 | 11.05 | 10.14 | 6.18 | 2.79 | 0.31 | −3.37 |
| (31.16) | (3.75) | (2.60) | (1.39) | (3.26) | (2.61) | (31.94) | |
| Utilities (2022) | 15.94 | 13.30 | 12.55 | 8.62 | 2.80 | 2.36 | −0.94 |
| (6.66) | (3.65) | (2.54) | (1.21) | (2.67) | (3.23) | (4.39) | |
| Energy (2022) | 16.50 | 16.06 | 12.77 | 7.32 | 9.72 | 56.16 | 5.15 |
| (11.83) | (4.32) | (3.56) | (1.72) | (5.31) | (6.61) | (5.76) |
| Variable | 0.01 | 0.05 | 0.1 | 0.5 | 0.9 | 0.95 | 0.99 |
|---|---|---|---|---|---|---|---|
| 5Y-1Y | |||||||
| −14.76 | −2.11 | −1.09 | −0.10 | 0.45 | 1.95 | −6.10 | |
| (11.37) | (2.05) | (0.70) | (0.31) | (1.00) | (2.06) | (10.88) | |
| −8.19 | −7.91 | −2.59 | −0.11 | −2.00 | −0.55 | −11.34 | |
| (25.21) | (5.05) | (2.85) | (0.74) | (1.80) | (2.48) | (15.32) | |
| −16.69 | 6.91 | 1.81 | −0.42 | 1.06 | −0.10 | −4.43 | |
| (26.09) | (5.19) | (2.29) | (0.70) | (1.61) | (3.20) | (18.17) | |
| 17.63 | 1.46 | −0.05 | −0.07 | 0.10 | −3.91 | 15.87 | |
| (15.07) | (2.39) | (1.01) | (0.46) | (1.28) | (2.68) | (8.84) | |
| 10Y−1Y | |||||||
| −22.42 | −3.19 | −2.71 | −1.04 | 0.61 | 1.58 | 4.89 | |
| (10.73) | (1.52) | (0.63) | (0.93) | (0.80) | (1.66) | (8.29) | |
| −67.92 | −4.03 | −5.32 | 3.01 | 2.74 | 1.77 | −0.58 | |
| (49.91) | (8.00) | (3.90) | (2.65) | (1.08) | (2.82) | (12.10) | |
| 43.50 | 1.89 | 1.07 | −1.44 | −0.92 | −2.73 | −6.35 | |
| (21.02) | (3.31) | (1.13) | (1.02) | (0.67) | (1.86) | (10.75) | |
| −18.38 | −2.86 | −0.36 | −0.93 | −1.87 | −3.19 | −6.75 | |
| (17.18) | (2.89) | (1.33) | (0.53) | (0.74) | (1.55) | (10.71) | |
| Variable | 0.01 | 0.05 | 0.1 | 0.5 | 0.9 | 0.95 | 0.99 |
|---|---|---|---|---|---|---|---|
| 2020 | |||||||
| CR Slope 5Y-1Y | 7.01 | −0.74 | 0.90 | −0.60 | 2.46 | 6.54 | 27.24 |
| (21.52) | (9.51) | (1.60) | (1.13) | (1.94) | (4.93) | (11.22) | |
| CR Slope 10Y-1Y | −20.89 | −1.84 | −0.48 | 1.73 | −1.86 | −0.72 | −0.27 |
| (16.81) | (8.36) | (3.36) | (1.68) | (1.62) | (1.86) | (11.70) | |
| 2021 | |||||||
| CR Slope 5Y-1Y | −21.11 | −4.67 | −2.93 | −1.15 | −2.63 | −0.44 | −8.90 |
| (14.51) | (6.81) | (2.18) | (0.67) | (2.01) | (7.60) | (12.37) | |
| CR Slope 10Y-1Y | −6.56 | −4.20 | −0.91 | −0.29 | 0.24 | 1.19 | 16.72 |
| (17.13) | (6.93) | (3.23) | (1.00) | (2.53) | (5.27) | (9.81) | |
| 2022 | |||||||
| CR Slope 5Y-1Y | 41.73 | −1.72 | 0.13 | 0.21 | −2.42 | −7.23 | −14.52 |
| (20.21) | (5.00) | (1.23) | (0.55) | (2.11) | (2.68) | (6.60) | |
| CR Slope 10Y-1Y | 0.49 | −8.14 | −3.23 | −2.57 | −3.53 | −8.21 | +17.52 |
| (29.82) | (6.82) | (2.74) | (1.09) | (1.89) | (4.94) | (10.91) | |
| 2023 | |||||||
| CR Slope 5Y-1Y | −15.59 | 14.21 | 9.07 | 3.13 | −1.65 | −1.16 | 23.28 |
| (33.49) | (9.97) | (7.14) | (3.33) | (8.73) | (17.41) | (20.91) | |
| CR Slope 10Y-1Y | −15.81 | 6.62 | 2.08 | −0.11 | −1.95 | −1.99 | 11.51 |
| (10.49) | (6.41) | (4.14) | (2.70) | (4.25) | (6.80) | (12.20) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Batoon, A.J.; Rroji, E. Analyzing the Impact of Carbon Risk on Firms’ Creditworthiness in the Context of Rising Interest Rates. Risks 2024, 12, 16. https://doi.org/10.3390/risks12010016
Batoon AJ, Rroji E. Analyzing the Impact of Carbon Risk on Firms’ Creditworthiness in the Context of Rising Interest Rates. Risks. 2024; 12(1):16. https://doi.org/10.3390/risks12010016
Chicago/Turabian StyleBatoon, Aimee Jean, and Edit Rroji. 2024. "Analyzing the Impact of Carbon Risk on Firms’ Creditworthiness in the Context of Rising Interest Rates" Risks 12, no. 1: 16. https://doi.org/10.3390/risks12010016
APA StyleBatoon, A. J., & Rroji, E. (2024). Analyzing the Impact of Carbon Risk on Firms’ Creditworthiness in the Context of Rising Interest Rates. Risks, 12(1), 16. https://doi.org/10.3390/risks12010016






