The Generalised Pareto Distribution Model Approach to Comparing Extreme Risk in the Exchange Rate Risk of BitCoin/US Dollar and South African Rand/US Dollar Returns
Abstract
1. Introduction
Literature Review
2. Methodology
2.1. The Generalised Pareto Distribution (GPD)
2.1.1. Parameter Estimation of GPD
2.1.2. Excess Distribution
2.2. Risk Measures
2.3. Model Adequacy
3. Results
3.1. Descriptive Statistics
3.2. Data Analysis
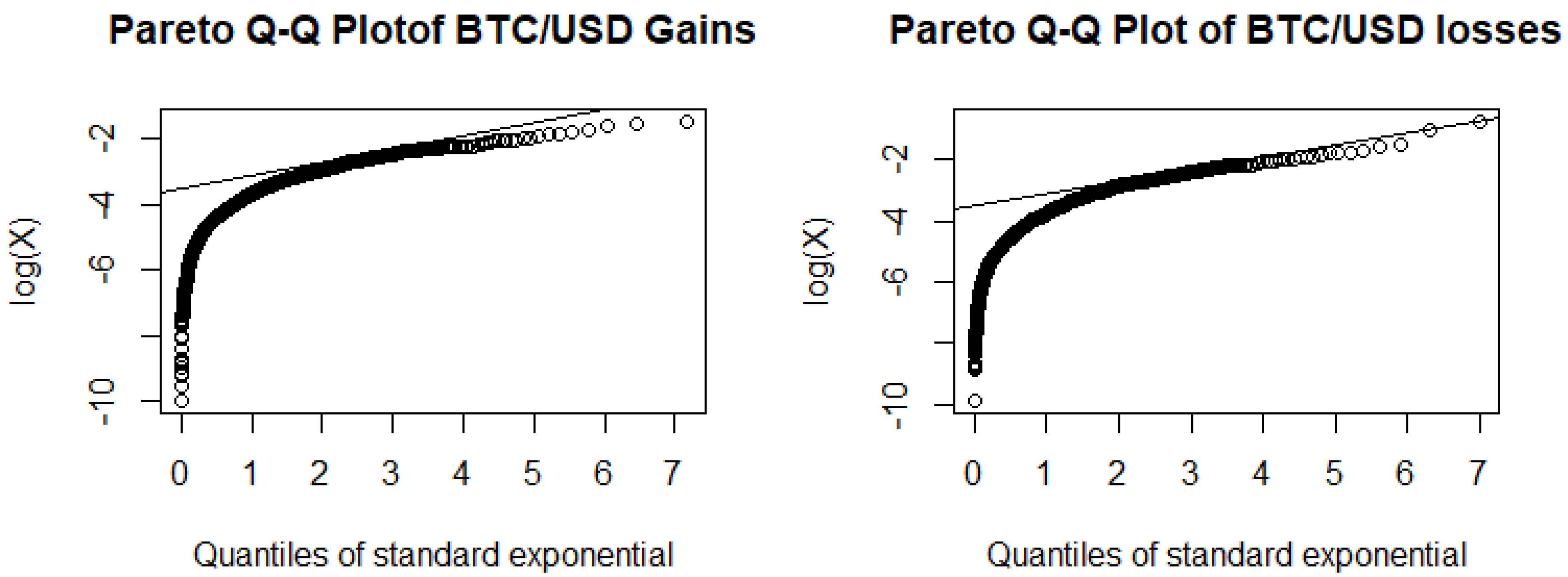
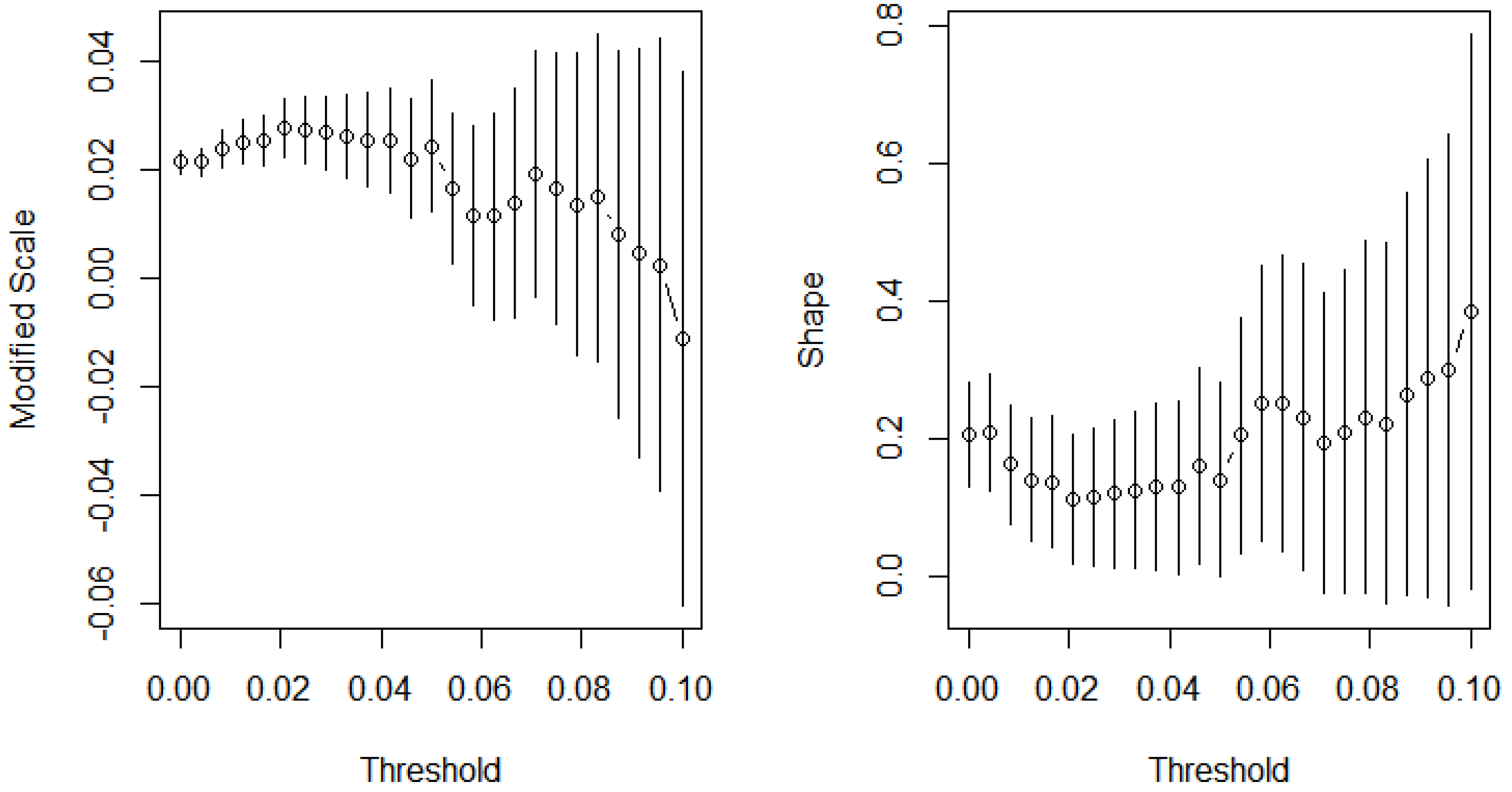
3.2.1. Analysing the BTC/USD Returns
3.2.2. Analysing ZAR/USD Returns
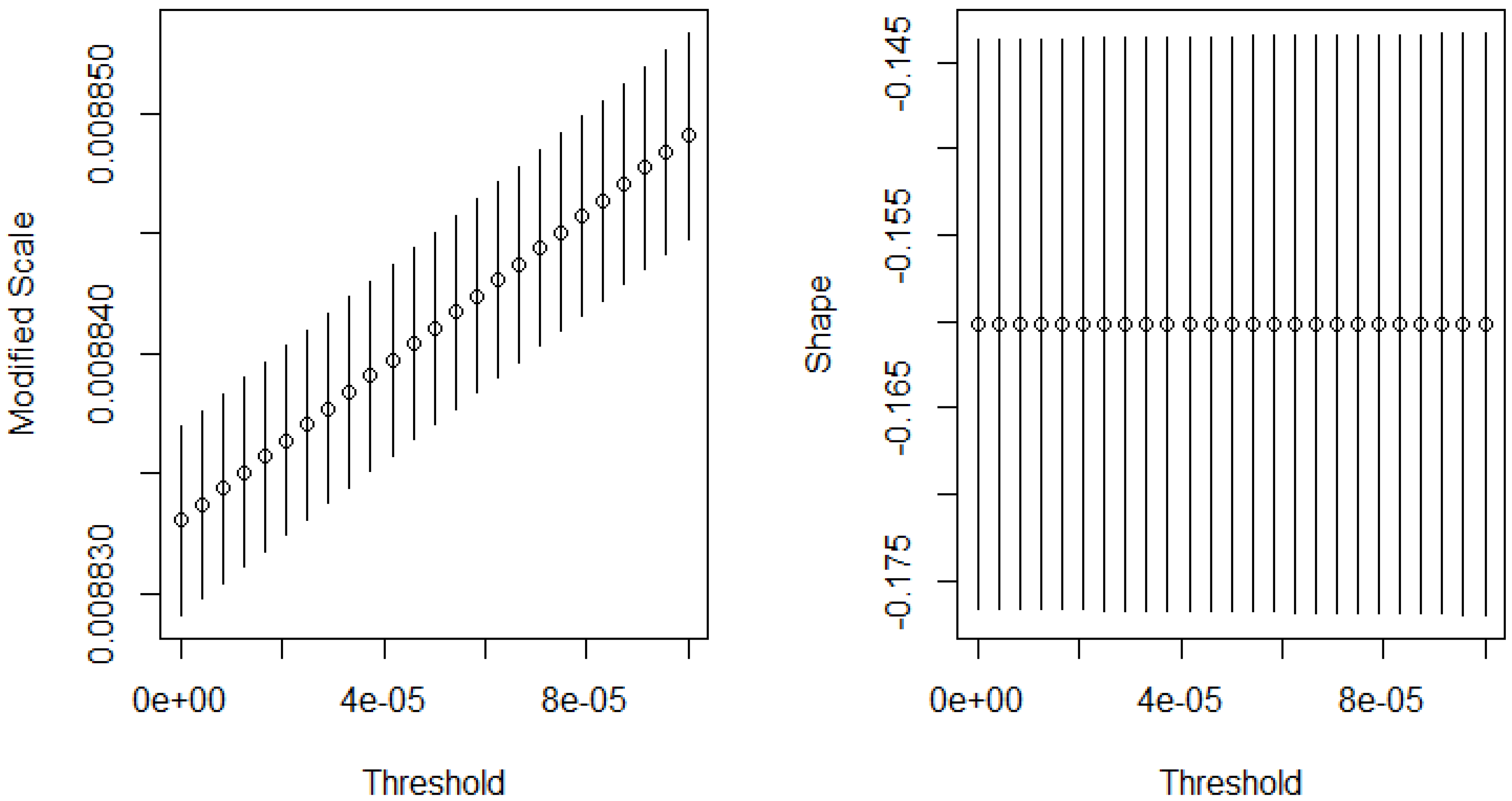
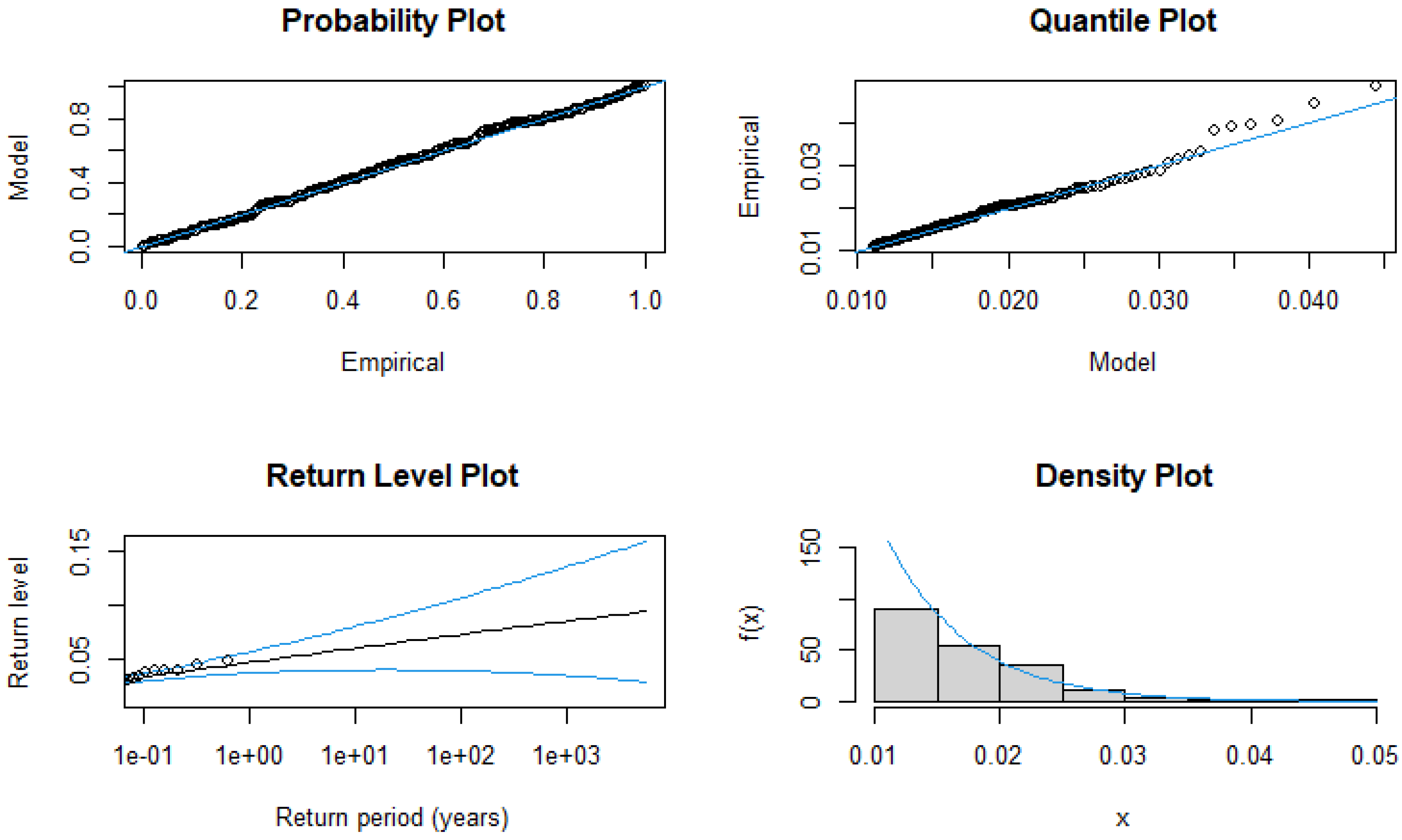
3.2.3. Model Diagnostics for the ZAR/USD Returns
3.3. Parameter Estimations
3.4. Risk Measures
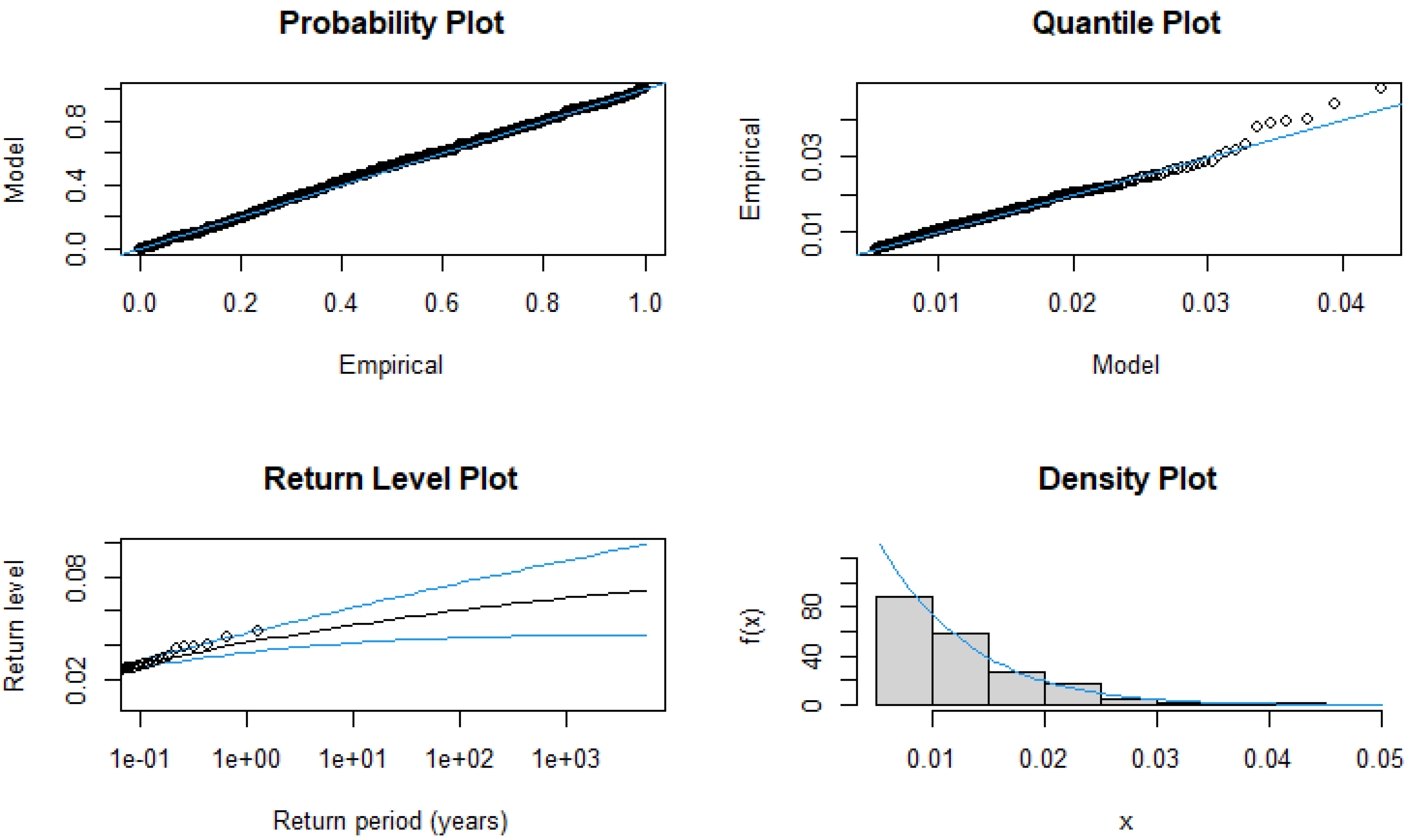
3.5. Model Adequacy
4. Discussion
Limitations and Further Related Studies
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Almeida, José, and Tiago Cruz Gonçalves. 2023. Portfolio Diversification, Hedge and Safe-Haven Properties in Cryptocurrency Investments and Financial Economics: A Systematic Literature Review. Journal of Risk and Financial Management 16: 3. [Google Scholar] [CrossRef]
- Artzner, Philippe, Freddy Delbaen, Eber Jean-Marc, and David D. Heath. 1999. Coherent Measures of Risk. Mathematical Finance 9: 203–28. [Google Scholar] [CrossRef]
- Bader, Brian, and Jun Yan. 2020. eva: Extreme Value Analysis with Goodness-of-Fit Testing. R Package Version 0.2.6. Available online: https://cran.r-project.org/web/packages/eva/eva.pdf (accessed on 10 December 2022).
- Balkema, August A., and Laurens de Haan. 1974. Residual lifetime at great age. Annals of Probability 2: 792–804. [Google Scholar] [CrossRef]
- Beirlant, Jan, Petra Vynckier, and Jozef L. Teugels. 1996. Tail index estimation, Pareto quantile plots, and regression diagnostics. Journal of American Statistical Association 91: 1659–67. [Google Scholar]
- Beirlant, Jan, Goedele Dierckx, and Armelle Guillou. 2005. Estimation of the extreme-value index and generalized quantile plots. Bernoulli 11: 949–70. [Google Scholar] [CrossRef]
- Bouri, Elie, Peter Molnár, Georges Azzi, David Roubaud, and Lars Ivar Hagfors. 2017. On the hedge and safe haven properties of BitCoin: Is it really more than a diversifier? Finance Research Letters 20: 192–98. [Google Scholar] [CrossRef]
- Caeiro, Frederico, Maria Ivette Gomes, and Dinis Pestana. 2005. Direct reduction of bias of the classical hill estimator. Revstat 3: 113–36. [Google Scholar]
- Cai, Juan-Juan, Laurens de Haan, and Chen Zhou. 2013. Bias correction in extreme value statistics with index around zero. Extremes 16: 173–201. [Google Scholar] [CrossRef]
- Chen, James Ming. 2018. On Exactitude in Financial Regulation: Value-at-Risk, Expected Shortfall, and Expectiles. Risks 6: 61. [Google Scholar] [CrossRef]
- Chikobvu, Delson, and Thabani Ndlovu. 2023. The Generalised Extreme Value Distribution Approach to Comparing the Riskiness of BitCoin/US Dollar and South African Rand/US Dollar Returns. Journal of Risk and Financial Management 16: 253. [Google Scholar] [CrossRef]
- Chou, Heng-Chih, and David K. Wang. 2014. Estimation of Tail-Related Value-at-Risk Measures: Range Based Extreme Value Approach. Quantitative Finance 14: 293–304. [Google Scholar] [CrossRef]
- Danielsson, Jon. 2011. Financial Risk Forecasting. London: Wiley. [Google Scholar]
- Davies, Martyn. 2017. Is South Africa the Next Brazil? Emerging Market Insights. Available online: https://www2.deloitte.com/content/dam/Deloitte/za/Documents/africa/DeloitteZA_Is_South_Africa_the_next_Brazil_Sep2017.pdf (accessed on 2 May 2023).
- Dekkers, Arnold L. M., John H. J. Einmahl, and Laurens de Haan. 1989. A moment estimator for the index of an extreme-value distribution. Annals of Statistics 17: 1833–55. [Google Scholar] [CrossRef]
- Dyhrberg, Anne Haubo. 2016. BitCoin, gold and the dollar—A Garch volatility analysis. Finance Research Letters 16: 85–92. [Google Scholar] [CrossRef]
- Fisher, Ronals, and Leonard Tippett. 1928. Limiting forms of the frequency distribution of the largest or smallest member of a sample. Mathematical Proceedings of the Cambridge Philosophical Society 24: 180–90. [Google Scholar] [CrossRef]
- Fratzscher, Marcel. 2002. On Currency Crises and Contagion. Working Paper Series 139; Franfurt am Main: European Central Bank. [Google Scholar]
- Ghalanos, Alexios. 2020. rugarch: Univariate GARCH Models. R Package Version 1.4-4. Available online: https://cran.r-project.org/web/packages/rugarch/index.html (accessed on 10 December 2022).
- Gneiting, Tilmann. 2011. Making and evaluating point forecasts. Journal of the American Statistical Association 106: 746–62. [Google Scholar] [CrossRef]
- Grable, John. 2000. Financial risk tolerance and additional factors that affect risk taking in everyday money matters. Journal of Business and Psychology 14: 625–30. [Google Scholar] [CrossRef]
- Heffernan, Janet E., and Alec G. Stephenson. 2018. ismev: An Introduction to Statistical Modeling of Extreme Values. R Package Version 1.42. Available online: https://cran.r-project.org/web/packages/ismev/ismev.pdf (accessed on 10 December 2022).
- Hull, John. 2006. Risk Management and Financial Institutions, 1st ed. Hoboken: Prentice Hall. [Google Scholar]
- Ibrahim, Mohamed, Walid Emam, Yusra Tashkandy, Mir Masoom Ali, and Haitham M. Yousof. 2023. Bayesian and Non-Bayesian Risk Analysis and Assessment under Left-Skewed Insurance Data and a Novel Compound Reciprocal Rayleigh Extension. Mathematics 11: 1593. [Google Scholar] [CrossRef]
- Joale, Dan. 2011. Analyzing the Effect of Exchange Rate Volatility on South Africa’s Exports to the US—Theory and Evidence. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Kaseke, Forbes, Shaun Ramroop, and Henry Mwambi. 2021. A Comparison of the Stylised Facts of BitCoin, Ethereum and the JSE Stock Returns. African Finance Journal 23: 50–64. [Google Scholar]
- Kupiec, Paul H. 1995. Techniques for verifying the accuracy of risk management models. Journal of Derivatives 3: 73–84. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1959. Portfolio Selection: Efficient Diversification of Investments. New York: John Wiley & Sons. [Google Scholar]
- Penalva, Helena, Sandra Nunes, and Manuela M. Neves. 2016. Extreme Value Analysis—A Brief Overview With an Application to Flow Discharge Rate Data in A Hydrometric Station In The North Of Portugal. REVSTAT—Statistical Journal Volume 14: 193–215. [Google Scholar]
- Pflug, Georg Ch. 2000. Some Remarks on the Value-at-Risk and the Conditional Value-at-Risk. Probabilistic Constrained Optimization. Boston: Springer, pp. 272–81. [Google Scholar]
- Pickands, James, III. 1975. Statistical inference using extreme order statistics. Annals of Statistics 3: 119–31. [Google Scholar] [CrossRef]
- Pretorius, Anmar, and Jesse De Beer. 2002. Financial Contagion in Africa: South Africa and a Troubled Neighbour, Zimbabwe. Paper presented at the 7th Annual Conference of the African Econometrics Society, Kruger National Park, South Africa, June 19–23. [Google Scholar]
- R Core Team. 2021. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 1 December 2021).
- Rached, Imen, and Elisabeth Larsson. 2019. Tail Distribution and Extreme Quantile Estimation Using Non-parametric Approaches. In High-Performance Modelling and Simulation for Big Data Applications. Cham: Springer, vol. 11400. [Google Scholar] [CrossRef]
- Rockafellar, Ralph Tyrrell, and Stan Uryasev. 2002. Conditional value-at-risk for general loss distributions. Journal of Banking & Finance 26: 1443–71. [Google Scholar] [CrossRef]
- RStudio Team. 2022. RStudio: Integrated Development Environment for R. Boston: RStudio, PBC. Available online: http://www.rstudio.com/ (accessed on 10 December 2022).
- Scarrott, Carl, and Anna MacDonald. 2012. A Review of Extreme Value Threshold Estimation and Uncertainty Quantification. REVSTAT-Statistical Journal 10: 33–60. [Google Scholar]
- Shanaev, Savva, and Binam Ghimire. 2021. A fitting return to fitting returns: Cryptocurrency distributions revisited. SSRN Electronic Journal 1: 1–33. [Google Scholar] [CrossRef]
- Smith, Richard L. 1987. Estimating Tails of Probability Distributions. The Annals of Statistics 15: 1174–207. [Google Scholar] [CrossRef]
- Takaishi, Tetsuya. 2018. Statistical properties and multifractality of BitCoin. Physica A: Statistical Mechanics and Its Applications 506: 507–19. [Google Scholar] [CrossRef]
- Tretina, Kat. 2023. Top 10 Cryptocurrencies of 2023. Forbes Advisor. Available online: https://www.forbes.com/advisor/investing/cryptocurrency/top-10-cryptocurrencies/ (accessed on 7 March 2023).
- Van Der Merwe, E. 1996. Exchange Rate Management Policies in South Africa: Recent Experience and Prospects. South African Reserve Bank Occasional Paper No. 8, June 1995. Pretoria: South African Reserve Bank Occasional. [Google Scholar]
- Yamai, Yasuhiro, and Toshinao Yoshiba. 2002. Comparative Analysis of Expected Shortfall and Value at Risk: Their Estimation Error, Decomposition, and Optimization. Monetary and Economic Studies 20: 87–121. [Google Scholar]
- Yousof, Haitham M., Walid Emam, Yusra Tashkandy, Mir Masoom Ali, Richard Minkah, and Mohamed Ibrahim. 2023a. A Novel Model for Quantitative Risk Assessment under Claim-Size Data with Bimodal and Symmetric Data Modeling. Mathematics 11: 1284. [Google Scholar] [CrossRef]
- Yousof, Haitham M., Yusra Tashkandy, Walid Emam, Mir Masoom Ali, and Mohamed Ibrahim. 2023b. A New Reciprocal Weibull Extension for Modeling Extreme Values with Risk Analysis under Insurance Data. Mathematics 11: 966. [Google Scholar] [CrossRef]
- Zhang, Yuanyuan, and Saralees Nadarajah. 2017. A review of backtesting for value at risk. Communications in Statistics—Theory and Methods 47: 3616–39. [Google Scholar] [CrossRef]







| Observations | Mean | Median | Maximum | Minimum | Skewness | Kurtosis | |
| BTC/USD | 2370 | 0.001990 | 0.001757 | 0.237220 | −0.480904 | −0.994382 | 16.15451 |
| ZAR/USD | 1694 | −0.000125 | 0.000000 | 0.049546 | −0.048252 | −0.264130 | 4.121644 |
| Test for normality, autocorrelation, and heteroscedasticity | |||||||
| BTC/USD | ZAR/USD | ||||||
| TEST | Statistic | p-value | Statistic | p-value | |||
| Jarque–Bera | 17,478.40 | 0.000000 | 108.4967 | 0.000000 | |||
| Ljung–Box | 11.7 | 0.0006249 | 0.40504 | 0.5245 | |||
| ARCH LM Test | 52.87 | 4.345 × 10−7 | 70.789 | 2.28 × 101 | |||
| Test for unit root and stationarity | |||||||
| BTC/USD | ZAR/USD | ||||||
| Unit Root Test | Statistic | p-value | Statistic | p-value | |||
| ADF Test | −52.20130 | 0.0001 | −40.47263 | 0.0000 | |||
| PP Test | −52.10963 | 0.0001 | −40.47011 | 0.0000 | |||
| KPSS Test | 0.092067 | 0.347000 | 0.090747 | 0.347000 | |||
| Model | Number of Exceedances | ||||
|---|---|---|---|---|---|
| BTC/USD Gains | 396 | 0.0302 | 0.0527 | 0.0284 | 0.0021 |
| BTC/USD Losses | 319 | 0.1096 | 0.0535 | 0.0311 | 0.0024 |
| ZAR/USD Gains | 229 | −0.0164 | 0.0650 | 0.0005 | 0.0064 |
| ZAR/USD Losses | 243 | −0.0844 | 0.0313 | 0.0065 | 0.0003 |
| BTC/USD | ZAR/USD | |||
|---|---|---|---|---|
| Losses | Gains | Losses | Gains | |
| 90% | 0.07 | 0.06 | 0.02 | 0.02 |
| 95% | 0.09 | 0.08 | 0.02 | 0.03 |
| 99% | 0.16 | 0.13 | 0.03 | 0.03 |
| BTC/USD | ZAR/USD | |||
|---|---|---|---|---|
| Losses | Gains | Losses | Gains | |
| 90% | 0.11 | 0.09 | 0.02 | 0.02 |
| 95% | 0.13 | 0.11 | 0.02 | 0.03 |
| 99% | 0.21 | 0.17 | 0.03 | 0.04 |
| BTC/USD | ZAR/USD | |||
|---|---|---|---|---|
| Losses | Gains | Losses | Gains | |
| 90% | 0.9901 | 0.96278 | 0.7140 | 0.9811 |
| 95% | 0.6725 | 0.4288 | 0.420 | 0.5514 |
| 99% | 0.3694 | 0.4212 | 0.8316 | 0.7375 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ndlovu, T.; Chikobvu, D. The Generalised Pareto Distribution Model Approach to Comparing Extreme Risk in the Exchange Rate Risk of BitCoin/US Dollar and South African Rand/US Dollar Returns. Risks 2023, 11, 100. https://doi.org/10.3390/risks11060100
Ndlovu T, Chikobvu D. The Generalised Pareto Distribution Model Approach to Comparing Extreme Risk in the Exchange Rate Risk of BitCoin/US Dollar and South African Rand/US Dollar Returns. Risks. 2023; 11(6):100. https://doi.org/10.3390/risks11060100
Chicago/Turabian StyleNdlovu, Thabani, and Delson Chikobvu. 2023. "The Generalised Pareto Distribution Model Approach to Comparing Extreme Risk in the Exchange Rate Risk of BitCoin/US Dollar and South African Rand/US Dollar Returns" Risks 11, no. 6: 100. https://doi.org/10.3390/risks11060100
APA StyleNdlovu, T., & Chikobvu, D. (2023). The Generalised Pareto Distribution Model Approach to Comparing Extreme Risk in the Exchange Rate Risk of BitCoin/US Dollar and South African Rand/US Dollar Returns. Risks, 11(6), 100. https://doi.org/10.3390/risks11060100






