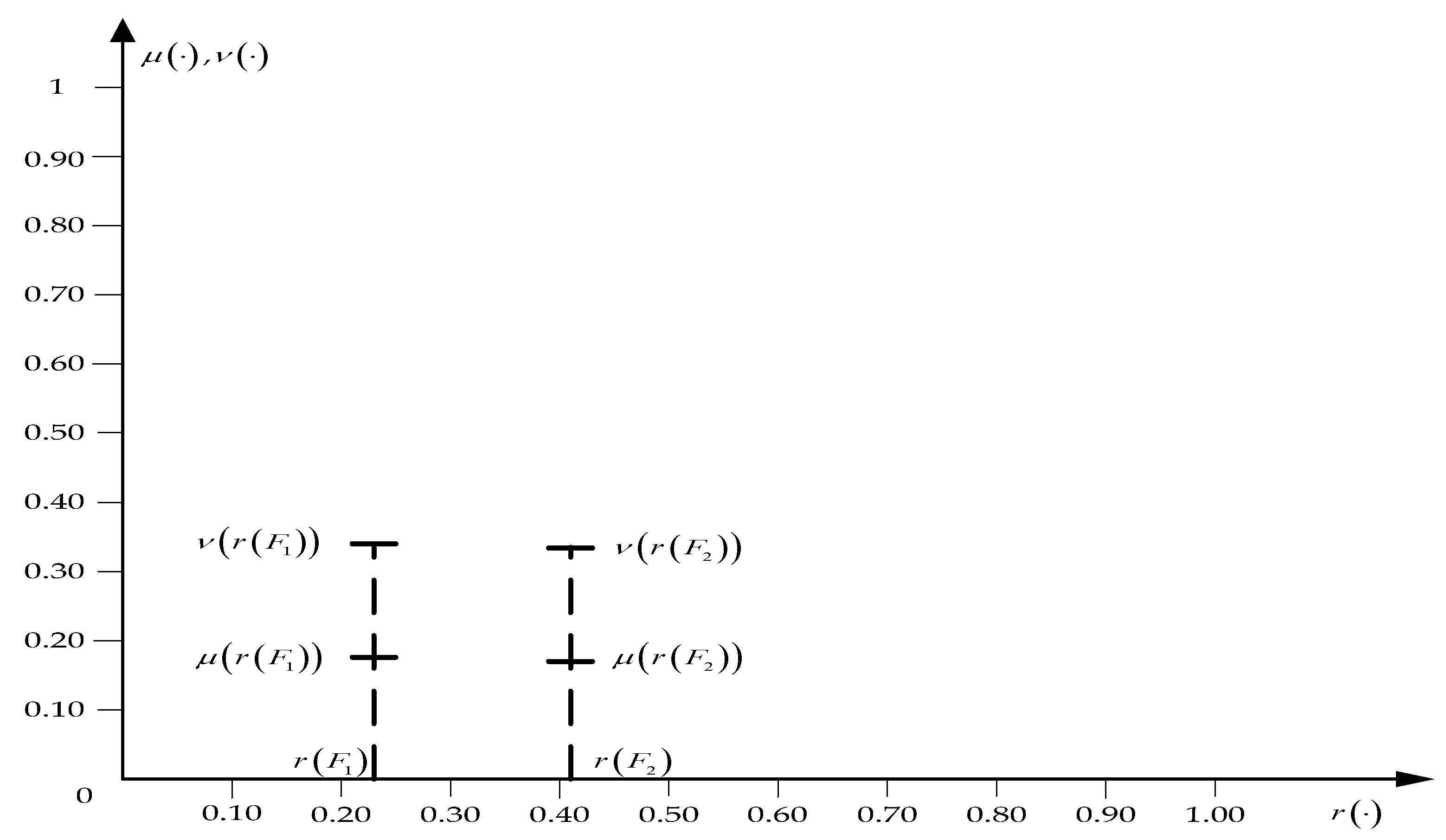Methodology for Environmental Risk Analysis Based on Intuitionistic Fuzzy Values

Abstract

Ecological risks are characterized by a high degree of uncertainty about the chances of unfavorable event outcomes and the losses associated with those outcomes. Subjective expert judgment is widely used when baseline data are insufficient. This introduces additional uncertainties in the results of risk analyses. In order to successfully model the existing uncertainties, this paper presents a methodology for ecological risk analysis that is based on input evaluations in the form of intuitionistic fuzzy values (IFVs). The advantage of this approach is the ability to model a wide range of uncertainties in ecological risk analysis tasks.

1. Introduction

Risks in a broad sense permeate all areas of human life and activities. Traveling on any kind of transport involves the risk of an accident in that vehicle. Ignoring the rules of behavior during an epidemic, a person can get sick. When investing in securities, an investor inevitably faces the risk of losing expected profits or even the risk of losing the invested funds. Any infrastructure at the national or local level is subject to risks of damage due to hurricanes, earthquakes, tsunamis, and other adverse natural impacts.

How can the concept of risk be formally defined? Many such definitions have been proposed. Extensive summaries of risk definitions are presented in (Aven and Renn 2010; Šotic and Radenko 2015). In this paper, we adopted the definition presented in (Aven and Renn 2010) as the basic universal definition. “Risk refers to uncertainties about the extent to which events and their consequences (or their outcomes) of some activity affect what constitutes human value”.

Let us present a generalized classification of risks based on the area of their occurrence.

• Technical and technological risks.
• Risks of negative impacts of natural factors on human activity and the external environment.
• Economic (commercial) risks.
• Organizational risks.
• Political risks.
• Ecological risks.

The last group of risks is associated with negative impacts on the external environment as the consequences of various activities of human society. Such negative impacts can be associated with production processes, as a result of which harmful substances enter the environment, for example, due to poor-quality fuel combustion, industrial accidents, and insufficient treatment of industrial and household waste.

This group may include the risks of degradation of territories due to various activities: deforestation, loss of large fertile areas through mining, construction of hydroelectric power stations, uncontrolled use of fertilizers, pesticides, and the like.

The cause of ecological risks may be the actions of people whose goal was to obtain positive results, but these actions lead to significant negative results. Here, we are talking about the negative impacts on the local environment associated with invasive plant and animal populations. The introduction of rabbits into Australia was supposed to have positive effects from this action. However, the uncontrolled growth of the rabbit population has led to negative impacts on local populations and has hampered economic activity in many agricultural areas.

Other examples of this kind are the spread of African bee populations in other countries, the spread of Asian carp in the lakes of the United States, and the spread of hogweed in countries in the former USSR.

A characteristic feature of the task of assigning environmental risks is the presence of various kinds of uncertainties. One source of uncertainty is the lack of initial data, the possible inconsistency, and the unreliability of the available data. Another source of uncertainty is expert assessments, which are an integral part of the task of assigning any risks. The credibility of expert assessments to a large extent depends on the knowledge and experience of experts. Therefore, the variability of expert assessments introduces significant uncertainties in the process of assigning any risks and environmental risks in particular.

Many methods have been proposed for modeling uncertainties in risk assignment problems. In the simplest cases, relevant estimates can be represented as intervals of possible values or as standard fuzzy numbers. In more complex situations, interval fuzzy numbers and intuitionistic fuzzy numbers can be used.

For modeling very high degrees of uncertainty, it seems more appropriate to use intuitionistic fuzzy numbers. This approach is already used in decision-making problems. The purpose of this work is to develop a methodology for assessing environmental risks in cases where relevant assessments are presented in the form of intuitionistic fuzzy numbers. This is the originality and novelty of this work.

The use of the proposed methodology will expand the possibilities of assigning environmental risks in situations where there are such uncertainties that existing approaches cannot handle.

The paper is structured as follows: Section 2 provides a review of the literature on the topic of this article. Section 3 introduces the basic concepts related to risks and risk assessment. Section 4 presents well-known methods for aggregating deterministic input data. The purpose of this presentation is to further extend these methods to an intuitionistic fuzzy environment. Section 5 introduces the theoretical foundations of intuitionistic fuzzy sets (IFSs) and intuitionistic fuzzy values (IFVs). Section 6 presents intuitionistic fuzzy versions of generalized aggregation operators OWA: IFWA, IFWG, a method for assigning fuzzy weights for experts, specific aggregation operators G-IFWA, and G-IFWG. Section 7 details the proposed methodology for fuzzy risk analysis. Section 8 presents a numerical example illustrating the proposed technique. Section 9 discusses the results obtained. Section 10 includes generalized conclusions and directions for further research.

2. Literature Review

The main guiding documents for assigning risks are ISO 31000 2018 and ISO 31010 2019. Broad overviews of the conceptual definitions of risk are presented in (Aven and Renn 2010; Šotic and Radenko 2015).

Among the many sources associated with fuzzy risk assignments, one should mention (Radionovs and Uzhga-Rebrov 2016, 2017). These works substantiate the possibility of using fuzzy logic to assign environmental risks.

A broad overview of data aggregation methods based on averages is presented in (Grabish et al. 2009).

In the works (Yager 1988, 1996), a family of special aggregation operators is proposed for deterministic values. Induced OWA operator (IOWA) is proposed in (Yager and Filev 1999). In (Yager 2004), a generalized operator GOWA is proposed.

The concept of intuitionistic fuzzy sets is proposed in (Atanassov 1986, 1999). Operations on IFVs are defined in (Xu 2007), and IFVS comparison methods are presented in (Chen and Tan 1994; Hong and Choi 2000).

An overview of data aggregation methods in an intuitionistic fuzzy environment is presented in (Xu and Cai 2012). Alternative methods for aggregating intuitionistic fuzzy data are presented in (Tepe and Kaya 2018; Liu et al. 2015; Rani et al. 2022).

Fuzzy approaches are used not only to assign risks but also to assess the reliability of systems. Let us take the following source as an example (Sahu and Srivastava 2018, 2020; Sahu et al. 2021).

3. Basic Concepts of Risk and Assessment

To effectively manage risks, these risks must be recognized, identified, and characterized. In other words, these risks must be assessed. Risk assessment processes are detailed in (ISO31000 2018; ISO31010 2019).

Let us introduce the basic concepts and procedures of risk assessment.

A hazard is a dangerous phenomenon, substance, human activity, or condition that causes death, injury, and other negative effects on someone’s health; loss of property; loss of livelihood; or damage to the environment.

A hazard mapping is a display that shows levels of probability of a hazard occurring. Such displays may focus on a single hazard or include different levels of hazards (multi-hazard display).

A risk mapping is a display that shows risk levels. Such a display may focus on only one risk or present different levels of risk.

A risk scenario is a representation of a single risk or a multi-risk situation that leads to important impacts and aims to assign more details to a particular risk for which they are representative or form an informative example or illustration.

The following concepts and definitions are taken from (ISO31010 2019):

Risk assessment is the overall process of risk identification, risk analysis, and risk assessment.

Risk analysis is the process of recognizing the nature of risk and determining the level of risk.

Risk evaluation is the process of comparing the results of a risk analysis with risk criteria to determine whether a risk and/or its magnitude is supportable or acceptable.

Risk criteria are links to agreements against which risk is assessed.

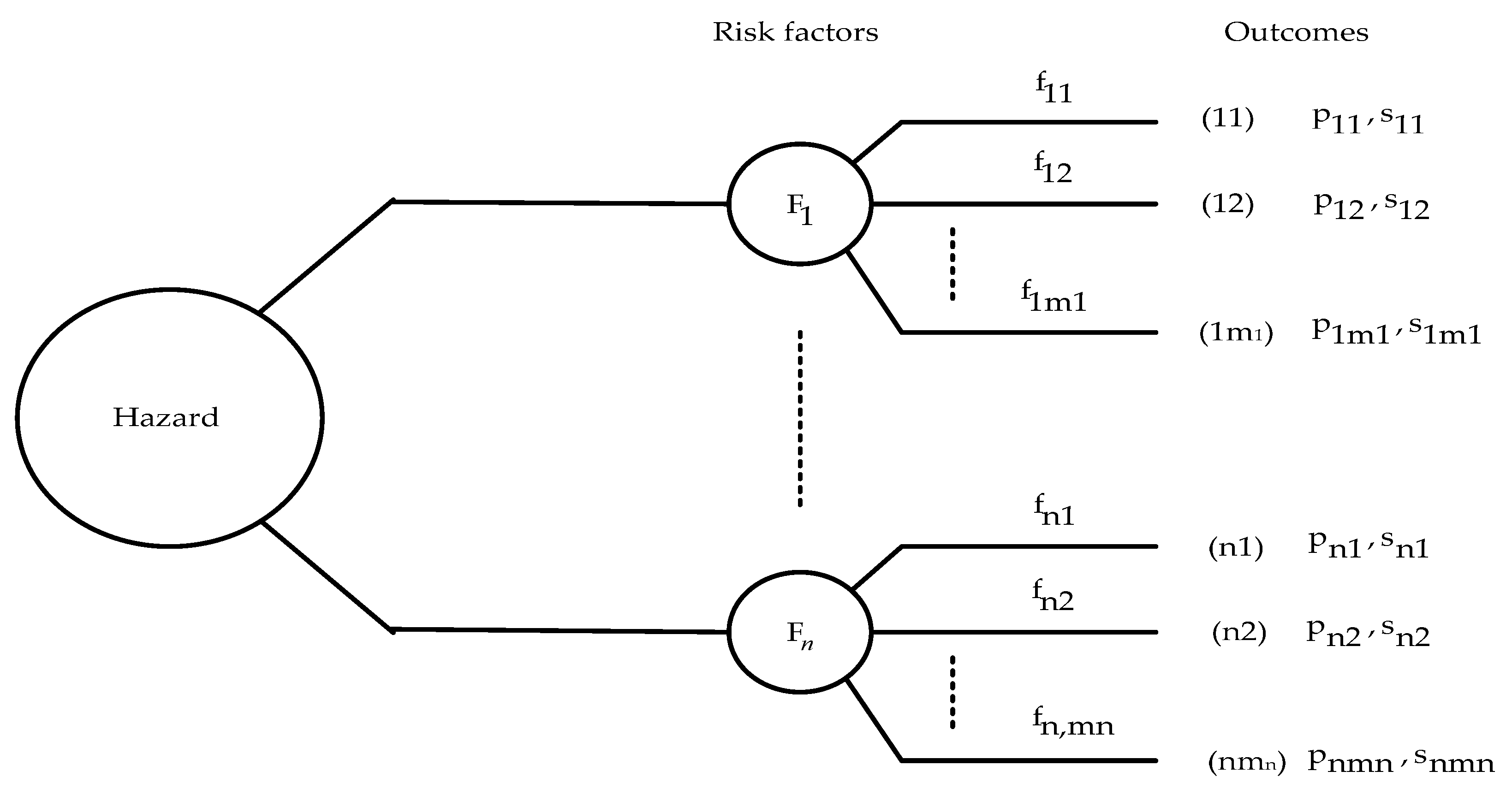
In this paper, we restricted ourselves to the following general framework of ecological risk analysis (see Figure 1).

In this diagram, “Hazard” is a generic representation of the current state of affairs that may lead to adverse ecological impacts.

A “risk factor” is a specification of a partial aspect of a general hazard.

${\mathrm{f}}_{\mathrm{i}\mathrm{j}},\mathrm{i}=1,\dots ,\mathrm{n}$—display the $j\text{-}th$ specific characteristic of the risk factor $F_i$.

The outcome $(\mathrm{i}\mathrm{j})$ represents the probability of the $j\text{-}th$ particular characteristic of the risk factor $F_i$ and the loss associated with that characteristic.

The use of probability and loss estimates to characterize particular outcomes of risk factors is not the only possible approach. The papers (Radionovs and Uzhga-Rebrov 2016, 2017; Oturakci 2018) present the ecological risk assessment methodology based on the fuzzy logic and fuzzy analytical hierarchy process (fuzzy AHP) approaches.

This paper’s aim is to present an ecological risk assessment methodology based on the traditional probability and loss approach, provided that all initial estimates are in the form of intuitionistic fuzzy values (IFVs).

4. Deterministic Versions of Aggregation Operators

In many practical applications, it is necessary to aggregate a certain set of initial estimates. In other words, on this set of estimates, it is necessary to determine the resulting estimate, which in some given sense characterizes the original set of estimates.

The simplest example of such aggregation is the calculation of the arithmetic mean on a given set of relevant estimates.

In addition to the well-known arithmetic mean, geometric mean, harmonic mean, and others are used in practical problems. A wide review of calculations of various types of average values is presented in (Grabish et al. 2009).

R. Yager (Yager 1988, 1996) proposed a family of special aggregation operators—the ordered weighted aggregation (OWA) operator—especially for aggregation of criterion estimates in multicriteria decision-making (MCDM).

Definition 1 

(Yager 1988). An OWA operator of dimension $n$ is a function ${\mathrm{F}}_{\mathrm{W}}:{\mathrm{R}}^{\mathrm{n}}\to \mathrm{R}$ that has an associated weight vector $\mathrm{W}=\left({\mathrm{w}}_1,{\mathrm{w}}_2,\dots ,{\mathrm{w}}_{\mathrm{n}}\right)$, such as ${\mathrm{w}}_{\mathrm{j}}\in \left[0,1\right]$ and ${\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{j}}}=1$. The function $F_W$ is defined as

$${\mathrm{F}}_{\mathrm{W}}=\left({\mathrm{a}}_1,{\mathrm{a}}_2,\dots ,{\mathrm{a}}_{\mathrm{n}}\right)={\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{j}}{\mathrm{a}}_{\mathsf{\sigma }\left(\mathrm{j}\right)}},$$

(1)

where ${\mathrm{a}}_{\mathsf{\sigma }\left(\mathrm{j}\right)}$ are the values of the argument $a_j$, ordered in non-decreasing order: ${\mathrm{a}}_{\mathsf{\sigma }\left(1\right)}\ge {\mathrm{a}}_{\mathsf{\sigma }\left(2\right)}\ge \dots \ge {\mathrm{a}}_{\mathsf{\sigma }\left(\mathrm{n}\right)}$.

The characteristic feature of the OWA operator is that, before the aggregation operation is performed, the argument $a_j$ values must be reordered in the form of a non-decreasing sequence of values ${\mathrm{a}}_{\mathsf{\sigma }\left(\mathrm{j}\right)}$, $\mathrm{j}=1,\dots ,\mathrm{n}$. The weights of the argument $w_j$ values are not related to the initial sequence of values $a_j$, but to the sequence of ordered values ${\mathrm{a}}_{\mathsf{\sigma }\left(\mathrm{j}\right)}.$

It should be noted that there is a variant of the OWA operator in which the initial values of the argument $a_j$ are ordered in the form of a non-increasing sequence of their values ${\mathrm{a}}_{\mathsf{\sigma }\left(\mathrm{j}\right)}$.

In general, applying the OWA operator to the initial sequence of values $\left\{a_j\right\}$ provides a specific averaging of these values. The magnitude of this average value depends both on the values of the argument $a_j$ and on the values of the weights $w_j$.

There are three specific cases of aggregation depending on the values of the weight vector $W$:

${\mathrm{F}}_{\max }\to \mathrm{W}={\mathrm{W}}^{*}={\left[0,0,\dots ,1\right]}^{\mathrm{T}}$. In this case, the aggregate value is taken as the maximum value of the argument ${\mathrm{a}}_{\mathsf{\sigma }\left(1\right)}$ in the ordered sequence of these values.

${\mathrm{F}}_{\min }\to \mathrm{W}={\mathrm{W}}_{\min }={\left[0,0,\dots ,1\right]}^{\mathrm{T}}$. In this case, the aggregate value is taken as the minimum value of the argument ${\mathrm{a}}_{\mathsf{\sigma }\left(\mathrm{n}\right)}$ in the ordered sequence of their values.

${\mathrm{F}}^{\mathrm{ave}}\to \mathrm{W}={\mathrm{W}}_{\mathrm{ave}}={\left[\frac{1}{\mathrm{n}},\frac{1}{\mathrm{n}},\dots ,\frac{1}{\mathrm{n}}\right]}^{\mathrm{T}}$. In this case, the OWA operator is reduced to the arithmetic mean operator.

Another type of weighted averaging operator is presented in (Yager and Filev 1999; Yager 2003). This operator is called the induced OWA operator (IOWA). We present the definition of this operator based on the data presented in (Yager and Filev 1999).

Using the above definition of the operator OWA (1), we introduce the following concept. Let $\mathrm{B}=\left\{{\mathrm{b}}_{\mathsf{\sigma }\left(\mathrm{j}\right)}={\mathrm{b}}_{\mathrm{j}}\right\},\mathrm{j}=1,\dots ,\mathrm{n}$ be an ordered non-decreasing sequence of initial values $a_j$. Then, the OWA operator can be represented in the following alternative form: ${\mathrm{F}}_{\mathrm{W}}=\left({\mathrm{a}}_1,{\mathrm{a}}_2,\dots ,{\mathrm{a}}_{\mathrm{n}}\right)={\mathrm{W}}^{\mathrm{T}}\mathrm{B}$, where $W^T$ is the vector of weights and $B$ is the ordered argument vector.

The idea of the IOWA operator is to aggregate tuples in the form of $\left({\mathrm{v}}_{\mathrm{i}},{\mathrm{a}}_{\mathrm{i}}\right)$. In this pair, $v_i$ is called an order-inducing value and $a_i$ is called an argument value. Note that here we are talking about the original values of the attribute $a_i$. Then, the IOWA execution procedure can be formally represented as

$${\mathrm{F}}_{\mathrm{W}}\left(<{\mathrm{v}}_1,{\mathrm{a}}_1>,\dots ,<{\mathrm{v}}_{\mathrm{n}},{\mathrm{a}}_{\mathrm{n}}>\right)={\mathrm{W}}^{\mathrm{T}}{\mathrm{B}}_{\mathrm{v}}.$$

(2)

In this expression, $W$ is a vector of weights $w_j$ such as ${\mathrm{w}}_{\mathrm{j}}\in \left[0,1\right]$ and ${\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{j}}}=1$. The elements of the vector $B_v$ are the initial values of the argument, ordered by the order-inducing value. Then expression (2) can be represented in the following expanded form

$${\mathrm{F}}_{\mathrm{W}}=\left(<{\mathrm{v}}_1,{\mathrm{a}}_1>,<{\mathrm{v}}_2,{\mathrm{a}}_2>,\dots ,<{\mathrm{v}}_{\mathrm{n}},{\mathrm{a}}_{\mathrm{n}}>\right)={\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{j}}}{\mathrm{a}}_{\mathrm{v}\text{-}index\left(\mathrm{j}\right)}.$$

(3)

Essentially, an IOWA operator is an OWA operator in which the reordering of the original values are explicitly done with the help of order inducing values.

In (Yager 2004), R. Yager introduced the generalized OWA operator GOWA.

Definition 2 

(Yager 2004). The mapping $\mathrm{M}:{\mathrm{R}}^{\mathrm{n}}\to \mathrm{R}$ is called generalized ordered weighted aggregation (GOWA) operator of a dimension if

$$\mathrm{M}\left({\mathrm{a}}_1,{\mathrm{a}}_2,\dots ,{\mathrm{a}}_{\mathrm{n}}\right)={\left({\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{j}}{\mathrm{b}}_{\mathrm{j}}^{\mathsf{\lambda }}}\right)}^{\frac{1}{\mathsf{\lambda }}},$$

(4)

where

• $w_j$ are the weights that satisfy the conditions ${\mathrm{w}}_{\mathrm{j}}\in \left[0,1\right]$, ${\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{j}}}=1$;
• $\lambda$ is a parameter such as $\mathsf{\lambda }\in \left[-\infty ,+\infty \right]$;
• $b_j$ is the $j\text{-}th$ largest of the $a_i$.

Operators OWA, IOWA, and GOWA were proposed to aggregate criteria estimates in MCDM. In decision-making problems at risk, not only criteria-based estimates of the outcomes of alternative decisions are used, but also the probabilities of these outcomes. To aggregate such mixed information, various variants of aggregation operators have been proposed. In this paper, we present one of the well-known operators of this kind (Yager 2004).

Let us have a weight vector $W$ with ${\mathrm{w}}_{\mathrm{j}}\in \left[0,1\right]$, ${\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{j}}}=1$, and a probability vector $P$ with ${\mathrm{p}}_{\mathrm{i}}\in \left[0,1\right]$. Then,

$$\mathrm{P}\mathrm{O}\mathrm{W}\mathrm{A}\left({\mathrm{a}}_1,{\mathrm{a}}_2,\dots ,{\mathrm{a}}_{\mathrm{n}}\right)=\mathsf{\gamma }{\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{j}}}{\mathrm{b}}_{\mathrm{j}}+\left(1-\mathsf{\gamma }\right){\mathrm{p}}_{\mathrm{i}}{\mathrm{a}}_{\mathrm{i}},$$

(5)

where $b_j$—$j\text{-}th$ largest of the argument $a_i$ and $\gamma \in \left[0,1\right]$.

In addition to arithmetic averaging operators, a geometric averaging operator is used:

$$\mathrm{OWG}\left({\mathrm{a}}_1,{\mathrm{a}}_2,\dots ,{\mathrm{a}}_{\mathrm{n}}\right)={\left({\displaystyle \prod _{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{a}}_{\mathrm{j}}}\right)}^{{\mathrm{w}}_{\mathrm{j}}},$$

(6)

where $w_j$ is the argument weight $a_j$, $w_j\in \left[0,1\right]$.

In the following sections, we present the basic theory of IFSs and IFVs and introduce extensions of the OWA and OWG operators to an intuitionistic fuzzy environment.

5. Brief Introduction to the Theory of IFSs and IFVS

In 1965, L. Zadeh (Zadeh 1965) introduced the concept of fuzzy sets. A fuzzy set is a set that does not have clear boundaries. The degree of membership of each of the elements in this set is a variable in the interval $\left[0,1\right]$.

Formally, a fuzzy set $A$ can be represented as a set of pairs

$$\mathrm{A}=\left\{<\mathrm{x},{\mathsf{\mu }}_{\mathrm{A}}\left(\mathrm{x}\right)>\right\},$$

(7)

where ${\mathsf{\mu }}_{\mathrm{A}}\left(\mathrm{x}\right)$ is the value of the membership function of an element $x$ to a fuzzy set $A$.

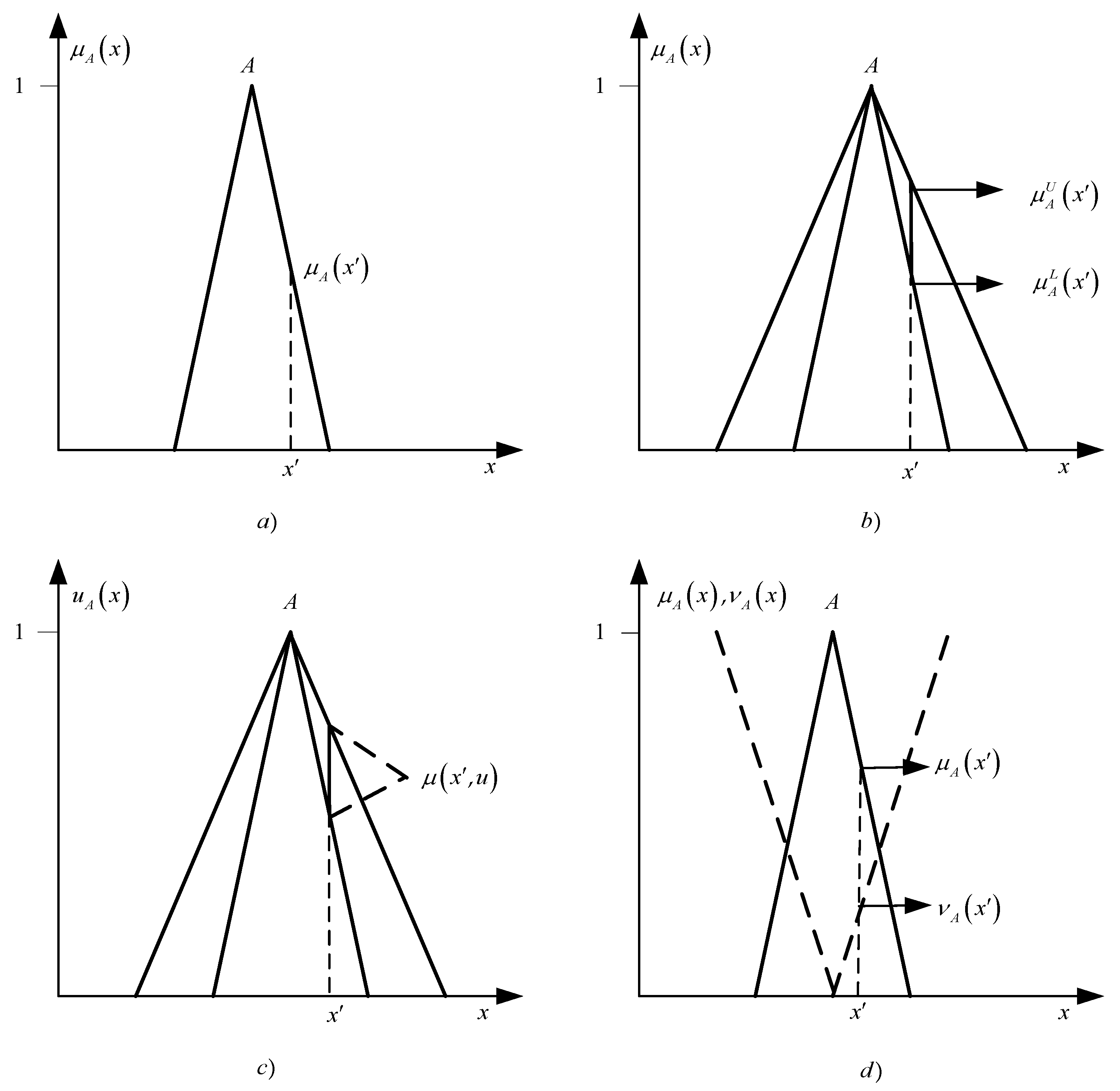
The graph of the membership function of a conditional fuzzy set $A$ is shown in Figure 2a.

As follows from expression (7) and Figure 2a, in the original theory of fuzzy sets, uncertainties are associated only with the membership of some entities to the corresponding fuzzy set (or to the corresponding fuzzy sets). The uncertainties of interest to us are uniquely modeled and evaluated using the corresponding values of the membership function.

The first extension of the original fuzzy sets was interval-valued fuzzy sets. The idea of fuzzy sets of this type was first proposed in (Sambuc 1975). The graph of the membership function of the conditional interval-valued fuzzy set $A$ is shown in Figure 2b. As can be seen from this figure, for a given value ${\mathrm{x}}^{\prime }\in \mathrm{A}$, the value of its membership function can be located in the interval $\left[{\mathsf{\mu }}_{\mathrm{A}}^{\mathrm{L}}\left({\mathrm{x}}^{\prime }\right),{\mathsf{\mu }}_{\mathrm{A}}^{\mathrm{U}}\left({\mathrm{x}}^{\prime }\right)\right]$. The main purpose of using fuzzy sets of this kind is to model uncertainties about the boundaries of the bases of the relevant fuzzy sets.

A further extension of interval-valued fuzzy sets is type-2 fuzzy sets (Mendel 2003, 2007). The graph of the membership function of the conditional type-2 fuzzy set $A$ is shown in Figure 2c. As can be seen from this figure, for each value ${\mathrm{x}}^{\prime }\in \mathrm{A}$, not only the interval of possible values of the primary membership function $u_A\left(x^{\prime }\right)$ is specified, but also the secondary membership function $\mathsf{\mu }\left({\mathrm{x}}^{\prime },\mathrm{u}\right)$ on this interval.

A specific extension of the original fuzzy sets is intuitionistic fuzzy sets (IFSs) (Atanassov 1986, 1999). A characteristic feature of any IFS is that for each value $\mathrm{x}\in \mathrm{A}$, the values of two functions are set:

-

the value of the membership function ${\mathsf{\mu }}_{\mathrm{A}}\left(\mathrm{x}\right)$;

-

the value of the non-membership function ${\mathsf{\nu }}_{\mathrm{A}}\left(\mathrm{x}\right)$.

Graphs of the membership and non-membership functions of the conditional IFS $A$ are shown in Figure 2d.

In general, IFS $A$ can be represented in the following form:

$$\mathrm{A}=\left\{\mathrm{x},{\mathsf{\mu }}_{\mathrm{A}}\left(\mathrm{x}\right),{\mathsf{\nu }}_{\mathrm{A}}\left(\mathrm{x}\right)\right\}, \forall \mathrm{x},{\mathsf{\mu }}_{\mathrm{A}}\left(\mathrm{x}\right)+{\mathsf{\nu }}_{\mathrm{A}}\left(\mathrm{x}\right)\le 1.$$

(8)

The difference ${\mathsf{\pi }}_{\mathrm{A}}\left(\mathrm{x}\right)=1-{\mathsf{\mu }}_{\mathrm{A}}\left(\mathrm{x}\right)-{\mathsf{\nu }}_{\mathrm{A}}\left(\mathrm{x}\right)$ represents the uncertainty about whether or not an element $x$ belongs to an IFS $A$. This value in the literature is usually called hesitation degree or intuitionistic fuzzy index.

Let there be two IFSs, $A$ and $B$. For these IFSs, the following relations can exist:

-

equality:

$$\mathrm{A}=\mathrm{B} \mathrm{if} \left(\forall \mathrm{x}\in \mathrm{E}\right)\left({\mathsf{\mu }}_{\mathrm{A}}\left(\mathrm{x}\right)={\mathsf{\mu }}_{\mathrm{B}}\left(\mathrm{x}\right)\&{\mathsf{\nu }}_{\mathrm{A}}\left(\mathrm{x}\right)={\mathsf{\nu }}_{\mathrm{B}}\left(\mathrm{x}\right)\right)$$

(9)

-

inequality:

$$\mathrm{A}\ne \mathrm{B} \mathrm{if} \left(\exists \mathrm{x}\in \mathrm{E}\right)\left({\mathsf{\mu }}_{\mathrm{A}}\left(\mathrm{x}\right)\ne {\mathsf{\mu }}_{\mathrm{B}}\left(\mathrm{x}\right)\right)$$

(10)

The main operations of IFSs are

-

union:

$$\mathrm{A}\cup \mathrm{B}=\left\{<\mathrm{x},\mathrm{m}\mathrm{a}\mathrm{x}\left({\mathsf{\mu }}_{\mathrm{A}}\left(\mathrm{x}\right),{\mathsf{\mu }}_{\mathrm{B}}\left(\mathrm{x}\right)\right),\mathrm{m}\mathrm{i}\mathrm{n}\left({\mathsf{\nu }}_{\mathrm{A}}\left(\mathrm{x}\right),{\mathsf{\nu }}_{\mathrm{B}}\left(\mathrm{x}\right)\right)>/\mathrm{x}\in \mathrm{E}\right\}$$

(11)

-

intersection:

$$\mathrm{A}\cap \mathrm{B}=\left\{<\mathrm{x},\mathrm{m}\mathrm{i}\mathrm{n}\left({\mathsf{\mu }}_{\mathrm{A}}\left(\mathrm{x}\right),{\mathsf{\mu }}_{\mathrm{B}}\left(\mathrm{x}\right)\right),\mathrm{m}\mathrm{a}\mathrm{x}\left({\mathsf{\nu }}_{\mathrm{A}}\left(\mathrm{x}\right),{\mathsf{\nu }}_{\mathrm{B}}\left(\mathrm{x}\right)\right)>/\mathrm{x}\in \mathrm{E}\right\}$$

(12)

Let us introduce one important concept, which is widely used in the present and subsequent sections of this paper. Let us have IFS $\mathrm{A}=\left\{<{\mathrm{a}}_{\mathrm{j}},{\mathsf{\mu }}_{\mathrm{A}}\left({\mathrm{a}}_{\mathrm{j}}\right),{\mathsf{\nu }}_{\mathrm{A}}\left({\mathrm{a}}_{\mathrm{j}}\right)>\right\}$ and assume that the membership function ${\mathsf{\mu }}_{\mathrm{A}}\left(\mathrm{a}\right)$ and the non-membership function ${\mathsf{\nu }}_{\mathrm{A}}\left(\mathrm{a}\right)$ are given in one way or another for all $\mathrm{a}\in \mathrm{A}$. Let us fix some value ${\mathrm{a}}_{\mathrm{j}}\in \mathrm{A}$. This value corresponds to the values of the functions ${\mathsf{\mu }}_{\mathrm{A}}\left({\mathrm{a}}_{\mathrm{j}}\right)$, ${\mathsf{\nu }}_{\mathrm{A}}\left({\mathrm{a}}_{\mathrm{j}}\right)$. Then, intuitionistic fuzzy value (IFV) $a_j$ is defined as ${\mathrm{a}}_{\mathrm{j}}=<{\mathsf{\mu }}_{\mathrm{A}}\left({\mathrm{a}}_{\mathrm{j}}\right),{\mathsf{\nu }}_{\mathrm{A}}\left({\mathrm{a}}_{\mathrm{j}}\right)>$, or for short, ${\mathrm{a}}_{\mathrm{j}}=<{\mathsf{\mu }}_{\mathrm{j}},{\mathsf{\nu }}_{\mathrm{j}}>$. We call the numerical value $a_j$ the basis of IFV $a_j$. Alternatively, we use the following notation for IFV: ${\mathrm{a}}_{\mathrm{j}}=\left({\mathsf{\mu }}_{\mathrm{j}},{\mathsf{\nu }}_{\mathrm{j}}\right)$.

Let us make the following remark. In the above definition, the equality “=” should not be understood in its direct sense. The left part of the IFV $a_j$ notation is the basis (numerical value) of this IFV, and the right part is a pair of values ${\mathsf{\mu }}_{\mathrm{j}}$, ${\mathsf{\nu }}_{\mathrm{j}}$ characterizing the basis $a_j$.

Using the concept of IFVs, it can be stated that an IFS $A$ is a set of IFVs forming it.

In the present paper, IFVs were constructed and interpreted in a different way. First, assume that there is no IFS $A$ in which IFVs $a_j$ are included, so there are no reference values of the membership function ${\mathsf{\mu }}_{\mathrm{j}}$ and non-membership function ${\mathsf{\nu }}_{\mathrm{j}}$.

Further, suppose that the expert needs to subjectively evaluate the value of some relevant parameter $a$. Using their knowledge and experience, the expert estimates the required value as $a_j$. However, the expert is not sure about the reliability of this assessment. Then, it can assign a pair of values $<{\mathsf{\mu }}_{\mathrm{j}},{\mathsf{\nu }}_{\mathrm{j}}>$. The value ${\mathsf{\mu }}_{\mathrm{j}}$ reflects how confident it is that the evaluated value $a_j$ is the true required value of the parameter $a$. On the other hand, the value ${\mathsf{\nu }}_{\mathrm{j}}$ reflects how confident it is that the evaluated value $a_j$ is not the true required value of the parameter $a$. All IFVs used further in this paper are interpreted in this way.

Let us define operations on IFVs based on the data presented in paper (Xu 2007). Let $\mathrm{a}=<{\mathsf{\mu }}_{\mathrm{a}},{\mathsf{\nu }}_{\mathrm{a}}>$, $\mathrm{b}=<{\mathsf{\mu }}_{\mathrm{b}},{\mathsf{\nu }}_{\mathrm{b}}>$ be two IFVs. Then,

$$\mathrm{a}\oplus \mathrm{b}=<{\mathsf{\mu }}_{\mathrm{a}}+{\mathsf{\mu }}_{\mathrm{b}}-{\mathsf{\mu }}_{\mathrm{a}}\ast {\mathsf{\mu }}_{\mathrm{b}},{\mathsf{\nu }}_{\mathrm{A}}\ast {\mathsf{\nu }}_{\mathrm{b}}>.$$

(13)

$$\mathrm{a}\otimes \mathrm{b}=<{\mathsf{\mu }}_{\mathrm{a}}\ast {\mathsf{\mu }}_{\mathrm{b}},{\mathsf{\nu }}_{\mathrm{A}}+{\mathsf{\nu }}_{\mathrm{b}}-{\mathsf{\nu }}_{\mathrm{a}}\ast {\mathsf{\nu }}_{\mathrm{b}}^{}>.$$

(14)

$$\mathsf{\lambda }\ast \mathrm{a}=1-{\left(1-{\mathsf{\mu }}_{\mathrm{a}}\right)}^{\mathsf{\lambda }},{\mathsf{\nu }}^{\mathsf{\lambda }},\mathsf{\lambda }>0.$$

(15)

$${\mathrm{a}}^{\mathsf{\lambda }}=<{\left({\mathsf{\mu }}_{\mathrm{a}}\right)}^{\mathsf{\lambda }},{\left(1-\left(1-{\mathsf{\nu }}_{\mathrm{a}}\right)\right)}^{\mathsf{\lambda }}>.$$

(16)

Operations (13)–(16) have the following properties (Xu 2007; Xu and Yager 2006):

$$\begin{array}{l}\mathrm{a}\oplus \mathrm{b}=\mathrm{b}\oplus \mathrm{a}.\\ \mathrm{a}\otimes \mathrm{b}=\mathrm{b}\otimes \mathrm{a}.\\ \mathsf{\lambda }\left(\mathrm{a}\otimes \mathrm{b}\right)=\mathsf{\lambda }\mathrm{a}\otimes \mathsf{\lambda }\mathrm{b}.\\ {\left(\mathrm{a}\otimes \mathrm{b}\right)}^{\mathsf{\lambda }}={\mathrm{a}}^{\mathsf{\lambda }}\otimes {\mathrm{b}}^{\mathsf{\lambda }}.\\ {\mathsf{\lambda }}_1\mathrm{a}\oplus {\mathsf{\lambda }}_2\mathrm{a}=\left({\mathsf{\lambda }}_1+{\mathsf{\lambda }}_2\right)\mathrm{a},{\mathsf{\lambda }}_1,{\mathsf{\lambda }}_2^{}>0.\\ {\mathrm{a}}^{{\mathsf{\lambda }}_1}\otimes {\mathrm{a}}^{{\mathsf{\lambda }}_2}={\mathrm{a}}^{\left({\mathsf{\lambda }}_1+{\mathsf{\lambda }}_2\right)},{\mathsf{\lambda }}_1,{\mathsf{\lambda }}_2>0.\end{array}$$

To compare and derive the order relation between a pair of IFVs $a$ and $b$, the label function $S\left(a\right)$ was introduced in (Chen and Tan 1994) and the accuracy function $H\left(a\right)$ was introduced in (Hong and Choi 2000):

$$\mathrm{S}\left(\mathrm{a}\right)={\mathsf{\mu }}_{\mathrm{a}}-{\mathsf{\nu }}_{\mathrm{a}}.$$

(17)

$$\mathrm{H}\left(\mathrm{a}\right)={\mathsf{\mu }}_{\mathrm{a}}+{\mathsf{\nu }}_{\mathrm{a}}.$$

(18)

Let $a$ and $b$ be two IFV. Then, from (Hong and Choi 2000):

• If $\mathrm{S}\left(\mathrm{a}\right)>\mathrm{S}\left(\mathrm{b}\right)$, then $\mathrm{a}>\mathrm{b}$.
• If $\mathrm{S}\left(\mathrm{a}\right)=\mathrm{S}\left(\mathrm{b}\right)$, then
• (a) If $\mathrm{H}\left(\mathrm{a}\right)=\mathrm{H}\left(\mathrm{b}\right)$ then $\mathrm{a}=\mathrm{b}$.
• (b) If $\mathrm{H}\left(\mathrm{a}\right)>\mathrm{H}\left(\mathrm{b}\right)$, then $\mathrm{a}>\mathrm{b}$.

Although it is common practice to compare IFVs on the basis of label function $S\left(a\right)$ values and accuracy function $H\left(a\right)$ values, this approach has significant drawbacks that have been repeatedly mentioned in the literature. Therefore, in this paper, in order to compare and rank IFVs, we used the intuitionistic fuzzy distance measure proposed in (Xu 2010):

$$\mathrm{d}\left({\mathrm{a}}_1,{\mathrm{a}}_2\right)=\left|{\mathrm{a}}_1-{\mathrm{a}}_2\right|=\frac{1}{2}\left(\left|{\mathsf{\mu }}_1-{\mathsf{\mu }}_2\right|,\left|{\mathsf{\nu }}_1-{\mathsf{\nu }}_2\right|\right).$$

(19)

6. Data Aggregation in an Intuitionistic Fuzzy Environment

Many methods have been proposed for aggregating data in an intuitionistic fuzzy environment. A detailed overview of these methods is presented in Section 1 (Xu and Cai 2012). In this section, we introduce and extend two methods that are used for risk analysis in an intuitionistic fuzzy environment.

Definition 3 

(Xu 2007). Let ${\mathrm{a}}_{\mathrm{j}}=<{\mathsf{\mu }}_{\mathrm{j}},{\mathsf{\nu }}_{\mathrm{j}}>=\left({\mathsf{\mu }}_{\mathrm{j}},{\mathsf{\nu }}_{\mathrm{j}}\right)$, $\mathrm{j}=1,\dots ,\mathrm{n}$ be a set of IFVs. The function IFWA is called an intuitionistic fuzzy weighted averaging (IFWA) operator. The aggregated value of a set of initial IFVs based on the IFWA operator is also an IFV, which is defined as

$$\mathrm{IFWA}\left({\mathrm{a}}_1,{\mathrm{a}}_2,\dots ,{\mathrm{a}}_{\mathrm{n}}\right)={\mathrm{w}}_1{\mathrm{a}}_1\oplus {\mathrm{w}}_2{\mathrm{a}}_2\oplus \dots \oplus {\mathrm{w}}_{\mathrm{n}}{\mathrm{a}}_{\mathrm{n}}=\left(1-{\displaystyle \prod _{\mathrm{j}=1}^{\mathrm{n}}{\left(1-{\mathsf{\mu }}_{\mathrm{j}}\right)}^{{\mathrm{w}}_{\mathrm{j}}},{\displaystyle \prod _{\mathrm{j}=1}^{\mathrm{n}}{\left({\mathsf{\nu }}_{\mathrm{j}}\right)}^{{\mathrm{w}}_{\mathrm{j}}}}}\right),$$

(20)

where $\mathrm{W}={\left({\mathrm{w}}_1,{\mathrm{w}}_2,\dots ,{\mathrm{w}}_{\mathrm{n}}\right)}^{\mathrm{T}}$ is a vector of weights with ${\mathrm{w}}_{\mathrm{j}}\in \left[0,1\right]$ and ${\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{j}}}=1$.

Definition 4 

(Xu and Yager 2006). The function IFWG is called an intuitionistic fuzzy weighted geometric (IFWG) operator. The aggregated value of a set of initial IFVs based on the IFWG operator is also an IFV, which is defined as

$$\mathrm{IFWG}\left({\mathrm{a}}_1,{\mathrm{a}}_2,\dots ,{\mathrm{a}}_{\mathrm{n}}\right)={\left({\mathrm{a}}_1\right)}^{{\mathrm{w}}_1}\otimes {\left({\mathrm{a}}_2\right)}^{{\mathrm{w}}_2}\otimes \dots \otimes {\left({\mathrm{a}}_{\mathrm{n}}\right)}^{{\mathrm{w}}_{\mathrm{n}}}=\left({\displaystyle \prod _{\mathrm{j}=1}^{\mathrm{n}}{\left({\mathsf{\mu }}_{\mathrm{j}}\right)}^{{\mathrm{w}}_{\mathrm{j}}},1-{\displaystyle \prod _{\mathrm{j}=1}^{\mathrm{n}}{\left(1-{\mathsf{\nu }}_{\mathrm{j}}\right)}^{{\mathrm{w}}_{\mathrm{j}}}}}\right),$$

(21)

where $\mathrm{W}={\left({\mathrm{w}}_1,{\mathrm{w}}_2,\dots ,{\mathrm{w}}_{\mathrm{n}}\right)}^{\mathrm{T}}$ is the exponential weighting vector with ${\mathrm{w}}_{\mathrm{j}}\in \left[0,1\right]$ and ${\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{j}}}=1$.

The structure of expressions (20) and (21) explicitly indicate that no preliminary reordering of the argument values (based of the initial IFVs) is required here.

The aggregation operators of expressions (20) and (21) assume that the values of the weights $w_j$, $\mathrm{j}=1,\dots ,\mathrm{n}$, are real numbers in the interval $\left[0,1\right]$. However, in many real situations, assigning deterministic values of weights is a difficult process. Then, alternatively, weight values can be assigned in the form of IFVs.

We present a technique for determining intuitionistic fuzzy values of weights that is based on the data presented in (Xu and Yager 2006). The idea of constructing such weights is based on an alternative representation of IFVs in the form of an interval (difference) formed by the membership and non-membership values: ${\mathrm{a}}_{\mathrm{j}}=\left({\mathsf{\mu }}_{\mathrm{j}}-{\mathsf{\nu }}_{\mathrm{j}}\right)$.

To demonstrate this approach, we considered assigning weights in the form of IFVs to a group of experts participating in a conditional risk analysis problem. It is obvious that individual experts have different knowledge and experience in the relevant field. Therefore, it is necessary to assess the degree of confidence in their assessments in some way. Such assessment is routinely carried out in the processes of group analysis and decision-making, using, for example, the Saaty scale (Saaty 1980) or other suitable scales.

Each of the experts is offered subjective weights in the form of IFVs to all experts, including the evaluating expert themselves. (We assume that each expert can, with a sufficient degree of objectivity, evaluate their own knowledge and experience in comparison with the knowledge and experience of other experts.)

Note that when performing such assessments in the Saaty scale, the value “1” is used as the self-assessment of each of the experts, which practically excludes subjective self-assessments of experts from the overall assessment process. However, when assessment is based on IFVs, it is not possible to exclude such self-assessments by experts. To resolve this issue, further research is required.

Taking as a basis the data presented in (Wang et al. 2016), we used the following notation. The interval that characterizes the expert’s uncertainty about the actual value of the weight $w_j$ we denote as ${\mathrm{w}}_{\mathrm{j}}=\left[{\mathrm{w}}_{\mathrm{j}}^{\mathrm{L}},{\mathrm{w}}_{\mathrm{j}}^{\mathrm{U}}\right]=\left[{\mathsf{\mu }}_{\mathrm{j}},{\mathsf{\nu }}_{\mathrm{j}}\right]=\left[{\mathsf{\eta }}_{\mathrm{j}},1-{\mathsf{\rho }}_{\mathrm{j}}\right]$.

In practice, an expert is required to assign three values: the basis $w_j$ of the corresponding IFV; ${\mathsf{\eta }}_{\mathrm{j}}$, which reflects the degree of his confidence that the value $w_j$ they assigned is the true value of this weight; and ${\mathsf{\rho }}_{\mathrm{j}}$, which reflects the degree of their confidence that the value $w_j$ they assigned is not the true value of this weight. However, the specificity of further calculations is that they use not estimated values ${\mathsf{\rho }}_{\mathrm{j}}$, but values $1-{\mathsf{\rho }}_{\mathrm{j}}$.

For deterministic values of the weight vector $W$, the normalization requirement is obligatory: ${\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{j}}}=1$. In the case of specifying weights in the form of IFVs, the normalization condition is formulated as follows (Wang and Elhag 2006). Let the vector of interval values of weights $\mathrm{W}={\left({\mathrm{w}}_1,{\mathrm{w}}_2,\dots ,{\mathrm{w}}_{\mathrm{n}}\right)}^{\mathrm{T}}$ with ${\mathrm{w}}_{\mathrm{j}}=\left[{\mathrm{w}}_{\mathrm{j}}^{\mathrm{L}},{\mathrm{w}}_{\mathrm{j}}^{\mathrm{U}}\right]$ and $0\le {\mathrm{w}}_{\mathrm{j}}^{\mathrm{L}}\le {\mathrm{w}}_{\mathrm{j}}^{\mathrm{U}}\le 1$, $\mathrm{j}=1,\dots ,\mathrm{q}$ be given. Then, if the conditions are met,

$${\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{q}}{\mathrm{w}}_{\mathrm{j}}^{\mathrm{U}}}-\left({\mathrm{w}}_{\mathrm{k}}^{\mathrm{U}}-{\mathrm{w}}_{\mathrm{k}}^{\mathrm{L}}\right)\ge 1, \forall \mathrm{k}\in \left\{1,\dots ,\mathrm{q}\right\}.$$

(22)

$${\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{q}}{\mathrm{w}}_{\mathrm{j}}^{\mathrm{L}}}+\left({\mathrm{w}}_{\mathrm{k}}^{\mathrm{U}}-{\mathrm{w}}_{\mathrm{k}}^{\mathrm{L}}\right)\le 1, \forall \mathrm{k}\in \left\{1,\dots ,\mathrm{q}\right\}.$$

(23)

Then, the weight vector $W$ is normalized; otherwise, the weight vector $W$ is not normalized.

Using the notation introduced earlier, the normalization conditions (22) and (23) can be expressed in the form of

$${\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{q}}\left(1-{\mathsf{\rho }}_{\mathrm{j}}\right)}-{\mathsf{\pi }}_{\mathrm{k}}\ge 1, \forall \mathrm{k}\in \left\{1,\dots ,\mathrm{q}\right\}.$$

(24)

$${\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{q}}{\mathsf{\eta }}_{\mathrm{j}}}+{\mathsf{\pi }}_{\mathrm{k}}\le 1, \forall \mathrm{k}\in \left\{1,\dots ,\mathrm{q}\right\}.$$

(25)

The values ${\mathsf{\pi }}_{\mathrm{k}}$ in expressions (24) and (25) are defined as ${\mathsf{\pi }}_{\mathrm{k}}=1-{\mathsf{\eta }}_{\mathrm{k}}-{\mathsf{\rho }}_{\mathrm{k}}$. The results of assessing the degrees of knowledge and experience of experts can be presented in the form of a table (see

Table 1. The results of evaluation the degrees of knowledge and experience of experts.

$E_i\backslash E_j$	$E_1$	.....	$E_1$	.....	$E_1$
$E_1$	$w_{11}=\left({\eta }_{11},1-{\rho }_{11}\right)$	.....	$w_{1j}=\left({\eta }_{1j},1-{\rho }_{1j}\right)$	.....	$w_{1q}=\left({\eta }_{1q},1-{\rho }_{1q}\right)$
.....	.....	.....	.....	.....	.....
$E_1$	$w_{i1}=\left({\eta }_{i1}^{},1-\rho \right)$	.....	$w_{ij}=\left({\eta }_{ij},1-{\rho }_{ij}\right)$	.....	$w_{iq}=\left({\eta }_{iq},1-{\rho }_{iq}\right)$
.....	.....	.....	.....	.....	.....
$E_1$	$w_{q1}=\left({\eta }_{q1},1-{\rho }_{q1}\right)$	.....	$w_{qj}=\left({\eta }_{qj},1-{\rho }_{qj}\right)$	.....	$w_{qq}=\left({\eta }_{qq},1-{\rho }_{qq}\right)$

).

In this table ${\mathrm{w}}_{\mathrm{i}\mathrm{j}}=\left({\mathsf{\eta }}_{\mathrm{i}\mathrm{j}},1-{\mathsf{\rho }}_{\mathrm{i}\mathrm{j}}\right)$—IFV displays the intuitionistic fuzzy assessment of the knowledge and experience of the $i\text{-}th$ expert by the $j\text{-}th$ expert, $\mathrm{i},\mathrm{j}=1,\dots ,\mathrm{q}$.

To obtain the resulting intuitionistic fuzzy values of weights $w_j$ $\mathrm{j}=1,\dots ,\mathrm{q}$, it is necessary to aggregate the values of IFVs in each column of Table 1. In this case, expressions (20) and (21) take the form:

$${\mathrm{w}}_{\mathrm{j}}=\mathrm{I}\mathrm{F}\mathrm{W}\mathrm{A}\left({\mathrm{w}}_{\mathrm{i}\mathrm{j}}\right)={\mathrm{w}}_1^{*}{\mathrm{w}}_{11}\oplus {\mathrm{w}}_2^{*}{\mathrm{w}}_{21}\oplus \dots \oplus {\mathrm{w}}_{\mathrm{q}}^{*}{\mathrm{w}}_{\mathrm{q}1}=\left(1-{\displaystyle \prod _{\mathrm{i}=1}^{\mathrm{q}}{\left(1-{\mathsf{\eta }}_{\mathrm{i}\mathrm{j}}\right)}^{{\mathrm{w}}_{\mathrm{i}}^{*}},{\displaystyle \prod _{\mathrm{i}=1}^{\mathrm{q}}{\left(1-{\mathsf{\rho }}_{\mathrm{i}\mathrm{j}}\right)}^{{\mathrm{w}}_{\mathrm{i}}^{*}}}}\right), \mathrm{i},\mathrm{j}=1,\dots ,\mathrm{q},$$

(26)

$${\mathrm{w}}_{\mathrm{i}}=\mathrm{I}\mathrm{F}\mathrm{W}\mathrm{G}\left({\mathrm{w}}_{\mathrm{i}\mathrm{j}}\right)={\left({\mathrm{w}}_{1\mathrm{j}}\right)}^{{\mathrm{w}}_1^{*}}\otimes {\left({\mathrm{w}}_{2\mathrm{j}}\right)}^{{\mathrm{w}}_2^{*}}\otimes \dots \otimes {\left({\mathrm{w}}_{\mathrm{q}\mathrm{j}}\right)}^{{\mathrm{w}}_{\mathrm{q}}^{*}}=\left({\displaystyle \prod _{\mathrm{i}=1}^{\mathrm{q}}{\left({\mathsf{\eta }}_{\mathrm{i}\mathrm{j}}\right)}^{{\mathrm{w}}_{\mathrm{i}}^{*}},{\displaystyle \coprod _{\mathrm{i}=1}^{\mathrm{q}}{\left({\mathsf{\rho }}_{\mathrm{i}\mathrm{j}}\right)}^{{\mathrm{w}}_{\mathrm{i}}^{*}}}}\right), \mathrm{i},\mathrm{j}=1,\dots ,\mathrm{q}.$$

(27)

In expressions (26) and (27) ${\mathrm{w}}_{\mathrm{i}}^{*}$ is the weight of the $i\text{-}th$ expert participating in the evaluation of other experts. If there is no reason to assume otherwise, we take the values ${\mathrm{w}}_{\mathrm{i}}^{*}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{q}$}\right.$, $\mathrm{i}=1,\dots ,\mathrm{q}$.

Let us consider an illustrative example. The group consists of three experts. It is necessary to determine the intuitionistic fuzzy weights of experts on the basis of the methodology presented above.

The initial assessments of experts are presented in

Table 2. Initial intuitionistic fuzzy values of expert weights.

$E_i\backslash E_j$	$E_1$				$E_2$				$E_3$
	$w_{i1}$	${\eta }_{i1}$	${\rho }_{i1}$	$1-{\rho }_{i1}$	$w_{i2}$	${\eta }_{i2}$	${\rho }_{i2}$	$1-{\rho }_{i2}$	$w_{i3}$	${\eta }_{i3}$	${\rho }_{i3}$	$1-{\rho }_{i3}$
$E_1$	0.20	0.30	0.60	0.40	0.30	0.20	0.50	0.50	0.50	0.20	0.50	0.50
$E_2$	0.30	0.20	0.50	0.50	0.30	0.30	0.50	0.50	0.40	0.20	0.50	0.50
$E_3$	0.20	0.20	0.50	0.50	0.40	0.20	0.50	0.50	0.40	0.20	0.50	0.50

.

Essentially, our task was to aggregate the intuitionistic fuzzy values of the weights in the columns of Table 2. First, we made sure that the normalization condition of the IFV bases in the rows of Table 2 was satisfied. A simple check shows that the sum of the values in each of the rows was equal to 1, which implies that the value vectors of the bases of the relevant IFVs were normalized.

Next, we checked whether the normalization conditions (24), (25) were satisfied for the expert assignment vectors.

-

For expert 1:

$$\begin{array}{l}{\displaystyle \sum _{\mathrm{j}=1}^3\left(1-{\mathsf{\rho }}_{1\mathrm{j}}\right)=0.40+0.50+0.50=1.40}.\\ {\mathsf{\pi }}_{11}=0.10, {\mathsf{\pi }}_{12}=0.30, {\mathsf{\pi }}_{13}=0.30.\end{array}$$

Since all differences ${\displaystyle \sum _{\mathrm{j}=1}^3\left(1-{\mathsf{\rho }}_{1\mathrm{j}}\right)}-{\mathsf{\pi }}_{1\mathrm{j}}$ were greater than 1, the normalization condition (24) was satisfied.

$${\displaystyle \sum _{\mathrm{j}=1}^3{\mathsf{\eta }}_{1\mathrm{j}}}=0.30+0.20+0.20=0.70.$$

Since all sums ${\displaystyle \sum _{\mathrm{j}=1}^3{\mathsf{\eta }}_{1\mathrm{j}}}+{\mathsf{\pi }}_{1\mathrm{j}}$ were less than or equal to 1, the normalization condition (25) was satisfied.

A similar check of the assignment vectors of experts 2 and 3 indicated that these vectors were normalized.

Let us calculate the aggregated values of expert weights ${\mathrm{w}}_{\mathrm{i}},\mathrm{i}=1,2,3$, on the basis of the IFWA aggregation operator (26).

-

For expert 1:

$$\begin{array}{l}{\mathrm{w}}_1=\mathrm{I}\mathrm{F}\mathrm{W}\mathrm{A}\left({\mathrm{w}}_{11},{\mathrm{w}}_{21},{\mathrm{w}}_{31}\right)\\ =\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\ast 0.30+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\ast 0.20+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\ast 0.20\right)=\left(1-{\left(1-0.30\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\ast {\left(1-0.20\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\ast {\left(1-0.20\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.},0.40^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\ast 0.50^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\ast 0.50^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\right)\\ =(0.100+0.067+0.100)=\left(1-0.70^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\ast 0.80^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\ast 0.80^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.},0.40^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\ast 0.50^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\ast 0.50^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\right)\\ =0.234=\left(1-0.889\ast 0.929\ast 0.929,0.739\ast 0.794\ast 0.794\right)\\ =0.234=\left(1-0.767,0.466\right)=0.234=\left(0.283,0.466\right).\end{array}$$

For experts 2 and 3, calculations are performed by analogy. As a result, we have

$$\begin{gathered} {\mathrm{w}}_1=0.234=\left(0.283,0.466\right); \\ {\mathrm{w}}_2=0.333=\left(0.232,0.502\right); \\ {\mathrm{w}}_3=0.433=\left(0.198,0.502\right). \end{gathered}$$

Let us calculate the aggregated expert weights ${\mathrm{w}}_{\mathrm{i}},\mathrm{i}=1,2,3$, on the basis of the IFWG aggregation operator (27).

-

For expert 1:

$$\begin{array}{c}{\mathrm{w}}_1=\mathrm{I}\mathrm{F}\mathrm{W}\mathrm{G}\left({\mathrm{w}}_{11},{\mathrm{w}}_{21},{\mathrm{w}}_{31}\right)=\left(0.30^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\ast 0.20^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\ast 0.20^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\right)=\left(0.30^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\ast 0.20^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\ast 0.20^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.},0.60^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\ast 0,50^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\ast 0.50^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\right)=\\ =0.672\ast 0.588\ast 0.588=\left(0.672\ast 0.588\ast 0.588,0.845\ast 0.795\ast 0.795\right)=0.232=\left(0.232,0.524\right).\end{array}$$

For experts 2 and 3, calculations are performed by analogy. As a result, we have

$$\begin{gathered} {\mathrm{w}}_1=0.232=\left(0.232,0.524\right); \\ {\mathrm{w}}_2=0.333=\left(0.225,0.502\right); \\ {\mathrm{w}}_3=0.434=\left(0.203,0.502\right). \end{gathered}$$

It is easy to verify that the resulting weights are fairly close to each other when using both aggregation methods.

Let the vector of argument values $\mathrm{A}=\left({\mathrm{a}}_1,{\mathrm{a}}_2,\dots ,{\mathrm{a}}_{\mathrm{q}}\right)$ and the vector of intuitionistic fuzzy weights $\mathrm{W}={\left({\mathrm{w}}_1,{\mathrm{w}}_2,\dots ,{\mathrm{w}}_{\mathrm{q}}\right)}^{\mathrm{T}}$ be given. How can such information be aggregated? The answer to this question is given by the following definition.

Definition 5 

(Li and He 2013). Let ${\mathrm{a}}_{\mathrm{j}}=\left({\mathsf{\mu }}_{\mathrm{a}\mathrm{j}},{\mathsf{\nu }}_{\mathrm{a}\mathrm{j}}\right)$ be a collection of intuitionistic fuzzy values, and $\mathrm{W}={\left({\mathrm{w}}_1,{\mathrm{w}}_2,\dots ,{\mathrm{w}}_{\mathrm{q}}\right)}^{\mathrm{T}}$ be the intuitionistic fuzzy weights vector such that ${\mathrm{w}}_{\mathrm{j}}=\left({\mathsf{\eta }}_{\mathrm{j}},{\mathsf{\rho }}_{\mathrm{j}}\right)$ for $\mathrm{j}=1,\dots ,\mathrm{q}$. Then, the generalized intuitionistic fuzzy weighted averaging operator (G-IFWA) and the generalized intuitionistic fuzzy weighted geometric operator (G-IFWG) can be defined as follows:

$$\begin{array}{l}\mathrm{G}\text{-}\mathrm{IFWA}\left({\mathrm{a}}_1,{\mathrm{a}}_2,\dots ,{\mathrm{a}}_{\mathrm{q}}\right)={\oplus }_{\mathrm{j}=1}^{\mathrm{q}}{\mathrm{w}}_{\mathrm{j}}{\mathrm{a}}_{\mathrm{j}}={\mathrm{w}}_1{\mathrm{a}}_1\oplus {\mathrm{w}}_2{\mathrm{a}}_2\oplus \dots \oplus {\mathrm{w}}_{\mathrm{q}}{\mathrm{a}}_{\mathrm{q}}\\ =\left(1-{\displaystyle \prod _{\mathrm{j}=1}^{\mathrm{q}}{\left(1-{\mathsf{\mu }}_{{\mathrm{a}}_{\mathrm{j}}}\right)}^{{\mathsf{\eta }}_{\mathrm{j}}},{\displaystyle \coprod _{\mathrm{j}=1}^{\mathrm{q}}{\left({\mathrm{v}}_{{\mathrm{a}}_{\mathrm{j}}}\right)}^{1-{\mathsf{\rho }}_{\mathrm{j}}}}}\right).\end{array}$$

(28)

$$\begin{array}{l}\mathrm{G}\text{-}\mathrm{IFWG}\left({\mathrm{a}}_1,{\mathrm{a}}_2,\dots ,{\mathrm{a}}_{\mathrm{q}}\right)={\otimes }_{\mathrm{j}=1}^{\mathrm{q}}\left({\mathrm{a}}_{\mathrm{j}}^{{\mathrm{w}}_{\mathrm{j}}}\right)={\mathrm{a}}_1^{{\mathrm{w}}_1}\otimes {\mathrm{a}}_2^{{\mathrm{w}}_2}\otimes \dots \otimes {\mathrm{a}}_{\mathrm{q}}^{{\mathrm{w}}_{\mathrm{q}}}\\ =\left({\displaystyle \coprod _{\mathrm{j}=1}^{\mathrm{q}}{\left({\mathsf{\mu }}_{{\mathrm{a}}_{\mathrm{j}}}\right)}^{1-{\mathsf{\rho }}_{\mathrm{j}}},1-{\displaystyle \coprod _{\mathrm{j}=1}^{\mathrm{q}}{\left(1-{\mathsf{\nu }}_{{\mathrm{a}}_{\mathrm{j}}^{}}\right)}^{{\mathsf{\eta }}_{\mathrm{j}}}}}\right). \end{array}$$

(29)

7. Proposed Methodology for Risk Analysis in an Intuitionistic Fuzzy Environment

This section presents a sequence of computational procedures that must be performed to obtain results that are necessary and sufficient for risk analysis in an intuitionistic fuzzy environment. We do not present hazard identification and analysis procedures here, as these procedures are context dependent and are performed individually for each risk situation.

Let us assume that a hazard has been identified, risk factors $F_i$ have been identified, and sub-factors ${\mathrm{f}}_{\mathrm{i}\mathrm{j}},\mathrm{i},\mathrm{j}=1,2,\dots$ have been identified for each factor. Each of the subfactors $f_{ij}$ corresponds to an outcome $\left(ij\right)$. The overall risk situation can be represented in detail in the form of a tree graph like that shown in Figure 1.

Assume that the task of risk analysis is performed by a group of $q$ experts. Then, this task is reduced to the following sequence of procedures.

1. Determining the weights of experts. These weights can be subjectively evaluated both in deterministic form and in the form of IFVs. In the first case, each expert assigns weight estimates in the form of real numbers in the interval $\left[0,1\right]$. After the initial evaluation, the condition must be checked for each expert’s evaluation vector: the sum of all evaluations must be equal to 1. If this requirement is not met for some experts’ evaluation vectors, these experts are offered to correct their initial evaluations.

The aggregation of the resulting evaluations is performed on the basis of a suitable deterministic aggregation operator.

If the weight evaluations of experts are given in the form of IFVs, then for each vector of these evaluations, a check should be made on the compliance of these evaluations with the normalization requirements (24) and (25). In the case of non-compliance with these requirements, individual experts may be asked to adjust their initial evaluations.

The aggregation of the initial intuitionistic fuzzy weight evaluations can be performed on the basis of the G-IFWA operator (26) or on the basis of the G-IFWG operator (27).

2. Assignment of probabilities of subfactors (outcomes) in the form of IFVs. This assignment is made by each of the experts on the basis of their knowledge and experience.

3. Aggregation of the obtained intuitionistic fuzzy probabilistic evaluations. In the case of deterministic weight values, the aggregation of these values is based on the IFWA operator (20) or based on the IFWG operator (21). If expert weights are specified in the form of IFVs, then they are aggregated on the basis of the G-IFWA operator (28) or on the basis of the G-IFWG operator (29).

4. Assigning potential loss values for all outcomes. Assuming that all potential loss values are expressed in a single form, each expert evaluates these losses on the basis of their knowledge and experience. If evaluations of potential losses for different outcomes are expressed in different units of measurement, these evaluations should be transformed into a common dimensionless form. In any case, it is assumed that all potential loss evaluations are in the form of IFVs.

5. Aggregation of initial evaluations of potential losses for each of the outcomes. If expert weight values are expressed in a deterministic form, then aggregation is performed on the basis of the IFWA operator (20) or on the basis of the IFWG operator (21). If expert weights are specified in the form of IFVs, then they are aggregated on the basis of the G-IFWA operator (28) or on the basis of the G-IFWG operator (29).

6. Calculation of expected losses for each of the outcomes. To do this, the intuitionistic fuzzy evaluations of losses for each of the outcomes are multiplied by the intuitionistic fuzzy evaluations of the probabilities of these outcomes. Calculations are performed according to expression (14).

7. The assignment of outcome weights for each of the risk factors $F_i$, $\mathrm{i}=1,2\dots$ This procedure is performed by analogy with the procedure for assigning expert weights. The aggregation of the obtained evaluations is performed on the basis of the IFWA operator (20) or on the basis of the IFWG operator (21). If the initial weight evaluations are in the form of IFVs, then the aggregation is performed on the basis of the G-IFWA aggregation operator (26) or on the basis of the G-IFWG operator (27).

8. Aggregation of expected losses for each risk factor $F_i$. If the weight evaluations are given in the deterministic form, they are aggregated on the IFWA operator basis (20) or the IFWG operator basis (21). If the weight evaluations are in the form of IFVs, then they are aggregated on the basis of the G-IFWA operator (26) or on the basis of the G-IFWG operator (27).

9. Comparison of generalized intuitionistic fuzzy risk evaluations for each pair of factors is performed on the basis of the evaluation of the distance (19) between these factors. Using the results of paired comparisons, all risk factors can be ranked according to the degree of risk associated with them.

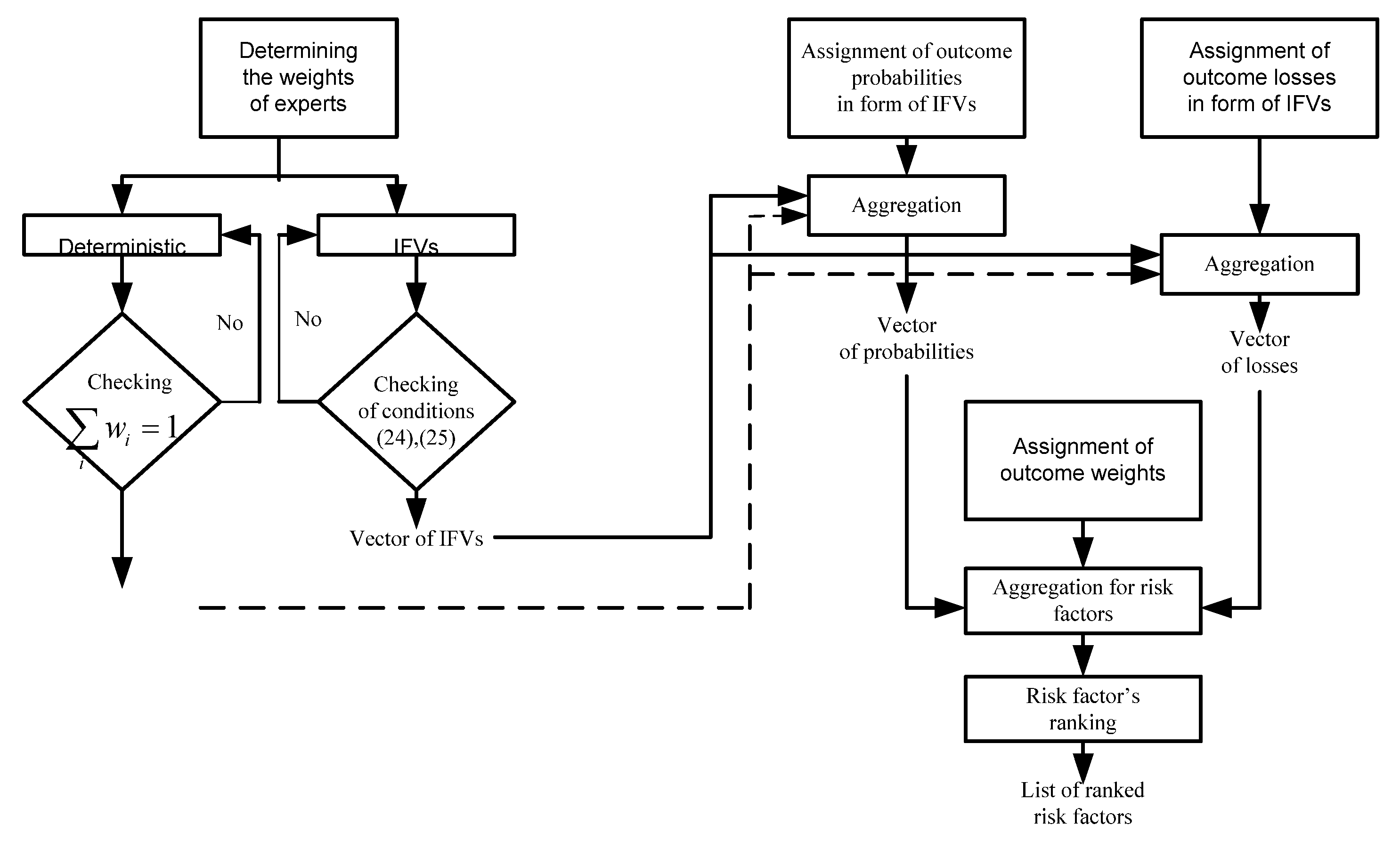
A flowchart of the proposed model is provided in Figure 3.

8. Illustrative Example

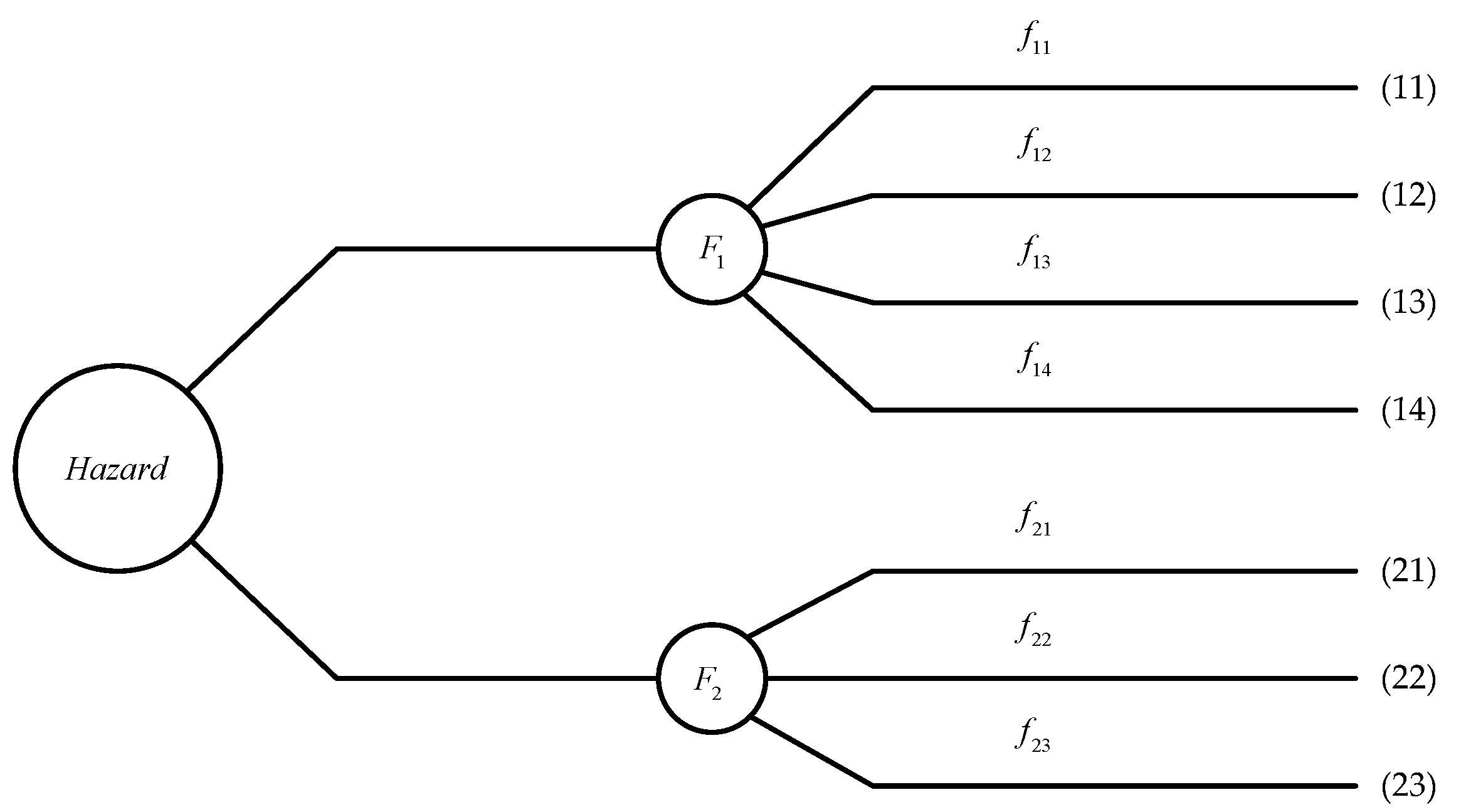
We here demonstrate the proposed risk analysis methodology in an intuitionistic fuzzy environment with the following simple example. Figure 4 schematically shows the structure of a risky situation. In this figure, “Hazard” represents an existing hazard. Factors ${\mathrm{F}}_1,{\mathrm{F}}_2$ reflect the possible manifestations of this danger. Subfactors ${\mathrm{f}}_{11}–{\mathrm{f}}_{12}$, ${\mathrm{f}}_{21}–{\mathrm{f}}_{23}$ characterize the possible manifestations of factors ${\mathrm{F}}_1,{\mathrm{F}}_2$. Each of the outcomes (11)–(14), (21)–(23) is associated with the corresponding subfactor.

There is a group of three experts. The tasks of this group are to evaluate the expected losses for each of the outcomes, to determine the total expected losses (risk levels) for the factors ${\mathrm{F}}_1,{\mathrm{F}}_2$, and to compare these levels. Relevant evaluations must be in the form of IFVs.

The first task is to subjectively evaluate the weights of experts, characterizing their knowledge and experience in the relevant field. We did not solve this problem but used the results obtained in the previous section on the basis of the application of the G-IFWA operator:

$$\begin{gathered} {\mathrm{w}}_1=0.233=\left(0.283,0.466\right); \\ {\mathrm{w}}_2=0.333=\left(0.232,0.502\right); \\ {\mathrm{w}}_3=0.433=\left(0.198,0.502\right). \end{gathered}$$

Since the values $\left(1-{\mathsf{\rho }}_{\mathrm{i}\mathrm{j}}\right)$ were used when aggregating the initial values of the weights by expression (26), the second term in parentheses in the resulting values of the weights $w_i$ corresponds to the value $\left(1-{\mathsf{\rho }}_{\mathrm{i}\mathrm{j}}\right)$.

The next task of experts is to subjectively evaluate the probabilities of all outcomes associated with risk factors ${\mathrm{F}}_1,{\mathrm{F}}_2$. The evaluation results for outcomes (11)–(14) are presented in

Table 3. The results of subjective evaluations of the probabilities of implementation outcomes (11)–(14).

	Outcome (11)	Outcome (12)	Outcome (13)	Outcome (14)
	${\mathrm{p}}_{\mathrm{i}1}=\left({\mathsf{\mu }}_{\mathrm{i}1},{\mathsf{\nu }}_{\mathrm{i}1}\right)$	${\mathrm{p}}_{\mathrm{i}2}=\left({\mathsf{\mu }}_{\mathrm{i}2},{\mathsf{\nu }}_{\mathrm{i}2}\right)$	${\mathrm{p}}_{\mathrm{i}3}=\left({\mathsf{\mu }}_{\mathrm{i}3},{\mathsf{\nu }}_{\mathrm{i}3}\right)$	${\mathrm{p}}_{\mathrm{i}4}=\left({\mathsf{\mu }}_{\mathrm{i}4},{\mathsf{\nu }}_{\mathrm{i}4}\right)$
E1	0.10 = (0.50, 0.40)	0.20 = (0.60, 0.30)	0.05 = (0.50, 0.30)	0.15 = (0.60, 0.30)
E2	0.15 = (0.50, 0.30)	0.25 = (0.50, 0.30)	0.10 = (0.50, 0.30)	0.20 = (0.50, 0.30)
E3	0.05 = (0.60, 0.30)	0.15 = (0.60, 0.30)	0.05 = (0.60, 0.30)	0.20 = (0.60, 0.30)

.

We aggregated the original evaluations in the columns of Table 3 on the basis of the G-IFWA operator (28).

$$\begin{array}{l}{\mathrm{p}}_{11}=\mathrm{G}\text{-}\mathrm{I}\mathrm{F}\mathrm{W}\mathrm{A}\left({\mathrm{p}}_{11},{\mathrm{p}}_{21},{\mathrm{p}}_{31}\right)={\mathrm{w}}_1{\mathrm{p}}_{11}\oplus {\mathrm{w}}_2{\mathrm{p}}_{21}\oplus {\mathrm{w}}_3{\mathrm{p}}_{31}\\ =\left(1-{\left(1-0.50\right)}^{0.283}\ast {\left(1-0.50\right)}^{0.232}\ast {\left(1-0.60\right)}^{0.198},0.40^{0.466}\ast 0.30^{0.502}\ast 0.30^{0.502}\right)\\ =0.234\ast 0.10+0.333\ast 0.15+0.433\ast 0.05\\ =\left(1-0.822\ast 0.851\ast 0.834,0.652\ast 0.546\ast 0.546\right)\\ =\left(0.022+0.050+0.022\right)=\left(1-0.583,0.194\right)=0.095=\left(0.417,0.194\right).\end{array}$$

The calculation of other aggregated values of the probabilities of outcomes is carried out by analogy. The calculation results are presented in the first column of

Table 4. Intuitionistic fuzzy values of probabilities, potential losses, and expected losses for outcomes (11)–(14) of the risk factor ${\mathrm{F}}_1$.

	${\mathrm{p}}_{1\mathrm{j}}=\left({\mathsf{\mu }}_{1\mathrm{j}},{\mathsf{\nu }}_{1\mathrm{j}}\right)$	${\mathrm{s}}_{1\mathrm{j}}=\left({\mathsf{\mu }}_{1\mathrm{j}},{\mathsf{\nu }}_{1\mathrm{j}}\right)$	${\mathrm{s}}_{1\mathrm{j}}^{*}=\left({\mathsf{\mu }}_{1\mathrm{j}}^{},{\mathsf{\nu }}_{1\mathrm{j}}\right)$
(11)	0.095 = (0.417, 0.194)	2.450 = (0.386, 0.216)	0.233 = (0.161, 0.318)
(12)	0.194 = (0.452, 0.194)	1.881 = (0.417, 0.194)	0.305 = (0.188, 0.350)
(13)	0.067 = (0.456, 0.176)	3.949 = (0.417, 0.194)	0.256 = (0.190, 0.331)
(14)	0.189 = (0.480, 0.170)	0.616 = (0.386, 0.249)	0.116 = (0.185, 0.377)

.

To evaluate the potential losses associated with all outcomes, we used the following conventional units of measurement: ${\mathrm{s}}_{\mathrm{i}\mathrm{j}}=\mathrm{x}*\left(10.000\right)$ conditional monetary units. To simplify the calculations, we used only the values $x$. The results of expert evaluation of potential losses for outcomes associated with the risk factor ${\mathrm{F}}_1$ are presented in

Table 5. Results of subjective evaluations of potential losses for outcomes (11)–(14).

	Outcome (11)	Outcome (12)	Outcome (13)	Outcome (14)
	${\mathrm{s}}_{\mathrm{i}1}=\left({\mathsf{\mu }}_{\mathrm{i}1},{\mathsf{\nu }}_{\mathrm{i}1}\right)$	${\mathrm{s}}_{\mathrm{i}2}=\left({\mathsf{\mu }}_{\mathrm{i}2},{\mathsf{\nu }}_{\mathrm{i}2}\right)$	${\mathrm{s}}_{\mathrm{i}3}=\left({\mathsf{\mu }}_{\mathrm{i}3},{\mathsf{\nu }}_{\mathrm{i}3}\right)$	${\mathrm{s}}_{\mathrm{i}4}=\left({\mathsf{\mu }}_{\mathrm{i}4},{\mathsf{\nu }}_{\mathrm{i}4}\right)$
E1	3.0 = (0.40, 0.50)	1.5 = (0.50, 0.40)	4.0 = (0.50, 0.40)	1.0 = (0.40, 0.50)
E2	2.0 = (0.50, 0.30)	2.0 = (0.50, 0.30)	4.5 = (0.50, 0.30)	0.5 = (0.50, 0.40)
E3	2.5 = (0.60, 0.30)	2.0 = (0.60, 0.30)	3.5 = (0.60, 0.30)	0.5 = (0.60, 0.30)

.

Using the G-IFWA aggregation operator (28), we aggregated the values of potential losses in the columns of Table 5.

$$\begin{array}{l}{\mathrm{s}}_{11}=\mathrm{G}\text{-}\mathrm{I}\mathrm{F}\mathrm{W}\mathrm{A}\left({\mathrm{s}}_{11},{\mathrm{s}}_{12},{\mathrm{s}}_{13}\right)=\left(0.234\ast 3.0+0.333\ast 2.0+0.433\ast 2.5\right)\\ =\left(1-{\left(1-0.40\right)}^{0.283}\ast {\left(1-0.50\right)}^{0.232}\ast {\left(1-0.60\right)}^{0.198},0.50^{0.406}\ast 0.30^{0.502}\ast 0.30^{0.502}\right)\\ =\left(0.302+0.667+1.182\right)=\left(1-0.865\ast 0.851\ast 0.834,0.724\ast 0.546\ast 0.546\right)\\ =2.45=\left(1-0.614,0.216\right)=2.45=\left(0.386,0.216\right).\end{array}$$

Aggregation of other initial values of potential losses is performed by analogy. The resulting evaluations of potential losses are presented in the second column of Table 4.

Let us calculate intuitionistic fuzzy values of expected losses for outcomes (11)–(14). Calculations are performed according to expression (14).

$$\begin{array}{l}{\mathrm{s}}_{11}^{\ast }={\mathrm{p}}_{11}\otimes {\mathrm{s}}_{11}=\left(0.095\ast 2.450\right)=\left(0.417\ast 0.386,\left(0.194+0.216\right)-0.194\ast 0.216\right)\\ =0.233=\left(0.161,0.318\right).\end{array}$$

The remaining calculations are performed by analogy. The resulting values of expected losses for outcomes (11)–(14) are presented in the third column of Table 4.

Table 6. The results of subjective evaluations of the probabilities of implementation outcomes (21)–(23).

	Outcome (21)	Outcome (22)	Outcome (23)
	${\mathrm{p}}_{\mathrm{i}1}=\left({\mathsf{\mu }}_{\mathrm{i}1},{\mathsf{\nu }}_{\mathrm{i}1}\right)$	${\mathrm{p}}_{\mathrm{i}2}=\left({\mathsf{\mu }}_{\mathrm{i}2},{\mathsf{\nu }}_{\mathrm{i}2}\right)$	${\mathrm{p}}_{\mathrm{i}3}=\left({\mathsf{\mu }}_{\mathrm{i}3},{\mathsf{\nu }}_{\mathrm{i}3}\right)$
E1	0.10 = (0.40, 0.40)	0.05 = (0.50, 0.30)	0.15 = (0.50, 0.40)
E2	0.10 = (0.50, 0.40)	0.10 = (0.50, 0.30)	0.10 = (0.50, 0.30)
E3	0.20 = (0.60, 0.30)	0.10 = (0.60, 0.30)	0.15 = (0.60, 0.30)

presents the initial intuitionistic fuzzy estimates of the probabilities of outcomes (21)–(23).

We aggregated the initial evaluations in the columns of Table 6 on the basis of the G-IFWA operator (28).

$$\begin{array}{l}{\mathrm{p}}_{21}=\mathrm{G}\text{-}\mathrm{I}\mathrm{F}\mathrm{W}\mathrm{A}\left({\mathrm{p}}_{11},{\mathrm{p}}_{21},{\mathrm{p}}_{31}\right)=\left(0.234\ast 0.10+0.333\ast 0.10+0.433\ast 0.20\right)\\ =\left(1-{\left(1-0.40\right)}^{0.283}\ast {\left(1-0.50\right)}^{0.232},{\left(1-0.60\right)}^{0.198},0.40^{0.466}\ast 0.40^{0.502}\ast 0.30^{0.502}\right)\\ =\left(0.023+0.033+0.087\right)=\left(1-0.865\ast 0.851\ast 0.834,0.652\ast 0.631\ast 0.546\right)\\ =0.143=\left(1-0.614,0.225\right)=0.143=\left(0.386,0.225\right).\end{array}$$

The aggregated values of the probabilities of the remaining outcomes are calculated by analogy. The resulting probability values are presented in the first column of

Table 7. Intuitionistic fuzzy values of probabilities, potential losses, and expected losses for outcomes (21)–(23) of the risk factor ${\mathrm{F}}_2$.

	${\mathrm{p}}_{1\mathrm{j}}=\left({\mathsf{\mu }}_{1\mathrm{j}},{\mathsf{\nu }}_{1\mathrm{j}}\right)$	${\mathrm{s}}_{1\mathrm{j}}=\left({\mathsf{\mu }}_{1\mathrm{j}},{\mathsf{\nu }}_{1\mathrm{j}}\right)$	${\mathrm{s}}_{1\mathrm{j}}^{*}=\left({\mathsf{\mu }}_{1\mathrm{j}}^{},{\mathsf{\nu }}_{1\mathrm{j}}\right)$
(21)	0.143 = (0.386, 0.225)	2.385 = (0.417, 0.170)	0.341 = (0.196, 0.317)
(22)	0.068 = (0.417, 0.170)	4.382 = (0.417, 0.225)	0.386 = (0.174, 0.352)
(23)	0.133 = (0.417, 0.194)	3.333 = (0.417, 0.194)	0.443 = (0.174, 0.350)

.

The results of expert evaluation of potential losses for outcomes associated with the risk ${\mathrm{F}}_2$ are presented in

Table 8. Results of subjective evaluations of potential losses for outcomes (21)–(23).

	Outcome (21)	Outcome (22)	Outcome (23)
	${\mathrm{s}}_{\mathrm{i}1}=\left({\mathsf{\mu }}_{\mathrm{i}1},{\mathsf{\nu }}_{\mathrm{i}1}\right)$	${\mathrm{s}}_{\mathrm{i}2}=\left({\mathsf{\mu }}_{\mathrm{i}2},{\mathsf{\nu }}_{\mathrm{i}2}\right)$	${\mathrm{s}}_{\mathrm{i}3}=\left({\mathsf{\mu }}_{\mathrm{i}3},{\mathsf{\nu }}_{\mathrm{i}3}\right)$
$E_1$	2.0 = (0.50, 0.30)	4.0 = (0.50, 0.40)	3.5 = (0.50, 0.40)
$E_2$	2.5 = (0.50, 0.30)	4.5 = (0.50, 0.40)	3.0 = (0.50, 0.30)
$E_3$	2.5 = (0.60, 0.30)	4.5 = (0.60, 0.30)	3.5 = (0.60, 0.30)

.

Using the G-IFWA aggregation operator (28), we aggregated the values of potential losses in the columns of Table 8.

$$\begin{array}{l}{\mathrm{s}}_{11}=\mathrm{G}\text{-}\mathrm{I}\mathrm{F}\mathrm{W}\mathrm{A}\left({\mathrm{s}}_{11},{\mathrm{s}}_{12},{\mathrm{s}}_{13}\right)=\left(0.234\ast 2.0+0.333\ast 2.5+0.433\ast 2.5\right)\\ =\left(1-{\left(1-0.50\right)}^{0.283}\ast {\left(1-0.50\right)}^{0.232}\ast {\left(1-0.60\right)}^{0.198},0.30^{0.466}\ast 0.30^{0.502}\ast 0.30^{0.502}\right)\\ =\left(0.468+0.835+1.082\right)=\left(1-0.827\ast 0.851\ast 0.834,0.571\ast 0.546\ast 0.546\right)\\ =2.385=\left(1-0.583,0.170\right)=2.385=\left(0.417,0.170\right).\end{array}$$

Aggregation of other values of potential losses is performed by analogy. The resulting evaluations of potential losses are presented in the second column of Table 7.

Intuitionistic fuzzy values of expected losses for outcomes (21)–(23) are calculated by expression (14). The factors are the corresponding intuitionistic fuzzy values of probabilities and potential losses. The calculation results are presented in the third column of Table 7.

We aggregated the values of intuitionistic fuzzy expected losses for risk factors ${\mathrm{F}}_1,{\mathrm{F}}_2$. To do this, we needed the values of the outcome weights. To simplify the further presentation, we assumed that the experts agreed to assign the following deterministic values for the required weights:

$$\begin{array}{l}{\mathrm{w}}_{11}=0.30; {\mathrm{w}}_{21}=0.20;\\ {\mathrm{w}}_{12}=0.30; {\mathrm{w}}_{22}=0.30;\\ {\mathrm{w}}_{13}=0.20; {\mathrm{w}}_{23}=0.50.\\ {\mathrm{w}}_{14}=0.20.\end{array}$$

Aggregation of expected loss values was performed on the basis of the IFWA operator (20). If the outcome weights were in the form of IFVs, then the aggregation needed to be performed on the basis of the G-IFWA operator (28).

-

Risk factor ${\mathrm{F}}_1$:

$$\begin{array}{l}\mathrm{r}\left({\mathrm{F}}_1\right)=\mathrm{I}\mathrm{F}\mathrm{W}\mathrm{A}\left({\mathrm{s}}_{11}^{\ast },{\mathrm{s}}_{12}^{\ast },{\mathrm{s}}_{13}^{\ast },{\mathrm{s}}_{14}^{\ast }\right)=\left(0.30\ast 0.233+0.30\ast 0.305+0.20\ast 0.265+0.20\ast 0.116\right)\\ =\left(1-{\left(1-0.161\right)}^{0.30}\ast {\left(1-0.188\right)}^{0.30}\ast {\left(1-0.190\right)}^{0.20}\ast {\left(1-0.185\right)}^{0.20},0.318^{0.30}\ast 0.350^{0.30}\ast 0.331^{0.20}\ast 0.377^{0.20}\right)\\ =\left(0.070+0.091+0.053+0.023\right)\\ =\left(1-0.949\ast 0.939\ast 0.959\ast 0.960,0.708\ast 0.802\ast 0.823\right)\\ =0.237=\left(1-0.820,0.342\right)=0.237=\left(0.180,0.342\right).\end{array}$$

-

Risk factor ${\mathrm{F}}_2$:

$$\begin{array}{l}\mathrm{r}\left({\mathrm{F}}_2\right)=\left(0.20\ast 0.341+0.30\ast 0.386+0.50\ast 0.443\right)\\ =\left(1-{\left(1-0.191\right)}^{0.20}\ast {\left(1-0.174\right)}^{0.30}\ast {\left(1-0.174\right)}^{0.50},0.317^{0.20}\ast 0.357^{0.30}\ast 0.350^{0.50}\right)\\ =\left(0.068+0.116+0.221\right)\\ =\left(1-0.958\ast 0.944\ast 0.909,0.795\ast 0.708\ast 0.592\right)\\ =0.405=\left(1-0.882,0.333\right)=0.405=\left(0.178,0.333\right).\end{array}$$

To compare the overall risks associated with the factors ${\mathrm{F}}_1,{\mathrm{F}}_2$, we evaluated the distance between the aggregated values of the expected losses associated with these factors, according to expression (19).

$$\mathrm{d}\left(\mathrm{r}\left({\mathrm{F}}_1\right),\mathrm{r}\left({\mathrm{F}}_2\right)\right)=\left|0.237-0.450\right|=\frac{1}{2}\left(\left|0.180-0.178\right|,\left|0.342-0.333\right|\right)=0.213=\left(0.002,0.009\right).$$

To better represent a further analysis, we present graphically aggregated intuitionistic fuzzy values of expected losses for risk factors ${\mathrm{F}}_1,{\mathrm{F}}_2$ (see Figure 5).

The difference in the bases of these IFVs was decisive in the distance evaluation $\mathrm{d}\left(\mathrm{r}\left({\mathrm{F}}_1\right),\mathrm{r}\left({\mathrm{F}}_2\right)\right)$. The value $\mathsf{\mu }(\times )$, $\mathsf{\nu }(\times )$ of the resulting distance evaluation was negligible, so the value of the distance in the first approximation can be taken as a deterministic value.

Since the difference between the values of the bases $\mathrm{r}\left({\mathrm{F}}_1\right)$, $\mathrm{r}\left({\mathrm{F}}_2\right)$ was negative, this implies the obvious fact that $\mathrm{r}\left({\mathrm{F}}_2\right)>\mathrm{r}\left({\mathrm{F}}_1\right)$. This conclusion follows even more clearly from the analysis of Figure 5.

Alternatively, all of the above calculations can be performed on the basis of the IFWG and G-IFWG aggregation operators.

9. Discussion

With the development of formal approaches to the analysis and choice of solutions, the role of various kinds of expert evaluations began to grow. Decisions had to be made, but often reliable data on the values of parameters in a particular problem simply did not exist. The use of subjective expert evaluations has become a forced necessity.

In connection with the widespread use of expert evaluations, the problem of modeling and taking into account the uncertain nature of such evaluations has arisen. The first step was to use interval evaluations instead of point evaluations. After the emergence and development of fuzzy set theory, this mathematical apparatus has become widely used for modeling various kinds of uncertainties.

With the emergence of other, more developed versions of the original fuzzy set theory, all these versions have found wide applications for modeling uncertainties.

The use of any type of fuzzy sets assumes that the actual value of the relevant evaluation is located in the interval corresponding to the basis of the corresponding fuzzy set (number). The degree of belonging of a particular evaluation to a given fuzzy set characterizes the degree of reliability of this evaluation.

The creation and development of the theory of intuitionistic fuzzy sets (IFSs) made it possible to successfully model both the degree of reliability of expert evaluations and the degree of doubt about the reliability of these evaluations.

The use of intuitionistic fuzzy values (IFVs) has become an important step in the race for successful uncertainty modeling. In this type of modeling, it is assumed that the expert sets the point values of his evaluations and evaluations of the degrees of confidence and doubt about these evaluations.

The use of group expert evaluations involves the subsequent aggregation of the evaluations of individual experts. The first variants of IFVs aggregation operators were developed for application in problems of decision analysis and decision making. Subsequently, these operators were extended in such a way as to take into account the preferences of decision makers on the sets of outcomes of alternative decisions and their subjective perception of the probabilities of these outcomes. Variants of aggregation operators of this kind are presented in (Zeng et al. 2016; Wei and Merigó 2012; He et al. 2014).

The IFV approach is also widely used in risk analysis problems. This concerns mainly the problems of evaluating the reliability of systems (Xun et al. 2022), fault trees analysis, and other practical applications.

As for the “classical” problems of risk analysis, here, IFVs are less common. (Note that by the “classical” problem of risk analysis, we mean a problem in which the expected losses of all outcomes for each risk factor are determined, then these losses are aggregated for each risk factor, and further analysis is performed on the set of these resulting evaluations.) We mention here the work (De et al. 2019), which deals with just such a “classical” problem.

What are the similarities and differences between the problems of analysis and choice of decisions and the problems of risk analysis? In the first case, it is required to evaluate the probabilities of outcomes of alternative decisions and the gains/losses associated with these outcomes. In the second case, it is required to evaluate the probabilities of outcomes of risk factors and the potential losses associated with these outcomes. However, the choice of the optimal solution is made on the basis of calculated data, using the system of preferences of the decision maker and his attitude to risk. In the tasks of risk analysis, the task is reduced only to a qualified statement of the current state of affairs and the possible projection of this state into the future. Therefore, in such problems, it seems reasonable to use fairly simple operators for aggregating initial data such as operators IFWA, IFWG, G-IFWG, and G-IFWG.

In this paper, we modeled and took into account an additional source of uncertainty in expert estimates, namely, uncertainty in the assignment of expert weights. These uncertainties are modeled by assigning weight values in the form of IFVs. This approach can also be used to model uncertainties in weights that characterize the relative importance of risk factor outcomes.

The advantage of such modeling is that it can be used to handle uncertainties that are often ignored in real risk analysis problems. Another advantage of this modeling is that the aggregation of the original evaluations is quite simple according to the G-IFWA and G-IFWG operators. The disadvantage of such modeling is that the vectors of evaluations of individual experts must satisfy the requirements of normalization (24), (25). These requirements are the “curse” of all vector interval evaluations. To meet these requirements, it may be necessary to repeatedly adjust the original expert evaluations.

The disadvantage of this methodology should be considered in the fact that it may be difficult for experts to express their subjective judgments in the form of IFVs.

In summary, we note that the proposed risk analysis methodology is a specific extension of the “classical” methodology to the initial expert evaluations expressed in the form of IFVs. By aggregating the evaluations of individual experts for the outcomes of each of the risk factors, we obtain a reliable basis for the overall risk analysis and subsequent decisions to reduce the existing level of risk to an acceptable level.

10. Concluding Remarks

In this paper, a risk analysis technique was proposed for situations where all initial evaluations of the parameters of these risks are given in the form of intuitionistic fuzzy values (IFVs). Additionally, a methodology for determining the weights of experts is presented where the initial evaluations are also provided in the form of IFVs.

This technique is suitable in conditions of extremely high uncertainty of initial risky situations. Typical examples of such situations are situations associated with environmental risks. In the future, we plan to apply the presented methodology to evaluate the risks of negative impacts on the external environment of populations of invasive plants and animals in Latvia.

In connection with the presented methodology, the following directions for further research can be outlined:

First, to simplify the process of extracting intuitionistic fuzzy expert evaluations, it seems appropriate to develop a scale of initial evaluations in the form of suitable linguistic categories. Variants of such scales have been proposed in the literature, but they do not seem appropriate in the present context.

Secondly, it seems desirable to develop a method for automatically checking sets of vector expert evaluations for the normalization of these vectors. This method should be essentially similar to the method of checking for consistency between pairwise comparisons in AHP but should be adapted to evaluations in the form of IFVs.

Thirdly, it is necessary to construct auxiliary linguistic variables (one for membership, the other for not membership). The use of suitable linguistic terms can simplify the processes of subjective expert evaluations. It is also necessary to determine the links between linguistic terms and their corresponding IFVs.