Dependency Modeling Approach of Cause-Related Mortality and Longevity Risks: HIV/AIDS
Abstract
1. Introduction
2. Copulas in Mortality Modelling
2.1. Copula Definition
- (1)
- is increasing in each
- (2)
- such that
- (3)
- , with we have the following:
2.2. Sklar Theorem
2.3. Complete Cause Elimination
2.4. Crude Survival Function
2.5. Net Survival Function
2.6. Dependence Measures
3. Methods and Materials
3.1. Data Source
3.2. Fitting the Multivariate Dependence Model
3.3. Multiple Decrement Model
3.4. Life Expectancy
4. Results and Discussion
4.1. All Causes of Death Distribution with and without HIV/AIDS in Terms of Time
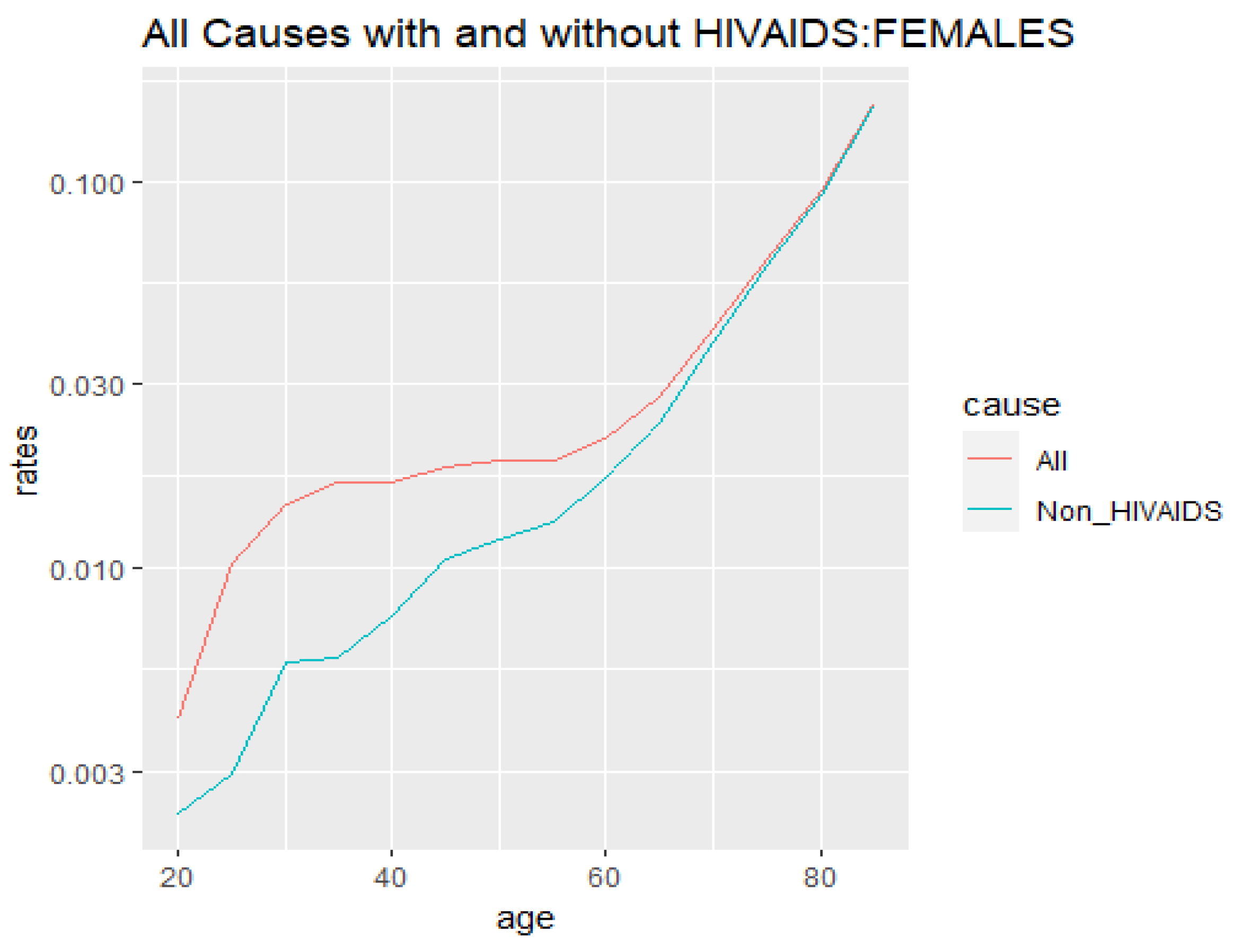
4.2. All Causes of Death Distribution with and without HIV/AIDS in Terms of Age
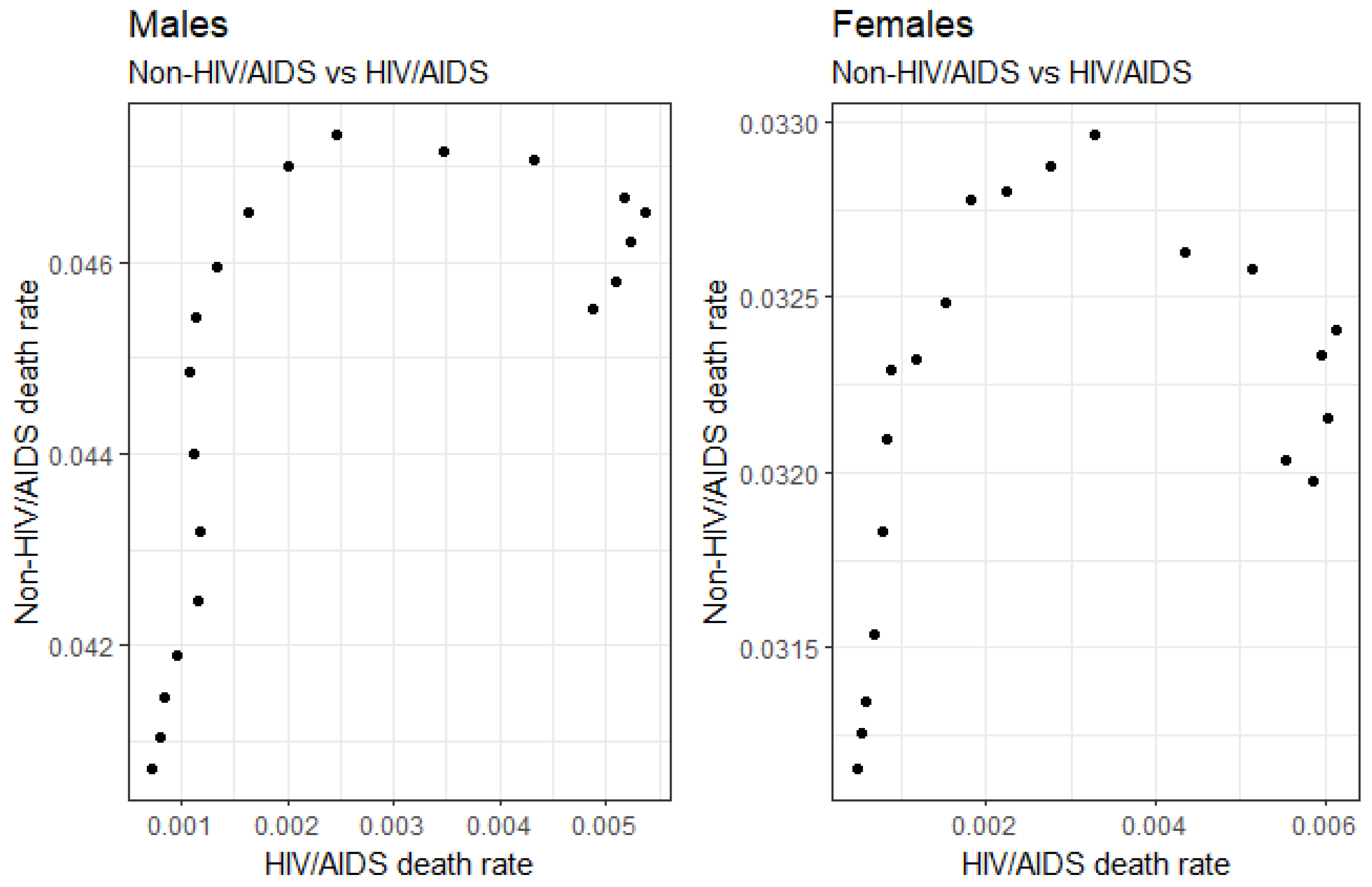
4.3. Joint Distribution for Non-HIV/AIDS against HIV/AIDS Death Rates for Males and Females
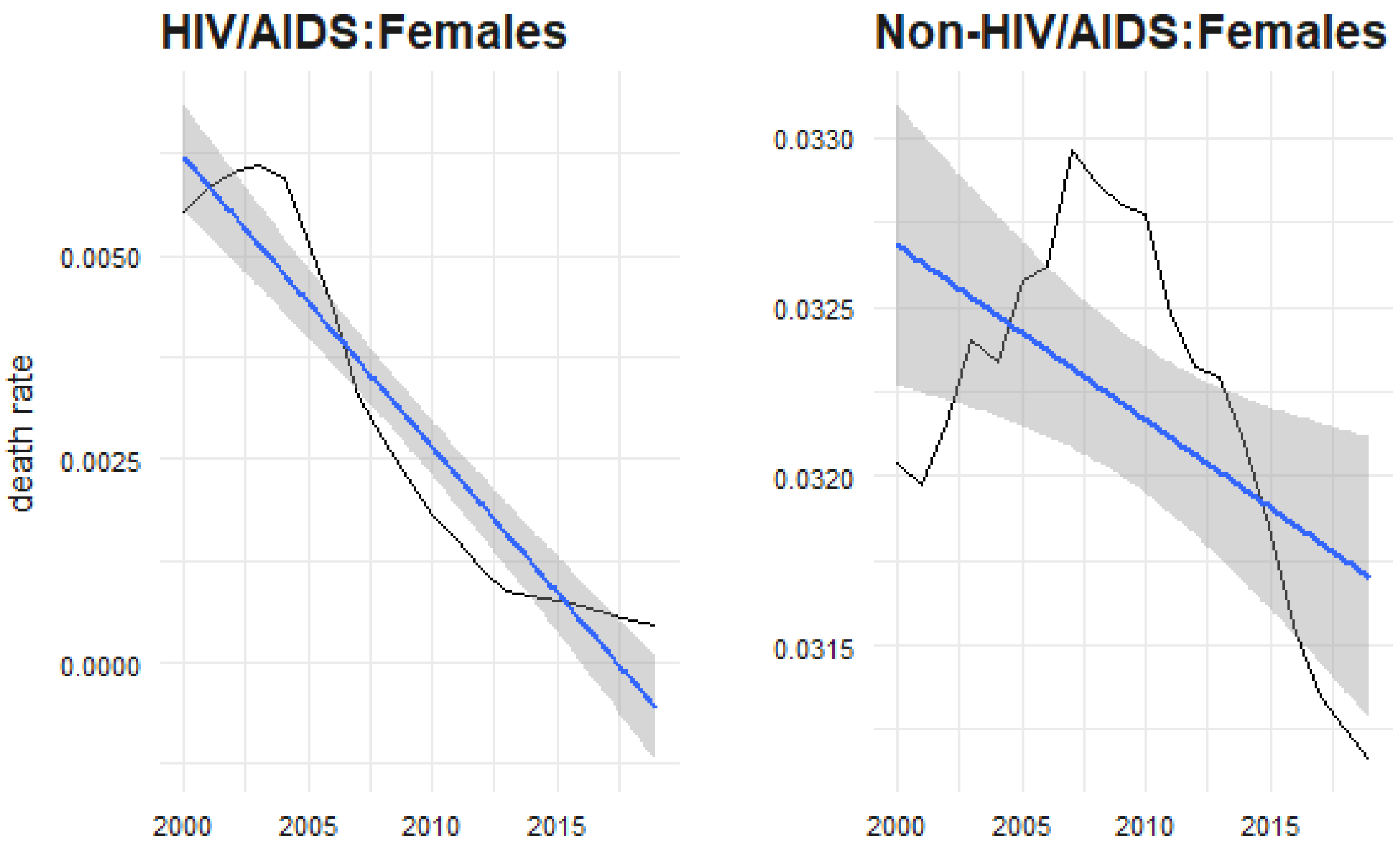
4.4. Marginal Distributions for HIV/AIDS and Non-HIV/AIDS for Males and Females
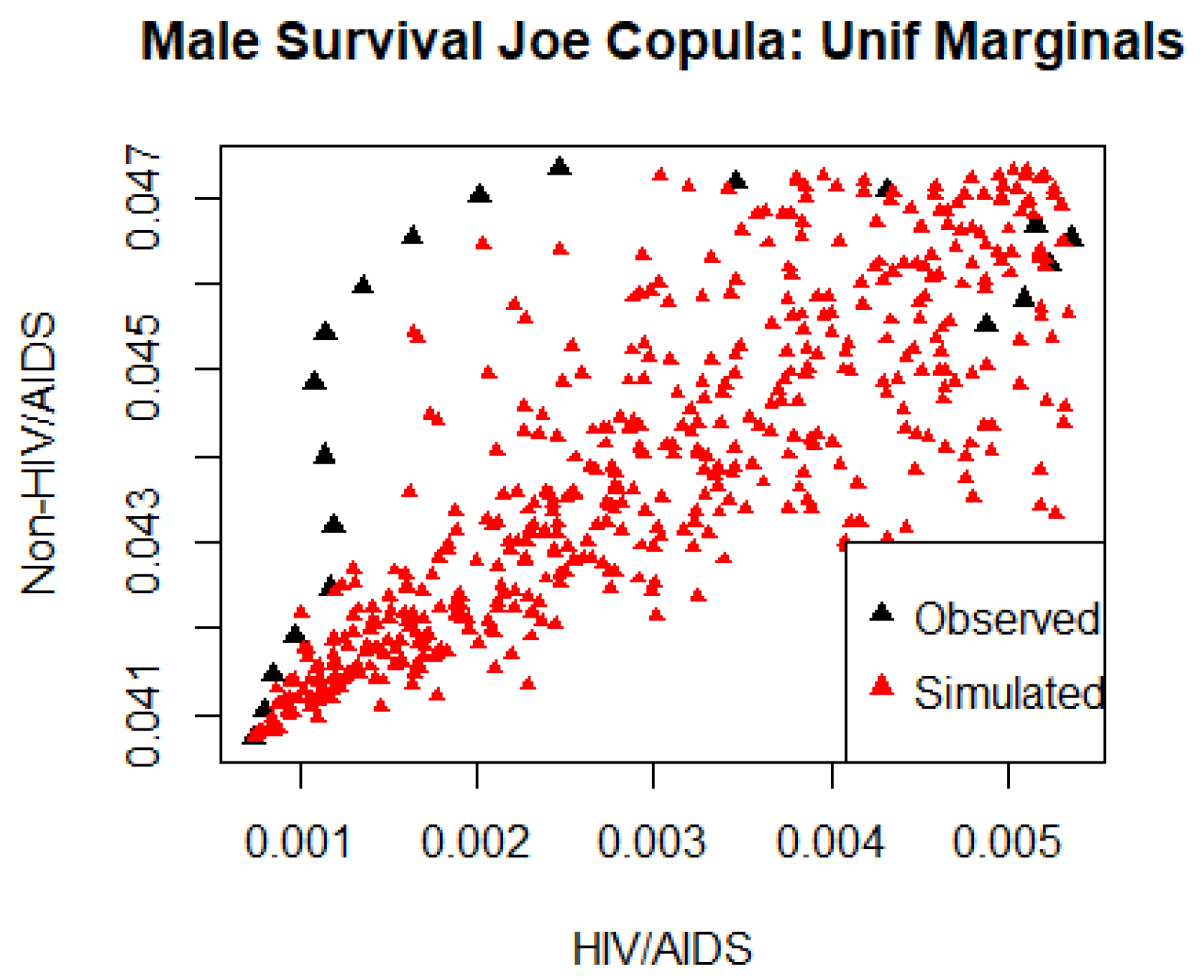
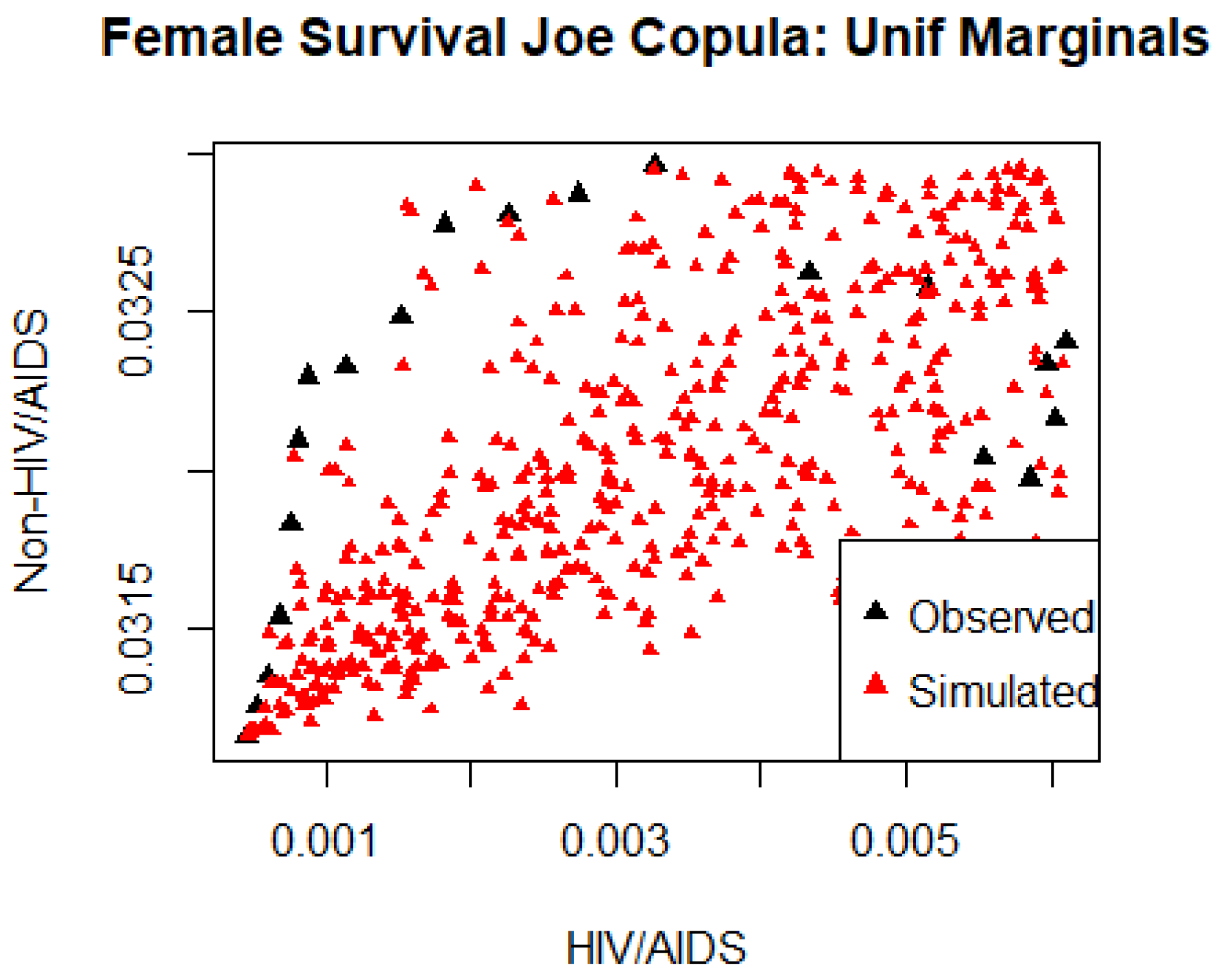
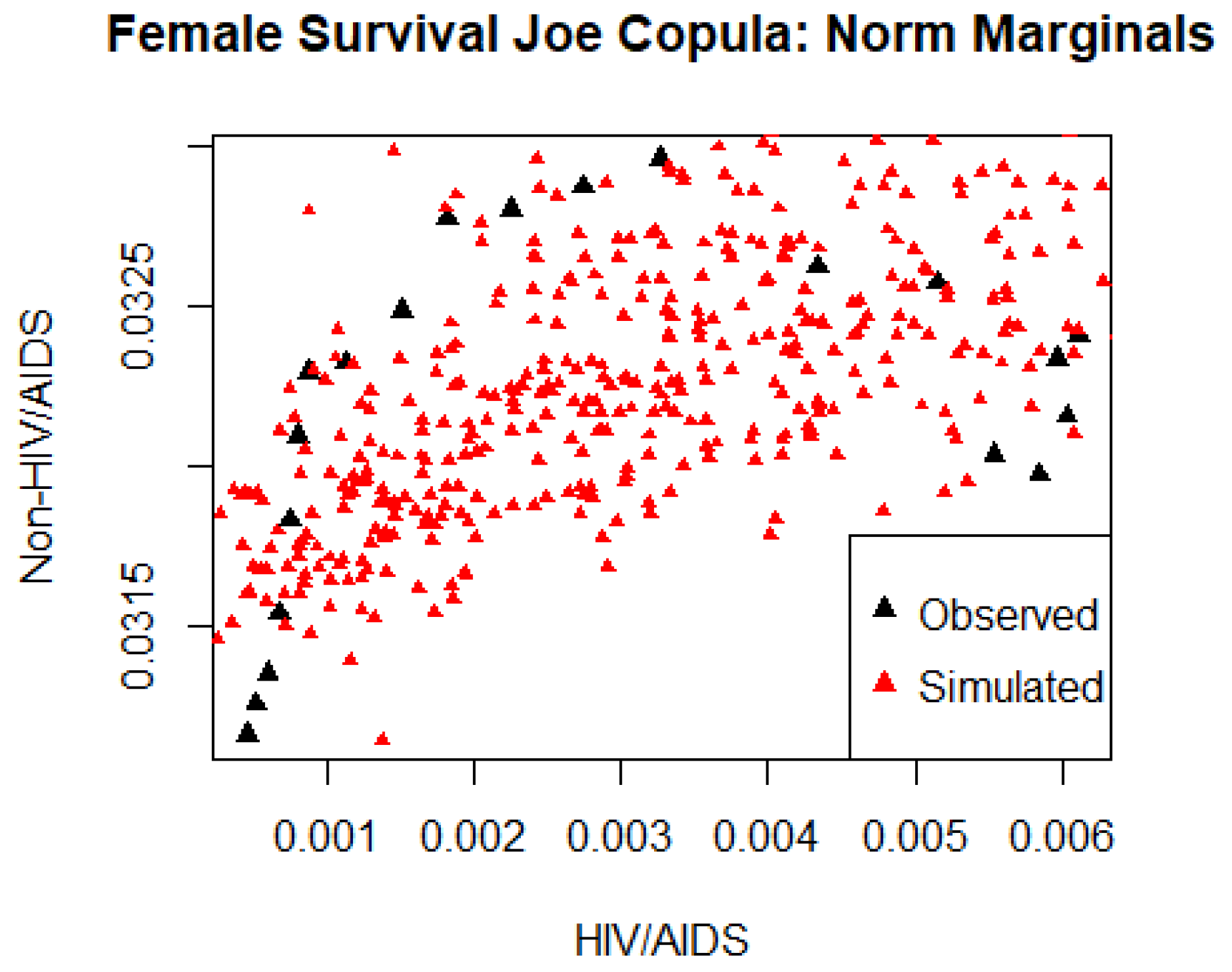
4.5. Bivariate Copula Analysis
4.6. Independence versus Dependence Assumption
4.7. Application of Cause-Specific Mortality Models to the Sensitivity to Life Expectancy
4.8. Life Expectancy Gain/Loss Analysis
4.9. All-Cause Mortality
4.10. Non-HIV/AIDS Mortality (Assuming Independence and Allowing Dependence)
4.11. Limitation of the Study
5. Conclusions and Further Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aas, Kjersti, Claudia Czado, Arnoldo Frigessi, and Henrik Bakken. 2009. Pair-Copula Constructions of Multiple Dependence. Insurance: Mathematics and Economics 44: 182–98. [Google Scholar] [CrossRef]
- Alai, Daniel H., Severine Gaille, and Michael Sherris. 2013. Modelling Cause-of-Death Mortality and the Impact of Cause-Elimination. UNSW Australian School of Business Research Paper. Sydney: UNSW Australian School of Business Research. [Google Scholar]
- Arias, Elizabeth, Jiaquan Xu, and Kenneth D. Kochanek. 2019. United States Life Tables, 2016. Available online: https://www.cdc.gov/nchs/data/nvsr/nvsr68/nvsr68_04-508.pdf (accessed on 20 September 2022).
- Arnold, Séverine, and Michael Sherris. 2015. Causes-of-Death Mortality: What Do We Know on Their Dependence? North American Actuarial Journal 19: 116–28. [Google Scholar] [CrossRef]
- Bedford, Tim, and Roger M. Cooke. 2002. Vines—A New Graphical Model for Dependent Random Variables. The Annals of Statistics 30: 1031–68. [Google Scholar] [CrossRef]
- Beltrán-Sánchez, Hiram, Samuel H. Preston, and Vladimir Canudas-Romo. 2008. An Integrated Approach to Cause-of-Death Analysis: Cause-Deleted Life Tables and Decompositions of Life Expectancy. Demographic Research 19: 1323. [Google Scholar] [CrossRef]
- Bengtsson, Tommy, and Nico Keilman. 2019. Old and New Perspectives on Mortality Forecasting. Berlin: Springer Nature. [Google Scholar]
- Bett, Nicholas, Juma Kasozi, and Daniel Ruturwa. 2022. Temporal Clustering of the Causes of Death for Mortality Modelling. Risks 10: 99. [Google Scholar] [CrossRef]
- Bryant, John, and James J. Dignam. 2004. Semiparametric Models for Cumulative Incidence Functions. Biometrics 60: 182–90. [Google Scholar] [CrossRef]
- Chiang, Chin Long. 1968. The Life Table and Its Construction. Introduction to Stochastic Processes in Biostatistics, 198–214. [Google Scholar]
- Delignette-Muller, Marie Laure, and Christophe Dutang. 2015. Fitdistrplus: An R Package for Fitting Distributions. Journal of Statistical Software 64: 1–34. [Google Scholar] [CrossRef]
- Dissmann, Jeffrey, Eike C. Brechmann, Claudia Czado, and Dorota Kurowicka. 2013. Selecting and Estimating Regular Vine Copulae and Application to Financial Returns. Computational Statistics & Data Analysis 59: 52–69. [Google Scholar]
- Elandt-Johnson, Regina C. 1976. Conditional Failure Time Distributions under Competing Risk Theory with Dependent Failure Times and Proportional Hazard Rates. Scandinavian Actuarial Journal 1976: 37–51. [Google Scholar] [CrossRef]
- Engle, Robert F., and Clive W. J. Granger. 1987. Co-Integration and Error Correction: Representation, Estimation, and Testing. Econometrica: Journal of the Econometric Society 1987: 251–76. [Google Scholar] [CrossRef]
- Fergany, Nader. 1971. On the Human Survivorship Function…-Google Scholar. Available online: https://scholar.google.com/scholar?hl=en&as_sdt=0%2C5&q=Fergany+%281971.+%22On+the+Human+Survivorship+Function+and+Life+Table+Construction%2C%22+Demography8%283%29%3A331-334%29&btnG= (accessed on 20 September 2022).
- Fréchet, Maurice. 1951. Sur Les Tableaux de Corrélation Dont Les Marges Sont Données. Annal Université Lyon, 3^e serie, Sciences, Section A 14: 53–77. [Google Scholar]
- Kaishev, Vladimir K., Dimitrina S. Dimitrova, and Steven Haberman. 2007. Modelling the Joint Distribution of Competing Risks Survival Times Using Copula Functions. Insurance: Mathematics and Economics 41: 339–61. [Google Scholar] [CrossRef]
- Keyfitz, Nathan, Samuel H. Preston, and Robert Schoen. 1972. Inferring Probabilities from Rates: Extension to Multiple Decrement. Scandinavian Actuarial Journal 1972: 1–13. [Google Scholar] [CrossRef]
- Kjærgaard, Søren, Yunus Emre Ergemen, Malene Kallestrup-Lamb, Jim Oeppen, and Rune Lindahl-Jacobsen. 2019. Forecasting Causes of Death by Using Compositional Data Analysis: The Case of Cancer Deaths. Journal of the Royal Statistical Society: Series C (Applied Statistics) 68: 1351–70. [Google Scholar] [CrossRef]
- Li, Hong, and Yang Lu. 2018. Modeling Cause-of-Death Mortality Using Hierarchical Archimedean Copula. Scandinavian Actuarial Journal 2019: 1–26. [Google Scholar] [CrossRef]
- McNeil, Alexander J., Rüdiger Frey, and Paul Embrechts. 2015. Quantitative Risk Management: Concepts, Techniques and Tools-Revised Edition. Princeton: Princeton University Press. [Google Scholar]
- Mueller, Steve. 2004. Strategically Managing AD&D Risk. Risk Management 51: 40. [Google Scholar]
- Murphy, Sherry L., Kenneth D. Kochanek, Jiaquan Xu, and Elizabeth Arias. 2021. Mortality in the United States, 2020. Available online: https://stacks.cdc.gov/view/cdc/112079 (accessed on 20 September 2022).
- Nall, Allison, Tiffany Chenneville, Lindsey M. Rodriguez, and Jennifer L. O’Brien. 2019. Factors Affecting HIV Testing among Youth in Kenya. International Journal of Environmental Research and Public Health 16: 1450. [Google Scholar] [CrossRef]
- Nelsen, Roger B. 2007. An Introduction to Copulas. Berlin: Springer Science & Business Media. [Google Scholar]
- Richmond, Douglas R. 2009. Drugs, Sex, and Accidental Death Insurance. Tort Trial & Insurance Practice Law Journal 2009: 57–96. [Google Scholar]
- Schober, Patrick, Christa Boer, and Lothar A. Schwarte. 2018. Correlation Coefficients: Appropriate Use and Interpretation. Anesthesia & Analgesia 126: 1763–68. [Google Scholar] [CrossRef]
- Sia, Drissa, Yentéma Onadja, Arijit Nandi, Anne Foro, and Timothy Brewer. 2014. What Lies behind Gender Inequalities in HIV/AIDS in Sub-Saharan African Countries: Evidence from Kenya, Lesotho and Tanzania. Health Policy and Planning 29: 938–49. [Google Scholar] [CrossRef] [PubMed]
- Sklar, Abe. 1973. Random Variables, Joint Distribution Functions, and Copulas. Kybernetika 9: 449–60. [Google Scholar]
- Sklar, M. 1959. Fonctions de Repartition an Dimensions et Leurs Marges. Publications de l’Institut de statistique de l’Université de Paris 8: 229–31. [Google Scholar]
- Stander, Y. S., D. J. Marais, and Ilse Botha. 2013. A Comparison of Cointegration and Copula Asset Allocation Approaches. Studies in Economics and Econometrics 37: 1–28. [Google Scholar] [CrossRef]
- Stracke, Andrea, and Winfried Heinen. 2020. SOA—Influenza Pandemic: The Impact on an Insured Lives Life Insurance Portfolio. Available online: https://www.soa.org/library/newsletters/the-actuary-magazine/2006/june/pub-influenza-the-impact-on-an-insured-lives-life-insurance-portfolio (accessed on 20 September 2022).
- Strauss, David J., Pierre J. Vachon, and Robert M. Shavelle. 2005. Estimation of Future Mortality Rates and Life Expectancy in Chronic Medical Conditions. Journal of Insurance Medicine 37: 20–34. [Google Scholar]







| Family Name | Copula Structure |
|---|---|
| Independence copula | = |
| Gaussian copula | is the C.D.F of the bivariate normal distribution with and correlation |
| Student t copula (t-copula) | where is the C.D.F of the bivariate t-distribution with mean 0 and degrees of freedom , with correlation |
| Clayton copula | where such that |
| Gumbel copula | where such that |
| Frank copula | where such that \{0} |
| Joe copula | where such that |
| Clayton-Gumbel = BB1 copula | where such that |
| Joe-Gumbel = BB6 copula | where such that |
| Joe-Clayton = BB7 copula | where such that |
| Joe-Frank = BB8 copula | where such that |
| 90 degrees rotated copulas | with c |
| 180 degrees rotated copulas | with c |
| 270 degrees rotated copulas | with c |
| Survival Copulas | |
| Tawn type 1 copula | with where w , 0 ≤, 0 ≤, |
| Tawn type 2 copula | with w + where w , 0 ≤ , , |
| Distribution | ||
|---|---|---|
| Joint | ||
| Marginal | ||
| Conditional |
| Males | Females | |||||
|---|---|---|---|---|---|---|
| Family Code and Name | logLik | AIC | BIC | logLik | AIC | BIC |
| 0 = independence copula | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 = Gaussian copula | 7.84 | 13.69 | −12.69 | 3.54 | −5.08 | −4.08 |
| 2 = Student t copula (t-copula) | 7.78 | −11.56 | −9.57 | 3.48 | −2.96 | −0.96 |
| 3 = Clayton copula | 14.62 | −27.23 | −26.23 | 8.68 | −15.36 | −14.36 |
| 4 = Gumbel copula | 4.6 | −7.21 | −6.21 | 1.41 | −0.82 | 0.17 |
| 5 = Frank copula | 7.73 | −13.45 | −12.45 | 2.97 | −3.93 | −2.94 |
| 6 = Joe copula | 2.03 | −2.05 | −1.06 | 0.16 | 1.69 | 2.68 |
| 7 = BB1 copula | 14.61 | −25.22 | −23.23 | 8.67 | −13.35 | −11.36 |
| 8 = BB6 copula | 4.6 | −5.2 | −3.21 | 1.41 | 1.18 | 3.17 |
| 9 = BB7 copula | 14.7 | −25.4 | −23.41 | 8.68 | −13.36 | −11.37 |
| 10 = BB8 copula | 5.58 | −7.16 | −5.17 | 2.13 | −0.25 | 1.74 |
| 13 = rotated Clayton copula (180 degrees; survival Clayton) | 2.86 | −3.73 | −2.73 | 0.63 | 0.73 | 1.73 |
| 14 = rotated Gumbel copula (180 degrees; survival Gumbel) | 10.83 | −19.67 | −18.67 | 5.87 | −9.74 | −8.74 |
| 16 = rotated Joe copula (180 degrees; survival Joe’) | 14.72 | −27.43 | −26.44 | 9.13 | −16.25 | −15.26 |
| 17 = rotated BB1 copula (180 degrees; survival BB1) | 10.83 | −17.66 | −15.66 | 5.86 | −7.73 | −5.74 |
| 18 = rotated BB6 copula (180 degrees; survival BB6) | 14.72 | −25.43 | −23.44 | 9.12 | −14.25 | −12.26 |
| 19 = rotated BB7 copula (180 degrees; survival BB7) | 14.72 | −25.43 | −23.44 | 9.13 | −14.25 | −12.26 |
| 20 = rotated BB8 copula (180 degrees; survival BB8) | 14.72 | −25.43 | −23.44 | 9.13 | −14.25 | −12.26 |
| 104 = Tawn type 1 copula | 4.2 | −4.39 | −2.4 | 1.87 | 0.25 | 2.24 |
| 114 = rotated Tawn type 1 copula (180 degrees) | 10.1 | −16.2 | −14.21 | 4.56 | −5.13 | −3.14 |
| 204 = Tawn type 2 copula | 4.11 | −4.21 | −2.22 | 0.99 | 2.03 | 4.02 |
| 214 = rotated Tawn type 2 copula (180 degrees) | 10.6 | −17.21 | −15.22 | 7.51 | −11.03 | −9.03 |
| Marginals | Pearson Linear Correlation Coefficient | Kendall’s Tau = 0.66 |
|---|---|---|
| Assuming Independence | 0.6417682 | 0.6 |
| Beta | 0.7215273 | 0.6687808 |
| Uniform | 0.8325042 | 0.6503343 |
| Marginals | Pearson Linear Correlation Coefficient | Kendall’s Tau = 0.55 |
|---|---|---|
| Assuming Independence | 0.3879891 | 0.4315789 |
| Beta | 0.5933727 | 0.5522082 |
| Uniform | 0.7142036 | 0.5313874 |
| Normal | 0.7361025 | 0.54 |
| 2019 | 2010 | 2000 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Age (x) | ex(All Cause) | ex(Non-HIVAIDS) Independence | ex(Non-HIVAIDS) Dependence | Gain/ (Loss) | ex(All Cause) | ex(Non-HIVAIDS) Independence | ex(Non-HIVAIDS) Dependence | Gain/ (Loss) | ex(All Cause) | ex(Non-HIVAIDS) Independence | ex(Non-HIVAIDS) Dependence | Gain/(Loss) |
| 20 | 44.0 | 44.9 | 44.6 | −0.3 | 40.4 | 42.0 | 41.0 | −1.0 | 36.1 | 41.8 | 37.4 | −4.4 |
| 25 | 43.1 | 44.0 | 43.7 | −0.3 | 39.4 | 41.1 | 40.1 | −1.0 | 35.2 | 40.9 | 36.4 | −4.5 |
| 30 | 39.5 | 40.3 | 40.1 | −0.2 | 35.9 | 37.5 | 36.5 | −1.0 | 31.8 | 37.2 | 33.0 | −4.2 |
| 35 | 35.1 | 35.8 | 35.6 | −0.2 | 31.7 | 33.1 | 32.3 | −0.8 | 28.2 | 32.8 | 29.4 | −3.4 |
| 40 | 30.8 | 31.5 | 31.4 | −0.1 | 27.9 | 29.0 | 28.5 | −0.5 | 25.4 | 28.8 | 26.5 | −2.3 |
| 45 | 26.9 | 27.4 | 27.4 | 0 | 24.4 | 25.2 | 25.0 | −0.2 | 23.0 | 25.4 | 24.0 | −1.4 |
| 50 | 23.1 | 23.5 | 23.6 | 0.1 | 21.3 | 21.7 | 21.8 | 0.1 | 20.6 | 22.1 | 21.4 | −0.7 |
| 55 | 19.6 | 19.8 | 20.0 | 0.2 | 18.2 | 18.5 | 18.6 | 0.1 | 17.7 | 18.7 | 18.5 | −0.2 |
| 60 | 16.2 | 16.4 | 16.6 | 0.2 | 15.1 | 15.3 | 15.5 | 0.2 | 14.8 | 15.3 | 15.5 | 0.2 |
| 65 | 13.2 | 13.2 | 13.5 | 0.3 | 12.3 | 12.4 | 12.6 | 0.2 | 12.0 | 12.3 | 12.6 | 0.3 |
| 70 | 10.3 | 10.4 | 10.6 | 0.2 | 9.7 | 9.7 | 9.9 | 0.2 | 9.5 | 9.7 | 10.0 | 0.3 |
| 75 | 7.8 | 7.8 | 8.0 | 0.2 | 7.4 | 7.4 | 7.6 | 0.2 | 7.3 | 7.4 | 7.6 | 0.2 |
| 80 | 5.5 | 5.5 | 5.6 | 0.1 | 5.2 | 5.2 | 5.4 | 0.2 | 5.3 | 5.3 | 5.5 | 0.2 |
| 85+ | 3.1 | 3.1 | 3.2 | 0.1 | 3.1 | 3.1 | 3.1 | 0 | 3.1 | 3.1 | 3.2 | 0.1 |
| 2019 | 2010 | 2000 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Age (x) | ex(All Cause) | ex(Non-HIVAIDS) Independence | ex(Non-HIVAIDS) Dependence | Gain/ (Loss) | ex(All Cause) | ex(Non-HIVAIDS) Independence | ex(Non-HIVAIDS) Dependence | Gain/ (Loss) | ex(All Cause) | ex(Non-HIVAIDS) Independence | ex(Non-HIVAIDS) Dependence | Gain/(Loss) |
| 20 | 48.0 | 48.7 | 48.9 | 0.2 | 43.6 | 46.5 | 44.7 | −2.2 | 37.8 | 45.6 | 39.1 | −6.5 |
| 25 | 47.1 | 47.7 | 48.0 | 0.3 | 42.7 | 45.5 | 43.8 | −1.7 | 36.9 | 44.7 | 38.3 | −6.4 |
| 30 | 43.4 | 44.0 | 44.3 | 0.3 | 39.3 | 42.0 | 40.4 | −1.6 | 34.4 | 41.2 | 35.7 | −5.5 |
| 35 | 39.0 | 39.6 | 39.9 | 0.3 | 35.5 | 37.8 | 36.6 | −1.2 | 31.8 | 37.3 | 33.0 | −4.3 |
| 40 | 34.8 | 35.2 | 35.6 | 0.4 | 32.1 | 33.7 | 33.1 | −0.6 | 29.4 | 33.3 | 30.4 | −2.9 |
| 45 | 30.7 | 31.1 | 31.5 | 0.4 | 28.8 | 29.8 | 29.7 | −0.1 | 26.7 | 29.5 | 27.6 | −1.9 |
| 50 | 26.8 | 27.0 | 27.5 | 0.5 | 25.5 | 26.1 | 26.3 | 0.2 | 24.0 | 26.0 | 24.8 | −1.2 |
| 55 | 22.9 | 23.0 | 23.5 | 0.5 | 22.0 | 22.4 | 22.7 | 0.3 | 21.1 | 22.4 | 21.9 | −0.5 |
| 60 | 19.1 | 19.2 | 19.6 | 0.4 | 18.5 | 18.7 | 19.1 | 0.4 | 18.0 | 18.8 | 18.6 | −0.2 |
| 65 | 15.4 | 15.4 | 15.9 | 0.5 | 15.0 | 15.1 | 15.5 | 0.4 | 14.8 | 15.3 | 15.3 | 0 |
| 70 | 11.9 | 12.0 | 12.4 | 0.4 | 11.7 | 11.8 | 12.1 | 0.3 | 11.6 | 11.9 | 12.1 | 0.2 |
| 75 | 8.9 | 8.9 | 9.2 | 0.3 | 8.7 | 8.8 | 9.1 | 0.3 | 8.8 | 8.9 | 9.1 | 0.2 |
| 80 | 6.1 | 6.1 | 6.3 | 0.2 | 6.0 | 6.0 | 6.3 | 0.3 | 6.1 | 6.2 | 6.4 | 0.2 |
| 85+ | 3.4 | 3.4 | 3.5 | 0.1 | 3.4 | 3.4 | 3.5 | 0.1 | 3.5 | 3.5 | 3.6 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bett, N.; Kasozi, J.; Ruturwa, D. Dependency Modeling Approach of Cause-Related Mortality and Longevity Risks: HIV/AIDS. Risks 2023, 11, 38. https://doi.org/10.3390/risks11020038
Bett N, Kasozi J, Ruturwa D. Dependency Modeling Approach of Cause-Related Mortality and Longevity Risks: HIV/AIDS. Risks. 2023; 11(2):38. https://doi.org/10.3390/risks11020038
Chicago/Turabian StyleBett, Nicholas, Juma Kasozi, and Daniel Ruturwa. 2023. "Dependency Modeling Approach of Cause-Related Mortality and Longevity Risks: HIV/AIDS" Risks 11, no. 2: 38. https://doi.org/10.3390/risks11020038
APA StyleBett, N., Kasozi, J., & Ruturwa, D. (2023). Dependency Modeling Approach of Cause-Related Mortality and Longevity Risks: HIV/AIDS. Risks, 11(2), 38. https://doi.org/10.3390/risks11020038








