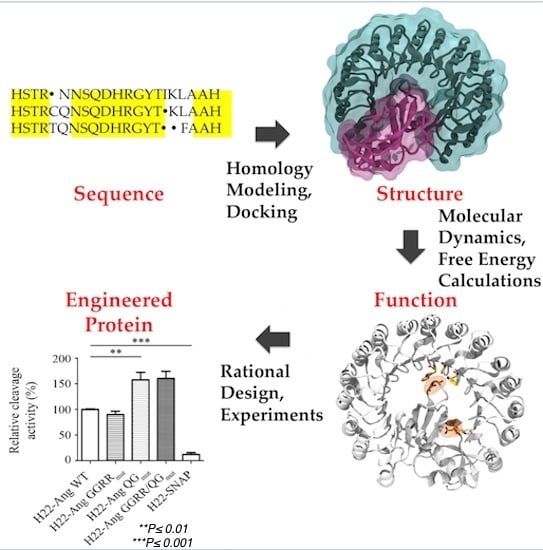
Designing the Sniper: Improving Targeted Human Cytolytic Fusion Proteins for Anti-Cancer Therapy via Molecular Simulation
Abstract
:1. Introduction
1.1. Specific Enzymes Used in Human Cytolytic Fusion Proteins (hCFPs) Therapy and Their Inhibitors
1.1.1. Granzyme B
1.1.2. Angiogenin
2. Computational Methods for Protein Engineering of Relevance for This Review
3. Proteins Structural Predictions
3.1. Template Search and Target-template Sequence Alignment
3.2. Template Selection
3.3. Model Construction
- Modeling by assembly of rigid bodies [61]. The model is assembled from a small number of rigid bodies obtained from aligned protein structures.
- Modeling by satisfaction of spatial restraints [64,65]. This method uses the structure of the templates to define restraints that are usually supplemented by stereochemical restraints on bond lengths, bond angles, dihedral angles, and non-bonded atom-atom contacts. The model is then derived by minimizing the violations of all the restraints in the aligned amino acids of the target sequence.
3.4. Model Quality Assessment
- The sequence identity between target and template
- The sequence alignment
4. Interface and Hot Spots Identification
5. Molecular Dynamics Simulations
6. Replica Exchange MD Simulations
7. Results: In Silico and In Vitro Studies on Granzyme B and Angiogenin
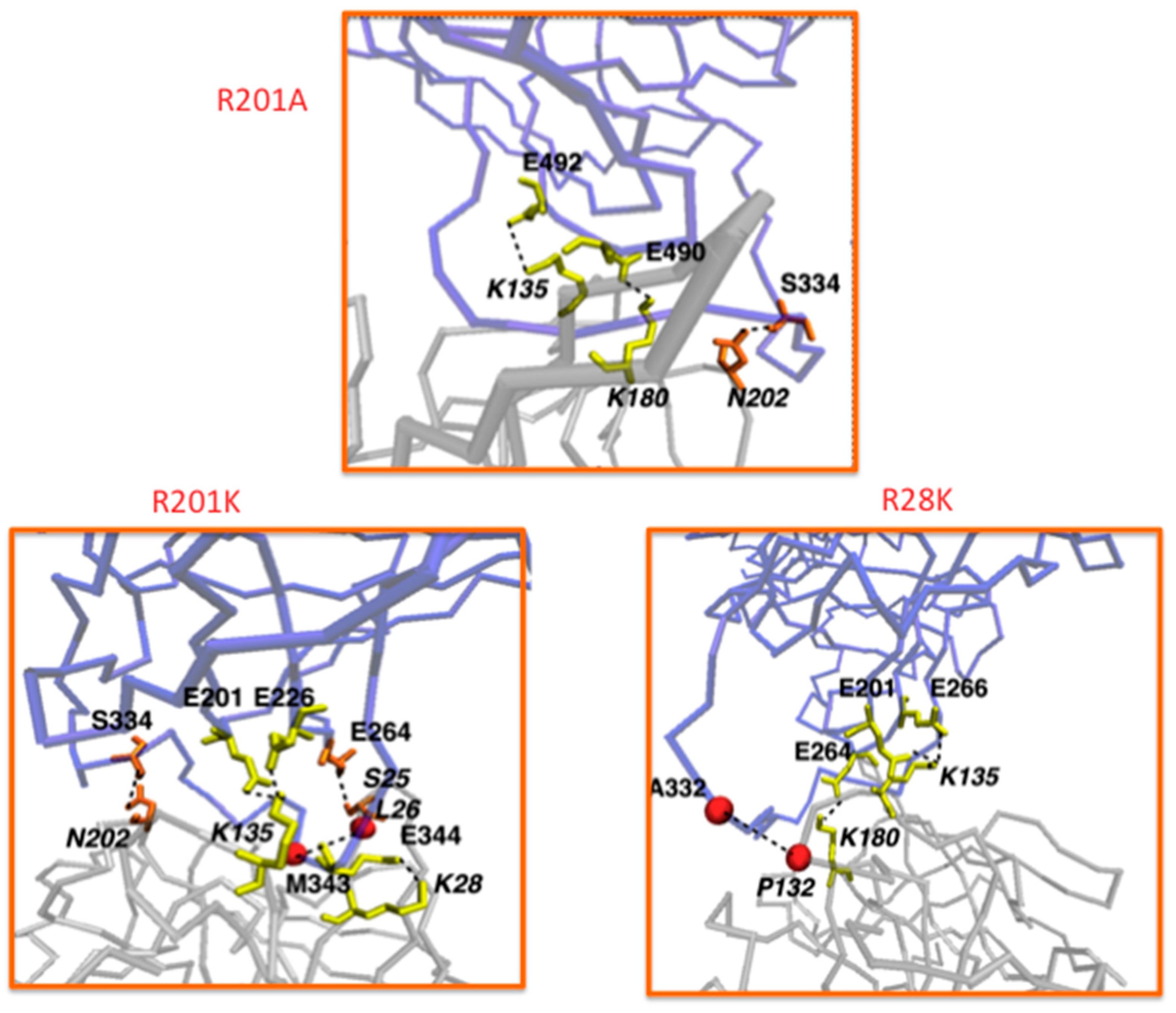
7.1. Granzyme B
7.2. Under Special Consideration: GBR201K as a Tool to Improve Other Immunotherapeutic Strategies Aiming to Attack Serpin B9 Positive Tumor Cells
7.2.1. hCFPs Against Liquid Tumors: Chronic and Acute Myelomonocytic Leukemia
7.2.2. hCFPs Against Solid Tumors: Hodgkin Lymphoma, Rhabdomyosarcoma, Triple-Negative Breast Cancer
7.2.3. Other Applications
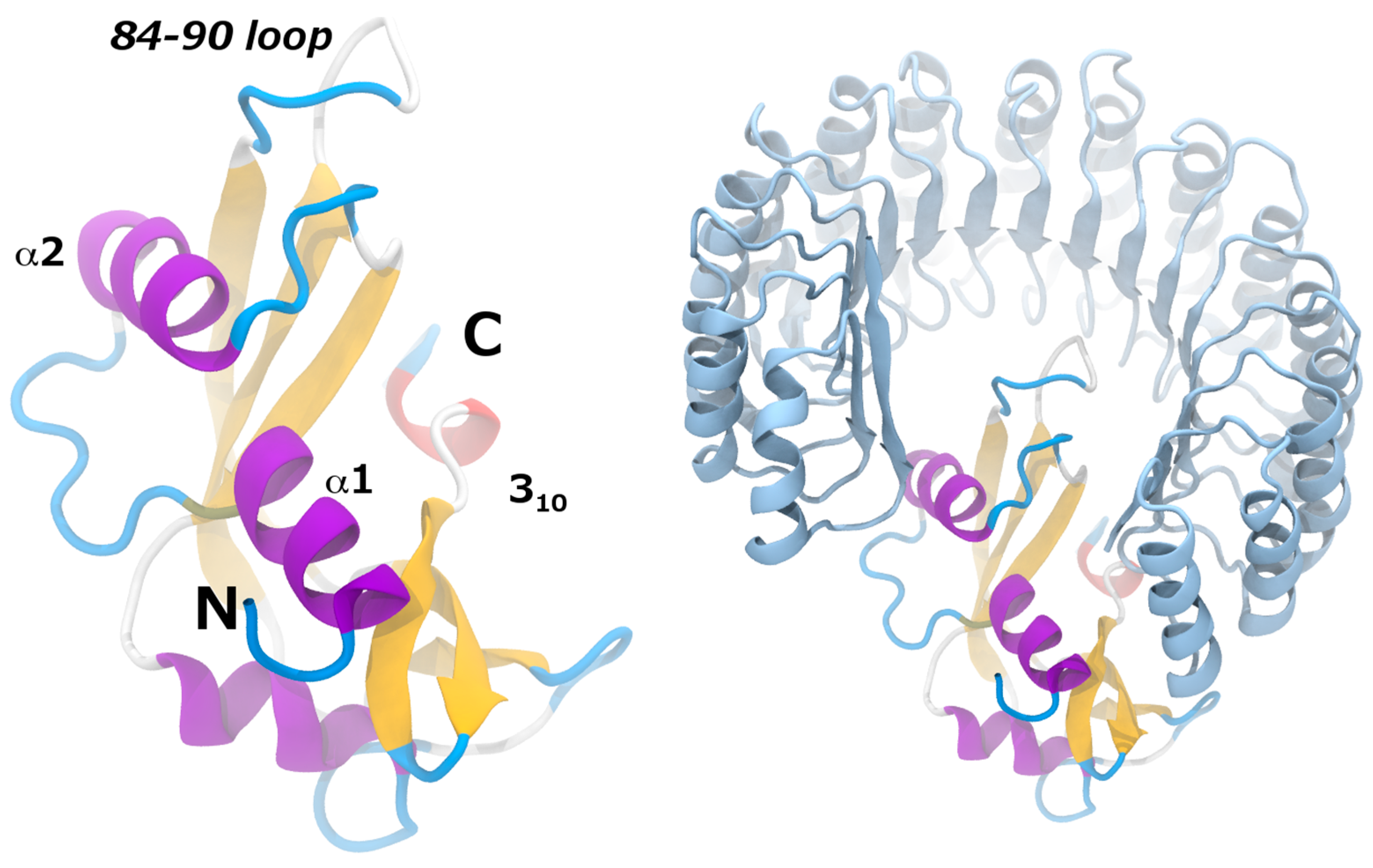
7.3. Angiogenin
8. Concluding Remarks
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Molecular Docking
- Force field based scoring functions that account large conformational changes by summing the strength of intermolecular van der Waals and electrostatic interactions between all atoms.
- Empirical scoring functions. Based on counting the number of various types of interactions between the two binding partners. Counting may be based, for example, on the number of atoms in the two proteins in contact with each other.
- Knowledge-based scoring functions (also known as statistical potentials). Based on statistical observations of intermolecular contacts in structural databases (e.g., the PDB). This approach assumes that atoms interacting with frequencies higher than those given by a random distribution are likely to be energetically more favorable.
- Machine learning scoring functions. The functional form for the relationship between the binding affinity and the structural features of the docked complex is inferred directly from the data. They have consistently been found to outperform classical scoring functions at predicting binding affinity of diverse protein-protein complexes [159].
Appendix A.2. MD-Based Enhanced Sampling Methods
- Collective-variable based methods. Free energy is calculated as a function of one or a few predefined collective variables (CVs), i.e., any differentiable function of the atomic coordinates associated to the degrees of freedom of the rare event under investigation in the system. Examples of these methods include thermodynamic integration [160], free energy perturbation [161], umbrella sampling [162], and weighted histogram techniques [163]. These approaches are very powerful but they do require a careful choice of the CVs that must provide a satisfactory description of the reaction coordinates. An alternative is offered by recently developed non-equilibrium methods; such as adaptive force bias [164], Wang-Landau sampling [165] and metadynamics [166]. In the latter approach, a history-dependent potential is added along selected CVs to compensate the underlying free energy landscape, allowing the system to escape from very stable minima and overcome high energy barriers. This way a reconstruction of the free energy profile along these variables can be performed. The application of the method is however limited to processes that can be described with a low number of CVs [167], constraining its applicability to biological events that are not high dimensional.
- Path sampling methods are aimed at exploring the transition mechanism and constructing reactive trajectories, such as finite-temperature string method [168], transition path sampling [169] or transition interface sampling [170]. These approaches are extremely powerful but they can be applied only if one knows in advance the initial and final states of the process that has to be simulated. Yet, these approaches are very expensive computationally.
- Generalized-ensemble approaches. These methods are based on non-Boltzmann probability weight factors so that a random walk in energy space may be realized [171,172]. This way such approaches allow the system to explore the phase space regardless the presence of high-energy barriers. In a single simulation it is possible to identify the energy minima and compute thermodynamic quantities in a wide temperature range. Two such well-known methods are the multi-canonical algorithm (random walk in energy space) [173] and the simulated tempering (random walk in temperature space) [174,175]. This approach is powerful but the probability weight factors that allow the random walk are not a priori known and usually are determined by several short trial simulations, a process usually laborious and not trivial. For this reason, an additional class of generalized-ensemble algorithms has been devised, the so-called replica-exchange methods (also referred to as replica Monte Carlo methods, multiple Markov chain method, and parallel tempering) [176], where the weight factor is essentially known and there is no complication in its determination. In practice, during these approaches the phase space is explored simultaneously by several copies of the system that differ for some specific properties (e.g., the temperature). Due to the replication approach, those methods are rather computational demanding and require HPC resources.
References
- Blythman, H.E.; Casellas, P.; Gros, O.; Gros, P.; Jansen, F.K.; Paolucci, F.; Pau, B.; Vidal, H. Immunotoxins: Hybrid molecules of monoclonal antibodies and a toxin subunit specifically kill tumour cells. Nature 1981, 290, 145–146. [Google Scholar] [CrossRef] [PubMed]
- Kreitman, R.J. Immunotoxins in cancer therapy. Curr. Opin. Immunol. 1999, 11, 570–578. [Google Scholar] [CrossRef]
- Kreitman, R.J. Immunotoxins for targeted cancer therapy. AAPS J. 2006, 8, E532–E551. [Google Scholar] [CrossRef] [PubMed]
- Hetzel, C.; Bachran, C.; Tur, M.K.; Fuchs, H.; Stocker, M. Improved immunotoxins with novel functional elements. Curr. Pharm. Des. 2009, 15, 2700–2711. [Google Scholar] [CrossRef] [PubMed]
- Weldon, J.E.; Pastan, I. A guide to taming a toxin—Recombinant immunotoxins constructed from Pseudomonas exotoxin A for the treatment of cancer. FEBS J. 2011, 278, 4683–4700. [Google Scholar] [CrossRef] [PubMed]
- Becker, N.; Benhar, I. Antibody-Based Immunotoxins for the Treatment of Cancer. Antibodies 2012, 1, 39–69. [Google Scholar] [CrossRef]
- Fuchs, H.; Weng, A.; Gilabert-Oriol, R. Augmenting the Efficacy of Immunotoxins and Other Targeted Protein Toxins by Endosomal Escape Enhancers. Toxins 2016, 8, 200. [Google Scholar] [CrossRef] [PubMed]
- Alley, S.C.; Okeley, N.M.; Senter, P.D. Antibody–drug conjugates: Targeted drug delivery for cancer. Curr. Opin. Chem. Biol. 2010, 14, 529–537. [Google Scholar] [CrossRef] [PubMed]
- Mazor, R.; Onda, M.; Pastan, I. Immunogenicity of therapeutic recombinant immunotoxins. Immunol. Rev. 2016, 270, 152–164. [Google Scholar] [CrossRef] [PubMed]
- Baluna, R.; Vitetta, E.S. Vascular leak syndrome: A side effect of immunotherapy. Immunopharmacology 1997, 37, 117–132. [Google Scholar] [CrossRef]
- Igney, F.H.; Krammer, P.H. Immune escape of tumors: Apoptosis resistance and tumor counterattack. J. Leukoc. Biol. 2002, 71, 907–920. [Google Scholar] [PubMed]
- Pastan, I. Immunotoxins containing Pseudomonas exotoxin A: A short history. Cancer Immunol. Immunother. 2003, 52, 338–341. [Google Scholar]
- Mathew, M.; Verma, R.S. Humanized immunotoxins: A new generation of immunotoxins for targeted cancer therapy. Cancer Sci. 2009, 100, 1359–1365. [Google Scholar] [CrossRef] [PubMed]
- Yokota, T.; Milenic, D.E.; Whitlow, M.; Schlom, J. Rapid tumor penetration of a single-chain Fv and comparison with other immunoglobulin forms. Cancer Res. 1992, 52, 3402–3408. [Google Scholar] [PubMed]
- Le Gall, F.; Kipriyanov, S.M.; Moldenhauer, G.; Little, M. Di-, tri- and tetrameric single chain Fv antibody fragments against human CD19: Effect of valency on cell binding. FEBS Lett. 1999, 453, 164–168. [Google Scholar] [CrossRef]
- Firer, M.A.; Gellerman, G. Targeted drug delivery for cancer therapy: The other side of antibodies. J. Hematol. Oncol. 2012, 5, 1. [Google Scholar] [CrossRef] [PubMed]
- Bazan, J.; Calkosinski, I.; Gamian, A. Phage display—A powerful technique for immunotherapy: 1. Introduction and potential of therapeutic applications. Hum. Vaccin. Immunother. 2012, 8, 1817–1828. [Google Scholar] [CrossRef] [PubMed]
- St Clair, D.K.; Rybak, S.M.; Riordan, J.F.; Vallee, B.L. Angiogenin abolishes cell-free protein synthesis by specific ribonucleolytic inactivation of ribosomes. Proc. Natl. Acad. Sci. USA 1987, 84, 8330–8334. [Google Scholar] [CrossRef] [PubMed]
- Saxena, S.; Rybak, S.; Davey, R.; Youle, R.; Ackerman, E. Angiogenin is a cytotoxic, tRNA-specific ribonuclease in the RNase A superfamily. J. Biol. Chem. 1992, 267, 21982–21986. [Google Scholar] [PubMed]
- Rybak, S.M.; Hoogenboom, H.R.; Meade, H.M.; Raus, J.; Schwartz, D.; Youle, R.J. Humanization of immunotoxins. Proc. Natl. Acad. Sci. USA 1992, 89, 3165–3169. [Google Scholar] [CrossRef] [PubMed]
- Huhn, M.; Sasse, S.; Tur, M.K.; Matthey, B.; Schinköthe, T.; Rybak, S.M.; Barth, S.; Engert, A. Human angiogenin fused to human CD30 ligand (Ang-CD30L) exhibits specific cytotoxicity against CD30-positive lymphoma. Cancer Res. 2001, 61, 8737–8742. [Google Scholar] [CrossRef]
- Lord, S.J.; Rajotte, R.V.; Korbutt, G.S.; Bleackley, R.C. Granzyme B: A natural born killer. Immunol. Rev. 2003, 193, 31–38. [Google Scholar] [CrossRef] [PubMed]
- Stahnke, B.; Thepen, T.; Stocker, M.; Rosinke, R.; Jost, E.; Fischer, R.; Tur, M.K.; Barth, S. Granzyme B-H22(scFv), a human immunotoxin targeting CD64 in acute myeloid leukemia of monocytic subtypes. Mol. Cancer Ther. 2008, 7, 2924–2932. [Google Scholar] [CrossRef]
- Hristodorov, D.; Nordlohne, J.; Mladenov, R.; Huhn, M.; Fischer, R.; Thepen, T.; Barth, S. Human microtubule-associated protein tau mediates targeted killing of CD30+ lymphoma cells in vitro and inhibits tumour growth in vivo. Br. J. Haematol. 2014, 164, 251–257. [Google Scholar] [CrossRef] [PubMed]
- Hristodorov, D.; Mladenov, R.; Pardo, A.; Pham, A.T.; Huhn, M.; Fischer, R.; Thepen, T.; Barth, S. Microtubule-associated protein tau facilitates the targeted killing of proliferating cancer cells in vitro and in a xenograft mouse tumour model in vivo. Br. J. Cancer 2013, 109, 1570–1578. [Google Scholar] [CrossRef] [PubMed]
- Amoury, M.; Mladenov, R.; Nachreiner, T.; Pham, A.T.; Hristodorov, D.; Di Fiore, S.; Helfrich, W.; Pardo, A.; Fey, G.; Schwenkert, M.; et al. A novel approach for targeted elimination of CSPG4-positive triple-negative breast cancer cells using a MAP tau-based fusion protein. Int. J. Cancer 2016, 139, 916–927. [Google Scholar] [CrossRef] [PubMed]
- Schiffer, S.; Letzian, S.; Jost, E.; Mladenov, R.; Hristodorov, D.; Huhn, M.; Fischer, R.; Barth, S.; Thepen, T. Granzyme M as a novel effector molecule for human cytolytic fusion proteins: CD64-specific cytotoxicity of Gm-H22(scFv) against leukemic cells. Cancer Lett. 2013, 341, 178–185. [Google Scholar] [CrossRef] [PubMed]
- Veugelers, K.; Motyka, B.; Goping, S.; Shostak, I.; Sawchuk, T.; Bleackley, R.C. Granule-mediated killing by granzyme B and perforin requires a mannose 6-phosphate receptor and is augmented by cell surface heparan sulfate. Mol. Biol. Cell 2006, 17, 623–633. [Google Scholar] [CrossRef] [PubMed]
- Heibein, J.A.; Goping, S.; Barry, M.; Pinkoski, M.J.; Shore, G.C.; Green, D.R.; Bleackley, R.C. Granzyme B–mediated cytochrome c release is regulated by the Bcl-2 family members bid and Bax. J. Exp. Med. 2000, 192, 1391–1402. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Bird, C.H.; Sutton, V.; McDonald, L.; Coughlin, P.B.; De Jong, T.A.; Trapani, J.A.; Bird, P.I. A cytosolic granzyme B inhibitor related to the viral apoptotic regulator cytokine response modifier A is present in cytotoxic lymphocytes. J. Biol. Chem. 1996, 271, 27802–27809. [Google Scholar] [CrossRef] [PubMed]
- Hirst, C.E.; Buzza, M.S.; Bird, C.H.; Warren, H.S.; Cameron, P.U.; Zhang, M.; Ashton-Rickardt, P.G.; Bird, P.I. The Intracellular Granzyme B Inhibitor, Proteinase Inhibitor 9, Is Up-Regulated During Accessory Cell Maturation and Effector Cell Degranulation, and Its Overexpression Enhances CTL Potency. J. Immunol. 2003, 170, 805–815. [Google Scholar] [CrossRef] [PubMed]
- Rousalova, I.; Krepela, E.; Prochazka, J.; Cermak, J.; Benkova, K. Expression of proteinase inhibitor-9/serpinB9 in non-small cell lung carcinoma cells and tissues. Int. J. Oncol. 2010, 36, 275–283. [Google Scholar] [PubMed]
- Losasso, V.; Schiffer, S.; Barth, S.; Carloni, P. Design of human granzyme B variants resistant to serpin B9. Proteins Struct. Funct. Bioinform. 2012, 80, 2514–2522. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Xu, Z. Mechanisms of action of angiogenin. Acta Biochim. Biophys. Sin. 2008, 40, 619–624. [Google Scholar] [CrossRef] [PubMed]
- Czech, A.; Wende, S.; Morl, M.; Pan, T.; Ignatova, Z. Reversible and rapid transfer-RNA deactivation as a mechanism of translational repression in stress. PLoS Genet. 2013, 9, e1003767. [Google Scholar] [CrossRef] [PubMed]
- Dickson, K.A.; Kang, D.K.; Kwon, Y.S.; Kim, J.C.; Leland, P.A.; Kim, B.M.; Chang, S.I.; Raines, R.T. Ribonuclease inhibitor regulates neovascularization by human angiogenin. Biochemistry 2009, 48, 3804–3806. [Google Scholar] [CrossRef] [PubMed]
- Pizzo, E.; Sarcinelli, C.; Sheng, J.; Fusco, S.; Formiggini, F.; Netti, P.; Yu, W.; D'Alessio, G.; Hu, G.F. Ribonuclease/angiogenin inhibitor 1 regulates stress-induced subcellular localization of angiogenin to control growth and survival. J. Cell Sci. 2013, 126, 4308–4319. [Google Scholar] [CrossRef] [PubMed]
- Cong, X.; Cremer, C.; Nachreiner, T.; Barth, S.; Carloni, P. Engineered human angiogenin mutations in the placental ribonuclease inhibitor complex for anticancer therapy: Insights from enhanced sampling simulations. Protein Sci. 2016, 25, 1451–1460. [Google Scholar] [CrossRef]
- Cremer, C.; Braun, H.; Mladenov, R.; Schenke, L.; Cong, X.; Jost, E.; Brummendorf, T.H.; Fischer, R.; Carloni, P.; Barth, S.; et al. Novel angiogenin mutants with increased cytotoxicity enhance the depletion of pro-inflammatory macrophages and leukemia cells ex vivo. Cancer Immunol. Immunother. 2015, 64, 1575–1586. [Google Scholar] [CrossRef]
- Bershtein, S.; Tawfik, D.S. Advances in laboratory evolution of enzymes. Curr. Opin. Chem. Biol. 2008, 12, 151–158. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, M.K.; Singh, R.; Singh, R.K.; Kim, I.-W.; Lee, J.-K. Computational approaches for rational design of proteins with novel functionalities. Comput. Struct. Biotechnol. J. 2012, 2, e201209002. [Google Scholar] [CrossRef] [PubMed]
- Mandell, D.J.; Kortemme, T. Computer-aided design of functional protein interactions. Nat. Chem. Biol. 2009, 5, 797–807. [Google Scholar] [CrossRef] [PubMed]
- Fiser, A. Protein structure modeling in the proteomics era. Expert Rev Proteom. 2004, 1, 97–110. [Google Scholar] [CrossRef] [PubMed]
- Karplus, M.; McCammon, J.A. Molecular dynamics simulations of biomolecules. Nat. Struct. Mol. Biol. 2002, 9, 646–652. [Google Scholar] [CrossRef] [PubMed]
- Krieger, E.; Nabuurs, S.B.; Vriend, G. Homology Modeling. Struct. Bioinform. 2003, 25, 507–520. [Google Scholar]
- Epstein, C.J.; Goldberger, R.F.; Anfinsen, C.B. The Genetic Control of Tertiary Protein Structure: Studies With Model Systems. Cold Spring Harb. Symp. Quant. Biol. 1963, 28, 439–449. [Google Scholar] [CrossRef]
- Chothia, C.; Lesk, A.M. The relation between the divergence of sequence and structure in proteins. EMBO J. 1986, 5, 823–826. [Google Scholar] [PubMed]
- Sander, C.; Schneider, R. Database of homology-derived protein structures and the structural meaning of sequence alignment. Proteins 1991, 9, 56–68. [Google Scholar] [CrossRef] [PubMed]
- Rost, B. Twilight zone of protein sequence alignments. Protein Eng. 1999, 12, 85–94. [Google Scholar] [CrossRef] [PubMed]
- Sternberg, M.J.E.; Bates, P.A.; Kelley, L.A.; MacCallum, R.M. Progress in protein structure prediction: Assessment of CASP3. Curr. Opin. Struct. Biol. 1999, 9, 368–373. [Google Scholar] [CrossRef]
- Marti-Renom, M.A.; Stuart, A.C.; Fiser, A.; Sanchez, R.; Melo, F.; Sali, A. Comparative protein structure modeling of genes and genomes. Annu. Rev. Biophys. Biomol. Struct. 2000, 29, 291–325. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, R.; Sali, A. Evaluation of comparative protein structure modeling by MODELLER-3. Proteins 1997, 1, 50–88. [Google Scholar] [CrossRef]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The protein data bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Altschul, S.F.; Gish, W.; Miller, W.; Myers, E.W.; Lipman, D.J. Basic local alignment search tool. J. Mol. Biol. 1990, 215, 403–410. [Google Scholar] [CrossRef]
- Pearson, W.R. Rapid and sensitive sequence comparison with FASTP and FASTA. Methods Enzymol. 1990, 183, 63–98. [Google Scholar] [PubMed]
- Thompson, J.D.; Higgins, D.G.; Gibson, T.J. CLUSTAL W: Improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 1994, 22, 4673–4680. [Google Scholar] [CrossRef] [PubMed]
- Lassmann, T.; Sonnhammer, E.L. Quality assessment of multiple alignment programs. FEBS Lett. 2002, 529, 126–130. [Google Scholar] [CrossRef]
- Feng, D.F.; Doolittle, R.F. Progressive sequence alignment as a prerequisite to correct phylogenetic trees. J. Mol. Evol. 1987, 25, 351–360. [Google Scholar] [CrossRef] [PubMed]
- Hirosawa, M.; Totoki, Y.; Hoshida, M.; Ishikawa, M. Comprehensive study on iterative algorithms of multiple sequence alignment. Bioinformatics 1995, 11, 13–18. [Google Scholar] [CrossRef]
- Tramontano, A.; Cozzetto, D. Evaluation of Protein Structure Prediction Methods: Issues and Strategies, in Multiscale Approaches to Protein Modeling; Springer: New York, NY, USA, 2011; pp. 315–339. [Google Scholar]
- Blundell, T.L.; Sibanda, B.L.; Sternberg, M.J.E.; Thornton, J.M. Knowledge-based prediction of protein structures and the design of novel molecules. Nature 1987, 326, 347–352. [Google Scholar] [CrossRef] [PubMed]
- Claessens, M.; van Cutsem, E.; Lasters, I.; Wodak, S. Modelling the polypeptide backbone with ‘spare parts’ from known protein structures. Protein Eng. 1989, 2, 335–345. [Google Scholar] [CrossRef] [PubMed]
- Levitt, M. Accurate modeling of protein conformation by automatic segment matching. J. Mol. Biol. 1992, 226, 39–46. [Google Scholar] [CrossRef]
- Srinivasan, S.; March, C.J.; Sudarsanam, S. An automated method for modeling proteins on known templates using distance geometry. Protein Sci. 1993, 2, 277–289. [Google Scholar] [CrossRef] [PubMed]
- Sali, A.; Blundell, T.L. Comparative protein modelling by satisfaction of spatial restraints. J. Mol. Biol. 1993, 234, 779–815. [Google Scholar] [CrossRef] [PubMed]
- Shen, M.Y.; Sali, A. Statistical potential for assessment and prediction of protein structures. Protein Sci. 2006, 15, 2507–2524. [Google Scholar] [CrossRef] [PubMed]
- Guex, N.; Peitsch, M.C. SWISS-MODEL and the Swiss-Pdb Viewer: An environment for comparative protein modeling. Electrophoresis 1997, 18, 2714–2723. [Google Scholar] [CrossRef] [PubMed]
- Bower, M.J.; Cohen, F.E.; Dunbrack, R.L., Jr. Prediction of protein side-chain rotamers from a backbone-dependent rotamer library: A new homology modeling tool. J. Mol. Biol. 1997, 267, 1268–1282. [Google Scholar] [CrossRef] [PubMed]
- Bates, P.A.; Kelley, L.A.; MacCallum, R.M.; Sternberg, M.J.E. Enhancement of protein modeling by human intervention in applying the automatic programs 3D-JIGSAW and 3D-PSSM. Proteins Struct. Funct. Bioinform. 2001, 45, 39–46. [Google Scholar] [CrossRef] [PubMed]
- Kopp, J.; Schwede, T. The SWISS-MODEL Repository of annotated three-dimensional protein structure homology models. Nucleic Acids Res. 2004, 32, D230–D234. [Google Scholar] [CrossRef] [PubMed]
- Fiser, A.; Do, R.K.; Sali, A. Modeling of loops in protein structures. Protein Sci. 2000, 9, 1753–1773. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Zhou, Y. Distance-scaled, finite ideal-gas reference state improves structure-derived potentials of mean force for structure selection and stability prediction. Protein Sci. 2002, 11, 2714–2726. [Google Scholar] [CrossRef] [PubMed]
- Benkert, P.; Fau, D.T.S.; Schomburg, D. QMEAN: A comprehensive scoring function for model quality assessment. Proteins Struct. Funct. Bioinform. 2008, 71, 261–277. [Google Scholar] [CrossRef] [PubMed]
- Laskowski, R.A.; Macarthur, M.W.; Moss, D.S.; Thornton, J.M. PROCHECK: A program to check the stereochemical quality of protein structures. J. Appl. Cryst. 1993, 26, 283–291. [Google Scholar] [CrossRef]
- Hooft, R.W.; Vriend, G.; Sander, C.; Abola, E.E. Errors in protein structures. Nature 1996, 381, 272. [Google Scholar] [CrossRef] [PubMed]
- Di Luccio, E.; Koehl, P. A quality metric for homology modeling: The H-factor. BMC Bioinform. 2011, 12, 48. [Google Scholar] [CrossRef] [PubMed]
- Clackson, T.; Wells, J.A. A hot spot of binding energy in a hormone-receptor interface. Science 1995, 267, 383. [Google Scholar] [CrossRef] [PubMed]
- Bogan, A.A.; Thorn, K.S. Anatomy of hot spots in protein interfaces1. J. Mol. Biol. 1998, 280, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Kortemme, T.; Kim, D.E.; Baker, D. Computational alanine scanning of protein-protein interfaces. Sci. STKE 2004, 2004. [Google Scholar] [CrossRef] [PubMed]
- Kortemme, T.; Baker, D. A simple physical model for binding energy hot spots in protein-protein complexes. Proc. Natl. Acad. Sci. USA 2002, 99, 14116–14121. [Google Scholar] [CrossRef] [PubMed]
- Guerois, R.; Nielsen, J.E.; Serrano, L. Predicting changes in the stability of proteins and protein complexes: A study of more than 1000 mutations. J. Mol. Biol. 2002, 320, 369–387. [Google Scholar] [CrossRef]
- Ribeiro, J.V.; Cerqueira, N.M.F.S.A.; Moreira, I.S.; Fernandes, P.A.; Ramos, M.J. CompASM: An Amber-VMD alanine scanning mutagenesis plug-in. Theor. Chem. Acc. 2012, 131, 1271. [Google Scholar] [CrossRef]
- Kim, D.E.; Chivian, D.; Baker, D. Protein structure prediction and analysis using the Robetta server. Nucleic Acids Res. 2004, 32, W526–W531. [Google Scholar] [CrossRef] [PubMed]
- Kortemme, T.; Morozov, A.V.; Baker, D. An orientation-dependent hydrogen bonding potential improves prediction of specificity and structure for proteins and protein-protein complexes. J. Mol. Biol. 2003, 326, 1239–1259. [Google Scholar] [CrossRef]
- Lazaridis, T.; Karplus, M. Discrimination of the native from misfolded protein models with an energy function including implicit solvation 1. J. Mol. Biol. 1999, 288, 477–487. [Google Scholar] [CrossRef] [PubMed]
- Fogolari, F.; Brigo, A.; Molinari, H. The Poisson-Boltzmann equation for biomolecular electrostatics: A tool for structural biology. J. Mol. Recognit. 2002, 15, 377–392. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.-J.; Zhang, Y.B.; Ding, Y. Binding mechanism between Hsp90 and Sgt1 explored by homology modeling and molecular dynamics simulations in rice. J. Mol. Model. 2012, 18, 4665–4673. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ding, Y. Molecular dynamics simulation and bioinformatics study on chloroplast stromal ridge complex from rice (Oryza sativa L.). BMC Bioinform. 2016, 17, 28. [Google Scholar] [CrossRef] [PubMed]
- Darnell, S.J.; PAGE, D.; Mitchell, J.C. An automated decision-tree approach to predicting protein interaction hot spots. Proteins Struct. Funct. Bioinform. 2007, 68, 813–823. [Google Scholar] [CrossRef] [PubMed]
- Ofran, Y.; Rost, B. Protein–Protein Interaction Hotspots Carved into Sequences. PLoS Comput. Biol. 2007, 3, e119. [Google Scholar] [CrossRef] [PubMed]
- Karplus, M.; Petsko, G.A. Molecular dynamics simulations in biology. Nature 1990, 347, 631–639. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: New York, NY, USA, 1989. [Google Scholar]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A 2nd generation force-field for the simulation of proteins, nucleic-acids, and organic-molecules. J. Am. Chem. Soc. 1995, 117, 5179. [Google Scholar] [CrossRef]
- MacKerell, A.D.; Bashford, D.; Bellott, M.; Dunbrack, R.L.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Tiradorives, J. The Opls Potential Functions for proteins—Energy minimizations for crystals of cyclic-peptides and crambin. J. Am. Chem. Soc. 1988, 110, 1657. [Google Scholar] [CrossRef] [PubMed]
- Brooks, B.R.; Bruccoleri, R.E.; Olafson, B.D.; States, D.J.; Swaminathan, S.; Karplus, M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh ewald method. J. Chem. Phys. 1995, 103, 8577. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N·log(N) method for ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089. [Google Scholar] [CrossRef]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; van der Spoel, D.; et al. GROMACS 4.5: A high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef] [PubMed]
- Miyamoto, S.; Kollman, P.A. Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Hünenberger, P.; Holm, C.; Kremer, K. Advanced Computer Simulation; Springer: Berlin, Germany, 2005; Volume 173, p. 105. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation; Academic Press, Inc.: Orlando, FL, USA, 2001; p. 638. [Google Scholar]
- Lebowitz, J.L. Hamiltonian Flows and Rigorous Results in Nonequilibrium Statistical Mechanics; Statistical Mechanics: New Concepts, New Problems, New Applications; University of Chicago Press: Chicago, IL, USA, 1972. [Google Scholar]
- Masetti, M.; Rocchia, W. Molecular mechanics and dynamics: Numerical tools to sample the configuration space. Front. Biosci. 2014, 1, 578–604. [Google Scholar] [CrossRef]
- Baker, C.M. Polarizable force fields for molecular dynamics simulations of biomolecules. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2015, 5, 241–254. [Google Scholar] [CrossRef]
- Sanbonmatsu, K.Y.; Tung, C.S. High performance computing in biology: Multimillion atom simulations of nanoscale systems. J. Struct. Biol. 2007, 157, 470–480. [Google Scholar] [CrossRef] [PubMed]
- Shaw, D.E.; Deneroff, M.M.; Dror, R.O.; Kuskin, J.S.; Larson, R.H.; Salmon, J.K.; Young, C.; Batson, B.; Bowers, K.J.; Chao, J.C.; et al. Anton, a special-purpose machine for molecular dynamics simulation. Commun. ACM 2008, 51, 91–97. [Google Scholar] [CrossRef]
- Shaw, D.E.; Dror, R.O.; Salmon, J.K.; Grossman, J.P.; Mackenzie, K.M.; Bank, J.A.; Young, C.; Deneroff, M.M.; Batson, B.; Bowers, K.J.; et al. Millisecond-scale molecular dynamics simulations on Anton. In Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis, Portland, OR, USA, 14–20 November 2009; ACM: Portland, OR, USA, 2009; pp. 1–11. [Google Scholar]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef]
- Oldziej, S.; Czaplewski, C.; Liwo, A.; Chinchio, M.; Nanias, M.; Khalili, M.; Arnautova, Y.A.; Jagielska, A.; Makowski, M.; Schafroth, H.D.; et al. Physics-based protein-structure prediction using a hierarchical protocol based on the UNRES force field: Assessment in two blind tests. Proc. Natl. Acad. Sci. USA 2005, 102, 7547–7552. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Saven, J.G. Computational methods for protein design and protein sequence variability: biased Monte Carlo and replica exchange. Chem. Phys. Lett. 2005, 401, 205–210. [Google Scholar] [CrossRef]
- Rosso, L.; Tuckerman, M.E. An Adiabatic Molecular Dynamics Method for the Calculation of Free Energy Profiles. Mol. Simul. 2002, 28, 91–112. [Google Scholar] [CrossRef]
- Laghaei, R.; Mousseau, N.; Wei, G. Effect of the disulfide bond on the monomeric structure of human amylin studied by combined Hamiltonian and temperature replica exchange molecular dynamics simulations. J. Phys. Chem. B 2010, 114, 7071–7077. [Google Scholar] [CrossRef] [PubMed]
- Bergonzo, C.; Henriksen, N.M.; Roe, D.R.; Cheatham, T.E. Highly sampled tetranucleotide and tetraloop motifs enable evaluation of common RNA force fields. RNA 2015, 21, 1578–1590. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Kim, B.; Friesner, R.A.; Berne, B.J. Replica exchange with solute tempering: A method for sampling biological systems in explicit water. Proc. Natl. Acad. Sci. USA 2005, 102, 13749–13754. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Hagen, M.; Kim, B.; Friesner, R.A.; Zhou, R.; Berne, B.J. Replica Exchange with Solute Tempering: Efficiency in Large Scale Systems. J. Phys. Chem. B 2007, 111, 5405–5410. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Friesner, R.A.; Berne, B.J. Replica exchange with solute scaling: A more efficient version of replica exchange with solute tempering (REST2). J. Phys. Chem. B 2011, 115, 9431–9438. [Google Scholar] [CrossRef] [PubMed]
- Schiffer, S.; Hristodorov, D.; Mladenov, R.; Aslanian, E.; Huhn, M.; Fischer, R.; Barth, S.; Thepen, T. Species-Dependent Functionality of the Human Cytolytic Fusion Proteins Granzyme B-H22(scFv) and H22(scFv)-Angiogenin in Macrophages. Antibodies 2013, 2, 9–18. [Google Scholar] [CrossRef]
- Kuan, C.T.; Pai, L.H.; Pastan, I. Immunotoxins containing Pseudomonas exotoxin that target LeY damage human endothelial cells in an antibody-specific mode: relevance to vascular leak syndrome. Clin. Cancer Res. 1995, 1, 1589–1594. [Google Scholar] [PubMed]
- Siegall, C.B.; Liggitt, D.; Chace, D.; Mixan, B.; Sugai, J.; Davidson, T.; Steinitz, M. Characterization of vascular leak syndrome induced by the toxin component of Pseudomonas exotoxin-based immunotoxins and its potential inhibition with nonsteroidal anti-inflammatory drugs. Clin. Cancer Res. 1997, 3, 339–345. [Google Scholar] [PubMed]
- Silverman, G.A.; Bird, P.I.; Carrell, R.W.; Church, F.C.; Coughlin, P.B.; Gettins, P.G.; Irving, J.A.; Lomas, D.A.; Luke, C.J.; Moyer, R.W.; et al. The serpins are an expanding superfamily of structurally similar but functionally diverse proteins. Evolution, mechanism of inhibition, novel functions, and a revised nomenclature. J. Biol. Chem. 2001, 276, 33293–33296. [Google Scholar] [CrossRef] [PubMed]
- Kurschus, F.C.; Jenne, D.E. Delivery and therapeutic potential of human granzyme B. Immunol. Rev. 2010, 235, 159–171. [Google Scholar] [CrossRef] [PubMed]
- Schechter, I.; Berger, A. On the size of the active site in proteases. I. Papain. 1967. Biochem. Biophys. Res. Commun. 2012, 425, 497–502. [Google Scholar] [PubMed]
- Huntington, J.A.; Read, R.J.; Carrell, R.W. Structure of a serpin-protease complex shows inhibition by deformation. Nature 2000, 407, 923–926. [Google Scholar] [CrossRef] [PubMed]
- Huntington, J.A.; Stein, P.E. Structure and properties of ovalbumin. J. Chromatogr. B Biomed. Sci. Appl. 2001, 756, 189–198. [Google Scholar] [CrossRef]
- Sun, J.; Ooms, L.; Bird, C.H.; Sutton, V.R.; Trapani, J.A.; Bird, P.I. A new family of 10 murine ovalbumin serpins includes two homologs of proteinase inhibitor 8 and two homologs of the granzyme B inhibitor (proteinase inhibitor 9). J. Biol. Chem. 1997, 272, 15434–15441. [Google Scholar] [CrossRef] [PubMed]
- Hehmann-Titt, G.; Schiffer, S.; Berges, N.; Melmer, G.; Barth, S. Improving the Therapeutic Potential of Human Granzyme B for Targeted Cancer Therapy. Antibodies 2013, 2, 19–49. [Google Scholar] [CrossRef]
- Jiang, X.; Ellison, S.J.; Alarid, E.T.; Shapiro, D.J. Interplay between the levels of estrogen and estrogen receptor controls the level of the granzyme inhibitor, proteinase inhibitor 9 and susceptibility to immune surveillance by natural killer cells. Oncogene 2007, 26, 4106–4114. [Google Scholar] [CrossRef] [PubMed]
- Van Houdt, I.S.; Oudejans, J.J.; van den Eertwegh, A.J.; Baars, A.; Vos, W.; Bladergroen, B.A.; Rimoldi, D.; Muris, J.J.; Hooijberg, E.; Gundy, C.M.; et al. Expression of the apoptosis inhibitor protease inhibitor 9 predicts clinical outcome in vaccinated patients with stage III and IV melanoma. Clin. Cancer Res. 2005, 11, 6400–6407. [Google Scholar] [CrossRef] [PubMed]
- Soriano, C.; Mukaro, V.; Hodge, G.; Ahern, J.; Holmes, M.; Jersmann, H.; Moffat, D.; Meredith, D.; Jurisevic, C.; Reynolds, P.N.; et al. Increased proteinase inhibitor-9 (PI-9) and reduced granzyme B in lung cancer: mechanism for immune evasion? Lung Cancer 2012, 77, 38–45. [Google Scholar] [CrossRef] [PubMed]
- Ray, M.; Hostetter, D.R.; Loeb, C.R.; Simko, J.; Craik, C.S. Inhibition of Granzyme B by PI-9 protects prostate cancer cells from apoptosis. Prostate 2012, 72, 846–855. [Google Scholar] [CrossRef] [PubMed]
- Courville, E.L.; Wu, Y.; Kourda, J.; Roth, C.G.; Brockmann, J.; Muzikansky, A.; Fathi, A.T.; de Leval, L.; Orazi, A.; Hasserjian, R.P. Clinicopathologic analysis of acute myeloid leukemia arising from chronic myelomonocytic leukemia. Mod. Pathol. 2013, 26, 751–761. [Google Scholar] [CrossRef] [PubMed]
- Schiffer, S.; Rosinke, R.; Jost, E.; Hehmann-Titt, G.; Huhn, M.; Melmer, G.; Barth, S.; Thepen, T. Targeted ex vivo reduction of CD64-positive monocytes in chronic myelomonocytic leukemia and acute myelomonocytic leukemia using human granzyme B-based cytolytic fusion proteins. Int. J. Cancer 2014, 135, 1497–1508. [Google Scholar] [CrossRef] [PubMed]
- Bladergroen, B.A.; Meijer, C.J.; ten Berge, R.L.; Hack, C.E.; Muris, J.J.; Dukers, D.F.; Chott, A.; Kazama, Y.; Oudejans, J.J.; van Berkum, O.; et al. Expression of the granzyme B inhibitor, protease inhibitor 9, by tumor cells in patients with non-Hodgkin and Hodgkin lymphoma: A novel protective mechanism for tumor cells to circumvent the immune system? Blood 2002, 99, 232–237. [Google Scholar] [CrossRef] [PubMed]
- Schiffer, S.; Hansen, H.P.; Hehmann-Titt, G.; Huhn, M.; Fischer, R.; Barth, S.; Thepen, T. Efficacy of an adapted granzyme B-based anti-CD30 cytolytic fusion protein against PI-9-positive classical Hodgkin lymphoma cells in a murine model. Blood Cancer J. 2013, 3, e106. [Google Scholar] [CrossRef] [PubMed]
- Niesen, J.; Stein, C.; Brehm, H.; Hehmann-Titt, G.; Fendel, R.; Melmer, G.; Fischer, R.; Barth, S. Novel EGFR-specific immunotoxins based on panitumumab and cetuximab show in vitro and ex vivo activity against different tumor entities. J. Cancer Res. Clin. Oncol. 2015, 141, 2079–2095. [Google Scholar] [CrossRef] [PubMed]
- Niesen, J.; Hehmann-Titt, G.; Woitok, M.; Fendel, R.; Barth, S.; Fischer, R.; Stein, C. A novel fully-human cytolytic fusion protein based on granzyme B shows in vitro cytotoxicity and ex vivo binding to solid tumors overexpressing the epidermal growth factor receptor. Cancer Lett 2016, 374, 229–240. [Google Scholar] [CrossRef] [PubMed]
- Soysal, S.D.; Muenst, S.; Barbie, T.; Fleming, T.; Gao, F.; Spizzo, G.; Oertli, D.; Viehl, C.T.; Obermann, E.C.; Gillanders, W.E. EpCAM expression varies significantly and is differentially associated with prognosis in the luminal B HER2+, basal-like, and HER2 intrinsic subtypes of breast cancer. Br. J. Cancer 2013, 108, 1480–1487. [Google Scholar] [CrossRef] [PubMed]
- Bottger, E.; Multhoff, G.; Kun, J.F.; Esen, M. Plasmodium falciparum-infected erythrocytes induce granzyme B by NK cells through expression of host-Hsp70. PLoS ONE 2012, 7, e33774. [Google Scholar] [CrossRef] [PubMed]
- Meslin, B.; Barnadas, C.; Boni, V.; Latour, C.; De Monbrison, F.; Kaiser, K.; Picot, S. Features of apoptosis in Plasmodium falciparum erythrocytic stage through a putative role of PfMCA1 metacaspase-like protein. J. Infect. Dis. 2007, 195, 1852–1859. [Google Scholar] [CrossRef]
- Kapelski, S.; de Almeida, M.; Fischer, R.; Barth, S.; Fendel, R. Antimalarial activity of granzyme B and its targeted delivery by a granzyme B-single-chain Fv fusion protein. Antimicrob. Agents Chemother. 2015, 59, 669–672. [Google Scholar] [CrossRef] [PubMed]
- Stöcker, M.; Tur, M.K.; Sasse, S.; Krüßmann, A.; Barth, S.; Engert, A. Secretion of functional anti-CD30-angiogenin immunotoxins into the supernatant of transfected 293T-cells. Protein Expr. Purif. 2003, 28, 211–219. [Google Scholar] [CrossRef]
- Krauss, J.; Arndt, M.A.E.; Vu, B.K.; Newton, D.L.; Rybak, S.M. Targeting malignant B-cell lymphoma with a humanized anti-CD22 scFv-angiogenin immunoenzyme. Br. J. Haematol. 2005, 128, 602–609. [Google Scholar] [CrossRef] [PubMed]
- Pons, C.; Grosdidier, S.; Solernou, A.; Pérez-Cano, L.; Fernández-Recio, J. Present and future challenges and limitations in protein–protein docking. Proteins Struct. Funct. Bioinform. 2010, 78, 95–108. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Recio, J.; Totrov, M.; Abagyan, R. ICM-DISCO docking by global energy optimization with fully flexible side-chains. Proteins Struct. Funct. Bioinform. 2003, 52, 113–117. [Google Scholar] [CrossRef] [PubMed]
- Gray, J.J.; Moughon, S.; Wang, C.; Schueler-Furman, O.; Kuhlman, B.; Rohl, C.A.; Baker, D. Protein–Protein Docking with Simultaneous Optimization of Rigid-body Displacement and Side-chain Conformations. J. Mol. Biol. 2003, 331, 281–299. [Google Scholar] [CrossRef]
- Van Zundert, G.C.P.; Rodrigues, J.P.G.L.M.; Trellet, M.; Schmitz, C.; Kastritis, P.L.; Karaca, E.; Melquiond, A.S.J.; van Dijk, M.; de Vries, S.J.; Bonvin, A.M.J.J. The HADDOCK2.2 Web Server: User-Friendly Integrative Modeling of Biomolecular Complexes. J. Mol. Biol. 2016, 428, 720–725. [Google Scholar] [CrossRef] [PubMed]
- Dominguez, C.; Boelens, R.; Bonvin, A.M.J.J. HADDOCK: A Protein−Protein Docking Approach Based on Biochemical or Biophysical Information. J. Am. Chem. Soc. 2003, 125, 1731–1737. [Google Scholar] [CrossRef] [PubMed]
- Andrusier, N.; Nussinov, R.; Wolfson, H.J. FireDock: Fast interaction refinement in molecular docking. Proteins Struct. Funct. Bioinform. 2007, 69, 139–159. [Google Scholar] [CrossRef] [PubMed]
- Mashiach, E.; Sklenar, H. FireDock: A web server for fast interaction refinement in molecular docking. Nucleic Acids Res. 2008, 36, W229–W232. [Google Scholar] [CrossRef] [PubMed]
- Zacharias, M. ATTRACT: Protein–protein docking in CAPRI using a reduced protein model. Proteins Struct. Funct. Bioinform. 2005, 60, 252–256. [Google Scholar] [CrossRef] [PubMed]
- Zacharias, M.; Sklenar, H. Harmonic modes as variables to approximately account for receptor flexibility in ligand–receptor docking simulations: Application to DNA minor groove ligand complex. J. Comput. Chem. 1999, 20, 287–300. [Google Scholar] [CrossRef]
- Ma, B.; Kumar, S.; Tsai, C.-J.; Nussinov, R. Folding funnels and binding mechanisms. Protein Eng. 1999, 12, 713–720. [Google Scholar] [CrossRef] [PubMed]
- Torchala, M.; Moal, I.H.; Chaleil, R.A.G.; Fernandez-Recio, J.; Bates, P.A. SwarmDock: A server for flexible protein–protein docking. Bioinformatics 2013, 29, 807–809. [Google Scholar] [CrossRef] [PubMed]
- Torchala, M.; Moal, I.H.; Chaleil, R.A.G.; Agius, R.; Bates, P.A. A Markov-chain model description of binding funnels to enhance the ranking of docked solutions. Proteins Struct. Funct. Bioinform. 2013, 81, 2143–2149. [Google Scholar] [CrossRef]
- Kennedy, J. Particle Swarm Optimization, in Encyclopedia of Machine Learning; Springer: New York, NY, USA, 2011; pp. 760–766. [Google Scholar]
- Schneidman-Duhovny, D.; Nussinov, R.; Wolfson, H.J. Automatic prediction of protein interactions with large scale motion. Proteins Struct. Funct. Bioinform. 2007, 69, 764–773. [Google Scholar] [CrossRef] [PubMed]
- Ain, Q.U.; Aleksandrova, A.; Roessler, F.D.; Ballester, P.J. Machine-learning scoring functions to improve structure-based binding affinity prediction and virtual screening. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2015, 5, 405–424. [Google Scholar] [CrossRef] [PubMed]
- Carter, E.A.; Ciccotti, G.; Hynes, J.T.; Kapral, R. Constrained reaction coordinate dynamics for the simulation of rare events. Chem. Phys. Lett. 1989, 156, 472–477. [Google Scholar] [CrossRef]
- Bash, P.A.; Singh, U.C.; Langridge, R.; Kollman, P.A. Free energy calculations by computer simulation. Science 1987, 1, 236, 564–568. [Google Scholar] [CrossRef]
- Kumar, S.; Payne, P.W.; Vásquez, M. Method for free-energy calculations using iterative techniques. J. Comput. Chem. 1996, 17, 1269–1275. [Google Scholar] [CrossRef]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Darve, E.; Pohorille, A. Calculating free energies using average force. J. Chem. Phys. 2001, 115, 9169–9183. [Google Scholar] [CrossRef]
- Wang, F.; Landau, D.P. Efficient, Multiple-Range Random Walk Algorithm to Calculate the Density of States. Phys. Rev. Lett. 2001, 86, 2050–2053. [Google Scholar] [CrossRef] [PubMed]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef] [PubMed]
- Alessandro, L.; Francesco, L.G. Metadynamics: A method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science. Rep. Prog. Phys. 2008, 71, 126601. [Google Scholar]
- E, W.; Ren, W.; Vanden-Eijnden, E. Finite Temperature String Method for the Study of Rare Events. J. Phys. Chem. B 2005, 109, 6688–6693. [Google Scholar] [CrossRef] [PubMed]
- Bolhuis, P.G.; Chandler, D.; Dellago, C.; Geissler, P.L. Transition Path Sampling: Throwing Ropes Over Rough Mountain Passes, in the Dark. Annu. Rev. Phys. Chem. 2002, 53, 291–318. [Google Scholar] [CrossRef] [PubMed]
- Van Erp, T.S.; Moroni, D.; Bolhuis, P.G. A novel path sampling method for the calculation of rate constants. J. Chem. Phys. 2003, 118, 7762–7774. [Google Scholar] [CrossRef]
- Hansmann, U.H.E.; Okamoto, Y. Numerical comparisons of three recently proposed algorithms in the protein folding problem. J. Comput. Chem. 1997, 18, 920–933. [Google Scholar] [CrossRef]
- Hansmann, U.H.E.; Okamoto, Y. New Monte Carlo algorithms for protein folding. Curr. Opin. Struct. Biol. 1999, 9, 177–183. [Google Scholar] [CrossRef]
- Berg, B.A.; Neuhaus, T. Multicanonical algorithms for first order phase transitions. Phys. Lett. B 1991, 267, 249–253. [Google Scholar] [CrossRef]
- Lyubartsev, A.P.; Martsinovski, A.A.; Shevkunov, S.V.; Vorontsov-Velyaminov, P.N. New approach to Monte Carlo calculation of the free energy: Method of expanded ensembles. J. Chem. Phys. 1992, 96, 1776–1783. [Google Scholar] [CrossRef]
- Marinari, E.; Parisi, G. Simulated Tempering: A New Monte Carlo Scheme. EPL (Europhys. Lett.) 1992, 19, 451. [Google Scholar] [CrossRef]
- Sugita, Y.; Okamoto, Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314, 141–151. [Google Scholar] [CrossRef]
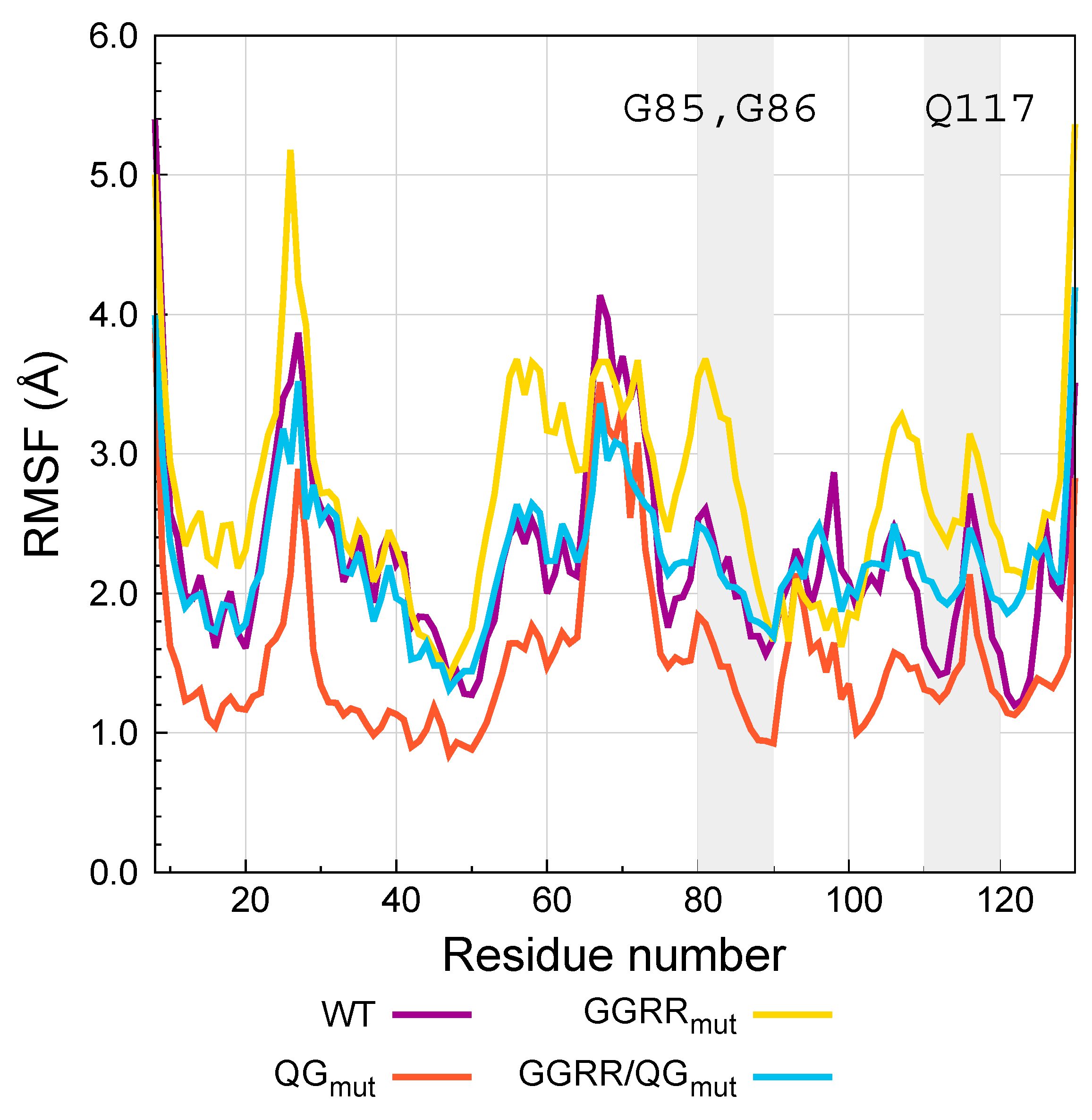
| Variant | RMSD (Å) |
|---|---|
| WT | 3.0 ± 0.6 |
| QGmut | 1.9 ± 0.4 |
| GGRRmut | 3.4 ± 0.8 |
| GGRR/QGmut | 4.2 ± 0.7 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bochicchio, A.; Jordaan, S.; Losasso, V.; Chetty, S.; Perera, R.C.; Ippoliti, E.; Barth, S.; Carloni, P. Designing the Sniper: Improving Targeted Human Cytolytic Fusion Proteins for Anti-Cancer Therapy via Molecular Simulation. Biomedicines 2017, 5, 9. https://doi.org/10.3390/biomedicines5010009
Bochicchio A, Jordaan S, Losasso V, Chetty S, Perera RC, Ippoliti E, Barth S, Carloni P. Designing the Sniper: Improving Targeted Human Cytolytic Fusion Proteins for Anti-Cancer Therapy via Molecular Simulation. Biomedicines. 2017; 5(1):9. https://doi.org/10.3390/biomedicines5010009
Chicago/Turabian StyleBochicchio, Anna, Sandra Jordaan, Valeria Losasso, Shivan Chetty, Rodrigo Casasnovas Perera, Emiliano Ippoliti, Stefan Barth, and Paolo Carloni. 2017. "Designing the Sniper: Improving Targeted Human Cytolytic Fusion Proteins for Anti-Cancer Therapy via Molecular Simulation" Biomedicines 5, no. 1: 9. https://doi.org/10.3390/biomedicines5010009
APA StyleBochicchio, A., Jordaan, S., Losasso, V., Chetty, S., Perera, R. C., Ippoliti, E., Barth, S., & Carloni, P. (2017). Designing the Sniper: Improving Targeted Human Cytolytic Fusion Proteins for Anti-Cancer Therapy via Molecular Simulation. Biomedicines, 5(1), 9. https://doi.org/10.3390/biomedicines5010009