Spike Timing-Dependent Plasticity and Random Inputs Shape Interspike Interval Regularity of Model STN Neurons
Abstract
1. Introduction
2. Materials and Methods
2.1. Keeping Track of Pre- and Postsynaptic Spikes
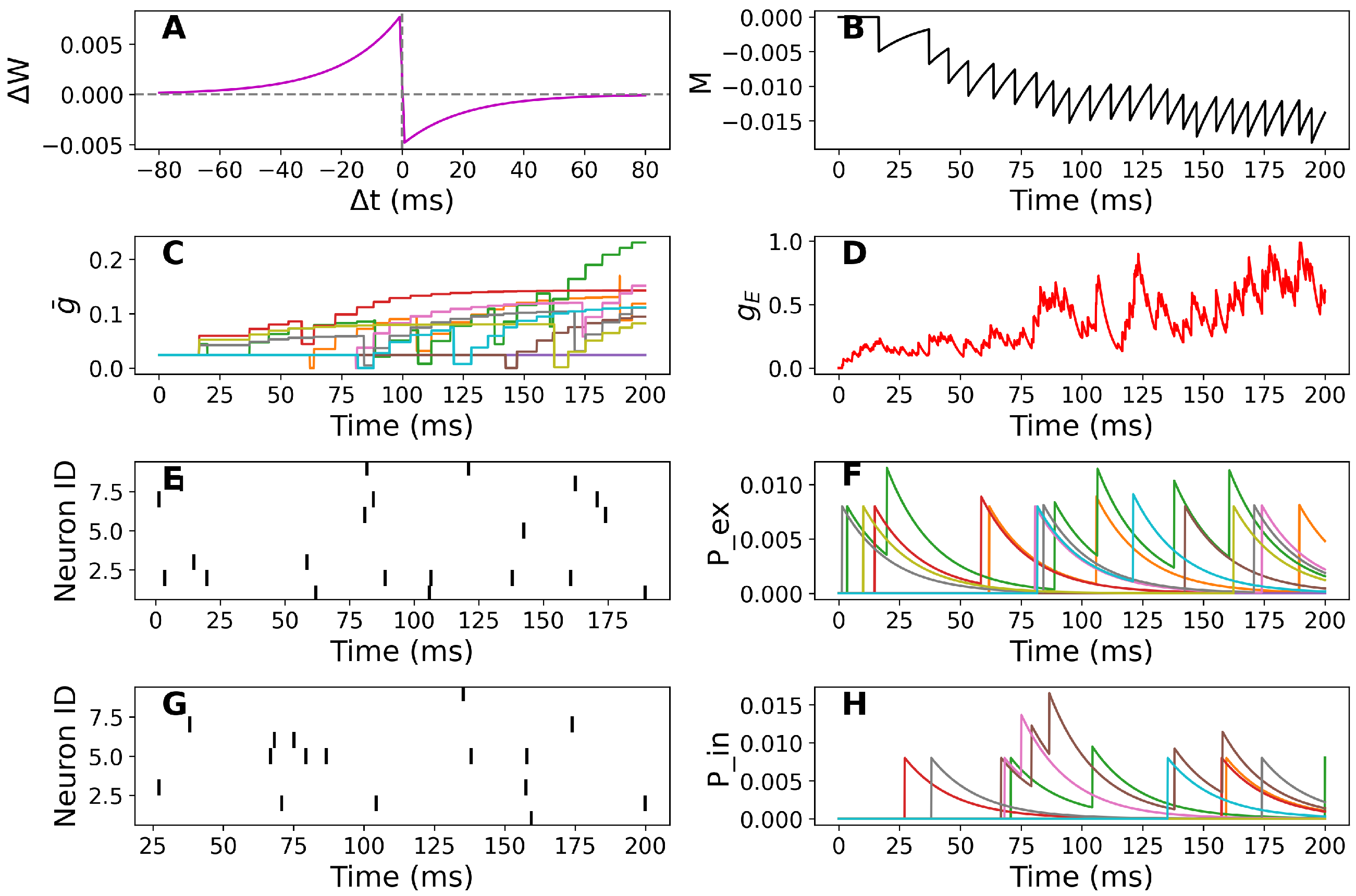
2.2. Implementation of STDP
- 1.
- When the i-th presynaptic neuron fires a spike, the peak conductance is updated as follows:Here, tracks the time since the last postsynaptic spike and is always negative. Therefore, if the postsynaptic neuron spikes shortly before the presynaptic neuron, the peak conductance will decrease, as indicated by the negative value of .
- 2.
- When the postsynaptic neuron fires a spike, the peak conductance of each synapse is updated as follows:Here, tracks the time since the last spike of the i-th presynaptic neuron and is always positive.Thus, if the presynaptic neuron spikes before the postsynaptic neuron, the peak conductance increases, as indicated by the positive value of .
2.3. Leaky Integrate-and-Fire Neuron Connected with Synapses That Show STDP
- For designing a spike generator of spike train, we define the probability of firing a spike within a short interval (see, e.g., [41]) as , where with representing the instantaneous excitatory and inhibitory firing rates, respectively.
- Then, a Poisson spike train is generated by first subdividing the time interval into a group of short sub-intervals through small time steps . In our model, we use (ms).
- We define a random variable with uniform distribution over the range between 0 and 1 at each time step.
- Finally, we compare the random variable with the probability of firing a spike, which reads as follows:
2.4. Effects of Input Correlations
- Common inputs: Neurons receiving input from the same sources tend to have correlated activity. The degree of correlation in their inputs influences the degree of correlation in their outputs.
- Pooling from correlated sources: Neurons may not share the same input neurons but could receive inputs from other neurons that are themselves correlated.
- Direct connections: Neurons connected to each other (either unidirectionally or bidirectionally) can exhibit time-delayed synchrony. Gap-junctions between neurons can also facilitate synchrony.
- Similar properties: Neurons with similar intrinsic parameters and initial conditions may also exhibit synchronous behavior.
2.5. STDP in Neuromorphic Systems and Other Applications
3. Results and Discussion
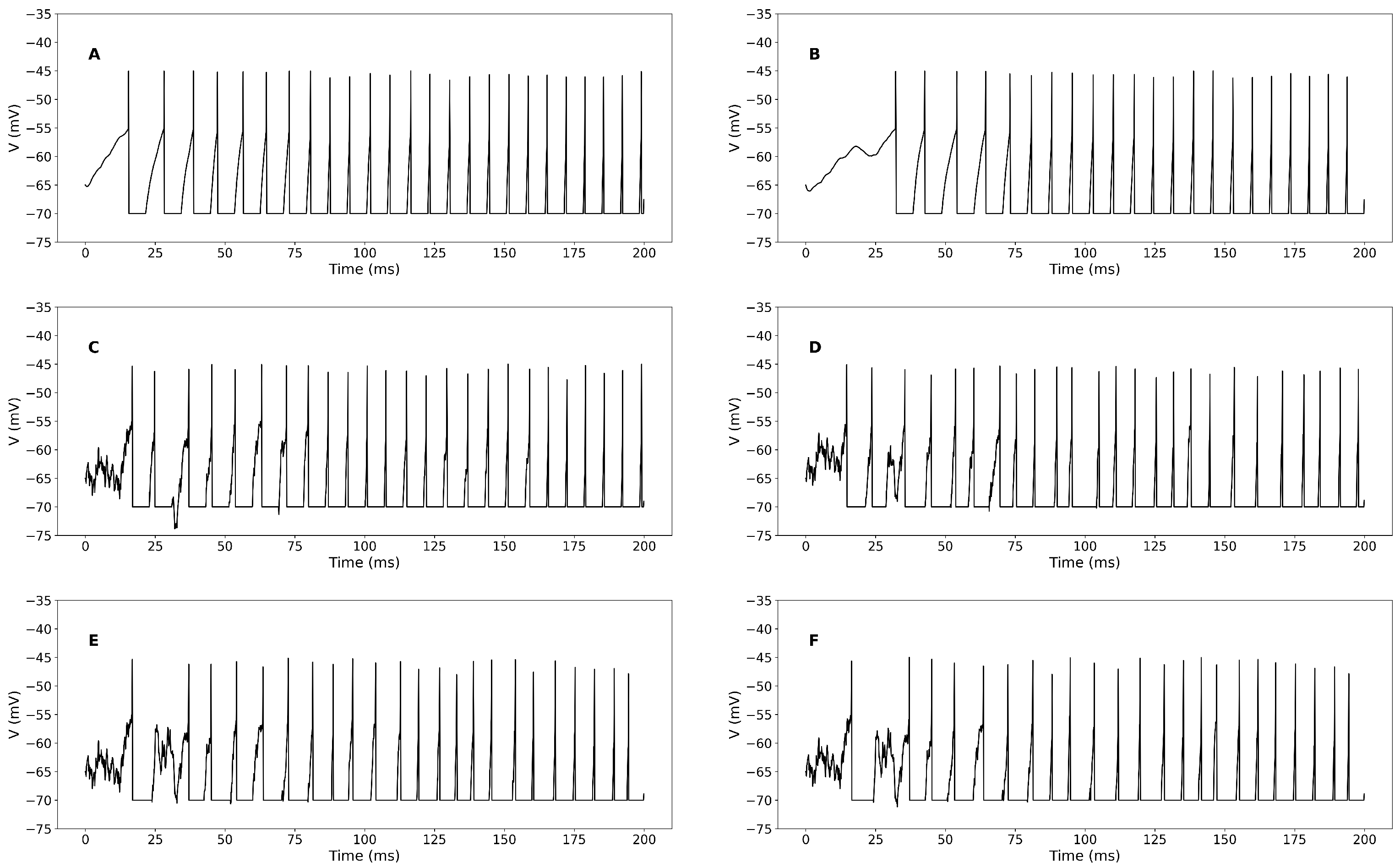
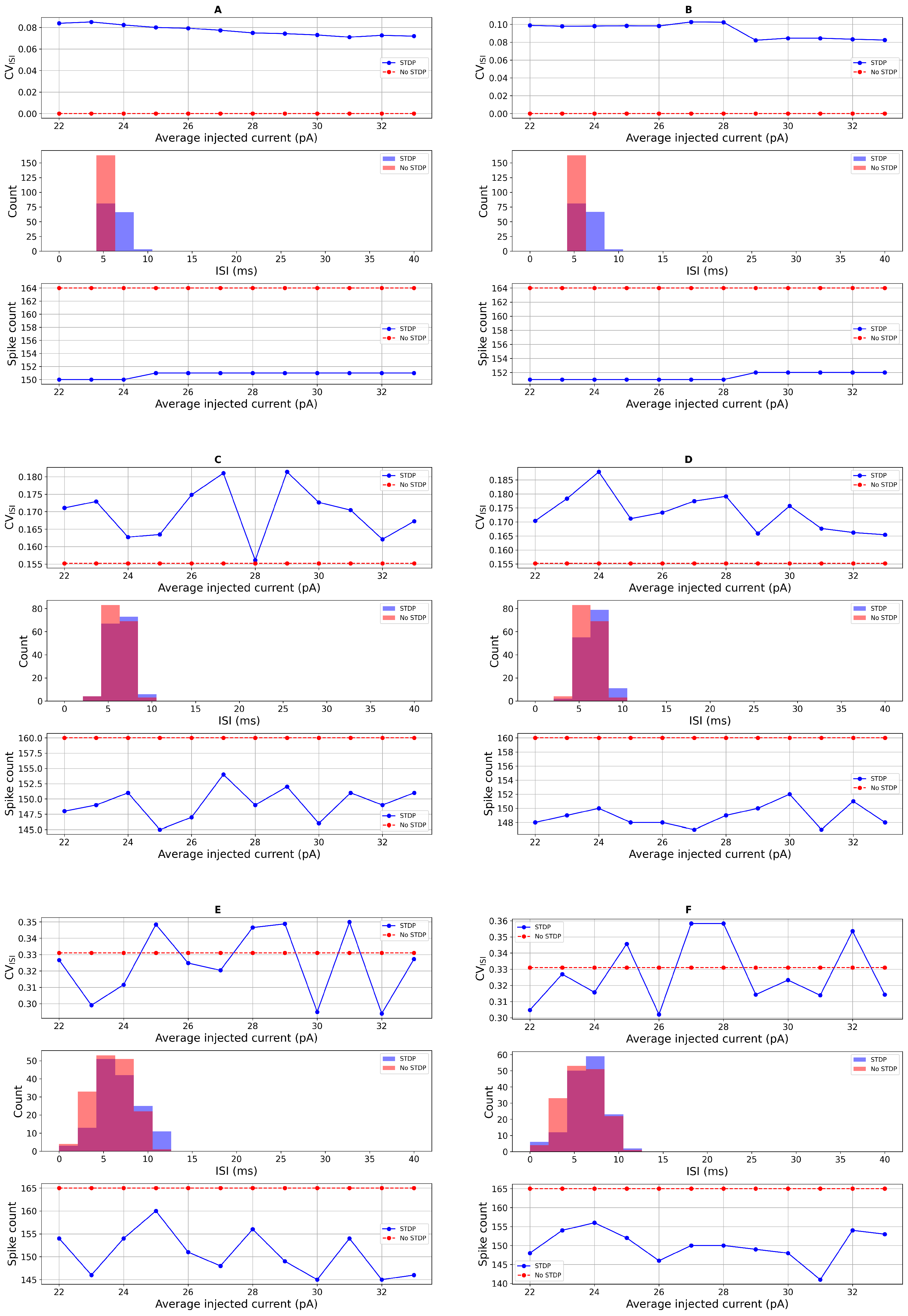
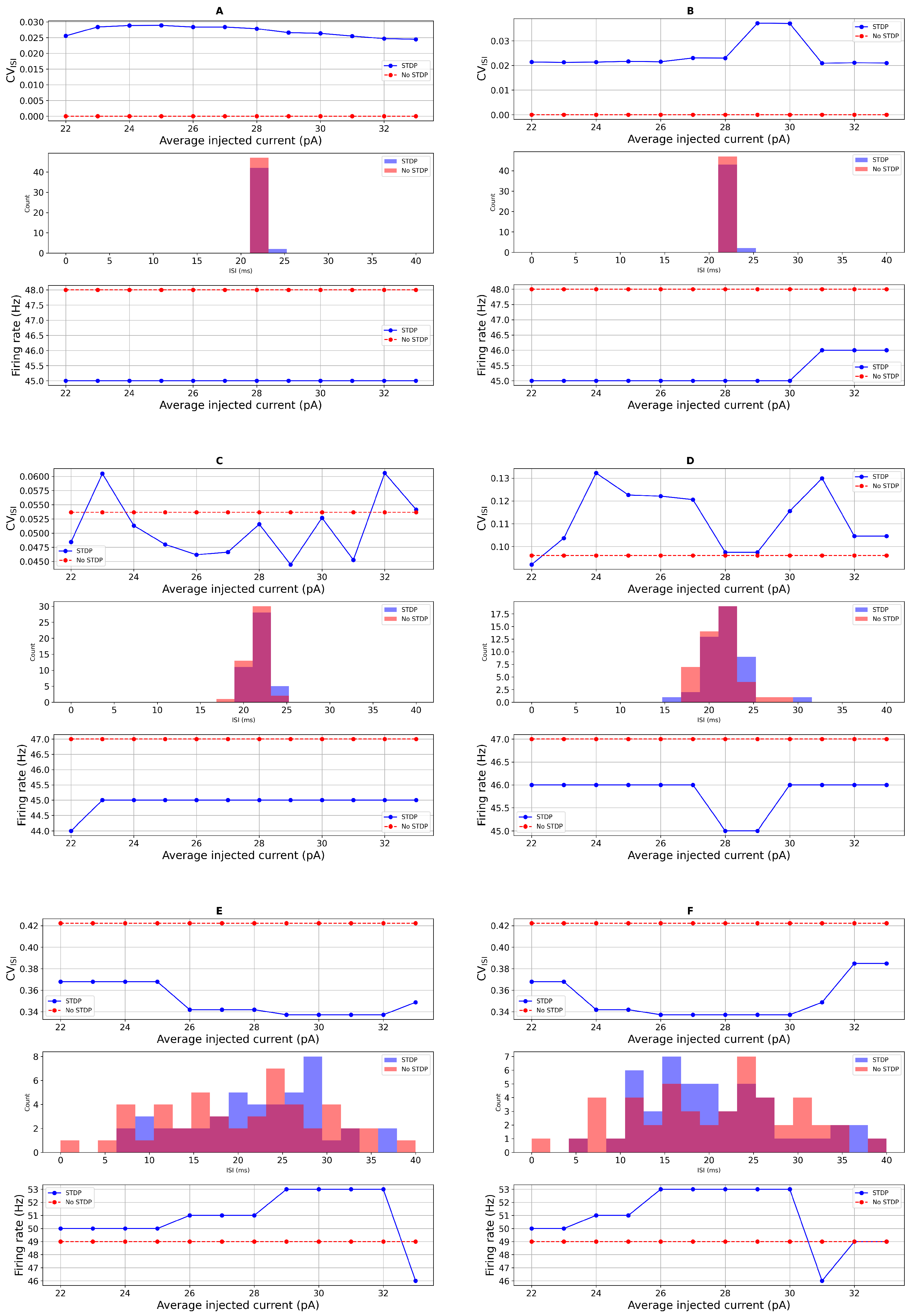
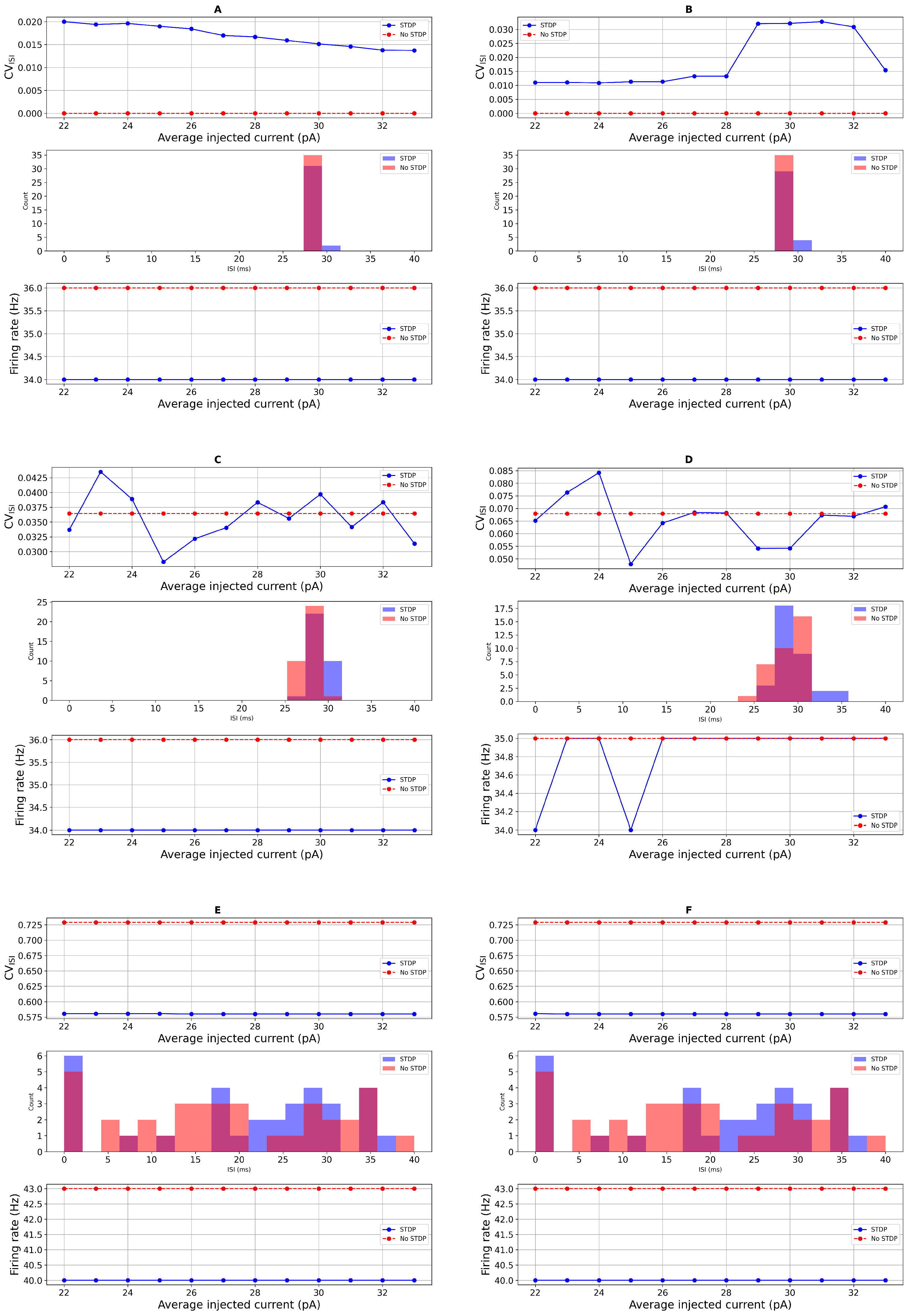
3.1. Simulation-Based Results
Sensitivity Analysis of STDP Parameters
3.2. Comparison with Real Data and Statistical Test
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hirschmann, J.; Steina, A.; Vesper, J.; Florin, E.; Schnitzler, A. Neuronal oscillations predict deep brain stimulation outcome in Parkinson’s disease. Brain Stimul. 2022, 15, 792–802. [Google Scholar] [CrossRef] [PubMed]
- David, F.J.; Munoz, M.J.; Corcos, D.M. The effect of STN DBS on modulating brain oscillations: Consequences for motor and cognitive behavior. Exp. Brain Res. 2020, 238, 1659–1676. [Google Scholar] [CrossRef]
- Rosa, M.; Giannicola, G.; Servello, D.; Marceglia, S.R.; Pacchetti, C.; Porta, M.; Sassi, M.; Scelzo, E.; Barbieri, S.; Priori, A. Subthalamic Local Field Beta Oscillations during Ongoing Deep Brain Stimulation in Parkinson’s Disease in Hyperacute and Chronic Phases. Neurosignals 2011, 19, 151–162. [Google Scholar] [CrossRef]
- Madadi Asl, M.; Vahabie, A.; Valizadeh, A.; Tass, P. Spike-timing-dependent Plasticity Mediated by Dopamine and its Role in Parkinson’s Disease Pathophysiology. Front. Netw. Physiol. 2022, 2, 817524. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, X.; Si, B.; Cheng, B.; Chen, J. Synchronization and oscillation behaviors of excitatory and inhibitory populations with spike-timing-dependent plasticity. Cogn. Neurodyn. 2022, 17, 715–727. [Google Scholar] [CrossRef]
- Lee, L.H.N.; Huang, C.S.; Wang, R.W.; Lai, H.J.; Chung, C.C.; Yang, Y.C.; Kuo, C.C. Deep brain stimulation rectifies the noisy cortex and irresponsive subthalamus to improve parkinsonian locomotor activities. npj Parkinsons Dis. 2022, 8, 77. [Google Scholar] [CrossRef]
- van der Groen, O.; Mattingley, J.B.; Wenderoth, N. Altering brain dynamics with transcranial random noise stimulation. Sci. Rep. 2019, 9, 4029. [Google Scholar] [CrossRef]
- Faisal, A.A.; Selen, L.P.J.; Wolpert, D.M. Noise in the nervous system. Nat. Rev. Neurosci. 2008, 9, 292–303. [Google Scholar] [CrossRef]
- Ebert, M.; Hauptmann, C.; Tass, P.A. Coordinated reset stimulation in a large-scale model of the STN-GPe circuit. Front. Comput. Neurosci. 2014, 8, 154. [Google Scholar] [CrossRef]
- Popovych, O.V.; Yanchuk, S.; Tass, P.A. Self-organized noise resistance of oscillatory neural networks with spike timing-dependent plasticity. Sci. Rep. 2013, 3, 2926. [Google Scholar] [CrossRef]
- Lücken, L.; Popovych, O.V.; Tass, P.A.; Yanchuk, S. Noise-enhanced coupling between two oscillators with long-term plasticity. Phys. Rev. E 2016, 93, 032210. [Google Scholar] [CrossRef] [PubMed]
- Nobukawa, S.; Nishimura, H. Enhancement of spike-timing-dependent plasticity in spiking neural systems with noise. Int. J. Neural Syst. 2016, 26, 1550040. [Google Scholar] [CrossRef] [PubMed]
- Baroni, F.; Varona, P. Spike timing-dependent plasticity is affected by the interplay of intrinsic and network oscillations. J.-Physiol.-Paris 2010, 104, 91–98. [Google Scholar] [CrossRef]
- Burkitt, A.N.; Meffin, H.; Grayden, D.B. Spike-timing-dependent plasticity: The relationship to rate-based learning for models with weight dynamics determined by a stable fixed point. Neural Comput. 2004, 16, 885–940. [Google Scholar] [CrossRef] [PubMed]
- Lindner, B. Superposition of many independent spike trains is generally not a Poisson process. Phys. Rev. E Statistical Nonlinear Soft Matter Phys. 2006, 73, 022901. [Google Scholar] [CrossRef]
- Zheng, T.; Kotani, K.; Jimbo, Y. Distinct effects of heterogeneity and noise on gamma oscillation in a model of neuronal network with different reversal potential. Sci. Rep. 2021, 11, 12960. [Google Scholar] [CrossRef]
- Powanwe, A.S.; Longtin, A. Brain rhythm bursts are enhanced by multiplicative noise. Chaos 2021, 31, 013117. [Google Scholar] [CrossRef]
- Thieu, T.; Melnik, R. Coupled effects of channels and synaptic dynamics in stochastic modelling of healthy and Parkinson’s-disease-affected brains. AIMS Bioeng. 2022, 9, 213–238. [Google Scholar] [CrossRef]
- Manos, T.; Zeitler, M.; Tass, P.A. Short-term dosage regimen for stimulation-induced long-lasting desynchronization. Front. Physiol. 2018, 9, 376. [Google Scholar] [CrossRef]
- Manos, T.; Zeitler, M.; Tass, P.A. How stimulation frequency and intensity impact on the long-lasting effects of coordinated reset stimulation. PLoS Comput. Biol. 2018, 14, e1006113. [Google Scholar] [CrossRef]
- Manos, T.; Diaz-Pier, S.; Tass, P.A. Long-term desynchronization by coordinated reset stimulation in a neural network model with synaptic and structural plasticity. Front. Physiol. 2021, 12, 716556. [Google Scholar] [CrossRef]
- Chauhan, K.; Neiman, A.B.; Tass, P.A. Synaptic reorganization of synchronized neuronal networks with synaptic weight and structural plasticity. PLoS Comput. Biol. 2024, 20, e1012261. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. Bull. Math. Biol. 1990, 52, 25–71. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef]
- Goldwyn, J.H.; Shea-Brown, E. The what and where of adding channel noise to the Hodgkin-Huxley equations. PLoS Comput. Biol. 2011, 7, e1002247. [Google Scholar] [CrossRef]
- Song, S.; Miller, K.D.; Abbott, L.F. Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 2000, 3, 919–926. [Google Scholar] [CrossRef]
- Sherf, N.; Shamir, M. Multiplexing rhythmic information by spike timing dependent plasticity. PLoS Comput. Biol. 2020, 16, e1008000. [Google Scholar] [CrossRef]
- Bujan, A.F.; Aertsen, A.; Kumar, A. Role of input correlations in shaping the variability and noise correlations of evoked activity in the neocortex. J. Neurosci. 2015, 35, 8611–8625. [Google Scholar] [CrossRef]
- Madadi Asl, M.; Valizadeh, A.; Tass, P.A. Propagation delays determine neuronal activity and synaptic connectivity patterns emerging in plastic neuronal networks. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 106308. [Google Scholar] [CrossRef]
- So, R.Q.; Kent, A.R.; Grill, W.M. Relative contributions of local cell and passing fiber activation and silencing to changes in thalamic fidelity during deep brain stimulation and lesioning: A computational modeling study. J. Comput. Neurosci. 2012, 32, 499–519. [Google Scholar] [CrossRef]
- Kim, S.Y.; Lim, W. Effect of interpopulation spike-timing-dependent plasticity on synchronized rhythms in neuronal networks with inhibitory and excitatory populations. Cogn. Neurodyn. 2020, 14, 535–567. [Google Scholar] [CrossRef] [PubMed]
- Thieu, T.; Melnik, R. Effects of noise on leaky integrate-and-fire neuron models for neuromorphic computing applications. In Proceedings of the Bioinformatics and Biomedical Engineering, Malaga, Spain, 4–7 July 2022; Springer: Cham, Switzerland, 2022; Volume 13375, pp. 3–18. [Google Scholar]
- Ranganathan, G.N.; Apostolides, P.F.; Harnett, M.T.; Xu, N.L.; Druckmann, S.; Magee, J.C. Active dendritic integration and mixed neocortical network representations during an adaptive sensing behavior. Nat. Neurosci. 2018, 21, 1583–1590. [Google Scholar] [CrossRef] [PubMed]
- Markram, H.; Lübke, J.; Frotscher, M.; Sakmann, B. Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 1997, 275, 213–215. [Google Scholar] [CrossRef]
- Bi, G.q.; Poo, M.m. Synaptic modifications in cultured hippocampal neurons: Dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 1998, 18, 10464–10472. [Google Scholar] [CrossRef]
- Vilimelis Aceituno, P.; Ehsani, M.; Jost, J. Spiking time-dependent plasticity leads to efficient coding of predictions. Biol. Cybern. 2020, 114, 43–61. [Google Scholar] [CrossRef]
- Yang, Y.C.; Tai, C.H.; Pan, M.K.; Kuo, C.C. The T-type calcium channel as a new therapeutic target for Parkinson’s disease. Pflugers Arch. Eur. J. Physiol. 2014, 446, 747–755. [Google Scholar] [CrossRef]
- Chen, X.; Xue, B.; Wang, J.; Liu, H.; Shi, L.; Xie, J. Potassium Channels: A Potential Therapeutic Target for Parkinson’s Disease. Neurosci. Bull. 2018, 34, 341–348. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, Y.; Xie, J.; Shi, L. Potassium channels and their emerging role in parkinson’s disease. Brain Res. Bull. 2020, 160, 1–7. [Google Scholar] [CrossRef]
- Gerstner, W.; Kistler, W.M.; Naud, R.; Paninski, L. Neuronal Dynamics: From Single Neurons to Networks and Models of Cognition; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Dayan, P.; Abbott, L.F. Theoretical Neuroscience; The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Li, S.; Liu, N.; Yao, L.; Zhang, X.; Zhou, D.; Cai, D. Determination of effective synaptic conductances using somatic voltage clamp. PLoS Comput. Biol. 2019, 15, e1006871. [Google Scholar] [CrossRef]
- Chiken, S.; Nambu, A. Mechanism of Deep Brain Stimulation: Inhibition, Excitation, or Disruption? The Neuroscientist 2016, 22, 313–322. [Google Scholar] [CrossRef]
- Traub, R.D.; Wong, R.K.; Miles, R.; Michelson, H. A Model of CA3 Hippocampal Pyramidal Neuron Incorporating Voltage-Clamp Data on Intrinsic Conductances. J. Neurophysiol. 1999, 66, 635–650. [Google Scholar] [CrossRef]
- Cornelisse, L.N.; Scheenen, W.J.J.M.; Koopman, W.J.H.; Roubos, E.W.; Gielen, S.C.A.M. Minimal Model for Intracellular Calcium Oscillations and Electrical Bursting in Melanotrope Cells of Xenopus Laevis. Neural Comput. 2000, 13, 113–137. [Google Scholar] [CrossRef]
- Roberts, J.A.; Friston, K.J.; Breakspear, M. Clinical Applications of Stochastic Dynamic Models of the Brain, Part I: A Primer. Biol. Psychiatry Cogn. Neurosci. Neuroimaging 2017, 2, 216–224. [Google Scholar] [CrossRef] [PubMed]
- Teka, W.; Marinov, T.M.; Santamaria, F. Neuronal Spike Timing Adaptation Described with a Fractional Leaky Integrate-and-Fire Model. PLoS Comput. Biol. 2014, 10, e1003526. [Google Scholar] [CrossRef] [PubMed]
- Brunel, N. Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J. Comput. Neurosci. 2000, 8, 183–208. [Google Scholar] [CrossRef]
- Gerstner, W.; Kistler, W.M. Spiking Neuron Models: Single Neurons, Populations, Plasticity; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Shinomoto, S.; Shima, K.; Tanji, J. Differences in spiking patterns among cortical neurons. Neural Comput. 2003, 15, 2823–2842. [Google Scholar] [CrossRef]
- Maimon, G.; Assad, J.A. Beyond Poisson: Increased spike-time regularity across primate parietal cortex. Neuron 2009, 62, 426–440. [Google Scholar] [CrossRef]
- van Rossum, M.C.; Turrigiano, G.G. Correlation based learning from spike timing dependent plasticity. Neurocomputing 2001, 38, 409–415. [Google Scholar] [CrossRef]
- Gallinaro, J.V.; Clopath, C. Memories in a network with excitatory and inhibitory plasticity are encoded in the spiking irregularity. PLoS Comput. Biol. 2021, 17, e1009593. [Google Scholar] [CrossRef]
- Christodoulou, C.; Bugmann, G. Coefficient of variation vs. mean interspike interval curves: What do they tell us about the brain? Neurocomputing 2001, 38–40, 1141–1149. [Google Scholar] [CrossRef]
- Salinas, E.; Sejnowski, T.J. Impact of correlated synaptic input on output firing rate and variability in simple neuronal models. J. Neurosci. 2000, 20, 6193–6209. [Google Scholar] [CrossRef] [PubMed]
- Hong, S.; Ratté, S.; Prescott, S.A.; De Schutter, E. Single neuron firing properties impact correlation-based population coding. J. Neurosci. 2012, 32, 1413–1428. [Google Scholar] [CrossRef] [PubMed]
- Tao, T.; Li, D.; Ma, H.; Li, Y.; Tan, S.; Liu, E.x.; Schutt-Aine, J.; Li, E.P. A new pre-conditioned STDP rule and its hardware implementation in neuromorphic crossbar array. Neurocomputing 2023, 557, 126682. [Google Scholar] [CrossRef]
- Lu, S.; Sengupta, A. Deep unsupervised learning using spike-timing-dependent plasticity. Neuromorphic Comput. Eng. 2024, 4, 024004. [Google Scholar] [CrossRef]
- Herculano-Houzel, S. Not all brains are made the same: New views on brain scaling in evolution. Brain, Behav. Evol. 2011, 78, 22–36. [Google Scholar] [CrossRef]
- Gupta, A.; Saurabh, S. Unsupervised Learning in a Ternary SNN Using STDP. IEEE J. Electron Devices Soc. 2024, 12, 211–220. [Google Scholar] [CrossRef]
- Gautam, A.; Kohno, T. An adaptive STDP learning rule for neuromorphic systems. Front. Neurosci. 2021, 15, 741116. [Google Scholar] [CrossRef]
- Gautam, A.; Kohno, T. Adaptive STDP-based on-chip spike pattern detection. Front. Neurosci. 2023, 17, 1203956. [Google Scholar] [CrossRef]
- Khoee, A.G.; Javaheri, A.; Kheradpisheh, S.R.; Ganjtabesh, M. Meta-learning in spiking neural networks with reward-modulated STDP. Neurocomputing 2024, 600, 128173. [Google Scholar] [CrossRef]
- Walters, B.; Kalatehbali, H.R.; Cai, Z.; Genov, R.; Amirsoleimani, A.; Eshraghian, J.; Azghadi, M.R. Efficient sparse spiking auto-encoder for reconstruction, denoising and classification. Neuromorphic Comput. Eng. 2024, 4, 034005. [Google Scholar] [CrossRef]
- Hussain, S.A.; Prasad, P.N.S.B.S.V.; Sanki, P.K. Efficient in situ learning of hybrid LIF neurons using WTA mechanism for high-speed low-power neuromorphic systems. Phys. Scr. 2024, 99, 106010. [Google Scholar] [CrossRef]
- Goupy, G.; Tirilly, P.; Bilasco, I.M. Paired competing neurons improving STDP supervised local learning in Spiking Neural Networks. Front. Neurosci. 2024, 18, 1401690. [Google Scholar] [CrossRef] [PubMed]
- Yamakou, M.E.; Desroches, M.; Rodrigues, S. Synchronization in STDP-driven memristive neural networks with time-varying topology. J. Biol. Phys. 2023, 49, 483–507. [Google Scholar] [CrossRef] [PubMed]
- Park, H.L.; Lee, Y.; Kim, N.; Seo, D.G.; Go, G.T.; Lee, T.W. Flexible neuromorphic electronics for computing, soft robotics, and neuroprosthetics. Adv. Mater. 2020, 32, 1903558. [Google Scholar] [CrossRef]
- Schuman, C.D.; Kulkarni, S.R.; Parsa, M.; Mitchell, J.P.; Date, P.; Kay, B. Opportunities for neuromorphic computing algorithms and applications. Nat. Comput. Sci. 2022, 2, 10–19. [Google Scholar] [CrossRef]
- De La Rocha, J.; Doiron, B.; Shea-Brown, E.; Josić, K.; Reyes, A. Correlation between neural spike trains increases with firing rate. Nature 2007, 448, 802–806. [Google Scholar] [CrossRef]
- Liu, S.; Wang, J.; Fan, Y.; Yi, G. Effects of dendritic properties on spike train correlations in biophysically-based model neurons. Int. J. Mod. Phys. B 2022, 36, 2250061. [Google Scholar] [CrossRef]
- Li, X.; Zhuang, P.; Li, Y. Altered neuronal firing pattern of the basal ganglia nucleus plays a role in levodopa-induced dyskinesia in patients with Parkinson’s disease. Front. Hum. Neurosci. 2015, 9, 630. [Google Scholar] [CrossRef]
- Casella, G.; Berger, R.L. Statistical Inference, 2nd ed.; Duxbury Press: Pacific Grove, CA, USA, 2002. [Google Scholar]
- Polyakova, Z.; Chiken, S.; Hatanaka, N.; Nambu, A. Cortical control of subthalamic neuronal activity through the hyperdirect and indirect pathways in monkeys. J. Neurosci. 2020, 40, 7451–7463. [Google Scholar] [CrossRef]
- Magill, P.J.; Bolam, J.P.; Bevan, M.D. Dopamine regulates the impact of the cerebral cortex on the subthalamic nucleus–globus pallidus network. Neuroscience 2001, 106, 313–330. [Google Scholar] [CrossRef]
- Sadeghi, S.G.; Chacron, M.J.; Taylor, M.C.; Cullen, K.E. Neural variability, detection thresholds, and information transmission in the vestibular system. J. Neurosci. 2007, 27, 771–781. [Google Scholar] [CrossRef] [PubMed]



| Current | Gating Variables | Gating Variables | Parameters |
|---|---|---|---|
| (nS) | |||
| (mV) | |||
| (mV) | |||
| (nS) | |||
| (mV) | |||
| (nS) | |||
| (mV) | |||
| (nS) | |||
| (mV) | |||
| (nS) | |||
| (mV) | |||
| (pA) |
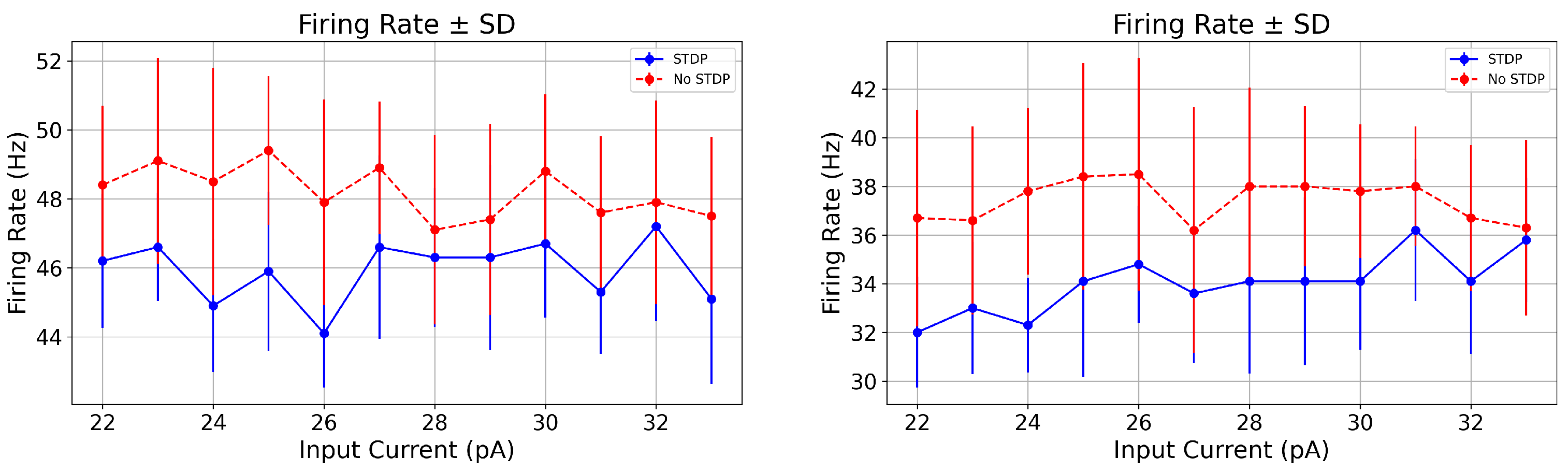
| Input (pA) | Condition | Firing Rate (Hz) | Spike Count | FR p-Value | CV p-Value | |
|---|---|---|---|---|---|---|
| 23.0 (PD) | STDP | 46.6 ± 1.56 | 0.348 ± 0.027 | 46.6 ± 1.56 | 0.056 (ns) | 0.017 |
| No STDP | 49.1 ± 2.98 | 0.379 ± 0.029 | 49.1 ± 2.98 |
| Input (pA) | Condition | Firing Rate (Hz) | Spike Count | FR p-Value | CV p-Value | |
|---|---|---|---|---|---|---|
| 23.0 (PD) | STDP | 33.0 ± 2.72 | 0.547 ± 0.060 | 33.0 ± 2.72 | 0.059 (ns) | 0.006 |
| No STDP | 36.6 ± 3.85 | 0.604 ± 0.067 | 36.6 ± 3.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thieu, T.; Melnik, R. Spike Timing-Dependent Plasticity and Random Inputs Shape Interspike Interval Regularity of Model STN Neurons. Biomedicines 2025, 13, 1718. https://doi.org/10.3390/biomedicines13071718
Thieu T, Melnik R. Spike Timing-Dependent Plasticity and Random Inputs Shape Interspike Interval Regularity of Model STN Neurons. Biomedicines. 2025; 13(7):1718. https://doi.org/10.3390/biomedicines13071718
Chicago/Turabian StyleThieu, Thoa, and Roderick Melnik. 2025. "Spike Timing-Dependent Plasticity and Random Inputs Shape Interspike Interval Regularity of Model STN Neurons" Biomedicines 13, no. 7: 1718. https://doi.org/10.3390/biomedicines13071718
APA StyleThieu, T., & Melnik, R. (2025). Spike Timing-Dependent Plasticity and Random Inputs Shape Interspike Interval Regularity of Model STN Neurons. Biomedicines, 13(7), 1718. https://doi.org/10.3390/biomedicines13071718






