In Silico Trials of Prosthetic Valves Replicate Methodologies for Evaluating the Fatigue Life of Artificial Leaflets to Expand Beyond In Vitro Tests and Conventional Clinical Trials
Abstract
1. Introduction
2. Materials and Methods
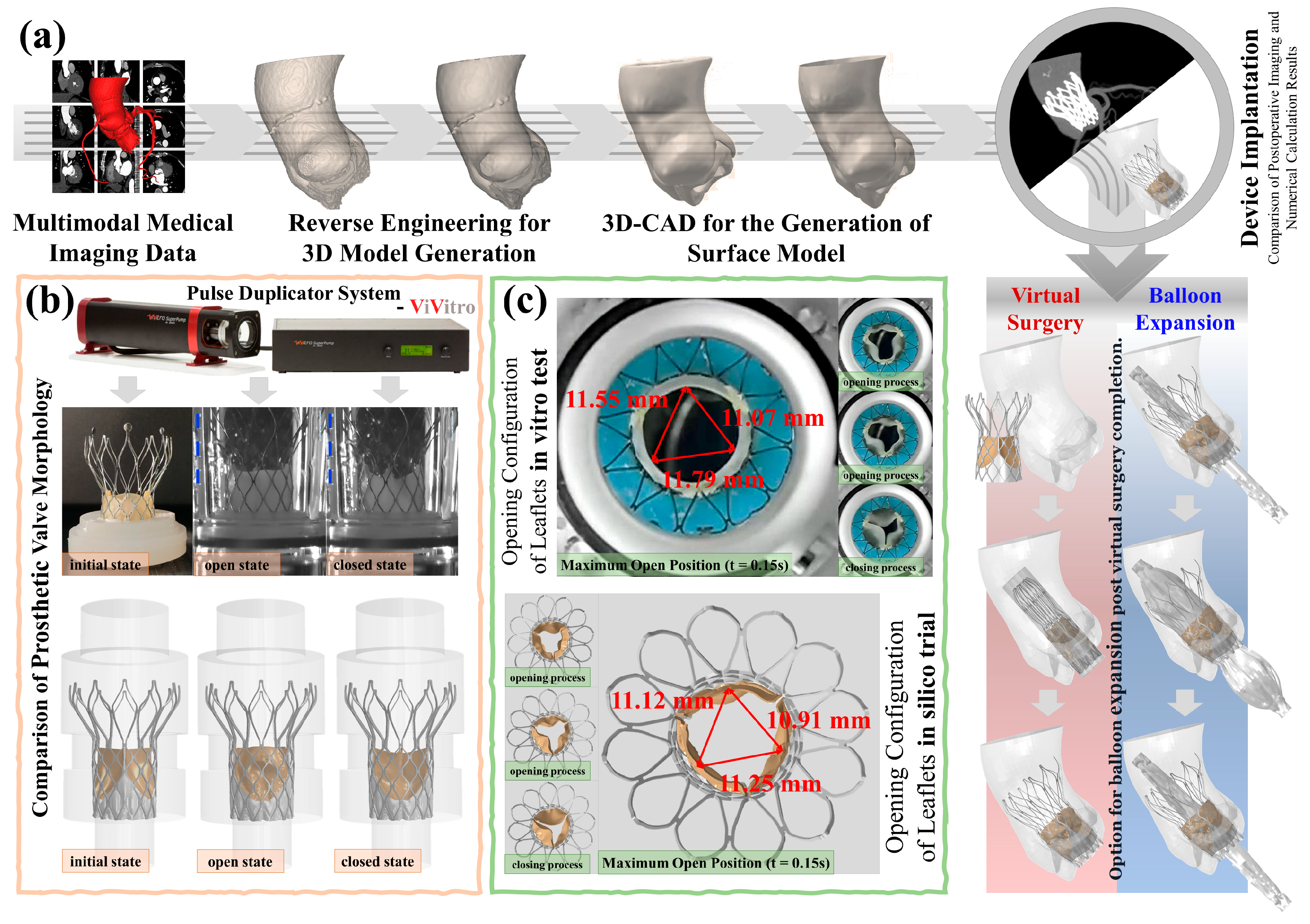
2.1. Clinical Patient and Image Acquisition
2.2. In Vitro Pulsatile Flow Tests
2.3. In Silico Trials of Prosthetic Valves
2.3.1. Establishing Virtual Patient Models
2.3.2. Material Properties
2.3.3. Virtual Surgeries
2.3.4. Virtual Postoperative Physiological Maintenance Simulation
2.4. Fatigue Life Prediction Model of the Artificial Leaflets
2.5. Crack Propagation Prediction Model of the Artificial Leaflets
3. Results
3.1. In Silico Process
3.2. Accuracy Analysis of the In Silico Trials
- i.
- Maximum leaflet displacement measurements during systole showed <1.5% variation between in vitro tests (11.07–11.79 mm) and computational results (10.91–11.25 mm, P > 0.05)
- ii.
- Peak systolic flow velocity in virtual patient B (3.11 m/s) differed by <3% from postoperative echocardiography (3.04 m/s, Figure 2c,d)
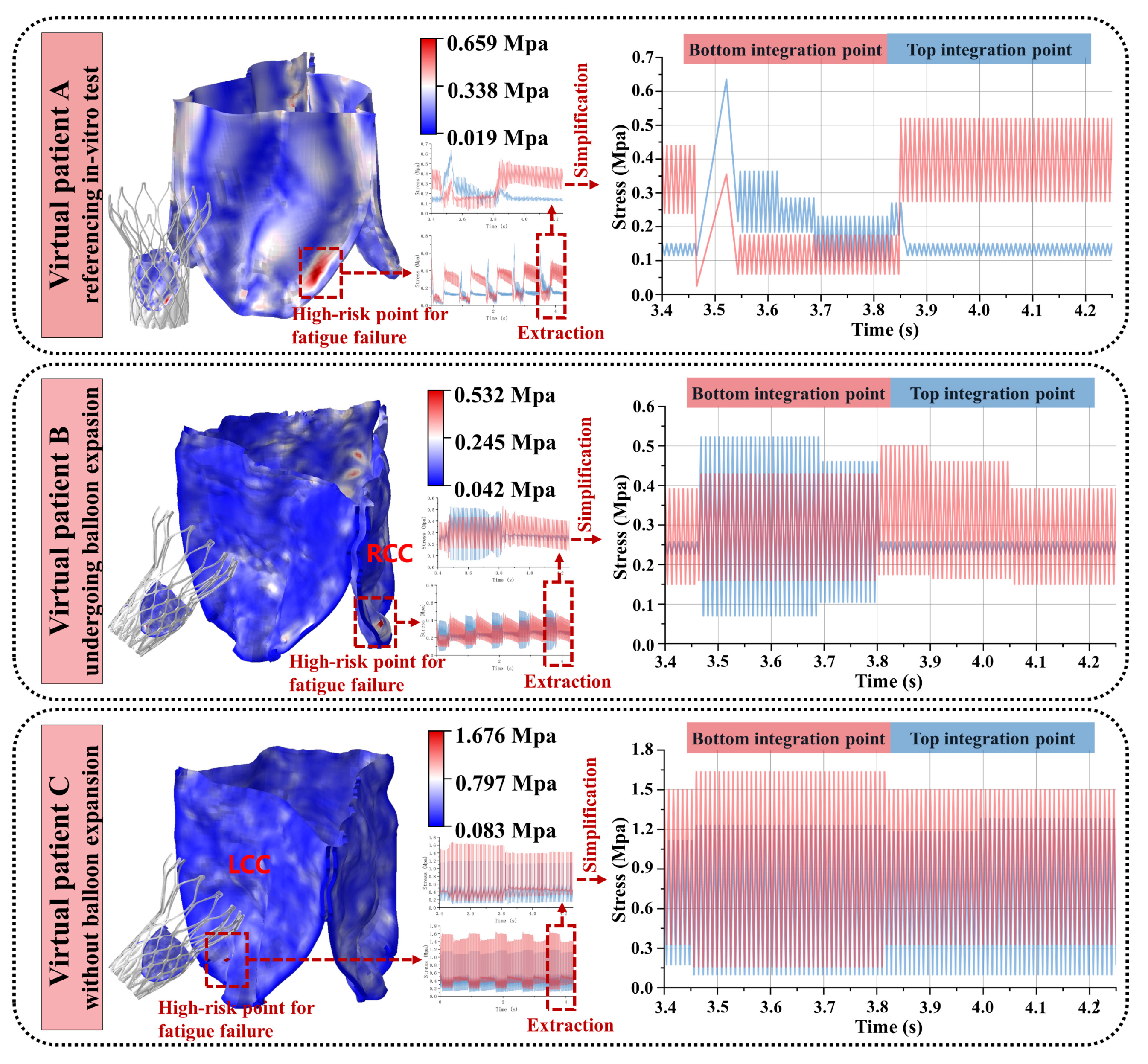
3.3. Variability in the Artificial Leaflet Fatigue Life
- i.
- Patient A demonstrated 0.659 MPa maximum stress within an elongated concentration zone at the side fold of the leaflet base. Systolic blood flow induced characteristic root bending, generating outer surface compression (0.659 MPa), surpassing inner surface tension—a mechanical reversal observed during diastolic closure.
- ii.
- Patient B exhibited 0.632 MPa circular stress localization at the right coronary cusp fold. Outer compressive stresses dominated systole (0.632 MPa vs. negligible inner tension < 0.05 MPa), with minimal diastolic variation (<5%) on the inner surface.
- iii.
- Patient C developed 1.676 MPa acute stress focusing on the sharply folded left coronary cusp base. Persistent inner surface stresses prevailed throughout the cardiac cycle (peak: 1.676 MPa; mean/stress amplitude exceeding outer surface by 38–62%), maintaining dual-surface high-stress states.
4. Discussion
5. Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CEL | Coupled Euler-Lagrange |
| CTA | Computed tomography angiography |
| FEA | Finite element analysis |
| FSI | Fluid–structure interaction |
| ISO | International Organization for Standardization |
| LCC | Left coronary cusp |
| NCC | Non-coronary cusp |
| NMPA | National Medical Products Administration |
| NISQ | Noisy intermediate-scale quantum |
| RCC | Right coronary cusp |
| S-N curve | Stress–number curve |
| TAVI | Transcatheter aortic valve implantation |
| TMVR | Transcatheter mitral valve repair |
References
- Bui, H.T.; Khair, N.; Yeats, B.; Gooden, S.; James, S.P.; Dasi, L.P. Transcatheter heart valves: A biomaterials perspective. Adv. Healthc. Mater. 2021, 10, 2100115. [Google Scholar] [CrossRef] [PubMed]
- Coffey, S.; Roberts-Thomson, R.; Brown, A.; Carapetis, J.; Chen, M.; Enriquez-Sarano, M.; Zühlke, L.; Prendergast, B.D. Global epidemiology of valvular heart disease. Nat. Rev. Cardiol. 2021, 18, 853–864. [Google Scholar] [CrossRef] [PubMed]
- Aluru, J.S.; Barsouk, A.; Saginala, K.; Rawla, P.; Barsouk, A. Valvular heart disease epidemiology. Med. Sci. 2022, 10, 32. [Google Scholar] [CrossRef] [PubMed]
- Khodaei, S.; Sadeghi, R.; Blanke, P.; Leipsic, J.; Emadi, A.; Keshavarz-Motamed, Z. Towards a non-invasive computational diagnostic framework for personalized cardiology of transcatheter aortic valve replacement in interactions with complex valvular, ventricular and vascular disease. Int. J. Mech. Sci. 2021, 202, 106506. [Google Scholar] [CrossRef]
- Oveissi, F.; Naficy, S.; Lee, A.; Winlaw, D.; Dehghani, F. Materials and manufacturing perspectives in engineering heart valves: A review. Mater. Today Bio 2020, 5, 100038. [Google Scholar] [CrossRef]
- Davidson, L.J.; Davidson, C.J. Transcatheter treatment of valvular heart disease: A review. JAMA 2021, 325, 2480–2494. [Google Scholar] [CrossRef]
- Zeng, L.; Liu, F.; Yu, Q.; Jin, C.; Yang, J.; Suo, Z.; Tang, J. Flaw-insensitive fatigue resistance of chemically fixed collagenous soft tissues. Sci. Adv. 2023, 9, eade7375. [Google Scholar] [CrossRef]
- Martin, C.; Sun, W. Comparison of transcatheter aortic valve and surgical bioprosthetic valve durability: A fatigue simulation study. J. Biomech. 2015, 48, 3026–3034. [Google Scholar] [CrossRef]
- Piñón, M.; Durán, D.; Pazos, P.; Pradas, G. Leaflets tear in a Trifecta aortic bioprosthesis 34 months after implantation. Interact. Cardiovasc. Thorac. Surg. 2015, 20, 281–282. [Google Scholar] [CrossRef]
- Hamamoto, M.; Kobayashi, T.; Ozawa, M.; Yoshimura, K. Pure cusp tear of Trifecta bioprosthesis 2 years after aortic valve replacement. Ann. Thorac. Cardiovasc. Surg. 2017, 23, 157–160. [Google Scholar] [CrossRef]
- Snyder, Y.; Jana, S. Strategies for development of decellularized heart valve scaffolds for tissue engineering. Biomaterials 2022, 288, 121675. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Wu, L.; Wu, Q. Structural stability of novel composite heart valve prostheses-Fatigue and wear performance. Biomed. Pharmacother. 2021, 136, 111288. [Google Scholar] [CrossRef] [PubMed]
- Ternacle, J.; Hecht, S.; Eltchaninoff, H.; Salaun, E.; Clavel, M.-A.; Côté, N.; Pibarot, P. Durability of transcatheter aortic valve implantation. EuroIntervention 2024, 20, e845–e864. [Google Scholar] [CrossRef] [PubMed]
- Noble, C.; Hooke, A.; Rajotia, A.; Morse, D.; Dragomir-Daescu, D.; Salisbury, J.; Young, M.D.; Lerman, A. Effect of mechanical fatigue on commercial bioprosthetic TAVR valve mechanical and microstructural properties. J. Mech. Behav. Biomed. Mater. 2024, 154, 106441. [Google Scholar] [CrossRef]
- Zhang, W.; Motiwale, S.; Hsu, M.-C.; Sacks, M.S. Simulating the time evolving geometry, mechanical properties, and fibrous structure of bioprosthetic heart valve leafletss under cyclic loading. J. Mech. Behav. Biomed. Mater. 2021, 123, 104745. [Google Scholar] [CrossRef]
- Martin, C.; Sun, W. Simulation of long-term fatigue damage in bioprosthetic heart valves: Effects of leaflets and stent elastic properties. Biomech. Model. Mechanobiol. 2014, 13, 759–770. [Google Scholar] [CrossRef]
- Abdulrazzaq, M.M.; Ramaha, N.T.A.; Hameed, A.A.; Salman, M.; Yon, D.K.; Fitriyani, N.L.; Syafrudin, M.; Lee, S.W. Consequential advancements of self-supervised learning (SSL) in deep learning contexts. Mathematics 2024, 12, 758. [Google Scholar] [CrossRef]
- Sarrami-Foroushani, A.; Lassila, T.; MacRaild, M.; Asquith, J.; Roes, K.C.B.; Byrne, J.V.; Frangi, A.F. In-silico trial of intracranial flow diverters replicates and expands insights from conventional clinical trials. Nat. Commun. 2021, 12, 3861. [Google Scholar] [CrossRef]
- Wu, X.; Ye, Y.; Sun, M.; Mei, Y.; Ji, B.; Wang, M.; Song, E. Recent progress of soft and bioactive materials in flexible bioelectronics. Cyborg Bionic Syst. 2025, 6, 0192. [Google Scholar] [CrossRef]
- ISO 5840-3:2021; Cardiovascular Implants—Cardiac Valve Prostheses—Part 3: Heart Valve Substitutes Implanted by Transcatheter Techniques. International Organization for Standardization: Geneva, Switzerland, 2021.
- Auricchio, F.; Reali, A.; Stefanelli, U. A macroscopic 1D model for shape memory alloys including asymmetric behaviors and transformation-dependent elastic properties. Comput. Methods Appl. Mech. Eng. 2009, 198, 1631–1637. [Google Scholar] [CrossRef]
- Liu, L.-W.; Lee, C.-H.; Aggarwal, A.; Chao, C.-M.; Ross, C.J.; Liao, Y.-K. Viscoelastic modelling of the tricuspid valve chordae tendineae tissue. Appl. Math. Model. 2022, 105, 648–669. [Google Scholar] [CrossRef]
- Zeidi, M.; Islam, S.; Park, C.B.; Kim, C.I. A pseudoelastic response of hyperelastic composites reinforced with nonlinear elastic fibrous materials: Continuum modeling and analysis. Int. J. Eng. Sci. 2024, 201, 104092. [Google Scholar] [CrossRef]
- Han, Y.; Liu, S.; Ochieng, B.O.; Gu, Y.; Kong, L.; Wang, G.; Ye, Z. Multiscale Mechanical Study of Proanthocyanidins for Recovering Residual Stress in Decellularized Blood Vessels. Adv. Healthc. Mater. 2025, 14, e2402250. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.; Liu, M.; Martin, C.; Sun, W. A residual stiffness-based model for the fatigue damage of biological soft tissues. J. Mech. Phys. Solids 2020, 143, 104074. [Google Scholar] [CrossRef]
- Weisbecker, H.; Pierce, D.M.; Regitnig, P.; Holzapfel, G.A. Layer-specific damage experiments and modeling of human thoracic and abdominal aortas with non-atherosclerotic intimal thickening. J. Mech. Behav. Biomed. Mater. 2012, 12, 93–106. [Google Scholar] [CrossRef]
- Puso, M.A.; Sanders, J.; Settgast, R.; Liu, B. An embedded mesh method in a multiple material ALE. Comput. Methods Appl. Mech. Eng. 2012, 245–246, 273–289. [Google Scholar] [CrossRef]
- Nowak, M.; Divo, E.; Adamczyk, W.P. Fluid–structure interaction methods for the progressive anatomical and artificial aortic valve stenosis. Int. J. Mech. Sci. 2022, 227, 107410. [Google Scholar] [CrossRef]
- Oks, D.; Reza, S.; Vázquez, M.; Houzeaux, G.; Kovarovic, B.; Samaniego, C.; Bluestein, D. Effect of sinotubular junction size on TAVR leaflet thrombosis: A fluid–structure interaction analysis. Ann. Biomed. Eng. 2024, 52, 719–733. [Google Scholar] [CrossRef]
- Li, J.; Yan, W.; Wang, W.; Wang, S.; Wei, L. Comparison of balloon-expandable valve and self-expandable valve in transcatheter aortic valve replacement: A patient-specific numerical study. J. Biomech. Eng. 2022, 144, 104501. [Google Scholar] [CrossRef]
- Yan, W.; Li, J.; Zhang, B.; Wang, W.; Wei, L.; Yu, H.; Wang, S. Patient-specific bicuspid aortic valve hemodynamics study based on computer simulation and in-vitro experiment. Acta Mech. Sin. 2024, 40, 324022. [Google Scholar] [CrossRef]
- Giannenas, A.E.; Laizet, S. A simple and scalable immersed boundary method for high-fidelity simulations of fixed and moving objects on a Cartesian mesh. Appl. Math. Model. 2021, 99, 606–627. [Google Scholar] [CrossRef]
- Wu, B.; Lee, H.; Shu, C.; Wan, M. Explicit boundary thickening direct forcing immersed boundary method. Int. J. Mech. Sci. 2024, 270, 109063. [Google Scholar] [CrossRef]
- Vahidkhah, K.; Abdollahi, V. Numerical simulation of a flexible fiber deformation in a viscous flow by the immersed boundary-lattice Boltzmann method. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1475–1484. [Google Scholar] [CrossRef]
- Jeong, D.; Choi, Y.; Kim, J. Modeling and simulation of the hexagonal pattern formation of honeycombs by the immersed boundary method. Commun. Nonlinear Sci. Numer. Simul. 2018, 62, 61–77. [Google Scholar] [CrossRef]
- Bi, Y.; Zhang, Z.; Liu, Q.; Liu, T. Research on nonlinear waves of blood flow in arterial vessels. Commun. Nonlinear Sci. Numer. Simul. 2021, 102, 105918. [Google Scholar] [CrossRef]
- Tang, W.; Yi, M.; Chen, L.-Q.; Guo, W. Classical fatigue theory informed phase-field model for high-cycle fatigue life and fatigue crack growth. Eng. Fract. Mech. 2024, 306, 110212. [Google Scholar] [CrossRef]
- Mallick, P.; Zhou, Y. Effect of mean stress on the stress-controlled fatigue of a short E-glass fiber reinforced polyamide-6,6. Int. J. Fatigue 2004, 26, 941–946. [Google Scholar] [CrossRef]
- Muñiz-Calvente, M.; Álvarez-Vázquez, A.; Pelayo, F.; Aenlle, M.; García-Fernández, N.; Lamela-Rey, M. A comparative review of time-and frequency-domain methods for fatigue damage assessment. Int. J. Fatigue 2022, 163, 107069. [Google Scholar] [CrossRef]
- Pyttel, B.; Canteli, A.F.; Ripoll, A.A. Comparison of different statistical models for description of fatigue including very high cycle fatigue. Int. J. Fatigue 2016, 93, 435–442. [Google Scholar] [CrossRef]
- Zou, Q.; Wen, J. A novel fatigue design modeling method under small-sample test data with generalized fiducial theory. Appl. Math. Model. 2024, 128, 260–271. [Google Scholar] [CrossRef]
- Proso, U.; Slavič, J.; Boltežar, M. Vibration-fatigue damage accumulation for structural dynamics with non-linearities. Int. J. Mech. Sci. 2016, 106, 72–77. [Google Scholar] [CrossRef]
- Xu, H.; Xiong, J.; Han, X.; Mei, Y.; Shi, Y.; Wang, D.; Zhang, M.; Chen, D. Computed tomography-based hemodynamic index for aortic dissection. J. Thorac. Cardiovasc. Surg. 2021, 162, e165–e176. [Google Scholar] [CrossRef] [PubMed]
- Knop, M.; Jones, R.; Molent, L.; Wang, C. On the Glinka and Neuber methods for calculating notch tip strains under cyclic load spectra. Int. J. Fatigue 2000, 22, 743–755. [Google Scholar] [CrossRef]
- Ozkan, M.T.; Erdemir, F. Determination of theoretical stress concentration factor for circular/elliptical holes with reinforcement using analytical, finite element method and artificial neural network techniques. Neural Comput. Appl. 2021, 33, 12641–12659. [Google Scholar] [CrossRef]
- Luo, L.; Xiang, Y.; Wang, Q. Stress concentration factor expression for tension strip with eccentric elliptical hole. Appl. Math. Mech. 2012, 33, 117–128. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, P.; Mu, S.; Dong, Y. Stress ratio influence on Paris parameter and fatigue driving force pertinent to material properties. Int. J. Fatigue 2024, 185, 108368. [Google Scholar] [CrossRef]
- Zhu, S.-P.; Hao, Y.-Z.; Liao, D. Probabilistic modeling and simulation of multiple surface crack propagation and coalescence. Appl. Math. Model. 2020, 78, 383–398. [Google Scholar] [CrossRef]
- Viceconti, M.; Juarez, M.A.; Curreli, C.; Pennisi, M.; Russo, G.; Pappalardo, F. Credibility of in silico trial technologies—A theoretical framing. IEEE J. Biomed. Health Inform. 2019, 24, 4–13. [Google Scholar] [CrossRef]
- Wang, M.; Song, G.; Chen, M.; Feng, Y.; Wang, J.; Liu, X.; Zhou, S.; Fang, Z.; Han, Y.; Xu, K.; et al. Twelve-month outcomes of the TaurusOne valve for transcatheter aortic valve implantation in patients with severe aortic stenosis. EuroIntervention 2022, 17, 1070–1076. [Google Scholar] [CrossRef]
- Nuis, R.J.; Yee, J.; Adrichem, R.; Hokken, T.W.; Lenzen, M.; Daemen, J.; de Jaegere, P.P.; Van Mieghem, N.M. Incidence and mechanisms of bioprosthetic dysfunction after transcatheter implantation of a mechanically-expandable heart valve. EuroIntervention 2022, 18, 769–776. [Google Scholar] [CrossRef]
- Tóth, A.; Balogh, E.; Jeney, V. In Vitro Models of Cardiovascular Calcification. Biomedicines 2024, 12, 2155. [Google Scholar] [CrossRef] [PubMed]
- Hanna, L.; Armour, C.; Xu, X.Y.; Gibbs, R. The Haemodynamic and pathophysiological mechanisms of calcific aortic valve disease. Biomedicines 2022, 10, 1317. [Google Scholar] [CrossRef] [PubMed]
- Yue, T.; Yang, H.; Wang, Y.; Jiang, N.; Yin, H.; Lu, X.; Liu, N.; Xu, Y. A Vascularized Multilayer Chip Reveals Shear Stress Induced Angiogenesis in Diverse Fluid Conditions. Cyborg Bionic Syst. 2025, 6, 0207. [Google Scholar] [CrossRef] [PubMed]
- Daryani, R.; Ersan, E.C.; Çelebi, M.S. Impact of multi-grade localized calcifications on aortic valve dynamics under helical inflow: A comparative hemodynamic study. Appl. Sci. 2023, 13, 12983. [Google Scholar] [CrossRef]
- Cai, Y.; Qu, S.; Jia, Z. Anomalous fracture behavior of soft layered materials. Int. J. Mech. Sci. 2024, 267, 109018. [Google Scholar] [CrossRef]
- Saito, J.; Kaneko, M.; Ishikawa, Y.; Yokoyama, U. Challenges and possibilities of cell-based tissue-engineered vascular grafts. Cyborg Bionic Syst. 2021, 2021, 1532103. [Google Scholar] [CrossRef]
- Peloquin, J.M.; Elliott, D.M. A comparison of stress in cracked fibrous tissue specimens with varied crack location, loading, and orientation using finite element analysis. J. Mech. Behav. Biomed. Mater. 2016, 57, 260–268. [Google Scholar] [CrossRef]
- Kim, S.-Y.; Kim, B.-S.; Kim, H.; Cho, S.-Y. Occlusal stress distribution and remaining crack propagation of a cracked tooth treated with different materials and designs: 3D finite element analysis. Dent. Mater. 2021, 37, 731–740. [Google Scholar] [CrossRef]
- Lyras, K.G.; Lee, J. Comparison of numerical implementations for modelling flow through arterial stenoses. Int. J. Mech. Sci. 2021, 211, 106780. [Google Scholar] [CrossRef]
- Wang, S.; Nikfar, M.; Agar, J.C.; Liu, Y. Stacked Deep Learning Models for Fast Approximations of Steady-State Navier–Stokes Equations for Low Re Flow. Intell. Comput. 2024, 3, 0093. [Google Scholar] [CrossRef]
- Khan, M.U.; Kamran, M.A.; Khan, W.R.; Ibrahim, M.M.; Ali, M.U.; Lee, S.W. Error Mitigation in the NISQ Era: Applying Measurement Error Mitigation Techniques to Enhance Quantum Circuit Performance. Mathematics 2024, 12, 2235. [Google Scholar] [CrossRef]

| Parameter | Metal Stent | Skirts | Artificial Leaflets | Balloon | |
|---|---|---|---|---|---|
| Density, g/cm3 | 7.45 | 1.38 | 1.06 | 1.01 | |
| Poisson’s ratio | 0.33 | 0.4 | - | 0.4 | |
| Young’s modulus, MPa | Austenite: | 53,875 | 1000 | 2 | 1100 |
| Martensite: | 29,600 | ||||
| Transformation strain | 0.055 | - | - | - | |
| Patient | Integration Point | Fatigue Life, Cycles |
|---|---|---|
| Virtual patient A | Top | 5.65 × 109 |
| Bottom | 4.58 × 109 | |
| Virtual patient B | Top | 4.58 × 108 |
| Bottom | 2.02 × 109 | |
| Virtual patient C | Top | 9.30 × 105 |
| Bottom | 4.40 × 105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, P.; Jin, M.; Li, W.; Zhang, H.; Li, H.; Li, S.; Yang, Y.; Zhu, M.; Shi, Y.; Zhang, X.; et al. In Silico Trials of Prosthetic Valves Replicate Methodologies for Evaluating the Fatigue Life of Artificial Leaflets to Expand Beyond In Vitro Tests and Conventional Clinical Trials. Biomedicines 2025, 13, 1135. https://doi.org/10.3390/biomedicines13051135
Mao P, Jin M, Li W, Zhang H, Li H, Li S, Yang Y, Zhu M, Shi Y, Zhang X, et al. In Silico Trials of Prosthetic Valves Replicate Methodologies for Evaluating the Fatigue Life of Artificial Leaflets to Expand Beyond In Vitro Tests and Conventional Clinical Trials. Biomedicines. 2025; 13(5):1135. https://doi.org/10.3390/biomedicines13051135
Chicago/Turabian StyleMao, Pengzhi, Min Jin, Wei Li, Haitao Zhang, Haozheng Li, Shilong Li, Yuting Yang, Minjia Zhu, Yue Shi, Xuehuan Zhang, and et al. 2025. "In Silico Trials of Prosthetic Valves Replicate Methodologies for Evaluating the Fatigue Life of Artificial Leaflets to Expand Beyond In Vitro Tests and Conventional Clinical Trials" Biomedicines 13, no. 5: 1135. https://doi.org/10.3390/biomedicines13051135
APA StyleMao, P., Jin, M., Li, W., Zhang, H., Li, H., Li, S., Yang, Y., Zhu, M., Shi, Y., Zhang, X., & Chen, D. (2025). In Silico Trials of Prosthetic Valves Replicate Methodologies for Evaluating the Fatigue Life of Artificial Leaflets to Expand Beyond In Vitro Tests and Conventional Clinical Trials. Biomedicines, 13(5), 1135. https://doi.org/10.3390/biomedicines13051135








