Numerical Simulation of the Effect of Electrical Stimulation on Disuse After Hip Replacement
Abstract
1. Introduction
2. Disuse Remodeling Model
2.1. Finite Element Model, Boundary Conditions, and Material Assignment
2.2. Bone Disuse Remodeling Model
3. Disuse Remodeling Process of the Proximal Femur
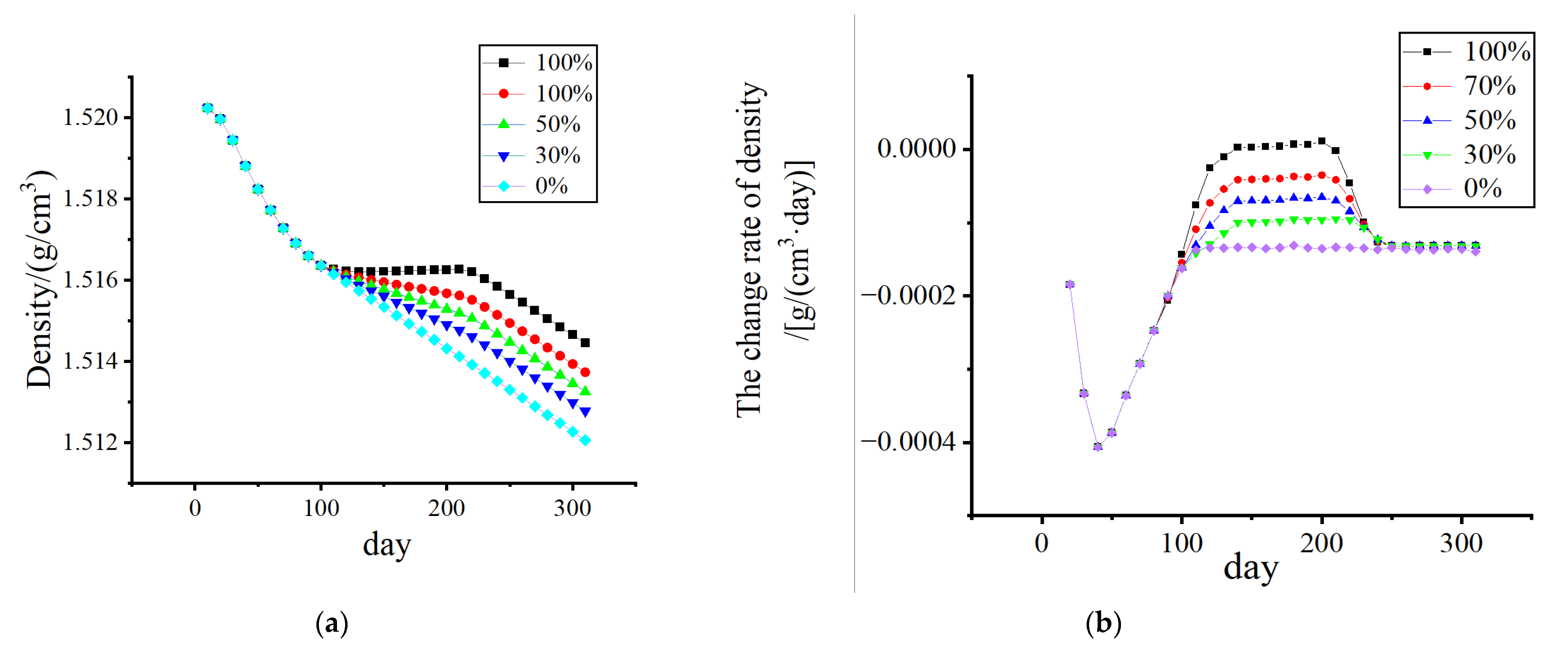
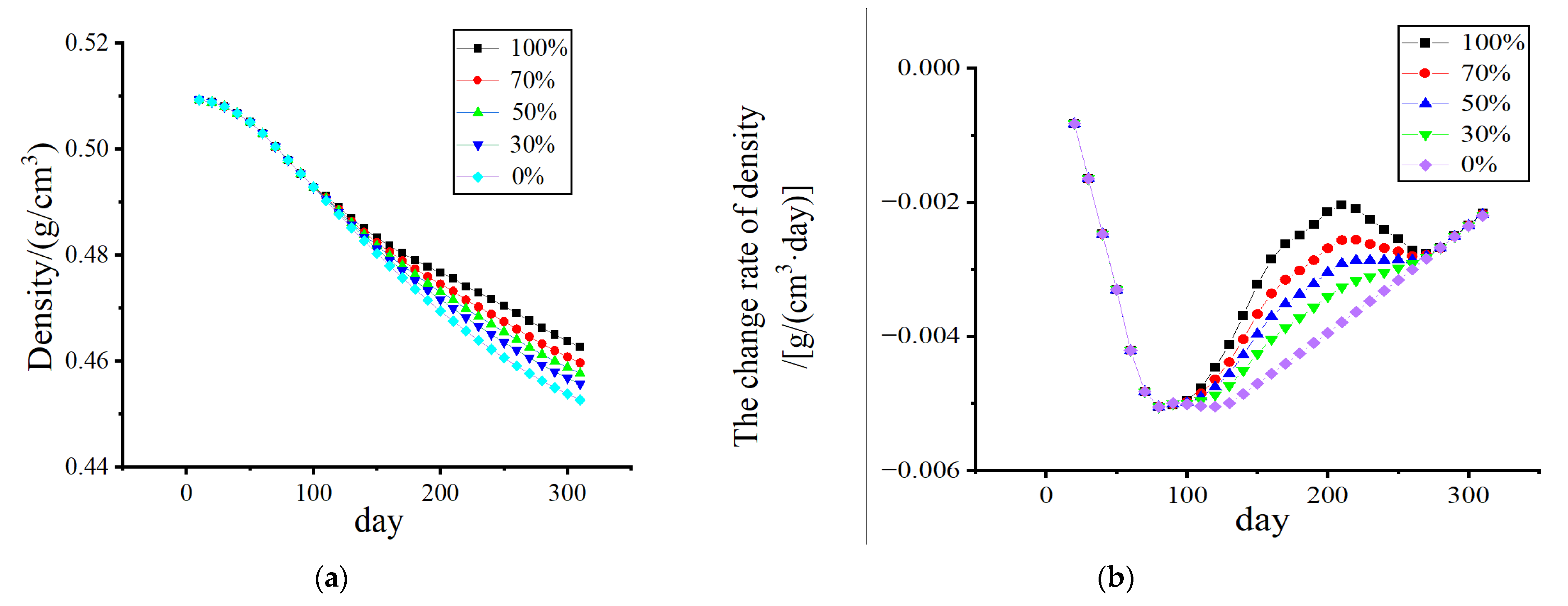
3.1. Stress-Shielding Effect
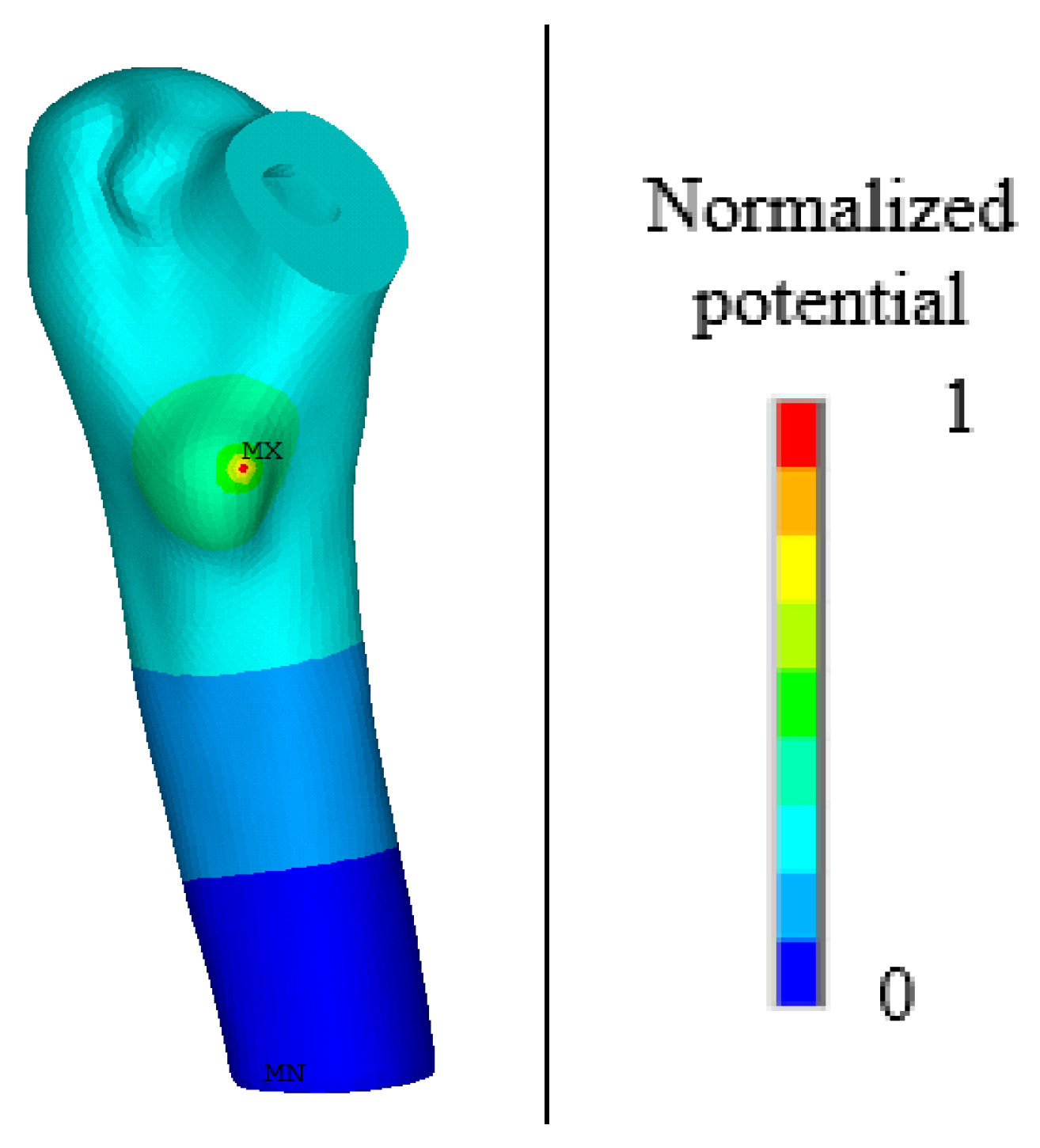
3.2. Numerical Simulation of Outages Under Mechanical–Electrical Coupling
4. Discussion
- In daily life activities, human bones are affected by a variety of loads. This paper discusses three types of typical working conditions: bone tissue with no loadings, bone tissue subjected to ligament forces, and bone subjected to muscle forces. Joint forces, such as the combined impact of a variety of loads, can be studied in future work [38]. A more complex boundary condition of the model will undoubtedly more closely approach the real situation of the simulation results;
- Bone tissue inside the material is assigned the CT value and density of a functional relationship for determination. In this work, the research on bone tissue, which is an isotropic homogeneous material, refers to the uniform internal porosity distribution in each unit without considering the location of the pore, as a typical anisotropic material [39]. Considering the uniqueness of the internal structure, more realistic simulation results can be obtained;
- There are also various blood vessels and tissue fluids in real bone tissue, which is essentially a biomaterial composed of solid and liquid [40]; real bone tissue needs to be further explored in future studies. In addition, individual differences in biomaterials must be discussed and analyzed;
- Electrical stimulation, as an in vitro physical stimulus, exhibits excellence in clinical application; however, at present, the internal mechanism of the impact of the bone-remodeling process still requires further exploration. This phenomenological model can provide a certain explanation for this phenomenon, but a specific parameter model remains to be further modified and perfected according to the experimental data.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Healy, W.L.; Iorio, R. Total hip arthroplasty: Optimal treatment for displaced femoral neck fractures in elderly patients. Clin. Orthop. Relat. Res. 2004, 429, 43–48. [Google Scholar] [CrossRef]
- Li, Z.; Li, M.; Yao, X.; Liu, B.; Liu, S.; Liu, Z.; Zhang, B.; Han, Y. Bone remodelling of the proximal femur after hip revision with a metaphyseal-fixation femoral stem component. Ther. Clin. Risk Manag. 2023, 19, 171–181. [Google Scholar] [CrossRef] [PubMed]
- Pannu, T.S.; Nezwek, T.; Villa, J.M.; Higuera, C.A. Total hip arthroplasty: Aseptic loosening. In Orthopaedics and Trauma: Current Concepts and Best Practices; Slullitel, P., Rossi, L., Camino-Willhuber, G., Eds.; Springer: Cham, Switzerland, 2024; pp. 1439–1447. [Google Scholar]
- Krishnamurthy, A.B.; MacDonald, S.J.; Paprosky, W.G. 5- to 13-year follow-up study on cementless femoral components in revision surgery. J. Arthroplasty 1997, 12, 839–847. [Google Scholar] [CrossRef]
- Avval, P.T.; Klika, V.; Bougherara, H. Predicting bone remodeling in response to total hip arthroplasty: Computational study using mechanobiochemical model. J. Biomech. Eng. 2014, 136, 051002. [Google Scholar] [CrossRef]
- Burchard, R.; Graw, J.A.; Soost, C.; Schmitt, J. Stress shielding effect after total hip arthroplasty varies between combinations of stem design and stiffness-a comparing biomechanical finite element analysis. Int. Orthop. 2023, 47, 1981–1987. [Google Scholar] [CrossRef]
- Liu, B.; Wang, H.; Zhang, M.; Li, J.; Zhang, N.; Luan, Y.; Fang, C.; Cheng, C.K. Capability of auxetic femoral stems to reduce stress shielding after total hip arthroplasty. J. Orthop. Translat. 2022, 38, 220–228. [Google Scholar] [CrossRef]
- Das, S.S.; Chakraborti, P. Development of biomaterial for total hip joint replacement. IOP Conf. Ser. Mater. Sci. Eng. 2018, 377, 012177. [Google Scholar] [CrossRef]
- Mihalko, W.M.; Haider, H.; Kurtz, S.; Marcolongo, M.; Urish, K. New materials for hip and knee joint replacement: What’s hip and what’s in kneed? J. Orthop. Res. 2020, 38, 1436–1444. [Google Scholar] [CrossRef]
- Oladapo, B.I.; Ismail, S.O.; Kayode, J.F.; Ikumapayi, O.M. Piezoelectric effects on bone modeling for enhanced sustainability. Mater. Chem. Phys. 2023, 305, 127960. [Google Scholar] [CrossRef]
- Rubin, J.; McLeod, K.J.; Titus, L.; Nanes, M.S.; Catherwood, B.D.; Rubin, C.T. Formation of osteoclast-like cells is suppressed by low frequency, low intensity electric fields. J. Orthop. Res. 1996, 14, 7–15. [Google Scholar] [CrossRef]
- Tschon, M.; Veronesi, F.; Contartese, D.; Sartori, M.; Martini, L.; Vincenzi, F.; Ravani, A.; Varani, K.; Fini, M. Effects of pulsed electromagnetic fields and platelet rich plasma in preventing osteoclastogenesis in an in vitro model of osteolysis. J. Cell. Physiol. 2018, 233, 2645–2656. [Google Scholar] [CrossRef] [PubMed]
- Hartig, M.; Joos, U.; Wiesmann, H.P. Capacitively coupled electric fields accelerate proliferation of osteoblast-like primary cells and increase bone extracellular matrix formation in vitro. Eur. Biophys. J. 2000, 29, 499–506. [Google Scholar] [CrossRef] [PubMed]
- Clark, C.C.; Wang, W.; Brighton, C.T. Up-regulation of expression of selected genes in human bone cells with specific capacitively coupled electric fields. J. Orthop. Res. 2014, 32, 894–903. [Google Scholar] [CrossRef]
- Wiesmann, H.; Hartig, M.; Stratmann, U.; Meyer, U.; Joos, U. Electrical stimulation influences mineral formation of osteoblast-like cells in vitro. Biochim. Biophys. Acta 2001, 1538, 28–37. [Google Scholar] [CrossRef]
- Wang, Q.; Zhong, S.; Ouyang, J.; Jiang, L.; Zhang, Z.; Xie, Y.; Luo, S. Osteogenesis of electrically stimulated bone cells mediated in part by calcium ions. Clin. Orthop. Relat. Res. 1998, 348, 259–268. [Google Scholar] [CrossRef]
- Yao, C.H.; Yang, B.Y.; Li, Y.E. Remodeling effects of the combination of GGT scaffolds, percutaneous electrical stimulation, and acupuncture on large bone defects in rats. Front. Bioeng. Biotechnol. 2022, 10, 832808. [Google Scholar] [CrossRef]
- Luo, S.; Zhang, C.; Xiong, W.; Song, Y.; Wang, Q.; Zhang, H.; Guo, S.; Yang, S.; Liu, H. Advances in electroactive biomaterials: Through the lens of electrical stimulation promoting bone regeneration strategy. J. Orthop. Translat. 2024, 47, 191–206. [Google Scholar] [CrossRef]
- Zhu, G.; Zhang, T.; Chen, M.; Yao, K.; Huang, X.; Zhang, B.; Li, Y.; Liu, J.; Wang, Y.; Zhao, Z. Bone physiological microenvironment and healing mechanism: Basis for future bone-tissue engineering scaffolds. Bioact. Mater. 2021, 6, 4110–4140. [Google Scholar] [CrossRef]
- Zhu, F.; Liu, W.; Li, P.; Zhao, H.; Deng, X.; Wang, H.L. Electric/magnetic intervention for bone regeneration: A systematic review and network meta-analysis. Tissue Eng. Part B Rev. 2023, 29, 217–231. [Google Scholar] [CrossRef]
- Jang, I.G.; Kim, I.Y. Computational simulation of simultaneous cortical and trabecular bone change in human proximal femur during bone remodeling. J. Biomech. 2010, 43, 294–301. [Google Scholar] [CrossRef]
- Garijo, N.; Verdonschot, N.; Engelborghs, K.; García-Aznar, J.M.; Pérez, M.A. Subject-specific musculoskeletal loading of the tibia: Computational load estimation. J. Mech. Behav. Biomed. Mater. 2017, 65, 334–343. [Google Scholar] [CrossRef] [PubMed]
- Mullender, M.G.; Huiskes, R.; Weinans, H. A physiological approach to the simulation of bone remodeling as a self-organizational control process. J. Biomech. 1994, 27, 1389–1394. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H. Research and Application of Computational Model of Osteoporosis of Cancellous Bone Conforming to Physiological Process. Ph.D. Thesis, Jilin University, Changchun, China, 2005. (In Chinese). [Google Scholar]
- Hazelwood, S.J.; Martin, R.B.; Rashid, M.M.; Rodrigo, J.J. A mechanistic model for internal bone remodeling exhibits different dynamic responses in disuse and overload. J. Biomech. 2001, 34, 299–308. [Google Scholar] [CrossRef]
- Lei, Z.J.X.; Wang, D.M.; Wang, C.H.; Chen, S.G. Effects of different mechanical incentives on numerical simulation of bone remodeling. J. Med. Biomech. 2015, 30, 299–303. [Google Scholar]
- Lei, Z.Q.X. Study on Theory and Method of Numerical Simulation of Bone Remodeling in Weightless Environment. Master’s Thesis, Shanghai Jiaotong University, Shanghai, China, 2015. (In Chinese). [Google Scholar]
- Hernandez, C.J.; Beaupré, G.S.; Carter, D.R. A model of mechanobiologic and metabolic influences on bone adaptation. J. Rehabil. Res. Dev. 2000, 37, 235–244. [Google Scholar]
- Qu, C. Simulation of Bone Remodeling Behavior under Multi-Field Coupling Loads. Ph.D. Dissertation, Tianjin University, Tianjin, China, 2007. (In Chinese). [Google Scholar]
- Martin, R.B. Porosity and specific surface of bone. Crit. Rev. Biomed. Eng. 1984, 10, 179–222. [Google Scholar]
- Fernandez, J.R.; Garcia-Aznar, J.M.; Martinez, R. Numerical analysis of a piezoelectric bone remodelling problem. Eur. J. Appl. Math. 2012, 23, 635–657. [Google Scholar] [CrossRef]
- Bansod, Y.D.; Kebbach, M.; Kluess, D.; Bader, R.; Van Rienen, U. Computational analysis of bone remodeling in the proximal tibia under electrical stimulation considering the piezoelectric properties. Front. Bioeng. Biotechnol. 2021, 9, 705199. [Google Scholar] [CrossRef]
- Jungwirth-Weinberger, A.; Boettner, F. Normal hip biomechanics. In Anterior Hip Replacement: From Origin to Current Advanced Techniques; Matta, J.M., Sah, A.P., Eds.; Springer: Cham, Switzerland, 2022; pp. 239–248. [Google Scholar]
- Zhang, B.; Liu, S.; Liu, Z.; Liu, B.; Huo, J.; Li, M.; Han, Y. Clinical and radiologic outcomes in patients undergoing primary total hip arthroplasty with Collum Femoris Preserving stems: A comparison between the direct anterior approach and the posterior approach. BMC Musculoskelet. Disord. 2022, 23, 77. [Google Scholar] [CrossRef]
- Nabudda, K.; Suriyawanakul, J.; Tangchaichit, K.; Pholdee, N.; Kosuwon, W.; Wisanuyotin, T.; Sukhonthamarn, K. Identification of flexural modulus and Poisson’s ratio of fresh femoral bone based on a finite element model. Int. J. Online Biomed. Eng. 2022, 18, 94–105. [Google Scholar] [CrossRef]
- Savio, D.; Bagno, A. When the total hip replacement fails: A review on the stress-shielding effect. Processes 2022, 10, 612. [Google Scholar] [CrossRef]
- Leppik, L.; Oliveira, K.M.C.; Bhavsar, M.B.; Barker, J.H. Electrical stimulation in bone tissue engineering treatments. Eur. J. Trauma Emerg. Surg. 2020, 46, 231–244. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.; Chen, Z.; Zhang, J.; Gao, Y.; Qiao, F.; Jin, Z. Musculoskeletal multibody dynamics investigation for the different medial-lateral installation position of the femoral component in unicompartmental knee arthroplasty. Sheng Wu Yi Xue Gong Cheng Xue Za Zhi 2023, 40, 508–514. [Google Scholar] [CrossRef] [PubMed]
- Rosa, N.; Moura, M.F.S.F.; Olhero, S.; Simoes, R.; Magalhães, F.D.; Marques, A.T.; Ferreira, J.P.S.; Reis, A.R.; Carvalho, M.; Parente, M. Bone: An outstanding composite material. Appl. Sci. 2022, 12, 3381. [Google Scholar] [CrossRef]
- Hong, M.H.; Lee, J.H.; Jung, H.S.; Shin, H.; Shin, H. Biomineralization of bone tissue: Calcium phosphate-based inorganics in collagen fibrillar organic matrices. Biomater. Res. 2022, 26, 42. [Google Scholar] [CrossRef]
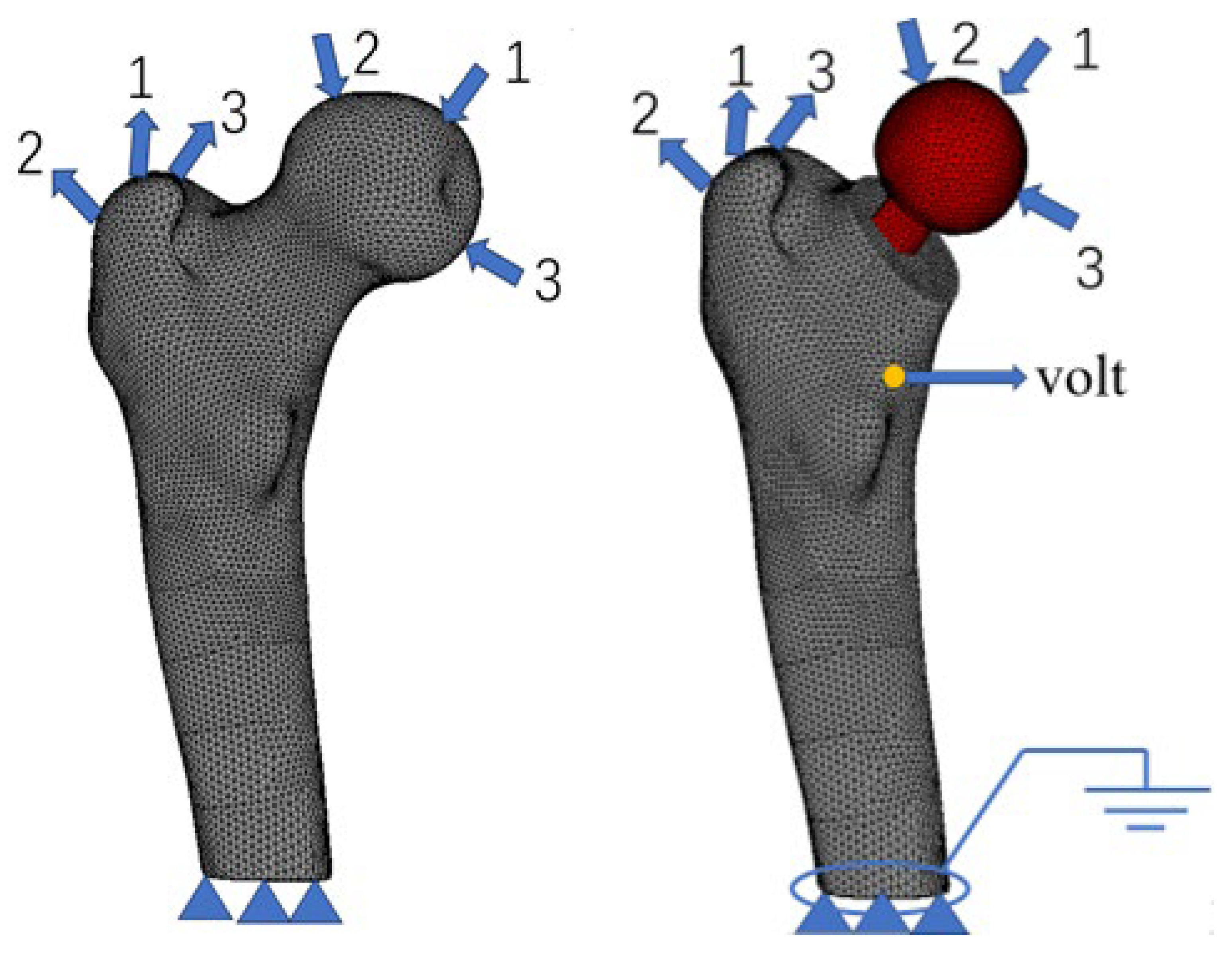



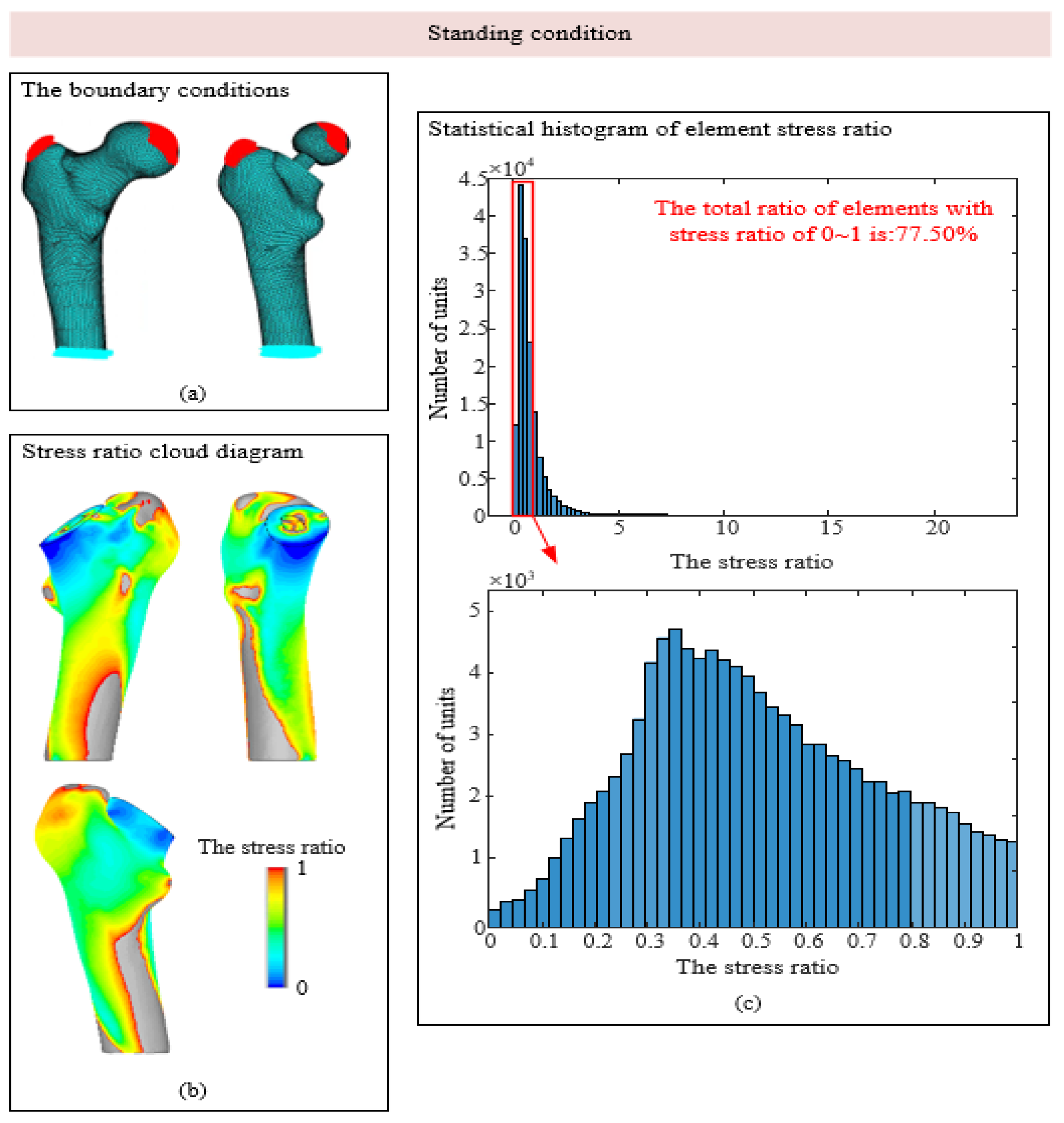
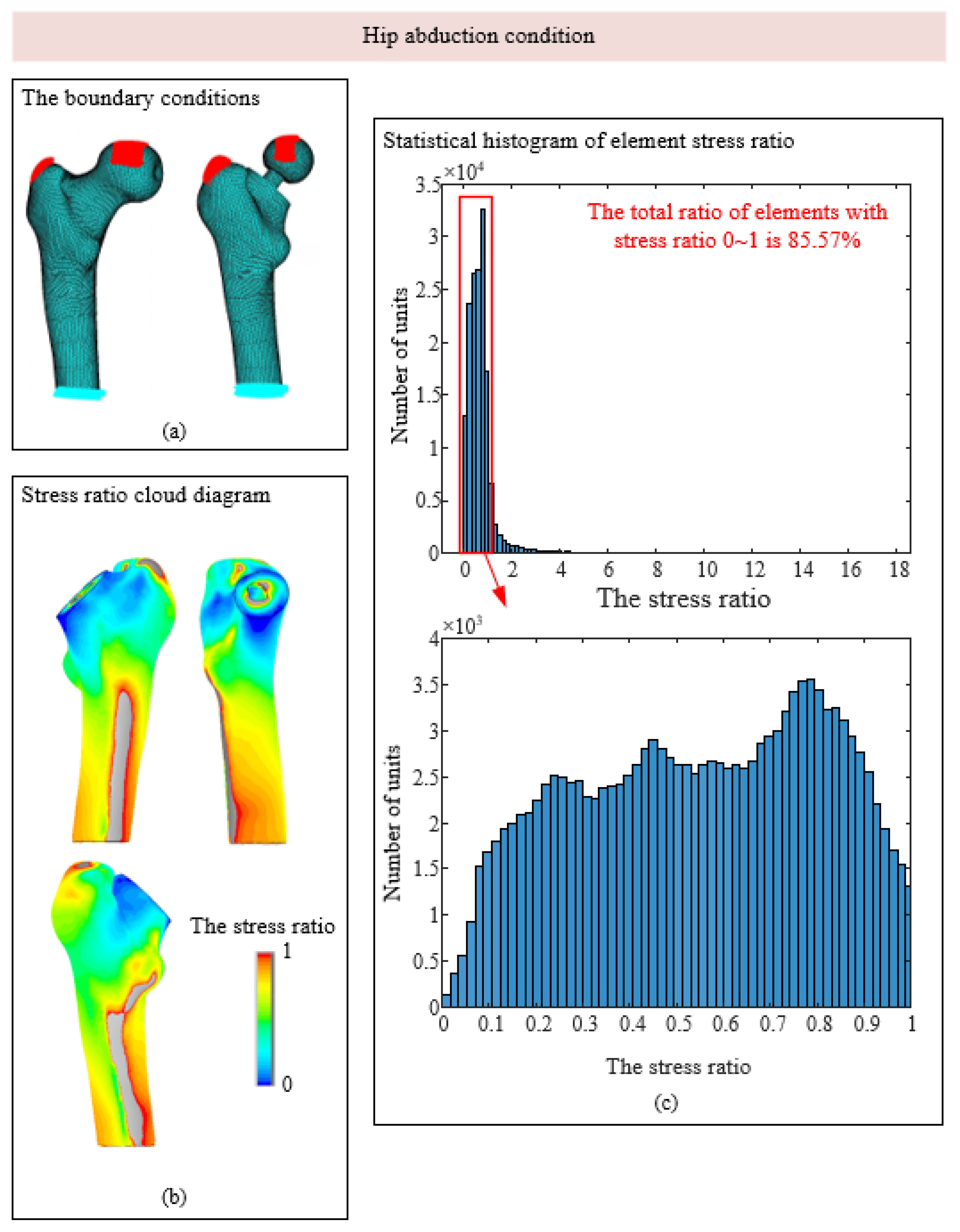
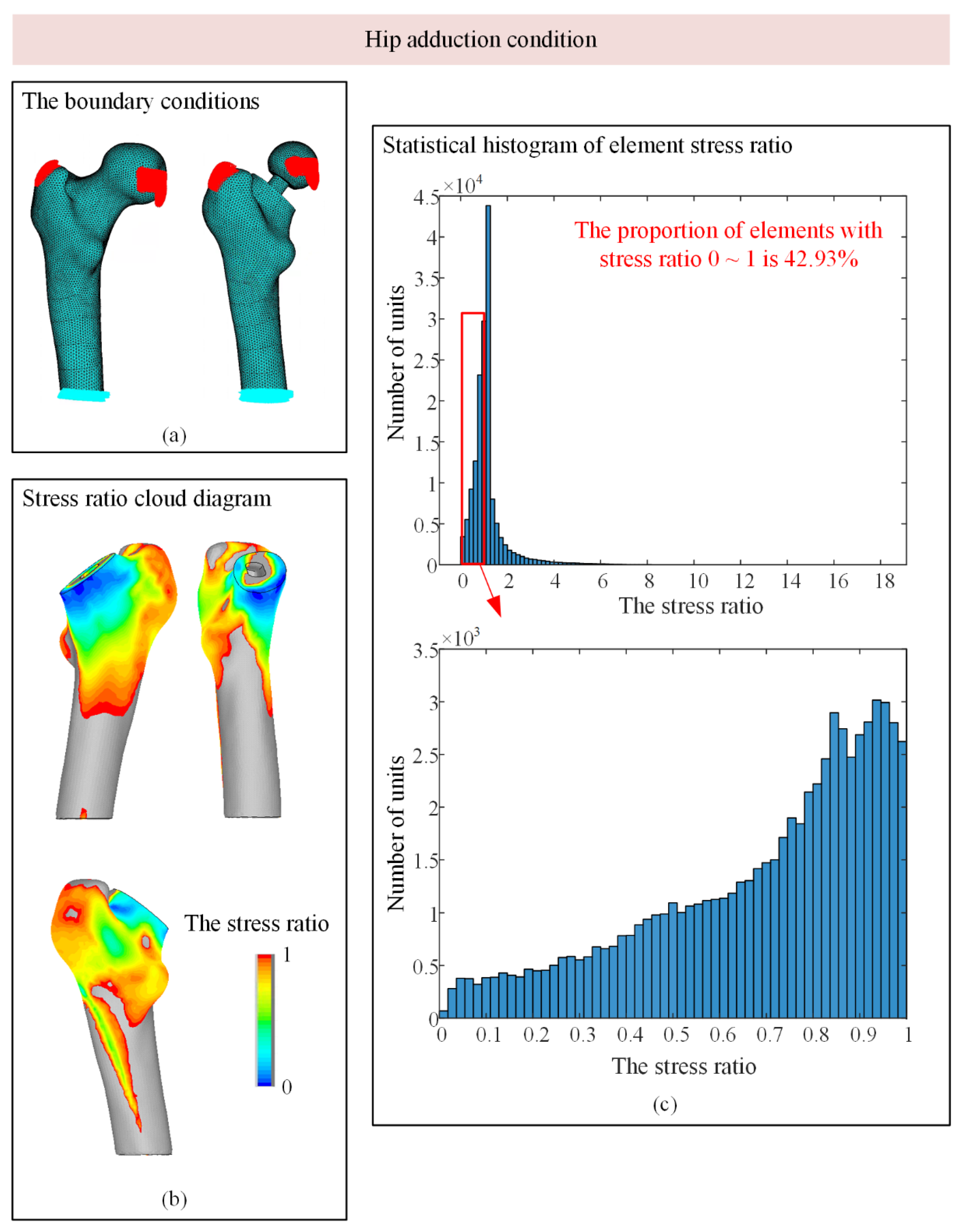




| Load Conditions | Cycles | Joint Force | Muscle Force | ||
|---|---|---|---|---|---|
| Size (N) | Direction (°) | Size (N) | Direction (°) | ||
| 1 Standing condition | 6000 | 2317 | 24 | 703 | 28 |
| 2 Hip abduction | 2000 | 1158 | −15 | 351 | −8 |
| 3 Hip adduction | 2000 | 1548 | 56 | 468 | 35 |
| Constant | Numerical Value | Unit |
|---|---|---|
| 0.5 [25] | ||
| 0.1 [25] | ||
| 0.1 [25] | BMUs/(mm3·day) | |
| TR (cortical bone) | 24 [25] | day |
| TI (cortical bone) | 8 [25] | day |
| TF (cortical bone) | 64 [25] | day |
| TR (cancellous bone) | 60 [28] | day |
| TI (cancellous bone) | 57 [28] | day |
| TF (cancellous bone) | 197 [28] | day |
| 0.01 [28] | mm | |
| 0.65 [28] | mm | |
| 0.05 [28] | mm | |
| 0.2 [29] | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Qu, C.; Li, X.; Yan, Y. Numerical Simulation of the Effect of Electrical Stimulation on Disuse After Hip Replacement. Biomedicines 2025, 13, 471. https://doi.org/10.3390/biomedicines13020471
Wang Q, Qu C, Li X, Yan Y. Numerical Simulation of the Effect of Electrical Stimulation on Disuse After Hip Replacement. Biomedicines. 2025; 13(2):471. https://doi.org/10.3390/biomedicines13020471
Chicago/Turabian StyleWang, Qian, Chuanyong Qu, Xiaohui Li, and Yufan Yan. 2025. "Numerical Simulation of the Effect of Electrical Stimulation on Disuse After Hip Replacement" Biomedicines 13, no. 2: 471. https://doi.org/10.3390/biomedicines13020471
APA StyleWang, Q., Qu, C., Li, X., & Yan, Y. (2025). Numerical Simulation of the Effect of Electrical Stimulation on Disuse After Hip Replacement. Biomedicines, 13(2), 471. https://doi.org/10.3390/biomedicines13020471







