Deformation Behaviour of Optimised Three-Dimensional Axisymmetric Chiral Auxetic Structures
Abstract
1. Introduction
2. Materials and Methods
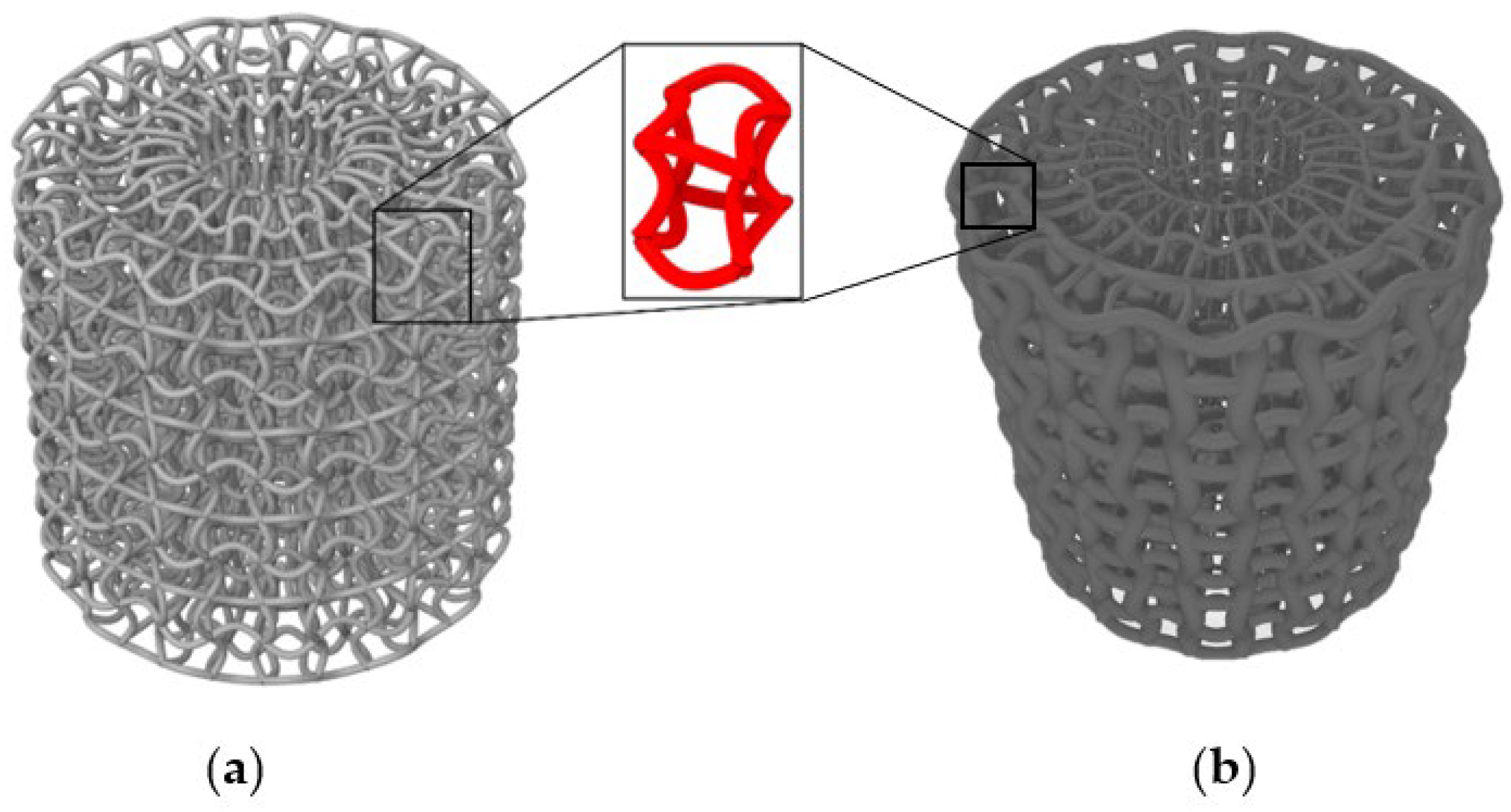
2.1. Design
2.2. Fabrication
2.3. Mechanical Testing
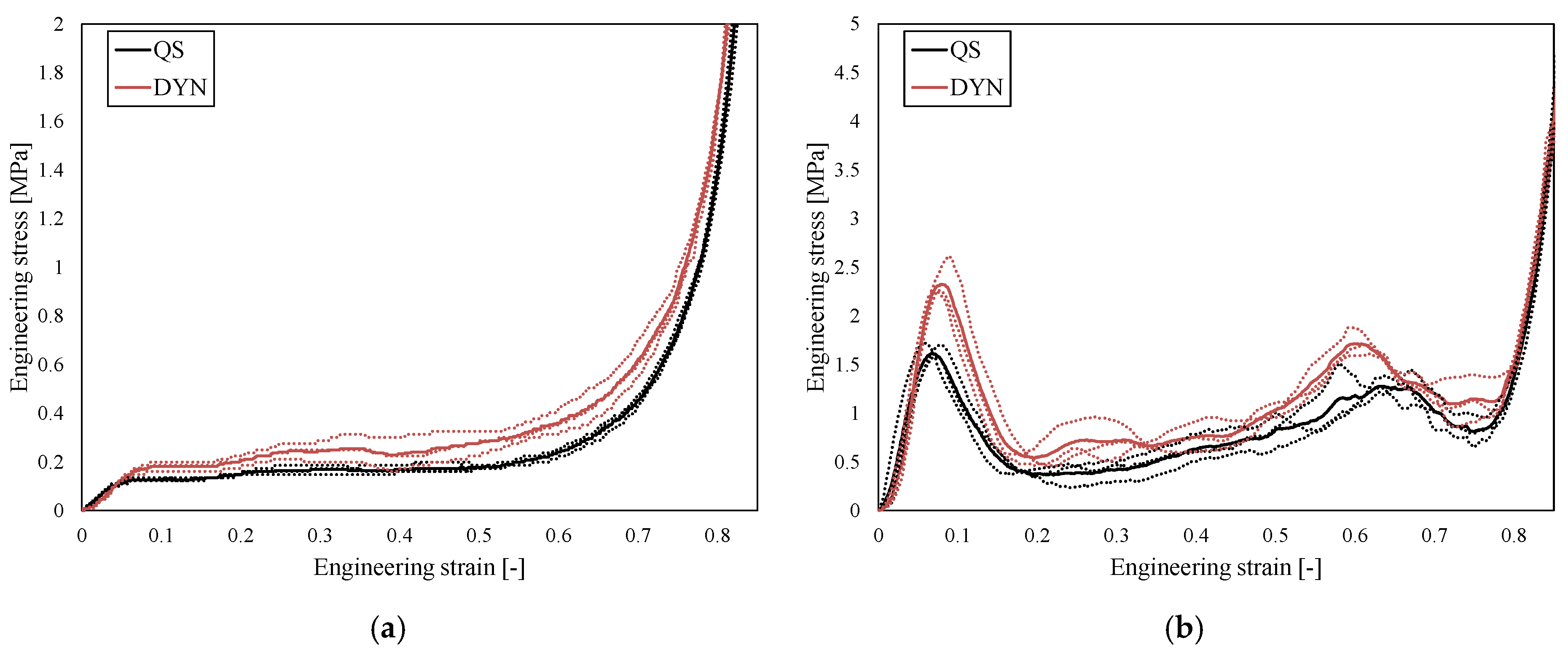
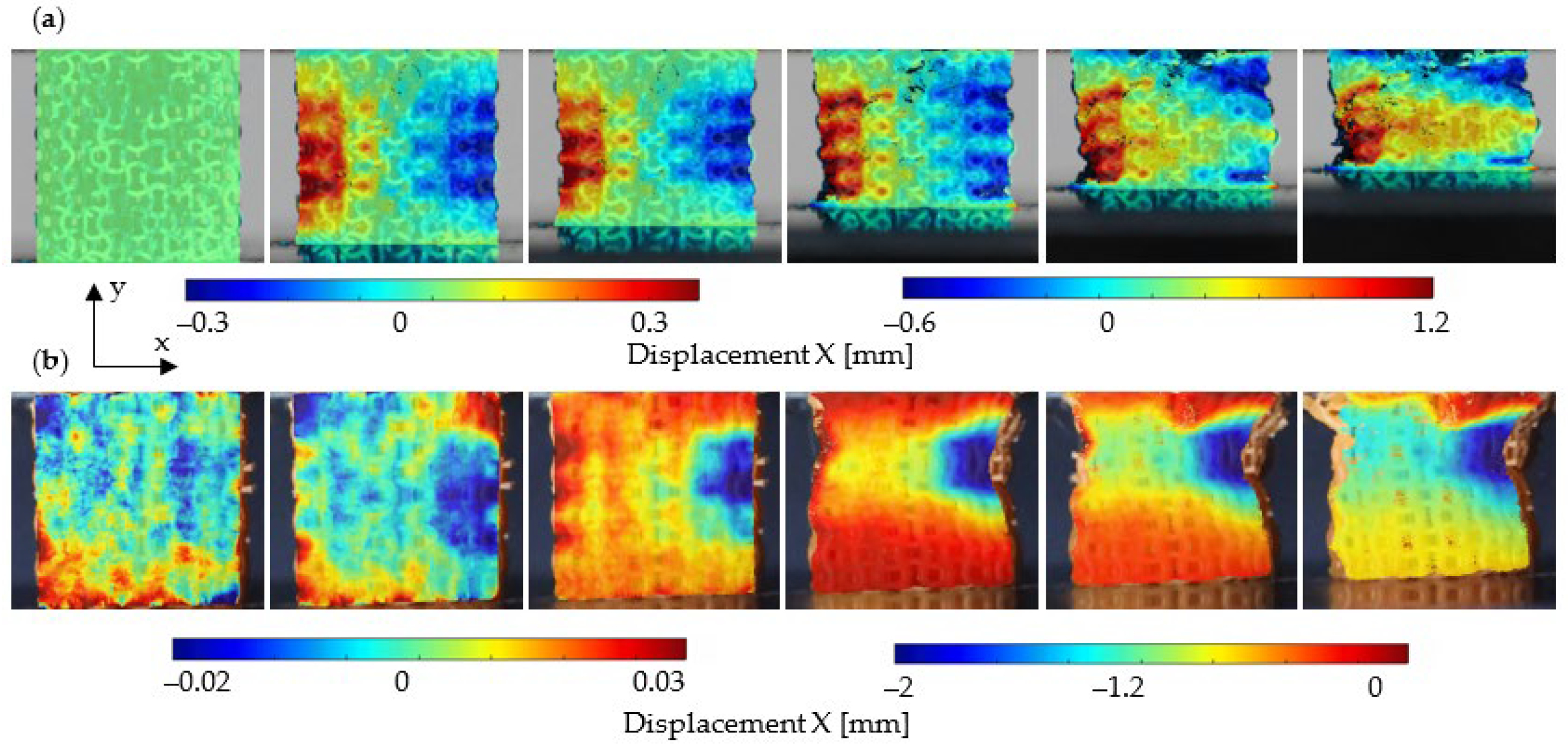
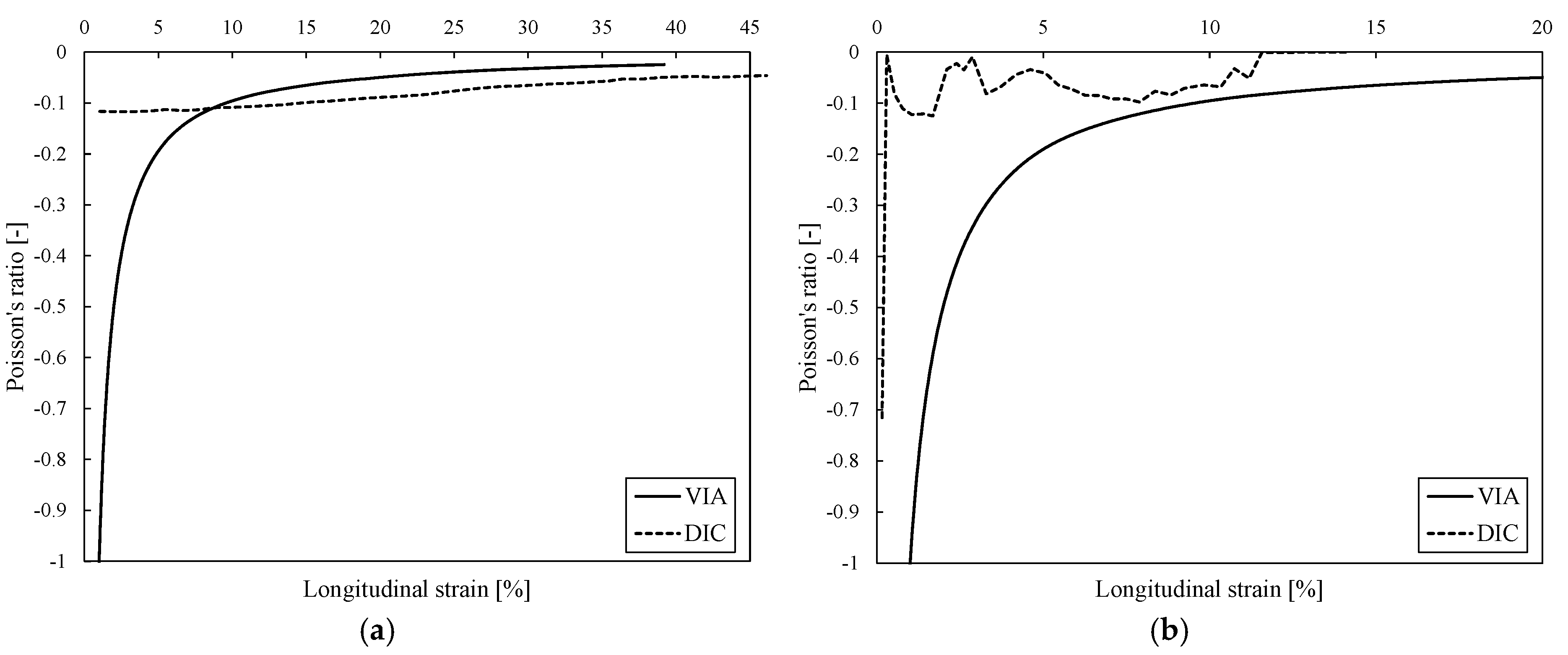
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bejoy, A.M.; Makkithaya, K.N.; Hunakunti, B.B.; Hegde, A.; Krishnamurthy, K.; Sarkar, A.; Lobo, C.F.; Keshav, D.V.S.; Dharshini, G.; Dhivya Dharshini, S.; et al. An insight on advances and applications of 3d bioprinting: A review. Bioprinting 2021, 24, e00176. [Google Scholar] [CrossRef]
- Stapenhorst, F.; Garrido dos Santos, M.; Prestes, J.P.; Alcantara, B.J.; Felisberto Borges, M.; Pranke, P. Bioprinting: A promising approach for tissue regeneration. Bioprinting 2021, 22, e00130. [Google Scholar] [CrossRef]
- Haleem, A.; Javaid, M. 3D printed medical parts with different materials using additive manufacturing. Clin. Epidemiol. Glob. Health 2020, 8, 215–223. [Google Scholar] [CrossRef]
- Mobarak, M.H.; Abid, A.S.; Munna, M.S.; Dutta, M.; Rimon, M.I.H. Additive manufacturing in biomedical: Applications, challenges, and prospects. Hybrid Adv. 2025, 10, 100467. [Google Scholar] [CrossRef]
- Ng, W.L.; Lee, J.M.; Zhou, M.; Chen, Y.-W.; Lee, K.-X.A.; Yeong, W.Y.; Shen, Y.-F. Vat polymerization-based bioprinting—Process, materials, applications and regulatory challenges. Biofabrication 2020, 12, 22001. [Google Scholar] [CrossRef]
- Guttridge, C.; Shannon, A.; O’Sullivan, A.; O’Sullivan, K.J.; O’Sullivan, L.W. Biocompatible 3D printing resins for medical applications: A review of marketed intended use, biocompatibility certification, and post-processing guidance. Ann. 3D Print. Med. 2022, 5, 100044. [Google Scholar] [CrossRef]
- Pesode, P.; Barve, S. Additive manufacturing of metallic biomaterials and its biocompatibility. Mater. Today Proc. 2022. [Google Scholar] [CrossRef]
- Ullah, M.W.; Ul-Islam, M.; Shehzad, A.; Manan, S.; Islam, S.U.; Fatima, A.; Al-Saidi, A.K.; Nokab, M.E.H.E.; Sanchez, J.Q.; Sebakhy, K.O. From Bioinks to Functional Tissues and Organs: Advances, Challenges, and the Promise of 3D Bioprinting. Macromol. Mater. Eng. 2025, e00251. [Google Scholar] [CrossRef]
- Lakes, R.S. Foam Structures with a Negative Poisson’s Ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef]
- Novak, N.; Vesenjak, M.; Ren, Z. Auxetic cellular materials—A Review. Stroj. Vestn.-J. Mech. Eng. 2016, 62, 485–493. [Google Scholar] [CrossRef]
- Evans, K.E.; Caddock, B.D. Microporous materials with negative Poisson’s ratios. II. Mechanisms and interpretation. J. Phys. D Appl. Phys. 1989, 22, 1883–1887. [Google Scholar] [CrossRef]
- Daynes, S. Isotropic cellular structure design strategies based on triply periodic minimal surfaces. Addit. Manuf. 2024, 81, 104010. [Google Scholar] [CrossRef]
- Weaver, J.C.; Milliron, G.W.; Allen, P.; Miserez, A.; Rawal, A.; Garay, J.; Thurner, P.J.; Seto, J.; Mayzel, B.; Friesen, L.J.; et al. Unifying design strategies in demosponge and hexactinellid skeletal systems. J. Adhes. 2010, 86, 72–95. [Google Scholar] [CrossRef]
- Han, S.F.; Miao, Y.R.; Pei, Y.J.; Yang, Y. Finite Element Study on the Effect of Fibrillar Morphology on Corneal Biomechanics. Int. J. Simul. Model. 2024, 23, 519–530. [Google Scholar] [CrossRef]
- Wegst, U.G.K.; Bai, H.; Saiz, E.; Tomsia, A.P.; Ritchie, R.O. Bioinspired structural materials. Nat. Mater. 2015, 14, 23–36. [Google Scholar] [CrossRef]
- Airoldi, A.; Quaranta, G.; Beltramin, A.; Sala, G. Design of a Morphing Actuated Aileron with Chiral Composite Internal Structure. Adv. Aircr. Spacecr. Sci. 2014, 1, 331–351. [Google Scholar] [CrossRef]
- Mauko, A.; Fíla, T.; Falta, J.; Koudelka, P.; Rada, V.; Neuhäuserová, M.; Zlámal, P.; Vesenjak, M.; Jiroušek, O.; Ren, Z. Dynamic deformation behaviour of chiral auxetic lattices at low and high strain-rates. Metals 2021, 11, 52. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Two-dimensional isotropic system with a negative poisson ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
- Narojczyk, J.W.; Tretiakov, K.V.; Smardzewski, J.; Wojciechowski, K.W. Hardening of fcc hard-sphere crystals by introducing nanochannels: Auxetic aspects. Phys. Rev. E 2023, 108, 45003. [Google Scholar] [CrossRef]
- Raamachandran, J.; Jayavenkateshwaran, K. Modeling of stents exhibiting negative Poisson’s ratio effect. Comput. Methods Biomech. Biomed. Eng. 2007, 10, 245–255. [Google Scholar] [CrossRef]
- Duncan, O.; Allen, T.; Foster, L.; Senior, T.; Alderson, A. Fabrication, characterisation and modelling of uniform and gradient auxetic foam sheets. Acta Mater. 2017, 126, 426–437. [Google Scholar] [CrossRef]
- Sadegh Ebrahimi, M.; Noruzi, M.; Hamzehei, R.; Etemadi, E.; Hashemi, R. Revolutionary auxetic intravascular medical stents for angioplasty applications. Mater. Des. 2023, 235, 112393. [Google Scholar] [CrossRef]
- Novak, N.; Mauko, A.; Ulbin, M.; Krstulović-Opara, L.; Ren, Z.; Vesenjak, M. Development and characterisation of novel three-dimensional axisymmetric chiral auxetic structures. J. Mater. Res. Technol. 2022, 17, 2701–2713. [Google Scholar] [CrossRef]
- Novak, N.; Nowak, M.; Vesenjak, M.; Ren, Z. Structural Optimization of the Novel 3D Graded Axisymmetric Chiral Auxetic Structure. Phys. Status Solidi (b) 2022, 259, 2200409. [Google Scholar] [CrossRef]
- Yi, J.; Yang, S.; Yue, L.; Lei, I.M. Digital light processing 3D printing of flexible devices: Actuators, sensors and energy devices. Microsyst. Nanoeng. 2025, 11, 51. [Google Scholar] [CrossRef]
- Siddique, S.H.; Hazell, P.J.; Wang, H.; Escobedo, J.P.; Ameri, A.A.H. Lessons from nature: 3D printed bio-inspired porous structures for impact energy absorption—A review. Addit. Manuf. 2022, 58, 103051. [Google Scholar] [CrossRef]
- Alparslan, C.; Bayraktar, Ş. Advances in Digital Light Processing (DLP) Bioprinting: A Review of Biomaterials and Its Applications, Innovations, Challenges, and Future Perspectives. Polymers 2025, 17, 1287. [Google Scholar] [CrossRef]
- Vesenjak, M.; Novak, N.; Ren, Z. Axisymmetric Chiral Auxetic Structure. EU Patent 3,970,941, 7 May 2025. [Google Scholar]
- Grygier, D.; Kurzawa, A.; Stachowicz, M.; Krawiec, K.; Stępczak, M.; Roszak, M.; Kazimierczak, M.; Aniszewska, D.; Pyka, D. Investigations into the Material Characteristics of Selected Plastics Manufactured Using SLA-Type Additive Methods. Polymers 2024, 16, 1607. [Google Scholar] [CrossRef]
- ISO 13314:2011; Mechanical Testing of Metals—Ductility Testing—Compression Test for Porous and Cellular Metals. International Organization for Standardization: Geneva, Switzerland, 2011. Available online: https://www.iso.org/standard/53669.html (accessed on 10 September 2025).
- Blaber, J.; Adair, B.; Antoniou, A. Ncorr: Open-Source 2D Digital Image Correlation Matlab Software. Exp. Mech. 2015, 55, 1105–1122. [Google Scholar] [CrossRef]
- Novak, N.; Dobnik Dubrovski, P.; Borovinšek, M.; Vesenjak, M.; Ren, Z. Deformation behaviour of advanced textile composites with auxetic structure. Compos. Struct. 2020, 252, 112761. [Google Scholar] [CrossRef]
- Neuhäuserová, M.; Fíla, T.; Koudelka, P.; Falta, J.; Rada, V.; Šleichrt, J.; Zlámal, P.; Jiroušek, O. Compressive Behaviour of Additively Manufactured Periodical Re-Entrant Tetrakaidecahedral Lattices at Low and High Strain-Rates. Metals 2021, 11, 1196. [Google Scholar] [CrossRef]



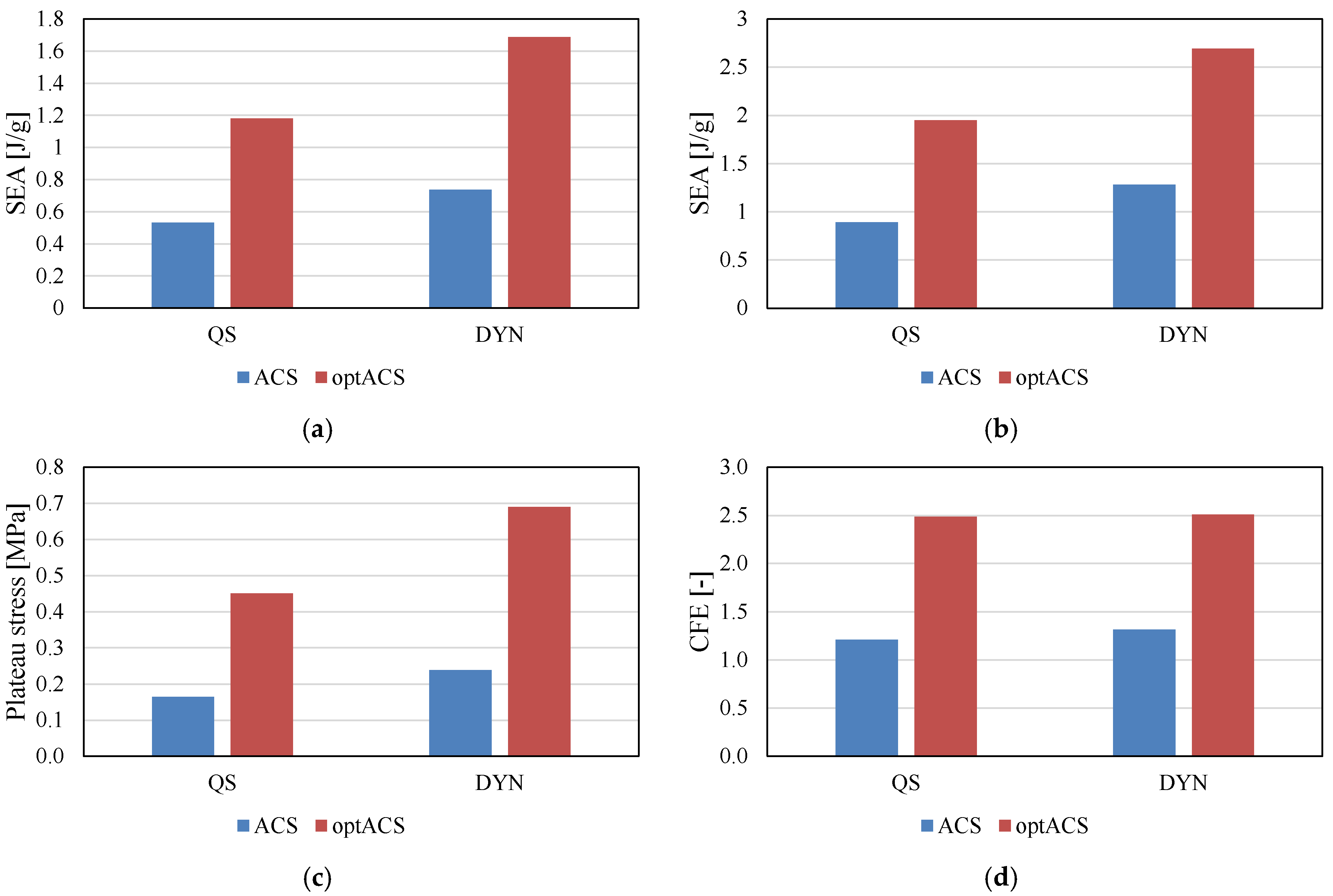
| Name | Dimensions | Weight [g] (st. dev.) | Relative Density [%] |
|---|---|---|---|
| ACS | Φ20 × 20 mm2 | 0.66 (0.016) | 9.67 |
| optACS | 1.38 (0.019) | 20.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Novak, N.; Grebo, A.; Borovinšek, M.; Krstulović-Opara, L.; Ren, Z.; Vesenjak, M. Deformation Behaviour of Optimised Three-Dimensional Axisymmetric Chiral Auxetic Structures. Biomedicines 2025, 13, 2816. https://doi.org/10.3390/biomedicines13112816
Novak N, Grebo A, Borovinšek M, Krstulović-Opara L, Ren Z, Vesenjak M. Deformation Behaviour of Optimised Three-Dimensional Axisymmetric Chiral Auxetic Structures. Biomedicines. 2025; 13(11):2816. https://doi.org/10.3390/biomedicines13112816
Chicago/Turabian StyleNovak, Nejc, Alen Grebo, Matej Borovinšek, Lovre Krstulović-Opara, Zoran Ren, and Matej Vesenjak. 2025. "Deformation Behaviour of Optimised Three-Dimensional Axisymmetric Chiral Auxetic Structures" Biomedicines 13, no. 11: 2816. https://doi.org/10.3390/biomedicines13112816
APA StyleNovak, N., Grebo, A., Borovinšek, M., Krstulović-Opara, L., Ren, Z., & Vesenjak, M. (2025). Deformation Behaviour of Optimised Three-Dimensional Axisymmetric Chiral Auxetic Structures. Biomedicines, 13(11), 2816. https://doi.org/10.3390/biomedicines13112816











