Why Intracranial Compliance Is Not Utilized as a Common Practical Tool in Clinical Practice
Abstract
:1. Introduction
2. Challenges in Measurement, Calculation, and Estimation of ICC
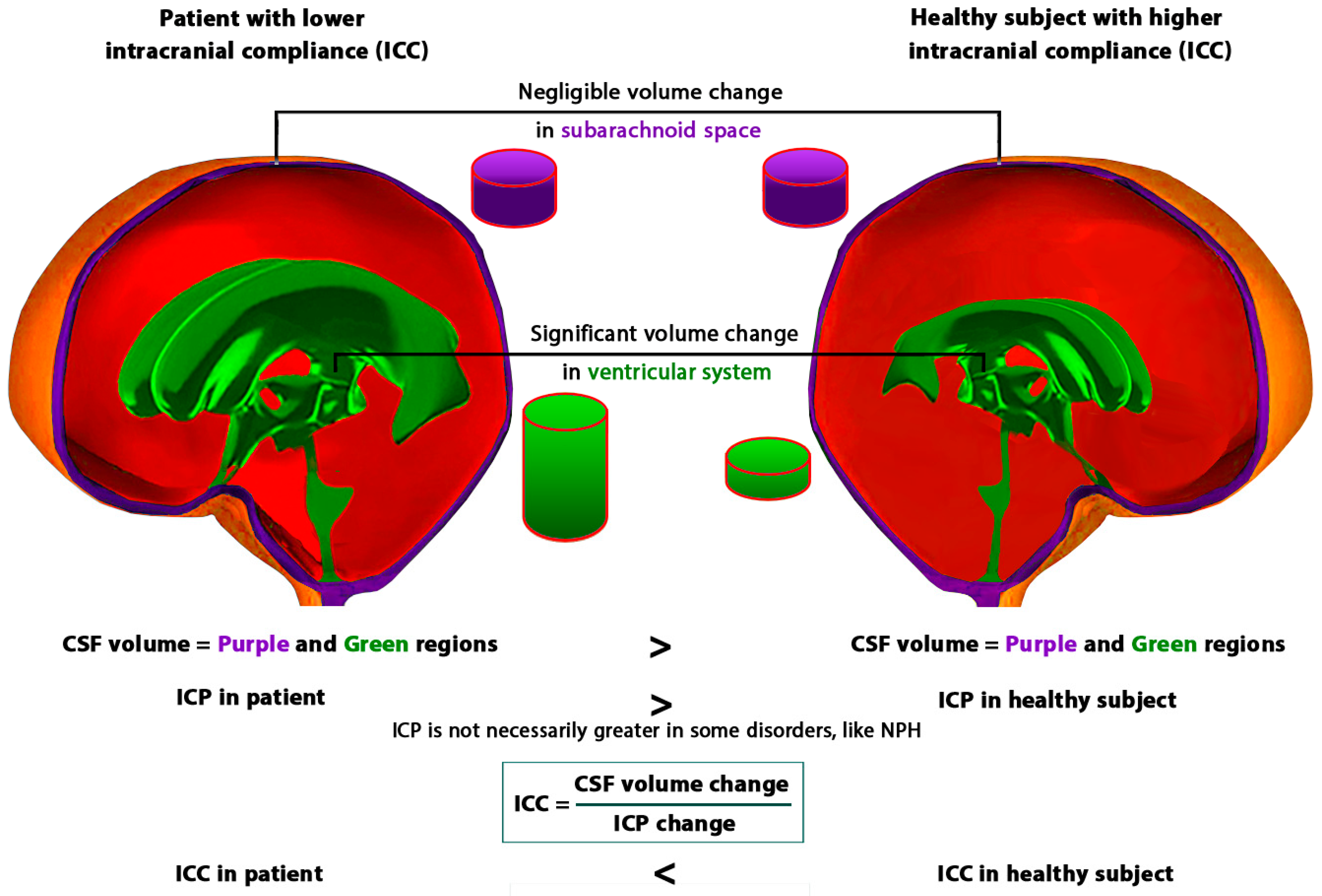
3. Challenges in the Definition and Concept of ICC
3.1. Time-Dependent Viscous Component of the Brain
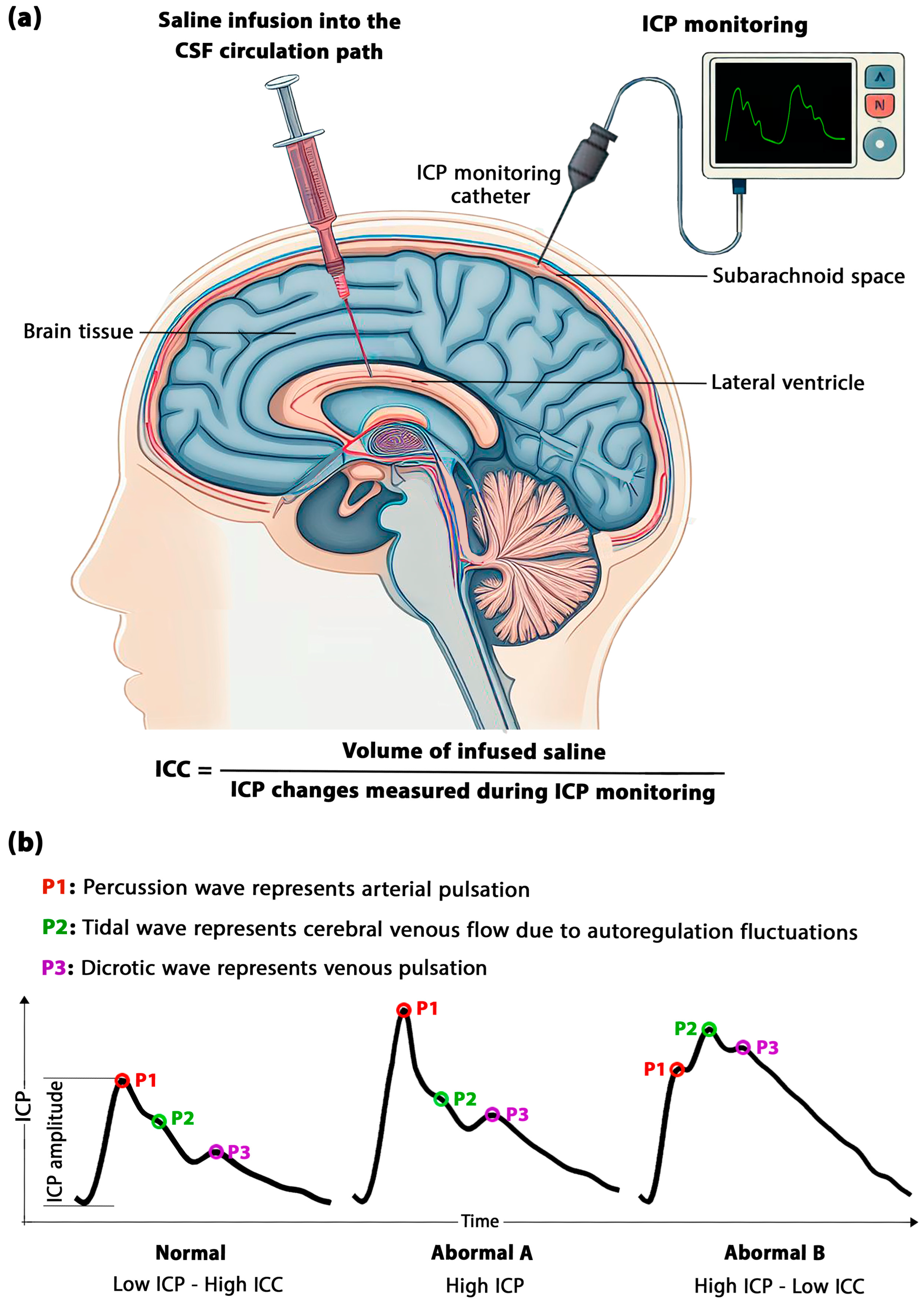
3.2. The Role of Time in the Formulation of ICC
3.3. Approaches to TE in ICC Assessment
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Borlongan, C.V.; Burns, J.; Tajiri, N.; Stahl, C.E.; Weinbren, N.L.; Shojo, H.; Sanberg, P.R.; Emerich, D.F.; Kaneko, Y.; van Loveren, H.R. Epidemiological survey-based formulae to approximate incidence and prevalence of neurological disorders in the United States: A meta-analysis. PLoS ONE 2013, 8, e78490. [Google Scholar] [CrossRef] [PubMed]
- Lima Giacobbo, B.; Doorduin, J.; Klein, H.C.; Dierckx, R.A.; Bromberg, E.; de Vries, E.F. Brain-derived neurotrophic factor in brain disorders: Focus on neuroinflammation. Mol. Neurobiol. 2019, 56, 3295–3312. [Google Scholar] [CrossRef] [PubMed]
- Reeves, B.C.; Karimy, J.K.; Kundishora, A.J.; Mestre, H.; Cerci, H.M.; Matouk, C.; Alper, S.L.; Lundgaard, I.; Nedergaard, M.; Kahle, K.T. Glymphatic system impairment in Alzheimer’s disease and idiopathic normal pressure hydrocephalus. Trends Mol. Med. 2020, 26, 285–295. [Google Scholar] [CrossRef] [PubMed]
- Ivkovic, M.; Liu, B.; Ahmed, F.; Moore, D.; Huang, C.; Raj, A.; Kovanlikaya, I.; Heier, L.; Relkin, N. Differential diagnosis of normal pressure hydrocephalus by MRI mean diffusivity histogram analysis. Am. J. Neuroradiol. 2013, 34, 1168–1174. [Google Scholar] [CrossRef] [PubMed]
- Gholampour, S.; Bahmani, M.; Shariati, A. Comparing the efficiency of two treatment methods of hydrocephalus: Shunt implantation and endoscopic third ventriculostomy. Basic Clin. Neurosci. 2019, 10, 185. [Google Scholar] [CrossRef]
- Gholampour, S.; Patel, J.; Yamini, B.; Frim, D. Cerebrospinal fluid hydrocephalus shunting: Cisterna magna, ventricular frontal, ventricular occipital. Neurosurg. Rev. 2022, 45, 2615–2638. [Google Scholar] [CrossRef]
- Gholampour, S.; Taher, M. Relationship of morphologic changes in the brain and spinal cord and disease symptoms with cerebrospinal fluid hydrodynamic changes in patients with Chiari malformation type I. World Neurosurg. 2018, 116, e830–e839. [Google Scholar] [CrossRef]
- Taher, M.; Gholampour, S. Effect of ambient temperature changes on blood flow in anterior cerebral artery of patients with skull prosthesis. World Neurosurg. 2020, 135, e358–e365. [Google Scholar] [CrossRef]
- Budday, S.; Ovaert, T.C.; Holzapfel, G.A.; Steinmann, P.; Kuhl, E. Fifty shades of brain: A review on the mechanical testing and modeling of brain tissue. Arch. Comput. Methods Eng. 2020, 27, 1187–1230. [Google Scholar] [CrossRef]
- Gholampour, S.; Gholampour, H. Correlation of a new hydrodynamic index with other effective indexes in Chiari I malformation patients with different associations. Sci. Rep. 2020, 10, 1–13. [Google Scholar] [CrossRef]
- Ocamoto, G.N.; Russo, T.L.; Zambetta, R.M.; Frigieri, G.; Hayashi, C.Y.; Brasil, S.; Rabelo, N.N.; Júnior, D.L.S. Intracranial Compliance Concepts and Assessment: A Scoping Review. Front. Neurol. 2021, 12, 756112. [Google Scholar] [CrossRef] [PubMed]
- Ursino, M.; Lodi, C.A. A simple mathematical model of the interaction between intracranial pressure and cerebral hemodynamics. J. Appl. Physiol. 1997, 82, 1256–1269. [Google Scholar] [CrossRef] [PubMed]
- Kiening, K.; Schoening, W.; Stover, J.; Unterberg, A. Continuous monitoring of intracranial compliance after severe head injury: Relation to data quality, intracranial pressure and brain tissue PO2. Br. J. Neurosurg. 2003, 17, 311–318. [Google Scholar] [CrossRef] [PubMed]
- Foreman, B.; Lissak, I.A.; Kamireddi, N.; Moberg, D.; Rosenthal, E.S. Challenges and opportunities in multimodal monitoring and data analytics in traumatic brain injury. Curr. Neurol. Neurosci. Rep. 2021, 21, 6. [Google Scholar] [CrossRef] [PubMed]
- Rabai, F.; Mohamed, B.; Seubert, C.N. Optimizing intraoperative neuromonitoring: Anesthetic considerations. Curr. Anesthesiol. Rep. 2018, 8, 306–317. [Google Scholar] [CrossRef]
- Cucciolini, G.; Motroni, V.; Czosnyka, M. Intracranial pressure for clinicians: It is not just a number. J. Anesth. Analg. Crit. Care 2023, 3, 31. [Google Scholar] [CrossRef]
- Ryder, H.W.; Espey, F.F.; Kimbell, F.D.; Penka, E.J.; Rosenauer, A.; Podolsky, B.; Evans, J.P. The mechanism of the change in cerebrospinal fluid pressure following an induced change in the volume of the fluid space. J. Lab. Clin. Med. 1953, 41, 428–435. [Google Scholar]
- Kanat, A.; Tsianaka, E.; Gasenzer, E.R.; Drosos, E. Some Interesting points of competition of X-ray using during the Greco-Ottoman War in 1897 and development of neurosurgical radiology: A reminiscence. Turk. Neurosurg. 2022, 32, 877–881. [Google Scholar] [CrossRef]
- Marmarou, A.; Shulman, K.; Lamorgese, J. Compartmental analysis of compliance and outflow resistance of the cerebrospinal fluid system. J. Neurosurg. 1975, 43, 523–534. [Google Scholar] [CrossRef]
- Evensen, K.B.; Eide, P.K. Measuring intracranial pressure by invasive, less invasive or non-invasive means: Limitations and avenues for improvement. Fluids Barriers CNS 2020, 17, 1–33. [Google Scholar] [CrossRef]
- Okon, M.D.; Roberts, C.J.; Mahmoud, A.M.; Springer, A.N.; Small, R.H.; McGregor, J.M.; Katz, S.E. Characteristics of the cerebrospinal fluid pressure waveform and craniospinal compliance in idiopathic intracranial hypertension subjects. Fluids Barriers CNS 2018, 15, 21. [Google Scholar] [CrossRef] [PubMed]
- Smielewski, P.; Czosnyka, M.; Roszkowski, M.; Walencik, A. Identification of the cerebrospinal compensatory mechanisms via computer-controlled drainage of the cerebrospinal fluid. Child’s Nerv. Syst. 1995, 11, 297–300. [Google Scholar] [CrossRef]
- Gholampour, S.; Nguyen, A.; Chaudry, S. Intracranial compliance, resistance to CSF-outflow, and pressure-volume index in hydrocephalus patients: A systematic review and meta-analysis. IRBM 2023, 44, 100785. [Google Scholar] [CrossRef]
- Alperin, N.J.; Lee, S.H.; Loth, F.; Raksin, P.B.; Lichtor, T. MR-Intracranial pressure (ICP): A method to measure intracranial elastance and pressure noninvasively by means of MR imaging: Baboon and human study. Radiology 2000, 217, 877–885. [Google Scholar] [CrossRef] [PubMed]
- Tain, R.-W.; Alperin, N. Noninvasive intracranial compliance from MRI-based measurements of transcranial blood and CSF flows: Indirect versus direct approach. IEEE Trans. Biomed. Eng. 2008, 56, 544–551. [Google Scholar] [CrossRef] [PubMed]
- Gholampour, S. FSI simulation of CSF hydrodynamic changes in a large population of non-communicating hydrocephalus patients during treatment process with regard to their clinical symptoms. PLoS ONE 2018, 13, e0196216. [Google Scholar] [CrossRef]
- Gholampour, S.; Frim, D.; Yamini, B. Long-term recovery behavior of brain tissue in hydrocephalus patients after shunting. Commun. Biol. 2022, 5, 1198. [Google Scholar] [CrossRef]
- Gholampour, S.; Fatouraee, N. Boundary conditions investigation to improve computer simulation of cerebrospinal fluid dynamics in hydrocephalus patients. Commun. Biol. 2021, 4, 394. [Google Scholar] [CrossRef]
- Gholampour, S.; Fatouraee, N.; Seddighi, A.; Seddighi, A. Numerical simulation of cerebrospinal fluid hydrodynamics in the healing process of hydrocephalus patients. J. Appl. Mech. Tech. Phys. 2017, 58, 386–391. [Google Scholar] [CrossRef]
- Gholampour, S.; Bahmani, M. Hydrodynamic comparison of shunt and endoscopic third ventriculostomy in adult hydrocephalus using in vitro models and fluid-structure interaction simulation. Comput. Methods Programs Biomed. 2021, 204, 106049. [Google Scholar] [CrossRef]
- Sahu, S.; Panda, N.; Swain, A.; Mathew, P.; Singla, N.; Gupta, S.; Jangra, K.; Bhardwaj, A.; Bhagat, H. Optic Nerve Sheath Diameter: Correlation with Intra-Ventricular Intracranial Measurements in Predicting Dysfunctional Intracranial Compliance. Cureus 2021, 13, e13008. [Google Scholar] [CrossRef] [PubMed]
- Wu, K.-C.; Sunwoo, J.; Sheriff, F.; Farzam, P.; Farzam, P.Y.; Orihuela-Espina, F.; LaRose, S.L.; Monk, A.D.; Aziz-Sultan, M.A.; Patel, N. Validation of diffuse correlation spectroscopy measures of critical closing pressure against transcranial Doppler ultrasound in stroke patients. J. Biomed. Opt. 2021, 26, 036008. [Google Scholar] [CrossRef] [PubMed]
- Eide, P.K.; Bentsen, G.; Sorteberg, A.G.; Marthinsen, P.B.; Stubhaug, A.; Sorteberg, W. A randomized and blinded single-center trial comparing the effect of intracranial pressure and intracranial pressure wave amplitude-guided intensive care management on early clinical state and 12-month outcome in patients with aneurysmal subarachnoid hemorrhage. Neurosurgery 2011, 69, 1105–1115. [Google Scholar] [PubMed]
- Ziółkowski, A.; Kasprowicz, M.; Czosnyka, M.; Czosnyka, Z. Brain blood flow pulse analysis may help to recognize individuals who suffer from hydrocephalus. Acta Neurochir. 2023; online ahead of print. [Google Scholar] [CrossRef]
- Baghbani, R. An Electrical Model of Hydrocephalus Shunt Incorporating the CSF Dynamics. Sci. Rep. 2019, 9, 9751. [Google Scholar] [CrossRef]
- Misra, J.; Chakravarty, S. A poroelastic spheroidal shell model for studying the problem of head injury. J. Math. Anal. Appl. 1984, 103, 332–343. [Google Scholar] [CrossRef]
- Chatelin, S.; Constantinesco, A.; Willinger, R. Fifty years of brain tissue mechanical testing: From in vitro to in vivo investigations. Biorheology 2010, 47, 255–276. [Google Scholar] [CrossRef]
- Franceschini, G.; Bigoni, D.; Regitnig, P.; Holzapfel, G.A. Brain tissue deforms similarly to filled elastomers and follows consolidation theory. J. Mech. Phys. Solids 2006, 54, 2592–2620. [Google Scholar] [CrossRef]
- Hrapko, M.; Van Dommelen, J.; Peters, G.; Wismans, J. The mechanical behaviour of brain tissue: Large strain response and constitutive modelling. Biorheology 2006, 43, 623–636. [Google Scholar]
- Cheng, S.; Bilston, L.E. Computational model of the cerebral ventricles in hydrocephalus. J. Biomech. Eng. 2010, 132, 054501. [Google Scholar] [CrossRef]
- Elkin, B.S.; Ilankovan, A.I.; Morrison, B., III. A detailed viscoelastic characterization of the P17 and adult rat brain. J. Neurotrauma 2011, 28, 2235–2244. [Google Scholar] [CrossRef] [PubMed]
- Yuan, T.; Zhan, W.; Jamal, A.; Dini, D. On the microstructurally driven heterogeneous response of brain white matter to drug infusion pressure. Biomech. Model. Mechanobiol. 2022, 21, 1299–1316. [Google Scholar] [CrossRef] [PubMed]
- Lambride, C.; Christodoulou, N.; Michail, A.; Vavourakis, V.; Stylianopoulos, T. Decompressive craniectomy of post-traumatic brain injury: An in silico modelling approach for intracranial hypertension management. Sci. Rep. 2020, 10, 18673. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Vardakis, J.C.; Lassila, T.; Mitolo, M.; Ravikumar, N.; Chou, D.; Lange, M.; Sarrami-Foroushani, A.; Tully, B.J.; Taylor, Z.A. Subject-specific multi-poroelastic model for exploring the risk factors associated with the early stages of Alzheimer’s disease. Interface Focus 2018, 8, 20170019. [Google Scholar] [CrossRef] [PubMed]
- Gholampour, S.; Fatouraee, N.; Seddighi, A.S.; Yazdani, S.O. A Hydrodynamical Study to propose a numerical Index for evaluating the CSF conditions in cerebralventricular system. Int. Clin. Neurosci. J. 2014, 1, 1–9. [Google Scholar]
- Gholampour, S.; Seddighi, A.; Fatouraee, N. Relationship between Spinal fluid and Cerebrospinal fluid as an index for assessment of non-communicating hydrocephalus. Modares Mech. Eng. 2015, 14, 308–314. [Google Scholar]
- Li, W.; Shepherd, D.E.; Espino, D.M. Investigation of the compressive viscoelastic properties of brain tissue under time and frequency dependent loading conditions. Ann. Biomed. Eng. 2021, 49, 3737–3747. [Google Scholar] [CrossRef]
- Siegkas, P.; Sharp, D.J.; Ghajari, M. The traumatic brain injury mitigation effects of a new viscoelastic add-on liner. Sci. Rep. 2019, 9, 3471. [Google Scholar] [CrossRef]
- Gholampour, S.; Fatouraee, N.; Seddighi, A.S.; Seddighi, A. Evaluating the effect of hydrocephalus cause on the manner of changes in the effective parameters and clinical symptoms of the disease. J. Clin. Neurosci. 2017, 35, 50–55. [Google Scholar] [CrossRef]
- Menghani, R.R.; Das, A.; Kraft, R.H. A sensor-enabled cloud-based computing platform for computational brain biomechanics. Comput. Methods Programs Biomed. 2023, 233, 107470. [Google Scholar] [CrossRef]
- Wang, F.; Han, Y.; Wang, B.; Peng, Q.; Huang, X.; Miller, K.; Wittek, A. Prediction of brain deformations and risk of traumatic brain injury due to closed-head impact: Quantitative analysis of the effects of boundary conditions and brain tissue constitutive model. Biomech. Model. Mechanobiol. 2018, 17, 1165–1185. [Google Scholar] [CrossRef] [PubMed]
- Wilkie, K.P.; Drapaca, C.S.; Sivaloganathan, S. A mathematical investigation of the role of intracranial pressure pulsations and small gradients in the pathogenesis of hydrocephalus. Int. J. Numer. Anal. Model. Ser. B 2012, 3, 36. [Google Scholar]
- Dutta-Roy, T. Does Normal Pressure Hydrocephalus Have Mechanistic Causes? University of Western Australia: Crawley, WA, Australia, 2011. [Google Scholar]
- Gholampour, S.; Balasundaram, H.; Thiyagarajan, P.; Droessler, J. A mathematical framework for the dynamic interaction of pulsatile blood, brain, and cerebrospinal fluid. Comput. Methods Programs Biomed. 2023, 231, 107209. [Google Scholar] [CrossRef] [PubMed]
- Gholampour, S.; Yamini, B.; Droessler, J.; Frim, D. A New Definition for Intracranial Compliance to Evaluate Adult Hydrocephalus After Shunting. Front. Bioeng. Biotechnol. 2022, 10, 900644. [Google Scholar] [CrossRef]
- Pavan, P.G.; Nasim, M.; Brasco, V.; Spadoni, S.; Paoloni, F.; d’Avella, D.; Khosroshahi, S.F.; de Cesare, N.; Gupta, K.; Galvanetto, U. Development of detailed finite element models for in silico analyses of brain impact dynamics. Comput. Methods Programs Biomed. 2022, 227, 107225. [Google Scholar] [CrossRef]
- Hosseini-Farid, M.; Ramzanpour, M.; McLean, J.; Ziejewski, M.; Karami, G. A poro-hyper-viscoelastic rate-dependent constitutive modeling for the analysis of brain tissues. J. Mech. Behav. Biomed. Mater. 2020, 102, 103475. [Google Scholar] [CrossRef]
- Forte, A.E.; Gentleman, S.M.; Dini, D. On the characterization of the heterogeneous mechanical response of human brain tissue. Biomech. Model. Mechanobiol. 2017, 16, 907–920. [Google Scholar] [CrossRef]
- Tuli, S.; O’Hayon, B.; Drake, J.; Clarke, M.; Kestle, J. Change in ventricular size and effect of ventricular catheter placement in pediatric patients with shunted hydrocephalus. Neurosurgery 1999, 45, 1329–1333; discussion 1333–1335. [Google Scholar] [CrossRef]
- Czosnyka, M.; Citerio, G. Brain compliance: The old story with a new ‘et cetera’. Intensive Care Med. 2012, 38, 925–927. [Google Scholar] [CrossRef]
- Portella, G.; Cormio, M.; Citerio, G.; Contant, C.; Kiening, K.; Enblad, P.; Piper, I. Continuous cerebral compliance monitoring in severe head injury: Its relationship with intracranial pressure and cerebral perfusion pressure. Acta Neurochir. 2005, 147, 707–713. [Google Scholar] [CrossRef]
- Gaohua, L.; Kimura, H. A mathematical model of intracranial pressure dynamics for brain hypothermia treatment. J. Theor. Biol. 2006, 238, 882–900. [Google Scholar] [CrossRef] [PubMed]
- Eklund, A.; Smielewski, P.; Chambers, I.; Alperin, N.; Malm, J.; Czosnyka, M.; Marmarou, A. Assessment of cerebrospinal fluid outflow resistance. Med. Biol. Eng. Comput. 2007, 45, 719–735. [Google Scholar] [CrossRef] [PubMed]
- Kazimierska, A.; Kasprowicz, M.; Czosnyka, M.; Placek, M.M.; Baledent, O.; Smielewski, P.; Czosnyka, Z. Compliance of the cerebrospinal space: Comparison of three methods. Acta Neurochir. 2021, 163, 1979–1989. [Google Scholar] [CrossRef] [PubMed]
- Czosnyka, M.; Czosnyka, Z.; Agarwal-Harding, K.J.; Pickard, J.D. Modeling of CSF dynamics: Legacy of Professor Anthony Marmarou. In Hydrocephalus; Springer: Berlin/Heidelberg, Germany, 2012; pp. 9–14. [Google Scholar]
- Xu, H.; Fame, R.M.; Sadegh, C.; Sutin, J.; Naranjo, C.; Syau, D.; Cui, J.; Shipley, F.B.; Vernon, A.; Gao, F. Choroid plexus NKCC1 mediates cerebrospinal fluid clearance during mouse early postnatal development. Nat. Commun. 2021, 12, 1–16. [Google Scholar] [CrossRef]
- Heldt, T.; Zoerle, T.; Teichmann, D.; Stocchetti, N. Intracranial pressure and intracranial elastance monitoring in neurocritical care. Annu. Rev. Biomed. Eng. 2019, 21, 523–549. [Google Scholar] [CrossRef]
- Sridharan, A.; Rajan, S.D.; Muthuswamy, J. Long-term changes in the material properties of brain tissue at the implant–tissue interface. J. Neural Eng. 2013, 10, 066001. [Google Scholar] [CrossRef]
- Boulet, T.; Kelso, M.L.; Othman, S.F. Microscopic magnetic resonance elastography of traumatic brain injury model. J. Neurosci. Methods 2011, 201, 296–306. [Google Scholar] [CrossRef]
- Eide, P.K. The pathophysiology of chronic noncommunicating hydrocephalus: Lessons from continuous intracranial pressure monitoring and ventricular infusion testing. J. Neurosurg. 2017, 129, 220–233. [Google Scholar] [CrossRef]
- Mase, M.; Miyati, T.; Yamada, K.; Kasai, H.; Hara, M.; Shibamoto, Y. Non-invasive measurement of intracranial compliance using cine MRI in normal pressure hydrocephalus. In Intracranial Pressure and Brain Monitoring XII; Springer: Berlin/Heidelberg, Germany, 2005; pp. 303–306. [Google Scholar]
- Meier, U.; Bartels, P. The importance of the intrathecal infusion test in the diagnostic of normal-pressure hydrocephalus. Eur. Neurol. 2001, 46, 178–186. [Google Scholar] [CrossRef]
- Sahuquillo, J.; Rubio, E.; Codina, A.; Molins, A.; Guitart, J.; Poca, M.; Chasampi, A. Reappraisal of the intracranial pressure and cerebrospinal fluid dynamics in patients with the so-called “normal pressure hydrocephalus” syndrome. Acta Neurochir. 1991, 112, 50–61. [Google Scholar] [CrossRef]
- Lokossou, A.; Balédent, O.; Garnotel, S.; Page, G.; Balardy, L.; Czosnyka, Z.; Payoux, P.; Schmidt, E. ICP monitoring and phase-contrast MRI to investigate intracranial compliance. In Intracranial Pressure & Neuromonitoring XVI; Springer: Berlin/Heidelberg, Germany, 2018; pp. 247–253. [Google Scholar]
- Eide, P.K. The correlation between pulsatile intracranial pressure and indices of intracranial pressure-volume reserve capacity: Results from ventricular infusion testing. J. Neurosurg. 2016, 125, 1493–1503. [Google Scholar] [CrossRef] [PubMed]
- Czosnyka, M.; Batorski, L.; Roszkowski, M.; Tomaszewski, J.; Wocjan, J.; Walencik, A.; Zabolotny, W. Cerebrospinal compensation in hydrocephalic children. Child’s Nerv. Syst. 1993, 9, 17–22. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, K.; Fried, A. Pressure-volume relationships in shunt-dependent childhood hydrocephalus: The zone of pressure instability in children with acute deterioration. J. Neurosurg. 1986, 64, 390–396. [Google Scholar] [CrossRef] [PubMed]
- Eide, P.K.; Brean, A. Cerebrospinal fluid pulse pressure amplitude during lumbar infusion in idiopathic normal pressure hydrocephalus can predict response to shunting. Cerebrospinal Fluid Res. 2010, 7, 5. [Google Scholar] [CrossRef]
- Jeong, J.-H. The Pathophysiology of Brain Edema and Intracranial Hypertension. J. Neurocritical Care 2016, 9, 59–62. [Google Scholar] [CrossRef]
- Piper, I. Intracranial pressure and elastance. In Head Injury; Chapman & Hall: London, UK, 1997; pp. 101–120. [Google Scholar]
- Tisell, M.; Edsbagge, M.; Stephensen, H.; Czosnyka, M.; Wikkelsø, C. Elastance correlates with outcome after endoscopic third ventriculostomy in adults with hydrocephalus caused by primary aqueductal stenosis. Neurosurgery 2002, 50, 70–77. [Google Scholar]
- Eide, P.; Park, E.H.; Madsen, J. Arterial blood pressure vs intracranial pressure in normal pressure hydrocephalus. Acta Neurol. Scand. 2010, 122, 262–269. [Google Scholar] [CrossRef]
- Thavarajasingam, S.G.; El-Khatib, M.; Rea, M.; Russo, S.; Lemcke, J.; Al-Nusair, L.; Vajkoczy, P. Clinical predictors of shunt response in the diagnosis and treatment of idiopathic normal pressure hydrocephalus: A systematic review and meta-analysis. Acta Neurochir. 2021, 163, 2641–2672. [Google Scholar] [CrossRef]
- Gholampour, S. Computerized biomechanical simulation of cerebrospinal fluid hydrodynamics: Challenges and opportunities. Comput. Methods Programs Biomed. 2021, 200, 105938. [Google Scholar] [CrossRef]
- Budday, S.; Sommer, G.; Holzapfel, G.; Steinmann, P.; Kuhl, E. Viscoelastic parameter identification of human brain tissue. J. Mech. Behav. Biomed. Mater. 2017, 74, 463–476. [Google Scholar] [CrossRef]
- Lesniak, M.; Clatterbuck, R.; Rigamonti, D.; Williams, M. Low pressure hydrocephalus and ventriculomegaly: Hysteresis, non-linear dynamics, and the benefits of CSF diversion. Br. J. Neurosurg. 2002, 16, 555–561. [Google Scholar] [CrossRef] [PubMed]
- Ringstad, G.; Vatnehol, S.A.S.; Eide, P.K. Glymphatic MRI in idiopathic normal pressure hydrocephalus. Brain 2017, 140, 2691–2705. [Google Scholar] [CrossRef] [PubMed]
- Taoka, T.; Masutani, Y.; Kawai, H.; Nakane, T.; Matsuoka, K.; Yasuno, F.; Kishimoto, T.; Naganawa, S. Evaluation of glymphatic system activity with the diffusion MR technique: Diffusion tensor image analysis along the perivascular space (DTI-ALPS) in Alzheimer’s disease cases. Jpn. J. Radiol. 2017, 35, 172–178. [Google Scholar] [CrossRef] [PubMed]
- Iliff, J.J.; Chen, M.J.; Plog, B.A.; Zeppenfeld, D.M.; Soltero, M.; Yang, L.; Singh, I.; Deane, R.; Nedergaard, M. Impairment of glymphatic pathway function promotes tau pathology after traumatic brain injury. J. Neurosci. 2014, 34, 16180–16193. [Google Scholar] [CrossRef]
- Behfar, M.H.; Björninen, T.; Moradi, E.; Sydänheimo, L.; Ukkonen, L. Biotelemetric wireless intracranial pressure monitoring: An in vitro study. Int. J. Antennas Propag. 2015, 2015, 918698. [Google Scholar] [CrossRef]


| Brain Model | Authors | Type of Brain Disorder | Solving Method | Brain Regions | Source |
|---|---|---|---|---|---|
| Poroelastic | Yuan et al. | Healthy subjects under drug infusion | Mathematical analysis based on arbitrary Lagrange–Eulerian equations | White matter | [42] |
| Lambride et al. | Brain injury | Finite element method | Single region | [43] | |
| Guo et al. | Alzheimer’s disease | Finite element method | White matter | [44] | |
| Gholampour et al. | Non-communicating hydrocephalus | Fluid-structure interaction | Single region | [45,46] | |
| Viscoelastic | Li et al. | Healthy subject | Finite element method | Grey and white matter | [47] |
| Siegkas et al. | Brain injury | Finite element method | Single region | [48] | |
| Gholampour et al. | Hydrocephalus | Fluid-structure interaction | Single region | [29,49] | |
| Harpko et al. | Healthy subject | Mathematical analysis | White matter | [39] | |
| Hyper-visco-elastic | Menghani et al. | Head impact | Finite element method | Basal ganglia, cerebral hemispheres, and corpus callosum | [50] |
| Wang et al. | Brain injury | Finite element method | Grey matter, white matter, and pia mater | [51] | |
| Wilkie et al. | Hydrocephalus | Mathematical analysis using fractional Zener model | Single region | [52] | |
| Dutta-Roy et al. | Normal pressure hydrocephalus | Finite element method | Single region | [53] | |
| Poro-visco-elastic | Gholampour et al. | Communicating hydrocephalus | Fluid-structure interaction | Single region | [27,54,55] |
| Pavan et al. | Brain injury | Finite element method | One region | [56] | |
| Gholampour | Non-communicating hydrocephalus | Fluid-structure interaction | Single region | [26] | |
| Cheng et al. | Non-communicating hydrocephalus | Finite element method | White matter | [40] | |
| Poro-hyper-viscoelastic | Hosseini-Farid et al. | Healthy subject | Finite element method | Grey and white matter | [57] |
| Forte et al. | Healthy subject | Finite element method | Grey and white matter | [58] |
| Age | Type of Hydrocephalus | Authors | Intracranial Compliance Assessment Method | Procedure Type | Intracranial Compliance (mL/mmHg) | Time Elapsed (Minute) | Source |
|---|---|---|---|---|---|---|---|
| Adult | Noncommunicating hydrocephalus | Gholampour et al. | Computer simulation | Non-invasive | 0.78 | 0.17 | [30] |
| Eide | Ventricular constant-flow infusion | Invasive | 0.60 | 15.5 | [70] | ||
| Normal pressure hydrocephalus | Kazmierska et al. | Computer-assisted constant-flow infusion | Invasive | 0.27 | 13.2 | [64] | |
| Mase et al. | Computer simulation | Non-invasive | 0.003 | <1 | [71] | ||
| Meier and Bartels | Computer-assisted constant-flow intrathecal infusion | Invasive | 0.36 | 10.5 | [72] | ||
| Sahuquillo et al. | Bolus injection, Lumbar and ventricular constant-flow infusion | Invasive | 0.33 | 15.0 | [73] | ||
| Communicating hydrocephalus | Eide | Ventricular constant-flow infusion | Invasive | 0.66 | 15.5 | [70] | |
| Hydrocephalus | Lokossou et al. | Lumbar constant-flow infusion | Invasive | 0.23 | --- | [74] | |
| Eide | Ventricular constant-flow infusion | Invasive | 0.6 | 15.5 | [75] | ||
| Pediatric | Noncommunicating hydrocephalus | Czosnyka et al. | Computer-assisted lumbar infusion | Invasive | 1.27 | 6.3 | [76] |
| Acute hydrocephalus | Czosnyka et al. | Computer-assisted lumbar infusion | Invasive | 0.97 | 6.3 | [76] | |
| Hydrocephalus | Shapiro and Fried | Bolus withdrawal and injection | Invasive | 0.32 | --- | [77] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gholampour, S. Why Intracranial Compliance Is Not Utilized as a Common Practical Tool in Clinical Practice. Biomedicines 2023, 11, 3083. https://doi.org/10.3390/biomedicines11113083
Gholampour S. Why Intracranial Compliance Is Not Utilized as a Common Practical Tool in Clinical Practice. Biomedicines. 2023; 11(11):3083. https://doi.org/10.3390/biomedicines11113083
Chicago/Turabian StyleGholampour, Seifollah. 2023. "Why Intracranial Compliance Is Not Utilized as a Common Practical Tool in Clinical Practice" Biomedicines 11, no. 11: 3083. https://doi.org/10.3390/biomedicines11113083
APA StyleGholampour, S. (2023). Why Intracranial Compliance Is Not Utilized as a Common Practical Tool in Clinical Practice. Biomedicines, 11(11), 3083. https://doi.org/10.3390/biomedicines11113083







