Validating Causal Diagrams of Human Health Risks for Spaceflight: An Example Using Bone Data from Rodents
Abstract
1. Introduction
2. Materials and Methods
3. Results
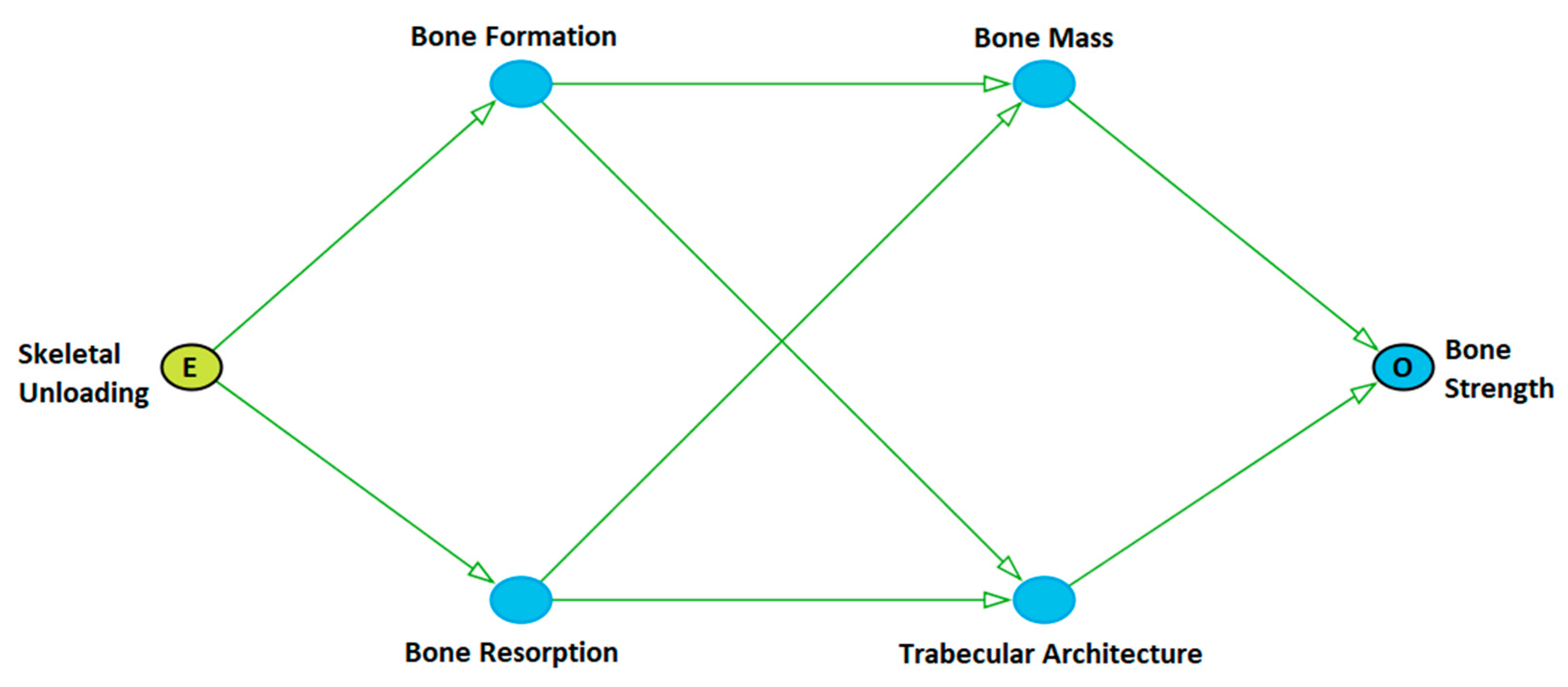
3.1. Causal Diagram
3.2. Variable Relationships
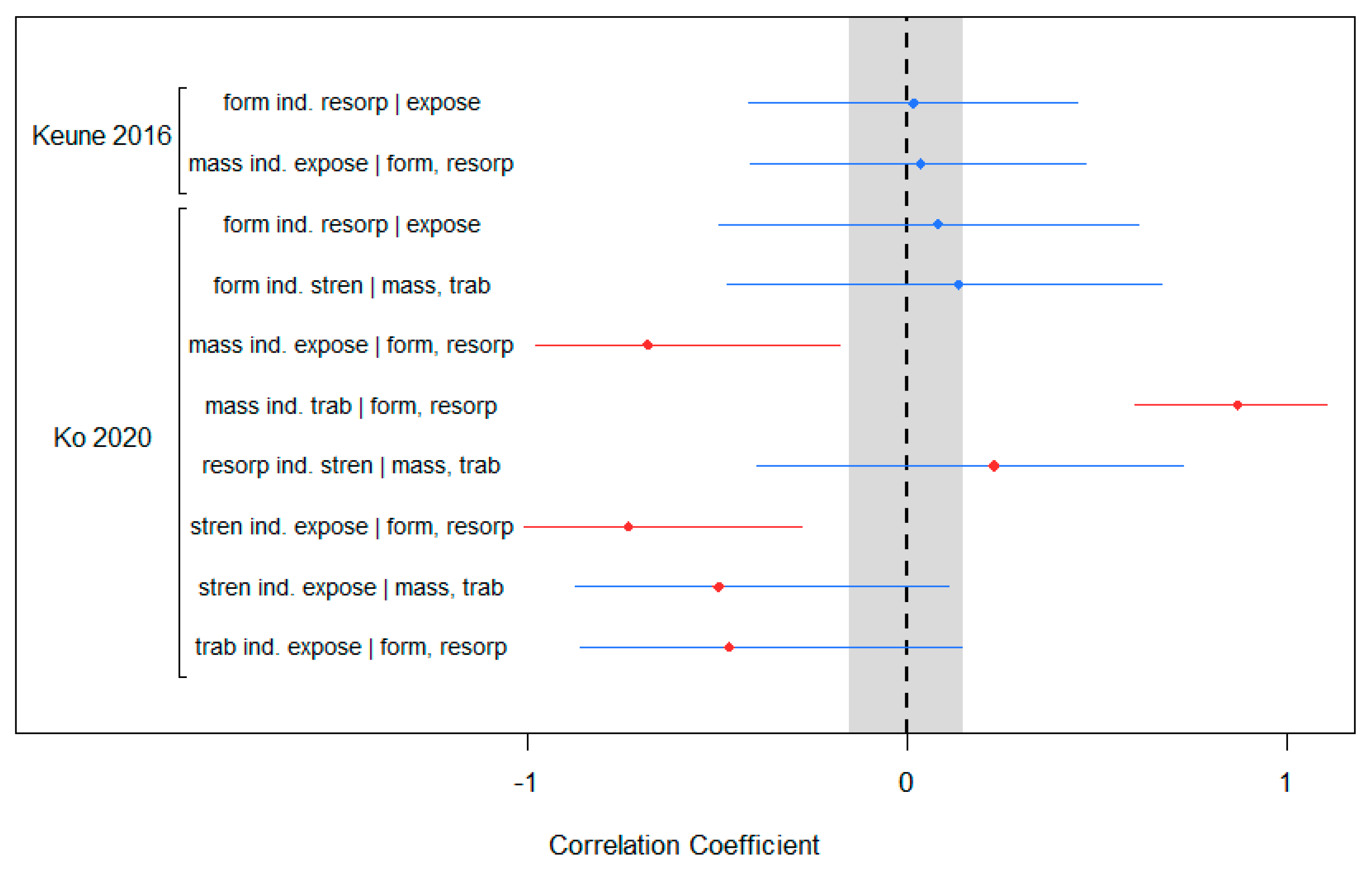
3.3. Tests of Marginal Correlation
3.4. Tests of Conditional Independencies
4. Discussion
4.1. Interpretation of Findings
- The causal diagram could be drawn incorrectly for the outcome. The first and most obvious reason a DAG is not validated by empirical data is that the DAG is fundamentally incorrect. This could be due to incorrect causal relationships drawn between variables, the lack of needed connections between variables, the erroneous inclusion of irrelevant variables, or the omission of needed explanatory variables or confounders (See Section 4.2 below for further discussion).
- Analogs could have a different mechanism. In this scenario the causal diagram is correct for the real-world system it explains, but incorrect for a particular analog dataset that is attempting to approximate it. In other words, the analog is an imperfect simulation of the causal mechanism under study. This is of the utmost concern when using animal models to approximate human exposures (e.g., sending rodents to space), when there may be interspecies differences in physiology, or when humans experience analog exposures (e.g., bed rest studies). In these situations, the correct DAG for the analog could have different nodes and/or slightly different causal mechanisms. For example, in this DAG the terms, bone mass, trabecular microarchitecture, and bone strength were originally modeled as bone density, bone structure, and skeletal fragility in the HSRB official DAG. Where “strength” may be a corollary of fragility, the effects of brittleness as opposed to a load-based conception of strength may impact these results.
- Variables used in the testing may not be appropriate measures of the random variables on the causal diagram. In this scenario, the DAG is drawn correctly, any analog in use is a good representation of the real causal system, but one or more measures in the data are inappropriate to represent random variables on the DAG. This can be because the measure is capturing the wrong phenomenon, or because it is measuring the correct phenomenon at the wrong time or in the wrong way.
4.2. Revising Incorrectly Drawn Causal Diagrams
4.3. Statistical Precision as a Criterion
4.4. Limitations of the Method
4.5. DAG Validation and NASA’s Level of Evidence Assessments
4.6. Future Directions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ball, J.R.; Evans, C.H., Jr. (Eds.) Institute of Medicine (US) Committee on Creating a Vision for Space Medicine During Travel Beyond Earth Orbit. In Safe Passage: Astronaut Care for Exploration Missions; National Academies Press: Washington, DC, USA, 2001. [Google Scholar] [PubMed]
- Romero, E.; Francisco, D. The NASA human system risk mitigation process for space exploration. Acta Astronaut. 2020, 175, 606–615. [Google Scholar] [CrossRef]
- Afshinnekoo, E.; Scott, R.T.; MacKay, M.J.; Pariset, E.; Cekanaviciute, E.; Barker, R.; Gilroy, S.; Hassane, D.; Smith, S.M.; Zwart, S.R.; et al. Fundamental Biological Features of Spaceflight: Advancing the Field to Enable Deep-Space Exploration. Cell 2021, 184, 6002. [Google Scholar] [CrossRef] [PubMed]
- Goswami, N.; Batzel, J.J.; Clément, G.; Stein, T.P.; Hargens, A.R.; Sharp, M.K.; Blaber, A.P.; Roma, P.G.; Hinghofer-Szalkay, H.G. Maximizing information from space data resources: A case for expanding integration across research disciplines. Eur. J. Appl. Physiol. 2013, 113, 1645–1654. [Google Scholar] [CrossRef] [PubMed]
- Antonsen, E.L.; Reynolds, R.J. Human System Risk Management Plan. 1 October 2020; (No. JSC 66705). Available online: https://ntrs.nasa.gov/citations/20205008887 (accessed on 21 June 2022).
- Austin, C.P. Opportunities and challenges in translational science. Clin. Transl. Sci. 2021, 14, 1629–1647. [Google Scholar] [CrossRef] [PubMed]
- Antonsen, E.L.; Reynolds, R.J.; Monti, A.; Charvat, J.; Petersen, D.; Connell, E.S.; Shelhamer, M.; Van Baalen, M.; Abukmail, A.; Marotta, K.; et al. Directed Acyclic Graph Guidance Documentation. 15 June 2022 (NASA/TM–20220006812). Available online: https://ntrs.nasa.gov/citations/20220006812 (accessed on 21 June 2022).
- Ankan, A.; Wortel, I.M.N.; Textor, J. Testing Graphical Causal Models Using the R Package “dagitty”. Curr. Protoc. 2021, 1, e45. Available online: https://www.ncbi.nlm.nih.gov/pubmed/33592130 (accessed on 21 June 2022). [CrossRef] [PubMed]
- Koller, D.; Friedman, N. Probabilistic graphical models: Principles and techniques. In Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Cucinotta, F.A.; Kim, M.Y.; Chappell, L. Space Radiation Cancer Risk Projections and Uncertainties NASA/TP-2013-217375, NASA, 2012. Available online: https://spaceradiation.jsc.nasa.gov/irModels/TP-2013-217375.pdf (accessed on 21 June 2022).
- Antonsen, E.L.; Van Baalen, M.; Kadwa, B.; Boley, L.; Arellano, J.; Kerstman, E.; Chappell, L.; Semones, E.; Elgart, S.R. Comparison of Health and Performance Risk for Accelerated Mars Mission Scenarios NASA/TM-20210009779, NASA, 2021. Available online: https://ntrs.nasa.gov/citations/20210009779 (accessed on 21 June 2022).
- Antonsen, E.L.; Myers, J.G.; Boley, L.; Arellano, J.; Kerstman, E.; Kadwa, B.; Buckland, D.M.; van Baalen, M. Estimating Medical Risk in Human Spaceflight. NPJ Microgravity 2022, 8, 8. [Google Scholar] [CrossRef] [PubMed]
- Scott, R.T.; Grigorev, K.; Mackintosh, G.; Gebre, S.G.; Mason, C.E.; del Alto, M.E.; Costes, S.V. Advancing the Integration of Biosciences Data Sharing to Further Enable Space Exploration. Cell Rep. 2020, 33, 108441. Available online: https://www.ncbi.nlm.nih.gov/pubmed/33242404 (accessed on 21 June 2022). [CrossRef]
- Berrios, D.C.; Galazka, J.; Grigorev, K.; Gebre, S.; Costes, S.V. NASA GeneLab: Interfaces for the Exploration of Space Omics Data. Nucleic Acids Res. 2021, 49, D1515–D1522. Available online: https://www.ncbi.nlm.nih.gov/pubmed/33080015 (accessed on 21 June 2022). [CrossRef]
- National Academies of Sciences Engineering and Medicine (U.S.); Committee on Toward an Open Science Enterprise, and National Academies of Sciences Engineering and Medicine (U.S.). Board on Research Data and Information. Open Science by Design: Realizing a Vision for 21st Century Research. In Consensus study report of the National Academies of Sciences, Engineering, Medicine; National Academies Press: Washington, DC, USA, 2018. Available online: https://www.ncbi.nlm.nih.gov/books/NBK525417/ (accessed on 21 June 2022).
- Wilkinson, M.D.; Dumontier, M.; Aalbersberg, I.J.; Appleton, G.; Axton, M.; Baak, A.; Blomberg, N.; Boiten, J.W.; da Silva Santos, L.B.; Bourne, P.E.; et al. The FAIR Guiding Principles for Scientific Data Management and Stewardship. Sci. Data 2016, 3, 160018. [Google Scholar] [CrossRef]
- Wickham, H. Tidy Data. J. Stat. Softw. 2014, 59, 1–23. Available online: https://www.jstatsoft.org/v59/i10/paper (accessed on 21 June 2022). [CrossRef]
- Haibe-Kains, B.; Adam, G.A.; Hosny, A.; Khodakarami, F.; Waldron, L.; Wang, B.; McIntosh, C.; Goldenberg, A.; Kundaje, A.; Greene, C.S.; et al. Transparency and Reproducibility in Artificial Intelligence. Nature 2020, 586, E14–E16. Available online: https://www.ncbi.nlm.nih.gov/pubmed/33057217 (accessed on 21 June 2022). [CrossRef]
- Lavin, A.; Gilligan-Lee, C.M.; Visnjic, A.; Ganju, S.; Newman, D.; Ganguly, S.; Lange, D.; Baydin, A.G.; Sharma, A.; Gibson, A.; et al. Technology Readiness Levels for Machine Learning Systems. arXiv 2021, arXiv:2101.03989. [Google Scholar] [CrossRef]
- Dubée, P.B.; Scott, R.T.; Thomas, N.H.; Pendleton, M.M.; Alwood, J.S. Quantifying Cancellous Bone Structural Changes in Microgravity: Axial Skeleton Results from the Rodent Research-1 Mission. In Proceedings of the American Society for Gravitational and Space Research, Cleveland, OH, USA, 26–29 October 2016. [Google Scholar]
- Keune, J.A.; Philbrick, K.A.; Branscum, A.J.; Iwaniec, U.T.; Turner, R.T. Spaceflight-Induced Vertebral Bone Loss in Ovariectomized Rats is Associated with Increased Bone Marrow Adiposity and no Change in Bone Formation. NPJ Microgravity 2016, 2, 16016. Available online: https://www.ncbi.nlm.nih.gov/pubmed/28725730 (accessed on 21 June 2022). [CrossRef][Green Version]
- Keune, J.A.; Branscum, A.J.; Iwaniec, U.T.; Turner, R.T. Effects of Spaceflight on Bone Microarchitecture in the Axial and Appendicular Skeleton in Growing Ovariectomized Rats. Sci Rep. 2015, 5, 18671. Available online: https://www.ncbi.nlm.nih.gov/pubmed/26691062 (accessed on 21 June 2022). [CrossRef]
- Ko, F.C.; Mortreux, M.; Riveros, D.; Nagy, J.A.; Rutkove, S.B.; Bouxsein, M.L. Dose-Dependent Skeletal Deficits Due to Varied Reductions in Mechanical Loading in Rats. NPJ Microgravity 2020, 6, 15. Available online: https://www.ncbi.nlm.nih.gov/pubmed/32435691 (accessed on 21 June 2022). [CrossRef]
- Bouxsein, M.L.; Boyd, S.K.; Christiansen, B.A.; Guldberg, R.E.; Jepsen, K.J.; Müller, R. Guidelines for Assessment of Bone Microstructure in Rodents Using Micro-Computed Tomography. J. Bone Miner. Res. 2010, 25, 1468–1486. Available online: https://www.ncbi.nlm.nih.gov/pubmed/20533309 (accessed on 21 June 2022). [CrossRef]
- Dempster, D.W.; Compston, J.E.; Drezner, M.K.; Glorieux, F.H.; Kanis, J.A.; Malluche, H.; Meunier, P.J.; Ott, S.M.; Recker, R.R.; Parfitt, A.M. Standardized Nomenclature, Symbols, and Units for Bone Histomorphometry: A 2012 Update of the Report of the ASBMR Histomorphometry Nomenclature Committee. J. Bone Miner. Res. 2013, 28, 2–17. Available online: https://www.ncbi.nlm.nih.gov/pubmed/23197339 (accessed on 21 June 2022). [CrossRef]
- Iwaniec, U.T.; Wronski, T.J.; Turner, R.T. 2008. Histological Analysis of Bone. Methods Mol. Biol. 2018, 447, 325–341. Available online: https://www.ncbi.nlm.nih.gov/pubmed/18369927 (accessed on 21 June 2022). [CrossRef]
- Jepsen, K.J.; Silva, M.J.; Vashishth, D.; Guo, X.E.; van der Meulen, M.C. Establishing Biomechanical Mechanisms in Mouse Models: Practical Guidelines for Systematically Evaluating Phenotypic Changes in the Diaphyses of Long Bones. J. Bone Miner. Res. 2015, 30, 951–966. Available online: https://www.ncbi.nlm.nih.gov/pubmed/25917136 (accessed on 21 June 2022). [CrossRef]
- Textor, J.; van der Zander, B.; Gilthorpe, M.S.; Liskiewicz, M.; Ellison, G.T. Robust Causal Inference Using Directed Acyclic Graphs: The R Package ‘Dagitty’. Int. J. Epidemiol. 2016, 45, 1887–1894. Available online: https://www.ncbi.nlm.nih.gov/pubmed/28089956 (accessed on 21 June 2022). [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019; Available online: https://www.R-project.org/ (accessed on 21 June 2022).
- Mayer, M. Confintr: Confidence Intervals. R Package Version 0.1.2. 2022. Available online: https://CRAN.R-project.org/package=confintr (accessed on 21 June 2022).
- Ploutz-Snyder, R.J.; Fiedler, J.; Feiveson, A.H. Justifying Small-n Research in Scientifically Amazing Settings: Challenging the Notion That Only “Big-n” Studies Are Worthwhile. J. Appl. Physiol. 2014, 116, 1251–1252. Available online: https://www.ncbi.nlm.nih.gov/pubmed/24408991 (accessed on 21 June 2022). [CrossRef]
- Reynolds, R.J.; Shelhamer, M. Introductory Chapter: Research Methods for the Next 60 Years of Space Exploration. In Beyond LEO—Human Health Issues for Deep Space Exploration; Reynolds, R.J., Ed.; IntechOpen: London, UK, 2020; pp. 3–8. Available online: https://www.intechopen.com/chapters/72023 (accessed on 21 June 2022).
- Popper, K.R. The Logic of Scientific Discovery; Basic Books: New York, NY, USA, 1959. [Google Scholar]
- Hill, A.B. The Environment and Disease: Association or Casation? Proc. R Soc. Med. 1965, 58, 295–300. Available online: https://www.ncbi.nlm.nih.gov/pubmed/14283879 (accessed on 21 June 2022). [CrossRef]
- Budd, S.; Blass, A.; Hoarfrost, A.; Khezeli, K.; D’Silva, K.; Soboczenski, F.; Mackintosh, G.; Chia, N.; Kalantari, J. Prototyping CRISP: A Causal Relation and Inference Search Platform applied to Colorectal Cancer Data. In Proceedings of the 2021 IEEE 3rd Global Conference on Life Sciences and Technologies (LifeTech), Nara, Japan, 9–11 March 2021. [Google Scholar]
- Yu, Y.; Chen, J.; Gao, T.; Yu, M. DAG Structure Learning with Graph Neural Networks. arXiv 2019, arXiv:1904.10098. Available online: https://arxiv.org/abs/1904.10098 (accessed on 21 June 2022).

| Study | Animal Type | Exposure | Control | Bone Assayed | Duration (days) | N |
|---|---|---|---|---|---|---|
| Dubeé [20] | C57BL/6 mice | Spaceflight | Terrestrial | L4 vertebra | 37 | 27 |
| Keune 2015 [22] | Fisher 344 rats | Spaceflight | Terrestrial | Femur | 14 | 24 |
| Keune 2016 [21] | Fisher 344 rats | Spaceflight | Terrestrial | L2 vertebra | 14 | 22 |
| Ko [23] | Wistar rats | Terrestrial: 80% or 60% unloaded | Terrestrial: 0% unloaded | Both femurs | 28 | 33 |
| Variable 1 | Variable 2 | Expected Direction |
|---|---|---|
| Unloading | Bone resorption | Positive |
| Bone formation | Negative | |
| Bone mass | Negative | |
| Trabecular microarchitecture | Negative | |
| Bone strength | Negative | |
| Bone resorption | Bone formation | Negative |
| Bone mass | Negative | |
| Trabecular microarchitecture | Negative | |
| Bone strength | Negative | |
| Bone formation | Bone mass | Positive |
| Trabecular microarchitecture | Positive | |
| Bone strength | Positive | |
| Bone mass | Trabecular microarchitecture | Positive |
| Bone strength | Positive | |
| Trabecular microarchitecture | Bone strength | Positive |
| Variable 1 | Variable 2 | Conditioning Set | ||
|---|---|---|---|---|
| Trabecular microarchitecture | ⊥ | Unloading | | | Bone formation, Bone resorption |
| Bone mass | ⊥ | Unloading | | | Bone formation, Bone resorption |
| Trabecular microarchitecture | ⊥ | Bone mass | | | Bone formation, Bone resorption |
| Bone Strength | ⊥ | Unloading | | | Bone formation, Bone resorption |
| Bone Strength | ⊥ | Unloading | | | Bone mass, Trabecular microarchitecture |
| Bone Strength | ⊥ | Bone Formation | | | Bone mass, Trabecular microarchitecture |
| Bone Strength | ⊥ | Bone resorption | | | Bone mass, Trabecular microarchitecture |
| Bone resorption | ⊥ | Bone formation | | | Skeletal unloading |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reynolds, R.J.; Scott, R.T.; Turner, R.T.; Iwaniec, U.T.; Bouxsein, M.L.; Sanders, L.M.; Antonsen, E.L. Validating Causal Diagrams of Human Health Risks for Spaceflight: An Example Using Bone Data from Rodents. Biomedicines 2022, 10, 2187. https://doi.org/10.3390/biomedicines10092187
Reynolds RJ, Scott RT, Turner RT, Iwaniec UT, Bouxsein ML, Sanders LM, Antonsen EL. Validating Causal Diagrams of Human Health Risks for Spaceflight: An Example Using Bone Data from Rodents. Biomedicines. 2022; 10(9):2187. https://doi.org/10.3390/biomedicines10092187
Chicago/Turabian StyleReynolds, Robert J., Ryan T. Scott, Russell T. Turner, Urszula T. Iwaniec, Mary L. Bouxsein, Lauren M. Sanders, and Erik L. Antonsen. 2022. "Validating Causal Diagrams of Human Health Risks for Spaceflight: An Example Using Bone Data from Rodents" Biomedicines 10, no. 9: 2187. https://doi.org/10.3390/biomedicines10092187
APA StyleReynolds, R. J., Scott, R. T., Turner, R. T., Iwaniec, U. T., Bouxsein, M. L., Sanders, L. M., & Antonsen, E. L. (2022). Validating Causal Diagrams of Human Health Risks for Spaceflight: An Example Using Bone Data from Rodents. Biomedicines, 10(9), 2187. https://doi.org/10.3390/biomedicines10092187






