Neural Network-Based Calculator for Rat Glomerular Filtration Rate
Abstract
1. Introduction
2. Materials and Methods
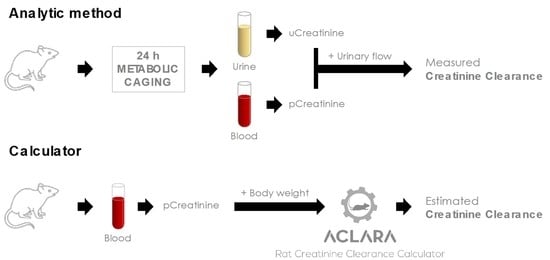
2.1. Data Mining and Database Generation
2.2. Algorithm Description
2.3. Data Preprocessing
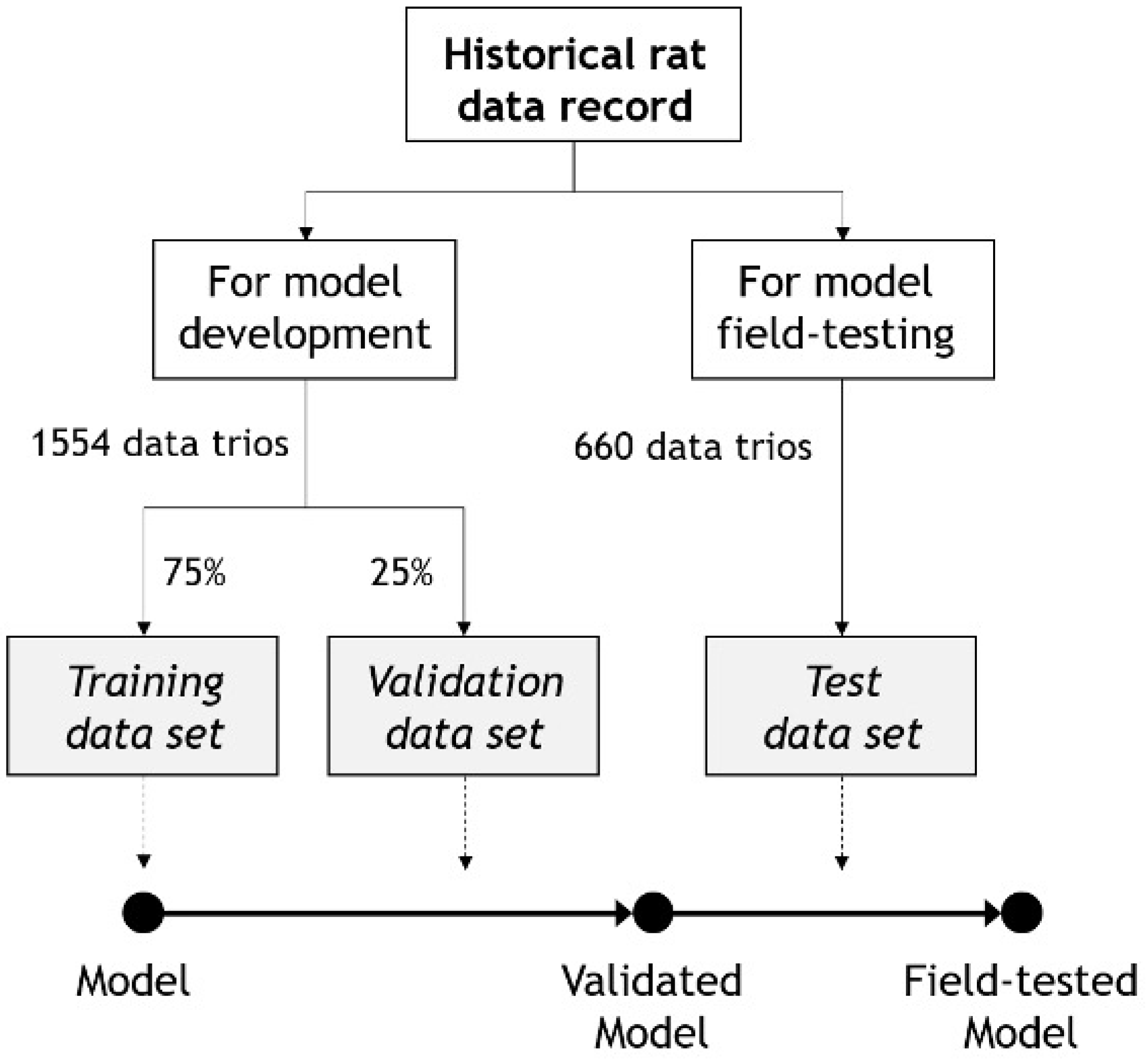
2.4. Neural Network Training, Validation, and Testing
3. Results
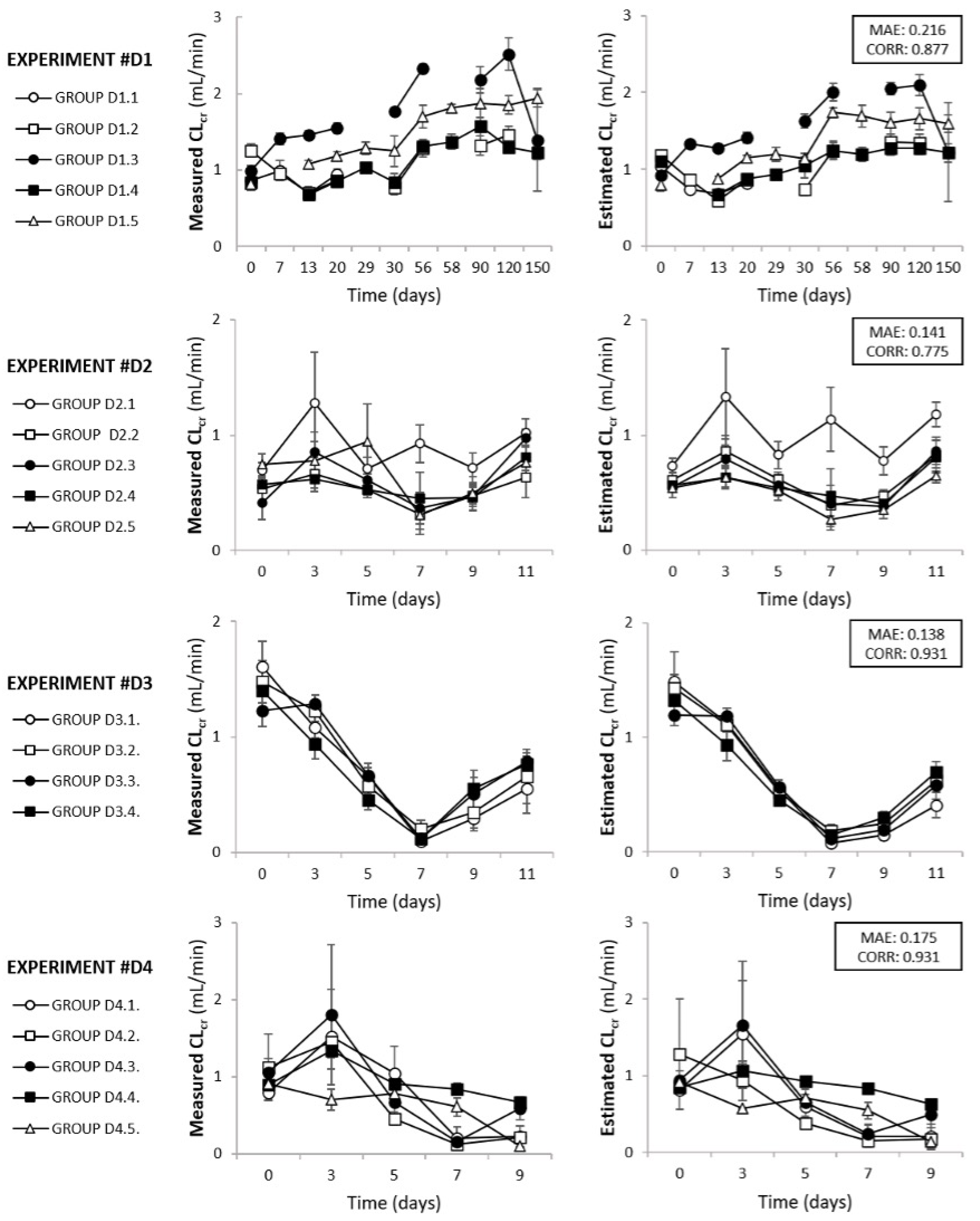
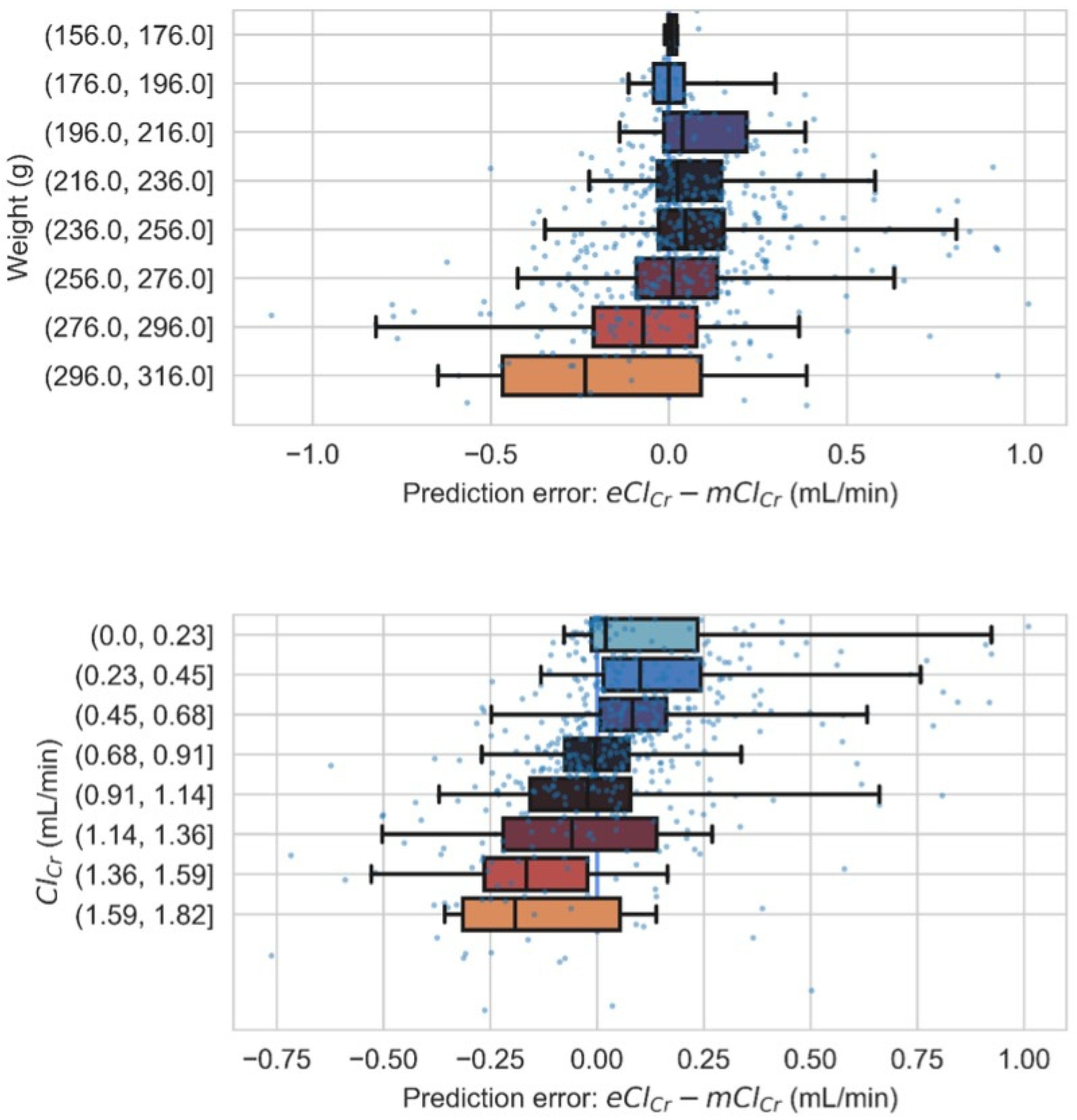
3.1. Model Development, Evaluation, and Validation
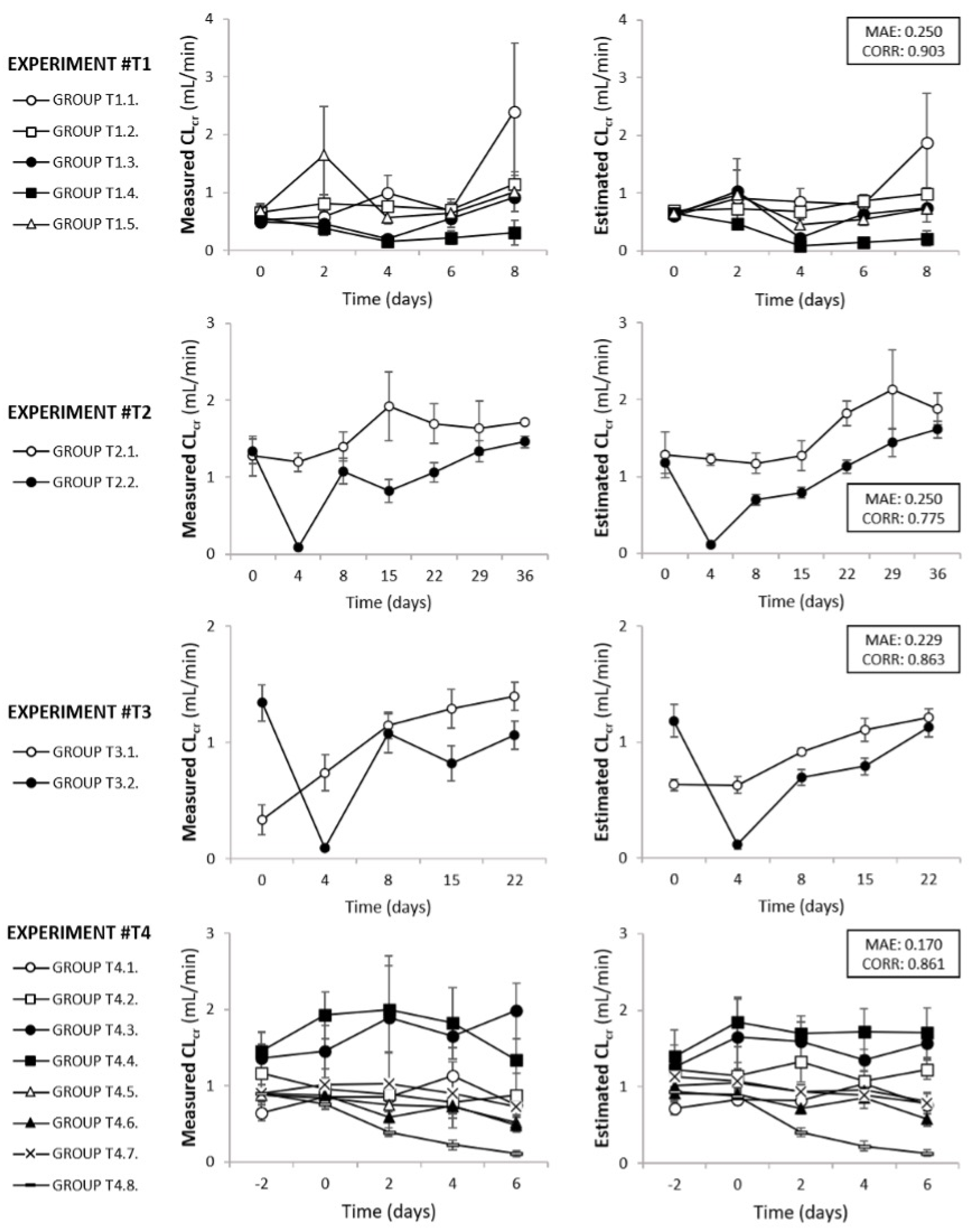
3.2. Model Field Testing
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Basile, D.P.; Anderson, M.D.; Sutton, T.A. Pathophysiology of acute kidney injury. Compr. Physiol. 2012, 2, 1303–1353. [Google Scholar] [CrossRef] [PubMed]
- López-Novoa, J.M.; Martínez-Salgado, C.; Rodríguez-Peña, A.B.; Hernández, F.J.L. Common pathophysiological mechanisms of chronic kidney disease: Therapeutic perspectives. Pharmacol. Ther. 2010, 128, 61–81. [Google Scholar] [CrossRef] [PubMed]
- López-Novoa, J.M.; Rodríguez-Peña, A.B.; Ortiz, A.; Martínez-Salgado, C.; López Hernández, F.J. Etiopathology of chronic tubular, glomerular and renovascular nephropathies: Clinical implications. J. Transl. Med. 2011, 9, 13. [Google Scholar] [CrossRef] [PubMed]
- Murphy, D.P.; Hsu, C.Y. Estimating glomerular filtration rate: Is it good enough? and is it time to move on? Curr. Opin. Nephrol. Hypertens. 2013, 22, 310–315. [Google Scholar] [CrossRef] [PubMed]
- Levey, A.S.; Becker, C.; Inker, L.A. Glomerular filtration rate and albuminuria for detection and staging of acute and chronic kidney disease in adults: A systematic review. JAMA J. Am. Med. Assoc. 2015, 313, 837–846. [Google Scholar] [CrossRef] [PubMed]
- KDIGO. Clinical Practice Guideline for Acute Kidney Injury. Kidney Int. Suppl. 2012. Available online: https://kdigo.org/guidelines/ckd-evaluation-and-management/ (accessed on 5 February 2022).
- Diskin, C.J. Creatinine and glomerular filtration rate: Evolution of an accommodation. Ann. Clin. Biochem. 2007, 44, 16–19. [Google Scholar] [CrossRef] [PubMed]
- Aurell, M. Accurate and feasible measurements of GFR-is the iohexol clearance the answer? Nephrol. Dial. Transplant. 1994, 9, 1222–1224. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, G.J.; Furth, S.L. Glomerular filtration rate measurement and estimation in chronic kidney disease. Pediatr. Nephrol. 2007, 22, 1839–1848. [Google Scholar] [CrossRef] [PubMed]
- Delanaye, P.; Ebert, N.; Melsom, T.; Gaspari, F.; Mariat, C.; Cavalier, E.; Björk, J.; Christensson, A.; Nyman, U.; Porrini, E.; et al. Iohexol plasma clearance for measuring glomerular filtration rate in clinical practice and research: A review. Part 1: How to measure glomerular filtration rate with iohexol? Clin. Kidney J. 2016, 9, 682–699. [Google Scholar] [CrossRef] [PubMed]
- Smith, H. The inulin clearance. In The Kidney; Smith, H., Ed.; Oxford University Press: New York, NY, USA, 1951; pp. 47–55. [Google Scholar]
- Filler, G.; Yasin, A.; Medeiros, M. Methods of assessing renal function. Pediatr. Nephrol. 2014, 29, 183–192. [Google Scholar] [CrossRef] [PubMed]
- Soveri, I.; Berg, U.B.; Björk, J.; Elinder, C.G.; Grubb, A.; Mejare, I.; Sterner, G.; Bäck, S.E. Measuring GFR: A systematic review. Am. J. Kidney Dis. 2014, 64, 411–424. [Google Scholar] [CrossRef] [PubMed]
- Inker, L.A.; Levey, A.S.; Coresh, J. Estimated Glomerular Filtration Rate from a Panel of Filtration Markers—Hope for Increased Accuracy Beyond Measured Glomerular Filtration Rate? Adv. Chronic Kidney Dis. 2018, 25, 67–75. [Google Scholar] [CrossRef] [PubMed]
- Prasad, N.; Barai, S.; Gambhir, S.; Parasar, D.; Ora, M.; Gupta, A.; Sharma, R. Comparison of glomerular filtration rate estimated by plasma clearance method with modification of diet in renal disease prediction equation and Gates method. Indian J. Nephrol. 2012, 22, 103–107. [Google Scholar] [CrossRef]
- Rizk, D.V.; Meier, D.; Sandoval, R.M.; Chacana, T.; Reilly, E.S.; Seegmiller, J.C.; DeNoia, E.; Strickland, J.S.; Muldoon, J.; Molitoris, B.A. A novel method for rapid bedside measurement of GFR. J. Am. Soc. Nephrol. 2018, 29, 1609–1613. [Google Scholar] [CrossRef] [PubMed]
- Wixom, R.L.; Davis, G.E.; Flynn, M.A.; Tsutakawa, R.T.; Hentges, D.J. Excretion of Creatine and Creatinine in Feces of Man. Proc. Soc. Exp. Biol. Med. 1979, 161, 452–457. [Google Scholar] [CrossRef] [PubMed]
- Levey, A.S.; Perrone, R.D.; Madias, N.E. Serum creatinine and renal function. Annu. Rev. Med. 1988, 39, 465–490. [Google Scholar] [CrossRef]
- Zhang, X.; Rule, A.D.; McCulloch, C.E.; Lieske, J.C.; Ku, E.; Hsu, C.Y. Tubular secretion of creatinine and kidney function: An observational study. BMC Nephrol. 2020, 21, 108. [Google Scholar] [CrossRef]
- Popper, H.; Mandel, E. Filtrations and reabsorptions leitung in dernierenpathologie. Erg. Inn. Med. Kinder 1937, 53, 685–695. [Google Scholar]
- Chasson, A.; Grady, H.; Stanley, M. Determination of creatinine by means of automatic chemical analysis. Tech. Bull. Regist Med. Technol. 1960, 30, 207–212. [Google Scholar] [CrossRef]
- Husdan, H.; Rapoport, A. Estimation of creatinine by the Jaffe reaction. A comparison of three methods. Clin. Chem. 1968, 14, 222–238. [Google Scholar] [CrossRef]
- Brück, K.; Jager, K.J.; Dounousi, E.; Kainz, A.; Nitsch, D.; Ärnlöv, J.; Rothenbacher, D.; Browne, G.; Capuano, V.; Ferraro, P.M.; et al. Methodology used in studies reporting chronic kidney disease prevalence: A systematic literature review. Nephrol. Dial. Transplant. 2015, 30, iv6–iv16. [Google Scholar] [CrossRef] [PubMed]
- Delanaye, P.; Cavalier, E.; Pottel, H. Serum Creatinine: Not so Simple! Nephron 2017, 136, 302–308. [Google Scholar] [CrossRef] [PubMed]
- Dennen, P.; Parikh, C.R. Biomarkers of acute kidney injury: Can we replace serum creatinine? Clin. Nephrol. 2007, 68, 269–278. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, G.; Haycock, G.; Edelmann, C., Jr.; Spitzer, A. A simple estimate of glomerular filtration rate in children derived from body length and plasma creatinine. Pediatrics 1976, 58, 259–263. [Google Scholar] [CrossRef]
- Cockcroft, D.W.; Gault, M.H. Prediction of creatinine clearance from serum creatinine. Nephron 1976, 16, 31–41. [Google Scholar] [CrossRef]
- Lamb, E.J.; Tomson, C.R.V.; Roderick, P.J. Estimating kidney function in adults using formulae. Ann. Clin. Biochem. 2005, 42, 321–345. [Google Scholar] [CrossRef]
- Levey, A.S.; Bosch, J.P.; Lewis, J.B.; Greene, T.; Rogers, N.; Roth, D. A more accurate method to estimate glomerular filtration rate from serum creatinine: A new prediction equation. Ann. Intern. Med. 1999, 130, 461–470. [Google Scholar] [CrossRef]
- Levey, A.S.; Stevens, L.A.; Schmid, C.H.; Zhang, Y.; Castro, A.F.; Feldman, H.I.; Kusek, J.W.; Eggers, P.; Van Lente, F.; Greene, T.; et al. A new equation to estimate glomerular filtration rate. Ann. Intern. Med. 2009, 150, 604–612. [Google Scholar] [CrossRef]
- Giles, S.N.; Fiori, S. Glomerular Filtration Rate Estimation by a Novel Numerical Binning-Less Isotonic Statistical Bivariate Numerical Modeling Method. Information 2019, 10, 100. [Google Scholar] [CrossRef]
- Passos, M.T.; Nishida, S.K.; Câmara, N.O.S.; Shimizu, M.H.; Mastroianni-Kirsztajn, G. Iohexol clearance for determination of glomerular filtration rate in rats induced to acute renal failure. PLoS ONE 2015, 10, e0123753. [Google Scholar] [CrossRef][Green Version]
- Zhu, X.R.; Ge, N.; Wang, Y.; Zhai, J.L.; Liu, C. Corticosteroids significantly increase cystatin C levels in the plasma by promoting cystatin C production in rats. Ren. Fail. 2019, 41, 698–703. [Google Scholar] [CrossRef] [PubMed]
- Zager, R.A. Exogenous Creatinine Clearance Accurately Assesses Filtration Failure in Rat Experimental Nephropathies. Am. J. Kidney Dis. 1987, 10, 427–430. [Google Scholar] [CrossRef]
- Van Liew, J.B.; Zamlauski-Tucker, M.J.; Feld, L.G. Endogenous creatinine clearance in the rat: Strain variation. Life Sci. 1993, 53, 1015–1021. [Google Scholar] [CrossRef]
- Ellery, S.J.; Cai, X.; Walker, D.D.; Dickinson, H.; Kett, M.M. Transcutaneous measurement of glomerular filtration rate in small rodents: Through the skin for the win? Nephrology 2015, 20, 117–123. [Google Scholar] [CrossRef]
- Sancho-Martínez, S.M.; Blanco-Gozalo, V.; Quiros, Y.; Prieto-García, L.; Montero-Gómez, M.J.; Docherty, N.G.; Martínez-Salgado, C.; Morales, A.I.; López-Novoa, J.M.; López-Hernández, F.J. Impaired Tubular Reabsorption Is the Main Mechanism Explaining Increases in Urinary NGAL Excretion Following Acute Kidney Injury in Rats. Toxicol. Sci. 2020, 175, 75–86. [Google Scholar] [CrossRef] [PubMed]
- Sancho-Martínez, S.M.; Sánchez-Juanes, F.; Blanco-Gozalo, V.; Fontecha-Barriuso, M.; Prieto-García, L.; Fuentes-Calvo, I.; González-Buitrago, J.M.; Morales, A.I.; Martínez-Salgado, C.; Ramos-Barron, M.A.; et al. Urinary TCP1-eta: A Cortical Damage Marker for the Pathophysiological Diagnosis and Prognosis of Acute Kidney Injury. Toxicol. Sci. 2020, 174, 3–15. [Google Scholar] [CrossRef]
- Quiros, Y.; Ferreira, L.; Sancho-Martínez, S.M.; González-Buitrago, J.M.; López-Novoa, J.M.; López-Hernández, F.J. Sub-nephrotoxic doses of gentamicin predispose animals to developing acute kidney injury and to excrete ganglioside M2 activator protein. Kidney Int. 2010, 78, 1006–1015. [Google Scholar] [CrossRef]
- Casanova, A.G.; Vicente-Vicente, L.; Hernández-Sánchez, M.T.; Prieto, M.; Rihuete, M.I.; Ramis, L.M.; del Barco, E.; Cruz, J.J.; Ortiz, A.; Cruz-González, I.; et al. Urinary transferrin pre-emptively identifies the risk of renal damage posed by subclinical tubular alterations. Biomed. Pharmacother. 2020, 121, 109684. [Google Scholar] [CrossRef]
- Vicente-Vicente, L.; Sánchez-Juanes, F.; García-Sánchez, O.; Blanco-Gozalo, V.; Pescador, M.; Sevilla, M.A.; González-Buitrago, J.M.; López-Hernández, F.J.; López-Novoa, J.M.; Morales, A.I. Sub-nephrotoxic cisplatin sensitizes rats to acute renal failure and increases urinary excretion of fumarylacetoacetase. Toxicol. Lett. 2015, 234, 99–109. [Google Scholar] [CrossRef]
- Casanova, A.G.; Fuentes-Calvo, I.; Hernández-Sánchez, M.T.; Quintero, M.; Toral, P.; Caballero, M.T.; Martínez-Salgado, C.; Morales, A.I.; Layton, A.T.; Eleno, N.; et al. The furosemide stress test and computational modeling identify renal damage sites associated with predisposition to acute kidney injury in rats. Transl. Res. 2020, 231, 76–91. [Google Scholar] [CrossRef]
- Alpaydin, E. Introduction to Machine Learning, 4th ed.; MT Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Breinman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Pedregosa, F.; Michel, V.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Vanderplas, J.; Cournapeau, D.; Pedregosa, F.; Varoquaux, G.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Kiefer, J.; Wolfowitz, J. Stochastic Estimation of the Maximum of a Regression Function. Ann. Math. Stat. 1952, 23, 462–466. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Whittaker, A.L.; Lymn, K.A.; Howarth, G.S. Effects of Metabolic Cage Housing on Rat Behavior and Performance in the Social Interaction Test. J. Appl. Anim. Welf. Sci. 2016, 19, 363–374. [Google Scholar] [CrossRef]
- Sneddon, L.U.; Halsey, L.G.; Bury, N.R. Considering aspects of the 3Rs principles within experimental animal biology. J. Exp. Biol. 2017, 220, 3007–3016. [Google Scholar] [CrossRef]
- Potter, D.; Jarrah, A.; Sakai, T.; Harrah, J.; Holliday, M.A. Character of function and size in kidney during normal growth of rats. Pediatr. Res. 1969, 3, 51–59. [Google Scholar] [CrossRef][Green Version]
- Filler, G.; Lee, M. Educational review: Measurement of GFR in special populations. Pediatr. Nephrol. 2018, 33, 2037–2046. [Google Scholar] [CrossRef]
| Model | n (Rats) | Age at Start (Weeks) | Duration (Weeks) | n (Data Trios) |
|---|---|---|---|---|
| Model Development (Training + Validation Datasets) | ||||
| CTRL | 9 | 8 | 1 | 51 |
| 34 | 8 | 2–28 | 194 | |
| T-AKI | 109 | 8 | 1 | 583 |
| 19 | 8 | 2–8 | 98 | |
| 64 | 8 | 2–28 | 381 | |
| I/R | 15 | 8 | 2–8 | 63 |
| RMR | 35 | 8 | 2–28 | 184 |
| Test Dataset | ||||
| CTRL | 13 | 8 | 1 | 59 |
| 2 | 8 | 5 | 10 | |
| 3 | 8 | 7 | 21 | |
| PRD | 61 | 8 | 1 | 279 |
| T-AKI | 9 | 8 | 5 | 38 |
| 7 | 8 | 7 | 49 | |
| 50 | 8 | 1 | 204 | |
| Training Set | Validation Set | Test Set | |||||||
|---|---|---|---|---|---|---|---|---|---|
| LR | RF | FFNN | LR | RF | FFNN | LR | RF | FFNN | |
| MAE | 0.2210 | 0.1801 | 0.1956 | 0.1975 | 0.1894 | 0.1780 | 0.2515 | 0.2257 | 0.2035 |
| Correlation | 0.8402 | 0.8869 | 0.8632 | 0.8732 | 0.8871 | 0.9028 | 0.7922 | 0.7450 | 0.8563 |
| P10 | 0.2635 | 0.3322 | 0.3099 | 0.2699 | 0.2828 | 0.2879 | 0.2530 | 0.2803 | 0.3136 |
| P30 | 0.6901 | 0.7751 | 0.7391 | 0.7044 | 0.7189 | 0.7532 | 0.6394 | 0.6727 | 0.6955 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pellicer-Valero, Ó.J.; Massaro, G.A.; Casanova, A.G.; Paniagua-Sancho, M.; Fuentes-Calvo, I.; Harvat, M.; Martín-Guerrero, J.D.; Martínez-Salgado, C.; López-Hernández, F.J. Neural Network-Based Calculator for Rat Glomerular Filtration Rate. Biomedicines 2022, 10, 610. https://doi.org/10.3390/biomedicines10030610
Pellicer-Valero ÓJ, Massaro GA, Casanova AG, Paniagua-Sancho M, Fuentes-Calvo I, Harvat M, Martín-Guerrero JD, Martínez-Salgado C, López-Hernández FJ. Neural Network-Based Calculator for Rat Glomerular Filtration Rate. Biomedicines. 2022; 10(3):610. https://doi.org/10.3390/biomedicines10030610
Chicago/Turabian StylePellicer-Valero, Óscar J., Giampiero A. Massaro, Alfredo G. Casanova, María Paniagua-Sancho, Isabel Fuentes-Calvo, Mykola Harvat, José D. Martín-Guerrero, Carlos Martínez-Salgado, and Francisco J. López-Hernández. 2022. "Neural Network-Based Calculator for Rat Glomerular Filtration Rate" Biomedicines 10, no. 3: 610. https://doi.org/10.3390/biomedicines10030610
APA StylePellicer-Valero, Ó. J., Massaro, G. A., Casanova, A. G., Paniagua-Sancho, M., Fuentes-Calvo, I., Harvat, M., Martín-Guerrero, J. D., Martínez-Salgado, C., & López-Hernández, F. J. (2022). Neural Network-Based Calculator for Rat Glomerular Filtration Rate. Biomedicines, 10(3), 610. https://doi.org/10.3390/biomedicines10030610