Computational Analysis of Enhanced Circulating Tumour Cell (CTC) Separation in a Microfluidic System with an Integrated Dielectrophoretic-Magnetophorectic (DEP-MAP) Technique
Abstract
:1. Introduction
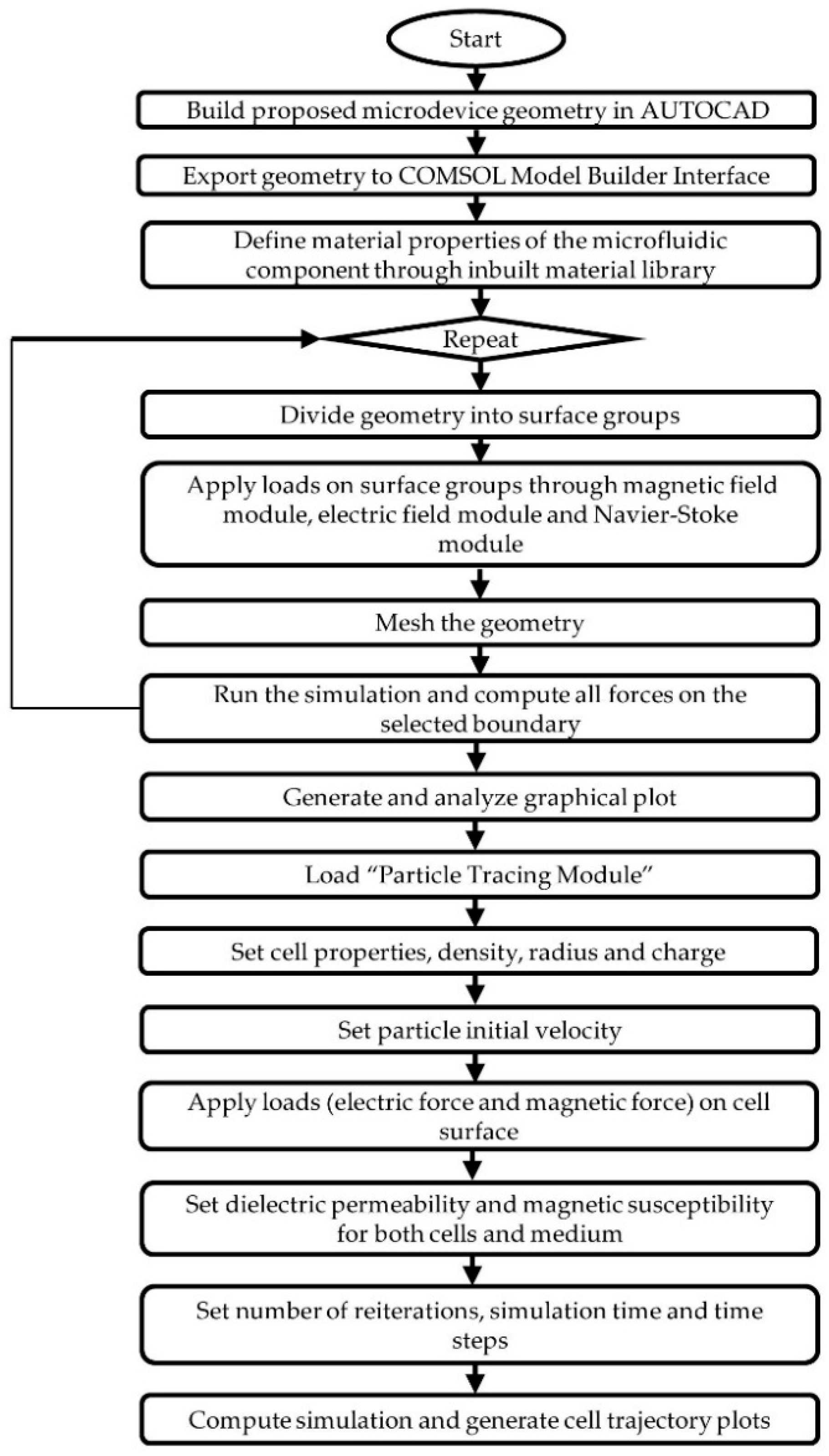
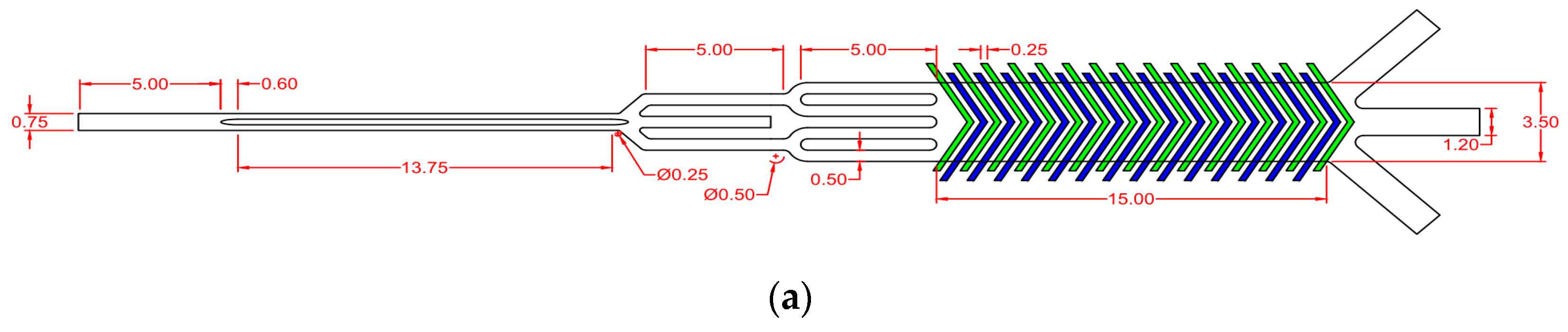
2. Computational Modelling Method
- The fluid injected at the inlet channel is non-Newtonian, whereby the viscous stress that arises from the flow is linear at every point.
- Cells are spherical.
- The flow within the microfluidic is incompressible such that it has constant density, viscosity, and concentration.
- As the cross sectional of the microchannel is less than 1 mm3, the Reynolds number generated within the fluid flow is less than 200. Therefore, the flow is considered laminar.
- Blood clotting did not occur within the microchannel.
- Both the surrounding medium and the system are considered to have uniform bulk conductivities, dielectric constants, and magnetic permeability. Hence no space charge with the system.
- The fluid has constant electric conductivity and magnetic permeability.
- A constant magnetic field gradient is generated across the fluid volume in the MAP stage. The electric conductivity is negligible in this stage.
- The magnetization of cells is collinear with the magnetic field.
- The presence of a non-magnetic cell does not distort the magnetic field lines in the MAP stage.
- Joule heating and electrochemical effects are assumed negligible in the DEP stage. This is because the electric field is low and the frequency is high.
- Cells flow according to the fluid stream. They do not stick to the boundaries.
3. Results and Discussions
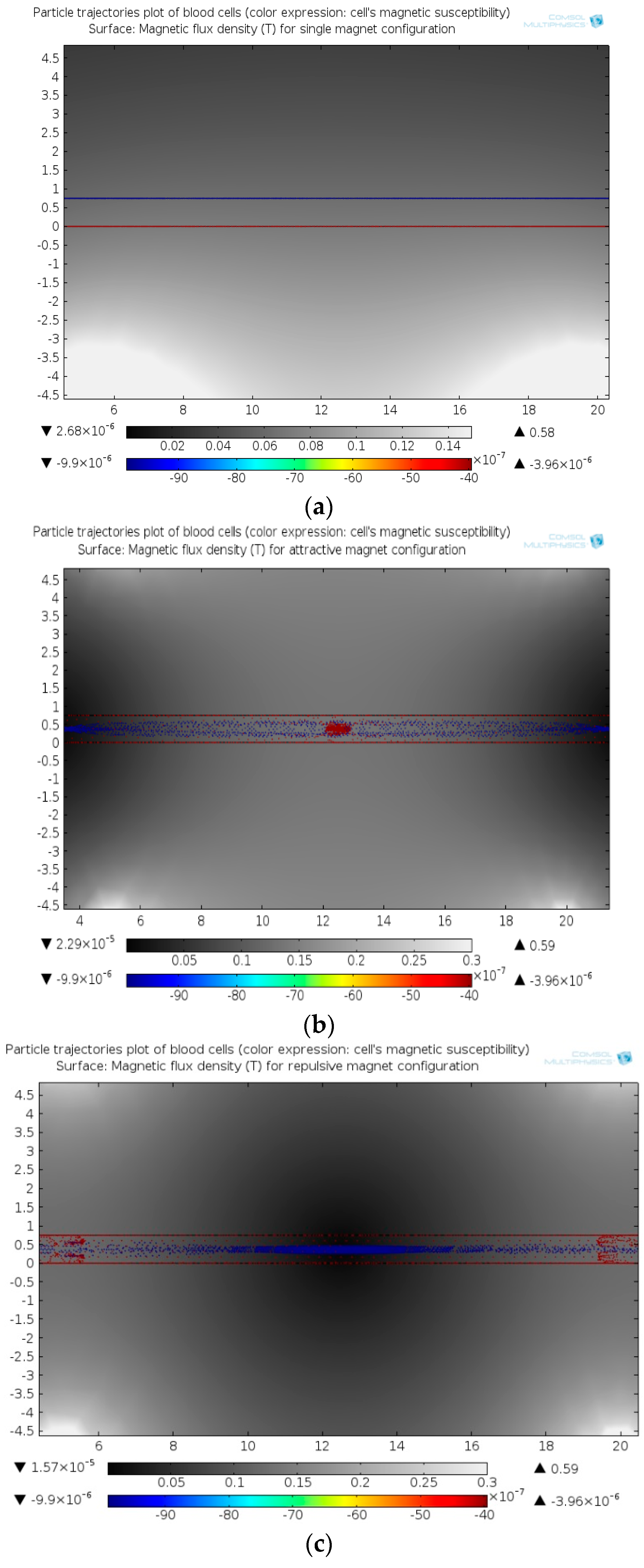
3.1. Magnetophoresis Stage
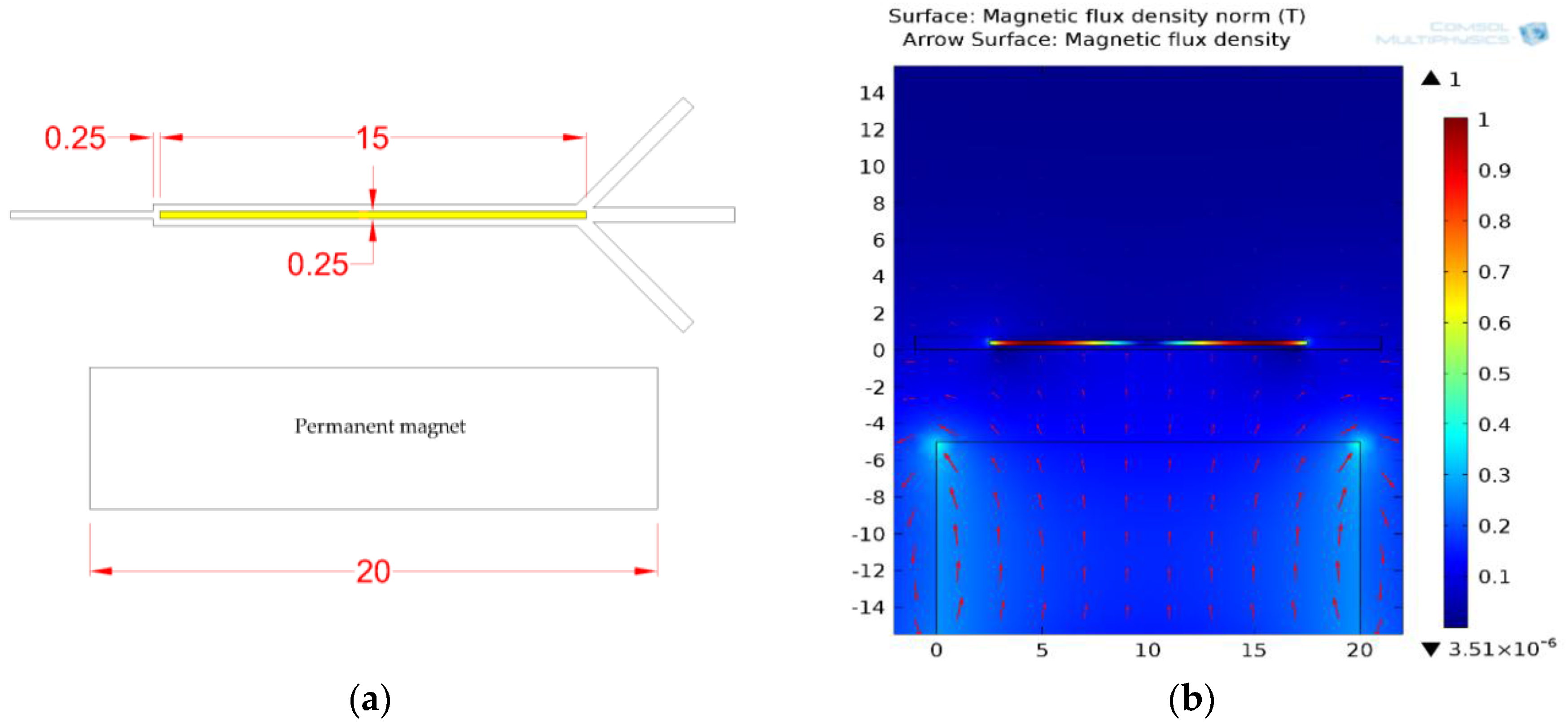
3.1.1. Permanent Magnet Configuration: Conventional vs. Face-to-Face Permanent Magnet
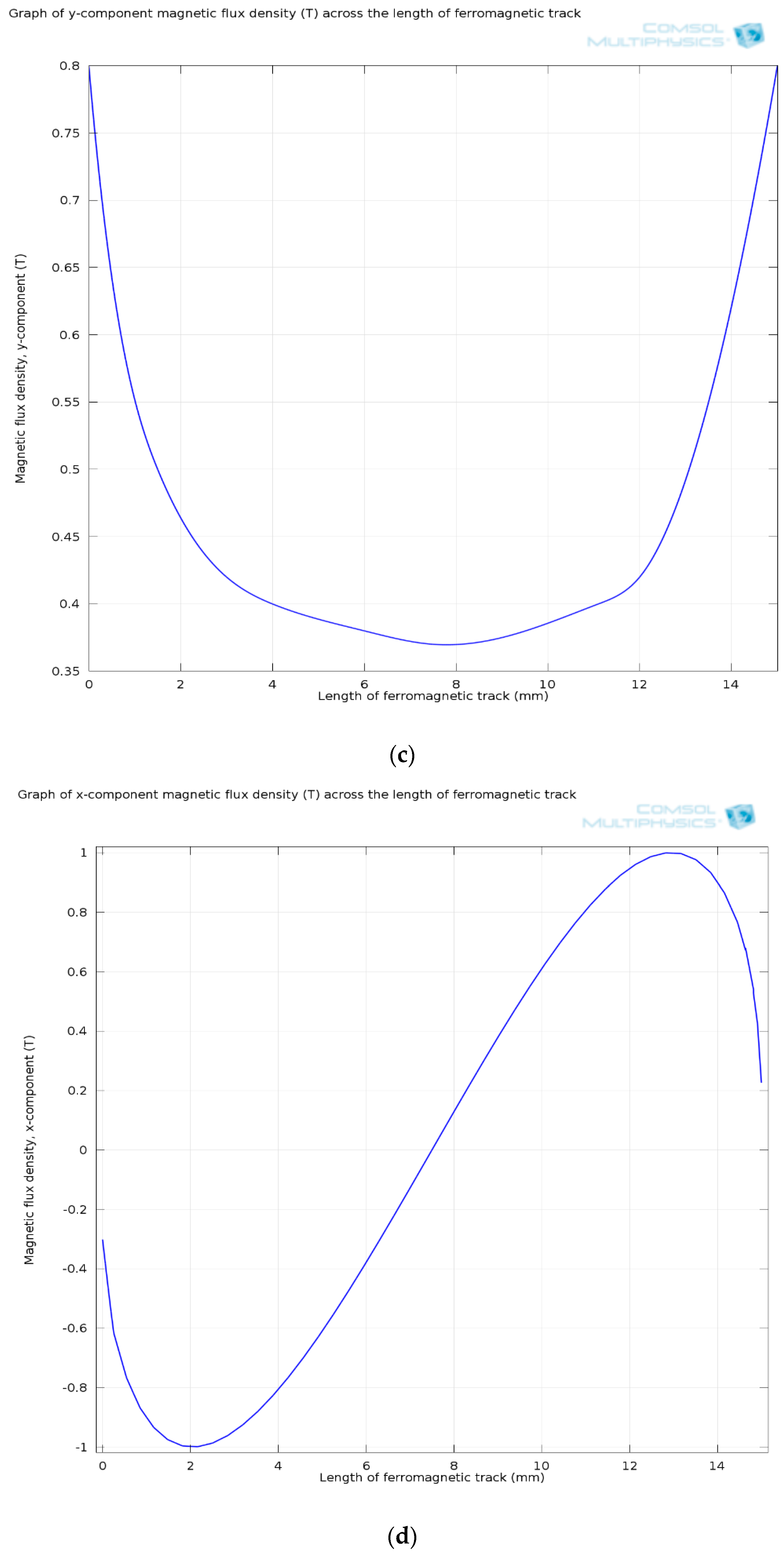
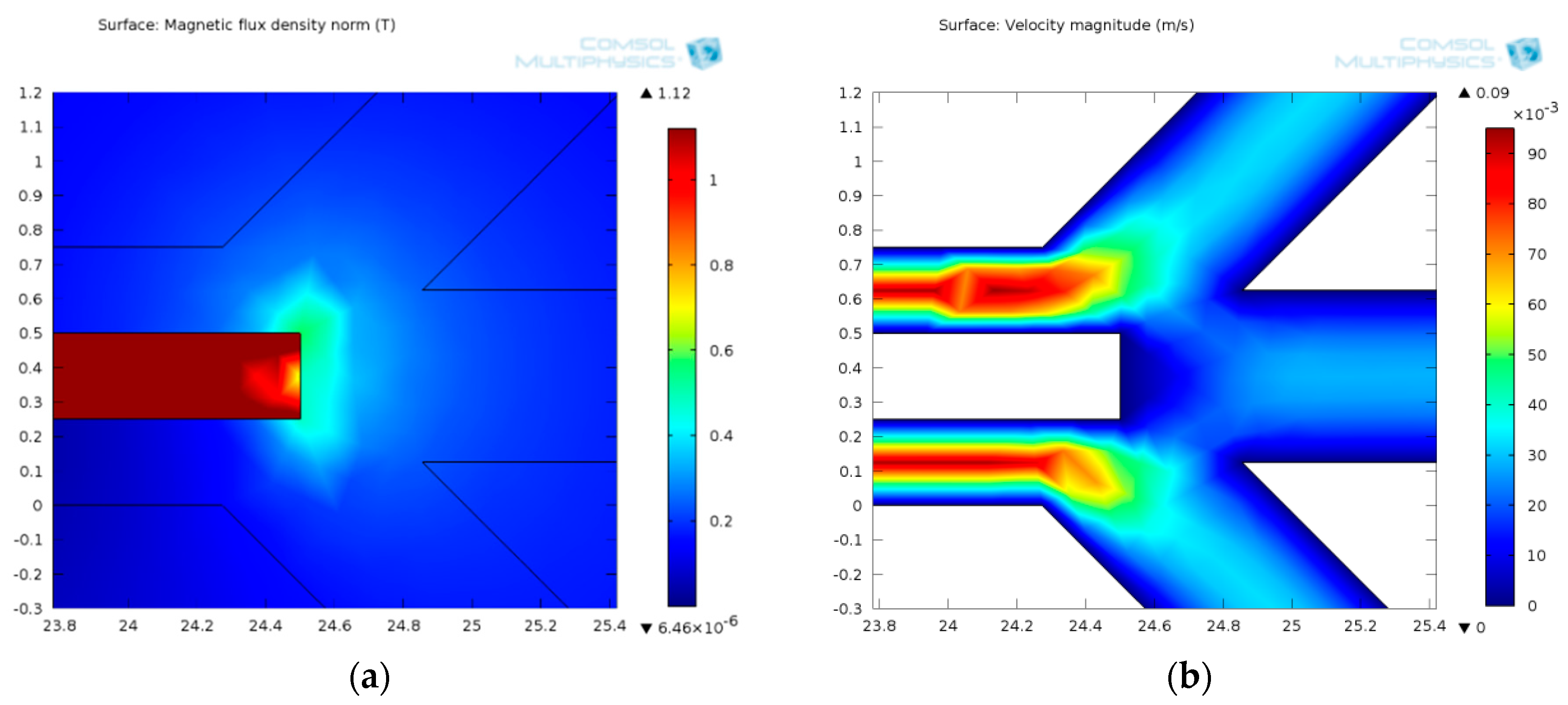
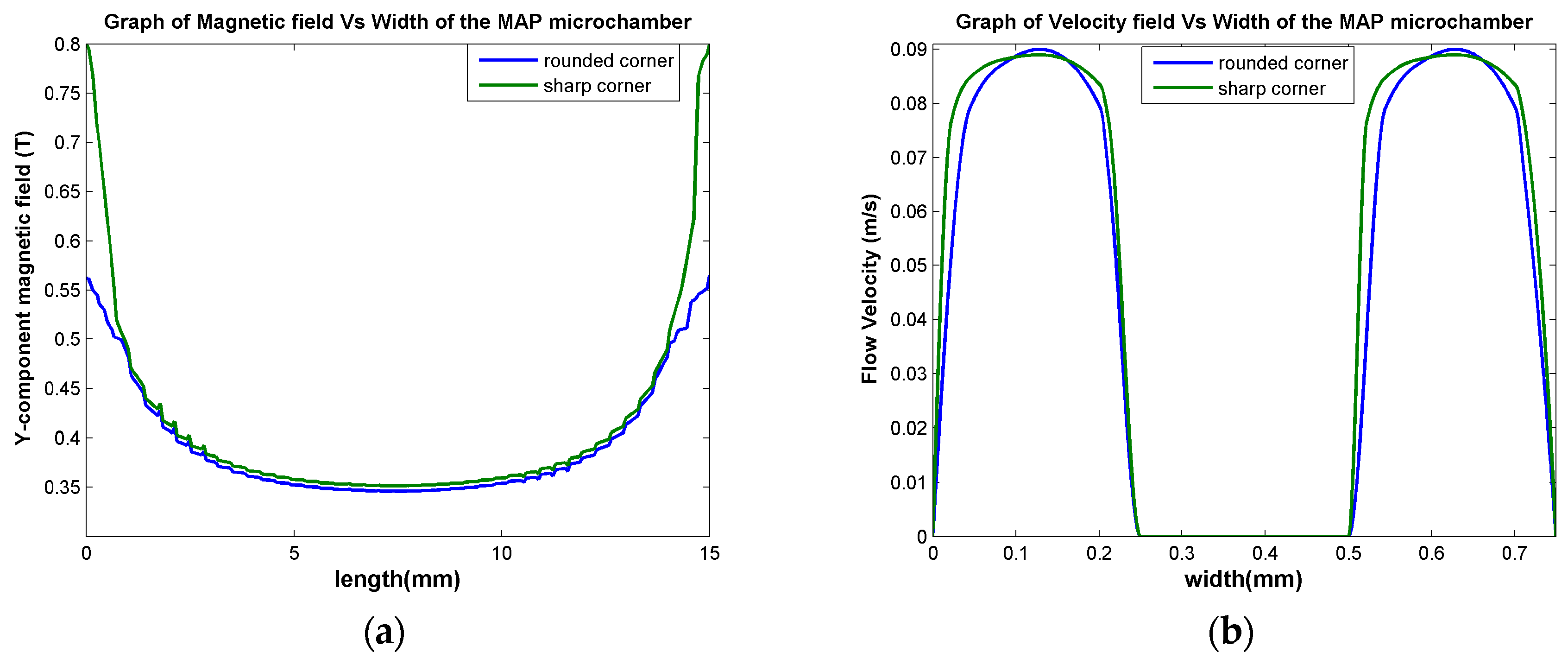
3.1.2. Ferromagnetic Track’s Configuration
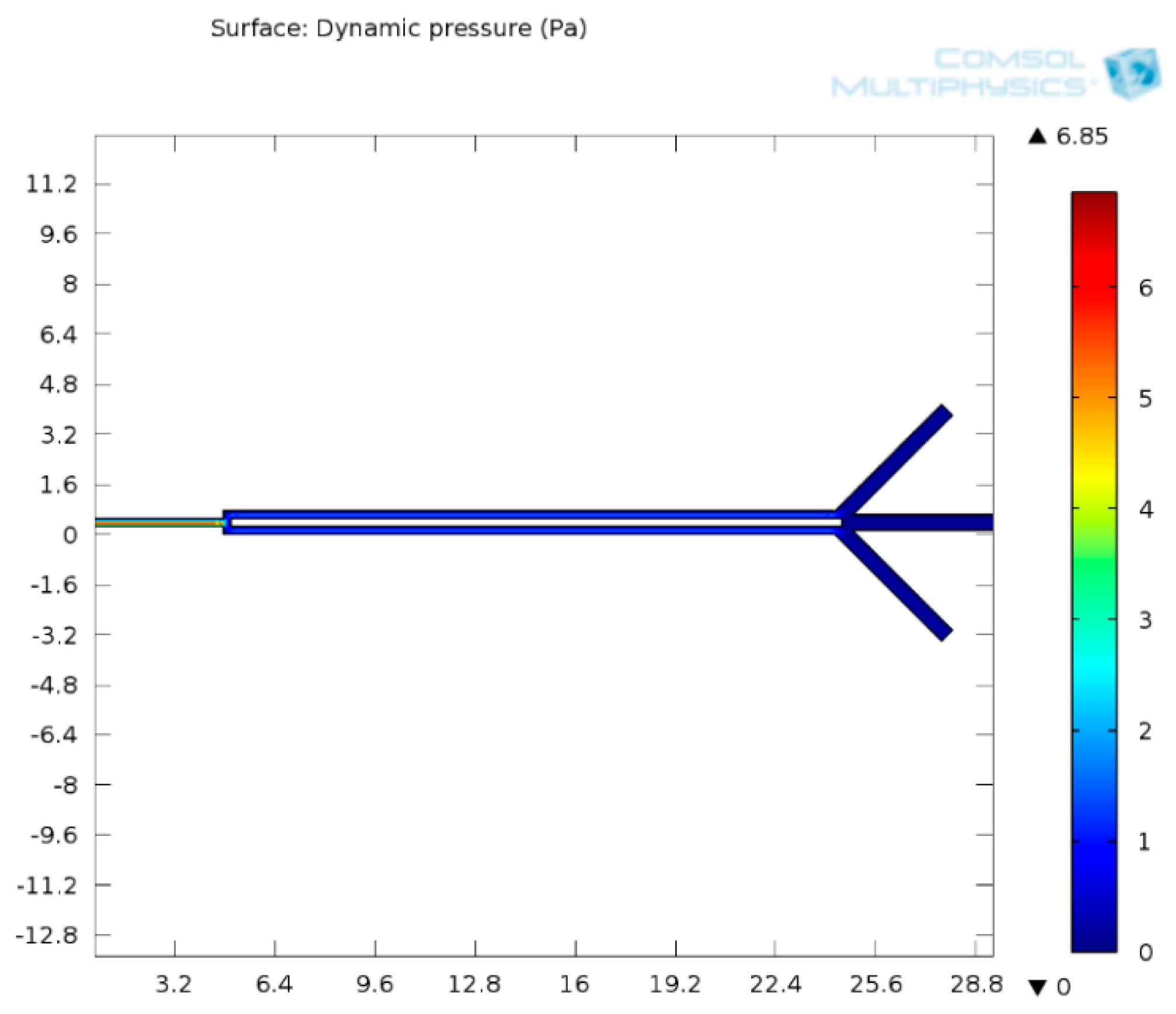
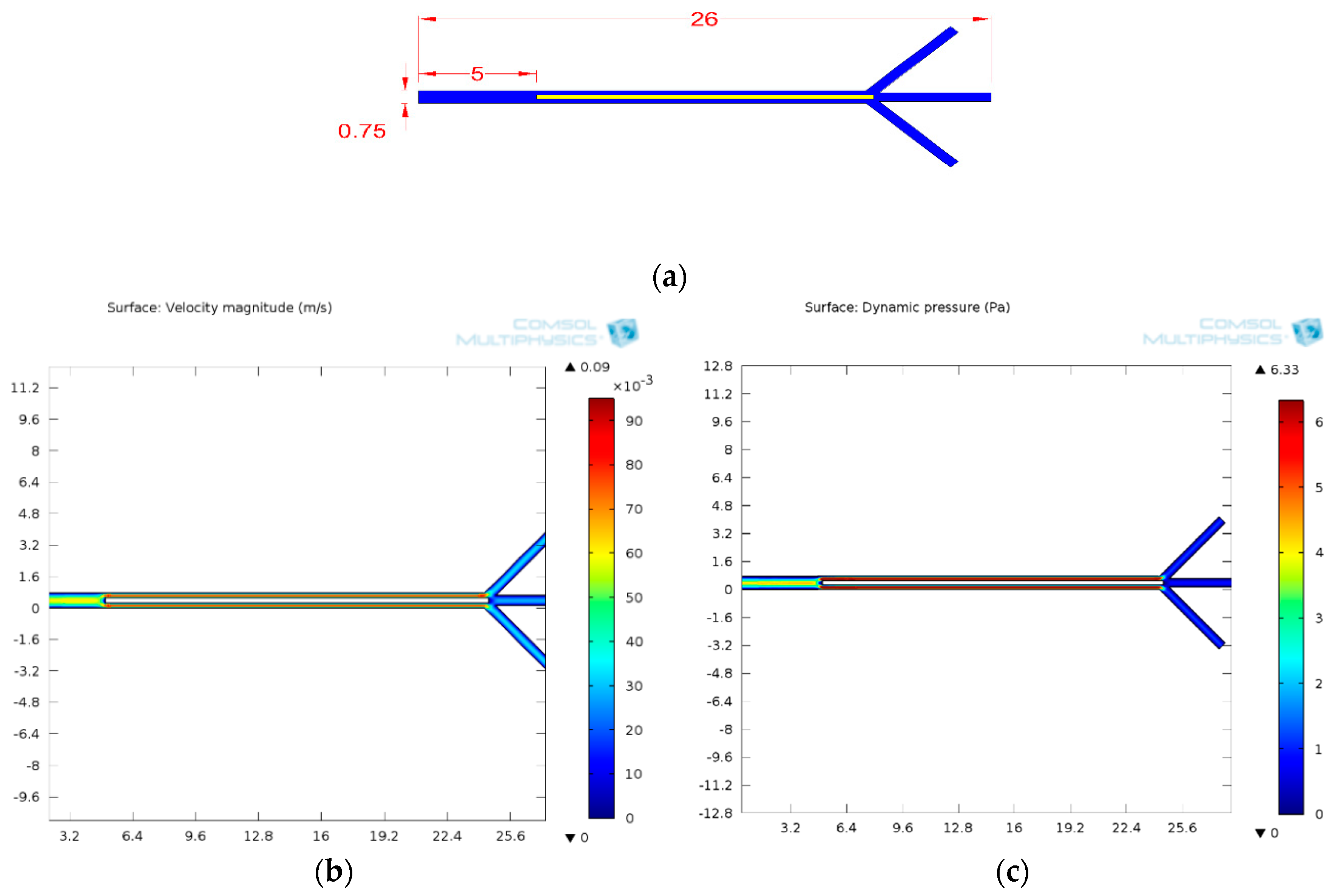
3.1.3. Fluid Flow Parameter and Dynamic Pressure of Proposed Microchannel
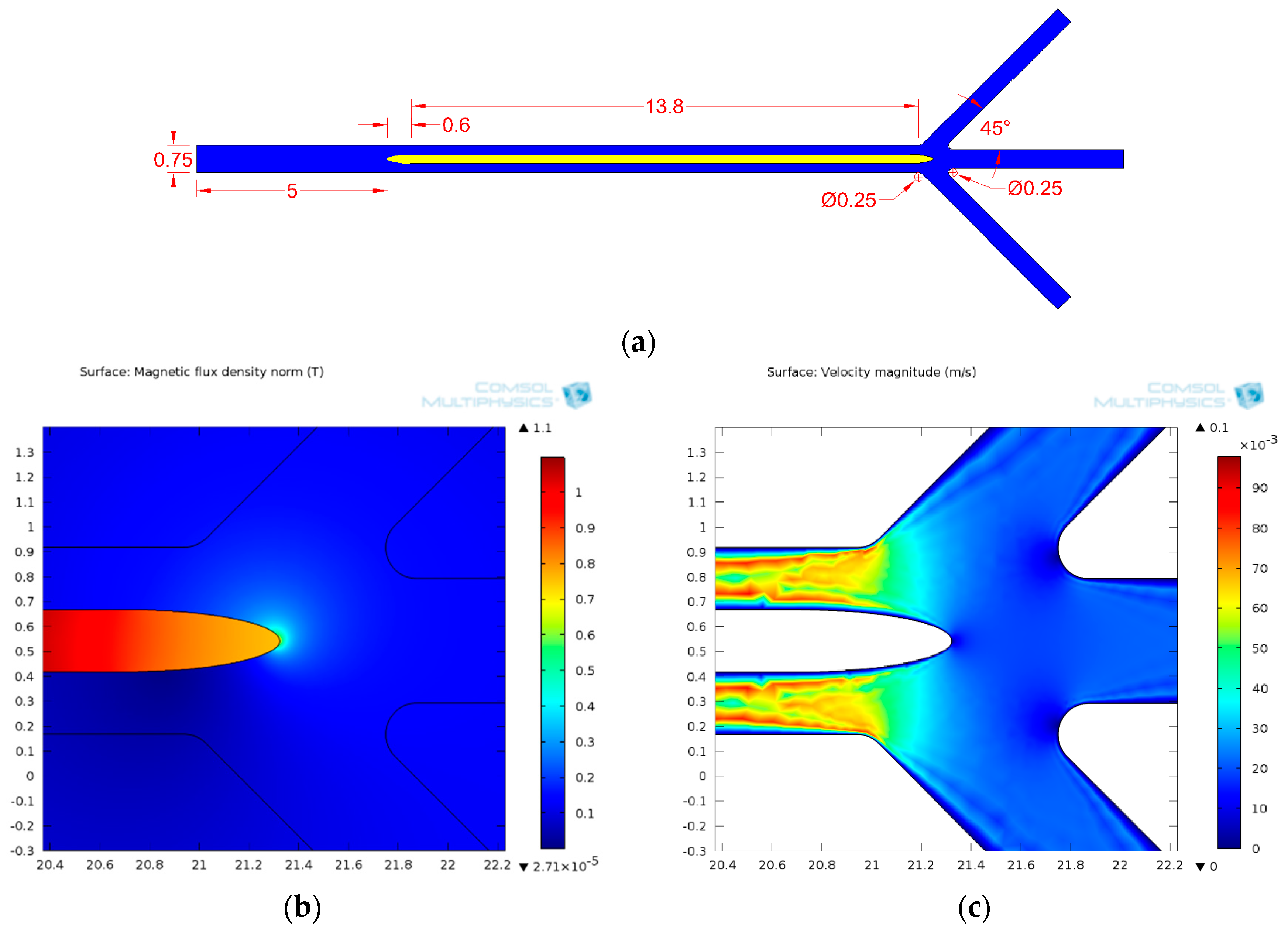
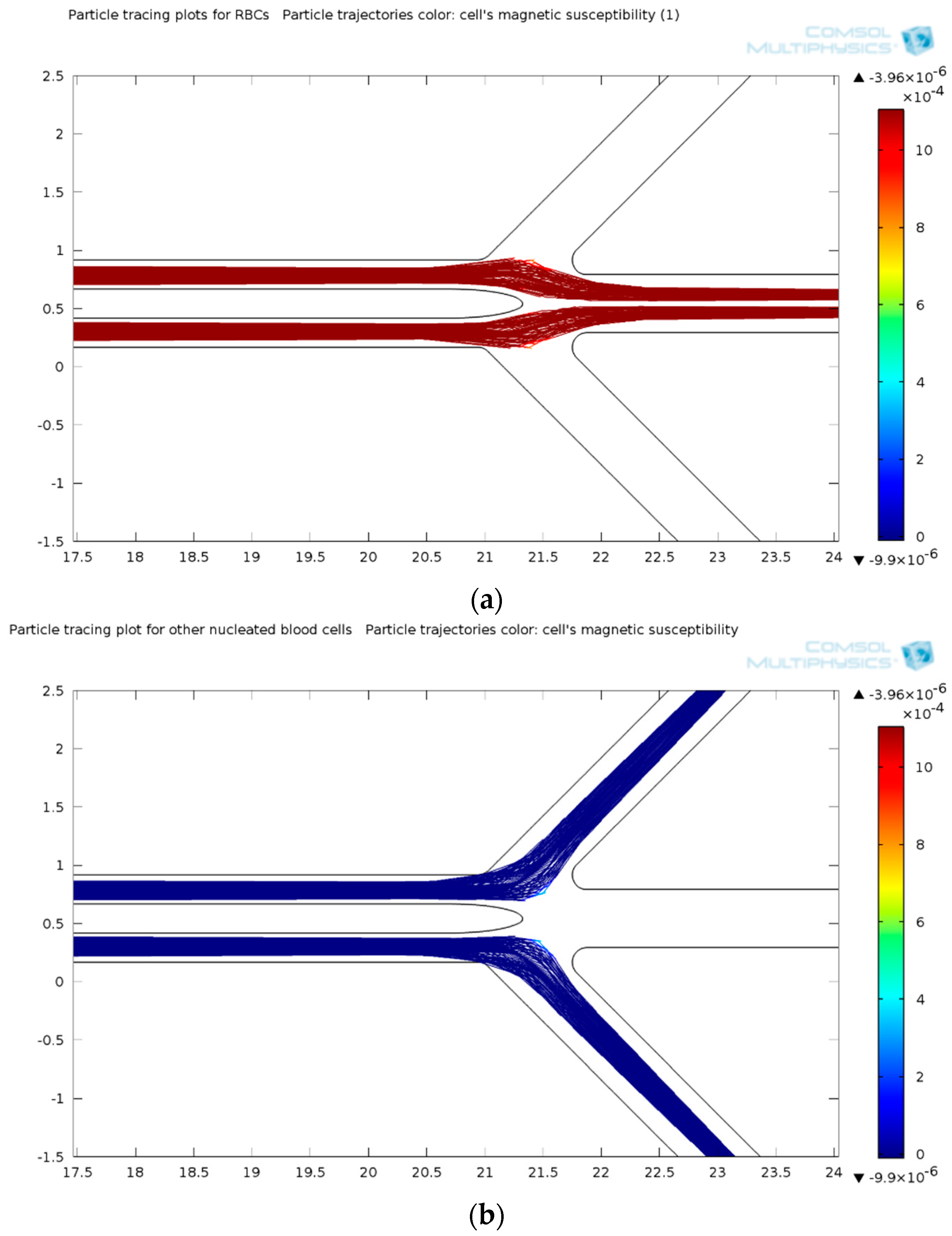
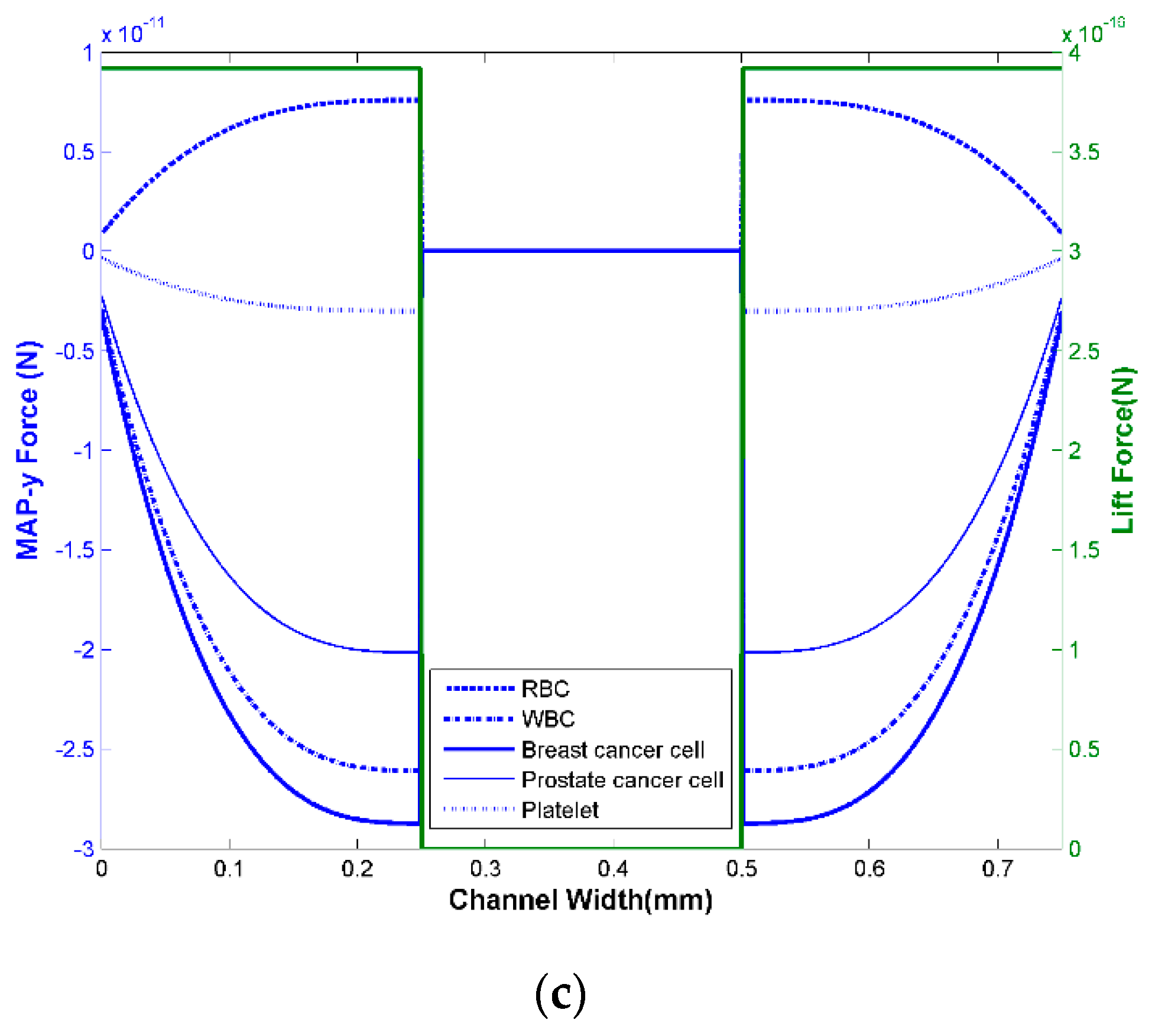
3.1.4. Design Optimization
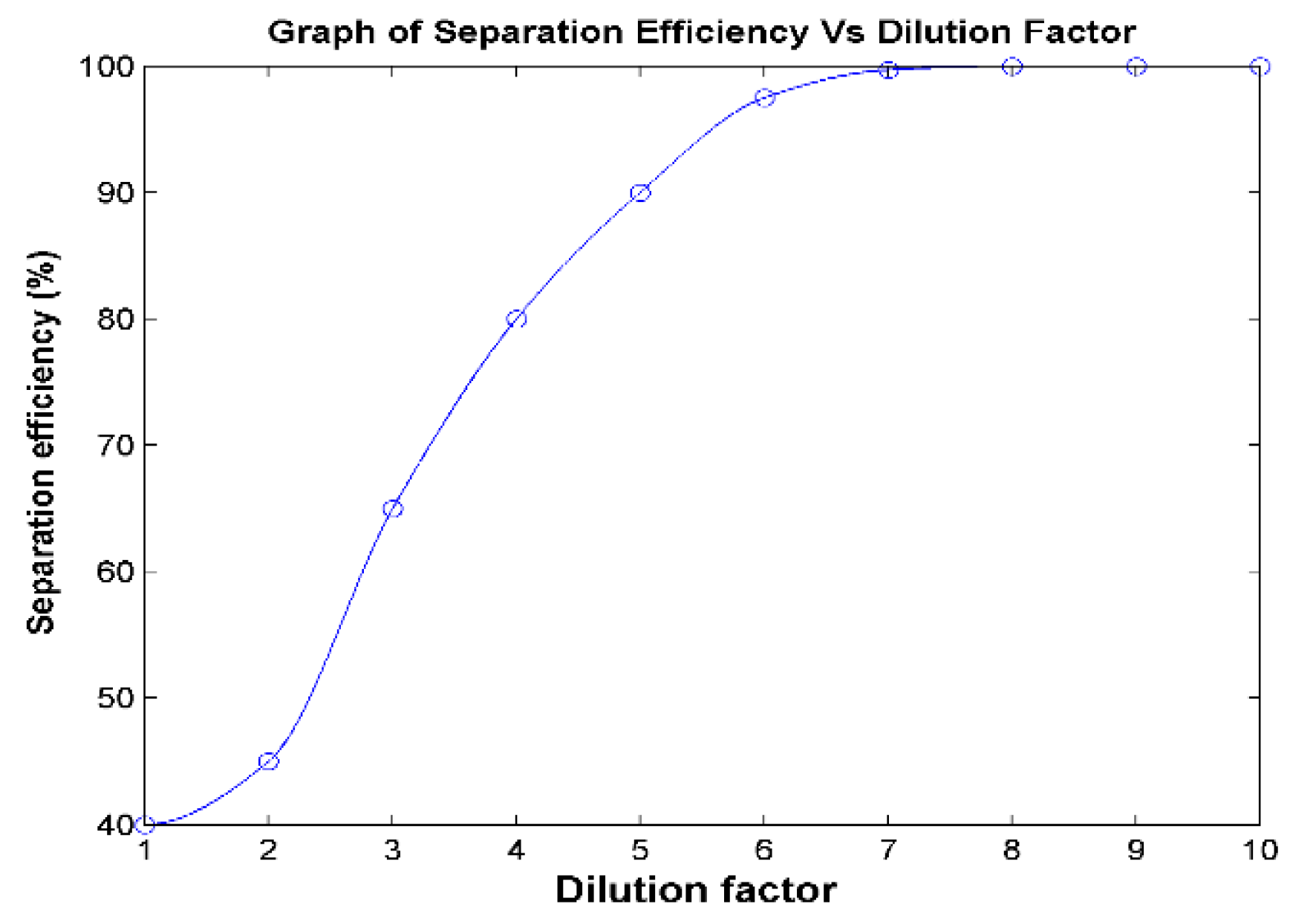
3.1.5. Separation Efficiency
3.2. Evaluation with DEP Stage
4. Conclusions and Future Works
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Maryam, F.; Hassali, M.A.; Knight, A.; Shafie, A.A.; Farooqui, M.A.; Saleem, F. A qualitative exploration of malaysian cancer patients’ perceptions of cancer screening. BMC Public Health 2013, 13, 1–7. [Google Scholar]
- Thiery, J.P. Epithelial-mesenchymal transitions in tumour progression. Nat. Rev. Cancer 2002, 2, 442–454. [Google Scholar] [CrossRef] [PubMed]
- Frangioni, J.V. New technologies for human cancer imaging. J. Clin. Oncol. 2008, 26, 4012–4021. [Google Scholar] [CrossRef] [PubMed]
- Husemann, Y.; Geigl, J.B.; Schubert, F.; Musiani, P.; Meyer, M.; Burghart, E.; Forni, G.; Eils, R.; Fehm, T.; Riethmuller, G.; et al. Systemic spread is an early step in breast cancer. Cancer Cell 2008, 13, 58–68. [Google Scholar] [CrossRef] [PubMed]
- Gerges, N.; Rak, J.; Jabado, N. New technologies for the detection of circulating tumour cells. Br. Med. Bull. 2010, 94, 49–64. [Google Scholar] [CrossRef] [PubMed]
- Allen, J.E.; El-Deiry, W.S. Circulating tumor cells and colorectal cancer. Curr. Colorectal Cancer Rep. 2010, 6, 212–220. [Google Scholar] [CrossRef] [PubMed]
- Dalum, G.V.; Holland, L.; Terstappen, L.W. Metastasis and circulating tumor cells. J. Int. Fed. Clin. Chem. Lab. Med. 2012, 23, 1–11. [Google Scholar]
- Michaelson, J.S.; Cheongsiatmoy, J.A.; Dewey, F.; Silverstein, M.J.; Sgroi, D.; Smith, B.; Tanabe, K.K. Spread of human cancer cells occurs with probabilities indicative of a nongenetic mechanism. Br. J. Cancer 2005, 93, 1244–1249. [Google Scholar] [CrossRef] [PubMed]
- Antolovic, D.; Galindo, L.; Carstens, A.; Rahbari, N.; Buchler, M.W.; Weitz, J.; Koch, M. Heterogeneous detection of circulating tumor cells in patients with colorectal cancer by immunomagnetic enrichment using different epcam-specific antibodies. BMC Biotechnol. 2010, 10, 35. [Google Scholar] [CrossRef] [PubMed]
- Khoo, B.L.; Chaudhuri, P.K.; Ramalingam, N.; Tan, D.S.; Lim, C.T.; Warkiani, M.E. Single-cell profiling approaches to probing tumor heterogeneity. Int. J. Cancer 2016, 139, 243–255. [Google Scholar] [CrossRef] [PubMed]
- Kallergi, G.; Papadaki, M.A.; Politaki, E.; Mavroudis, D.; Georgoulias, V.; Agelaki, S. Epithelial to mesenchymal transition markers expressed in circulating tumour cells of early and metastatic breast cancer patients. Breast Cancer Res. 2011, 13, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Marrinucci, D.; Bethel, K.; Lazar, D.; Fisher, J.; Huynh, E.; Clark, P.; Bruce, R.; Nieva, J.; Kuhn, P. Cytomorphology of circulating colorectal tumor cells: A small case series. J. Oncol. 2010, 2010. [Google Scholar] [CrossRef] [PubMed]
- Cima, I.; Wen Yee, C.; Iliescu, F.S.; Min Phyo, W.; Hon Lim, K.; Iliescu, C.; Han Tan, M. Label-free isolation of circulating tumor cells in microfluidic devices: Current research and perspectives. Biomicrofluidics 2013, 7. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.; Lin, H.K.; Lu, B.; Williams, A.; Datar, R.; Cote, R.J.; Tai, Y.C. 3D microfilter device for viable circulating tumor cell (CTC) enrichment from blood. Biomed. Microdevices 2011, 13, 203–213. [Google Scholar] [CrossRef] [PubMed]
- Coumans, F.A.; van Dalum, G.; Beck, M.; Terstappen, L.W. Filter characteristics influencing circulating tumor cell enrichment from whole blood. PLoS ONE 2013, 8, e61770. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Liu, C.; Li, M.; Wang, J.; Xianyu, Y.; Hu, G.; Jiang, X. Size-based hydrodynamic rare tumor cell separation in curved microfluidic channels. Biomicrofluidics 2013, 7. [Google Scholar] [CrossRef] [PubMed]
- Warkiani, M.E.; Guan, G.; Luan, K.B.; Lee, W.C.; Bhagat, A.A.S.; Kant Chaudhuri, P.; Tan, D.S.-W.; Lim, W.T.; Lee, S.C.; Chen, P.C.Y.; et al. Slanted spiral microfluidics for the ultra-fast, label-free isolation of circulating tumor cells. Lab Chip 2014, 14, 128–137. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.-T.; Amstislavskaya, T.G.; Chen, G.-H.; Chang, H.-H.; Chen, Y.-H.; Jen, C.-P. Selectively concentrating cervical carconoma cells from rare blood cells utilizing dielectrophoresis with circular ito electrodes in stepping electric fields. J. Med. Biol. Eng. 2012, 33, 51–59. [Google Scholar] [CrossRef]
- Moon, H.S.; Kwon, K.; Kim, S.I.; Han, H.; Sohn, J.; Lee, S.; Jung, H.I. Continuous separation of breast cancer cells from blood samples using multi-orifice flow fractionation (moff) and dielectrophoresis (dep). Lab Chip 2011, 11, 1118–1125. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Ang, R.R.; Duffy, S.P.; Bazov, J.; Chi, K.N.; Black, P.C.; Ma, H. Morphological differences between circulating tumor cells from prostate cancer patients and cultured prostate cancer cells. PLoS ONE 2014, 9, e85264. [Google Scholar] [CrossRef] [PubMed]
- Mulhall, H.J.; Labeed, F.H.; Kazmi, B.; Costea, D.E.; Hughes, M.P.; Lewis, M.P. Cancer, pre-cancer and normal oral cells distinguished by dielectrophoresis. Anal. Bioanal. Chem. 2011, 401, 2455–2463. [Google Scholar] [CrossRef] [PubMed]
- Broche, L.M.; Bhadal, N.; Lewis, M.P.; Porter, S.; Hughes, M.P.; Labeed, F.H. Early detection of oral cancer—Is dielectrophoresis the answer? Oral Oncol. 2007, 43, 199–203. [Google Scholar] [CrossRef] [PubMed]
- Fabbri, F.; Carloni, S.; Zoli, W.; Ulivi, P.; Gallerani, G.; Fici, P.; Chiadini, E.; Passardi, A.; Frassineti, G.L.; Ragazzini, A.; et al. Detection and recovery of circulating colon cancer cells using a dielectrophoresis-based device: Kras mutation status in pure CTCs. Cancer Lett. 2013, 335, 225–231. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Liu, H.; Bander, N.H.; Kirby, B.J. Enrichment of prostate cancer cells from blood cells with a hybrid dielectrophoresis and immunocapture microfluidic system. Biomed. Microdevices 2013, 15, 941–948. [Google Scholar] [CrossRef] [PubMed]
- Vykoukal, D.M.; Gascoyne, P.R.; Vykoukal, J. Dielectric characterization of complete mononuclear and polymorphonuclear blood cell subpopulations for label-free discrimination. Integr. Biol. 2009, 1, 477–484. [Google Scholar] [CrossRef] [PubMed]
- Leu, T.-S.; Liao, Z.-F. Separating plasma and blood cells by dielectrophoresis in microfluidic chips. Int. J. Mod. Phys. Conf. Ser. 2012, 19, 185–189. [Google Scholar] [CrossRef]
- Toner, M.; Irimia, D. Blood-on-a-chip. Annu. Rev. Biomed. Eng. 2008, 7, 77–103. [Google Scholar] [CrossRef] [PubMed]
- Gascoyne, P.R.C.; Noshari, J.; Anderson, T.J.; Becker, F.F. Isolation of rare cells from cell mixtures by dielectrophoresis. Electrophoresis 2009, 30, 1388–1398. [Google Scholar] [CrossRef] [PubMed]
- Shim, S.; Gascoyne, P.; Noshari, J.; Hale, K.S. Dynamic physical properties of dissociated tumor cells revealed by dielectrophoretic field-flow fractionation. Integr. Biol. 2011, 3, 850–862. [Google Scholar] [CrossRef] [PubMed]
- Gupta, V.; Jafferji, I.; Garza, M.; Melnikova, V.O.; Hasegawa, D.K.; Pethig, R.; Davis, D.W. Apostream(™), a new dielectrophoretic device for antibody independent isolation and recovery of viable cancer cells from blood. Biomicrofluidics 2012, 6. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.H.; Lawrence, S.M.; Navas, T.; Kinderss, R.J. Characterization of CTCs from peripheral blood specimens of patients (using aposteam instruments). In American Society of Clinical Oncolgy Annual Meeting 2014; American Society of Clinical Oncology: Chicago, IL, USA, 2014. [Google Scholar]
- Gascoyne, P.R.C.; Shim, S. Isolation of circulating tumor cells by dielectrophoresis. Cancers 2014, 6, 545–579. [Google Scholar] [CrossRef] [PubMed]
- Pommer, M.S.; Zhang, Y.; Keerthi, N.; Chen, D.; Thomson, J.A.; Meinhart, C.D.; Soh, H.T. Dielectrophoretic separation of platelets from diluted whole blood in microfluidic channels. Electrophoresis 2008, 29, 1213–1218. [Google Scholar] [CrossRef] [PubMed]
- Liao, S.H.; Chang, C.Y.; Chang, H.C. A capillary dielectrophoretic chip for real-time blood cell separation from a drop of whole blood. Biomicrofluidics 2013, 7. [Google Scholar] [CrossRef] [PubMed]
- Takaori, M. Changes of ph of blood diluted with plasma and plasma substitutes in vitro. Transfusion 1966, 6, 597–599. [Google Scholar] [CrossRef] [PubMed]
- Lynch, E.C. Peripheral blood smear. In Clinical Methods: The History, Physical, and Laboratory Examinations; Walker, H.K., Hall, W.D., Hurst, J.W., Eds.; Butterworths: Boston, MA, USA, 1990. [Google Scholar]
- Gassner, A.L.; Abonnenc, M.; Chen, H.X.; Morandini, J.; Josserand, J.; Rossier, J.S.; Busnel, J.M.; Girault, H.H. Magnetic forces produced by rectangular permanent magnets in static microsystems. Lab Chip 2009, 9, 2356–2363. [Google Scholar] [CrossRef] [PubMed]
- Tomlinson, M.J.; Tomlinson, S.; Yang, X.B.; Kirkham, J. Cell separation: Terminology and practical considerations. J. Tissue Eng. 2013, 4. [Google Scholar] [CrossRef] [PubMed]
- Essakali, S.; Carney, D.; Westerman, D.; Gambell, P.; Seymour, J.F.; Dobrovic, A. Negative selection of chronic lymphocytic leukaemia cells using a bifunctional rosette-based antibody cocktail. BMC Biotechnol. 2008, 8, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Esmaeilsabzali, H.; Beischlag, T.V.; Cox, M.E.; Parameswaran, A.M.; Park, E.J. Detection and isolation of circulating tumor cells: Principles and methods. Biotechnol. Adv. 2013, 31, 1063–1084. [Google Scholar] [CrossRef] [PubMed]
- Iliescu, C.; Xu, G.; Barbarini, E.; Avram, M.; Avram, A. Microfluidic device for continuous magnetophoretic separation of white blood cells. Microsyst. Technol. 2008, 15, 1157–1162. [Google Scholar] [CrossRef]
- Shen, F.; Hwang, H.; Hahn, Y.K.; Park, J.-K. Label-free cell separation using a tunable magnetophoretic repulsion force. Anal. Chem. 2012, 84, 3075–3081. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.; Han, K.-H. Lateral-driven continuous magnetophoretic separation of blood cells. Appl. Phys. Lett. 2008, 93. [Google Scholar] [CrossRef]
- Chen, J.; Abdelgawad, M.; Yu, L.; Shakiba, N.; Chien, W.-Y.; Lu, Z.; Geddie, W.R.; Jewett, M.A.S.; Sun, Y. Electrodeformation for single cell mechanical characterization. J. Micromech. Microeng. 2011, 21. [Google Scholar] [CrossRef]
- Furiani, E.P. Magnetophoretic separation of blood cells at microscale. J. Appl. Phys. 2007, 40, 1313. [Google Scholar]
- Baccelli, I.; Schneeweiss, A.; Riethdorf, S.; Stenzinger, A.; Schillert, A.; Vogel, V.; Klein, C.; Saini, M.; Bauerle, T.; Wallwiener, M.; et al. Identification of a population of blood circulating tumor cells from breast cancer patients that initiates metastasis in a xenograft assay. Nat. Biotechnol. 2013, 31, 539–544. [Google Scholar] [CrossRef] [PubMed]
- Krawczyk, N.; Banys, M.; Hartkopf, A.; Hagenbeck, C.; Melcher, C.; Fehm, T. Circulating tumour cells in breast cancer. Ecancermedicalscience 2013, 7, 352. [Google Scholar] [PubMed]
- Furtado, P.; Lima, M.V.A.; Nogueira, C.; Franco, M.; Tavora, F. Review of small cell carcinomas of the prostate. Prostate Cancer 2011, 2011. [Google Scholar] [CrossRef] [PubMed]
- Newton, M.R.; Phillips, S.; Chang, S.S.; Clark, P.E.; Cookson, M.S.; Davis, R.; Fowke, J.H.; Herrell, S.D.; Baumgartner, R.; Chan, R.; et al. Smaller prostate size predicts high grade prostate cancer at final pathology. J. Urol. 2010, 184, 930–937. [Google Scholar] [CrossRef] [PubMed]
- Zagoria, R.J. Genitourinary Radiology: The Requisites; Mosby: Philadelphia, PA, USA, 2004. [Google Scholar]
- Elblbesy, M.A. Effect of static magnetic field on erythrocytes characterizations. J. Biomed. Sci. Eng. 2010, 3, 300–303. [Google Scholar] [CrossRef]
- Chen, P.; Huang, Y.Y.; Hoshino, K.; Zhang, J.X. Microscale magnetic field modulation for enhanced capture and distribution of rare circulating tumor cells. Sci. Rep. 2015, 5, 8745. [Google Scholar] [CrossRef] [PubMed]
- Albrecht, M.; Furubayashi, T.; Przybylski, M.; Korecki, J.; Gradman, U. Magnetic step anisotropies. J. Magn. Magn. Mater. 1992, 113, 207–220. [Google Scholar] [CrossRef]
- Emerson, D.R.; Cieslicki, K.; Gu, X.; Barber, R.W. Biomimetic design of microfluidic manifolds based on a generalised Murray’s law. Lab Chip 2006, 6, 447–454. [Google Scholar] [CrossRef] [PubMed]
- Lee, A.M.; Tormoen, G.W.; Kanso, E.; McCarty, O.J.; Newton, P.K. Modeling and simulation of procoagulant circulating tumor cells in flow. Front. Oncol. 2012, 2, 108. [Google Scholar] [CrossRef] [PubMed]
- Low, W.S.; Kadri, N.A.; Wan Abas, W.A.B.B. Computational fluid dynamics modelling of microfluidic channel for dielectrophoretic biomems application. Sci. World J. 2014, 2014, 11. [Google Scholar] [CrossRef] [PubMed]
- Berthier, E.; Young, E.W.K.; Beebe, D. Engineers are from pdms-land, biologists are from polystyrenia. Lab Chip 2012, 12, 1224–1237. [Google Scholar] [CrossRef] [PubMed]
- Mortensen, N.A.; Okkels, F.; Bruus, H. Reexamination of hagen-poiseuille flow: Shape dependence of the hydraulic resistance in microchannels. Phys. Rev. E 2005, 71. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.; Chuncheng, Z.; Peng, Z.; Deyi, Z. Optimization of turn geometries in microfluidic channels. In Proceedings of the 2005 International Conference on MEMS, NANO and Smart Systems, Banff, AB, Canada, 24–27 July 2005; pp. 32–35.
- Green, J.V.; Kniazeva, T.; Abedi, M.; Sokhey, D.S.; Taslim, M.E.; Murthy, S.K. Effect of channel geometry on cell adhesion in microfluidic devices. Lab Chip 2009, 9, 677–685. [Google Scholar] [CrossRef] [PubMed]
- Peeters, F.M.; Jo, D.B. Hybrid magnetic-semiconductor nanostructures. In Nanostructured Materials and Nanotechnology; Nalwa, H.S., Ed.; AcademicPress: San Diego, CA, USA, 2002; pp. 247–328. [Google Scholar]
- Issa, D.; Albeldawi, M.; Lopez, R.; Alkhouri, N. Hematocrit levels and red blood cell indices in patients with nonalcoholic fatty liver disease. Eur. J. Gastroenterol. Hepatol. 2014, 26, 363–364. [Google Scholar] [CrossRef] [PubMed]
- Guldiken, R.; Jo, M.C.; Gallant, N.D.; Demirci, U.; Zhe, J. Sheathless size-based acoustic particle separation. Sensors 2012, 12, 905–922. [Google Scholar] [CrossRef] [PubMed]

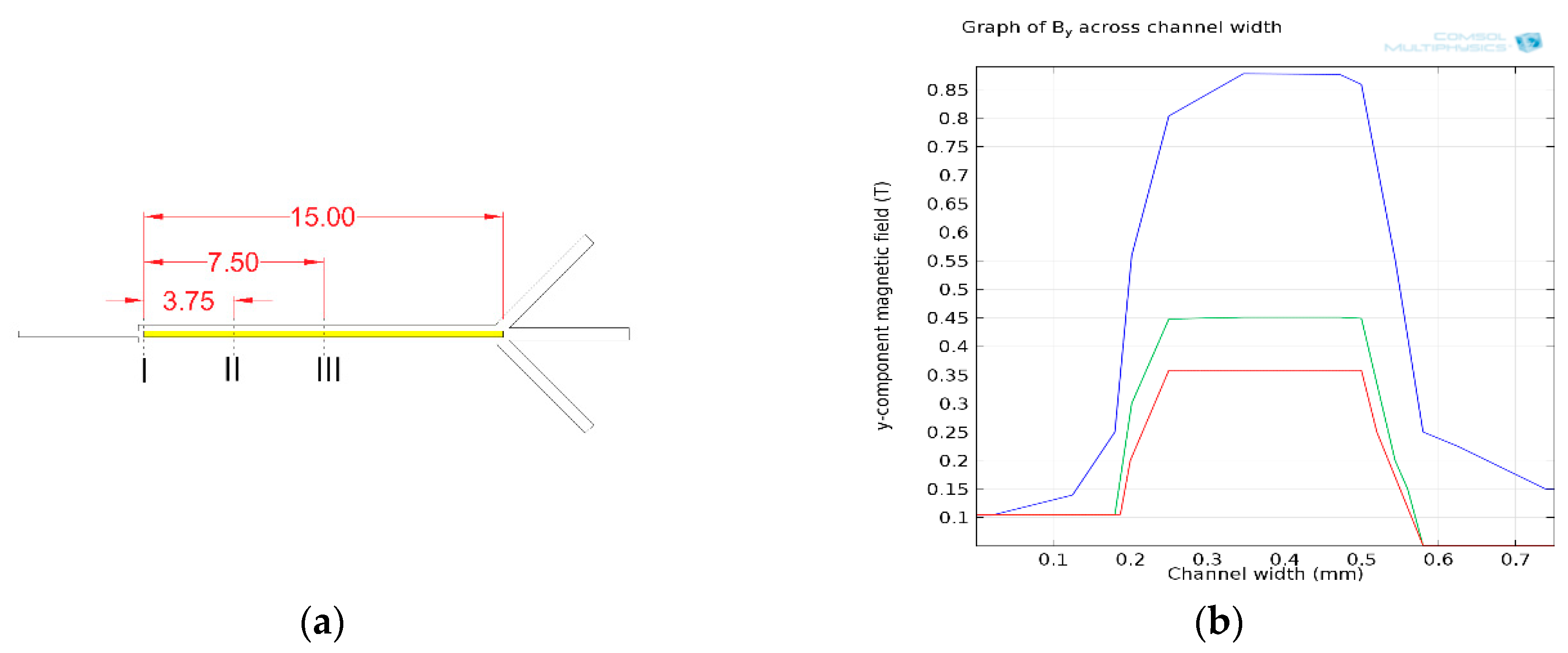
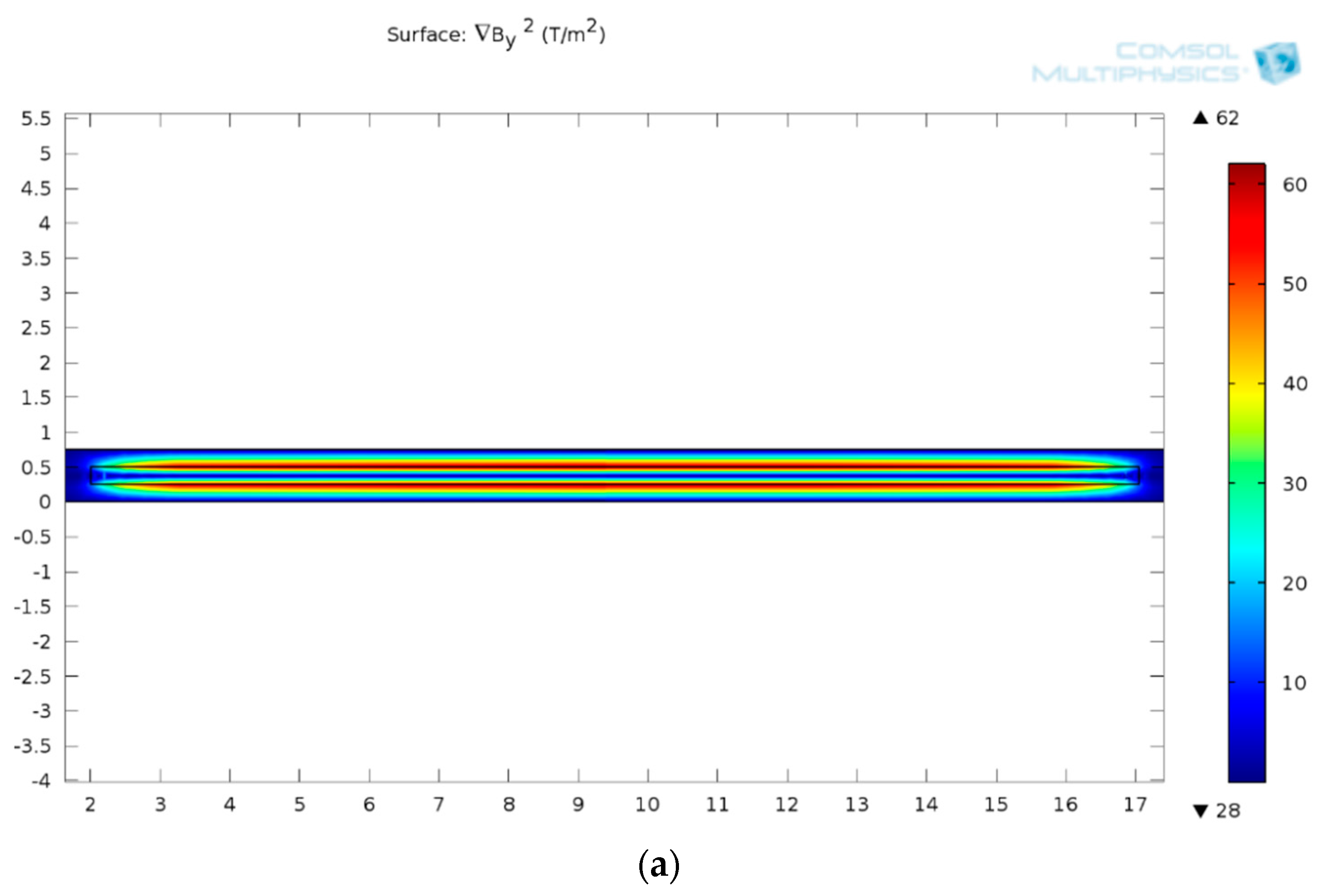
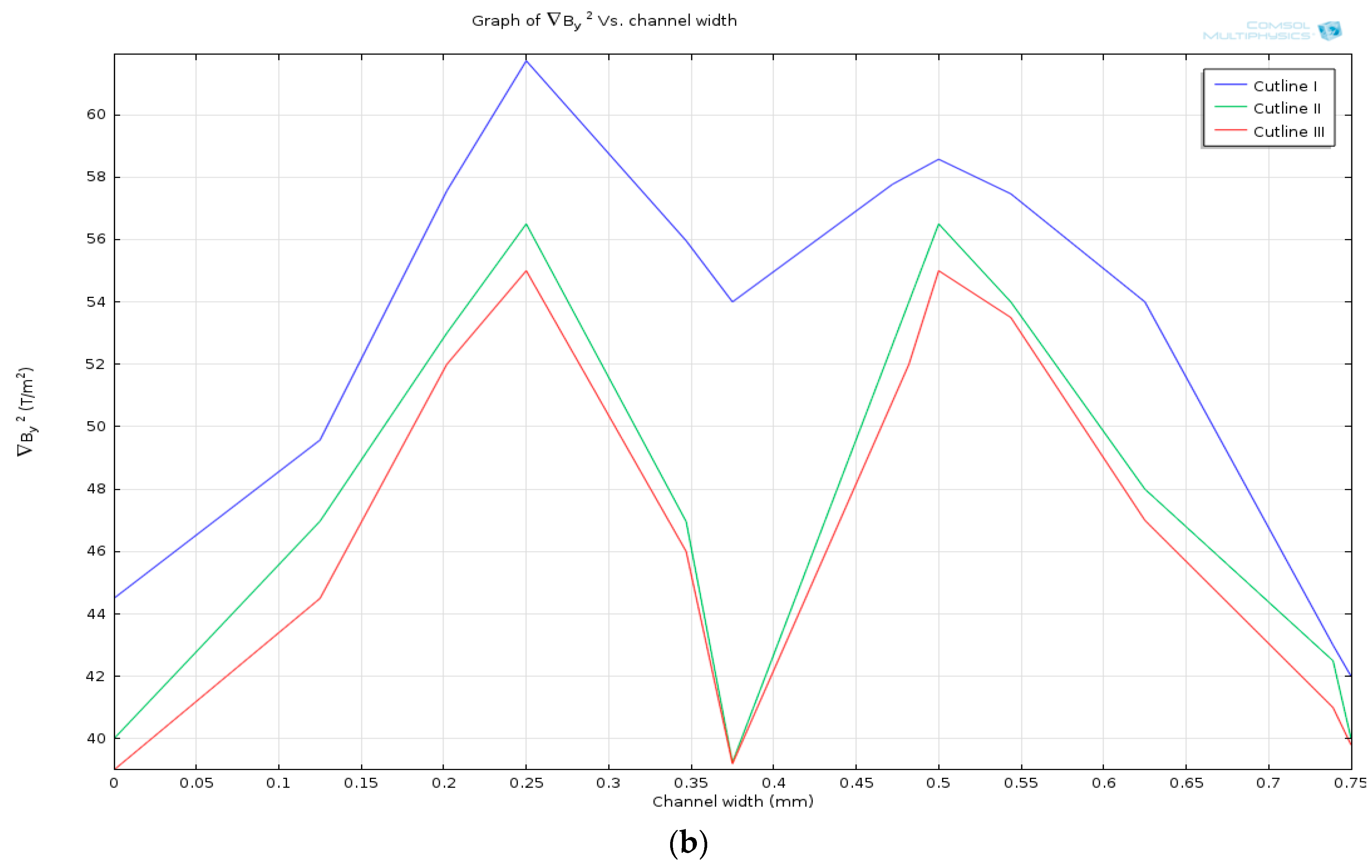
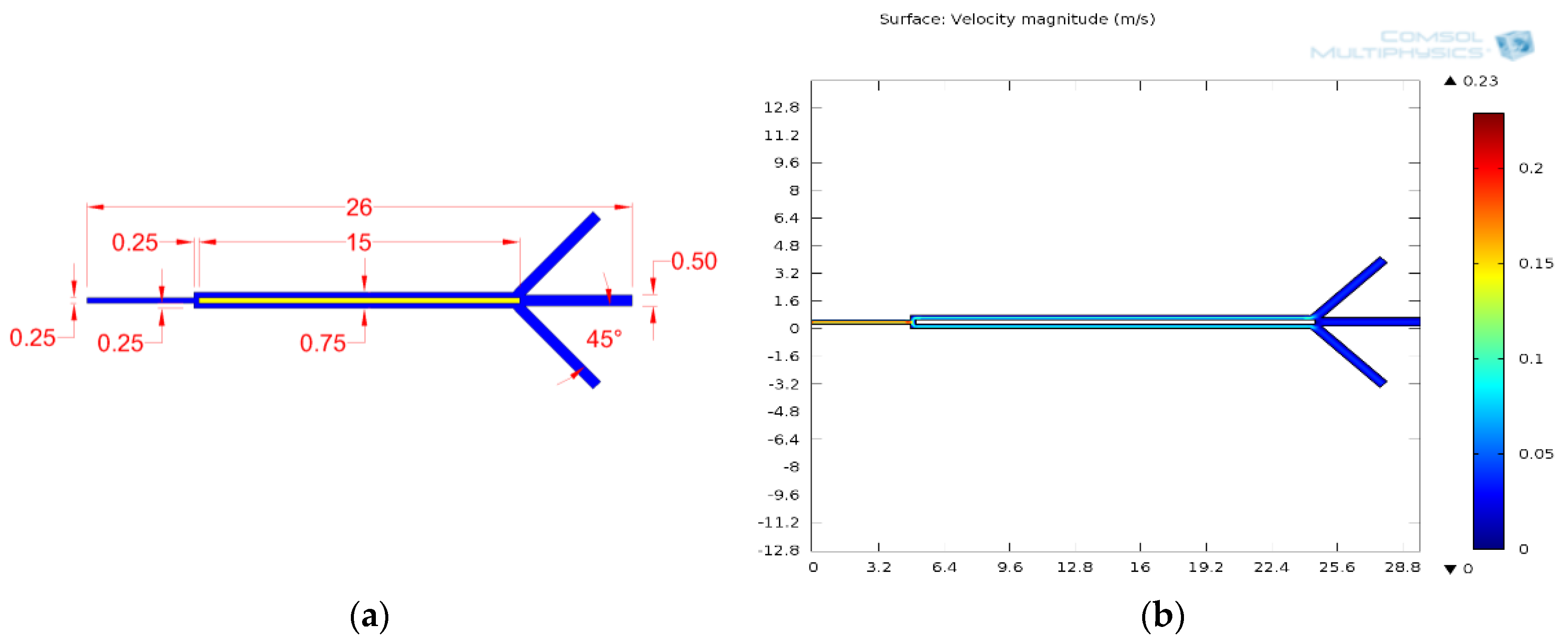

| Cell Type | Mean Radius, r | Magnetic Susceptibility, χcell | Electrical Properties | |
|---|---|---|---|---|
| σcytoplasm (S/m) | εcytoplasm | |||
| Red blood cell (RBC) | 4 | −3.69 × 10−6 | 0.52 | 57 |
| White blood cell (WBC) | 7 | −9.9 × 10−6 | 0.76 | 150.9 |
| Human breast cancer MDA-231 | 20 | −9.5143 × 10−6 | 0.62 | 52 |
| Human prostate cancer HeLa | 7.36 | −9.4966 × 10−6 | 0.21 | 52 |
| Platelet | 2 | −9.2 × 10−6 | 0.25 | 1 × 10−7 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Low, W.S.; Kadri, N.A. Computational Analysis of Enhanced Circulating Tumour Cell (CTC) Separation in a Microfluidic System with an Integrated Dielectrophoretic-Magnetophorectic (DEP-MAP) Technique. Chemosensors 2016, 4, 14. https://doi.org/10.3390/chemosensors4030014
Low WS, Kadri NA. Computational Analysis of Enhanced Circulating Tumour Cell (CTC) Separation in a Microfluidic System with an Integrated Dielectrophoretic-Magnetophorectic (DEP-MAP) Technique. Chemosensors. 2016; 4(3):14. https://doi.org/10.3390/chemosensors4030014
Chicago/Turabian StyleLow, Wan Shi, and Nahrizul Adib Kadri. 2016. "Computational Analysis of Enhanced Circulating Tumour Cell (CTC) Separation in a Microfluidic System with an Integrated Dielectrophoretic-Magnetophorectic (DEP-MAP) Technique" Chemosensors 4, no. 3: 14. https://doi.org/10.3390/chemosensors4030014
APA StyleLow, W. S., & Kadri, N. A. (2016). Computational Analysis of Enhanced Circulating Tumour Cell (CTC) Separation in a Microfluidic System with an Integrated Dielectrophoretic-Magnetophorectic (DEP-MAP) Technique. Chemosensors, 4(3), 14. https://doi.org/10.3390/chemosensors4030014






