Author Contributions
The contributions of individual authors to this study and manuscript are as follows: methodology, Y.C. and T.S.; software, statistical analysis, and data validation, T.S.; formal analysis, Y.C. and T.Z.; investigation, K.S.; resources, D.C.; data curation, T.S.; writing—original draft preparation, Y.C.; writing—review and editing, W.X., W.Z. and Y.C. All authors have read and agreed to the published version of the manuscript.
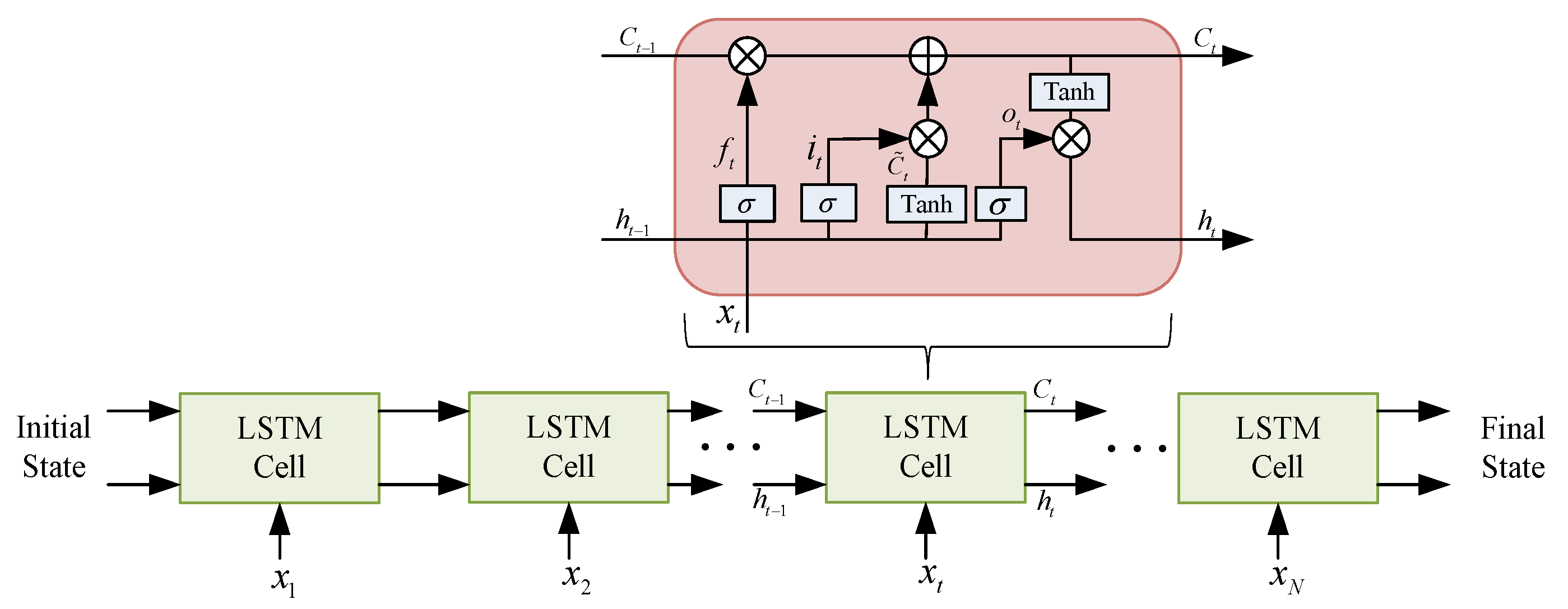
Figure 1.
The structure of a standard LSTM network.
Figure 1.
The structure of a standard LSTM network.
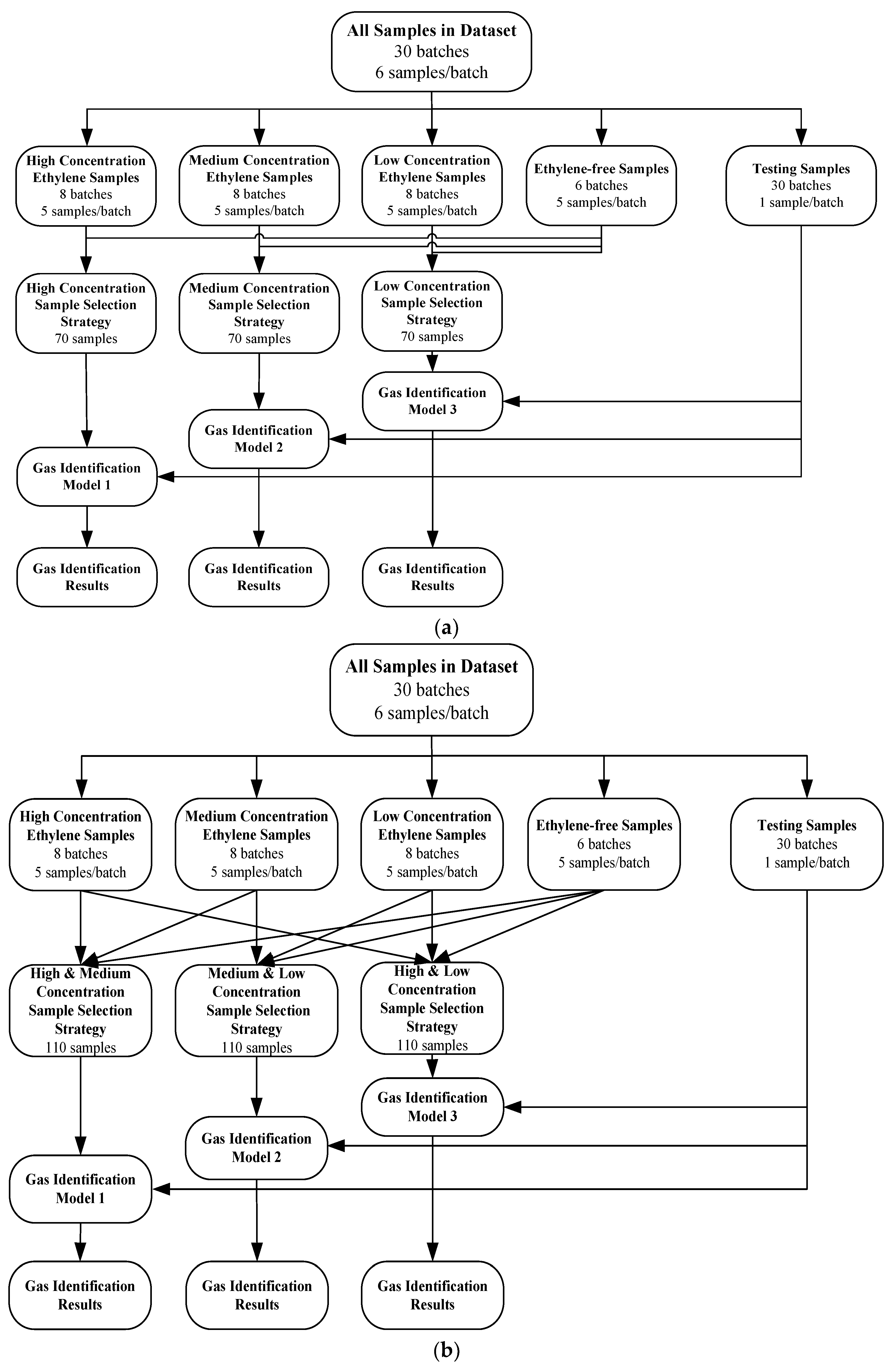
Figure 4.
Flow chart of the proposed qualitative and quantitative analysis strategy. (a) The data preprocessing and feature extraction performed to create the sample feature set. (b) The modeling process of the WOA-LSTM model and PSO-LSSVM model.
Figure 4.
Flow chart of the proposed qualitative and quantitative analysis strategy. (a) The data preprocessing and feature extraction performed to create the sample feature set. (b) The modeling process of the WOA-LSTM model and PSO-LSSVM model.
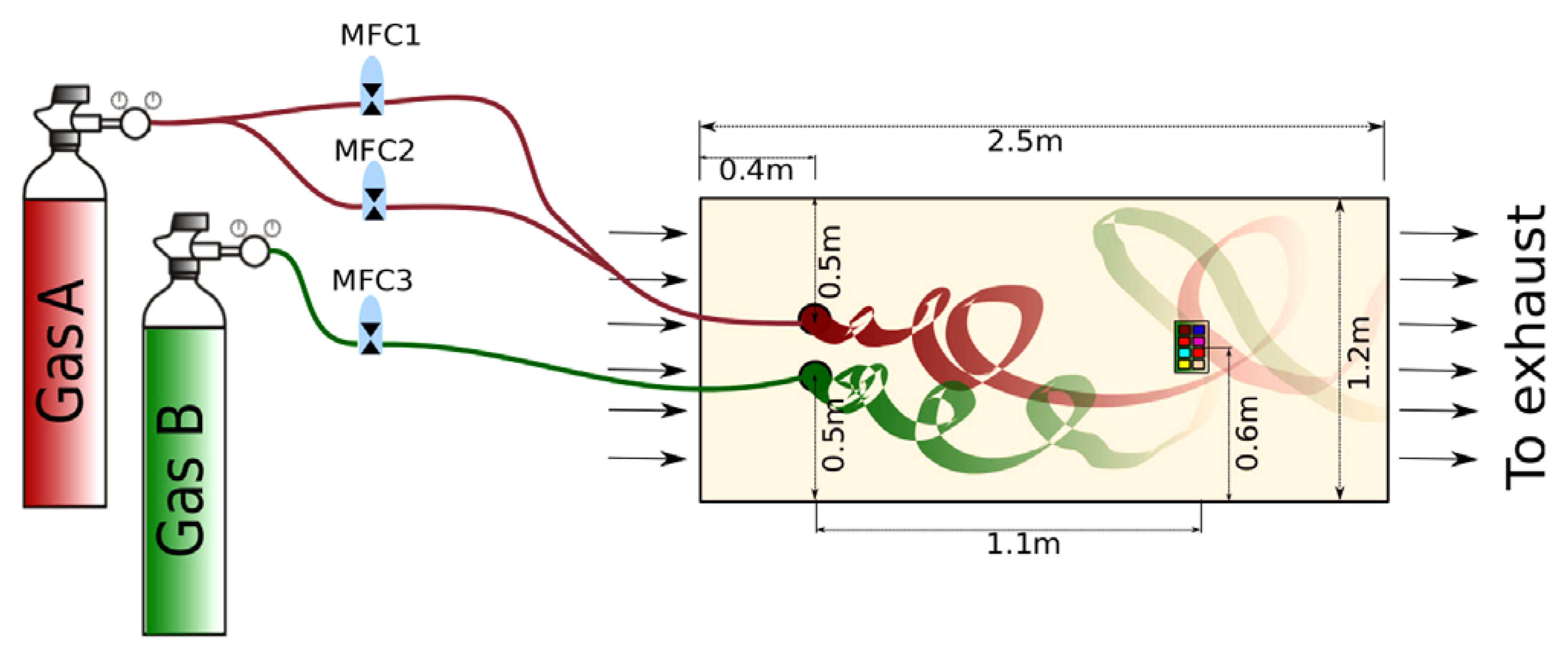
Figure 5.
Schematic diagram of the experimental setup of the public dataset used in this paper. The wind tunnel includes two gas sources that generate two independent gas plumes. The facility collected sensor responses when placed in a turbulent environment [
14].
Figure 5.
Schematic diagram of the experimental setup of the public dataset used in this paper. The wind tunnel includes two gas sources that generate two independent gas plumes. The facility collected sensor responses when placed in a turbulent environment [
14].
Figure 6.
Response curves of ethylene and carbon monoxide gas mixtures.
Figure 6.
Response curves of ethylene and carbon monoxide gas mixtures.
Figure 7.
Two different training sample selection strategies for identifying a certain gas component in the gas mixtures. (a) Single-concentration level sample selection strategy; (b) compound-concentration level sample selection strategy.
Figure 7.
Two different training sample selection strategies for identifying a certain gas component in the gas mixtures. (a) Single-concentration level sample selection strategy; (b) compound-concentration level sample selection strategy.
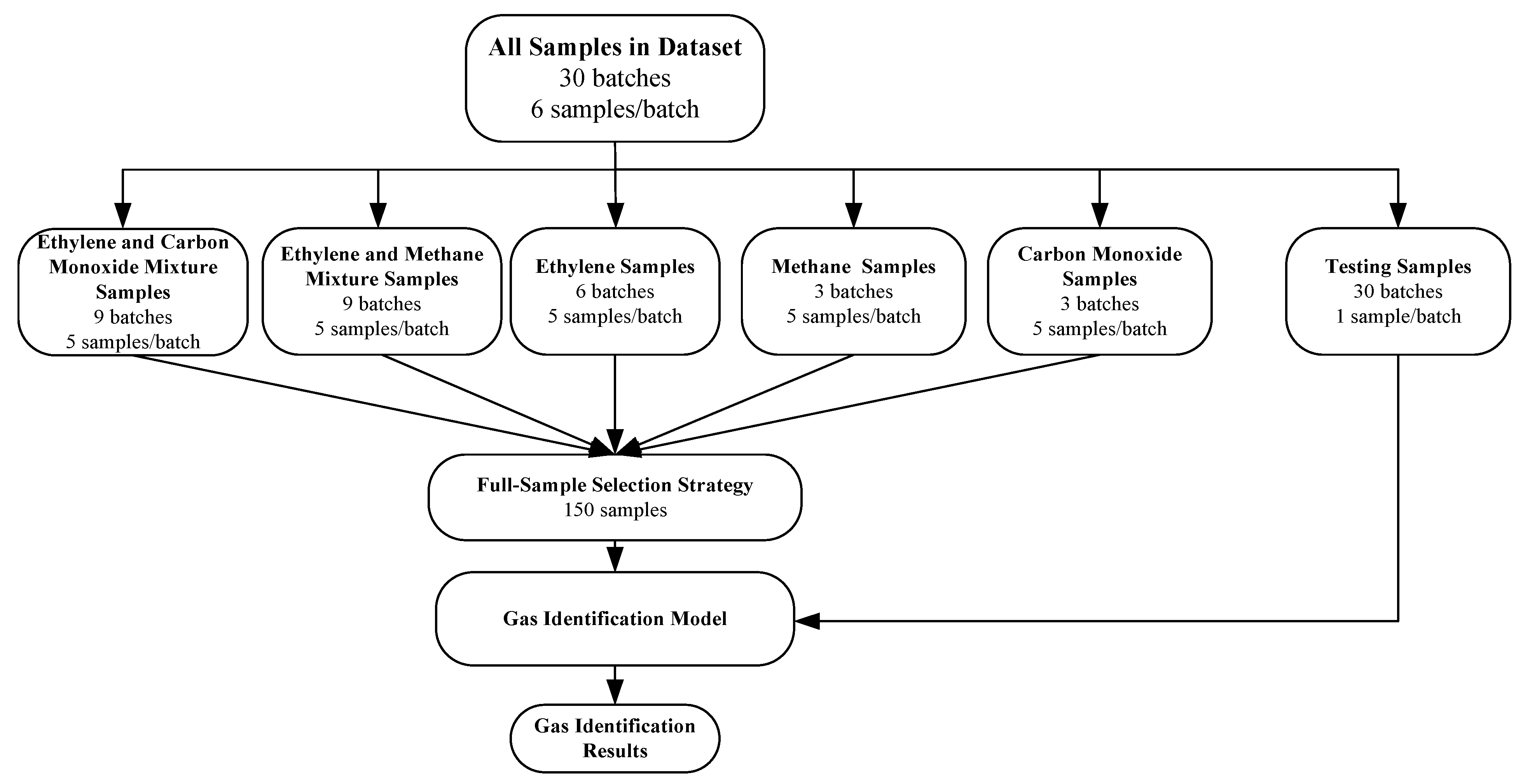
Figure 8.
Full-sample selection strategy for gas mixture identification.
Figure 8.
Full-sample selection strategy for gas mixture identification.
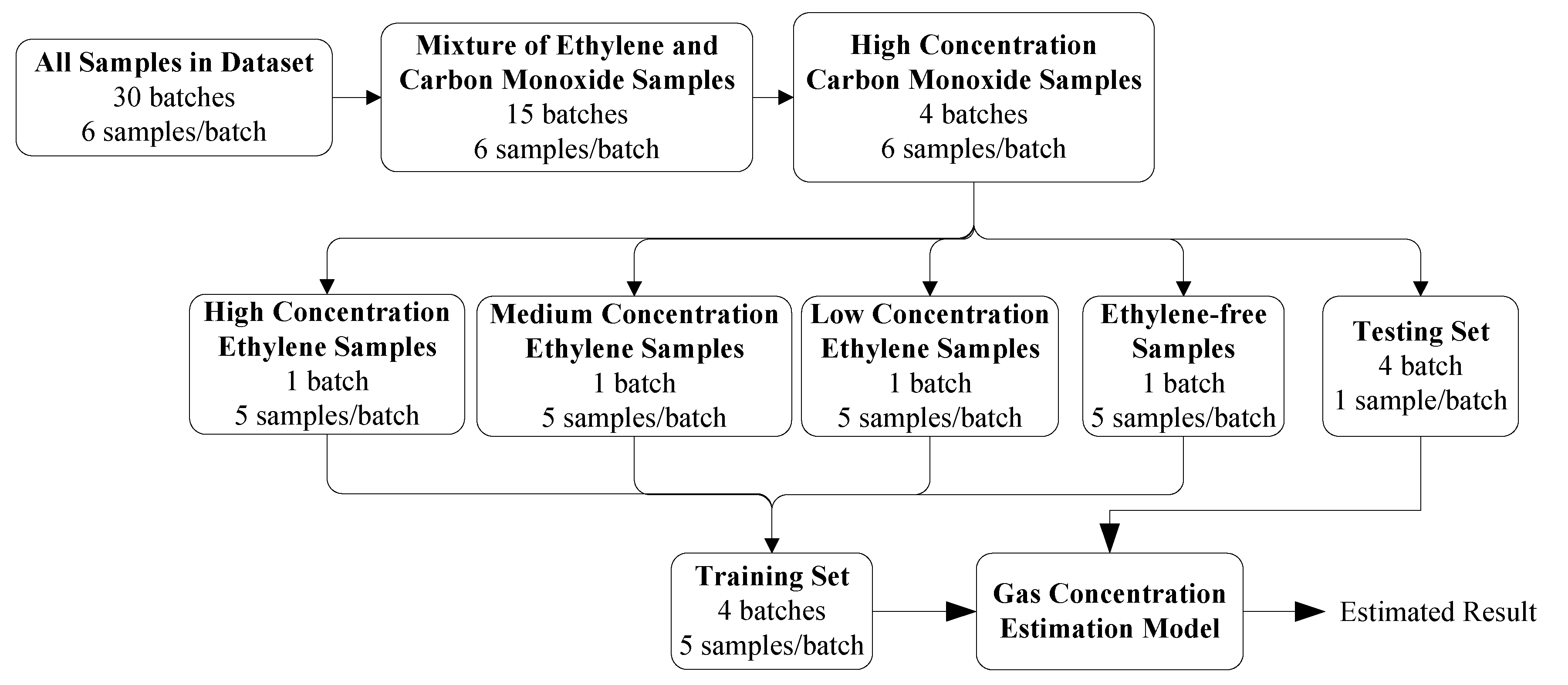
Figure 9.
Sample selection strategy for ethylene as a target gas under the conditions of high-concentration carbon monoxide as a background gas.
Figure 9.
Sample selection strategy for ethylene as a target gas under the conditions of high-concentration carbon monoxide as a background gas.
Figure 10.
Full-sample selection strategy for estimating ethylene concentration.
Figure 10.
Full-sample selection strategy for estimating ethylene concentration.
Figure 11.
Predicted results of ethylene gas concentration using the PSO-LSSVM method under the condition of a high concentration of carbon monoxide as the background gas.
Figure 11.
Predicted results of ethylene gas concentration using the PSO-LSSVM method under the condition of a high concentration of carbon monoxide as the background gas.
Figure 12.
Box plots of ethylene concentration prediction errors under the condition of a high concentration of carbon monoxide as the background gas. (a) RMSE; (b) MAPE.
Figure 12.
Box plots of ethylene concentration prediction errors under the condition of a high concentration of carbon monoxide as the background gas. (a) RMSE; (b) MAPE.
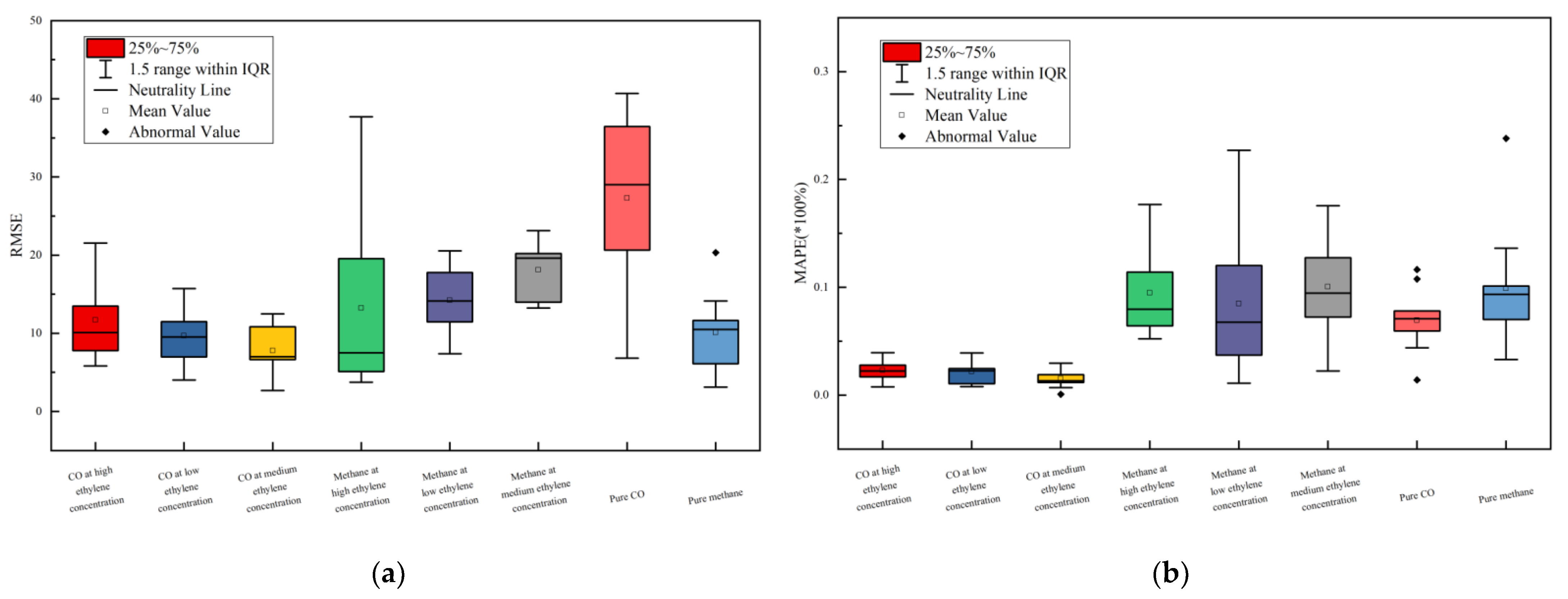
Figure 13.
Box plots of carbon monoxide and methane concentration prediction errors under the condition of ethylene as the background gas. (a) RMSE; (b) MAPE.
Figure 13.
Box plots of carbon monoxide and methane concentration prediction errors under the condition of ethylene as the background gas. (a) RMSE; (b) MAPE.
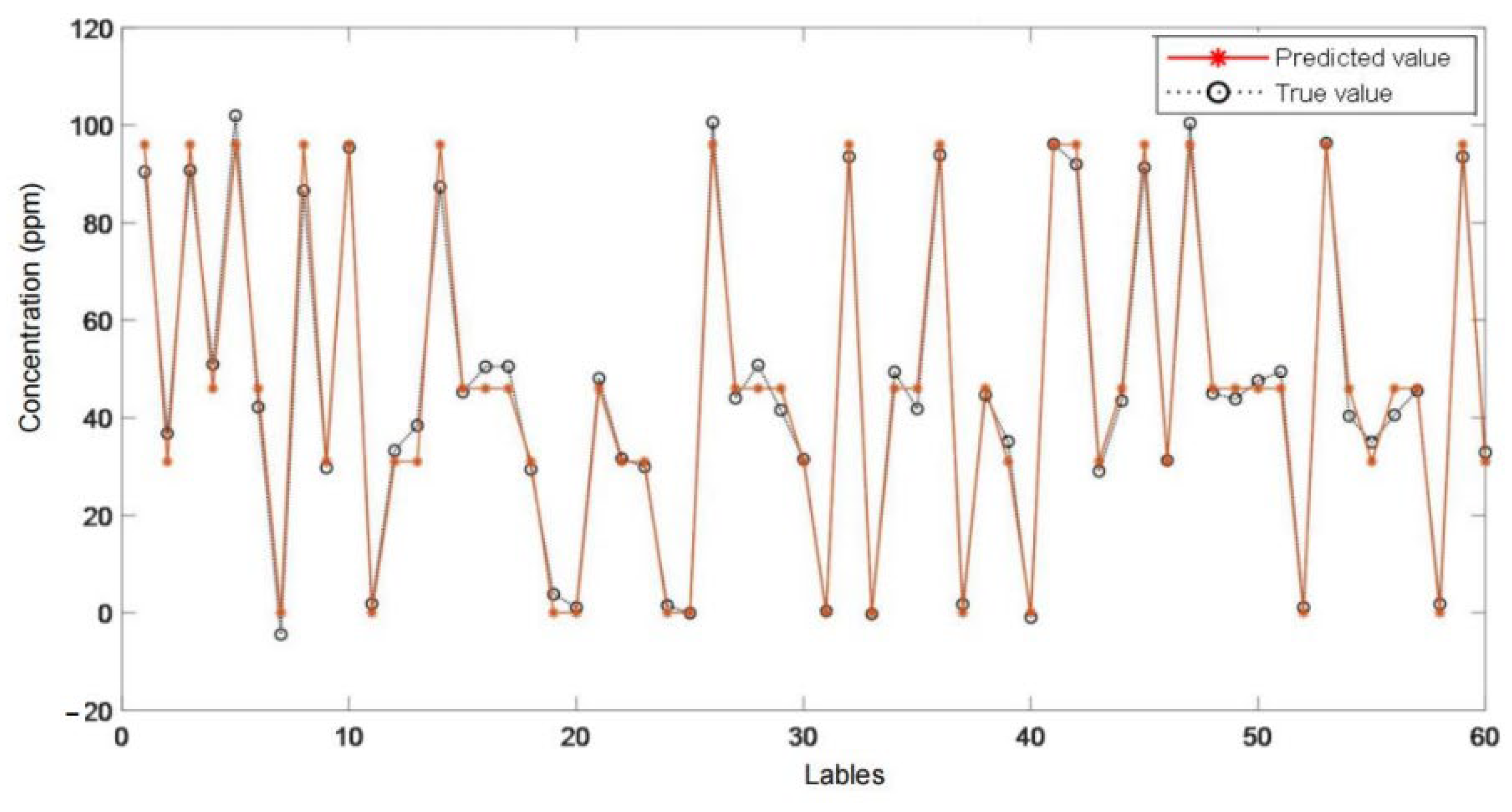
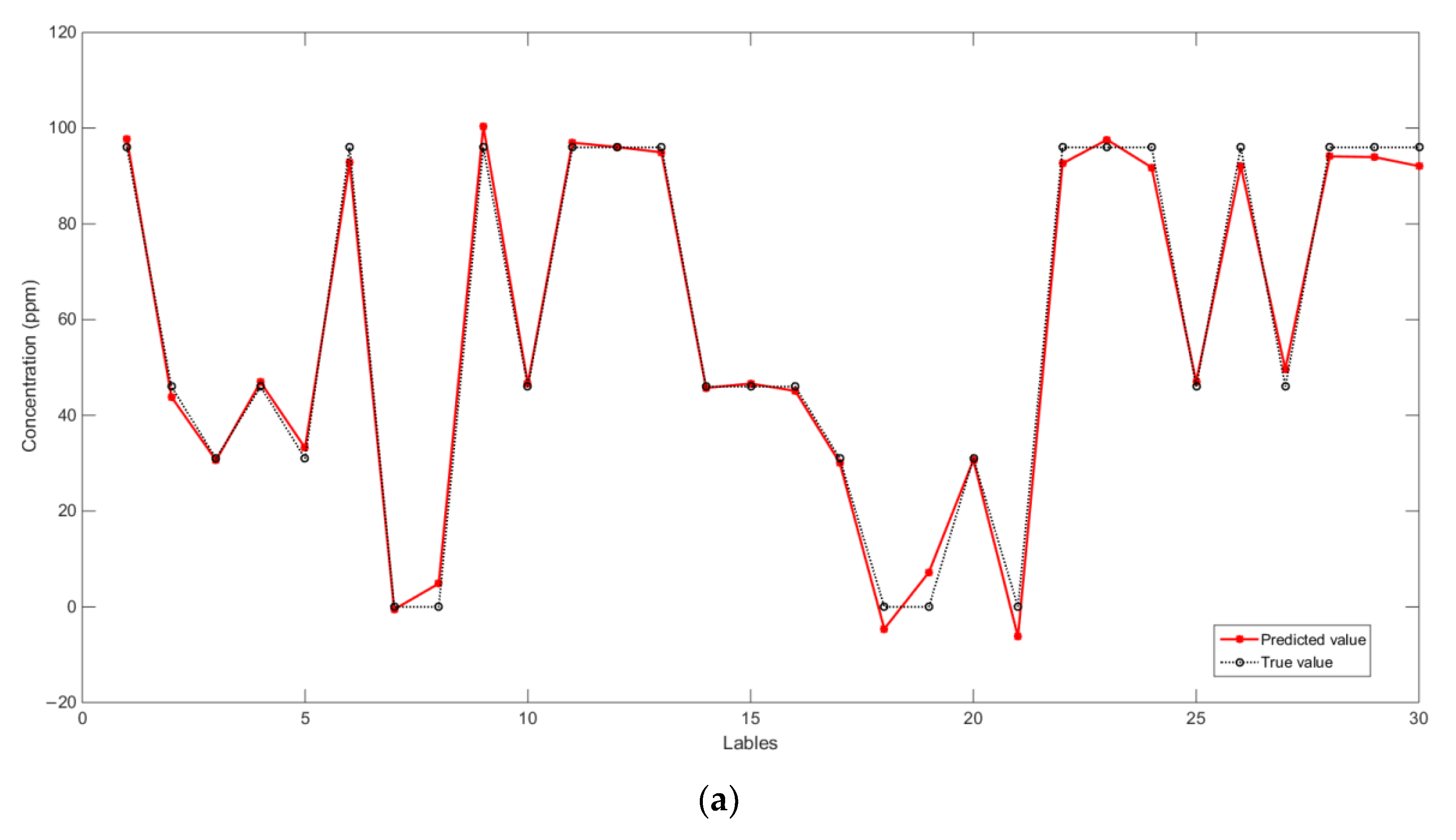
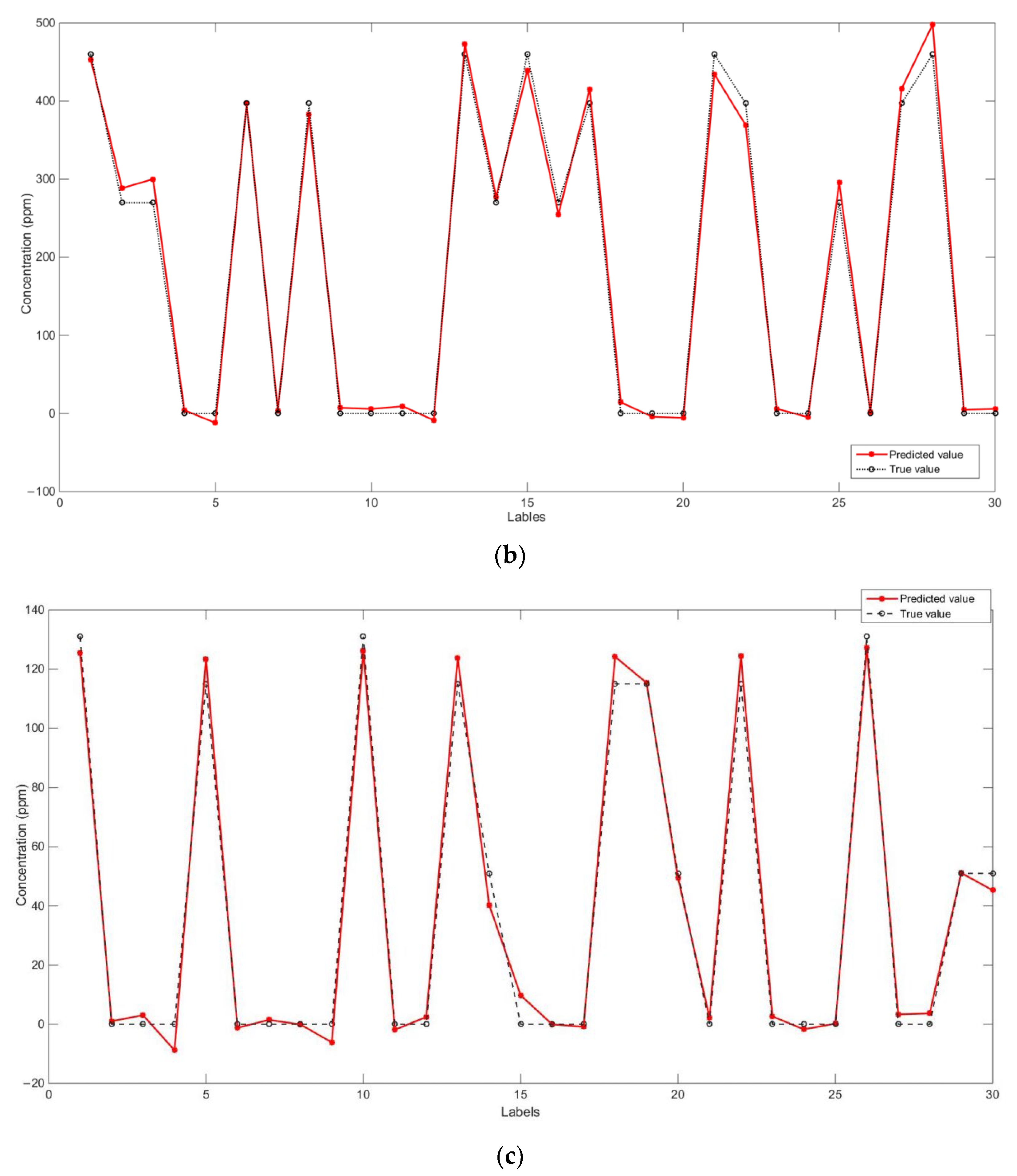
Figure 14.
Prediction results for three gas concentrations under the full-sample selection strategy. (a) Comparison of predicted and real ethylene concentration; (b) comparison of predicted and true values of carbon monoxide concentration; (c) comparison of predicted and true methane concentrations.
Figure 14.
Prediction results for three gas concentrations under the full-sample selection strategy. (a) Comparison of predicted and real ethylene concentration; (b) comparison of predicted and true values of carbon monoxide concentration; (c) comparison of predicted and true methane concentrations.
Table 1.
Details of the eight MOS gas sensors assembled on the gas sensor array.
Table 1.
Details of the eight MOS gas sensors assembled on the gas sensor array.
| Sensor Types | Number of Units | Target Gases |
|---|
| TGS2611 | 1 | CH4 |
| TGS2612 | 1 | CH4, C3H8, C4H10 |
| TGS2610 | 1 | C3H8 |
| TGS2600 | 1 | H2, CO |
| TGS2602 | 2 | NH3, H2S, VOCs |
| TGS2620 | 2 | CO, flammable gas, VOCs |
Table 2.
Average estimated concentrations of the three gases at different flow rates obtained by gas chromatography-mass spectrometry.
Table 2.
Average estimated concentrations of the three gases at different flow rates obtained by gas chromatography-mass spectrometry.
| Volatile Gases | Flow Rate (sccm) | Estimated Concentration (ppm) |
|---|
| Ethylene@2500 ppm | 20 | 96 |
| 14 | 46 |
| 8 | 31 |
Carbon monoxide
@4000 ppm | 200 | 460 |
| 180 | 397 |
| 140 | 270 |
| Methane@1000 ppm | 300 | 131 |
| 200 | 115 |
| 100 | 51 |
Table 3.
Sample distribution in the dataset along with rate of chemical release (in sccm) and corresponding induced gas concentration level (in ppm) in the vicinity of the sensors. In total, 180 measurements were performed. The labels H, M, L, and n indicate high, medium, low, and zero concentrations of the corresponding volatiles, respectively.
Table 3.
Sample distribution in the dataset along with rate of chemical release (in sccm) and corresponding induced gas concentration level (in ppm) in the vicinity of the sensors. In total, 180 measurements were performed. The labels H, M, L, and n indicate high, medium, low, and zero concentrations of the corresponding volatiles, respectively.
| Volatiles | Ethylene@2500 ppm |
|---|
| 20 sccm | 14 sccm | 8 sccm | 0 sccm |
|---|
| H:96 ppm | M:46 ppm | L:31 ppm | n:0 ppm |
|---|
Carbon Monoxide
@4000 ppm | 200 sccm | H: 460 ppm | 6 | 6 | 6 | 6 |
| 140 sccm | M: 397 ppm | 6 | 6 | 6 | 6 |
| 800 sccm | L: 270 ppm | 6 | 6 | 6 | 6 |
| 0 sccm | n: 0 ppm | 6 | 6 | 6 | — |
Methane
@1000 ppm | 300 sccm | H: 131 ppm | 6 | 6 | 6 | 6 |
| 200 sccm | M: 115 ppm | 6 | 6 | 6 | 6 |
| 100 sccm | L: 51 ppm | 6 | 6 | 6 | 6 |
| 0 sccm | n: 0 ppm | 6 | 6 | 6 | — |
Table 4.
Average ethylene gas identification accuracy of WOA-LSTM with the single-concentration level sample selection strategy. The training samples were selected from high-concentration, medium-concentration, or low-concentration ethylene samples.
Table 4.
Average ethylene gas identification accuracy of WOA-LSTM with the single-concentration level sample selection strategy. The training samples were selected from high-concentration, medium-concentration, or low-concentration ethylene samples.
| Sample Selection Strategies | Average Identification Accuracy (%) |
|---|
| High-concentration sample selection strategy | 88.17 ± 6.09 |
| Medium-concentration sample selection strategy | 91.56 ± 3.30 |
| Low-concentration sample selection strategy | 94.40 ± 2.57 |
Table 5.
Average ethylene gas identification accuracy of WOA-LSTM with compound ethylene concentration sample selection strategies. The training samples were selected from high- and low-concentration, medium- and low-concentration, or high- and medium-concentration ethylene samples.
Table 5.
Average ethylene gas identification accuracy of WOA-LSTM with compound ethylene concentration sample selection strategies. The training samples were selected from high- and low-concentration, medium- and low-concentration, or high- and medium-concentration ethylene samples.
| Sample Selection Strategies | Average Identification Accuracy (%) |
|---|
| High- and low-concentration sample selection strategy | 94.00 ± 2.08 |
| Medium- and low-concentration sample selection strategy | 96.39 ± 1.48 |
| High- and medium-concentration sample selection strategy | 93.39 ± 3.22 |
Table 6.
Average identification accuracy of different gas recognition models with compound ethylene concentration sample selection strategies.
Table 6.
Average identification accuracy of different gas recognition models with compound ethylene concentration sample selection strategies.
| Models | SVM | KNN | BP | Softmax | LSTM | WOA-LSTM |
|---|
| Average identification accuracy (%) | 88.93 ± 2.25 | 95.91 ± 1.65 | 86.21 ± 3.17 | 86.70 ± 2.78 | 94.67 ± 1.98 | 96.39 ± 1.48 |
Table 7.
Identification accuracy of WOA-LSTM for different gas components.
Table 7.
Identification accuracy of WOA-LSTM for different gas components.
| Gas Categories | Ethylene and Methane | Ethylene and
Carbon Monoxide | Ethylene | Methane | Carbon Monoxide |
|---|
| Identification accuracy (%) | 95.24 ± 2.91 | 94.97 ± 3.21 | 90.48 ± 2.28 | 95.24 ± 2.51 | 95.24 ± 3.03 |
Table 8.
Average identification accuracy of different gas identification models for multi-gas components with the full-sample selection strategy.
Table 8.
Average identification accuracy of different gas identification models for multi-gas components with the full-sample selection strategy.
| Models | SVM | KNN | BP | Softmax | LSTM | WOA-LSTM |
|---|
| Identification accuracy (%) | 72.2 ± 2.08 | 76.84 ± 3.05 | 84.45 ± 3.43 | 66.7 ± 3.73 | 88.32 ± 2.39 | 94.61 ± 2.74 |
Table 9.
Concentration prediction results for carbon monoxide and methane with ethylene as the background gas.
Table 9.
Concentration prediction results for carbon monoxide and methane with ethylene as the background gas.
| Target Gas | RMSE | MAPE (%) |
|---|
| Ethylene under the background of a high concentration of carbon monoxide | 4.7212 | 5.49 |
| Ethylene under the background of a medium concentration of carbon monoxide | 4.1134 | 5.38 |
| Ethylene under the background of a low concentration of carbon monoxide | 3.0786 | 5.10 |
| Ethylene under the background of a high concentration of methane | 2.8608 | 4.56 |
| Ethylene under the background of a medium concentration of methane | 2.8826 | 4.03 |
| Ethylene under the background of a low concentration of methane | 3.7376 | 4.82 |
| Pure ethylene | 4.3210 | 7.58 |
Table 10.
Concentration prediction results for carbon monoxide and methane with ethylene as the background gas.
Table 10.
Concentration prediction results for carbon monoxide and methane with ethylene as the background gas.
| Target Gas | RMSE | MAPE (%) |
|---|
| Carbon monoxide with high-concentration ethylene as the background gas | 8.3818 | 2.38 |
| Carbon monoxide with medium-concentration ethylene as the background gas | 8.2541 | 2.26 |
| Carbon monoxide with low-concentration ethylene as the background gas | 8.2358 | 2.19 |
| Pure carbon monoxide | 27.3094 | 6.94 |
| Methane with high-concentration ethylene as the background gas | 16.9220 | 9.47 |
| Methane with medium-concentration ethylene as the background gas | 18.4146 | 10.06 |
| Methane with low-concentration ethylene as the background gas | 14.7585 | 8.49 |
| Pure methane | 10.0737 | 9.88 |
Table 11.
Overall prediction effect of the PSO-LSSVM model on turbulent gas mixtures.
Table 11.
Overall prediction effect of the PSO-LSSVM model on turbulent gas mixtures.
| Target Gas | RMSE | MAPE (%) |
|---|
| Ethylene | 3.6736 | 5.28 |
| Methane | 15.0442 | 9.48 |
| Carbon monoxide | 13.0453 | 3.44 |
Table 12.
Concentration prediction results of ethylene gas in mixed gas using different concentration prediction methods.
Table 12.
Concentration prediction results of ethylene gas in mixed gas using different concentration prediction methods.
| Target Gas | RMSE | MAPE (%) |
|---|
| PSO-LSSVM | 3.6736 | 5.28 |
| SVM | 15.0442 | 9.16 |
| LSSVM | 9.941 | 7.61 |
Table 13.
Prediction results for three gas concentrations with the full-sample selection strategy.
Table 13.
Prediction results for three gas concentrations with the full-sample selection strategy.
| Target Gas | RMSE | MAPE (%) |
|---|
| Ethylene | 3.2609 | 4.19 |
| Methane | 3.3391 | 1.29 |
| Carbon monoxide | 5.1919 | 2.58 |
Table 14.
Ethylene concentration prediction results of different algorithms under the full-sample selection strategy.
Table 14.
Ethylene concentration prediction results of different algorithms under the full-sample selection strategy.
| Target Gas | RMSE | MAPE (%) |
|---|
| SVM | 12.8261 | 7.21 |
| LSSVM | 8.2998 | 6.73 |
| PSO-LSSVM | 3.2609 | 4.19 |