Mathematical Contact Tracing Models for the COVID-19 Pandemic: A Systematic Review of the Literature
Abstract
1. Introduction
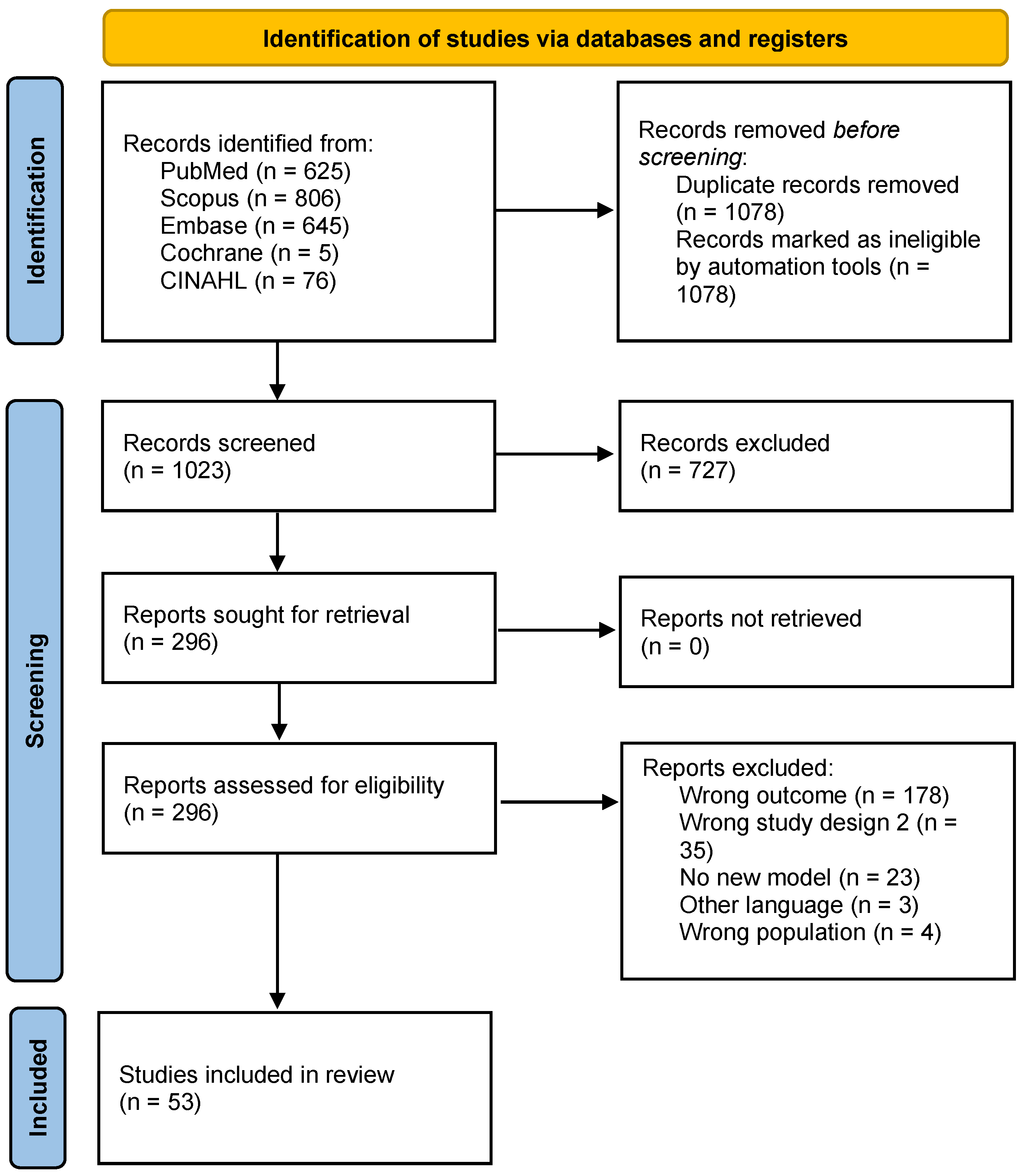
2. Materials and Methods
2.1. Eligibility Criteria
2.2. Search Strategy and Information Source
2.3. Study Selection
2.4. Data Extraction
2.5. Synthesis Methods
2.6. Risk of Bias
3. Results
3.1. Study Characteristics
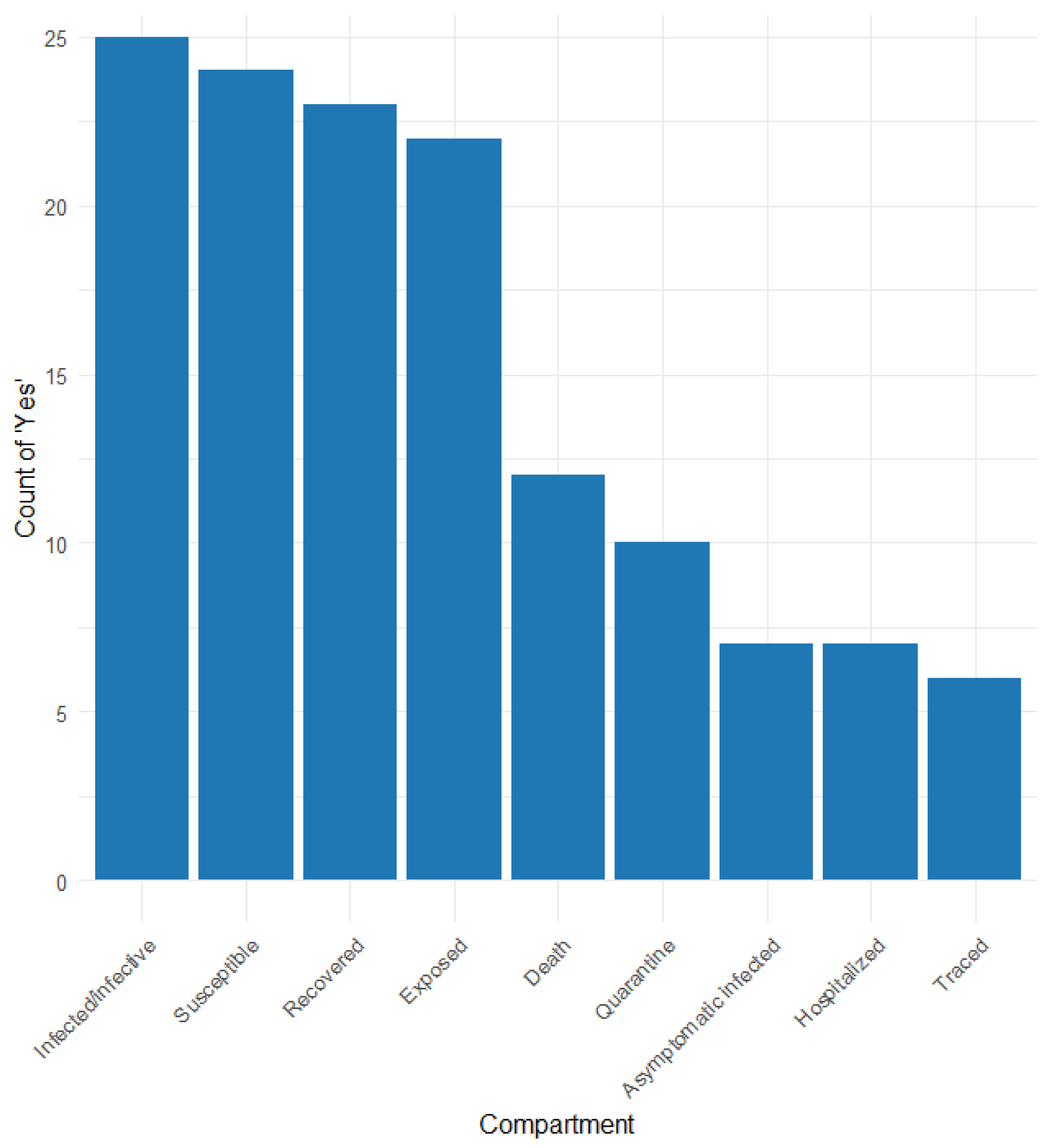
3.2. Ccontact Tracing
3.3. Characteristics of the Models
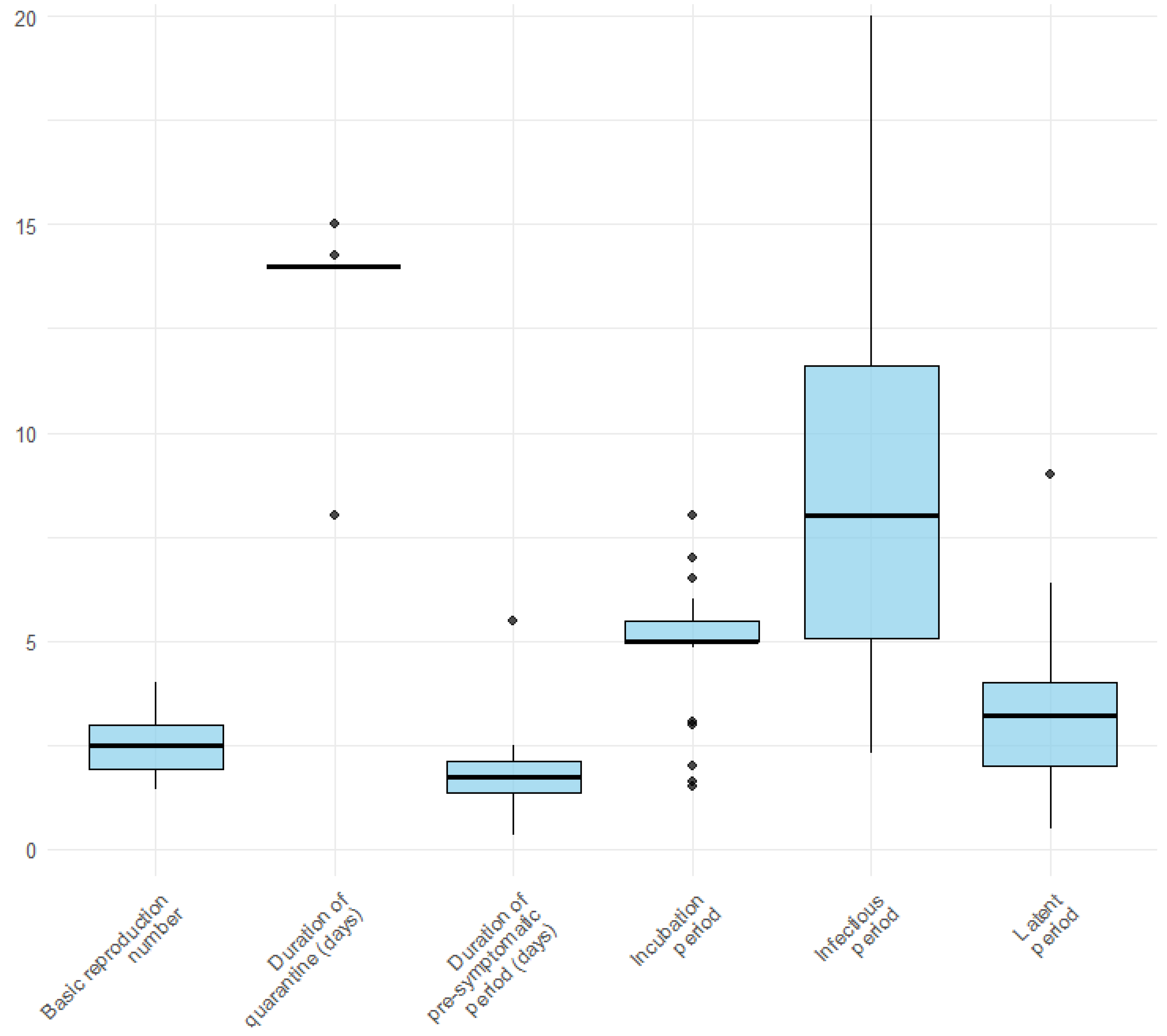
3.4. Infection-Related Parameters
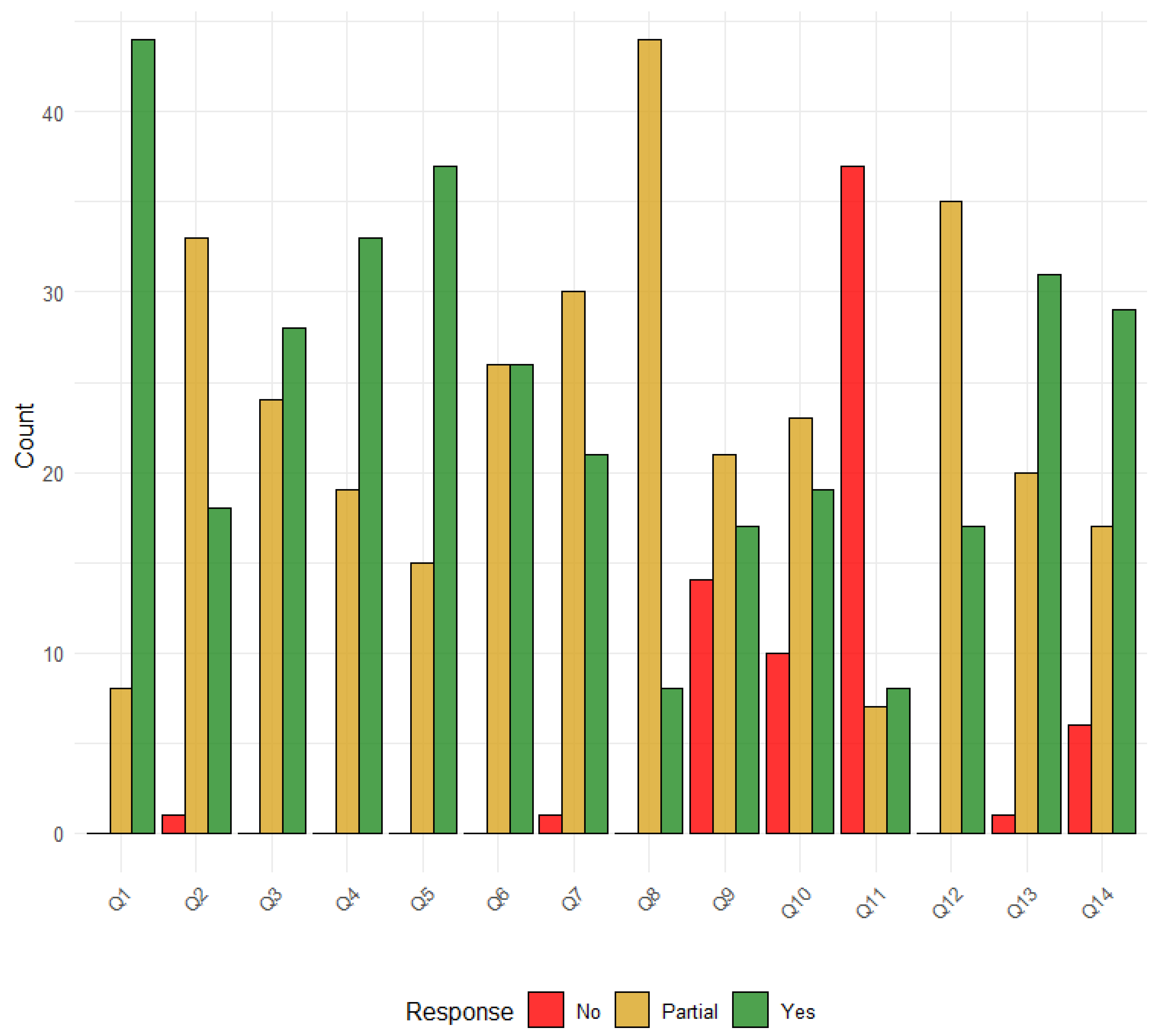
3.5. Reporting Biases
4. Discussion
4.1. Stochastic and Deterministic
4.2. Infection-Related Parameters
4.3. Study Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Search String Strategy for Pubmed
| PUBMED | |
| Concept 1 | (“contact tracing”(MeSH Terms) OR “contact tracing”(Text Word)) |
| AND | |
| Concept 2 | (“modeling” OR “models” OR “model” OR “statistical models” OR “models, theoretical”(MeSH Terms) OR mathematical model(Text Word)) |
| AND | |
| Concept 3 | (“COVID-19” OR “COVID-19”(MeSH Terms) OR “COVID-19 Vaccines” OR “COVID-19 Vaccines”(MeSH Terms) OR “COVID-19 serotherapy” OR “COVID-19 serotherapy”(Supplementary Concept) OR “COVID-19 Nucleic Acid Testing” OR “covid-19 nucleic acid testing”(MeSH Terms) OR “COVID-19 Serological Testing” OR “covid-19 serological testing”(MeSH Terms) OR “COVID-19 Testing” OR “covid-19 testing”(MeSH Terms) OR “SARS-CoV-2” OR “sars-cov-2”(MeSH Terms) OR “Severe Acute Respiratory Syndrome Coronavirus 2” OR “NCOV” OR “2019 NCOV” OR “COVID-19 breakthrough infections” (Supplementary Concept) OR “spike protein, SARS-CoV-2” (Supplementary Concept) OR “COVID-19 vaccine booster shot” (Supplementary Concept) OR “SARS-CoV-2 variants” (Supplementary Concept) OR ((“coronavirus”(MeSH Terms) OR “coronavirus” OR “COV”) AND 2019/11/01(PDAT): 3000/12/31(PDAT))) |
| SCOPUS | |
| Concept 1 | (“contact tracing”) |
| AND | |
| Concept 2 | (“modeling” OR “models” OR “model” OR “statistical models” OR “models, theoretical” OR “mathematical model”) |
| AND | |
| Concept 3 | (“COVID-19” OR “COVID-19 Vaccines” OR “COVID-19 serotherapy” OR “COVID-19 Nucleic Acid Testing” OR “COVID-19 Serological Testing” OR “covid-19 serological testing” OR “COVID-19 Testing” OR “SARS-CoV-2” OR “Severe Acute Respiratory Syndrome Coronavirus 2” OR “NCOV” OR “2019 NCOV” OR “COVID-19 breakthrough infections” OR “spike protein, SARS-CoV-2” OR “COVID-19 vaccine booster shot” OR “SARS-CoV-2 variants” OR “coronavirus” OR “COV”) |
| EMBASE | |
| Concept 1 | (contact tracing.mp. or exp contact examination/) |
| AND | |
| Concept 2 | (modelling OR models OR model OR “statistical models” OR exp “models, theoretical”/ OR statistical models.mp. or exp *statistical model/ OR mathematical models.mp. or exp *mathematical model/) |
| AND | |
| Concept 3 | (COVID-19 OR exp COVID-19/ OR “COVID-19 Vaccines” OR exp “COVID-19 Vaccines”/ OR “COVID-19 serotherapy” OR “COVID-19 Nucleic Acid Testing” OR exp “covid-19 nucleic acid testing”/ OR “COVID-19 Serological Testing” OR exp “covid-19 serological testing”/ OR “COVID-19 Testing” OR exp “covid-19 testing”/ OR SARS-CoV-2 OR exp sars-cov-2/ OR “Severe Acute Respiratory Syndrome Coronavirus 2” OR NCOV OR “2019 NCOV”) |
| Cochrane central | |
| Concept 1 | exp “contact tracing”/ or “contact tracing”.mp.) |
| AND | |
| Concept 2 | ((modelling or models or model or “statistical models”).mp. or exp “models, theoretical”/or statistical models.mp. or exp *statistical model/ or mathematical models.mp. or exp *mathematical model/) |
| AND | |
| Concept 3 | (COVID-19.mp. or exp COVID-19/ or “COVID-19 Vaccines”.mp. or exp “COVID-19 Vaccines”/ or “COVID-19 serotherapy”.mp. or “COVID-19 Nucleic Acid Testing”.mp. or exp “covid-19 nucleic acid testing”/ or “COVID-19 Serological Testing”.mp. or exp “covid-19 serological testing”/ or “COVID-19 Testing”.mp. or exp “covid-19 testing”/ or SARS-CoV-2.mp. or exp sars-cov-2/ or “Severe Acute Respiratory Syndrome Coronavirus 2”.mp. or NCOV.mp. or “2019 NCOV”.mp.) (mp = title, original title, abstract, floating sub-heading word, mesh headings, heading words, keyword) |
| CINAHL | |
| Concept 1 | ((MM “Contact Tracing”) OR “contact tracing”) |
| AND | |
| Concept 2 | (“mathematical models” OR (MH “Models, Statistical”) OR “statistical models” OR “model” OR “modelling” OR “models”) |
| AND | |
| Concept 3 | ((MH “COVID-19”) OR (MH “COVID-19 Testing”) OR (MH “COVID-19 Vaccines”) OR (MH “COVID-19 Pandemic”) OR (MH “SARS-CoV-2”) OR “covid 19”) |
Appendix B
| Author, Year | Outcome |
|---|---|
| Almagor 2020 [53] | Modelling the COVID-19 considering rates of the CT app, different levels of testing capacity, and behavioural factors to assess the impact on the epidemic |
| Amaku 2021 [20] | Assess CT on the number of cases and deaths |
| Ashcroft 2022 [21] | Assess impact of quarantine duration |
| BahaRaja 2022 [22] | Assess CT effect |
| Biala 2022 [23] | Assess CT effect |
| Browne 2022 [24] | Assess CT and social distancing in different scenarios |
| Chen 2021 [25] | Assess testing-CT, non-lockdown social distancing in different scenarios |
| Chiba 2021 [26] | Assess CT apps |
| Chiu 2020 [27] | Assess the impact of social distancing, testing and CT |
| Colomer 2021 [28] | Assess vaccination and CT with and without social control |
| Elias 2022 [54] | Model COVID-19 abd find optimal methods of CT |
| Endo 2021 [62] | Modelling with CT (backward and forward) with overdispersed transmission |
| Ferrari 2021 [55] | Modelling the COVID-19 epidemic in different scenarios |
| Ferretti 2020 [29] | Model COVID-19 with different transmissio routes; Assess the speed and scale of CT to stop the epidemic |
| Gardner 2021 [30] | Assess CT efficiency in different scenarios |
| Ge 2021 [46] | Forecast effectiveness of non-pharmaceutical interventions |
| Getz 2021 [31] | Assess surveillance, social distancing, quarantine, etc; forecast the impacts of these drivers |
| Gill 2020 [47] | Forecasting COVID-19 transmission |
| Giordano 2020 [48] | Forecast COVID-19 |
| Grantz 2021 [63] | Modelling test trace isolate on transmission |
| Grimm 2021 [32] | Assess effectiveness of epidemic control measure |
| Hellewell 2020 [33] | Assess effect of CT and isolation |
| Hernandez-Orallo 2020 [34] | Assess effect of CT |
| Hinch 2021 [56] | Modelling non-pharmaceutical interventions |
| Hoops 2021 [57] | Modelling CT |
| Hornstein 2022 [35] | Assess quarantine, CT, random testing effects in terms of lives saved and costs |
| Hu 2021 [64] | Modelling testing and tracing |
| Humphrey 2021 [49] | Forecasting with social distance, testing and tracing strategies |
| James 2021 [52] | Modelling CT |
| Kerr 2021 [36] | Assess test-trace-quarantine strategies with different scenarios |
| Khajanchi 2021 [65] | Modelling CT and hospitalisation |
| Kim 2021 [43] | Evaluating the effectiveness of testing and CT |
| Kretzschmar 2020 [44] | Identify key factors for a successful CT |
| Kucharski 2020 [37] | Assess control measures to estimate reduction in different scenarios |
| Lanzarotti 2021 [38] | Assess different CT strategies in reducing infection |
| Maiorana 2021 [50] | Forecast effectiveness of control measure |
| Mancastroppa 2021 [45] | Compare manual and digital CT |
| McQuade 2021 [58] | Modelling with different data |
| Mettler 2021 [66] | Modelling simulated scenario |
| Pollmann 2021 [39] | Assess digital CT, random testing, social distancing on the spread of the COVID-19 |
| Rajabi 2021 [67] | Modelling spread and containment |
| Ramos 2021 [59] | Modelling different scenario of control measures |
| Rusu 2021 [68] | Modelling CT in different scenarios |
| Ryu 2021 [40] | Model COVID-19 considering CT, Assess effectiveness of case isolation, CT in different scenarios |
| Sasmita 2020 [51] | Forecasting the peak of COVID-19 |
| Scarabel 2021 [69] | Model COVID-19 including CT in different scenarios |
| Shayak 2021 [70] | Model COVID-19 transmission |
| Soldano 2021 [71] | Model different strategies (CT, app) |
| Sturniolo 2021 [72] | Modelling with testing, CT and isolation |
| Tatapudi 2020 [41] | Assess the impact of social intervention strategy |
| Traore 2020 [60] | Modelling that include CT |
| Wang 2020 [42] | assess effectiveness of disease control measure; forecasting to exit lockdown |
Appendix C
| Criterion | Frequencies |
|---|---|
| Aim and objectives fc: Partial | 15% (8) |
| Yes | 85% (45) |
| Setting and population fc: No | 2% (1) |
| Partial | 64% (34) |
| Yes | 34% (18) |
| Intervention comparators fc: Partial | 45% (24) |
| Yes | 55% (29) |
| Outcome measures fc: Partial | 36% (19) |
| Yes | 64% (34) |
| Model structure and time horizon fc: Partial | 28% (15) |
| Yes | 72% (38) |
| Modelling methods fc: Partial | 49% (26) |
| Yes | 51% (27) |
| Parameters ranges and data sources fc: No | 2% (1) |
| Partial | 58% (31) |
| Yes | 40% (21) |
| Assumptions explicit and justified fc: Partial | 85% (45) |
| Yes | 15% (8) |
| Quality of data and uncertainty ad or sensitivity analysis fc: No | 28% (15) |
| Partial | 40% (21) |
| Yes | 32% (17) |
| Method of fitting fc: No | 19% (10) |
| Partial | 45% (24) |
| Yes | 36% (19) |
| Model validation fc: No | 72% (38) |
| Partial | 13% (7) |
| Yes | 15% (8) |
| Presentation of results and uncertainty fc: Partial | 66% (35) |
| Yes | 34% (18) |
| Interpetation and discussion of results fc: No | 2% (1) |
| Partial | 38% (20) |
| Yes | 60% (32) |
| Funding source and conflicts of interest fc: No | 13% (7) |
| Partial | 32% (17) |
| Yes | 55% (29) |
| Final score | 17/19/22 |
| Rating: High | 34% (18) |
| Low | 4% (2) |
| Medium | 45% (24) |
| Very high | 17% (9) |
References
- Guan, W.; Ni, Z.; Hu, Y.; Liang, W.; Ou, C.; He, J.; Liu, L.; Shan, H.; Lei, C.; Hui, D.S.C.; et al. Clinical Characteristics of Coronavirus Disease 2019 in China. N. Engl. J. Med. 2020, 382, 1708–1720. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Coronavirus Disease (COVID-19). Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019 (accessed on 3 April 2025).
- Iezadi, S.; Gholipour, K.; Azami-Aghdash, S.; Ghiasi, A.; Rezapour, A.; Pourasghari, H.; Pashazadeh, F. Effectiveness of Non-Pharmaceutical Public Health Interventions against COVID-19: A Systematic Review and Meta-Analysis. PLoS ONE 2021, 16, e0260371. [Google Scholar] [CrossRef] [PubMed]
- Coronavirus Disease (COVID-19): Contact Tracing. Available online: https://www.who.int/news-room/questions-and-answers/item/coronavirus-disease-covid-19-contact-tracing (accessed on 24 May 2022).
- Armbruster, B.; Brandeau, M.L. Contact Tracing to Control Infectious Disease: When Enough Is Enough. Health Care Manag. Sci. 2007, 10, 341–355. [Google Scholar] [CrossRef] [PubMed]
- Hossain, A.D.; Jarolimova, J.; Elnaiem, A.; Huang, C.X.; Richterman, A.; Ivers, L.C. Effectiveness of Contact Tracing in the Control of Infectious Diseases: A Systematic Review. Lancet Public Health 2022, 7, e259–e273. [Google Scholar] [CrossRef]
- Saurabh, S.; Prateek, S. Role of Contact Tracing in Containing the 2014 Ebola Outbreak: A Review. Afr. Health Sci. 2017, 17, 225–236. [Google Scholar] [CrossRef]
- Müller, J.; Kretzschmar, M.; Dietz, K. Contact Tracing in Stochastic and Deterministic Epidemic Models. Math. Biosci. 2000, 164, 39–64. [Google Scholar] [CrossRef]
- Hethcote, H.W.; Yorke, J.A. Gonorrhea Transmission Dynamics and Control; Springer: Berlin, Germany, 2014; ISBN 978-3-662-07544-9. [Google Scholar]
- Girum, T.; Lentiro, K.; Geremew, M.; Migora, B.; Shewamare, S. Global Strategies and Effectiveness for COVID-19 Prevention through Contact Tracing, Screening, Quarantine, and Isolation: A Systematic Review. Trop. Med. Health 2020, 48, 91. [Google Scholar] [CrossRef]
- Raymenants, J.; Geenen, C.; Thibaut, J.; Nelissen, K.; Gorissen, S.; Andre, E. Empirical Evidence on the Efficiency of Backward Contact Tracing in COVID-19. Nat. Commun. 2022, 13, 4750. [Google Scholar] [CrossRef]
- Saleem, F.; Al-Ghamdi, A.S.A.-M.; Alassafi, M.O.; AlGhamdi, S.A. Machine Learning, Deep Learning, and Mathematical Models to Analyze Forecasting and Epidemiology of COVID-19: A Systematic Literature Review. Int. J. Environ. Res. Public Health 2022, 19, 5099. [Google Scholar] [CrossRef]
- Afzal, A.; Saleel, C.A.; Bhattacharyya, S.; Satish, N.; Samuel, O.D.; Badruddin, I.A. Merits and Limitations of Mathematical Modeling and Computational Simulations in Mitigation of COVID-19 Pandemic: A Comprehensive Review. Arch. Comput. Methods Eng. State Art. Rev. 2022, 29, 1311–1337. [Google Scholar] [CrossRef]
- Fair, J.M.; LeClaire, R.J.; Dauelsberg, L.R.; Ewers, M.; Pasqualini, D.; Cleland, T.; Rosenberger, W. Systems Dynamics and the Uncertainties of Diagnostics, Testing and Contact Tracing for COVID-19. Methods 2021, 195, 77–91. [Google Scholar] [CrossRef] [PubMed]
- Yusoff, M.; Izhan, M. The Use of System Dynamics Methodology in Building a COVID-19 Confirmed Case Model. Comput. Math. Methods Med. 2020, 2020, e9328414. [Google Scholar] [CrossRef]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G.; PRISMA Group. Preferred Reporting Items for Systematic Reviews and Meta-Analyses: The PRISMA Statement. Ann. Intern. Med. 2009, 151, 264–269. [Google Scholar] [CrossRef] [PubMed]
- Covidence Covidence—Better Systematic Review Management. Available online: https://www.covidence.org/ (accessed on 3 June 2022).
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 Statement: An Updated Guideline for Reporting Systematic Reviews. BMJ 2021, 372, n71. [Google Scholar] [CrossRef]
- Harris, R.C.; Sumner, T.; Knight, G.M.; White, R.G. Systematic Review of Mathematical Models Exploring the Epidemiological Impact of Future TB Vaccines. Hum. Vaccines Immunother. 2016, 12, 2813–2832. [Google Scholar] [CrossRef]
- Amaku, M.; Covas, D.T.; Bezerra Coutinho, F.A.; Azevedo, R.S.; Massad, E. Modelling the Impact of Contact Tracing of Symptomatic Individuals on the COVID-19 Epidemic. Clinics 2021, 76, e2639. [Google Scholar] [CrossRef]
- Ashcroft, P.; Lehtinen, S.; Bonhoeffer, S. Test-Trace-Isolate-Quarantine (TTIQ) Intervention Strategies after Symptomatic COVID-19 Case Identification. PLoS ONE 2022, 17, e0263597. [Google Scholar] [CrossRef]
- Baha Raja, D.; Abdul Taib, N.A.; Teo, A.K.J.; Jayaraj, V.J.; Ting, C.-Y. Vaccines Alone Are No Silver Bullets: A Modeling Study on the Impact of Efficient Contact Tracing on COVID-19 Infection and Transmission in Malaysia. Int. Health 2022, 15, 37–46. [Google Scholar] [CrossRef]
- Biala, T.A.; Afolabi, Y.O.; Khaliq, A.Q.M. How Efficient Is Contact Tracing in Mitigating the Spread of COVID-19? A Mathematical Modeling Approach. Appl. Math. Model. 2022, 103, 714–730. [Google Scholar] [CrossRef]
- Browne, C.J.; Gulbudak, H.; Macdonald, J.C. Differential Impacts of Contact Tracing and Lockdowns on Outbreak Size in COVID-19 Model Applied to China. J. Theor. Biol. 2022, 532, 110919. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Fang, C.-T.; Huang, Y.-L. Effect of Non-Lockdown Social Distancing and Testing-Contact Tracing During a COVID-19 Outbreak in Daegu, South Korea, February to April 2020: A Modeling Study. Int. J. Infect. Dis. 2021, 110, 213–221. [Google Scholar] [CrossRef] [PubMed]
- Chiba, A. Modeling the Effects of Contact-Tracing Apps on the Spread of the Coronavirus Disease: Mechanisms, Conditions, and Efficiency. PLoS ONE 2021, 16, e0256151. [Google Scholar] [CrossRef] [PubMed]
- Chiu, W.A.; Fischer, R.; Ndeffo-Mbah, M.L. State-Level Needs for Social Distancing and Contact Tracing to Contain COVID-19 in the United States. Nat. Hum. Behav. 2020, 4, 1080–1090. [Google Scholar] [CrossRef] [PubMed]
- Colomer, M.À.; Margalida, A.; Alòs, F.; Oliva-Vidal, P.; Vilella, A.; Fraile, L. Modeling of Vaccination and Contact Tracing as Tools to Control the COVID-19 Outbreak in Spain. Vaccines 2021, 9, 386. [Google Scholar] [CrossRef]
- Ferretti, L.; Wymant, C.; Kendall, M.; Zhao, L.; Nurtay, A.; Abeler-Dörner, L.; Parker, M.; Bonsall, D.; Fraser, C. Quantifying SARS-CoV-2 Transmission Suggests Epidemic Control with Digital Contact Tracing. Science 2020, 368, eabb6936. [Google Scholar] [CrossRef]
- Gardner, B.J.; Kilpatrick, A.M. Contact Tracing Efficiency, Transmission Heterogeneity, and Accelerating COVID-19 Epidemics. PLoS Comput. Biol. 2021, 17, e1009122. [Google Scholar] [CrossRef]
- Getz, W.M.; Salter, R.; Luisa Vissat, L.; Horvitz, N. A Versatile Web App for Identifying the Drivers of COVID-19 Epidemics. J. Transl. Med. 2021, 19, 109. [Google Scholar] [CrossRef]
- Grimm, V.; Mengel, F.; Schmidt, M. Extensions of the SEIR Model for the Analysis of Tailored Social Distancing and Tracing Approaches to Cope with COVID-19. Sci. Rep. 2021, 11, 4214. [Google Scholar] [CrossRef]
- Hellewell, J.; Abbott, S.; Gimma, A.; Bosse, N.I.; Jarvis, C.I.; Russell, T.W.; Munday, J.D.; Kucharski, A.J.; Edmunds, W.J.; Sun, F.; et al. Feasibility of Controlling COVID-19 Outbreaks by Isolation of Cases and Contacts. Lancet Glob. Health 2020, 8, e488–e496. [Google Scholar] [CrossRef]
- Hernandez-Orallo, E.; Manzoni, P.; Calafate, C.T.; Cano, J.-C. Evaluating How Smartphone Contact Tracing Technology Can Reduce the Spread of Infectious Diseases: The Case of COVID-19. IEEE Access 2020, 8, 99083–99097. [Google Scholar] [CrossRef]
- Hornstein, A. Quarantine, Contact Tracing, and Testing: Implications of an Augmented SEIR Model. BE J. Macroecon. 2022, 22, 53–88. [Google Scholar] [CrossRef]
- Kerr, C.C.; Mistry, D.; Stuart, R.M.; Rosenfeld, K.; Hart, G.R.; Núñez, R.C.; Cohen, J.A.; Selvaraj, P.; Abeysuriya, R.G.; Jastrzębski, M.; et al. Controlling COVID-19 via Test-Trace-Quarantine. Nat. Commun. 2021, 12, 2993. [Google Scholar] [CrossRef] [PubMed]
- Kucharski, A.J.; Klepac, P.; Conlan, A.J.K.; Kissler, S.M.; Tang, M.L.; Fry, H.; Gog, J.R.; Edmunds, W.J.; Emery, J.C.; Medley, G.; et al. Effectiveness of Isolation, Testing, Contact Tracing, and Physical Distancing on Reducing Transmission of SARS-CoV-2 in Different Settings: A Mathematical Modelling Study. Lancet Infect. Dis. 2020, 20, 1151–1160. [Google Scholar] [CrossRef] [PubMed]
- Lanzarotti, E.; Santi, L.; Castro, R.; Roslan, F.; Groisman, L. A Multi-Aspect Agent-Based Model of COVID-19: Disease Dynamics, Contact Tracing Interventions and Shared Space-Driven Contagions; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2021; Volume 2021. [Google Scholar]
- Pollmann, T.R.; Schönert, S.; Müller, J.; Pollmann, J.; Resconi, E.; Wiesinger, C.; Haack, C.; Shtembari, L.; Turcati, A.; Neumair, B.; et al. The Impact of Digital Contact Tracing on the SARS-CoV-2 Pandemic—A Comprehensive Modelling Study. EPJ Data Sci. 2021, 10, 37. [Google Scholar] [CrossRef]
- Ryu, H.; Abulali, A.; Lee, S. Assessing the Effectiveness of Isolation and Contact-Tracing Interventions for Early Transmission Dynamics of COVID-19 in South Korea. IEEE Access 2021, 9, 41456–41467. [Google Scholar] [CrossRef]
- Tatapudi, H.; Das, R.; Das, T.K. Impact Assessment of Full and Partial Stay-at-Home Orders, Face Mask Usage, and Contact Tracing: An Agent-Based Simulation Study of COVID-19 for an Urban Region. Glob. Epidemiol. 2020, 2, 100036. [Google Scholar] [CrossRef]
- Wang, T.; Wu, Y.; Lau, J.Y.-N.; Yu, Y.; Liu, L.; Li, J.; Zhang, K.; Tong, W.; Jiang, B. A Four-Compartment Model for the COVID-19 Infection-Implications on Infection Kinetics, Control Measures, and Lockdown Exit Strategies. Precis. Clin. Med. 2020, 3, 104–112. [Google Scholar] [CrossRef]
- Kim, Y.J.; Koo, P.-H. Effectiveness of Testing and Contact-Tracing to Counter COVID-19 Pandemic: Designed Experiments of Agent-Based Simulation. Healthc. Switz. 2021, 9, 625. [Google Scholar] [CrossRef]
- Kretzschmar, M.E.; Rozhnova, G.; Bootsma, M.C.J.; van Boven, M.; van de Wijgert, J.H.H.M.; Bonten, M.J.M. Impact of Delays on Effectiveness of Contact Tracing Strategies for COVID-19: A Modelling Study. Lancet Public Health 2020, 5, e452–e459. [Google Scholar] [CrossRef]
- Mancastroppa, M.; Castellano, C.; Vezzani, A.; Burioni, R. Stochastic Sampling Effects Favor Manual over Digital Contact Tracing. Nat. Commun. 2021, 12, 1919. [Google Scholar] [CrossRef]
- Ge, Y.; Chen, Z.; Handel, A.; Martinez, L.; Xiao, Q.; Li, C.; Chen, E.; Pan, J.; Li, Y.; Ling, F.; et al. The Impact of Social Distancing, Contact Tracing, and Case Isolation Interventions to Suppress the COVID-19 Epidemic: A Modeling Study. Epidemics 2021, 36, 100483. [Google Scholar] [CrossRef] [PubMed]
- Gill, B.S.; Jayaraj, V.J.; Singh, S.; Ghazali, S.M.; Cheong, Y.L.; Md Iderus, N.H.; Sundram, B.M.; Aris, T.B.; Mohd Ibrahim, H.; Hong, B.H.; et al. Modelling the Effectiveness of Epidemic Control Measures in Preventing the Transmission of COVID-19 in Malaysia. Int. J. Environ. Res. Public Health 2020, 17, 5509. [Google Scholar] [CrossRef] [PubMed]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Di Filippo, A.; Di Matteo, A.; Colaneri, M. Modelling the COVID-19 Epidemic and Implementation of Population-Wide Interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, L.; Thommes, E.W.; Fields, R.; Coudeville, L.; Hakim, N.; Chit, A.; Wu, J.; Cojocaru, M.G. Large-Scale Frequent Testing and Tracing to Supplement Control of Covid-19 and Vaccination Rollout Constrained by Supply. Infect. Dis. Model. 2021, 6, 955–974. [Google Scholar] [CrossRef]
- Maiorana, A.; Meneghelli, M.; Resnati, M. Effectiveness of Isolation Measures with App Support to Contain COVID-19 Epidemics: A Parametric Approach. J. Math. Biol. 2021, 83, 46. [Google Scholar] [CrossRef]
- Sasmita, N.R.; Ikhwan, M.; Suyanto, S.; Chongsuvivatwong, V. Optimal Control on a Mathematical Model to Pattern the Progression of Coronavirus Disease 2019 (COVID-19) in Indonesia. Glob. Health Res. Policy 2020, 5, 38. [Google Scholar] [CrossRef]
- James, A.; Plank, M.J.; Hendy, S.; Binny, R.; Lustig, A.; Steyn, N.; Nesdale, A.; Verrall, A. Successful Contact Tracing Systems for COVID-19 Rely on Effective Quarantine and Isolation. PLoS ONE 2021, 16, e0252499. [Google Scholar] [CrossRef]
- Almagor, J.; Picascia, S. Exploring the Effectiveness of a COVID-19 Contact Tracing App Using an Agent-Based Model. Sci. Rep. 2020, 10, 22235. [Google Scholar] [CrossRef]
- Elías, L.L.; Elías, S.L.; del Rey, A.M. An Analysis of Contact Tracing Protocol in an Over-Dispersed SEIQR Covid-like Disease. Phys. Stat. Mech. Its Appl. 2022, 590, 126754. [Google Scholar] [CrossRef]
- Ferrari, A.; Santus, E.; Cirillo, D.; Ponce-de-Leon, M.; Marino, N.; Ferretti, M.T.; Santuccione Chadha, A.; Mavridis, N.; Valencia, A. Simulating SARS-CoV-2 Epidemics by Region-Specific Variables and Modeling Contact Tracing App Containment. NPJ Digit. Med. 2021, 4, 9. [Google Scholar] [CrossRef]
- Hinch, R.; Probert, W.J.M.; Nurtay, A.; Kendall, M.; Wymant, C.; Hall, M.; Lythgoe, K.; Bulas Cruz, A.; Zhao, L.; Stewart, A.; et al. OpenABM-Covid19-An Agent-Based Model for Non-Pharmaceutical Interventions against COVID-19 Including Contact Tracing. PLoS Comput. Biol. 2021, 17, e1009146. [Google Scholar] [CrossRef] [PubMed]
- Hoops, S.; Chen, J.; Adiga, A.; Lewis, B.; Mortveit, H.; Baek, H.; Wilson, M.; Xie, D.; Swarup, S.; Venkatramanan, S.; et al. High Performance Agent-Based Modeling to Study Realistic Contact Tracing Protocols; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2021; Volume 2021. [Google Scholar]
- McQuade, S.T.; Weightman, R.; Merrill, N.J.; Yadav, A.; Trélat, E.; Allred, S.R.; Piccoli, B. Control of COVID-19 Outbreak Using an Extended SEIR Model. Math. Models Methods Appl. Sci. 2021, 31, 2399–2424. [Google Scholar] [CrossRef]
- Ramos, A.M.; Ferrández, M.R.; Vela-Pérez, M.; Kubik, A.B.; Ivorra, B. A Simple but Complex Enough θ-SIR Type Model to Be Used with COVID-19 Real Data. Application to the Case of Italy. Phys. Nonlinear Phenom. 2021, 421, 132839. [Google Scholar] [CrossRef]
- Traoré, A.; Konané, F.V. Modeling the Effects of Contact Tracing on COVID-19 Transmission. Adv. Differ. Equ. 2020, 2020, 509. [Google Scholar] [CrossRef] [PubMed]
- Mahmood, M.; Mateu, J.; Hernández-Orallo, E. Contextual Contact Tracing Based on Stochastic Compartment Modeling and Spatial Risk Assessment. Stoch. Environ. Res. Risk Assess. 2022, 36, 893–917. [Google Scholar] [CrossRef]
- Endo, A.; Leclerc, Q.J.; Knight, G.M.; Medley, G.F.; Atkins, K.E.; Funk, S.; Kucharski, A.J. Implication of Backward Contact Tracing in the Presence of Overdispersed Transmission in COVID-19 Outbreaks. Wellcome Open Res. 2021, 5, 239. [Google Scholar] [CrossRef]
- Grantz, K.H.; Lee, E.C.; D’Agostino McGowan, L.; Lee, K.H.; Metcalf, J.C.E.; Gurley, E.S.; Lessler, J. Maximizing and Evaluating the Impact of Test-Trace-Isolate Programs: A Modeling Study. PLoS Med. 2021, 18, e1003585. [Google Scholar] [CrossRef]
- Hu, Y.; Guo, J.; Li, G.; Lu, X.; Li, X.; Zhang, Y.; Cong, L.; Kang, Y.; Jia, X.; Shi, X.; et al. Role of Efficient Testing and Contact Tracing in Mitigating the COVID-19 Pandemic: A Network Modelling Study. BMJ Open 2021, 11, e045886. [Google Scholar] [CrossRef]
- Khajanchi, S.; Sarkar, K.; Mondal, J.; Nisar, K.S.; Abdelwahab, S.F. Mathematical Modeling of the COVID-19 Pandemic with Intervention Strategies. Results Phys. 2021, 25, 104285. [Google Scholar] [CrossRef]
- Mettler, S.K.; Park, J.; Özbek, O.; Mettler, L.K.; Ho, P.-H.; Rhim, H.C.; Maathuis, M.H. The Importance of Timely Contact Tracing —A Simulation Study. Int. J. Infect. Dis. 2021, 108, 309–319. [Google Scholar] [CrossRef]
- Rajabi, A.; Mantzaris, A.V.; Mutlu, E.C.; Garibay, O.O. Investigating Dynamics of Covid-19 Spread and Containment with Agent-Based Modeling. Appl. Sci. Switz. 2021, 11, 5367. [Google Scholar] [CrossRef]
- Rusu, A.C.; Emonet, R.; Farrahi, K. Modelling Digital and Manual Contact Tracing for COVID-19. Are Low Uptakes and Missed Contacts Deal-Breakers? PLoS ONE 2021, 16, e0259969. [Google Scholar] [CrossRef] [PubMed]
- Scarabel, F.; Pellis, L.; Ogden, N.H.; Wu, J. A Renewal Equation Model to Assess Roles and Limitations of Contact Tracing for Disease Outbreak Control. R. Soc. Open Sci. 2021, 8, 202091. [Google Scholar] [CrossRef] [PubMed]
- Shayak, B.; Sharma, M.M. Contact Tracing Can Explain Counter-Intuitive COVID-19 Trajectories, Mitigate Disease Transmission and Provide an Early Warning Indicator—A Mathematical Modeling Study. medRxiv 2021. [Google Scholar] [CrossRef]
- Soldano, G.J.; Fraire, J.A.; Finochietto, J.M.; Quiroga, R. COVID-19 Mitigation by Digital Contact Tracing and Contact Prevention (App-Based Social Exposure Warnings). Sci. Rep. 2021, 11, 14421. [Google Scholar] [CrossRef]
- Sturniolo, S.; Waites, W.; Colbourn, T.; Manheim, D.; Panovska-Griffiths, J. Testing, Tracing and Isolation in Compartmental Models. PLoS Comput. Biol. 2021, 17, e1008633. [Google Scholar] [CrossRef]
- Hart, W.S.; Maini, P.K.; Thompson, R.N. High Infectiousness Immediately before Covid-19 Symptom Onset Highlights the Importance of Continued Contact Tracing. eLife 2021, 10, e65534. [Google Scholar] [CrossRef]
- Xin, H.; Li, Y.; Wu, P.; Li, Z.; Lau, E.H.Y.; Qin, Y.; Wang, L.; Cowling, B.J.; Tsang, T.K.; Li, Z. Estimating the Latent Period of Coronavirus Disease 2019 (COVID-19). Clin. Infect. Dis. 2022, 74, 1678–1681. [Google Scholar] [CrossRef]
- Prieto, D.M.; Das, T.K.; Savachkin, A.A.; Uribe, A.; Izurieta, R.; Malavade, S. A Systematic Review to Identify Areas of Enhancements of Pandemic Simulation Models for Operational Use at Provincial and Local Levels. BMC Public Health 2012, 12, 251. [Google Scholar] [CrossRef]
- Shankar, S.; Mohakuda, S.S.; Kumar, A.; Nazneen, P.S.; Yadav, A.K.; Chatterjee, K.; Chatterjee, K. Systematic Review of Predictive Mathematical Models of COVID-19 Epidemic. Med. J. Armed Forces India 2021, 77, S385–S392. [Google Scholar] [CrossRef]
- Kojaku, S.; Hébert-Dufresne, L.; Mones, E.; Lehmann, S.; Ahn, Y.-Y. The Effectiveness of Backward Contact Tracing in Networks. Nat. Phys. 2021, 17, 652–658. [Google Scholar] [CrossRef] [PubMed]
- Jenniskens, K.; Bootsma, M.C.J.; Damen, J.A.A.G.; Oerbekke, M.S.; Vernooij, R.W.M.; Spijker, R.; Moons, K.G.M.; Kretzschmar, M.E.E.; Hooft, L. Effectiveness of Contact Tracing Apps for SARS-CoV-2: A Rapid Systematic Review. BMJ Open 2021, 11, e050519. [Google Scholar] [CrossRef] [PubMed]
- Pegollo, L.; Mazza, C.; Girardi, D.; Maggioni, E.; Valente, G.; Gaeta, M.; Odone, A. Use and Effectiveness of Digital Contact Tracing during COVID-19 Pandemic: A Systematic Review. Eur. J. Public Health 2021, 31, ckab165.171. [Google Scholar] [CrossRef]
- da Costa, A.L.P.; Pires, M.A.; Resque, R.L.; de Almeida, S.S.M.D.S. Mathematical Modeling of the Infectious Diseases: Key Concepts and Applications. J. Infect. Dis. Epidemiol. 2021, 7, 209. [Google Scholar] [CrossRef]
- Grimm, V.; Berger, U.; Bastiansen, F.; Eliassen, S.; Ginot, V.; Giske, J.; Goss-Custard, J.; Grand, T.; Heinz, S.K.; Huse, G.; et al. A Standard Protocol for Describing Individual-Based and Agent-Based Models. Ecol. Model. 2006, 198, 115–126. [Google Scholar] [CrossRef]
- Patlolla, P.; Gunupudi, V.; Mikler, A.; Jacob, R.T. Agent-Based Simulation Tools in Computational Epidemiology. In International Workshop on Innovative Internet Community Systems; Springer: Berlin, Germany, 2004. [Google Scholar] [CrossRef]
- Perez, L.; Dragicevic, S. An Agent-Based Approach for Modeling Dynamics of Contagious Disease Spread. Int. J. Health Geogr. 2009, 8, 50. [Google Scholar] [CrossRef]
- Tillett, H.E. Infectious Diseases of Humans: Dynamics and Control. R. M. Anderson, R. M. May, Pp. 757. Oxford University Press; 1991 (£50.00). Epidemiol. Infect. 1992, 108, 211. [Google Scholar] [CrossRef]
- Liu, Y.; Rocklöv, J. The Effective Reproductive Number of the Omicron Variant of SARS-CoV-2 Is Several Times Relative to Delta. J. Travel Med. 2022, 29, taac037. [Google Scholar] [CrossRef]
- Rai, B.; Shukla, A.; Dwivedi, L.K. Incubation Period for COVID-19: A Systematic Review and Meta-Analysis. J. Public Health 2021, 30, 2649–2656. [Google Scholar] [CrossRef]
- Brookmeyer, R. Incubation Period of Infectious Diseases. In Encyclopedia of Biostatistics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005; ISBN 978-0-470-01181-2. [Google Scholar]
- Dhouib, W.; Maatoug, J.; Ayouni, I.; Zammit, N.; Ghammem, R.; Fredj, S.B.; Ghannem, H. The Incubation Period during the Pandemic of COVID-19: A Systematic Review and Meta-Analysis. Syst. Rev. 2021, 10, 101. [Google Scholar] [CrossRef]
- Cheng, C.; Zhang, D.; Dang, D.; Geng, J.; Zhu, P.; Yuan, M.; Liang, R.; Yang, H.; Jin, Y.; Xie, J.; et al. The Incubation Period of COVID-19: A Global Meta-Analysis of 53 Studies and a Chinese Observation Study of 11 545 Patients. Infect. Dis. Poverty 2021, 10, 119. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Kang, L.; Guo, Z.; Liu, J.; Liu, M.; Liang, W. Incubation Period of COVID-19 Caused by Unique SARS-CoV-2 Strains: A Systematic Review and Meta-Analysis. JAMA Netw. Open 2022, 5, e2228008. [Google Scholar] [CrossRef] [PubMed]
- Puhach, O.; Meyer, B.; Eckerle, I. SARS-CoV-2 Viral Load and Shedding Kinetics. Nat. Rev. Microbiol. 2022, 21, 147–161. [Google Scholar] [CrossRef] [PubMed]
- Khadem Charvadeh, Y.; Yi, G.Y.; Bian, Y.; He, W. Is 14-Days a Sensible Quarantine Length for COVID-19? Examinations of Some Associated Issues with a Case Study of COVID-19 Incubation Times. Stat. Biosci. 2022, 14, 175–190. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ocagli, H.; Brigiari, G.; Marcolin, E.; Mongillo, M.; Tonon, M.; Da Re, F.; Gentili, D.; Michieletto, F.; Russo, F.; Gregori, D. Mathematical Contact Tracing Models for the COVID-19 Pandemic: A Systematic Review of the Literature. Healthcare 2025, 13, 935. https://doi.org/10.3390/healthcare13080935
Ocagli H, Brigiari G, Marcolin E, Mongillo M, Tonon M, Da Re F, Gentili D, Michieletto F, Russo F, Gregori D. Mathematical Contact Tracing Models for the COVID-19 Pandemic: A Systematic Review of the Literature. Healthcare. 2025; 13(8):935. https://doi.org/10.3390/healthcare13080935
Chicago/Turabian StyleOcagli, Honoria, Gloria Brigiari, Erica Marcolin, Michele Mongillo, Michele Tonon, Filippo Da Re, Davide Gentili, Federica Michieletto, Francesca Russo, and Dario Gregori. 2025. "Mathematical Contact Tracing Models for the COVID-19 Pandemic: A Systematic Review of the Literature" Healthcare 13, no. 8: 935. https://doi.org/10.3390/healthcare13080935
APA StyleOcagli, H., Brigiari, G., Marcolin, E., Mongillo, M., Tonon, M., Da Re, F., Gentili, D., Michieletto, F., Russo, F., & Gregori, D. (2025). Mathematical Contact Tracing Models for the COVID-19 Pandemic: A Systematic Review of the Literature. Healthcare, 13(8), 935. https://doi.org/10.3390/healthcare13080935







