Pulmonary Function Prediction Method Based on Convolutional Surface Modeling and Computational Fluid Dynamics Simulation
Abstract
1. Introduction
- (1)
- Pulmonary function tests require patients’ cooperation. The accuracy of their results is affected by patients’ compliance. For patients with severe respiratory distress, cognitive impairment, or vocal cord edema, pulmonary function tests are not suitable for obtaining their pulmonary function data. Additionally, patients experiencing coughing, shortness of breath, or high anxiety tend to have reduced compliance, which leads to decreased accuracy and consistency of test outcomes, as well as lower work efficiency of clinicians [11,12,13,14].
- (2)
- Pulmonary function tests can only reflect patients’ current lung function status. For patients with airway tumor compression or other airway stenoses, they cannot predict patients’ future lung function based on changes in tumor size or the degree of airway narrowing. Additionally, they cannot provide preoperative predictions of lung function after airway expansion surgery.
2. Methods
2.1. Overview
2.2. Model Construction
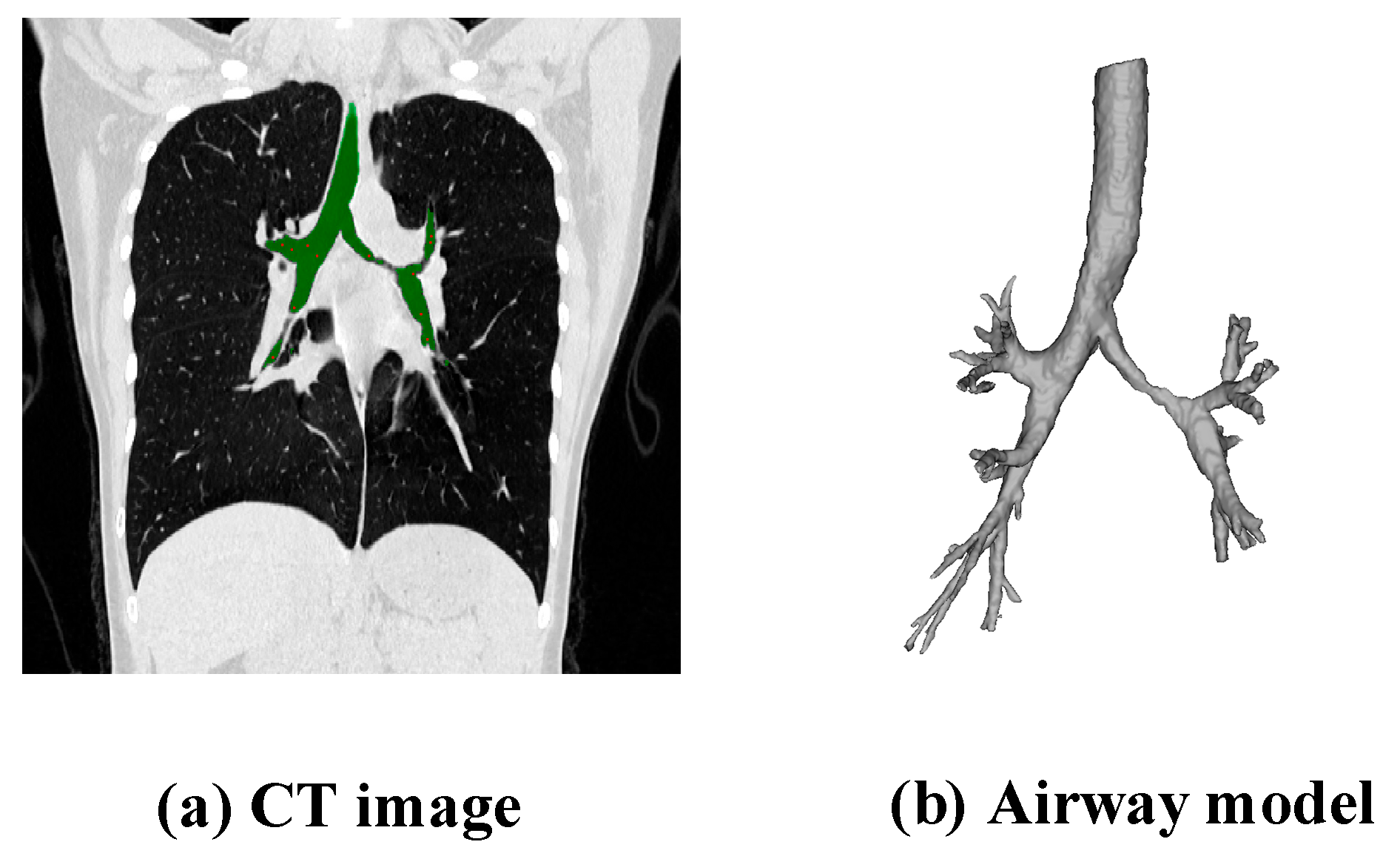
2.2.1. Extraction of Airway Data
2.2.2. Generation of Skeleton Data
2.2.3. Establishment of the Airway Model
- (1)
- Calculation of the Skeletal Potential Function
- (2)
- Rendering of the Skeleton Convolution Surface
2.3. Settings for Model Simulation
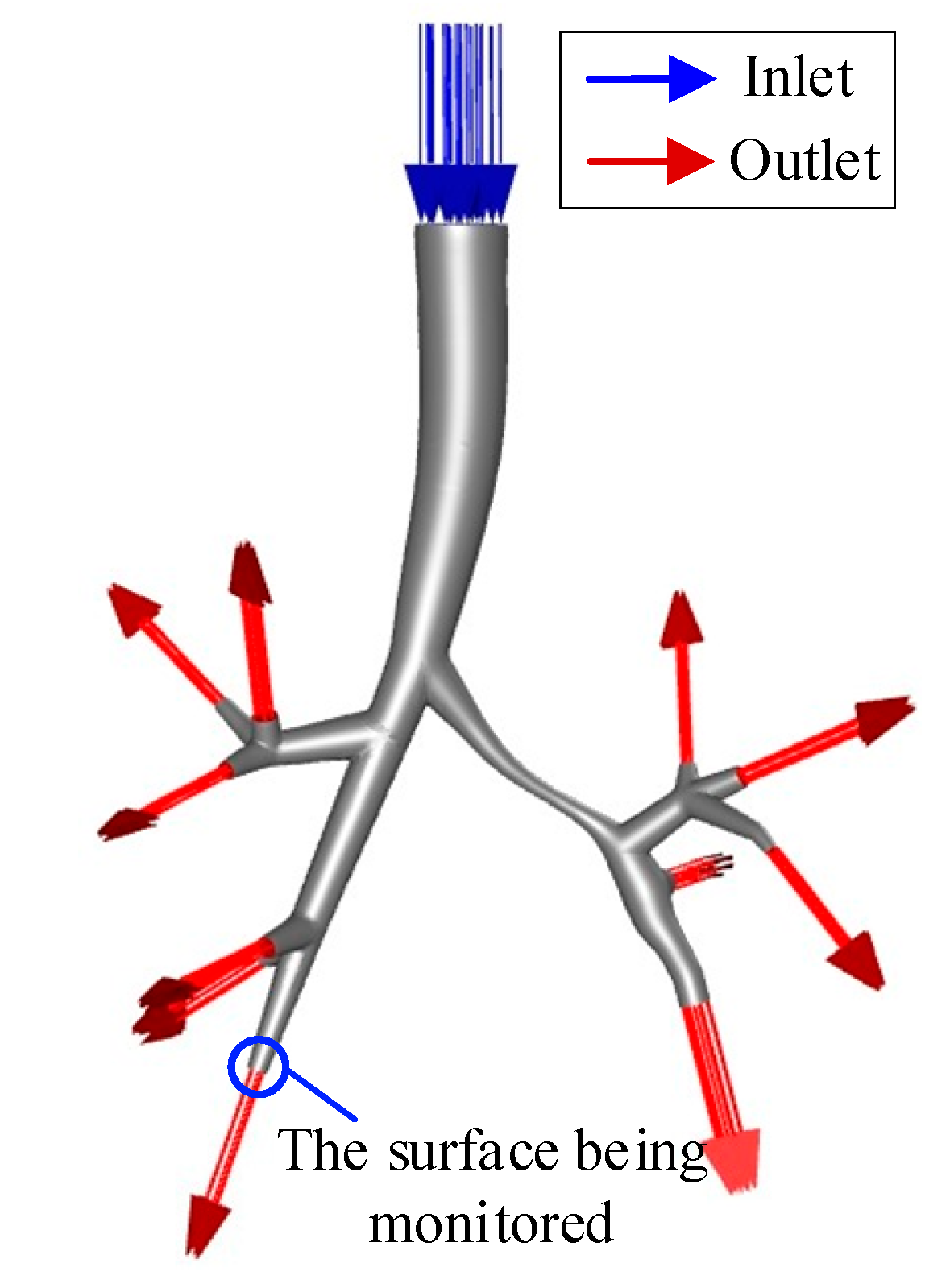
2.3.1. Mesh Generation
2.3.2. Boundary Condition Setting
- (1)
- Lung Segment Function Proportion Assumption
- (2)
- Assumption of Equal Pressure
2.3.3. Other Parameter Settings
2.4. Prediction of FEV1 Based on Large Airway Flow Simulation
3. Results
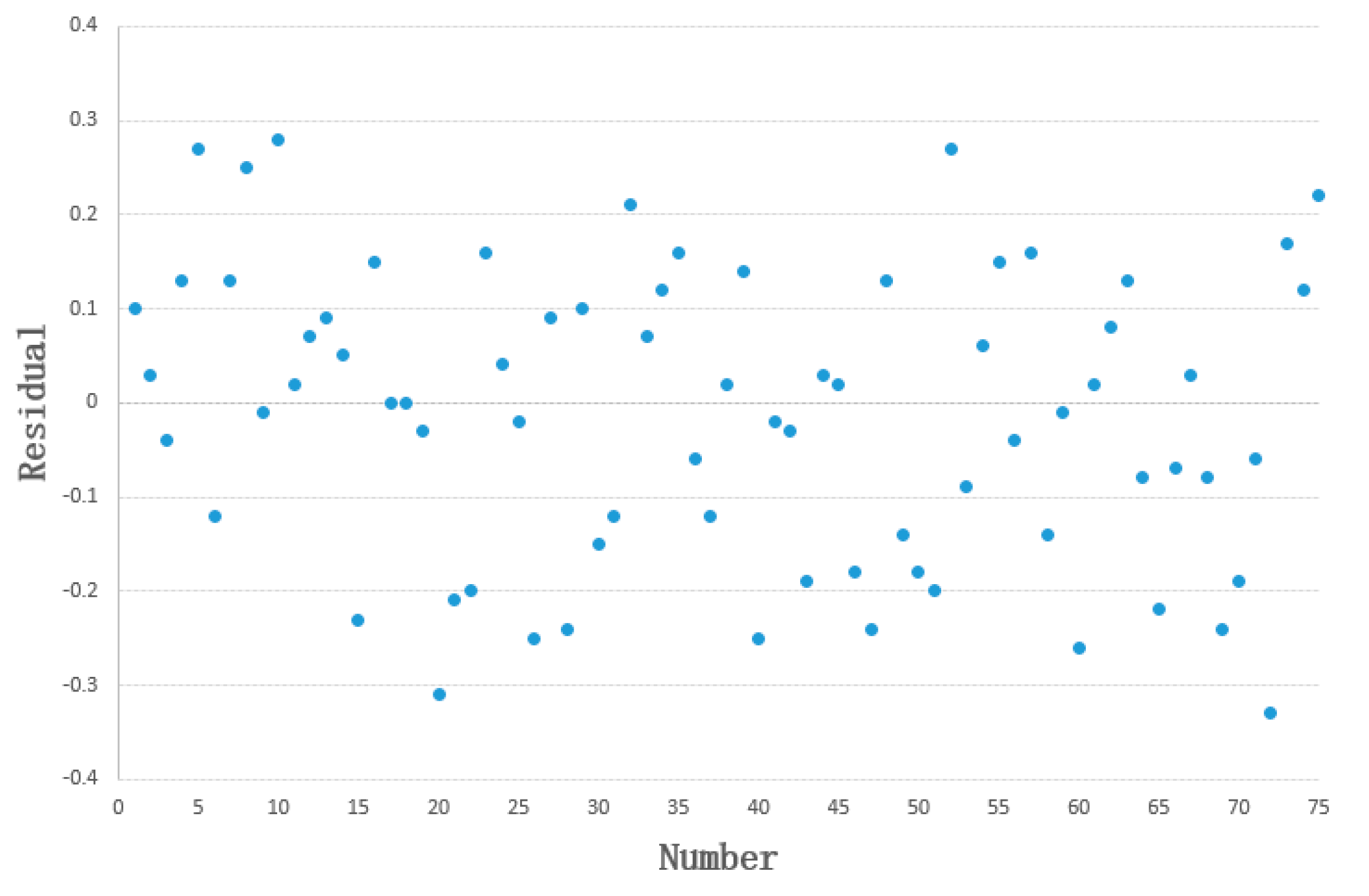
3.1. Development and Validation Results of the FEV1 Prediction Model
3.1.1. Build a Model Using the Training Set
3.1.2. Exploring Feasibility Using the Test Set
3.2. Visualization of Flow Field Characteristics
3.3. Preoperative Evaluation Method for Airway Dilation Surgery
4. Discussion
4.1. Clinical Significance of the Pulmonary Function Prediction Model
- (1)
- Sample size limitation: Only six samples were included, which did not cover all subtypes of large airway stenosis. This may lead to prediction bias for special cases (e.g., the relative error of 8.8% for Patient F was slightly higher, possibly due to their stenotic location near the right main bronchus).
- (2)
- CFD simulation error: Assumptions such as lung segmental function proportion and the equal pressure assumption for small airways may introduce calculation bias in volume flow rate, indirectly affecting the accuracy of the input variable x.
- (3)
- Limitation in variable selection: The model only incorporates volume flow rate and does not account for clinical factors such as patient age and disease duration, which may result in unexplained variation in residuals.
4.2. Application Value of Preoperative Evaluation in Airway Dilation Therapy
4.3. Limitations and Future Works
- (1)
- Limitations
- Sample size limitation
- Operational limitation
- Applicability limitation
- (2)
- Future Works
- Expanding sample size
- Model optimization
- Technical optimization
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- West, J.B.; Luks, A.M. West’s Respiratory Physiology; Lippincott Williams & Wilkins: Ambler, PA, USA, 2020. [Google Scholar]
- Widmaier, E.; Raff, H.; Strang, K.T. Vander’s Human Physiology; McGraw-Hill US Higher Ed USE: New York, NY, USA, 2022. [Google Scholar]
- Da, A.; Ps, B.; Yz, C.; Phc, A.; Pas, A.; Envelope, P.; Unit, N. Global, regional, and national prevalence of, and risk factors for, chronic obstructive pulmonary disease (COPD) in 2019: A systematic review and modelling analysis—ScienceDirect. Ann. Surg. 2022, 10, 447–458. [Google Scholar] [CrossRef]
- Labaki, W.W.; Han, M.K. Chronic respiratory diseases: A global view. Lancet Respir. Med. 2020, 8, 531–533. [Google Scholar] [CrossRef]
- Tran, H.M.; Tsai, F.-J.; Lee, Y.-L.; Chang, J.-H.; Chang, L.-T.; Chang, T.-Y.; Chung, K.F.; Kuo, H.-P.; Lee, K.-Y.; Chuang, K.-J. The impact of air pollution on respiratory diseases in an era of climate change: A review of the current evidence. Sci. Total Environ. 2023, 898, 166340. [Google Scholar] [CrossRef]
- Baral, N.; Jabbar, A.B.A.; Noor, A.; Mirza, M.; DeVrieze, B.; Hildenbrand, A.; Tauseef, A. Demographic and geographical trends in chronic lower respiratory diseases mortality in the United States, 1999 to 2020. Respir. Res. 2024, 25, 258. [Google Scholar] [CrossRef] [PubMed]
- Wanger, J. Pulmonary Function Testing: A Practical Approach: A Practical Approach; Jones & Bartlett Publishers: Burlington, MA, USA, 2011. [Google Scholar]
- Huang, Y.; Tan, C.; Wu, J.; Chen, M.; Wang, Z.; Luo, L.; Zhou, X.; Liu, X.; Huang, X.; Yuan, S. Impact of coronavirus disease 2019 on pulmonary function in early convalescence phase. Respir. Res. 2020, 21, 163. [Google Scholar] [CrossRef]
- Chawes, B.; Elenius, V. Pulmonary function testing for the diagnosis of asthma in preschool children. Curr. Opin. Allergy Clin. Immunol. 2022, 22, 101–106. [Google Scholar] [CrossRef]
- Schnabel, E.; Chen, C.-M.; Koch, B.; Karrasch, S.; Jörres, R.A.; Schäfer, T.; Vogelmeier, C.; Ewert, R.; Schäper, C.; Völzke, H.; et al. Regional differences in prediction models of lung function in Germany. Respir. Res. 2010, 11, 40. [Google Scholar] [CrossRef]
- Ma, Y.e.; Cai, M.; Chen, Q.; Jiang, D.; Yang, Z.; Cui, M. Psychological Experience of the First Pulmonary Function Test in Elderly Patients with Poor Cooperation: A Qualitative Study. Am. J. Health Behav. 2023, 47, 965–973. [Google Scholar] [CrossRef]
- Johnson, B.; Steenbruggen, I.; Graham, B.L.; Coleman, C. Improving spirometry testing by understanding patient preferences. ERJ Open Res. 2021, 7, 1. [Google Scholar] [CrossRef] [PubMed]
- Kakavas, S.; Kotsiou, O.S.; Perlikos, F.; Mermiri, M.; Mavrovounis, G.; Gourgoulianis, K.; Pantazopoulos, I. Pulmonary function testing in COPD: Looking beyond the curtain of FEV1. NPJ Prim. Care Respir. Med. 2021, 31, 23. [Google Scholar] [CrossRef]
- Stanojevic, S.; Kaminsky, D.A.; Miller, M.R.; Thompson, B.; Aliverti, A.; Barjaktarevic, I.; Cooper, B.G.; Culver, B.; Derom, E.; Hall, G.L. ERS/ATS technical standard on interpretive strategies for routine lung function tests. Eur. Respir. J. 2022, 60, 1. [Google Scholar] [CrossRef]
- Dong, D.; Tang, Z.; Wang, S.; Hui, H.; Gong, L.; Lu, Y.; Xue, Z.; Liao, H.; Chen, F.; Yang, F. The role of imaging in the detection and management of COVID-19: A review. IEEE Rev. Biomed. Eng. 2020, 14, 16–29. [Google Scholar] [CrossRef]
- Soldati, G.; Demi, M.; Smargiassi, A.; Inchingolo, R.; Demi, L. The role of ultrasound lung artifacts in the diagnosis of respiratory diseases. Expert Rev. Respir. Med. 2019, 13, 163–172. [Google Scholar] [CrossRef]
- Zhou, T.; Guan, Y.; Lin, X.; Zhou, X.; Mao, L.; Ma, Y.; Fan, B.; Li, J.; Liu, S.; Fan, L. CT-based whole lung radiomics nomogram for identification of PRISm from non-COPD subjects. Respir. Res. 2024, 25, 329. [Google Scholar] [CrossRef] [PubMed]
- Tanabe, N.; Sato, S.; Oguma, T.; Shima, H.; Sato, A.; Muro, S.; Hirai, T. Associations of airway tree to lung volume ratio on computed tomography with lung function and symptoms in chronic obstructive pulmonary disease. Respir. Res. 2019, 20, 77. [Google Scholar] [CrossRef] [PubMed]
- Langton, D.; Sloan, G.; Banks, C.; Bennetts, K.; Plummer, V.; Thien, F. Bronchial thermoplasty increases airway volume measured by functional respiratory imaging. Respir. Res. 2019, 20, 157. [Google Scholar] [CrossRef] [PubMed]
- Li, W.-I.; Perzl, M.; Heyder, J.; Langer, R.; Brain, J.D.; Englmeier, K.-H.; Niven, R.W.; Edwards, D.A. Aerodynamics and aerosol particle deaggregation phenomena in model oral-pharyngeal cavities. J. Aerosol Sci. 1996, 27, 1269–1286. [Google Scholar] [CrossRef]
- Stapleton, K.W.; Guentsch, E.; Hoskinson, M.; Finlay, W.H. On the suitability of k–ε turbulence modeling for aerosol deposition in the mouth and throat: A comparison with experiment. J. Aerosol Sci. 2000, 31, 739–749. [Google Scholar] [CrossRef]
- Zhang, Z.; Kleinstreuer, C.; Kim, C.S. Comparison of analytical and CFD models with regard to micron particle deposition in a human 16-generation tracheobronchial airway model. J. Aerosol Sci. 2009, 40, 16–28. [Google Scholar] [CrossRef]
- Augusto, L.; Lopes, G.; Gonçalves, J. A CFD study of deposition of pharmaceutical aerosols under different respiratory conditions. Braz. J. Chem. Eng. 2016, 33, 549–558. [Google Scholar] [CrossRef]
- Farkhadnia, F.; Gorji, T.B.; Gorji-Bandpy, M. Airflow, transport and regional deposition of aerosol particles during chronic bronchitis of human central airways. Australas. Phys. Eng. Sci. Med. 2016, 39, 43–58. [Google Scholar] [CrossRef]
- Tian, G.; Longest, P.W.; Su, G.; Hindle, M. Characterization of respiratory drug delivery with enhanced condensational growth using an individual path model of the entire tracheobronchial airways. Ann. Biomed. Eng. 2011, 39, 1136–1153. [Google Scholar] [CrossRef]
- Tena, A.; Casan, P.; Fernández, J.; Ferrera, C.; Marcos, A. Characterization of particle deposition in a lung model using an individual path. EPJ Web Conf. 2013, 45, 01079. [Google Scholar] [CrossRef]
- Xi, J.; Kim, J.; Si, X.A.; Corley, R.A.; Kabilan, S.; Wang, S. CFD modeling and image analysis of exhaled aerosols due to a growing bronchial tumor: Towards non-invasive diagnosis and treatment of respiratory obstructive diseases. Theranostics 2015, 5, 443. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Xiang, Y.; Lu, C.; Ou, C.; Deng, Q. Numerical modeling of particle deposition in the conducting airways of asthmatic children. Med. Eng. Phys. 2020, 76, 40–46. [Google Scholar] [CrossRef]
- Mohite, V.; Deoghare, A.B.; Pandey, K.M. Modeling of Human Airways CAD model Using CT Scan Data. Mater. Today: Proc. 2020, 22, 1710–1714. [Google Scholar] [CrossRef]
- Kharat, S.B.; Deoghare, A.B.; Pandey, K.M. Development of human airways model for CFD analysis. Mater. Today: Proc. 2018, 5, 12920–12926. [Google Scholar] [CrossRef]
- Bloomenthal, J.; Shoemake, K. Convolution surfaces. In Proceedings of the 18th Annual Conference on Computer Graphics and Interactive Techniques, Las Vegas, NV, USA, 28 July–2 August 1991; pp. 251–256. [Google Scholar]
- Sherstyuk, A. Kernel functions in convolution surfaces: A comparative analysis. Vis. Comput. 1999, 15, 171–182. [Google Scholar] [CrossRef]
- Bærentzen, J.A.; Villesen, I.B.; Dellwik, E. Reconstruction of a Botanical Tree from a 3D Point Cloud. In Proceedings of the INdAM Workshop on Mathematical Methods for Objects Reconstruction: From 3D Vision to 3D Printing, Online, 10–12 February 2021; pp. 103–120. [Google Scholar]
- Oeltze, S.; Preim, B. Visualization of vasculature with convolution surfaces: Method, validation and evaluation. IEEE Trans. Med. Imaging 2005, 24, 540–548. [Google Scholar] [CrossRef] [PubMed]
- Pizaine, G.; Angelini, E.D.; Bloch, I.; Makram-Ebeid, S. Vessel geometry modeling and segmentation using convolution surfaces and an implicit medial axis. In Proceedings of the 2011 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Chicago, IL, USA, 30 March–2 April 2011; pp. 1421–1424. [Google Scholar]
- Bošnjak, D.; Pepe, A.; Schussnig, R.; Schmalstieg, D.; Fries, T.-P. Higher-order block-structured hex meshing of tubular structures. Eng. Comput. 2024, 40, 931–951. [Google Scholar] [CrossRef]
- Hailin, Z. Convolution Surface Modeling for Cubic B-Spline Skeletons. J. Comput.—Aided Des. Comput. Graph. 2006, 18, 1300. [Google Scholar]
- Dancer, R.; Thickett, D. Pulmonary function tests. Medicine 2012, 40, 186–189. [Google Scholar] [CrossRef]
- Wang, K.; Zeng, R. Pulmonary function test. Handb. Clin. Diagn. 2020, 337–342. [Google Scholar]
- Cooper, B.G. Republished review: An update on contraindications for lung function testing. Postgrad. Med. J. 2011, 87, 724–733. [Google Scholar] [CrossRef] [PubMed]
- Park, H.; Yun, J.; Lee, S.M.; Hwang, H.J.; Seo, J.B.; Jung, Y.J.; Hwang, J.; Lee, S.H.; Lee, S.W.; Kim, N. Deep learning–based approach to predict pulmonary function at chest CT. Radiology 2023, 307, e221488. [Google Scholar] [CrossRef] [PubMed]
- Ohno, Y.; Koyama, H.; Nogami, M.; Takenaka, D.; Matsumoto, S.; Yoshimura, M.; Kotani, Y.; Sugimura, K. Postoperative lung function in lung cancer patients: Comparative analysis of predictive capability of MRI, CT, and SPECT. Am. J. Roentgenol. 2007, 189, 400–408. [Google Scholar] [CrossRef] [PubMed]






| Number | Gender | Age | Height | Weight | FVC | FEV1 | ||
|---|---|---|---|---|---|---|---|---|
| Measured | Predicted | Measured | Predicted | |||||
| A | Female | 23 | 166 | 56 | 3.74 | 3.81 | 2.29 | 3.33 |
| B | Female | 37 | 147.5 | 56 | 2.84 | 2.66 | 0.89 | 2.28 |
| C | Female | 68 | 156.5 | 47 | 2.79 | 2.25 | 0.73 | 1.86 |
| D | Female | 67 | 145.3 | 40 | 2.29 | 1.78 | 0.24 | 1.44 |
| E | Female | 62 | 162 | 61.8 | 2.26 | 2.67 | 0.7 | 2.25 |
| F | Female | 70 | 159 | 68 | 1.92 | 2.31 | 1.27 | 1.91 |
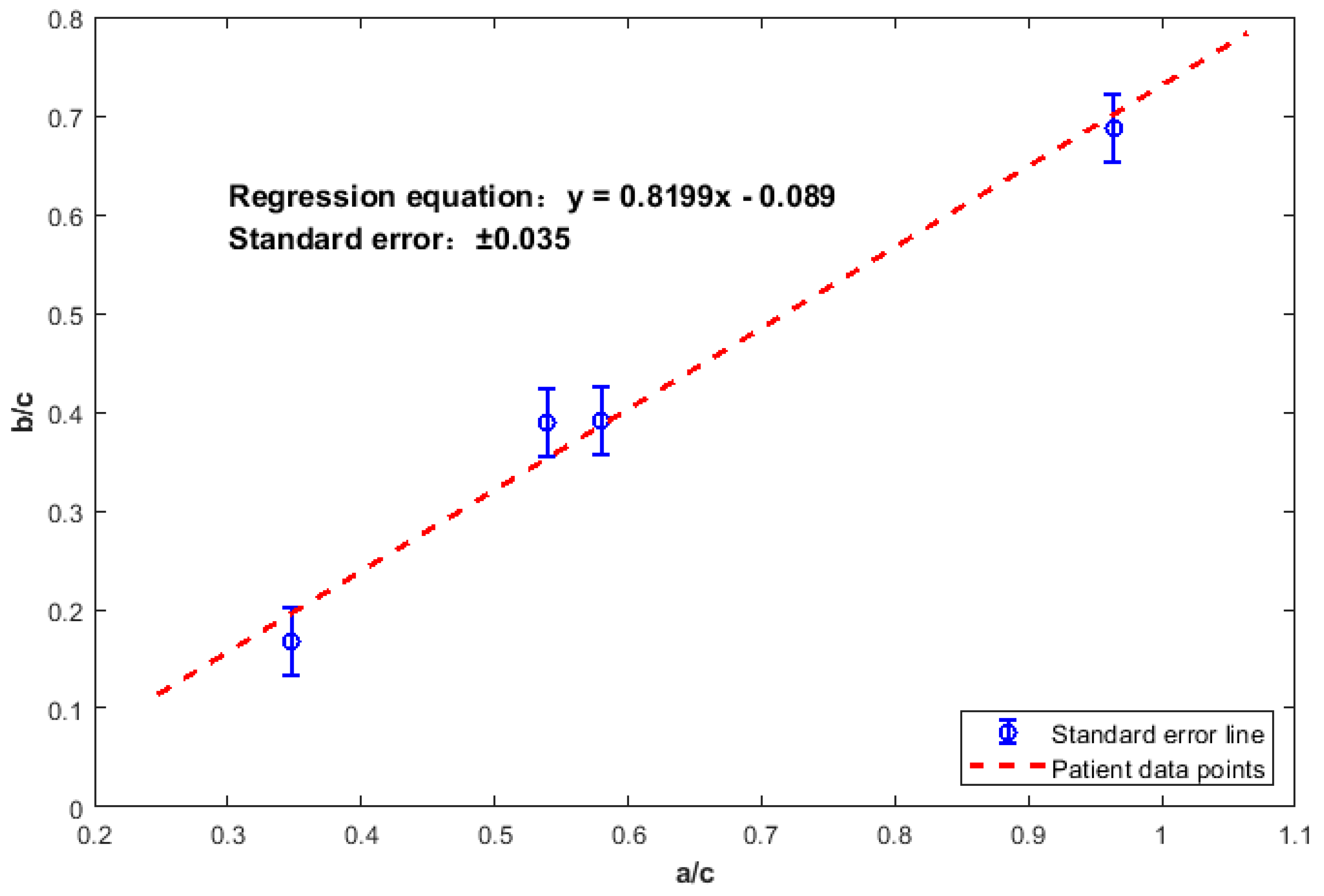
| Patient ID | a (L/s) | b (L/s) | c (L/s) | a/c | b/c |
|---|---|---|---|---|---|
| A | 3.210 | 2.29 | 3.33 | 0.964 | 0.688 |
| B | 1.230 | 0.89 | 2.28 | 0.539 | 0.390 |
| C | 1.079 | 0.73 | 1.86 | 0.580 | 0.392 |
| D | 0.500 | 0.24 | 1.44 | 0.347 | 0.167 |
| Patient ID | a (L/s) | b (L/s) | c (L/s) | a/c | b/c |
|---|---|---|---|---|---|
| E | 1.135 | 0.700 | 2.250 | 0.504 | 0.311 |
| F | 1.620 | 1.270 | 1.910 | 0.848 | 0.665 |
| Patient ID | The Predicted Value of b/c | The Measured Value of b/c | The Predicted Value of b | The Measured Value of b | |
|---|---|---|---|---|---|
| Value | 95% CI | ||||
| E | 0.325 | [0.298, 0.352] | 0.311 | 0.730 | 0.700 |
| F | 0.606 | [0.572, 0.640] | 0.665 | 1.158 | 1.270 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lian, X.; Hu, T.; Ma, S.; Ma, D. Pulmonary Function Prediction Method Based on Convolutional Surface Modeling and Computational Fluid Dynamics Simulation. Healthcare 2025, 13, 2196. https://doi.org/10.3390/healthcare13172196
Lian X, Hu T, Ma S, Ma D. Pulmonary Function Prediction Method Based on Convolutional Surface Modeling and Computational Fluid Dynamics Simulation. Healthcare. 2025; 13(17):2196. https://doi.org/10.3390/healthcare13172196
Chicago/Turabian StyleLian, Xianhui, Tianliang Hu, Songhua Ma, and Dedong Ma. 2025. "Pulmonary Function Prediction Method Based on Convolutional Surface Modeling and Computational Fluid Dynamics Simulation" Healthcare 13, no. 17: 2196. https://doi.org/10.3390/healthcare13172196
APA StyleLian, X., Hu, T., Ma, S., & Ma, D. (2025). Pulmonary Function Prediction Method Based on Convolutional Surface Modeling and Computational Fluid Dynamics Simulation. Healthcare, 13(17), 2196. https://doi.org/10.3390/healthcare13172196





