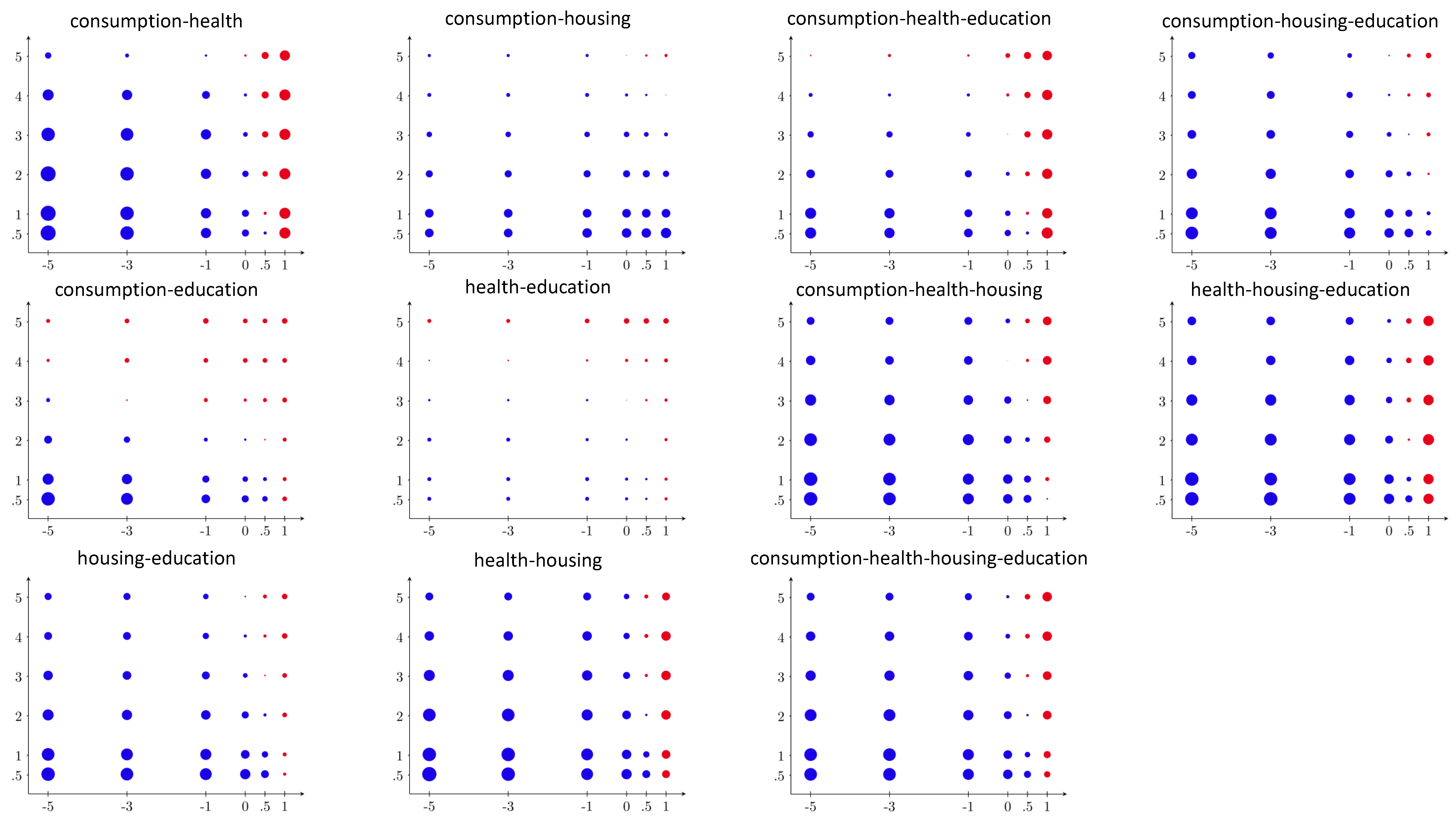
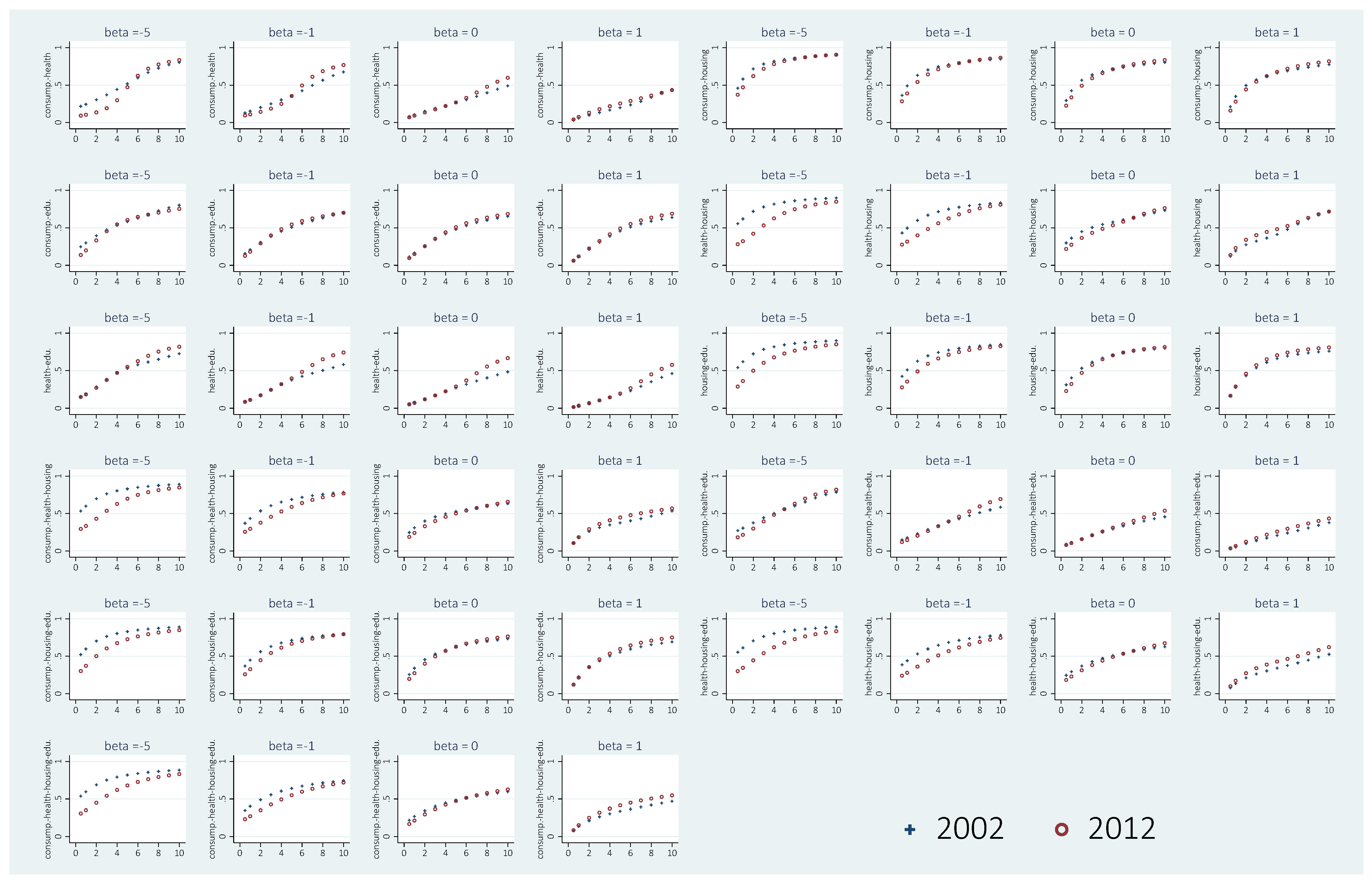
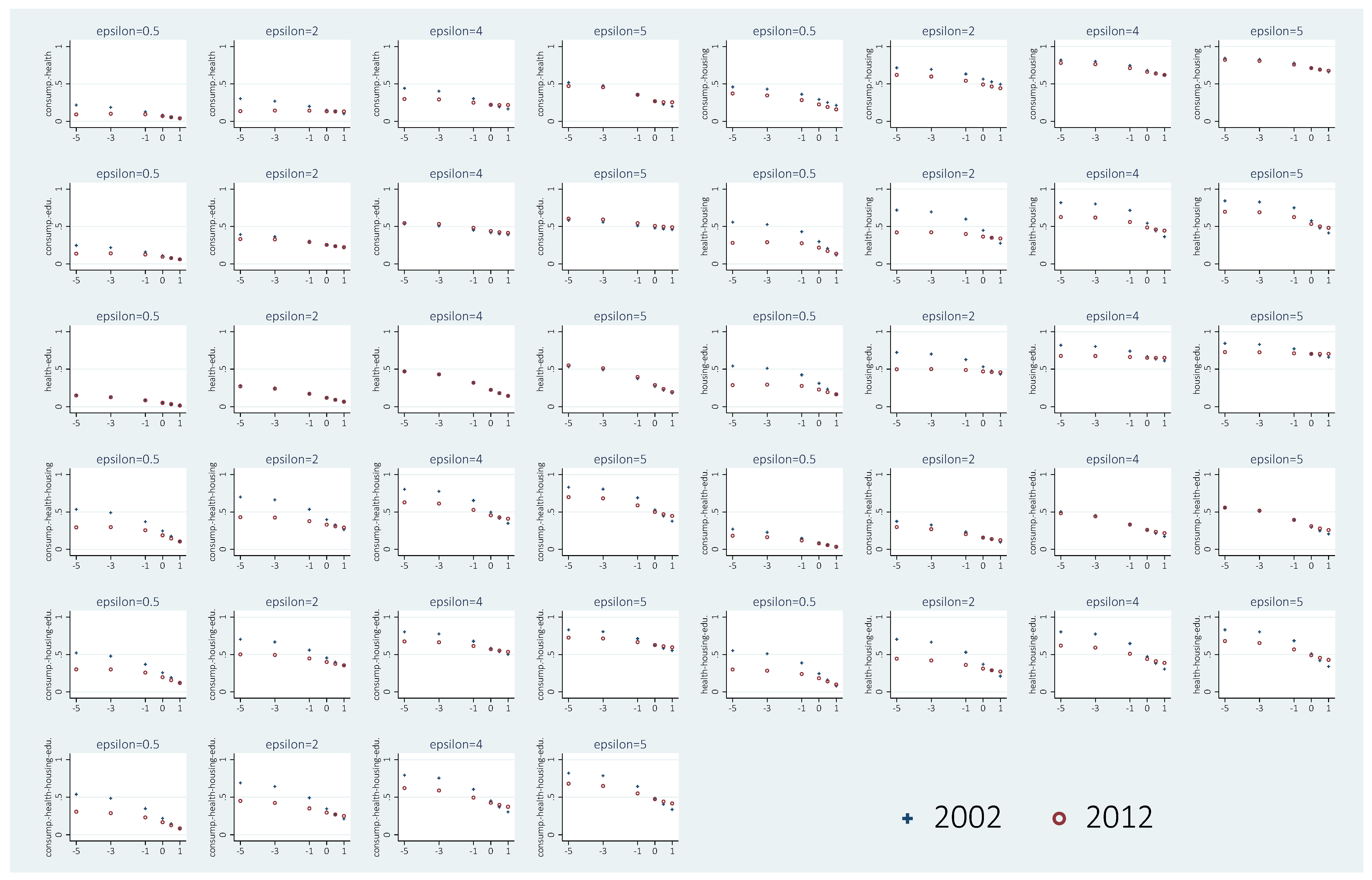
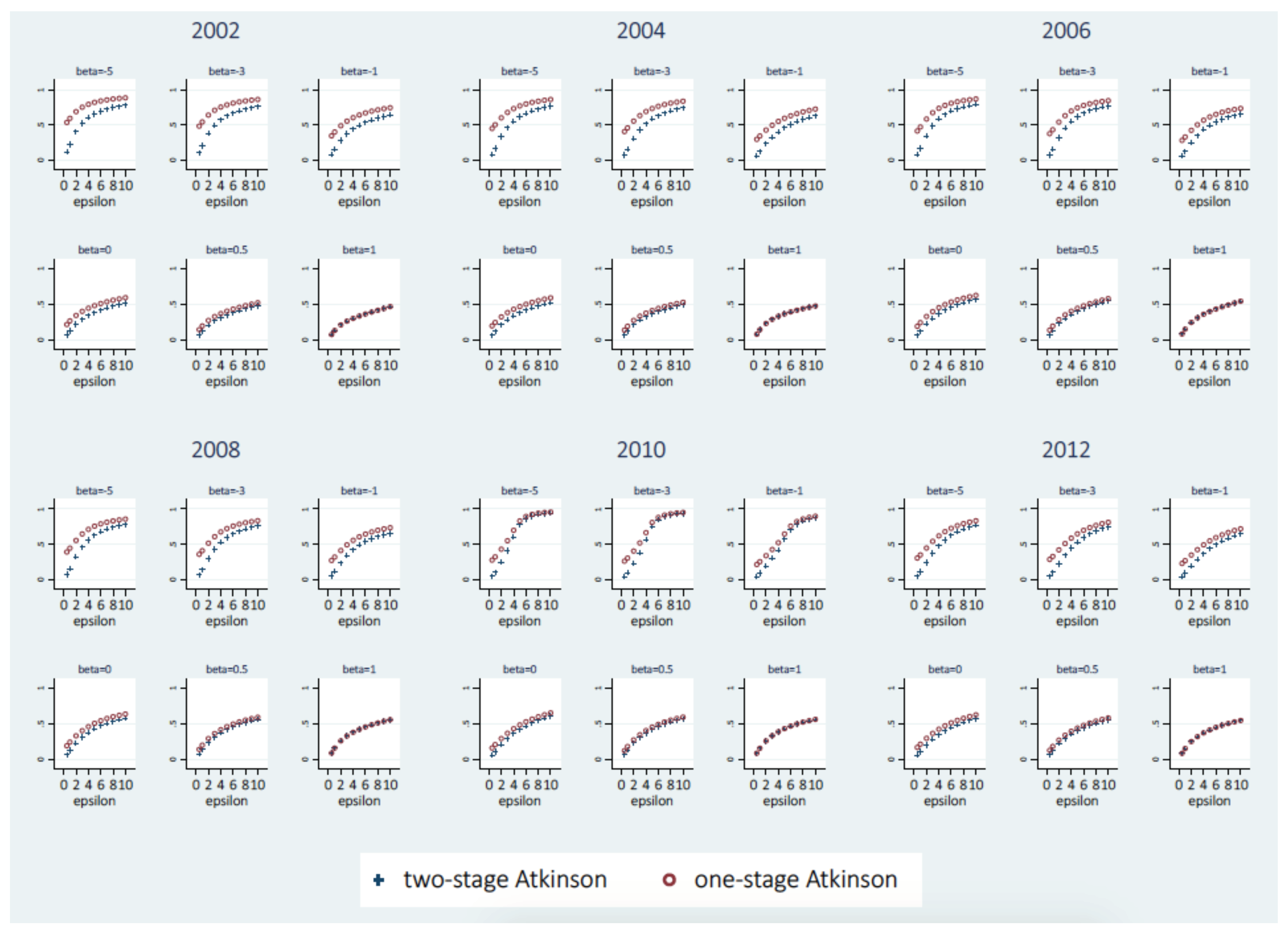
Economists have tended to study the distribution of well-being by looking at one dimension only: monetary income. Income was conceived as the most important means to attain well-being (see, e.g.,
Dalton 1920). It is now generally accepted, however, that well-being involves more than just money. This has led to a growing literature on multidimensional inequality (with the capability approach of
Sen (
1995), as an important source of inspiration) and to various attempts to extend the analysis of unidimensional inequality to a multidimensional framework. The multidimensional approach to the study of well-being was pioneered by
Fisher (
1956), who introduced a multidimensional distribution matrix to reflect the notion that besides monetary income other attributes also matter for individual welfare. Since then, the multidimensional aspects of inequality have received attention from many economists, such as
Atkinson and Bourguignon (
1982);
Maasoumi (
1986,
1989);
Savaglio (
2006);
Weymark (
2006) and
Muller and Trannoy (
2012).
Cowell (
2000) also mentioned briefly the multidimensional approaches in his discussion of the measurement of inequality.
2.1. Properties of Multidimensional Inequality Measures
When it comes to the measurement of one-dimensional inequality (typically inequality of per capita income or consumption), it is now customary to focus on measures of relative inequality that satisfy the properties of symmetry, replication invariance, mean independence and the Pigou–Dalton (or transfer) principle (
Sen 1997, p. 139). Sometimes additive decomposability is added to the list of desirable properties.
The symmetry principle demands that individuals are treated anonymously; for the measurement of inequality, it should not matter which specific individual earns which specific income. Replication invariance means that the population size of the studied society should play no role in inequality measurement. According to this principle, if we construct a new distribution by merging exact replicas of a given distribution, then the new distribution is considered to have exactly the same level of inequality as the original one. The mean independence property indicates that inequality does not change when all individuals of a given society experience a change of their attainments by the same proportion. If everyone’s income doubles, the level of inequality should remain the same as before. The Pigou–Dalton principle refers to the reaction of the index to mean-preserving transfers. Suppose income is transferred from a relatively poor individual to a relatively rich individual, while everything else remains unchanged. Since the relatively poor person gets poorer and the relatively rich person richer, this is a regressive transfer: it increases the dispersion of income within society. The Pigou–Dalton principle states that a regressive transfer must lead to an increase in the measured degree of inequality (
Sen 1973, p. 27). Finally, the property of subgroup decomposability deals with the relationship between the level of inequality in society as a whole, and the levels of inequality within and between subgroups of the population. Subgroup decomposability requires that it must be possible to express the degree of inequality in society as a whole as a sum of two components: the degree of inequality within the subgroups, and the degree of inequality between the subgroups. Moreover, the first component must be a simple function of the degrees of inequality within the subgroups.
It is possible to extend these properties to the multidimensional context. If we are considering g dimensions and n individuals, we have to use matrices to study the distribution of well-being. In what follows, we assume the () matrices X and Y represent two distributions of the g attributes of well-being (e.g., health and income) over the n individuals, with the rows corresponding to the individuals and the columns to the attributes.
Nothing essential needs to be changed to the definition of the symmetry property. Y is considered to be a permutation of X if there exists a permutation matrix P such that . The inequality index I has the symmetry principle if for any distribution Y that is a permutation of distribution X, the two distributions have the same level of inequality: . Likewise, it is straightforward to generalize the replication invariance property to the multidimensional case. If distribution Z consists of m exact replicas of distribution X, the property requires the two distributions to have the same levels of inequality.
The extension of the mean independence property is also immediate. For those attributes for which it is relevant (these are typically measured by ratio-scale variables, such as income) it means that the multiplication of the corresponding columns by an arbitrary positive scalar should have no influence on the measured degree of inequality. For instance, if we want the mean independence property to hold for the first attribute, then the following two distributions should have the same level of inequality:
The extension of the Pigou–Dalton principle to more than one dimension poses a few challenges. In general, the ranking of individuals according to one dimension (say health) does not concord with the ranking according to another (say income). An individual who is top-ranked by one attribute may very well be bottom-ranked by another. It is not immediately clear how individuals should be ranked for the multidimensional Pigou–Dalton principle. For example, if in matrix X the first column refers to health and the second to income, the second individual has a lower income rank but a higher health rank in comparison to the first individual. Does an income transfer from the first individual to the second still satisfy the Pigou–Dalton principle?
There is a large literature on this topic, and a good survey was made by
Aaberge and Brandolini (
2015, Section 3.4.1). The adoption of the uniform majorization criterion (
Kolm 1977;
Marshall et al. 1979;
Tsui 1995;
Weymark 2006) is one way of tackling the issue. It relies on the idea that a bistochastic transformation of a matrix generalizes the concept of a progressive Pigou–Dalton transfer. If matrix
Y can be obtained from matrix
X by a bistochastic transformation, distribution
Y is on the whole closer to the average than distribution
X, and therefore
Y is considered to be socially preferable to
X. Uniform majorization can be illustrated by the following example from
Decancq and Lugo (
2012). Let us compare two matrices,
X and
Y, as well as the bistochastic matrix
B:
Since
Y =
, it follows that
Y should be socially preferred to
X. As a result of the bistochastic transformation, every column of matrix
Y has the same mean but a less severe dispersion than the corresponding column of matrix
X. Uniform majorization states that on the whole well-being is more equally distributed in
Y than it is in
X.
Although the uniform majorization criterion succeeds in translating the idea of the Pigou–Dalton principle to a multidimensional setting, it has been criticized for its lack of taking into account the association between dimensional distributions. In reality, dimensions of well-being are often positively correlated; think of income and health. The inequality indices proposed by
Hicks (
1997);
Foster et al. (
2005) and
Gajdos and Weymark (
2005), as well as the poverty index suggested by
Alkire and Foster (
2011), also fail to capture the dimensional associations.
It has been argued that a good multidimensional index should be at least sensitive to the correlations between different welfare dimensions, since “various types of inequalities may strengthen each other” (
Stiglitz et al. 2009, p. 205). This implies that an additional criterion is required which explicitly captures these correlations in the multidimensional context.
Atkinson and Bourguignon (
1982) and
Walzer (
1983) were among the first to point out that multidimensional inequality should be sensitive to such dimensional associations.
Tsui (
1999) formalized their intuitions by means of the criterion of correlation increasing majorization, which is motivated by the concept of correlation increasing transfer studied by
Boland and Proschan (
1988). Imagine that we switch the positions of elements in the first column of matrix
X to form the following matrix
Y:
The element switching boosts the inter-attribute association. The association between the two considered attributes is obviously higher in matrix
Y than in matrix
X. In matrix
Y, the first individual is better placed than the others in not only one but two dimensions at the same time. In the same manner, the second and the third individuals are, respectively, the worst and the second worst off in both dimensions. In matrix
X, each individual attains less in one attribute but more in the other attribute in comparison to the other individuals. This means the relative shortfall in one dimension of an individual is compensated by his or her relatively better achievement in the other dimension. Hence, no one is best (or worst) off in both dimensions simultaneously.
According to this reasoning, the two-dimensional distribution is deemed more equal in matrix X than in matrix Y. The difference between the two matrices illustrates the criterion of correlation increasing majorization: element switching which strengthens the inter-attribute correlation increases multidimensional inequality.
Finally, the definition of subgroup decomposability remains the same as before.
2.2. Multidimensional Inequality Measurement
We have considered necessary properties for the measurement of multidimensional inequality. In this subsection, we summarize the ways in which multidimensional inequality has been measured. Typically, two fundamental procedures are required to measure the distribution of individuals’ attainments in all dimensions. One procedure compares the well-being attainments across individuals and another aggregates the attainments of different dimensions. In the literature, these two procedures are incorporated into the measurement process in a different ways. Three measurement approaches can be distinguished.
The first approach executes the two mentioned procedures in two consecutive calculation stages, and is normally referred to as the two-stage measurement approach which aggregates across individuals first (
Aaberge and Brandolini 2015, p. 194). In the first stage, inequality across individuals is measured for each separate dimension using the unidimensional measurement. In the second stage, these calculated levels of unidimensional inequality of all dimensions are aggregated into one summary level of multidimensional inequality. The relative importance of each dimension can be taken into account through the dimensional weights introduced in the second stage. For example, the well-known inequality-adjusted Human Development Index introduced in the 2010 edition of the Human Development Report (
UNDP 2010) and the multidimensional generalized Gini indices (
Gajdos and Weymark 2005) follow this approach. Since the distribution in each dimension is separately summarized before being incorporated into the multidimensional inequality, the potential correlations between component dimensions are completely ignored. The measurement cannot satisfy the criterion of correlation increasing majorization, but it still can meet the uniform majorization criterion (
Aaberge and Brandolini 2015).
The second approach also needs two separate calculation stages for the two fundamental procedures and is commonly referred to as the two-stage measurement approach which aggregates across dimensions first (
Aaberge and Brandolini 2015, p. 195). The first stage aggregates all dimensional attainments for each individual, and dimensional weights are incorporated into this step. The second stage measures the multidimensional inequality across individuals based on the distribution of the levels of well-being of individuals. This approach has been widely applied in a number of studies. For instance,
Maasoumi (
1986,
1989,
1999) employed a utility-like function to calculate well-being attainments for each individual, and then measured the inequality across individuals using unidimensional measurement.
Nilsson (
2010);
Justino (
2012) and
Rohde and Guest (
2013) used Theil indices, while
List (
1999);
Banerjee (
2010) and
Decancq and Lugo (
2012) used the Gini coefficient. By aggregating dimensional attainments for each individual, this measurement approach includes the correlations between component dimensions, hence can satisfy the correlation increasing majorization criterion, and also can satisfy the criterion of uniform majorization (
Aaberge and Brandolini 2015).
The third approach incorporates the procedures of aggregating across individuals and across dimensions into a unified multidimensional inequality index in only one rather than two separate stages. For this reason, it is called the direct one-stage approach (
Aaberge and Brandolini 2015, p. 196). Attainments in separate dimensions of an individual are combined into a function of well-being. This well-being function is embedded in the inequality function to form a one-stage multidimensional inequality index. In this way, the distributions of different attributes enter directly into the multidimensional inequality index. The one-stage approach can satisfy the criteria of uniform majorization and correlation increasing majorization since it takes the dimensional correlations into account while examining the attainments of individuals for all dimensions (
Aaberge and Brandolini 2015).
Tsui (
1995,
1999) adopted this approach using the Atkinson index.
List (
1999),
Brandolini (
2008) and
Decancq et al. (
2009) also extended Atkinson indices for multivariate measurement.
Erreygers (
2013) developed the dual and joint Atkinson indices, which require a specific social evaluation function, for the measurement of socioeconomic inequality of health.
Besides measuring the multidimensional inequality by means of a normative index, many researchers have employed stochastic dominance criteria (
Shorrocks 1983;
Lambert 2001) to examine multidimensional inequality (
Duclos et al. 2011;
Muller and Trannoy 2011;
Cowell et al. 2017;
Petrillo 2017) and multidimensional poverty (
Arndt et al. 2012;
Nanivazo 2015). The advantage of this method is that it is based on the comparison of the entire distributions of different dimensions rather than on the comparison of aggregated index values. However, the drawback is that it very often leads to an incomplete ranking of distributions, which reduces its usefulness for policymakers.