Industrial Productivity Divergence and Input-Output Network Structures: Evidence from Japan 1973–2012
Abstract
1. Introduction
2. Methods and Data
2.1. Input-Output Network Analysis
2.2. Stationary and Transitional Communities
2.3. Sigma and Beta Convergence Analysis
2.4. Data
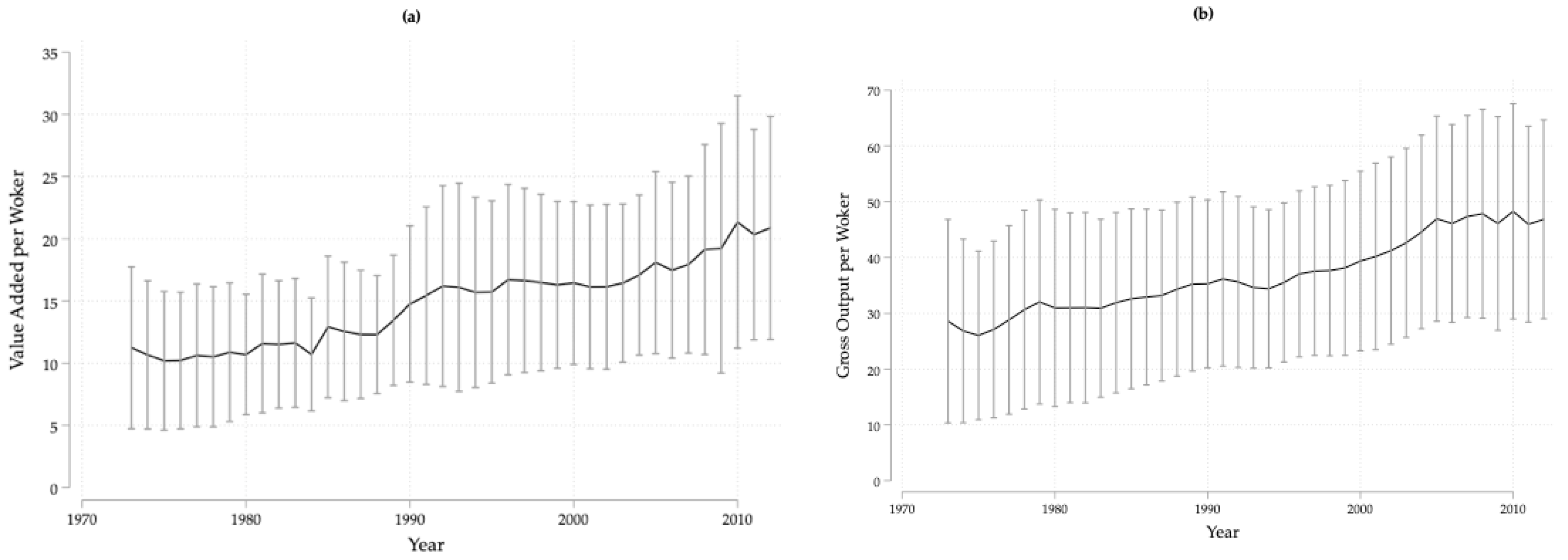
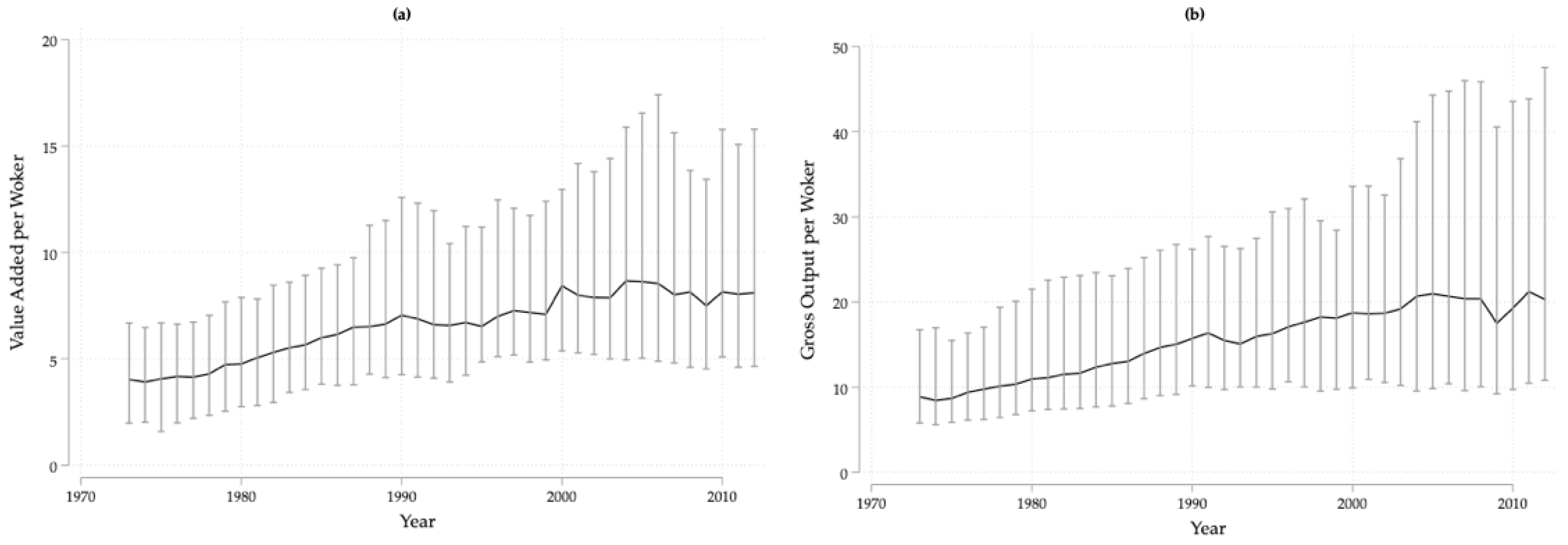
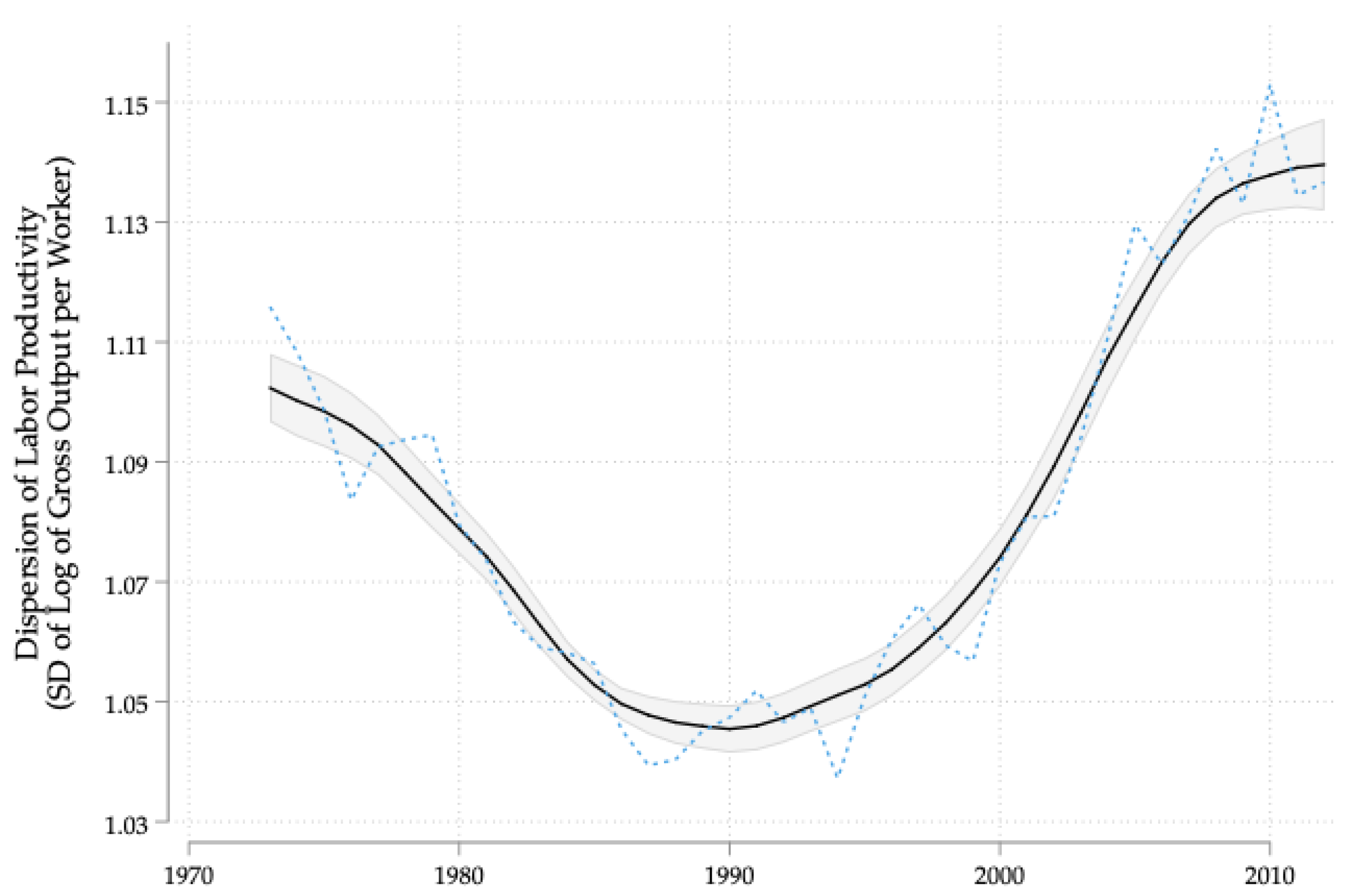
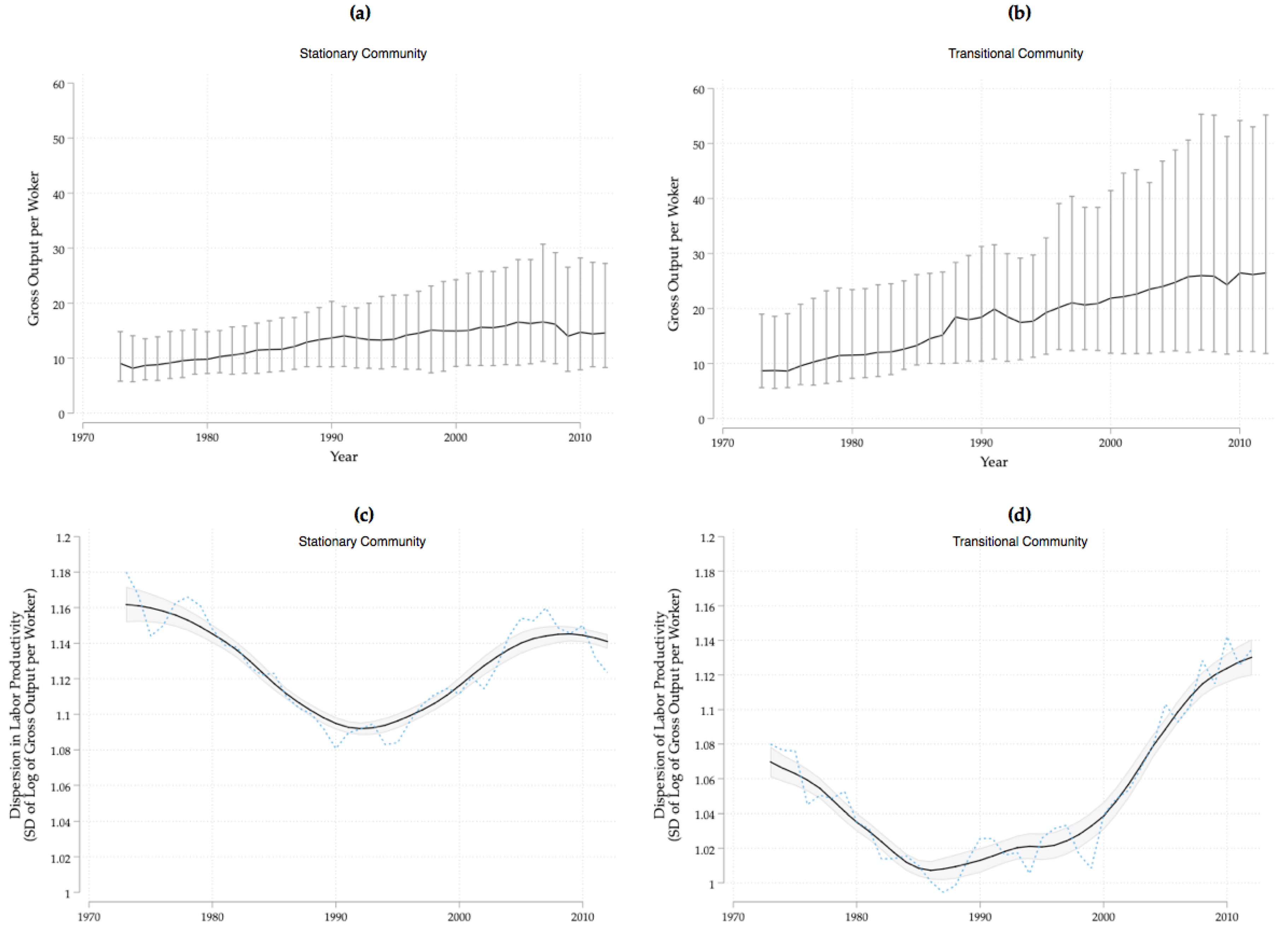
3. Some Stylized Facts: Productivity Dispersion and Divergence
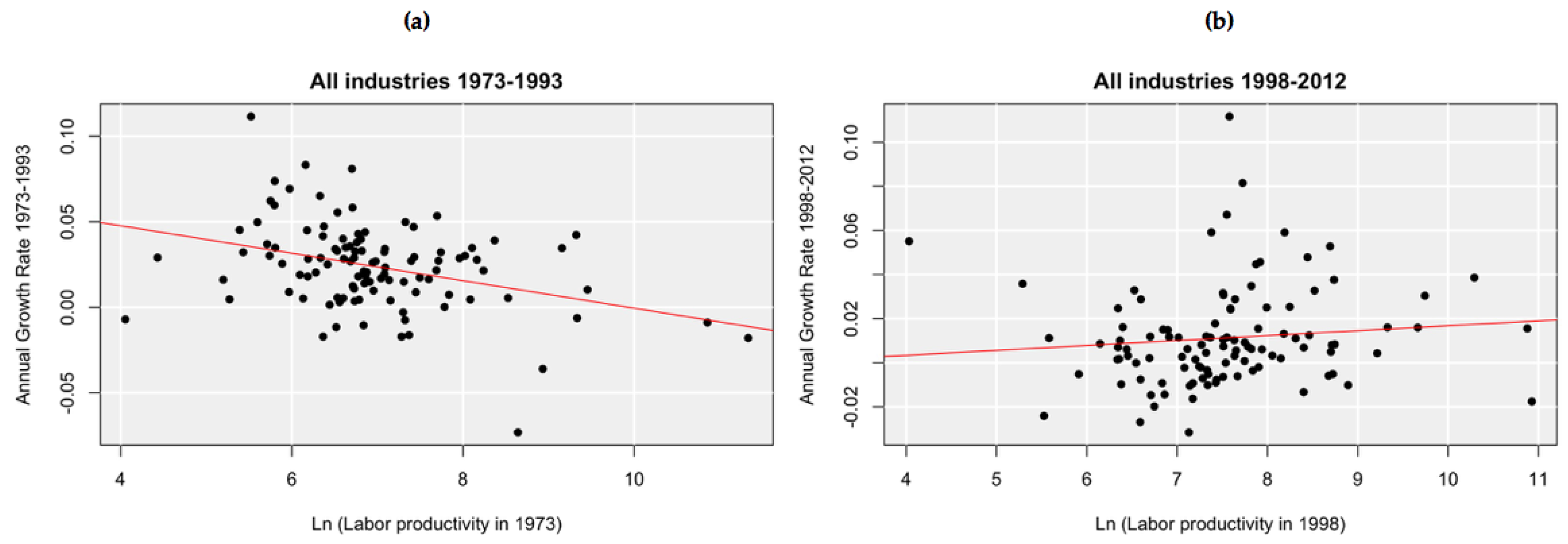
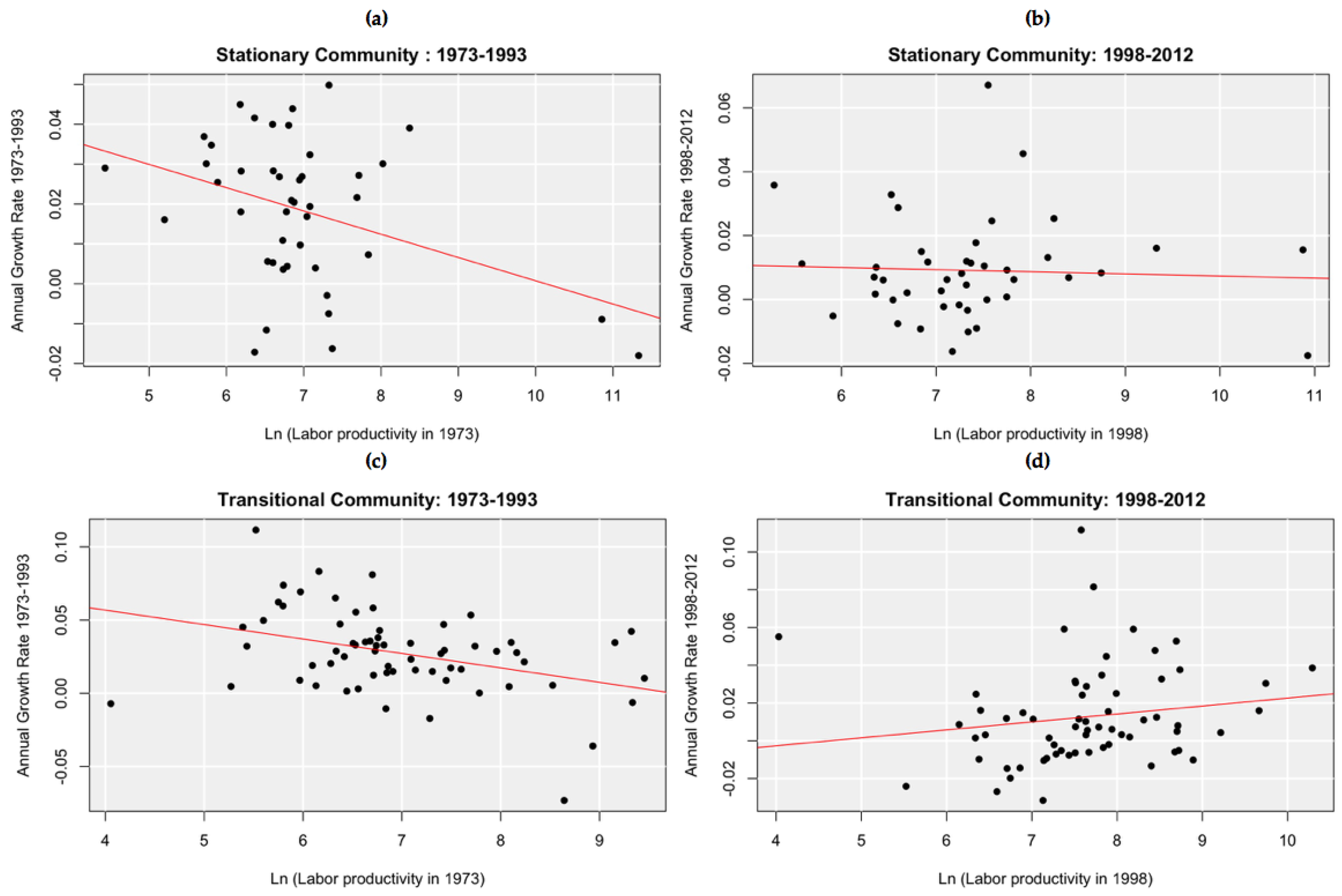
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| JIP 2015 | ||
|---|---|---|
| No. | Industry No. | Industry Name |
| 1 | 1 | Rice, wheat production |
| 2 | 2 | Miscellaneous crop farming |
| 3 | 4 | Agricultural services |
| 4 | 5 | Forestry |
| 5 | 11 | Miscellaneous foods and related products |
| 6 | 13 | Beverages |
| 7 | 15 | Textile products |
| 8 | 18 | Pulp, paper, and coated and glazed paper |
| 9 | 19 | Paper products |
| 10 | 21 | Leather and leather products |
| 11 | 22 | Rubber products |
| 12 | 27 | Chemical fibers |
| 13 | 28 | Miscellaneous chemical products |
| 14 | 30 | Petroleum products |
| 15 | 35 | Miscellaneous ceramic, stone and clay products |
| 16 | 41 | Miscellaneous fabricated metal products |
| 17 | 57 | Precision machinery and equipment |
| 18 | 58 | Plastic products |
| 19 | 59 | Miscellaneous manufacturing industries |
| 20 | 60 | Construction |
| 21 | 62 | Electricity |
| 22 | 64 | Waterworks |
| 23 | 67 | Wholesale |
| 24 | 68 | Retail |
| 25 | 69 | Finance |
| 26 | 70 | Insurance |
| 27 | 71 | Real estate |
| 28 | 72 | Housing |
| 29 | 73 | Railway |
| 30 | 74 | Road transportation |
| 31 | 75 | Water transportation |
| 32 | 77 | Other transportation and packing |
| 33 | 86 | Rental of office equipment and goods |
| 34 | 87 | Automobile maintenance services |
| 35 | 88 | Other services for businesses |
| 36 | 89 | Entertainment |
| 37 | 98 | Education (public) |
| 38 | 100 | Medical (public) |
| 39 | 101 | Hygiene (public) |
| 40 | 102 | Social insurance and social welfare (public) |
| 41 | 104 | Medical (non-profit) |
| 42 | 105 | Social insurance and social welfare (non-profit) |
| 43 | 107 | Others (non-profit) |
| 44 | 108 | Activities not elsewhere classified |
| JIP 2015 | ||
|---|---|---|
| No. | Industry No. | Industry Name |
| 1 | 3 | Livestock and sericulture farming |
| 2 | 6 | Fisheries |
| 3 | 7 | Mining |
| 4 | 8 | Livestock products |
| 5 | 9 | Seafood products |
| 6 | 10 | Flour and grain mill products |
| 7 | 12 | Prepared animal foods and organic fertilizers |
| 8 | 14 | Tobacco |
| 9 | 16 | Lumber and wood products |
| 10 | 17 | Furniture and fixtures |
| 11 | 20 | Printing, plate making for printing and bookbinding |
| 12 | 23 | Chemical fertilizers |
| 13 | 24 | Basic inorganic chemicals |
| 14 | 25 | Basic organic chemicals |
| 15 | 26 | Organic chemicals |
| 16 | 29 | Pharmaceutical products |
| 17 | 31 | Coal products |
| 18 | 32 | Glass and its products |
| 19 | 33 | Cement and its products |
| 20 | 34 | Pottery |
| 21 | 36 | Pig iron and crude steel |
| 22 | 37 | Miscellaneous iron and steel |
| 23 | 38 | Smelting and refining of non-ferrous metals |
| 24 | 39 | Non-ferrous metal products |
| 25 | 40 | Fabricated constructional and architectural metal products |
| 26 | 42 | General industry machinery |
| 27 | 43 | Special industry machinery |
| 28 | 44 | Miscellaneous machinery |
| 29 | 45 | Office and service industry machines |
| 30 | 46 | Electrical generating, transmission, distribution and industrial apparatus |
| 31 | 47 | Household electric appliances |
| 32 | 48 | Electronic data processing machines, digital and analog computer equipment and accessories |
| 33 | 49 | Communication equipment |
| 34 | 50 | Electronic equipment and electric measuring instruments |
| 35 | 51 | Semiconductor devices and integrated circuits |
| 36 | 52 | Electronic parts |
| 37 | 53 | Miscellaneous electrical machinery equipment |
| 38 | 54 | Motor vehicles |
| 39 | 55 | Motor vehicle parts and accessories |
| 40 | 56 | Other transportation equipment |
| 41 | 61 | Civil engineering |
| 42 | 63 | Gas, heat supply |
| 43 | 65 | Water supply for industrial use |
| 44 | 66 | Waste disposal |
| 45 | 76 | Air transportation |
| 46 | 78 | Telegraph and telephone |
| 47 | 79 | |
| 48 | 80 | Education (private and non-profit) |
| 49 | 81 | Research (private) |
| 50 | 82 | Medical (private) |
| 51 | 83 | Hygiene (private and non-profit) |
| 52 | 84 | Other public services |
| 53 | 85 | Advertising |
| 54 | 90 | Broadcasting |
| 55 | 91 | Information services and internet-based services |
| 56 | 92 | Publishing |
| 57 | 93 | Video picture, sound information, character information production and distribution |
| 58 | 94 | Eating and drinking places |
| 59 | 95 | Accommodation |
| 60 | 96 | Laundry, beauty and bath services |
| 61 | 97 | Other services for individuals |
| 62 | 99 | Research (public) |
| 63 | 103 | Public administration |
| 64 | 106 | Research (non-profit) |
References
- Abreu, Maria, Henri L. F. De Groot, and Raymond J. G. M. Florax. 2005. A meta-analysis of β-convergence: The legendary 2%. Journal of Economic Surveys 19: 389–420. [Google Scholar] [CrossRef]
- Acemoglu, Daron, Ufuk Akcigit, and William Kerr. 2016. Networks and the macroeconomy: An empirical exploration. NBER Macroeconomics Annual 30: 273–335. [Google Scholar] [CrossRef]
- Acemoglu, Daron, Vasco M. Carvalho, Asuman Ozdaglar, and Alireza Tahbaz-Salehi. 2012. The network origins of aggregate fluctuations. Econometrica 80: 1977–2016. [Google Scholar] [CrossRef]
- Barro, Robert J., and Xavier Sala-i Martin. 1992a. Convergence. Journal of Political Economy 100: 223–51. [Google Scholar] [CrossRef]
- Barro, Robert T., and Xavier Sala-i Martin. 1992b. Regional growth and migration: A Japan-United States comparison. Journal of the Japanese and International Economies 6: 312–46. [Google Scholar] [CrossRef]
- Baumol, William J. 1986. Productivity growth, convergence, and welfare: What the long-run data show. The American Economic Review 76: 1072–85. [Google Scholar]
- Bernard, Andrew B., and Charles I. Jones. 1996. Comparing apples to oranges: Productivity convergence and measurement across industries and countries. The American Economic Review 86: 1216–38. [Google Scholar] [CrossRef][Green Version]
- Blondel, Vincent D., Jean-Loup Guillaume, Renaud Lambiotte, and Etienne Lefebvre. 2008. Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment 2008: P10008. [Google Scholar] [CrossRef]
- Carvalho, Vasco M. 2014. From micro to macro via production networks. Journal of Economic Perspectives 28: 23–48. [Google Scholar] [CrossRef]
- Cerina, Federica, Zhen Zhu, Alessandro Chessa, and Massimo Riccaboni. 2015. World input-output network. PLoS ONE 10: e0134025. [Google Scholar] [CrossRef]
- Del Río-Chanona, Rita María, Jelena Grujić, and Henrik Jeldtoft Jensen. 2017. Trends of the world input and output network of global trade. PLoS ONE 12: e0170817. [Google Scholar] [CrossRef]
- Fortunato, Santo. 2010. Community detection in graphs. Physics Reports 486: 75–174. [Google Scholar] [CrossRef]
- Fortunato, Santo, and Darko Hric. 2016. Community detection in networks: A user guide. Physics Reports 659: 1–44. [Google Scholar] [CrossRef]
- Furceri, Davide. 2005. β and σ-convergence: A mathematical relation of causality. Economics Letters 89: 212–15. [Google Scholar] [CrossRef]
- Girvan, Michelle, and Mark E. J. Newman. 2002. Community structure in social and biological networks. Proceedings of the National Academy of Sciences USA 99: 7821–26. [Google Scholar] [CrossRef]
- Islam, Nazrul. 2003. What have we learnt from the convergence debate? Journal of Economic Surveys 17: 309–62. [Google Scholar] [CrossRef]
- Kagawa, Shigemi, Shunsuke Okamoto, Sangwon Suh, Yasushi Kondo, and Keisuke Nansai. 2013. Finding environmentally important industry clusters: Multiway cut approach using nonnegative matrix factorization. Social Networks 35: 423–38. [Google Scholar] [CrossRef]
- Karrer, Brian, and Mark E. J. Newman. 2011. Stochastic blockmodels and community structure in networks. Physical Review E 83: 016107. [Google Scholar] [CrossRef]
- Leontief, Wassily. 1944. Output, employment, consumption, and investment. The Quarterly Journal of Economics 58: 290–314. [Google Scholar] [CrossRef]
- Melitz, Marc J. 2003. The impact of trade on intra-industry reallocations and aggregate industry productivity. Econometrica 71: 1695–725. [Google Scholar] [CrossRef]
- Newman, Mark E. J. 2006. Finding community structure in networks using the eigenvectors of matrices. Physical Review E 74: 036104. [Google Scholar] [CrossRef]
- Newman, Mark E. J., and Michelle Girvan. 2004. Finding and evaluating community structure in networks. Physical Review E 69: 026113. [Google Scholar] [CrossRef]
- Phillips, Peter C. B., and Donggyu Sul. 2007a. Some empirics on economic growth under heterogeneous technology. Journal of Macroeconomics 29: 455–69. [Google Scholar] [CrossRef]
- Phillips, Peter C. B., and Donggyu Sul. 2007b. Transition modeling and econometric convergence tests. Econometrica 75: 1771–855. [Google Scholar] [CrossRef]
- Sala-i-Martin, Xavier. 1996. The classical approach to convergence analysis. The Economic Journal 106: 1019–36. [Google Scholar] [CrossRef]
- Solow, Robert M. 1956. A contribution to the theory of economic growth. Quarterly Journal of Economics 70: 65–94. [Google Scholar] [CrossRef]
- Zhu, Zhen, Federica Cerina, Alessandro Chessa, Guido Caldarelli, and Massimo Riccaboni. 2014. The rise of china in the international trade network: A community core detection approach. PLoS ONE 9: e105496. [Google Scholar] [CrossRef]
| 1. | Directed networks can have a node connect to another without the latter necessarily connecting to the first. Weighted networks are those with weights in their links, which allows for asymmetric relationships. |
| 2. | We acknowledge and thank the insightful comments of an anonymous referee who helped improving this section. |
| 3. | See the work of Abreu et al. (2005) and Islam (2003) for some comprehensive reviews of this literature. |
| 4. | Assortativity refers to the tendency of nodes in a network to connect with others with similar characteristics while dissasortativity implies the opposite case. |
| 5. | The simplest form of beta convergence, also known as absolute beta convergence, is commonly used for the study of production units that share common technological and institutional environments. |
| 6. | For the labor productivity convergence analysis, however, 107 industries are considered. This is because there is no systematic data on the number of workers for the Housing industry (JIP code 72). |
| 7. | From a conceptual standpoint, however, using the number of work-hours allows for a more precise definition of labor productivity. |
| 8. | We do not take into account self-loops in the networks since communities are defined considering only linkages between different nodes. |
| 9. | There is an important statistical difference when comparing the regression lines of Figure 4. In panel (a) the relationship is statistically significant, whereas in panel (b) it is not. Indeed, when we estimate a linear relationship for the 1990–2012 period the regression line is actually flat. |
| 10. | Based on panel (a) of Figure 4, relatively low productivity industries are those whose labor productivity was less than 6 in log terms. Although this threshold is arbitrary, its selection is just for illustration purposes. |
| 11. | As we noted in the introduction, community detection algorithms sometimes produce communities with some overlap. In our case this means that there may be some industries from the non-service sector present too. Ways to solve this type of issues are actively being researched in the field. |
| 12. | We tested and compared these results with the Louvain algorithm (Blondel et al. 2008) as a robustness check. The resulting communities obtained mostly coincide with those from the Newman (2006) algorithm we used. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domínguez, A.; Mendez, C. Industrial Productivity Divergence and Input-Output Network Structures: Evidence from Japan 1973–2012. Economies 2019, 7, 52. https://doi.org/10.3390/economies7020052
Domínguez A, Mendez C. Industrial Productivity Divergence and Input-Output Network Structures: Evidence from Japan 1973–2012. Economies. 2019; 7(2):52. https://doi.org/10.3390/economies7020052
Chicago/Turabian StyleDomínguez, Alvaro, and Carlos Mendez. 2019. "Industrial Productivity Divergence and Input-Output Network Structures: Evidence from Japan 1973–2012" Economies 7, no. 2: 52. https://doi.org/10.3390/economies7020052
APA StyleDomínguez, A., & Mendez, C. (2019). Industrial Productivity Divergence and Input-Output Network Structures: Evidence from Japan 1973–2012. Economies, 7(2), 52. https://doi.org/10.3390/economies7020052





