Abstract
The present study applies a bootstrapped data envelopment analysis (DEA) procedure to compute bias-corrected measures of agricultural total factor productivity (TFP) change and its components (technical change and technical efficiency change) using a panel data of 19 regions of Bangladesh covering a 23-year period (1987–2009), thereby overcoming the limitation of the lack of statistical inference of the conventional non-parametric DEA. Results revealed that overall productivity grew at a modest rate of 0.03%, mainly powered by technological progress at 0.03% and a negligible decline in technical efficiency at 0.004% with large disparities amongst regions. Six regions in the middle order shifted ranks with regard to TFP change following bias correction. The estimated confidence intervals demonstrated that many regions underwent either progress or regress in productivity performance over time. Investments in research and development (R&D), agricultural extension, and crop diversification are suggested to improve regional inequality and declining technical efficiency.
Keywords:
total factor productivity change; efficiency change; technical change; bootstrapped DEA; Malmquist indices; agriculture; Bangladesh JEL Classification:
C14; C150; O47; Q16
1. Introduction
Agriculture is one of the most important economic sectors in Bangladesh, as it contributes 14.23% to the country’s GDP (BER 2018) and employs 41% of the labor force (BBS 2018). Bangladesh is also one of the most densely populated nations of the world (964 persons per Km2) with an estimated population of 142.3million, of which 75% live in rural areas (BBS 2010). The nation also suffers from one of the lowest land–man ratios of the world (0.2 ha per person), making it very difficult to achieve food security (Rahman and Salim 2013). As a result, Bangladesh has designed and implemented various agricultural policies for quick transformation of the agricultural sector through rapid technological progress aimed at alleviating poverty and raising the standard of living of its increasing population (Rahman 2003). The process started from the early 1960s to diffuse High Yielding Varieties (HYV) of rice technology with corresponding support in the provision of modern inputs, such as chemical fertilizers, pesticides, irrigation equipment, institutional credit, product procurement, storage and marketing facilities (Rahman 2003). However, the diffusion of HYV technology went through various cycles, picking up during its inception stage (i.e., 1970s), then slowing during the early 1980s, then picking up again from the late 1980s in response to policy reforms aimed at liberalization of the procurement and distribution of agricultural inputs and a reduction of import duties on agricultural equipment (Hossain and Akash 1994). As a result, irrigation coverage, which is a major pre-requisite for the expansion of HYV rice technology, increased dramatically to 51.5% of gross cropped area in 2000–2001 from 22.5% in 1980-1981 (Praduman et al. 2008). In addition, various polices were also undertaken gradually from the 1990s, aimed at ensuring food grain availability and food security in the long run. However, the realization of these aims remained unfulfilled as the country is still identified as a food deficit nation with occasional self-sufficiency in some years (Alam et al. 2011). Therefore, agricultural productivity growth and efficiency improvement remain a top priority for Bangladesh in order to meet food needs for its rapidly increasing population.
Improving productivity and efficiency are the two fundamental strategies to develop a country’s economy. Productivity growth in agriculture has been the subject matter of intense research over the last five decades due to: (i) its determinant role in economic growth of low-income regions; (ii) its ability to produce higher quality goods in a more efficient manner, thereby leading to lower costs to consumers, as well as release resources to other sectors and raise per capita income; and (iii) its ability to grow output at a sufficiently rapid rate to meet increasing demands for food, owing to steady population growth (Trueblood and Coggins 2003). Bangladesh is no exception as it requires these three aspects to be fulfilled by its agricultural sector.
Several studies have used the non-parametric Data Envelopment Analysis (DEA) approach to measure productivity and efficiency in the agricultural sector. Chen et al. (2008) and Yao and Li (2010) used DEA to construct their best-practice frontier in the agricultural sector. DEA was also used by Suhariyanto and Thirtle (2001), Trueblood and Coggins (2003), Coelli and Rao (2005), and Headey et al. (2010) to estimate growth in agricultural productivity and its components at an international scale. The principal advantage of DEA is that it does not require any assumption regarding the behaviour of the market and price information (Rahman 2003). However, the use of DEA and Malmquist indices to measure productivity and efficiency were criticized for not providing statistical precision of the estimates (Caves et al. 1982; Färe et al. 1994; Coelli et al. 1998), which is required to determine whether the observed differences of the estimated results are systematic or not. To overcome this drawback, the present study employs the bootstrap method proposed by Simar and Wilson (1999), originally introduced by Efron (1979), to provide statistical accuracy of the DEA estimator. In this process, the DEA estimator is re-sampled and then the re-sampled estimates are used to calculate bootstrap confidence intervals that determine desired statistical inferences. Simar and Wilson (1998, 1999) have proven that DEA can allow for the addition of random errors while maintaining all of the method’s advantages. Bootstrapping to estimate confidence intervals for the DEA scores have previously been used in several studies (e.g., Odeck 2009; Vasiliev et al. 2011; Čechura 2012) who pointed out that the observed differences in the estimates obtained by applying conventional DEA methods may not be significant.
Many studies have analyzed total factor productivity (TFP) growth of Bangladesh agriculture using non-parametric approaches but none has computed confidence intervals of the efficiency and productivity scores to provide statistical inferences. For example, Pray and Ahmed (1991), Dey and Evenson (1991), Suhariyanto and Thirtle (2001), Rahman (2007), and Rahman and Salim (2013) measured Bangladesh agricultural TFP growth using a range of non-parametric approaches including DEA. However, none of these studies used bootstrapping procedure to correct bias of the DEA or TFP indices, which may lead to biased conclusions. Also, except Rahman and Salim (2013), all previous studies of productivity growth in Bangladesh agriculture used dated data ending in1992. Therefore, this research contributes to the existing literature by providing a bias-corrected measure of agricultural TFP change and its components for 19 regions of Bangladesh for a recent 23-year period (1987–2009), so that the results complement or conform with Rahman and Salim (2013), who used data for a longest 61-year period (1948–2008) using a linear programming technique.
Given this background, the objectives of this study are to: (i) examine growth of TFP and its components (i.e., technical change (TECH) and technical efficiency change (EC)); and (ii) test the robustness of these results by estimating confidence intervals using bootstrap method. To fulfill these objectives, we first use DEA to estimate Malmquist indices to assess TFP growth, TECH, and EC over the study period of 1987–2009, and finally use the bootstrapping technique to determine accuracy of the DEA estimates.
2. Methodology
2.1. Efficiency and Productivity Measurement Using Data Envelopment Analysis (DEA)
The non-parametric DEA and Malmquist index method was pioneered by Caves et al. (1982) and developed further by Färe et al. (1994), and it provides a decomposition of firms’ productivity change into efficiency change and technological change (Coelli et al. 1998). The use of non-parametric DEA approach is quite popular for several reasons. First, it does not need the assumptions regarding the functional form of the production technology and does not require price data. Second, for multiple inputs and outputs, DEA does not require aggregation. Third, because DEA is predicated on linear programming techniques, it is possible to identify the “best practice” for every firm. Finally, its ability to decompose productivity growth into two components: changes in technical efficiency over time (catching-up) and technical change (shifts in technology over time) (Färe et al. 1994).
DEA is a linear programming methodology suitable for both input-oriented and output-oriented specification of the production technology. Input-oriented measure refers to production technology that considers maximum possible proportional reduction in input usage, with output levels held fixed. In the output-oriented case, the DEA method seeks maximum proportional increase in output production, with input levels held constant. Both measures derive the same technical efficiency scores when technology exhibits constant returns to scale (CRS), but not when technology exhibits variable returns to scale (VRS). In this study we considered an output distance function under CRS technology because it would be fair to assume that one usually attempts to maximize output from a given set of inputs in agriculture, rather than the inverse.
2.2. The Malmquist TFP Index
The Malmquist index is defined using distance functions. By estimating input or output distance functions, DEA can also be used to decompose Malmquist TFP change into movements of the frontier (technical change—TECH) and movements toward the frontier (technical efficiency change—EC) (see Coelli and Rao 2005 for further discussion). Specifically, for a pair of input–output vectors (xs, ys) and (xt, yt) at two time points, s and t, the Malmquist TFP index is defined using the output distance functions computed for the observed input–output vectors in periods s and t, evaluated at the technologies prevailing in periods s and t. Following Caves et al. (1982), Färe et al. (1994), and Coelli and Rao (2005), the Malmquist TFP index can be defined as follows:
where represents the output distance from the period t observation to the period s technology as the reference technology. A value of mo greater than one will indicate positive TFP growth while a value less than one indicates a TFP decline. Note that Equation (1) is the geometric mean of two TFP indices. The first index is estimated with respect to period s technology and the second with respect to period t technology. An equivalent way of writing this productivity index is
The ratio outside the square brackets measures the technical efficiency change (EC) between period s and t. That is, the efficiency change is equivalent to the ratio of the technical efficiency in two periods. The technical efficiency change can be further decomposed into ‘pure’ efficiency and scale efficiency (Coelli et al. 1998). The remaining part of the index in Equation (2) is a measure of technological change (TECH). It is the geometric mean of the shift in technology between the two periods. EC is greater than, equal to, or less than unity as technical efficiency improves, remains unchanged, or declines between two periods.
Equation (2) indicates that the computation of TFP change between two periods, s and t. requires solution of four output-distance functions. Following Färe et al. (1994), the distance functions are calculated by using DEA-like linear programming (LP) models. The required LPs under the constant returns to scale (CRS) technology are:
and
In production economics, solving these linear programming problems is called Data Envelopment Analysis (Yin 2000).
2.3. Bootstrapping to Estimate Confidence Intervals
The DEA approach is best suited for measuring productivity in multi-output and multi-input technologies even in the absence of price data (Headey et al. 2010). However, the major criticism of the DEA approach is the lack of information about estimates’ uncertainty and biased measures of estimates of efficiency. The other drawback of the DEA is that its results may be affected by sampling variation. Bootstrapping methods have been developed to correct bias in DEA estimators and to construct confidence intervals for assessing sampling variability of the results using homogenous bootstrap procedure (Simar and Wilson 1999). A number of studies have applied this method (e.g., Kuosmanen et al. 2006; Abatania et al. 2012; Gitto and Mancuso 2012). However, most of the bootstrap applications are in the non-agricultural sector (e.g., Simar and Wilson 1999; Gitto and Mancuso 2012). Use of the bootstrap method to determine precision of the estimates in the agricultural sector is rare and a few available are confined to only farm-level cross-sectional data (Balcombe et al. 2008; Abatania et al. 2012; Bagchi and Zhuang 2016). Therefore, our application of the bootstrap procedure to panel data for the agricultural sector is another aspect of our contribution to the existing relevant literature.
According to Simar and Wilson (1998), the idea underlying bootstrapping is to approximate a true sampling distribution by mimicking data generating process (DGP). However, the problem arises due to simulation of a true sampling distribution by consistent mimicking of DGP. They argued that if the distance estimation values are close to unity and resampling done directly from the set of original data to build pseudo-samples, then it will provide inconsistent bootstrap estimation of the confidence intervals. To overcome this problem, Simar and Wilson (1998) suggested using a smooth bootstrap procedure. They applied a univariate kernel estimator of the density of the original distance function estimates to construct the pseudo-data. In addition, the Malmquist index uses panel data instead of a single cross-section of data, with the possibility of temporal correlation. For this reason, Simar and Wilson (1999) modified the bootstrap procedure to protect the temporal correlation that exist in the data by employing a bivariate smoothing procedure that takes all these features into account to achieve consistent replication of the DGP.
The basics of obtaining bootstrapping efficiency scores are to construct a large number of pseudo-data set and re-estimate the DEA model with this new data set. After many repetitions of the process, we obtain a good approximation of the true distribution of the sampling. This implies that the DGP is now different. Once we have a large bootstrap sample , then our most important task is to know how to make inference. If we have a consistent DGP estimator, the bootstrap distribution will mimic the original sampling distribution of the estimators of interest. Then, by using the bootstrap sample we can estimate the level of bias of each of the estimations as:
where, then it is possible to obtain a bias-corrected estimator for as:
Furthermore, the empirical distribution of provides, after correction for bias, confidence intervals for :
where is the 100 th percentile of the empirical distribution of the corrected for bias distribution denoted by .
To estimate confidence intervals through bootstrap technique, consider the unknown distribution to be approximated by the distribution where is the DEA estimate of index as indicated previously and to be the bootstrap estimator of the Malmquist productivity index. If we knew the distribution of , then the ideal confidence interval would be
To find the values of and would be trivial for the usual confidence levels (α = 0.10, α = 0.05). Unfortunately, the distribution is unknown. Since we do not know the distribution, we can use the bootstrap values such that (Simar and Wilson 1999):
Also, as it is true that when B→∞
It can be written from Equations (11) and (12)
It involves mechanical sorting of the values b = 1, …, B in increasing order and then deleting ((α/2) × 100) percent of the elements at either end of this sorted array, and finally setting and at that two extreme points, meeting the condition . This method is known as the percentile method.
Once we obtain both values, by rearranging the terms in (13) we then obtain:
which is a (1 − α)% confidence interval indicating that productivity indices progress or regress at a significant level from its base if the interval does not include unity.
This bootstrap procedure for Malmquist productivity indices was implemented using FEAR software package program developed by (Wilson 2010).
2.4. Data and Variables
This section presents definition of inputs and outputs and the dataset used in this research. The panel data used for this study covers a 23-year period (1987–2009) disaggregated into 19 regions of Bangladesh. At present there are 64 districts which are conventionally divided into 19 regions (greater districts), as most of the time series data are still available only at the greater district level. All data comes from various issues of the Yearbook of Agricultural Statistics for the years 1992–2012 published annually by the Bangladesh Bureau of Statistics (BBS).
Aggregate crop output includes four major crop groups at the regional level over the study period 1987–2009 and is measured in metric tons, namely (i) ‘cereals’—includes local varieties of rice and HYV rice grown in each of the three seasons (Aus—pre-monsoon, Aman—monsoon, and Boro—dry winter season), wheat, and maize; (ii) ‘cash crops’—includes jute, cotton, and sugarcane; (iii) ‘pulses’—includes gram, mungbean, lentil, khesari, and arhar; and (iv) ‘potatoes’—includes potatoes and sweet potatoes.
Five inputs are specified: land, labor, animal power, fertilizer, and irrigation. Area (in hectares) under all crops recorded for the output series is considered as the ‘land area under cultivation’. ‘Labor’ refers to economically active population engaged in agriculture. Economically active population is defined as all persons engaged or seeking employment in an economic activity, whether as employers, own-account workers, salaried employees or unpaid workers assisting in the operation of a family farm or business. This variable obviously overstates labor input used in agricultural production. However, since Bangladesh is still at the lower end of the development stage, the level of overstatement is likely to be low as the sector employs 48% of the labor force (BBS 2010). ‘Animal power’ refers to the number of draft animals and is estimated using linear trend interpolation from actual counts available in the agricultural censuses of 1983–1984, 1996, and 2008. ‘Fertilizer’ is measured in actual nutrient content (in metric tons) of three major types of fertilizers, i.e., active ingredients of nitrogen (N), potassium (K), and phosphorus (P) obtained from urea, triple super phosphate, muriate of potash, and di-ammonium phosphate fertilizers. ‘Irrigation’ refers to the proportion of total cultivated land area under irrigation and includes irrigation by all means, such as power pump, shallow tube-well, deep tube-well, hand tube-well, and traditional methods.
Although the data used in this study are 10 years old, little has changed in cultivation methods, intercultural operation, and practices over this period in Bangladesh. Consequently, we assume that there will be no significant changes in the result. Many research articles have also been published using many-years-old data. For example, Coelli et al. (2003) and Rahman (2007) used dataset for the period of 1961–1992 and 1964–1992 but published in 2003 and 2007, respectively. Therefore, we argue that our findings are capable of providing important information to policy makers.
3. Results and Discussion
We present the results in subsections. The discussion begins by regional analyses of the changes in productivity, technology, and efficiency indices based on original and bootstrapped methods. Finally, overall growth rate of productivity, technology, and efficiency indices for the nation as a whole over the study period based on original and bootstrapped methods are discussed.
3.1. Growth in TFP and Its Components by Region
In this section, we examine movements in the level of TFP growth and its components (TECH and EC). This section also illustrates the annual growth rate of TECH, EC, and TFP including ranking of regions based on both original and bootstrapped TFP indices. Table 1 presents the movements in the level of TFP growth and its components (TECH and EC) from the initial year (1987) to the terminal year (2009) for both original and bootstrapped measures across the regions. The first two columns show that for most of the regions, the level of efficiency change increased, except for Noakhali, whose initial level of efficiency change is higher than the terminal level. The level of technological change for most of the regions also increased, which indicates that the technology has improved in agricultural practices in Bangladesh.

Table 1.
Technical efficiency change, technological change, and level of productivity across the regions for both original and bootstrapped measures.
This finding is supported by Hossain et al. (2012) and Rahman and Barmon (2018). Rahman and Barmon (2018) reported that the total factor energy productivity was mainly driven by the technological progress of the gher farming system in Bangladesh. Hossain et al. (2012) reported that technological change was the main driving force for the improvement of TFP of rice in Bangladesh, whereas Rodriguez and Elasraag (2015) reported that the technological change negatively contributes to the TFP growth. It can be argued that the upward shift in technological progress is the result of diffusion of Green Revolution (GR) technology and other factors, such as significant increase in use of chemical fertilizer, extended the irrigated area, infrastructural development, research and extension expenditure, farmers’ accessibility to high yielding varieties (HYV) of seed, and availability of market information. For example, fertilizer consumption (in the form of active nutrients) increased from 0.18 million tons in 1973 to 1.70 million tons in 2006, and the proportion of irrigated area in gross cropped area (GCA) increased from 11.0% in1973 to 37.5% in 2006 in Bangladesh agriculture (Rahman 2010).
The last four columns in Table 1 reveal that the level of productivity change has improved for both original and bootstrapped method. The average rate of productivity growth rate is estimated at 0.03% per annum (p.a.) for Bangladesh over the period (though this low growth rate is not satisfactory (Table 2). The lower productivity growth rate may partly be attributed to the static or declining yield rate of major crop and increased requirement to use inputs and partly to other factors such as reduced sown area due to increasing population, land fragmentation, deterioration of soil fertility, and rapid depletion of groundwater. In fact, the total rice output of the nation declined at a rate of 1.1% p.a. during 1987–1998 (Otsuka 2000). The yield rate of modern rice also declined at an annual rate of 1.2% over the period 1968–1969 to 1993–1994 (Rahman 2002). However, the input use rate significantly increased due to the widespread diffusion of GR technology. For example, the growth rate of fertilizer use increased (in the form of active nutrient) from 14.25 kg/ha in 1973 to 127.18 kg/ha in 2006, and annual growth rate was6.3%. Similarly, pesticides use increased at an annual growth rate of 8.5% over the period 1977 to 2002. The HYV seed of rice and wheat uses increased at an annual growth rate 5.9% during the period of 1973–2006 (Rahman 2010). These imply that the comparatively high proportion of these inputs is required just to attain the existing level of productivity. Rahman and Salim (2013) noted that average farm in Bangladesh agriculture has been declining from 1.4 ha in 1960 to 0.6 ha in 2008. Giang et al. (2019) observed that the farm size was positively correlated with the total factor productivity. The reduction in average farm has a significant negative impact on technical efficiency and productivity of crop (Rahman and Rahman 2009). Losses of soil fertility is also an important factor for low productivity level of Bangladesh agriculture. Bangladesh has suffered declining soil fertility more than 65% of its total agricultural land (Task Force Report 1991). It is reported by the MOA (2008) that the soil fertility had losses of 10–70% in 11 out of 30 agroecological zones in Bangladesh over the period of 1968–1998. Due to this serious loss of soil fertility, productivity of two key inputs, fertilizer and pesticides, have declined by 3.8% and 6.5%, respectively, which has an adverse impact on crop productivity (Rahman 2007). Over-exploitation of ground water may cause salinization and rising the sea level, and most importantly it will seriously affect irrigation as well as drinking water. During Boro rice cultivation, 80% of the country’s irrigation comes from the groundwater, and in the dry season 63% of irrigation is provided by the groundwater extraction by shallow tube wells. Due to this over-exploitation of groundwater, the non-renewable water input becomes more expensive or unavailable and the groundwater level go down to the sea level, resulting in the salinization problem that may seriously affect the crop productivity (Sattar 2011).

Table 2.
Annual Growth Rate (%) of Malmquist Productivity Indices and its components and ranking based on TFP scores across the regions.
Pabna experienced the highest technical efficiency improvements growing at the rate of 0.04% p.a., followed by Noakhali at 0.03% p.a., shown in Table 2. Overall, technical efficiency change is greater than unity for five regions (26%), whereas 11 regions recorded stagnant EC, and the remaining three regions experienced declining EC estimated at 0.09% p.a. for Khulna, 0.04% for Chittagong, and 0.03% for Sylhet. Khulna is the coastal region with salinity problems in the south and Sylhet is a hilly region at the upper north-east of the country and, therefore, efficiency decline is not surprising.
Rahman and Salim (2013) also reported that Noakhali is the second highest region on the basis of technical efficiency improvement and that the south and north-eastern part of the country (i.e., Khulna, Barisal, and Sylhet) showed declining technical efficiency. In our study, Chittagong includes Chittagong Hill Tracts, which is not suitable for conventional agriculture as the region is mainly characterized by mountainous terrain with most areas being classified as state forests. The resident tribal population of this region is mostly familiar with the jhum (slash and burn) agriculture (Rahman and Salim 2013). Therefore, the observed decline in EC of Chittagong may have been influenced by poor performance of Chittagong Hill Tracts. Rahman and Salim (2013) identified Chittagong Hill Tracts as the poorest performing region for the reasons cited above.
Rangpur had the highest level of TFP growth estimated at 0.2% p.a. followed by Rajshahi, Comilla, and Jessore (with TFP growth rates of above 0.1% p.a.), largely powered by technological progress. Rajshahi has the second leading position over the study period. Several factors contribute to increased productivity and technological progress in these four regions. It can be argued that the TFP growth in this region may partly be attributable to the Barind Multipurpose Development Authority (BMDA) and partly to other factors such as soil structure, as it is located in floodplain on the bank of a major river Padma. BMDA expanded the irrigated area in this region, allowing at least three crops to be harvested as opposed to only a single rain fed crop in the past (MoEF 2002). Because of the Padma river, all three types of rich soils (i.e., loamy, sandy-loam, and silt) are available in Rajshahi, which are highly suitable for all types of crops. Comilla is one of the most intensive agricultural regions of Bangladesh and has been at the forefront of adaptation of modern technology where the adoption rate of HYV rice technology reached 80% and 100% in Aman and Boro season by 1999 (BBS 1999).Despite being an economically backward region, Rangpur experienced an outstanding performance due to rapid expansion of irrigated area at a rate of 18–19% p.a. and an increase in fertilizer usage at 13–15% p.a. (Rahman 2002).
In contrast, three regions, namely Dhaka, Khulna, and Barisal experienced large decline in TFP. Lack of technical progress as well as decline in efficiency can be attributed to the biophysical constraints faced by these regions. Khulna and Barisal are coastal regions with low lying areas that face major cyclones and flood almost every year. Another reason for poor performance in Khulna region is that most of the farmers in this region have now adopted the integrated prawn–fish–rice culture (Rahman et al. 2011). Soil quality of the Khulna region has deteriorated because of gradual accumulation of salt over the years due to the shrimp cultivation, which is also an important reason for large decline in TFP in this region. Karim (2006) reported that shrimp cultivation needs salt water and the sluice gates are allowed to open for the exchange of saline water from river water, which causes water lodging in the agricultural land. He argued that salinization is the main reason of low yield of most of the field crops including transplanted rice in the Khulna region, and wheat, jute, sugarcane production was seriously affected because of soil salinization. The result of large decline in TFP score in Dhaka is similar to the result found by Dey and Evenson (1991) for the period 1973–1989 and Rahman and Salim (2013) for the period 1948–2008, but in contrast with Rahman (2007) for the period 1964–1992. Rahman (2007) reported that the intensive use of modern inputs in the less advantaged areas such as coastal and north-eastern regions did not produce the same level of increase in output, and efficiency differences increased, leading to TFP decline. He also argued that TFP decline may be attributed to the re-use of HYV rice seeds from generation to generation, which yields lower productivity since genetic purity is compromised.
3.2. Ranking of Regions with regard to TFP Growth after Correction for Bias
Now we consider the bias-corrected TFP scores of the regions, which are somewhat different from the original TFP scores. The last two columns of Table 2 show that after correcting for bias, six regions (32%) changed ranks. However, one should also note that the top five ranks and the bottom six ranks are identical between both methods. The shift in ranks is in the middle order of the regions. Nevertheless, this ranking comparison demonstrates the need and power of bootstrapping for evaluating performance of individual regions. It also suggests that caution is necessary when we compare performance considering only the original scores as highlighted by Simar and Wilson (1999). The confidence intervals for Malmquist indices and its components are relatively wider, which provides additional justification for bootstrapping. The original TFP estimates revealed that 12 out of 19 regions experienced productivity improvements and the remaining declined. Simar and Wilson (1999) suggest that it is more important to know that whether the observed differences are statistically significant or not rather than whether the estimates are increasing or decreasing. It is argued that if a firm demonstrates lower bound of confidence interval value greater than 1 and upper bound confidence interval value of less than 1, then it implies that the firm has experienced significant progress and regress, respectively. Therefore, given the evidence presented in Table 2, we can conclude that there is a large uncertainty about the extent of agricultural TFP growth in the regions of Bangladesh.
3.3. TFP Change and Its Components by Year
Table 3 summarizes overall TFP growth performance by year using both original and bootstrapped estimates. Overall, TFP growth is estimated at a rate of 0.03% p.a. with overall increase of 0.6% over the sample period. The overall TFP growth rate is mainly powered by technical progress at an annual rate of 0.03% and slight decline in efficiency 0.004% over the period. This situation is similar to the results obtained by Rahman (2007) for 1964–1992. Rahman (2007) applied the sequential Malmquist index to calculate the TFP index for Bangladesh agriculture. He concluded that TFP grew at an average rate of 0.9% per annum, mainly powered by technological progress estimated at 1.9% p.a. and overall technical efficiency decline of 1.0% p.a. This result is also similar with Chen et al. (2008) for China for the period of 1990–2003, which reported that the national TFP grew at 1.5% p.a. due to technological progress at 4.7% and declined in technical efficiency at 1.9%. Anik et al. (2017) observed the positive TFP growth rate of Bangladesh with a similar growth pattern of residual scale and mix efficiency change but they experienced no change in technical scale and mix efficiency for the period of 1980–2013.

Table 3.
Summary of overall growth rate of Bootstrap Malmquist productivity indices across the all regions over the study period 1987−2009.
Table 3 shows that the increase in TFP index has not been uniform and fluctuation has occurred from year to year. It has also revealed that the progress/regress of TFP index is not only powered by increase or decrease in technology or technical efficiency. For instance, in 1993, technical efficiency improved (as expressed by EC index) but failed to maintain output maximizing technology. This lagging performance in technology outweighed improvement in efficiency, such that overall productivity fell. Conversely, in 1991, technical efficiency diminished but experienced overall productivity growth due to progress in technology. Yet another example is 2008, which showed a negative TECH and a positive EC, resulting in no change of TFP. These examples demonstrate the advantages of a decomposable productivity measure where productivity growth/regress is explained by either efficiency improvements or technological progress, or both. Finally, the dynamic behavior of TFP index over the study period across the regions can be attributed to a number of factors including biophysical character of the regions; natural disaster; mechanical, biological, and organizational aspects of technical progress; and increase in the number of economically active population owing to steady increase in population over time.
The comparison of the original and bootstrapped Malmquist indices revealed the same direction in productivity and technology change but opposite directions in efficiency change. From Table 3, we noticed that the overall progress in bias-corrected productivity appears to be larger than the original estimate, while the technological progress is smaller than the original TECH. In the original sample, efficiency change is declining (at 0.01% p.a.) but the bias-corrected estimate shows improvement in efficiency change (at 0.04% p.a.).It indicates that the lack of correction of original sampling variability might be the cause of improving or declining TFP indices and its components. For this reason, Simar and Wilson (1998) suggest that one should be careful when making performance comparisons based on original efficiency scores.
Figure 1a–c present graphical representation of bootstrapped TFP and its components for all regions over the study period. We observe that the confidence interval is highest for EC compared to TFP and TECH. Frequency distribution of original and bootstrap TFP, EC, and TECH for the regions is presented in Figure 1d. Comparing the bootstrap to the original estimates, it can be concluded that the bootstrap technique helps in reducing ambiguity of the result.
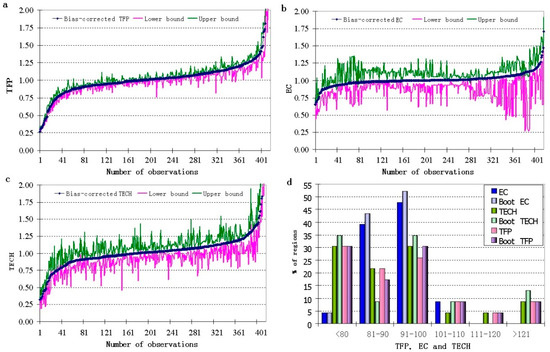
Figure 1.
Bias-corrected Malmquist indices with upper bound and lower bound (a) TFP, (b) EC, (c) TECH. (d) Frequency distribution of original and bootstrap TFP, EC, and TECH.
4. Conclusions and Policy Implications
The study applies both DEA and bootstrapped methods to Malmquist indices of agricultural TFP change and its components (TECH and EC) for 19 regions of Bangladesh covering a 23-year period (1987–2009).
The productivity of Bangladesh agriculture grew at a rate of 0.03% p.a., powered mainly by technological progress which is estimated at the same rate of 0.03% p.a. However, efficiency change over time has deteriorated at a negligible rate of 0.004% p.a. Large regional disparities exist with respect to TFP growth and its components over time. Correction of bias using bootstrapped procedure resulted in six regions changing ranks, which are in the middle order, while the top five and bottom six ranks remained identical with regard to mean TFP indices. From the regional results, it was found that there exist large disparities among the regions in TFP growth performance.
The use of bootstrapped procedure provided confidence in our results, corrected bias of original estimates, and also demonstrated existence of wide range of variations across regions and over time with respect to estimated TFP, TECH, and EC indices.
A number of policy implications can be drawn from the results. In order to stimulate TFP growth, it is important to address the underlying causes of declining efficiency and the thrust in policy should be aimed at measures to improve production efficiency by removing misallocation of resources. Attention is also needed to address regional inequality by focusing on failing and inefficient regions. One obvious pathway to improve resource allocation amongst farmers is to invest in well-functioning agricultural extension systems. Rahman and Salim (2013) noted that mix-efficiency in Bangladesh agriculture is declining sharply, implying that farmers are failing to gain from economies of scope. They have demonstrated that investment in extension significantly improves mix-efficiency improvements. For improving the technical efficiency, better education should be provided to the farming populations (Liu et al. 2019).
Furthermore, attention should be paid to develop varieties that are suitable for unfavorable regions (e.g., regions which are frequently affected by flood, coastal regions affected by saline water, and regions mainly dependent on monsoon rain), which can be made possible through increased investment in Research and Development (R&D). Rahman and Salim (2013) and Coelli et al. (2003) noted that R&D investment positively influences technical progress as well as TFP growth. Policy should be taken to grow fewer water consuming crops and make the most of use of surface water by digging canals and dredging rivers to reduce the overemphasizing groundwater extraction.
Diversification of the cropping system also positively influences technical progress (Rahman and Salim 2013). Government of Bangladesh already realized the need to diversify its cropping system in order to move away from cereal monoculture dominated by rice and has allocated 8.9% of the total agricultural budget to promote crop diversification (Rahman 2009). In this context, policy should be taken to increase the extension expenditure and irrigation infrastructure facilities that will significantly increase the crop diversity (Rahman and Kazal 2015).
The challenge faced by Bangladesh is formidable but the realization of these policies will result in a growing agricultural sector, which is the main source of providing food, income, and employment for its rapidly increasing population.
Author Contributions
Conceived & design the research: M.B. and Y.S. Data collection & analysis: M.B. Writing—the original draft: M.B. Writing—review & editing: S.R.
Funding
Financial support for this study was provided by the National Social Science Fund projects in China. It was one of the stage achievements of Research on Policy Evaluation of Forestry Ecological Construction and the Improvement of Ecosystem in Western China (project number: 11&ZD042).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abatania, Luke N., Atakelty Hailu, and Amin W. Mugera. 2012. Analysis of farm household technical efficiency in Northern Ghana using bootstrap DEA. Paper presented at 56th Annual Conference of the Australian Agricultural and Resource Economics Society, Fremantle, WA, USA, February 7–10. [Google Scholar]
- Alam, Mohammad Jahangir, Ismat Ara Begum, Sanzidur Rahman, Jeroen Buysse, and Guido Van Huylenbroeck. 2011. Total Factor Productivity and the Efficiency of Rice Farms in Bangladesh: A Farm Level Panel Data Comparison of the Pre- and Post-Market Reform Period. Paper presented at 85th Annual Conference of the Agricultural Economics Society, Warwick University, UK, April 18–20. [Google Scholar]
- Anik, Asif, Sanzidur Rahman, and Jaba Sarker. 2017. Agricultural Productivity Growth and the Role of Capital in South Asia (1980–2013). Sustainability 9: 470. [Google Scholar] [CrossRef]
- Bagchi, Mita, and Lijuan Zhuang. 2016. Analysis of farm household technical efficiency in Chinese litchi farm using bootstrap DEA. Custos e@ gronegcio 12: 278–93. [Google Scholar]
- Balcombe, Kelvin, Iain Mcpherson Fraser, Laure Latruffe, Mizanur Rahman, and Laurence Smith. 2008. An Application of the DEA double Bootstap to Examine Sources of Efficiency in Bangladesh Rice Farming. Applied Economics 40: 1919–25. [Google Scholar] [CrossRef]
- BBS. 1999. Statistical Yearbook of Bangladesh. Dhaka: Bangladesh Bureau of Statistics. [Google Scholar]
- BBS. 2010. Statistical Yearbook of Bangladesh. Dhaka: Bangladesh Bureau of Statistics. [Google Scholar]
- BBS. 2018. Statistical Yearbook of Bangladesh. Dhaka: Bangladesh Bureau of Statistics. [Google Scholar]
- BER. 2018. Bangladesh Economic Review; Dhaka: Finance Division, Ministry of Finance, Government of Peoples’ Republic of Bangladesh.
- Caves, Douglas W., Laurits R. Christensen, and Walter Erwin Diewert. 1982. The economic theory of index numbers and the measurement of input, output and productivity. Econometrica 50: 1393–414. [Google Scholar] [CrossRef]
- Čechura, Lukáš. 2012. Technical efficiency and total factor productivity in Czech agriculture. Agricultural Economics Czech 58: 147–56. [Google Scholar] [CrossRef]
- Chen, Po-Chi, Ming-Miin Yu, Ching-Cheng Chang, and Shih-Hsun Hsu. 2008. Total factor productivity growth in China’s agricultural sector. China Economic Review 19: 580–93. [Google Scholar] [CrossRef]
- Coelli, Tim J., and Dodla Sai Prasada Rao. 2005. Total Factor Productivity Growth in Agriculture: A Malmquist Index Analysis of 93 Countries, 1980–2000. Agricultural Economics 32: 115–34. [Google Scholar] [CrossRef]
- Coelli, Tim J., Dodla Sai Prasada Rao, and George Battese. 1998. An Introduction to Efficiency and Productivity Analysis. Norwell: Springer. [Google Scholar]
- Coelli, Tim, Sanzidur Rahman, and Colin Thirtle. 2003. A stochastic frontier approach to total factor productivity measurement in Bangladesh crop agriculture, 1961–1992. Journal of International Development 15: 321–33. [Google Scholar] [CrossRef]
- Dey, Madan Mohan, and Robert Eugene Evenson. 1991. The Economic Impact of Rice Research in Bangladesh; Dhaka: BRRI/IRRI/BARC. Available online: http://agris.fao.org/agris-search/search.do?recordID=QR19960024497 (accessed on 1 May 2019).
- Efron, Bradley. 1979. Bootstrap methods: Another look at the jackknife. The Annals of Statistics 7: 1–26. [Google Scholar] [CrossRef]
- Färe, Rolf, Shawna Grosskopf, Mary Norris, and Zhongyang Zhang. 1994. Productivity Growth, Technical Progress and Efficiency Changes in Industrialised Countries. American Economic Review 84: 66–83. [Google Scholar]
- Giang, Mai Huong, Tran Dang Xuan, Bui Huy Trung, and Mai Thanh Que. 2019. Total Factor Productivity of Agricultural Firms in Vietnam and Its Relevant Determinants. Economies 7: 4. [Google Scholar] [CrossRef]
- Gitto, Simone, and Paolo Mancuso. 2012. Bootstrapping the Malmquist indexes for Italian airports. International Journal ofProduction Economics 135: 403–11. [Google Scholar] [CrossRef]
- Headey, Derek, Mohammad Alauddin, and Dodla Sai Prasada Rao. 2010. Explaining agricultural productivity growth: An international perspective. Agricultural Economics 41: 1–14. [Google Scholar] [CrossRef]
- Hossain, Mahabub, and Mokaddem M. Akash. 1994. Public Rural Works for Relief and Development. Washington, DC: IFPRI. [Google Scholar]
- Hossain, Md Kamrul, Anton Abdulbasah Kamil, Md Azizul Baten, and Adli Mustafa. 2012. Stochastic frontier approach and data envelopment analysis to total factor productivity and efficiency measurement of Bangladeshi rice. PLoS ONE 7: 10. [Google Scholar] [CrossRef] [PubMed]
- Karim, Md Rezaul. 2006. Brackish-water shrimp cultivation threatens permanent damage to coastal agriculture in Bangladesh. Environment and Livelihoods in Tropical Coastal Zones: Managing Agriculture-Fishery-Aquaculture Conflicts 2: 61–71. [Google Scholar]
- Kuosmanen, Timo, Diemuth Pemsl, and Justus Wesseler. 2006. Specification and estimation of production functions involving damage control inputs: A two-stage, semi parametric approach. American Journal of Agricultural Economics 88: 499–511. [Google Scholar] [CrossRef]
- Liu, Jianxu, Hui Li, Songsak Sriboonchitta, and Sanzidur Rahman. 2019. Technical Efficiency Analysis of Top Agriculture Producing Countries in Asia: Zero Inefficiency Meta-Frontier Approach. In Structural Changes and Their Econometric Modeling. TES 2019. Studies in Computational Intelligence, 1st ed. Edited by Kreinovich Vladik and Sriboonchitta Songsak. Cham: Springer, p. 808. [Google Scholar]
- MOA. 2008. Ministry of Agriculture. Handbook of Agricultural Statistics of Bangladesh. December 2007; Dhaka: MOA, Government of Bangladesh. Available online: http://www.moa.gov.bd/statistics/ statistics.htm (accessed on 1 May 2019).
- MoEF. 2002. Second National Report on Implementation of United Nations Convention to Combat Desertification Bangladesh; Dhaka: Ministry of Environment and Forests, Government of Bangladesh.
- Odeck, James. 2009. Statistical precision of DEA and Malmquist indices: A bootstrap application to Norwegian grain producers. Omega 37: 1007–17. [Google Scholar] [CrossRef]
- Otsuka, Keijiro. 2000. Role of agricultural research in poverty reduction: Lessons from the Asian experience. Food Policy 25: 447–62. [Google Scholar] [CrossRef]
- Praduman, Kumar, Surabhi Mittal, and Mahabub Hossain. 2008. Agricultural Growth Accounting and Total Factor Productivity in South Asia: A Review and Policy Implications. Agricultural Economics Research Review 21: 145–72. [Google Scholar]
- Pray, Carl, and Zafar Ahm. 1991. Research and Agricultural Productivity Growth in Bangladesh. In Research and Productivity in Asian Agriculture. Edited by Robert EugeneEvenson and Carl E. Pray. New York: Cornell University Press. [Google Scholar]
- Rahman, Sanzidur. 2002. Technological change and food production sustainability in Bangladesh agriculture. Asian Profile 30: 233–45. [Google Scholar]
- Rahman, Sanzidur. 2003. Environmental impacts of modern agricultural technology diffusion in Bangladesh: An analysis of farmers’ perceptions and their determinants. Journal of Environmental Management 68: 183–91. [Google Scholar] [CrossRef]
- Rahman, Sanzidur. 2007. Regional productivity and convergence in Bangladesh agriculture, (1964–1992). Journal of Developing Areas 41: 221–36. [Google Scholar] [CrossRef]
- Rahman, Sanzidur. 2009. Whether crop diversification is a desired strategy for agricultural growth in Bangladesh? Food Policy 34: 340–49. [Google Scholar] [CrossRef]
- Rahman, Sanzidur. 2010. Six decades of agricultural land use change in Bangladesh: Effects on crop diversity, productivity, food availability and the environment, 1948–2006. Singapore Journal of Tropical Geography 31: 254–69. [Google Scholar] [CrossRef]
- Rahman, Sanzidur, and Basanta Kumar Barmon. 2018. Total Factor Energy Productivity and Efficiency Changes of theGher(Prawn-Carp-Rice) Farming System in Bangladesh: A Stochastic Input Distance Function Approach. Energies 11: 3482. [Google Scholar] [CrossRef]
- Rahman, Sanzidur, and Mohammad Mizanul Haque Kazal. 2015. Determinants of crop diversity in the regions of Bangladesh (1990–2008). Singapore Journal of Tropical Geography 36: 83–97. [Google Scholar] [CrossRef]
- Rahman, Sanzidur, and Mizanur Rahman. 2009. Impact of land fragmentation and resource ownership on productivity and efficiency: The case of rice producers in Bangladesh. Land Use Policy 26: 95–103. [Google Scholar] [CrossRef]
- Rahman, Sanzidur, and Ruhul Salim. 2013. Six Decades of Total Factor Productivity Change and Sources of Growth in Bangladesh Agriculture (1948–2008). Journal of Agricultural Economics 64: 275–94. [Google Scholar] [CrossRef]
- Rahman, Sanzidur, Basanta K. Barmon, and Nesar Ahm. 2011. Diversification economies and efficiencies in a ‘Blue-Green Revolution’ combination: A case study of prawn-carp-rice farming in the ‘gher’ system in Bangladesh. Aquaculture International 19: 665–82. [Google Scholar] [CrossRef]
- Rodriguez, Xosé A., and Yahia H. Elasraag. 2015. Assessing the Total Factor Productivity of Cotton Production in Egypt. PLoS ONE 10: e0116085. [Google Scholar] [CrossRef]
- Sattar, M. 2011. “Invisible Hazard” of Groundwater Depletion. The New Humanitarian. December 13. Available online: http://www.thenewhumanitarian.org/feature/2011/12/13/%E2%80%9Cinvisible-hazard%E2%80%9D-groundwater-depletion (accessed on 1 May 2019).
- Simar, Leopold, and Paul W. Wilson. 1998. Sensitivity analysis of efficiency scores: How to bootstrap in nonparametric frontier models. Management Science 44: 49–61. [Google Scholar] [CrossRef]
- Simar, Leopold, and Paul W. Wilson. 1999. Estimating and bootstrapping Malmquist indices. European Journal of Operational Research 115: 459–71. [Google Scholar] [CrossRef]
- Suhariyanto, Kecuk, and Colin Thirtle. 2001. Asian Agricultural Productivity and Convergence. Journal of Agricultural Economics 52: 96–110. [Google Scholar] [CrossRef]
- Task Force Report. 1991. Bangladesh Development Strategies: Environment and Development. Dhaka: University Press Ltd., vol. 4. [Google Scholar]
- Trueblood, Michael A., and Jay Coggins. 2003. Intercountry Agricultural Efficiency and Productivity: A Malmquist Index Approach. Washington, DC: Mimeo, World Bank. [Google Scholar]
- Vasiliev, Nikolay, Elsa Suuster, Helis Luik, Rando Värnik, Eduard Matveev, and Alar Astover. 2011. Productivity of Estonian dairy farms decline after the accession to the European Union. Agricultural Economics-Zemedelska Ekonomika 57: 457–63. [Google Scholar] [CrossRef]
- Wilson, Paul W. 2010. FEAR 1.15 User’s Guide. Clemson: Department of Economics, Clemson University. [Google Scholar]
- Yao, Shunbo, and Hua Li. 2010. Agricultural Productivity Changes Induced by the Sloping Land Conversion Program: An Analysis of Wuqi County in the Loess Plateau Region. Environmental Management 45: 541–50. [Google Scholar] [CrossRef] [PubMed]
- Yin, Runsheng. 2000. Alternative measurements of production efficiency in the global pulp sector. Forest Science 46: 558–69. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).