1. Introduction
Tourism-led growth literature proposed that the tourism industry plays a vital role in economic growth. In recent decades, tourism and the growth hypothesis has been a focal point for economists. The traditional analysis under debate is that development in tourism led to faster economic growth. Tourism is vital for developing countries as it contributes heavily to foreign exchange confronted by foreign exchange constraints (
Oh 2005); furthermore, because tourism receipts together with export revenues well ameliorate current account deficits, promoting the tourism industry in those countries has become a primary development strategy.
Similarly, budget deficits may also be improved through increments of the tax revenues as tourism contributes to every single economic sector. On the basis of the assumption that tourism is an effective mechanism for economic growth, tourism promoters consistently lobby for investments and support in either way through infrastructure and developments (
Becker and George 2011;
Liasidou 2013) and the creation of new attractions (
Getz 2008).
Lew (
2011) argued that tourism is the largest service sector in international trade and comprises a significant part of the global economy. According to united nation world tourism organization (
2001UNWTO), tourism is within the top five bases of foreign export income in the world. Tourism contributes heavily to world revenue by providing an employment opportunity to the peoples of around 225 million and adds 6 billion dollars, which is 9% of total world revenue (
Chou 2013). According to the World Travel & Tourism Council’s annual research, and Oxford Economics, Travel, & Tourism’s contribution to world gross domestic product (GDP) outpaced the global economy for the sixth consecutive year in 2016, raised to a total of 10.2% to world GDP. The sector now supports 292 million people in employment—that is, 1 in 10 jobs all over. Travel & Tourism forecasts for the next ten years also show promising results with predicted growth rates of 3.9% annually in the same context.
Roe and Urquhart (
2001) stated that in developing countries, tourism has become an important sector owing to its positive effects on infrastructure and superstructure, creating income, employment, and balance payment, as well as its high added value and impact on other industries. Tourism has been considered as a critical foundation of economic growth.
Nowak et al. (
2003) stated that to redouble tourism with economic growth, many governments carry out projects about infrastructure services. The importance and form of tourism have mostly changed especially, after 1990, by the effect of globalization.
Binns and Nel (
2002) highlight that tourism generally had sub-sectors. These sectors are motivated by input and output exchange, employment, transportation component, exporting, and other similar industries.
There is an interactive relationship between the tourism industry and economic growth. As the study is conducted worldwide by different researchers and over an unusual period, still there is a question mark as to whether the relationship between tourism and economic growth is unidirectional or bidirectional. Therefore, this sort of study is essential from time to time to check the results, implication, and reliability of the previous research. This study is conducted using the cointegration test, vector autoregression (VAR) model, error correction model (ECM), and Granger causality to analyze the relationship between the tourism industry and economic growth in Beijing, China for the period of 1994–2015. The study uses the three models together in order to gain a better understanding of the survey, which is missed in the limited empirical literature about tourism and economic growth. From a regional economic perspective, this study is first looking to the real link between the tourism industry and economic growth on one side and, at the same time, any importance from the economic growth toward the tourism industry in the context of Beijing, China. Second, the nexus between the tourism industry and economic growth will provide an experimental design with additional arguments to demonstrate the relationship between the tourism industry and economic growth. Third, the study is vital for a policymaker to show some discussions to make the right decisions for the future growth of Beijing’s sustainable tourism sector. Although tourism is important and fast-growing, it is somewhat a facet of globalization, especially in an underdeveloped country. Excellent empirical literature shed light on the tourism industry pros and cons using cross country data. However, this paper uses the domestic data to unleash the determinant and consequence of tourism and economic growth.
Further, the proposed study is planned in the following order.
Section 2 highlights the literature of relevant research, and domestic tourism development and economic growth.
Section 3 presents the data and methodology added by the econometric model of the study. Chapter 4 describes the empirical results and discussion, aided by regression estimates of all the model used in the study, which are been explained in this section.
Section 5 includes the conclusion, limitations, and some future research concepts. The references are listed under “References”.
2. Literature Review
Economists emphasize the industrial properties of tourism growth in the economy while analyzing tourism.
Schroenn and Tecle (
2006) argued that the benefits of tourism are spread over a broader segment of society as compared with other sectors of the economy, because tourism is a multidisciplinary activity that involves several industries and draws upon a variety of skills. The revolutionary studies of the tourism led-growth hypothesis (
Lea 1993;
Sinclair 1998) unleashed that the possible results of the tourism industry are jobs creation, developed growth, and generate revenue for the government. On the basis of this hypothesis,
Sinclair and Stabler (
2002) stated that the potential strategic factor for economic growth is considered international tourism, as it provides the foreign exchange earnings, tourist spending, and an alternative form of exports.
Looking at the relationship between tourism and economic growth, the previous study shows ambiguous results using a different technique. There is no clear understanding of whether there are unidirectional or bidirectional results between the variables.
Mohammadzade and Najafinasab (
2009) used pool data and the Granger causality test to analyze the causal relationship between the tourism industry and gross domestic product in the selected Islamic countries during the period 1995–2005. The results claimed the existence of a one-way causal relation from gross domestic product towards a number of tourists.
Tang and Jang (
2009) study the same sort of relationship while using Granger causality for U.S. economic growth and the results highlight that there is no unified relationship between the two variables. Similarly,
Lean and Tang (
2010) studied the same model for Malaysian market for the period from 1989 to 2010 and unleashed a bilateral relationship between tourism and economic growth only in short run, while in the long run, only economic growth affects tourism, which confirms the unidirectional link.
Lee and Chang (
2008) used a different test for organization of economic cooperation and development (OECD) and non-OECD countries to test the hypothesis, and the results demonstrate different outcomes for OECD and non-OECD countries, as OECD countries show a unidirectional causal relationship in the long run, while the non-OECD countries show a bidirectional relationship between tourism and economic growth.
Gunduz and Hatemi-J (
2005) highlight that ambiguous results may stem from various reasons, such as using different econometric techniques; the relative weight of international tourism in the economies; missing crucial explanatory variables such as real exchange rates; and, most significantly, the poor quality of data in the empirical studies. The tourism-led growth hypothesis is strongly supported by
Balaguer and Cantavella-Jordá (
2002) in their research for Spain, which is the second largest recipient of international tourism revenues (5.9% of its GDP) next to the United States.
Dritsakis (
2004) found a bidirectional causal relationship between international tourism and economic growth in Greece, furthermore, both the hypothesis of tourism-led growth and growth-led tourism were valid for the Greek economy. Contrary to the Greek study,
Sanchez Carrera et al. (
2008) found a unidirectional causal relationship from international tourism toward economic growth for the Mexican economy and supported the tourism-led growth hypothesis. However,
Oh’s (
2005) results show no long-run cointegration connection for the Korea economy between tourism and growth.
Furthermore, it should be added that the tourism-led growth hypothesis for an economy highly depends on the relative weight in GDP from tourism.
Kim and Chen (
2006) results are in support of
Dritsakis (
2004), who find a bidirectional relationship between tourism and economic growth for Taiwan. That is, both the growth-led tourism and tourism-led growth hypotheses are valid to the economy of Taiwan, where the comparative weight of tourism revenues is similar to that of Korea.
Proenca and Soukiazis (
2005) tested the same sort of hypothesis for Portuguese regions and found that if the supply characteristics of the tourism sector are improved, it can be considered as a substitute method for attractive regional growth in Portugal.
Cunado and De Gracia (
2006) find some limited evidence for the African region.
Domestic Tourism Development and Economic Growth
Domestic tourism in China is as old as Chinese history. However, development in the tourism industry of China, Beijing is a new phenomenon, as China was closed to the outside world for an extended period. According to
Sofield and Li (
1998), domestic tourism in China dates back three thousand years ago, while international tourists have started coming into the country in the recent past. Therefore, it is essential to study the historical perspective of domestic tourism back to its emperors, scholars, and philosophers.
After the 1920s, modern domestic tourism started in China—first in Shanghai, where some travel agencies began working. These new travel agencies were used initially both for local tourism and outbound tourism (
Qiao 1995), but this service of tourism was not the initiative for tourism in China, because those agencies were stopped their services forcefully by civil war and war against Japan. Before the communist party ruling in the country, leisure travel for ordinary people was restricted only to the temple. This was mainly because of the lack of time, money, and facilities, as well as strict government control over internal migration (
Gormsen 1995).
With time and especially after 1949, traveling and tourism was considered in the lifestyle of ordinary people and the government realized that they should always guard against (
Zhang 1989). Still, however, there was some restriction and essential documents were needed, such as a permit to travel outside from one’s local district. Over time, however, the tourism industry grew, and was considered one of the crucial elements of economic growth.
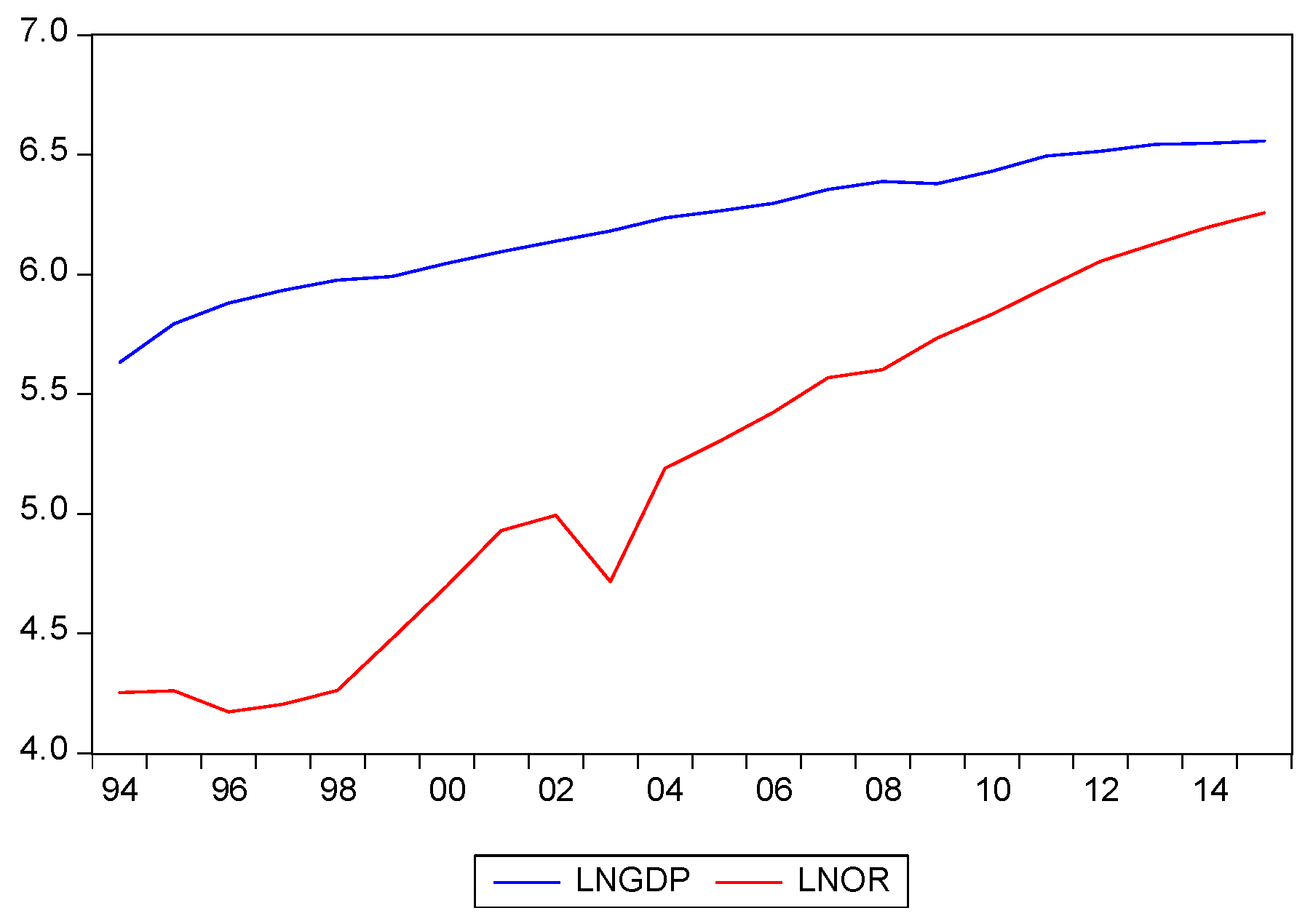
According to the facts and figures for tourism in China, in 2017, domestic tourism revenue was around CNY 4.57 trillion, with an increasing rate of 15.9%. The overall tourism industry contribution to the economy in every field—such as employment, where the direct employment is around 28.25 million people and indirect employment is 80 million peoples who contribute as a result to the total employment—is approximately 10.28%. Therefore, the study of domestic tourism and economic growth is vital to analyze the data in a different period. Thus, the hypothesis is developed like as follows:
Hypothesis 1. There is no relationship between domestic tourism and economic growth in Beijing.
Hypothesis 2. There is a healthy interdependent relationship between domestic tourism and economic growth in Beijing.
5. Conclusions
Beijing tourism industry has expanded rapidly over the past two decades and brought changes to China’s various industries with strong functional characteristics. The tourism industry absorbs foreign currency with low cost, improves regional economic development, and increases economic vitality. Several industries such as telecommunication, transportation, insurance, finance, and commerce relating to tourism range from traditional to modern. Recently, a total of 5 million staff working directly in the Chinese tourism industry has been recorded. According to
Zhu (
2001), 25 million employees are working directly and indirectly in the Chinese tourism industry. This study conceptualized an econometric model of the tourism industry and economic growth for analysis. The results have shown a positive effect of tourism and economic growth for Beijing.
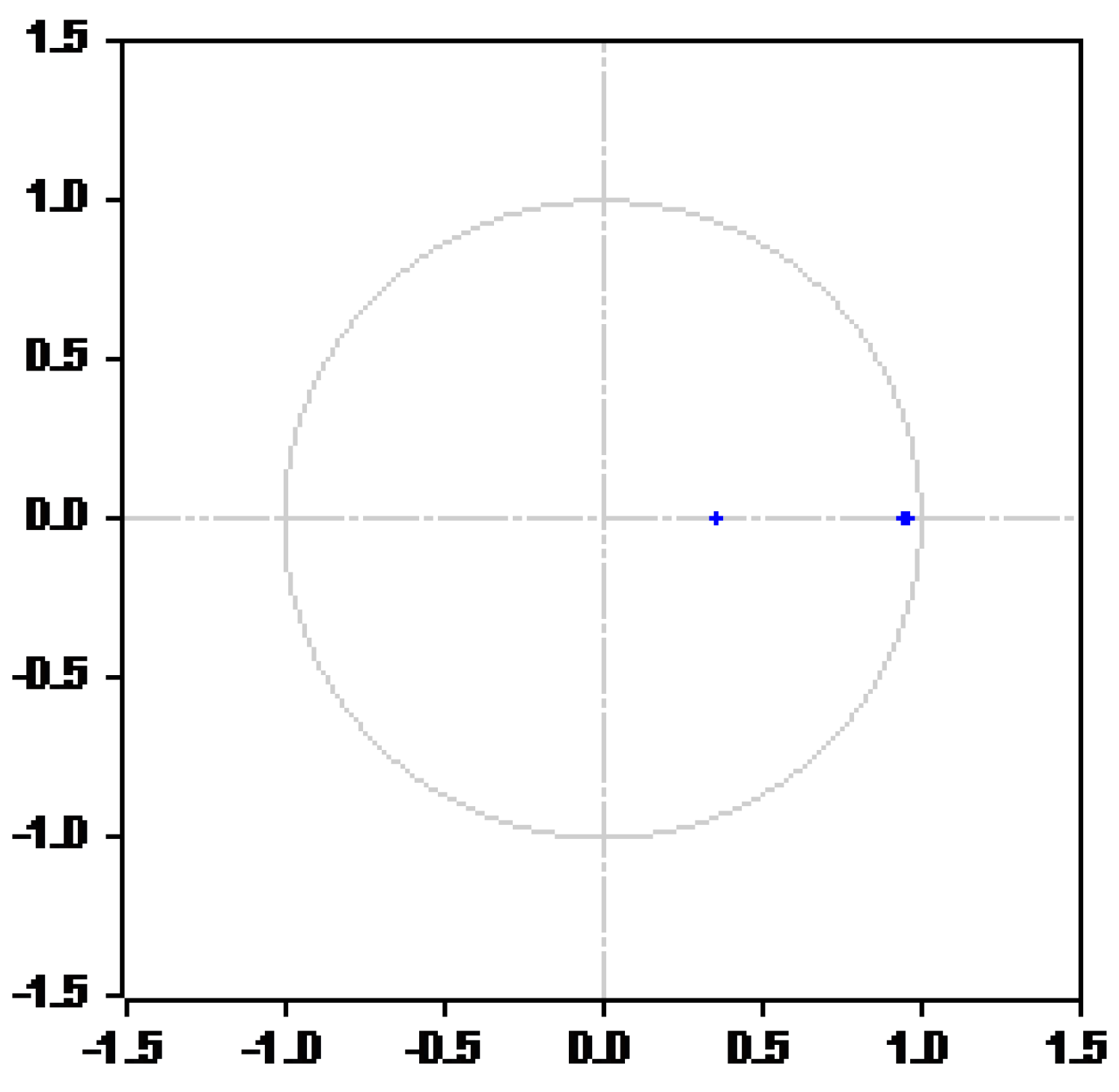
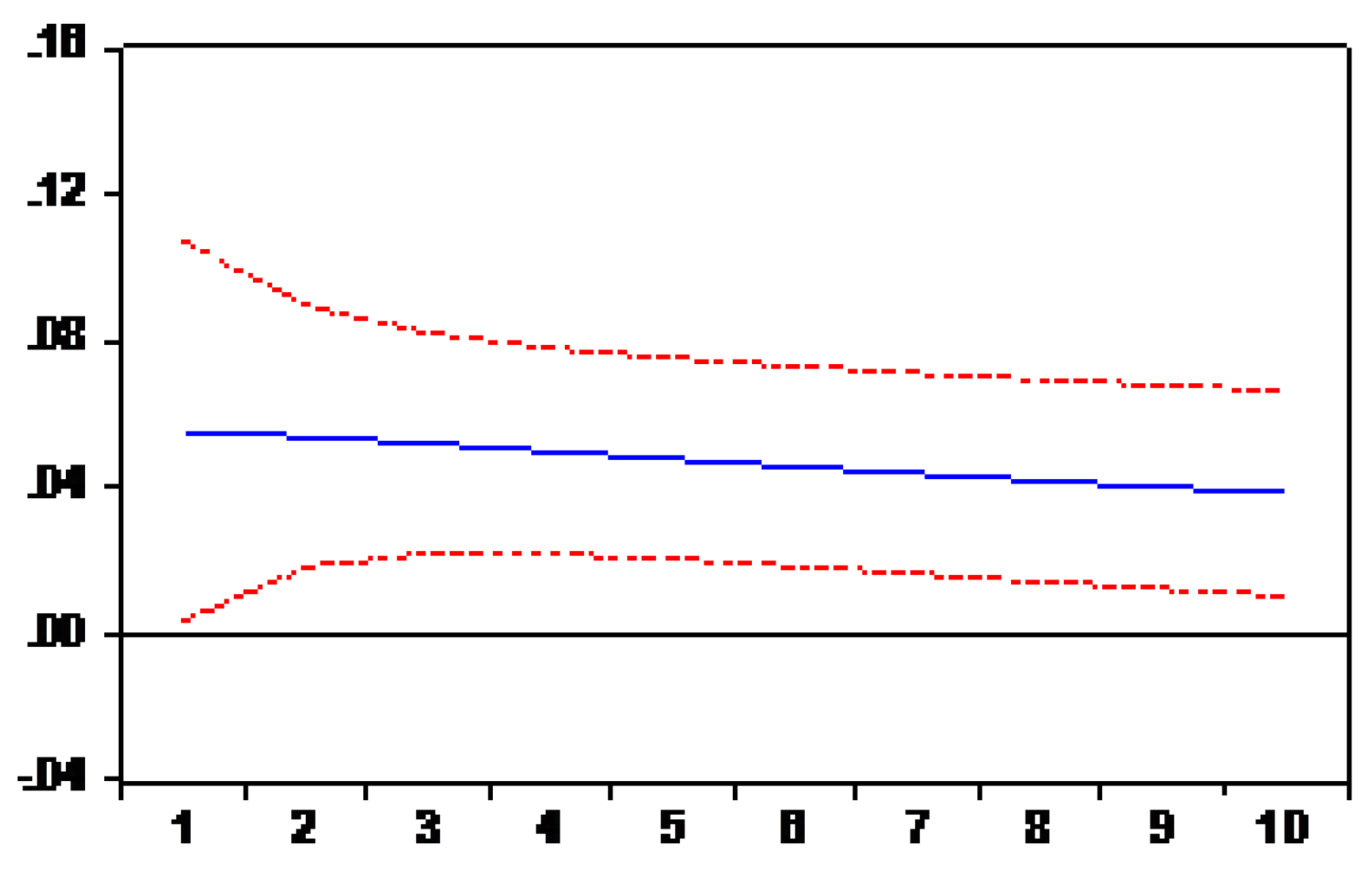
The tourism industry is the most important sector in Beijing, and it is stimulated by numerous policies set by China’s government that encourage the growth of tourism industry, as well as the reformation of the People’s Republic of China. Beijing’s tourism has grown from a small number of servicing units into the most important sector of the economy in Beijing, China. The Chinese government is aiming to double domestic spending on tourism soon. Therefore, this study is conducted to check the vital relationship between the tourism industry and economic growth with time-series analysis for the period of 1994 to 2015. The results of the cointegration analysis show that there exists a long-run cointegration relation between the total domestic tourism revenue and GDP for Beijing. Although the long run implication of the tourism industry and economic development is critical in the existing social sciences literature in a developing country, around the globe, government and international aid organizations are involved and show interest in the tourism industry, and invest a good amount of public funds to promote regional tourism. The results are consistent with the literature in the case of Beijing, where domestic tourism and economic growth are essential for one another in the long run.
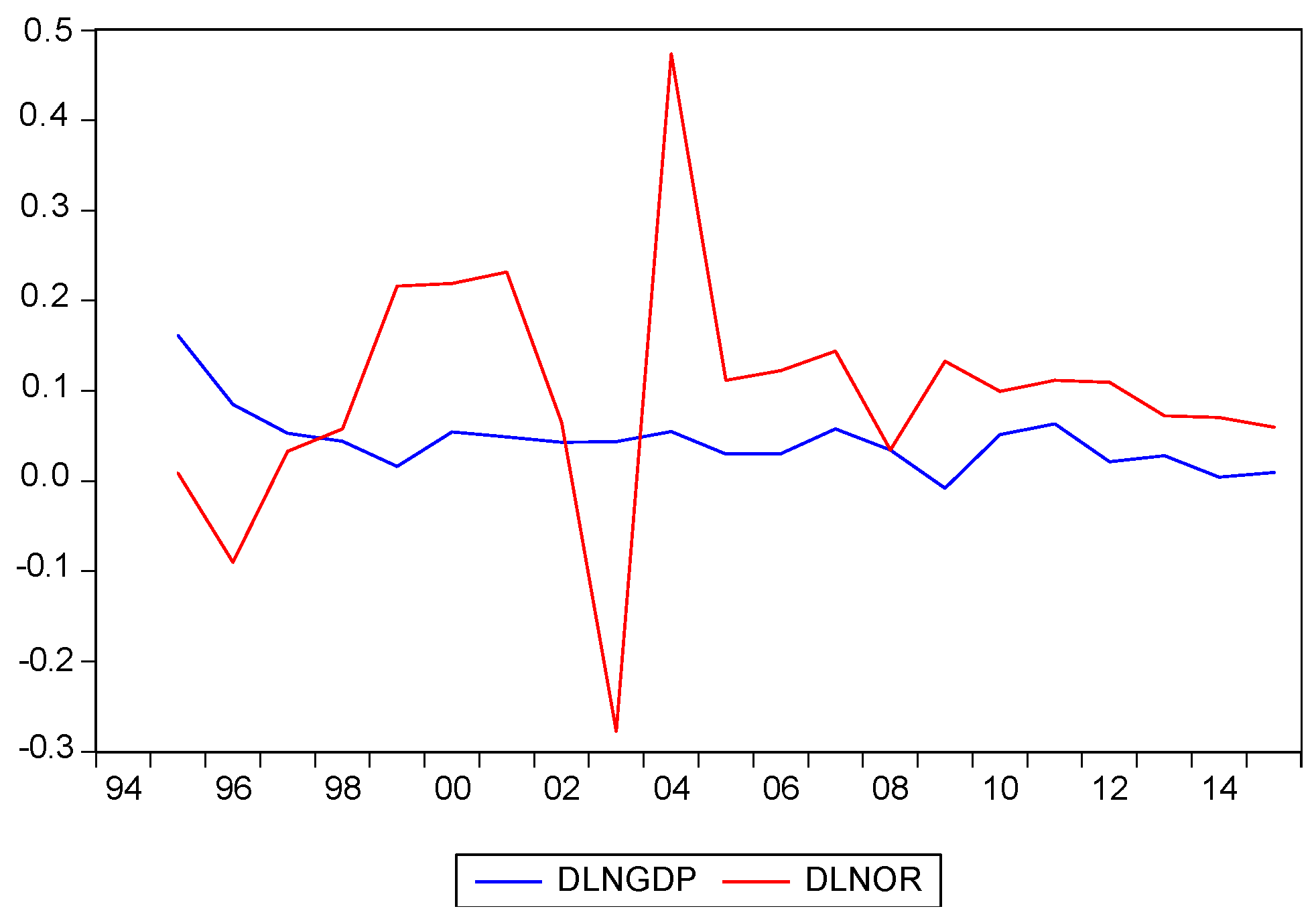
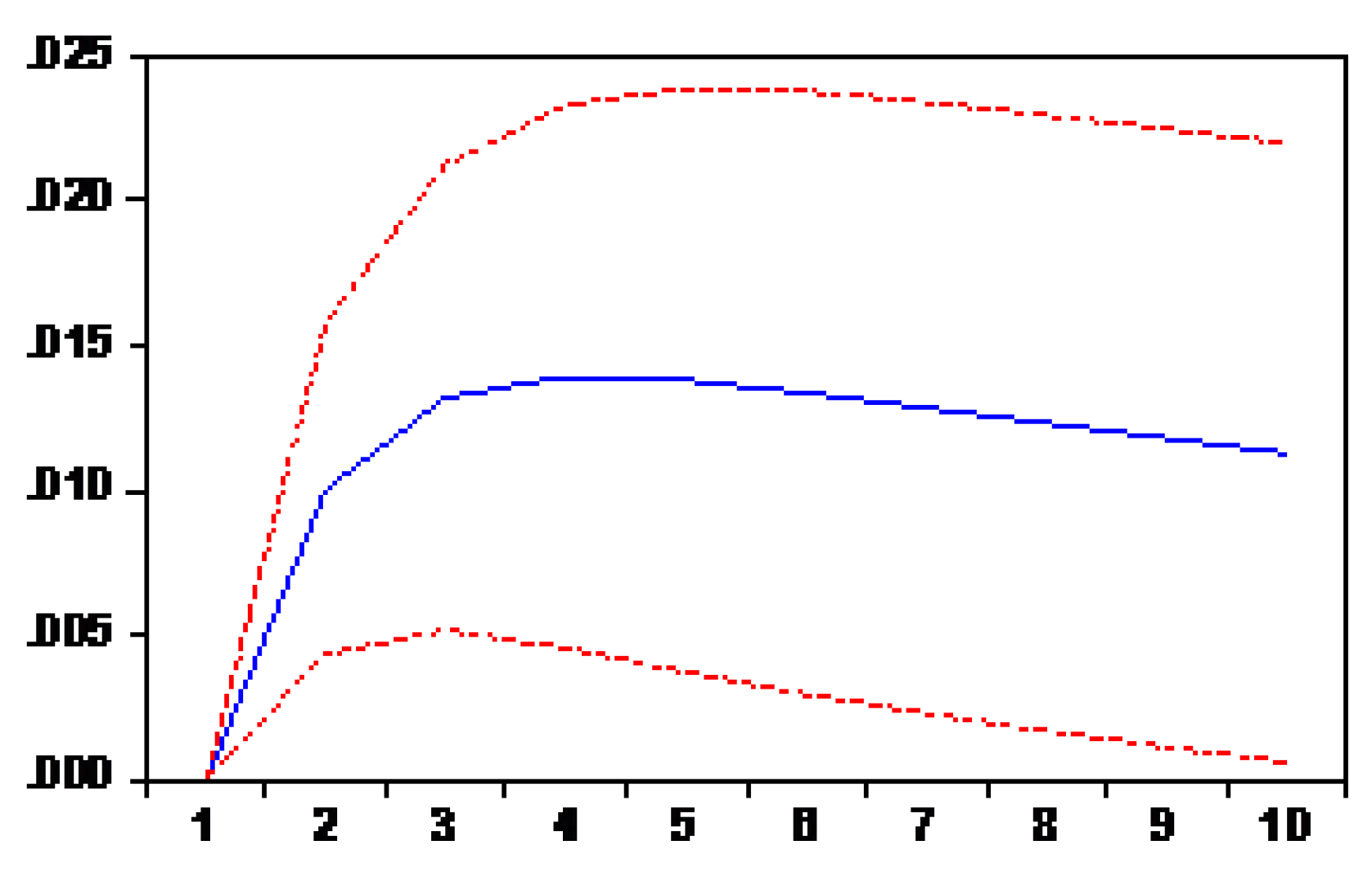
The results of the VAR model indicate Beijing’s economic growth will be affected by both the lag length domestic tourism revenue and the lag length economic growth, because tourism is becoming an important sector in the national economy and has been playing an active role in the economy of Beijing, China. Because of the rapid growth of domestic tourism, all related industries are growing. On the basis of the ECM model results in the short term, local tourism revenue and economic growth show a unidirectional relationship, supporting the findings in the previous study of
Sanchez Carrera et al. (
2008).
The proposed study results are significant for the policy maker about tourism in Beijing. This study shows robust empirical findings regarding the long- and short-run relationship between tourism and economic growth. The policy maker should give considerable attention to domestic and international tourism in Beijing. The sustainable position is also vital for the tourism industry in Beijing. The tourism industry can maintain its position and improve further by lowering the cost of traveling, living, and relaxation in the international tourism process. This study also used a different model at the same time to gain more insight information and fruitful results for future research.
Limitation and Future Research Direction
Although the study has significant implications and an essential contribution to the empirical literature in the context of tourism and economic growth, still it is not beyond the limitation. The results show a positive influence on tourism and economic growth in Beijing, but this does not mean that the development in Beijing is the result of the tourism industry as a whole. This is one of the most significant limitations of the study. This study used domestic tourism for Beijing as a tourism industry indicator. Future research can use international tourism together with domestic tourism to see the difference in linkage with economic growth. The study used data only for Beijing, so future research can use pool data from more cities in China to see overall results. More variables for the representation of the tourism industry, such as a number of tourists arriving, the number of nights stayed in the host country, and real exchange rate, among others, can also be used in future research with more advanced techniques. The prospective study can also control the crucial factors that influence the growth in Beijing’s economy to find a clearer picture of the concept.