Put–Call Ratio Volume vs. Open Interest in Predicting Market Return: A Frequency Domain Rolling Causality Analysis
Abstract
:1. Introduction
2. Data and Methodology
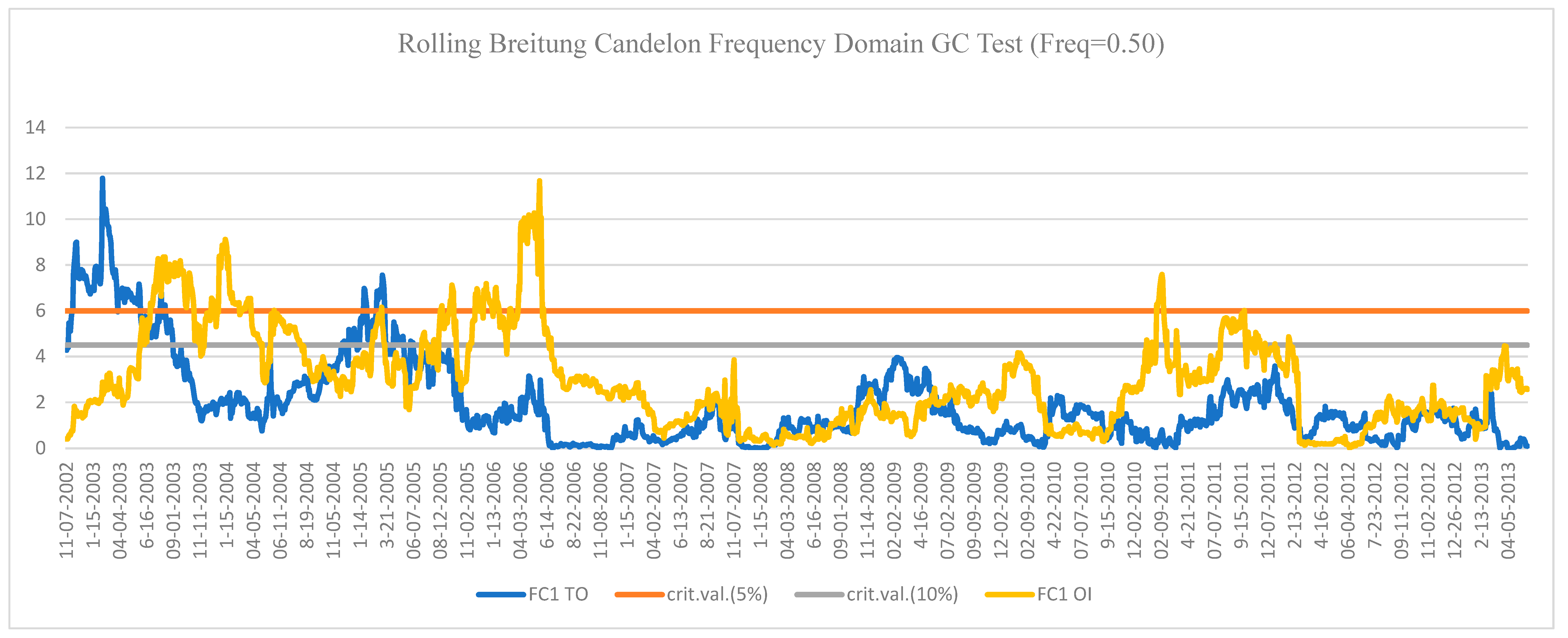
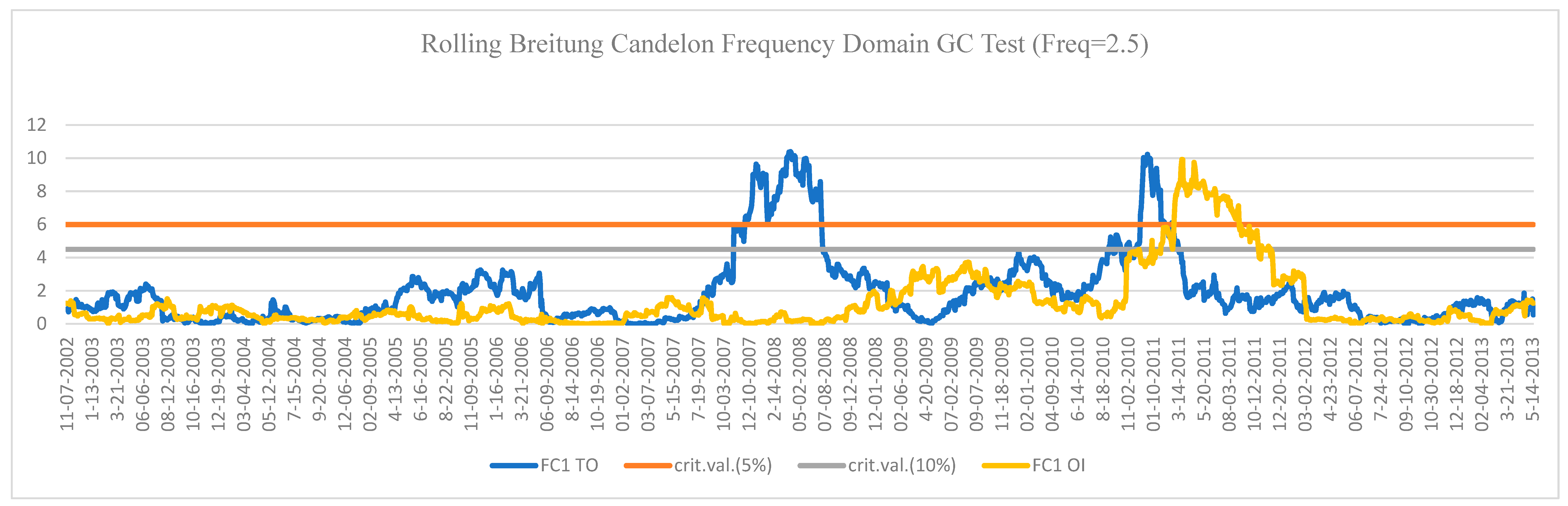
3. Empirical Analysis
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
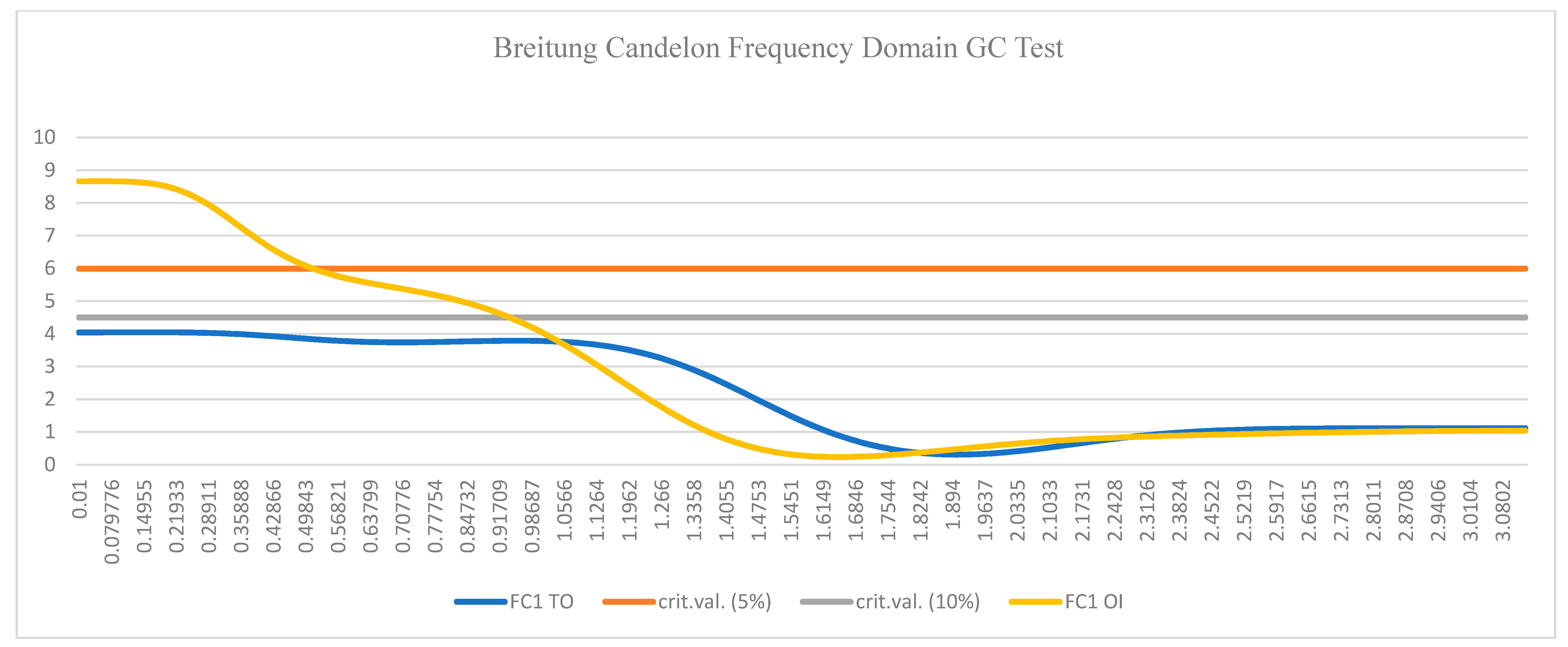
Appendix A
| In Sample | Out of Sample (Freq. 0.5) | Out of Sample (Freq. 2.5) | ||||
|---|---|---|---|---|---|---|
| FC1 TO | FC1 OI | FC1 TO | FC1 OI | FC1 TO | FC1 OI | |
| Mean | 2.195 | 2.785 | 1.953 | 2.955 | 1.942 | 1.323 |
| Median | 1.332 | 1.026 | 1.359 | 2.571 | 1.350 | 0.565 |
| Standard Deviation | 1.441 | 2.772 | 1.888 | 2.112 | 2.157 | 1.849 |
| Kurtosis | −1.783 | −0.620 | 3.032 | 0.621 | 4.114 | 5.483 |
| Skewness | 0.140 | 0.929 | 1.719 | 0.948 | 2.050 | 2.380 |
| Minimum | 0.308 | 0.232 | 0.002 | 0.009 | 0.000 | 0.001 |
| Maximum | 4.046 | 8.662 | 11.784 | 11.674 | 10.391 | 9.919 |
| No of Obs. | 314 | 314 | 1917 | 1917 | 1917 | 1917 |
References
- Back, Kerry. 1993. Asymmetric information and options. The Review of Financial Studies 6: 435–72. [Google Scholar] [CrossRef]
- Bai, Jushan, and Pierre Perron. 2003. Computation and analysis of multiple structural change models. Journal of Applied Econometrics 18: 1–22. [Google Scholar] [CrossRef]
- Bandopadhyaya, Arindam, and Anne Leah Jones. 2008. Measures of investor sentiment: A comparative analysis put-call ratio vs. volatility index. Journal of Business & Economics Research 6: 27–34. [Google Scholar]
- Batten, Jonathan A., Cetin Ciner, and Brian M. Lucey. 2017. The dynamic linkages between crude oil and natural gas markets. Energy Economics 62: 155–70. [Google Scholar] [CrossRef]
- Biais, Bruno, and Pierre Hillion. 1994. Insider and liquidity trading in stock and options markets. The Review of Financial Studies 7: 743–80. [Google Scholar] [CrossRef]
- Billingsley, Randall S., and Don M. Chance. 1988. Put-call ratios and market timing effectiveness. Journal of Portfolio Management 15: 25. [Google Scholar] [CrossRef]
- Black, Fischer. 1975. Fact and Fantasy in the Use of Options. Financial Analysts Journal 31: 36–41. [Google Scholar] [CrossRef]
- Blau, Benjamin M., and Tyler J. Brough. 2015. Are put-call ratios a substitute for short sales? Review of Derivatives Research 18: 51–73. [Google Scholar] [CrossRef]
- Blau, Benjamin M., Nga Nguyen, and Ryan J. Whitby. 2014. The information content of option ratios. Journal of Banking & Finance 43: 179–87. [Google Scholar]
- Bouri, Elie, David Roubaud, Rania Jammazi, and Ata Assaf. 2017. Uncovering frequency domain causality between gold and the stock markets of China and India: Evidence from implied volatility indices. Finance Research Letters 23: 23–30. [Google Scholar] [CrossRef]
- Breitung, Jörg, and Bertrand Candelon. 2006. Testing for short-and long-run causality: A frequency-domain approach. Journal of Econometrics 132: 363–78. [Google Scholar] [CrossRef]
- Brennan, Michael J., and H. Henry Cao. 1996. Information, trade, and derivative securities. The Review of Financial Studies 9: 163–208. [Google Scholar] [CrossRef]
- Cao, H. Henry, and Dongyan Ye. 2016. Transaction Risk, Derivative Assets, and Equilibrium. Quarterly Journal of Finance 6: 1650001. [Google Scholar] [CrossRef]
- Chang, Chuang-Chang, Pei-Fang Hsieh, and Hung-Neng Lai. 2009. Do informed option investors predict stock returns? Evidence from the Taiwan stock exchange. Journal of Banking & Finance 33: 757–64. [Google Scholar]
- Chordia, Tarun, Alexander Kurov, Dmitriy Muravyev, and Avanidhar Subrahmanyam. 2018. Index Option Trading Activity and Market Returns. Available online: http://dx.doi.org/10.2139/ssrn.2798390 (accessed on 17 May 2018).
- Du, Brian, Scott Fung, and Robert Loveland. 2018. The Informational Role of Options Markets: Evidence from FOMC Announcements. Journal of Banking & Finance 92: 237–56. [Google Scholar]
- Easley, David, Maureen O’hara, and Pulle Subrahmanya Srinivas. 1998. Option volume and stock prices: Evidence on where informed traders trade. The Journal of Finance 53: 431–65. [Google Scholar] [CrossRef]
- Fodor, Andy, Kevin Krieger, and James S. Doran. 2011. Do option open-interest changes foreshadow future equity returns? Financial Markets and Portfolio Management 25: 265–80. [Google Scholar] [CrossRef]
- Granger, Clive W. J. 1969. Investigating causal relations by econometric models and cross-spectral methods. Econometrica: Journal of the Econometric Society 37: 424–38. [Google Scholar] [CrossRef]
- Grossman, Sanford J. 1988. An analysis of the implications for stock and futures price volatility of program trading and dynamic hedging strategies. Journal of Business 61: 275–98. [Google Scholar] [CrossRef]
- Hosoya, Yuzo. 1991. The decomposition and measurement of the interdependency between second-order stationary processes. Probability Theory and Related Fields 88: 429–44. [Google Scholar] [CrossRef]
- Jena, Sangram Keshari, and Ashutosh Dash. 2014. Trading activity and Nifty index futures volatility: An empirical analysis. Applied Financial Economics 24: 1167–76. [Google Scholar] [CrossRef]
- John, Kose, Apoorva Koticha, Ranga Narayanan, and Marti Subrahmanyam. 2000. Margin Rules, Informed Trading and Price Dynamics. Working Paper. New York: Stern School of Business, New York University. [Google Scholar]
- Johnson, Travis L., and Eric C. So. 2012. The option to stock volume ratio and future returns. Journal of Financial Economics 106: 262–86. [Google Scholar] [CrossRef]
- Li, Wei-Xuan, Clara Chia-Sheng Chen, and Joseph J. French. 2015. Toward an early warning system of financial crises: What can index futures and options tell us? The Quarterly Review of Economics and Finance 55: 87–99. [Google Scholar] [CrossRef]
- Pan, Jun, and Allen M. Poteshman. 2006. The information in option volume for future stock prices. The Review of Financial Studies 19: 871–908. [Google Scholar] [CrossRef]
- Roll, Richard, Eduardo Schwartz, and Avanidhar Subrahmanyam. 2009. Options trading activity and firm valuation. Journal of Financial Economics 94: 345–60. [Google Scholar] [CrossRef]
- Roll, Richard, Eduardo Schwartz, and Avanidhar Subrahmanyam. 2010. O/S: The relative trading activity in options and stock. Journal of Financial Economics 96: 1–17. [Google Scholar] [CrossRef]
- Ryu, Doojin. 2015. The information content of trades: An analysis of KOSPI 200 index derivatives. Journal of Futures Markets 35: 201–21. [Google Scholar] [CrossRef]
- Tiwari, Aviral Kumar, Mohamed Arouri, and Frederic Teulon. 2014. Oil prices and trade balance: A frequency domain analysis for India. Economics Bulletin 34: 663–80. [Google Scholar]
- Tiwari, Aviral Kumar, Mihai Ioan Mutascu, Claudiu Tiberiu Albulescu, and Phouphet Kyophilavong. 2015. Frequency domain causality analysis of stock market and economic activity in India. International Review of Economics & Finance 39: 224–38. [Google Scholar]
- Yamada, Hiroshi, and Wei Yanfeng. 2014. Some theoretical and simulation results on the frequency domain causality test. Econometric Reviews 33: 936–47. [Google Scholar] [CrossRef]
| 1 | Informational role of derivative markets was discussed by Back (1993), Biais and Hillion (1994), Brennan and Cao (1996) and John et al. (2000) and others who further enriched the linkage among trade, price and private information in derivative market. In addition, few empirical studies support the informational role of derivative markets (e.g., Dubrian et al. (2018), Ryu (2015), Cao and Ye (2016) and Chordia et al. (2018)). |
| 2 | |
| 3 | |
| 4 | We estimated the Bai and Perron (2003) test and the results show five breakpoints in both the cases, i.e., volume PCR and market return, and open interest PCR and market return. The results are available on request. |
| 5 | The bellwether index of National Stock Exchange of India (NSE) represents 65% of the total market capitalization and 12 sectors of the economy. |
| 6 | |
| 7 | Yamada and Yanfeng (2014) through theoretical evaluation tested the usefulness of the methodology even at a frequency close to zero. |
| 8 | We are thankful to the anonymous referees for this suggestion. |
| 9 | The descriptive statistics of the F-statics of the frequency domain causality results are presented in Appendix A Table A1. |
| 10 | We also estimated conditional frequency domain rolling causality analysis after controlling for the futures market activities. The results are quite similar and available upon request. |
| PCROI | PCRTO | RET | LFTO | |
|---|---|---|---|---|
| Mean | 1.124 | 0.904 | 0.001 | 12.790 |
| Median | 1.140 | 0.911 | 0.001 | 13.473 |
| Maximum | 3.049 | 2.773 | 0.162 | 14.944 |
| Minimum | 0.210 | 0.136 | −0.163 | 6.862 |
| Std. Dev. | 0.414 | 0.264 | 0.019 | 1.703 |
| Skewness | 0.155 | 0.370 | −0.136 | −1.420 |
| Kurtosis | 3.177 | 4.969 | 12.447 | 3.840 |
| Jarque–Bera | 11.491 | 399.741 | 8065.200 | 791.801 |
| Probability | 0.003 *** | 0.000 *** | 0.000 *** | 0.000 *** |
| Observations | 2168 | 2168 | 2167 | 2168 |
| Augmented Dickey–Fuller test statistic (p-values) | −7.892 (0.000 ***) | −7.682 (0.000 ***) | −46.776 (0.000 ***) | −3.314 (0.014 **) |
| Unconditional Chi-sq. Test Statistic (p-Values) | Conditional Chi-sq. Test Statistic (p-Values) | |
|---|---|---|
| PCR TO ≠> RET | 3.548 (0.470) | 5.887 (0.207) |
| NIFTY RET ≠> PCR TO | 23.403 (0.000 ***) | 26.213 (0.000 ***) |
| PCR OI ≠> RET | 9.326 (0.009 ***) | 15.999 (0.000 ***) |
| NIFTY RET ≠> PCR OI | 27.469 (0.000 ***) | 36.878 (0.000 ***) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jena, S.K.; Tiwari, A.K.; Mitra, A. Put–Call Ratio Volume vs. Open Interest in Predicting Market Return: A Frequency Domain Rolling Causality Analysis. Economies 2019, 7, 24. https://doi.org/10.3390/economies7010024
Jena SK, Tiwari AK, Mitra A. Put–Call Ratio Volume vs. Open Interest in Predicting Market Return: A Frequency Domain Rolling Causality Analysis. Economies. 2019; 7(1):24. https://doi.org/10.3390/economies7010024
Chicago/Turabian StyleJena, Sangram Keshari, Aviral Kumar Tiwari, and Amarnath Mitra. 2019. "Put–Call Ratio Volume vs. Open Interest in Predicting Market Return: A Frequency Domain Rolling Causality Analysis" Economies 7, no. 1: 24. https://doi.org/10.3390/economies7010024
APA StyleJena, S. K., Tiwari, A. K., & Mitra, A. (2019). Put–Call Ratio Volume vs. Open Interest in Predicting Market Return: A Frequency Domain Rolling Causality Analysis. Economies, 7(1), 24. https://doi.org/10.3390/economies7010024






