On the Samaritan’s Dilemma, Foreign Aid, and Freedom

Abstract

This paper presents an extension of the two-period Samaritan’s Dilemma in order to analyze the potential for foreign aid to promote freedom. An example is the United States’ recent opening towards Cuba. It is shown that a donor nation’s dual concern for economic reforms and greater freedoms can exacerbate the Samaritan’s Dilemma, even when economic aid is coupled with targets for freedom. By contrast, a policy that is focused on freedom alone can potentially resolve the Samaritan’s Dilemma. Such a policy requires the donor to temper the degree of altruism that motivates its provision of economic aid to the recipient nation.

1. Introduction

Donor nations may seek to attain multiple goals when providing foreign aid to a recipient nation. For example, if the recipient nation is a dictatorship, then the donor may be interested in fostering both economic growth and political freedoms. By contrast, the recipient dictatorship might not be interested in achieving both goals, particularly if political freedoms would lead to a reduction in power. In such a situation, what is a donor nation to do?

Cuba is a motivating example of this phenomenon. In the first 30 years of communist rule it was a USSR satellite in that Cuba’s economy critically depended on Soviet aid (Morris 2007). Given the effects of the United States (U.S.) embargo that resulted from Cuba’s nationalization of U.S. oil refineries, it was impossible for Cuba to sustain its economy without receiving external support (Pérez 2002). With the demise of the Soviet Union, Cuba’s primary source of aid dried up and it looked for new partners to economically and financially support the communist regime. Subsequently, Hugo Chavez’s Venezuela became the main provider of aid to Cuba (Amegashie et al. 2013). Yet, under the combination of falling oil prices and the death of Chavez, Venezuela could no longer afford to support Cuba (Piccone and Trinkunas 2014). Brazil, under the Lula and Rousseff administrations, then became Cuba’s new life-line.1 Over time, the Brazilian government was plagued by corruption and also committed itself to vast expenditures associated with its hosting of The World Cup and Rio Olympics. Finally, during Rousseff’s presidency, the Brazilian economy entered into the nadir of a recession (Economist 2016), at which point it could no longer maintain its support of Cuba.

This history of aid to Cuba characterizes the regime as parasitic in the sense of Buchanan’s (Buchanan 1975) Samaritan’s Dilemma. That is, sponsors directed international aid to Cuba primarily for the purpose of maintaining Cuba’s communist regime, and, knowing this, Cuba has had no incentive to conduct meaningful economic reform. Cuba’s leaders were well-aware that aid would not be withdrawn in the absence of reform because the maintenance of Cuba’s communist system was of first-order importance to its donors. This is consistent with Gibson et al.’s (2005) characterization of the Samaritan’s Dilemma as being a motivational problem, rather one than stemming from the asymmetry or absence of information. Moreover, Gibson et al. (2005) recognize that the dynamics of the Samaritan’s Dilemma are such that not only is meaningful reform unlikely, but also aid recipients may actually lose skills and motivation over time (p. 39).

Such behavior is not limited to Cuba. For example, North Korea and other dictatorial clientele states do the same; they have an incentive to avoid reforming their own economies in order to extract rents from the rest of the world in the form of foreign aid. Although not framed within the context of the Samaritan’s Dilemma, Bapat (2011) notes that donors of anti-terrorism aid face a similar situation. Specifically, it is the existence of terrorism in the recipient nation that prompts the need for aid. This then begs the question as to the incentive for true counterterror efforts within the recipient nation if counterterror success leads to less aid.

What happens if, in addition to economic performance, the donor is also interested in promoting freedom? For example, as outlined above, without the help of the Soviet Union, Venezuela, or Brazil the Cuban regime had no obvious source of aid. Within this vacuum, the Obama administration saw a clear opportunity to engage Cuba and reestablish diplomatic and commercial relations with it. For the Obama administration, opening its relationship with Cuba was seen as an opportunity to renew its leadership in the Americas “and promote more effective change that supports the Cuban people and our national security interests” [https://www.whitehouse.gov/issues/foreign-policy/cuba]. In particular,

“A critical focus of these actions will include continued strong support for improved human rights conditions and democratic reforms in Cuba. The promotion of democracy supports universal human rights by empowering civil society and a person’s right to speak freely, peacefully assemble, and associate, and by supporting the ability of people to freely determine their future. The U.S. efforts are aimed at promoting the independence of the Cuban people so they do not need to rely on the Cuban state”.

[https://www.whitehouse.gov/issues/foreign-policy/cuba, emphasis added]

In sum, the aim of the Obama administration’s policy was to improve Cuba’s economic performance, and, at the same time, increase the freedom of its people so that they do not have to rely on the Cuban state.2 Indeed, promoting freedom is often used as a justifying rationale for foreign aid. For freedom promotion to work, it would appear that, at a minimum, the donor must resolve the Samaritan’s Dilemma. Moreover, we show how changes to this policy under the Trump administration will have the effect of testing the administration’s resolve.

The issues here are quite general and extend beyond U.S.-Cuba relations. Consequently, this paper introduces an explicitly dynamic model as a context for analyzing the possible outcomes of a change in donor-recipient relations that emphasizes both increased economic performance and freedoms. In particular, we ask whether a focus on resolving the Samaritan’s Dilemma with respect to the aid-income relationship is enough to successfully increase freedoms as well. That is, is a focus on the Samaritan’s Dilemma an example of Kerr’s (Kerr 1975) classic trap of rewarding A while hoping for B? Here, ‘A’ is rewarding recipient economic reform with increased aid, consistent with resolving the Samaritan’s Dilemma. The ‘B’ is the donor’s objective of increased freedoms for the recipient population.

Within this context, we consider three different types of policies and two policymaking environments. The policies are (i) an aid policy that is targeted on recipient economic performance; (ii) a policy that couples aid with freedom and (iii) a freedom target that affects the recipient’s economic performance indirectly via entrepreneurial reforms. The two policy environments are Stackelberg (leader-follower) and Nash. The Stackelberg environment with the recipient treated as the leader is most closely associated with the Samaritan’s Dilemma within two-period models (Pedersen 2001; Dijkstra 2007); hence, it serves as a benchmark. Within this environment, we show that a policy that is designed to avoid Kerr’s (1975) trap by coupling aid with freedom neither resolves the Samaritan’s Dilemma nor does it foster freedom. This leads us to consider Nash interaction between donor and recipient because Nash behavior involves sufficient donor commitment to resolve the two-period Samaritan’s Dilemma (Gintis 2009). However, this turns out to be a classic case of rewarding A while hoping for B. Specifically, in a Nash environment, the policy of coupling aid with freedom resolves the Samaritan’s Dilemma, but it does not commensurately increase freedoms within the recipient nation. Our final consideration, Nash play (representing donor commitment) and an explicitly freedom-based policy, succeeds at resolving both the Samaritan’s Dilemma and increasing freedoms. To be successful; however, such a policy requires the donor to temper its altruistic motivation for supporting the recipient. This is especially true if the recipient is willing to test the donor’s resolve.

The paper is organized as follows. The next section presents a literature review. Section 3 introduces a baseline dynamic version of a Samaritan’s Dilemma between a donor and recipient. Section 4 considers several policies designed to resolve the Samaritan’s Dilemma, and shows that in all cases, the recipient is able to accept donor aid and maintain its restrictions on freedoms. In Section 5 we analyze the effect of the donor pre-committing to a freedom-based target, and show how this causes meaningful reform within the recipient. Concluding remarks appear in Section 6.

2. Literature Review

Many countries engage in foreign aid and yet the literature on the efficacy of aid is equivocal. For example, Easterly (2003) disputes that aid promotes growth. By contrast, Dalgaard et al. (2004) show that aid increases long-run productivity. Boone (1996) finds that foreign aid has little impact reducing poverty, or increasing investment; its main effect is to increase the size of government. Tavares (2003) shows that foreign aid reduces corruption. Goldsmith (2001) finds a small, positive relationship between foreign aid and democracy or freedom in Africa. Conversely, Knack (2004) does not find any empirical evidence that aid promotes democracy for a sample of recipient nations over 1975–2000. Power and Ryan (2006) analyze recipient nations over a 30-year time span (1970–2000) and find no significant effect of foreign aid on economic freedom. Regarding the equivocal relationship between aid and freedom, it is our contention that such observations can be partially explained by mixed results on the part of donors to resolve the Samaritan’s Dilemma.

Indeed, The Elusive Quest for Growth (Easterly 2002) raised awareness of the importance of accounting for economic and political incentives when it comes to development aid. Much earlier, Buchanan (1975) similarly observed that suitable incentives and institutions for both donors and recipients are necessary in order to be able to successfully institute aid-based reforms. Buchanan called such a situation the Samaritan’s Dilemma, where a donor that is motivated by altruism (the proverbial Samaritan) might have to restrict the extent of their altruism in order to provide the necessary incentives for a recipient nation to conduct reform. For example, suppose that, as an altruist, a donor’s aid to a recipient nation is negatively related to the recipient’s GDP. Then, if the recipient nation’s economy fares poorly—owing to the absence of economic reforms—the recipient nation may receive more aid than it would have under reforms that produced better economic outcomes. Buchanan (1975) calls such recipient behavior parasitic. Moreover, Buchanan (1975) sees the issue in terms of being as much of a problem of the donor’s behavior as that of the recipient.

In particular, when a donor is altruistic, the donor’s utility places positive weight on the recipient’s utility. Aid has a direct cost in that it subtracts from the donor’s income but it also constitutes an altruistic benefit for the donor because it increases the recipient’s utility. Hence, if the recipient underachieves economically an altruistic donor finds it in its interest to augment the recipient’s income via aid. In addition, in Buchanan’s (1975) active Samaritan’s Dilemma, the donor’s utility is not only a function of the amount of aid given to the recipient but it is also a function of the recipient’s actions. Typically, this means that the donor prefers that the recipient conduct economic reforms rather than exhibit parasitic behavior. In this paper, we put a twist on the donor’s preferences over the recipient’s actions. Specifically, donor aid policy is motivated by both a concern for recipient economic performance and also as a means for promoting freedom. Consequently, an altruistic donor prefers that aid results in actions by the recipient that ultimately lead to increased freedoms.

In order to avoid the counterproductive incentive structure between the lack of reform and the provision of aid, the donor nation may have to tie its hands and act against its altruistic interests. Whether or not the donor should abandon its altruistic tendencies, thereby temporarily penalizing both itself and the recipient, is the Samaritan’s Dilemma. In making such a commitment, the donor must weigh the utility of the recipient in both the short and long run. Yet, the dynamic asymmetries present between donor and recipient are absent from Buchanan’s (1975) model because it is a static game in strategic form. Consequently, a literature has emerged that examines the dynamic means for tying the hands of altruistic donors and aligning the incentives for the recipient with those of the donor.

Within a dynamic context the Samaritan’s Dilemma typically arises when the recipient acts as a Stackelberg leader, thereby capitalizing on the donor’s altruism to its full extent (Bruce and Waldman 1990). The Stackelberg relation applies because recipients know that the greater the need that an altruistic donor observes, the more aid the donor will give. To summarize Pedersen (2001, p. 698): upon observing a low level of recipient income, it is in the donor’s interest to increase aid, which is exactly what the recipient anticipated the donor to do. This is because if the donor does not give extra aid it will lower the recipient’s utility, and, by the donor’s altruism, the utility of the donor itself. The recipient’s understanding of this incentive structure allows for it to behave like a Stackelberg leader in that it anticipates the donor’s likely response.

The solution therefore requires the donor to commit to not giving extra aid if the recipient underperforms economically. Gintis (2009) demonstrates that if the donor is able to commit to Nash play with the recipient, then the Samaritan’s Dilemma may be resolved. It is also well-established that the two-period passive version of Buchanan’s Samaritan’s Dilemma can be resolved if the donor acts as a leader in the Stackelberg sense (e.g., Dijkstra 2007).3 Another resolution is provided by Lagerlöf (2004), where the donor has incomplete information regarding the recipient’s preferences over the aid-augmented term in the recipient’s utility. As is often the case, the introduction of incomplete information increases the set of equilibria. In particular, equilibrium exists where the recipient truthfully signals its need for aid. In an alternative environment, where the donor has asymmetric information regarding the recipient’s degree of reform, Svensson (2000) shows that a second-best solution can be achieved when the donor delegates its aid decision to an agent that is less altruistic than the donor. This is consistent with Buchanan’s (1975) intuition that resolving the Samaritan’s Dilemma requires the donor to tie its hands against its altruistic interests.

In terms of the literature reviewed above, there are two defining aspects of our analysis. First, the recipient is engaged in an active Samaritan’s Dilemma with the donor, owing to the donor’s concerns for freedoms that extend beyond its altruistic motivation for providing aid. That is, the donor is concerned with both the recipient’s welfare and actions. Second, it is a complete information analysis. This is in keeping with donor’s understanding of the recipient as a dictatorship with well-defined preferences for remaining in power. In addition, it is consistent with the treatment of the Samaritan’s Dilemma in the foreign aid literature as being a motivational problem for donor and recipient alike, rather than stemming from asymmetric information (Gibson et al. 2005). The corresponding model is presented in the following section.

3. The Model

Our framework is based on an explicitly dynamic version of the Samaritan’s Dilemma. This two-period baseline model allows for us to begin by formally addressing Buchanan’s (1975) assertion that the resolution of the Samaritan’s Dilemma may require a commitment that is costly to an altruistic aid donor in order to convince the aid recipient that it is in the recipient’s best interest to undertake reform. Moreover, the two-period horizon captures the inability of elected governments to commit to longer-term criteria for aid.

In expressing the model, the upper-case symbols U and V are used to denote the donor and recipient’s two-period utility functions, respectively. The first-period components of the donor’s and recipient’s utilities are denoted as u and v, respectively, with the second-period component of the recipient’s utility being denoted as $\widehat{v}.$ We do not specify a second-period component of the donor’s utility because, by the definition of altruism, the donor’s second-period utility will be a function of the recipient’s utility, V.

The two-period utility function of the recipient’s leadership, V, is defined to be consistent with that of a dictatorship.4 In the first period, prior to receiving donor aid, the recipient’s welfare depends positively on the state of its economy, as measured by its GDP, y, and negatively on the freedom, F, of its people. The greater the freedom, the lower the dictator’s utility. These considerations are captured by the following partial derivatives of the first-period utility function, $v(y,F):$

$$v_y>0,v_{yy}<0,v_F<0,v_{FF}<0,v_{yF}>0.$$

(1)

For example, the cross-partial derivative $v_{yF}>0$ reflects the following phenomena. Aid is a second-period decision for the donor Hence, one way that the recipient can augment its first period income in the absence of aid is by increasing freedoms that lead to increased entrepreneurship. In the Cuban example, when the Soviet Union fell, its aid and trade subsidization policies with Cuba ended as well. In order to make up the output gap, Cuba responded by legalizing microenterprises in various sectors during 1993–1995 (Ritter 1998). The tradeoff that is involved for a dictatorship considering such freedoms in the first period is captured by $v_F<0,v_{FF}<0,$ implying that the dictatorship dislikes freedom; and, $v_{yF}>0,$ implying that entrepreneurial freedom is good for growth. The short-term use of entrepreneurial freedoms to augment growth is a hallmark of dictatorships.5

In the second period, aid from the donor is now possible. Aid/help from the donor is denoted by H, which adds to the recipient’s second-period income; i.e., y + H. The recipient’s second-period utility, $\widehat{v}(y+H,F),$ is characterized by the following set of partial derivatives:

$${\widehat{v}}_1>0,{\widehat{v}}_{11}<0,{\widehat{v}}_F<0,{\widehat{v}}_{FF}<0,{\widehat{v}}_{1F}=0,$$

(2)

where ${\widehat{v}}_1$ denotes the partial derivative of the recipient’s second-period utility function, $\widehat{v},$ with respect to its first argument, y + H. The possibility of aid in the second period means that freedom loses its income-augmenting appeal in the recipient’s second-period utility function; which is captured by ${\widehat{v}}_{1F}=0.$ That is, in the second period the recipient behaves strategically by substituting aid for reform, as is the case in the Samaritan’s Dilemma. The inconsistent way that the recipient views freedom when aid is not present (in the first period) versus how it views freedom when aid is a possibility (in the second period) is a characteristic of dictatorial behavior [see footnote 5].

The recipient’s utility function for both periods is

$$V(y,F,H)=v(y,F)+\delta \widehat{v}(y+H,F),$$

(3)

where δ > 0 is the recipient’s discount factor. Being a dictatorship, the recipient’s control variable is its income, y. To wit, in choosing y the recipient is effectively determining its degree of economic reform. Moreover, given the relationship between entrepreneurial freedom and y, in selecting y the recipient imputes a corresponding level of F. Measures that have been used to monitor F are discussed below.

The donor acts as an altruistic agent, in that it wants to improve the well-being of the recipient’s people via income-augmenting aid to the recipient at a material cost to itself. Specifically, aid/help (H) comes out of the donor’s GDP, Y. The donor’s two-period utility function is

$$U\left(Y,H,y,F\right)=u(Y-H)+\alpha V(y,F,H),$$

(4)

where α > 0 is the donor’s degree of altruism. The presence of altruism in this form is a defining characteristic of the Samaritan’s Dilemma. The donor’s first-period utility function is increasing and concave in its own net income, Y–H. That is, $u^{\prime }>0\mathrm{and}{u}^{″}<0.$ As an altruist, the donor’s second-period utility is the α-weighted utility of the recipient. In particular, given that $\alpha {\widehat{v}}_1>0,$ if y is low, then an altruistic donor sees it as in its interest to augment the low y with aid, H. Hence, the potential for the Samaritan’s Dilemma is present.

Given these utility functions, the interaction between the recipient and donor hinges upon two relationships. The first is $dH/dy;$ i.e., the effect that the recipient’s economic performance has on donor aid. A parasitic relationship exists when $dH/dy<0.$ Lower recipient economic performance leads to a lower value of y, which in turn induces the donor to give greater aid. This in keeping with the Samaritan’s Dilemma approach to foreign aid. As an extension to this approach, note that one determinant of y is F. When freedoms increase this facilitates entrepreneurial behavior that spurs growth. Such freedoms reduce dictatorial power, however. It follows that if the dictatorship infringes on F this limits y. The dictator’s cost of reducing economic-enhancing freedom is offset when $dH/dy<0$ because aid can potentially make up the difference. This exacerbates the Samaritan’s Dilemma. Moreover, this characterization of strategic interaction between recipient and donor captures the observed equivocal relationship between aid and freedom. Indeed, in resolving the Samaritan’s Dilemma by creating an aid policy that leads to $dH/dy>0,$ the question remains as to how this will ultimately affect freedom. Kerr’s (1975) trap is a potentiality. Only when the interaction between the donor and the recipient results in $dH/dF>0$ is the donor aid policy in alignment with its desire to promote freedom for the recipient’s people. We now turn to three aid policies that address this issue.

4. Aid without Commitment

In the Samaritan’s Dilemma, if the donor is unable to commit to a policy of no aid when the recipient does not undertake economic reform, then the donor’s altruism causes the donor to react optimally to the economic situation that is produced by the recipient’s reforms or lack thereof. In terms of the model, this means that, if the donor cannot commit to an aid level that is independent of the recipient’s economic situation, then altruism leads the donor to make its aid policy contingent on the recipient’s economic situation. Expressed in terms of the choice variables, this means that the donor observes the recipient’s choice of y and then the donor sets its choice of H. That is, the donor’s policy is its best reply function. The donor’s inability to commit is therefore indicative of a leader-follower relationship where the recipient is the leader and the donor is the follower. In this section we consider two cases that can arise in the absence of donor commitment. The difference between the two cases is whether the donor selects aid, H, in reaction to the recipient’s choice of y (Case A); or, if the donor instead couples aid, H, with freedom, F. Case A is the classic Samaritan’s Dilemma and Case B is a new wrinkle that recognizes the donor’s ultimate rationale for engaging the recipient: increasing freedoms.

Case A: No Donor Link between Aid and Reform

The donor’s choice variable is aid, H (help). In Case A, the donor selects aid in reaction to the current economic situation in the recipient nation, y. Solving the model backwards, for a given y the donor maximizes (4) with respect to H. The donor’s first order condition is

$$-u^{\prime }(Y-H)+\alpha \delta {\widehat{v}}_1(y+H,F)=0\Rightarrow H=H(\alpha ,y,Y),$$

(5)

which characterizes the donor’s best reply function.

The result is a parasitic relationship, as the impact of y on H is negative [all comparative static calculations are derived in Appendix A]:

$$H_y=\frac{dH}{dy}=\frac{-\alpha \delta {\widehat{v}}_{11}}{u^{″}+\alpha \delta {\widehat{v}}_{11}}<0.$$

(6)

Equation (6) describes a counterproductive incentive at play. When the recipient underperforms economically, this induces the donor to give more aid. This is a classic parasitic relationship in the sense of Buchanan’s (1975) Samaritan’s Dilemma. A failing recipient economy leads to increased aid. Hence, this is our starting point for donor-recipient relations.

Given donor aid policy (the donor’s best reply function), $H(\alpha ,Y,y),$ the recipient maximizes (3) with respect to y, yielding

$$v_y(y,F)+\delta {\widehat{v}}_1(y+H,F)(1+H_y)=0\Rightarrow y_A^{*}=y(\alpha ,F,H).$$

(7)

Equation (7) determines the optimal value of the recipient’s income for Case A: $y_A^{*}.$ Note that the impact of freedom on the optimal $y_A^{*}$ is positive:

$$\frac{d{y}_A^{*}}{dF}=\frac{-v_{yF}}{v_{yy}+\delta {(1+H_y)}^2{\widehat{v}}_{11}}>0.$$

(8)

By Equation (8), a dictatorship’s restrictions on freedom allows a parasite to underperform with respect to income, thereby further facilitating the parasitic relationship. This exacerbates the Samaritan’s Dilemma.

Inserting $y_A^{*}$ into Equation (5) yields the donor’s optimal aid for Case A, $H_A^{*}:$

$$H_A^{*}=H(\alpha ,y_A^{*},Y)=H(\alpha ,y_A^{*}(\alpha ,F,Y),Y).$$

(9)

Now, one can assess the impact of donor aid on the freedom on the recipient’s people [taking into account Equations (6) and (8)]:

$$\frac{d{H}_A^{*}}{dF}=\frac{dH}{d{y}_A^{*}}\frac{d{y}_A^{*}}{dF}<0.$$

(10)

That is, although freedom has a positive impact on income, $d{y}_A^{*}/dF>0,$ this is offset by the parasitic donor-recipient relationship, $d{H}_A^{*}/d{y}_A^{*}<0.$ Increased freedoms that might be necessary for augmenting a regime’s income are instead neglected, because the resulting decrease in income causes the altruistic donor to be more generous. Consequently, the recipient does not reform either economically or in the dimension of freedom for its people. As expected, this case is consistent with the Samaritan’s Dilemma.

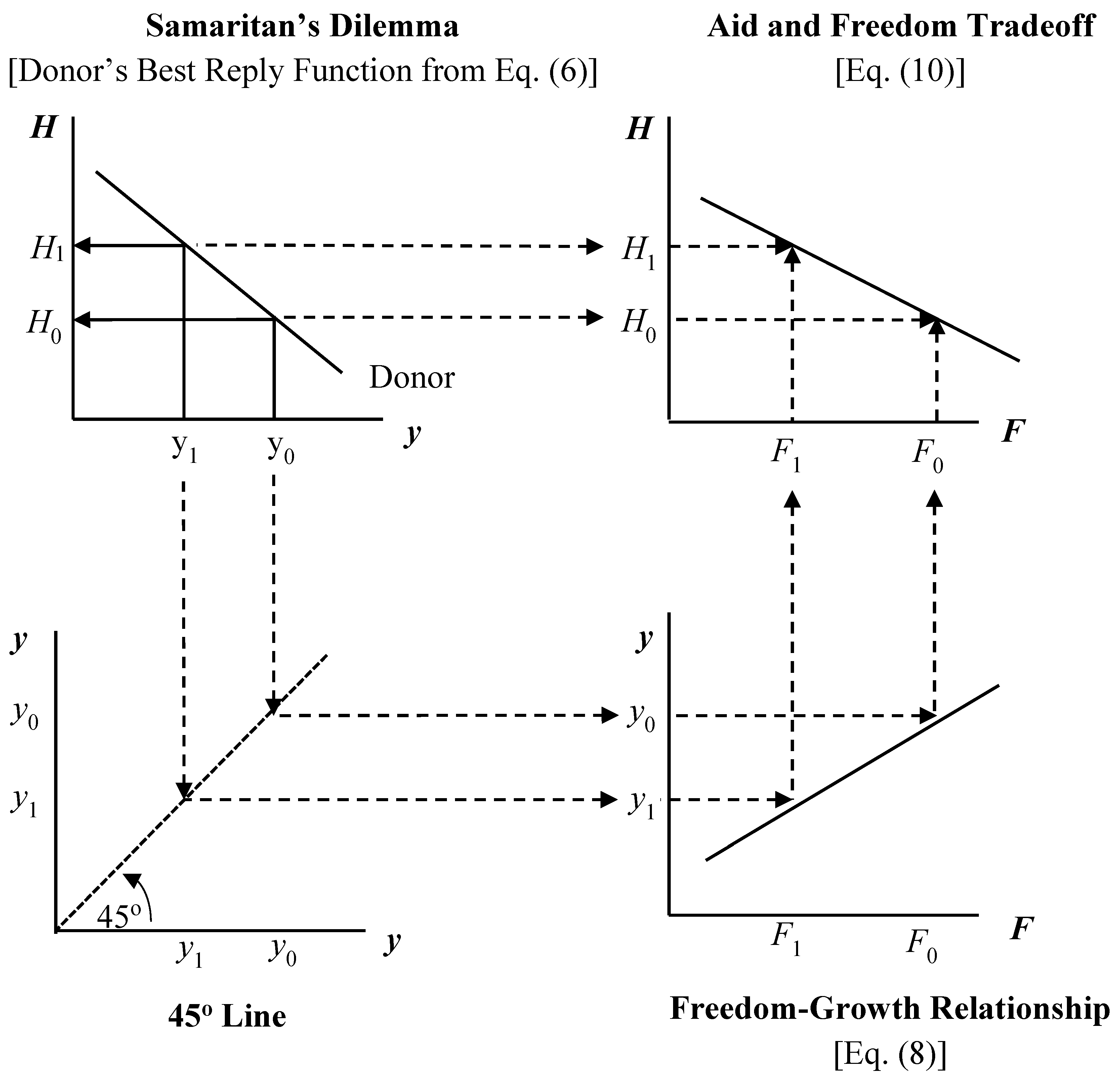
Figure 1 illustrates the inner workings of Case A. First, the top left graph depicts Equation (6): the negative relation between donor aid, H, and the recipient’s income, y. If the recipient’s income falls from y₀ to y₁, donor aid is increased from H₀ to H₁. This is the Samaritan’s Dilemma: the recipient finds it in its interest to underperform economically in order to extract more aid. Second, the bottom left graph uses a 45° line in (y, y) space to transform the measurement of y, which is on the horizontal axis of the top left graph, to the measurement of y on the vertical axis of (F, y) space in the bottom right graph of Figure 1. Third, the bottom right graph depicts the relationship given in Equation (8): the positive relationship between freedom and the recipient’s income. When the recipient makes its choice of income y₁ instead of y₀ it does not need the entrepreneurial freedoms, F₀, associated with y₀. Instead, it imputes that the freedoms necessary for y₁ are those that are given by F₁. Fourth, the top right graph depicts Equation (10): the impact of donor aid on the freedom of the recipient’s people. It captures the tradeoff between these two variables, in which a decrease in freedoms from F₀ to F₁ leads to an increase in donor aid from H₀ to H₁. Figure 1 presents the two main tradeoffs identified within this paper: the Samaritan’s Dilemma, which captures the tradeoff between income and aid; and, the resulting tradeoff between freedom and aid, which, to the best of our knowledge, has gone unidentified until now.

Case B: The Donor Couples Aid to Reform

Of course, both outcomes of Case A: (i) the recipient’s parasitic ability to receive aid when it engages in less reform; and, (ii) the negative relationship between freedom and aid; run against the donor’s goodwill and intentions. As an alternative, the donor can use aid to augment the recipient’s income, but do so in a way that couples aid to freedom.

A coupled donor aid policy is expressed as the product FH, where H is again the donor’s choice variable. This implies that rather than aid augmenting the recipient’s income through the term y + H, it does so through the term y + FH. From an operational perspective, the term FH can be directly estimated if F is a freedom index that lies along the [0, 1] interval, where 0 represents no freedom and 1 the freedom level the donor is targeting. Such freedom scores allow for the monitoring of changes in freedom in the recipient nations, and have been used in empirical work on the composition and efficacy of aid (Amegashie et al. 2013; Power and Ryan 2006; Medvedev 1972). Therefore, the recipient’s and donor’s utility functions are, respectively,

$$V(y,F,H)=v(y,F)+\delta \widehat{v}(y+FH);$$

(11)

$$U\left(Y,H,y,F\right)=u(Y-FH)+\alpha V(y,F,H).$$

(12)

Throughout this section, we retain the leader-follower structure consistent with an altruistic donor that makes its aid policy contingent upon the recipient’s income. Consequently, the donor takes y as given and maximizes (12) with respect to aid, H, yielding the following best reply function:

$$-u^{\prime }(Y-FH)F+\alpha \delta {\widehat{v}}_1(y+FH)F=0\Rightarrow H=H(\alpha ,y,Y,F).$$

(13)

From (13), one can see that in this context the aid-income relationship remains parasitic:

$$H_y=\frac{dH}{dy}=\frac{-\alpha \delta {\widehat{v}}_{11}}{[u^{″}+\alpha \delta {\widehat{v}}_{11}]F}<0.$$

(14)

Once again, it is in the recipient’s interest to underperform economically, thereby receiving more aid.

Moreover, in contrast to Case A, from (13) F now has a direct impact on H:

$$\frac{dH}{dF}=\frac{-H}{F}<0,$$

(15)

which can be best understood in terms of the elasticity of donor aid, H, with respect to freedom in the recipient, F:

$${\epsilon }_{HF}=\frac{dH}{dF}\frac{F}{H}=-1$$

(13′)

As the absolute value of ${\epsilon }_{HF}$ is equal to one, $\left|{\epsilon }_{HF}\right|=1$, the donor’s best reply function is of unit elasticity, i.e., the marginal impact of freedom on aid is equal to the average impact.

The recipient takes the donor’s best reply in (13) into account and selects a level of reform that determines y. Effectively, the recipient maximizes (11) with respect to y given (13), yielding

$$v_y(y,F)+\delta {\widehat{v}}_1[y+FH(\alpha ,y,Y,F)](1+F{H}_y)=0\Rightarrow y_B^{*}=y(\alpha ,Y,F).$$

(16)

Equation (16) determines the optimal recipient income in Case B: $y_B^{*}$. The impact of freedom on $y_B^{*}$ is given by

$$\frac{dy}{dF}=\frac{-v_{yF}-\delta {\widehat{v}}_{11}(F{H}_F+H)(1+F{H}_y)-\delta {\widehat{v}}_1{H}_y}{[v_{yy}+\delta {\widehat{v}}_{11}{(1+F{H}_y)}^2]}$$

(17)

Substituting (16) into (13) yields the optimal donor aid for Case B: $H_B^{*}=H(\alpha ,y_B^{*},Y,F),$ which allows for an assessment of the impact of donor aid on the freedom when aid is coupled with freedom. Note that now there exists both a direct and an indirect impact of F on $H_B^{*}.$ Policy FH results in the direct channel between F and $H_B^{*}.$ The indirect channel between F and $H_B^{*}$ occurs by combining of the effect of F on y with the effect of y on H via the chain rule:

$$\frac{d{H}_B^{*}}{dF}=\frac{dH}{dF}+\frac{dH}{d{y}_B^{*}}\frac{d{y}_B^{*}}{dF}=\frac{-H}{F}+\frac{(-\alpha \delta {\widehat{v}}_{11})}{[u^{″}+\alpha \delta {\widehat{v}}_{11}]F}\left[\frac{-v_{yF}-\delta {\widehat{v}}_{11}(F{H}_F+H)(1+F{H}_y)-\delta {\widehat{v}}_1{H}_y}{[v_{yy}+\delta {\widehat{v}}_{11}{(1+F{H}_y)}^2]}\right]$$

(18)

Given a positive effect of entrepreneurial freedom on growth, $\partial y/\partial F>0,$ by Equations (14) and (15), one must conclude that $\partial H_B^{*}/\partial F<0.$

In both cases addressed in this section, a parasitic relationship exists between donor aid and recipient economic reform. Moreover, aid is a negative function of freedom in that the dictatorship uses restrictions on freedoms to inhibit growth, thereby exacerbating the Samaritan’s Dilemma. Notably, this occurs even when the donor follows a policy that couples aid and freedom. The desired result is not obtained, and this is due to the structure of the game in which the donor does not commit to an aid level, but instead follows a policy in which aid is a best reply to the recipient’s income level.

5. The Donor Pre-Commits Its Aid to the Recipient

In this section, we allow for the donor to commit to a particular aid strategy, rather than reacting to the prevailing economic situation in the recipient. Instead of a leader-follower relationship, in which the recipient takes the donor’s best reply function as given, the two countries engage in Nash behavior, implying that in equilibrium the donor’s aid policy is a best reply to the recipient’s economic policy and vice-versa. In other words, each country creates the conditions under which the other sets its policy. We therefore analyze two aid strategies for the donor. In the first (Case C), the donor follows the aid-freedom coupling policy FH. In the second (Case D), the donor specifies aid as an increasing function of freedom in the recipient nation.

Case C: The Freedom-Aid Coupling Policy

Here, the donor again couples its aid to freedom; i.e., policy FH, but aid no longer moves in tandem with the recipient’s income, y. The two are instead co-determined as part of a Nash equilibrium. Given policy FH, the donor’s utility is as expressed in Equation (12) and the recipient’s is as expressed in Equation (11). The first order conditions for the donor (with respect to H) and the recipient (with respect to y) are

$$-u^{\prime }(Y-FH)F+\alpha \delta {\widehat{v}}_1(y+FH)F=0;$$

(19)

$$v_y(y,F)+\delta {\widehat{v}}_1[y+FH]=0.$$

(20)

When y and H are determined simultaneously, as is the case in Equations (19) and (20), by definition, there is no longer a parasitic relationship between the recipient and donor. Changing the game from a Stackelberg game in which the recipient is the leader, to a Nash game in which recipient income and donor aid are co-determined, eliminates the recipient’s parasitism, thereby resolving the Samaritan’s dilemma.

The impact of freedom on aid is given by (proof in Appendix A):

$$\frac{d{H}_C^{*}}{dF}=\frac{\alpha \delta {\widehat{v}}_{11}{v}_{yF}-(H{u}^{″}[v_{yy}+\delta {\widehat{v}}_{11}]+\alpha \delta H{\widehat{v}}_{11}{v}_{yy})}{\Delta }<0.$$

(21)

where $\Delta =[u^{″}F+\alpha \delta F{\widehat{v}}_{11}][v_{yy}+\delta {\widehat{v}}_{11}]-\alpha {\delta }^{2}F{\left({\widehat{v}}_{11}\right)}^2=[v_{yy}+\delta {\widehat{v}}_{11}]u^{″}F+\alpha \delta F{\widehat{v}}_{11}{v}_{yy}>0$.

Unfortunately, the tradeoff between freedom and aid persists, as $\partial H_C^{*}/\partial F<0.$ In Case C, the donor has fallen into Kerr’s (1975) trap in that it has committed to a policy that couples aid with freedom, thereby resolving the Samaritan’s Dilemma, but the ultimate goal of establishing a positive relationship between freedom and aid is not achieved. Per Equation (21), there is a tradeoff between freedom and aid. Therefore, the ability to pre-commit eliminates the recipient’s parasitism, thereby resolving the Samaritan’s Dilemma. At the same time, pre-commitment to aid coupled with freedom does not remove the tradeoff between freedom and aid.

Figure 2 illustrates Case C. The donor’s best reply function is given by Equation (19), denoted as D. The recipient’s best reply function is given by Equation (20), denoted as R. Strategies H and y are strategic substitutes for both the donor and recipient, as depicted by their downward-sloping best reply functions in (y, H) space. Indeed, the fact that aid and income are strategic substitutes lies at the heart of the Samaritan’s Dilemma, because when the recipient can act as a Stackelberg leader, the recipient maximizes its utility function along the donor’s negatively-sloped best reply function, implying that the recipient can substitute aid for income, as occurs in Cases A and B. In a Nash environment, the equilibrium instead takes place at the intersection of the best reply functions.

An increase in recipient freedom from F to F′ shifts both best reply functions outward from the origin and the equilibrium changes from the original point (y*, H*) to (y′, H′). Consequently, there is a tradeoff between F and H; i.e., optimal donor aid falls when the recipient’s freedom increases.

Case D: The Donor Explicitly Targets Freedom

In this case the donor’s aid is based on the following policy:

$$H=H(F)=hF,h>0.$$

(22)

Under this policy, the donor aims at directly influencing freedom in the recipient, treating F as its strategy. Aid is no longer a policy itself but is instead the result of the policy that makes the donor’s aid an increasing function of freedom in the recipient nation. Differently from the other cases, where the donor attempts to influence freedom indirectly through aid, in Case D, aid is explicitly tied to freedom. In other words, the donor recognizes the potential for Kerr’s (1975) trap if it rewards economic reform with aid and hopes that freedom will be bolstered as well. Instead, the donor targets freedom directly.

The utility functions of the recipient and donor are, respectively:

$$V(y,F,H)=v(y,F)+\delta \widehat{v}(y+hF);$$

(23)

$$U\left(Y,H,y,F\right)=u(Y-hF)+\alpha V(y,F,H).$$

(24)

The first order conditions for a Nash equilibrium are

$$v_y(y,F)+\delta {\widehat{v}}_1(y+hF)=0;$$

(25)

$$-h{u}^{\prime }(Y-hF)+\alpha \delta h{\widehat{v}}_1(y+hF)=0,$$

(26)

where in (25) the recipient maximizes its payoff with respect to its income, y, and in (26) the donor maximizes its payoff with respect to freedom, F.

For Case D, Equations (25) and (26) jointly determine the optimal levels of freedom, $F_D^{*}$, and income, $y_D^{*}$. With $F_D^{*}$ one can calculate optimal aid, through Equation (22), to obtain $H_D^{*}$. In this case, the donor designs and enforces an aid policy which increases aid to the recipient only when freedom in the recipient increases. By definition, then, aid is an increasing function of freedom. It is clear that committing to the hF policy obtains the ultimate goal of the donor’s aid policy. By targeting F instead of H the donor reduces the recipient’s incentive to underperform economically via restrictions on freedom.

Interestingly, this creates a potential dilemma for a recipient dictatorship. As a dictatorship, the recipient may likely reject the freedom targets set by the donor. Absent any viable alternative donor, a rejecting recipient faces two alternatives. First, it could allow for growth-enhancing freedoms in order to reform itself out of the parasitic/clientele existence it has been sustaining via the Samaritan’s Dilemma. But, this is tantamount to acquiescing to what the donor wanted in the first place. Second, the recipient could test the donor’s resolve. For example, citing a need for U.S.-Cuban relations to be more closely tied with economic freedoms for the Cuban people, the Trump administration decided to rescind several Obama administration foreign-aid initiatives. Consequently, Cuba’s government “has stopped allowing self-employed entrepreneurs to form company-like cooperatives” (Economist 2017). Again, like freedom scores, it is possible for donors to observe the evolution of such policies.

Recipient efforts at testing a freedom-targeting donor’s resolve are captured by our model. Specifically, in the previous cases, altruism, α, is positively correlated with aid, H, and freedom, F (not shown). By contrast, under the hF policy this need not be the case:

$$\frac{d{F}_D^{*}}{d\alpha }=\frac{h\delta {\widehat{v}}_{11}[v_{yy}+\delta {\widehat{v}}_{11}]}{\Delta }<0\iff \Delta <0\iff \alpha \delta {\widehat{v}}_{11}{v}_{yF}<h\{[u^{″}+\alpha \delta {\widehat{v}}_{11}]v_{yy}+u^{″}\delta \}$$

(27)

$$\frac{d{H}_D^{*}}{d\alpha }=\frac{h^2\delta {\widehat{v}}_{11}[v_{yy}+\delta {\widehat{v}}_{11}]}{\Delta }<0\iff \Delta <0$$

(28)

One of Buchanan’s (1975) primary points about the relationship between incentives and aid is that a donor may have to restrict the extent of their altruism to temper a recipient’s incentive to underperform in order to receive more aid. This is captured by the two equations above. If the donor can reduce the way in which altruism enters into the aid decision, thereby lowering $\alpha ,$ then both aid and freedom increase and the Kerr’s (1975) trap is averted. Hence, the donor must be prepared to demonstrate resolve.

An even more convincing example of the need to reduce altruism in the aid decision is given by a fully cooperative model in which both donor and recipient are coordinated by an agreement in which they aim at maximizing the sum of their payoffs:

$$\begin{gathered} \underset{y,F}{Max}V(y,F,H)+U(Y,H,y,F)=u(Y-hF)+(1+\alpha )V(y,F,H);\mathrm{i}.\mathrm{e}. \\ \underset{y,F}{Max}u(Y-hF)+(1+\alpha )[v(y,F)+\delta \widehat{v}(y+hF)] \end{gathered}$$

(29)

The impact of altruism in this fully cooperative case is negative for reasonable conditions [less restrictive than the one underlying (27) and (28)] (see calculations in the Appendix A):

$$\begin{array}{c}\frac{d{F}_{coop}}{d\alpha }={\Delta }^{-1}\left\{v_{yy}(v_F+h\delta {\widehat{v}}_1)-v_y(v_{Fy}+h\delta {\widehat{v}}_{11})\right\}{(1+\alpha )}^{-1}<0\\ \iff \Delta >0\mathrm{and}{v}_{yy}(v_F+h\delta {\widehat{v}}_1)<v_y(v_{Fy}+h\delta {\widehat{v}}_{11})\end{array}$$

(30)

In Equation (30), note that, in contrast with (27) and (28), the denominator Δ, must be positive, $\Delta >0$, because it corresponds to the optimal second order condition of the maximization in Equation (29). According to (30), the marginal impact of altruism is negative on the optimal choice of freedom of the cooperative solution. This is because, in the cooperative solution, the joint externality between donor and recipient is internalized; namely, the penchant for the recipient to reduce income owing to the presence of the Samaritan’s Dilemma. The effects of this externality are further decreased via a reduction in the donor’s altruism.

Surprisingly, neither the cooperative solution, nor its comparative statics relative to the donor’s level of altruism, have been characterized in prior treatments of the Samaritan’s Dilemma. By doing so, we verify Buchanan’s (1975) intuition that the donor needs to temper its altruism if it is to fully resolve the Samaritan’s Dilemma.

6. Concluding Remarks

This paper presents a two-period game based on the Samaritan’s dilemma to analyze the relationship between a foreign aid donor nation and a dictatorial recipient. Our model extends past analyses in that the donor nation is interested in fostering both economic growth and freedom within the recipient nation. This is consistent with many nations’ underlying objectives for foreign aid. It is also consistent with the existing empirical literature, in which the observed relationship between aid and freedom is equivocal. This indeterminacy is often attributed to the existence of a Samaritan’s Dilemma between donor and recipient. We show that it is further exacerbated by the donor’s concern for freedom. Specifically, resolving the Samaritan’s Dilemma can come at the cost of economic freedoms in the recipient nation.

In particular, prescriptions for resolving the Samaritan’s Dilemma typically involve donor commitment to aid policies that force the recipient into a relationship where aid and economic performance are co-determined (in the Nash sense). Yet, we show that a focus on resolving the Samaritan’s Dilemma represents a potential trap for the donor in that it need not ultimately foster recipient nation freedoms. An example of such a trap is an aid-freedom coupling policy. Within a Nash framework, the coupling policy resolves the Samaritan’s Dilemma but recipient freedoms do not commensurately increase.

Finally, we examine an alternative policy that avoids this trap because the donor provides aid in direct proportion to increases in freedom. Given that the donor pre-commits, the Samaritan’s Dilemma does not arise, and because aid increases with freedom, the donor achieves its dual goals of increasing economic performance and freedom in the recipient nation. Yet, the policy is not as simple as it may seem because the optimal commitment requires the donor to reduce its altruistic motivations for helping the recipient and replace them with a commitment to freedom targets. This may be difficult for altruistic policymakers, especially if the recipient is willing to test the donor’s resolve. In the absence of such a policy, what this paper has identified is a fundamental tradeoff for a donor nation in terms of resolving the Samaritan’s Dilemma versus promoting freedom. As such, this tradeoff should be recognized and accounted for in empirical analyses of the performance of foreign aid.