Leaning against the Wind Policies on Vietnam’s Economy with DSGE Model
Abstract
:1. Introduction
2. Literature Overview
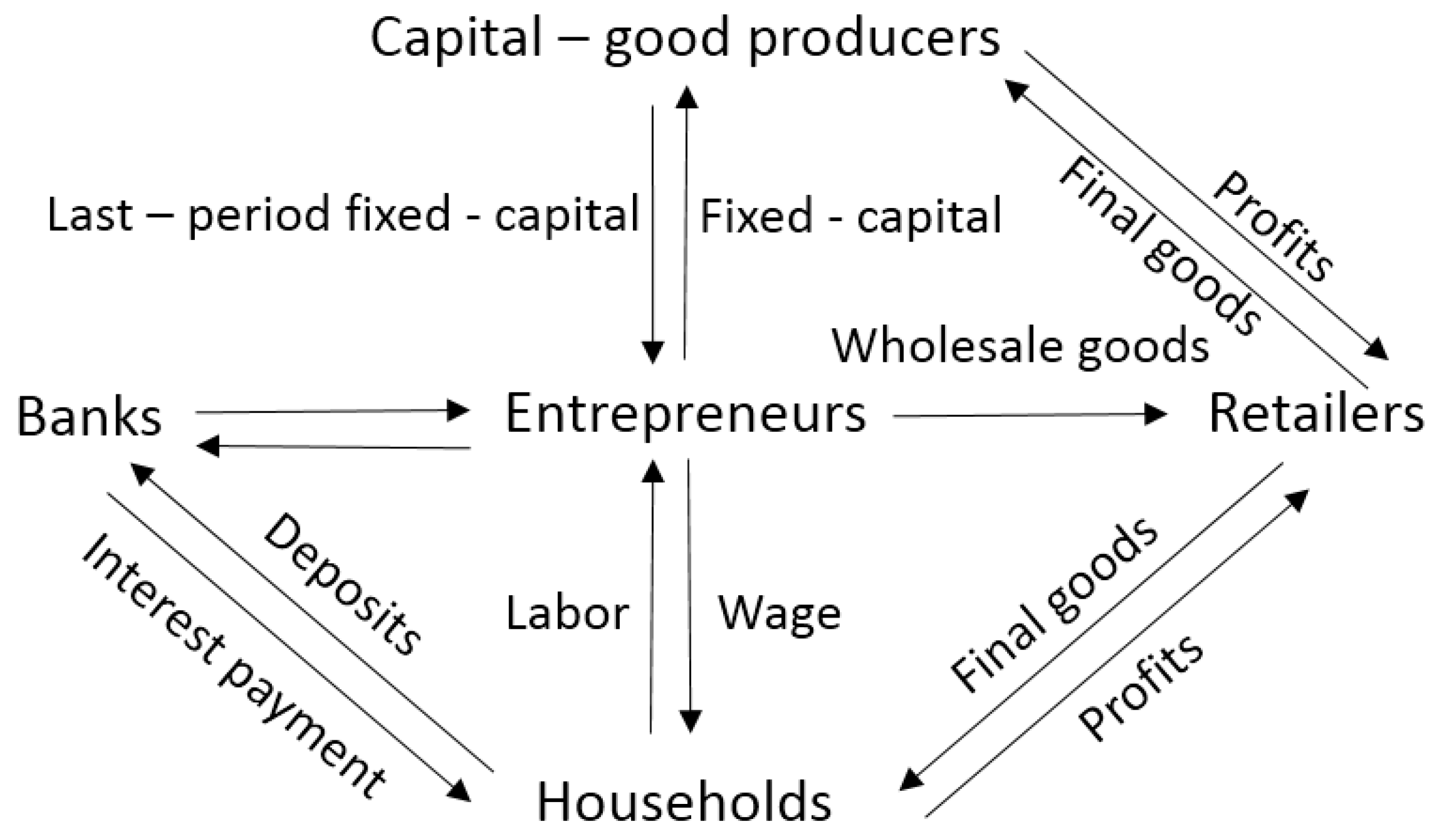
3. DSGE Model
3.1. Households
3.2. Entrepreneurs
3.3. Capital Good Producers
3.4. Retailers
3.5. Banks
4. The Transmission Channels
- (i)
- Equation (25) shows that the leverage ratio depends positively on the parameter and future asset prices and negatively on the loan interest rate.
- (ii)
- The asset prices and the lending rates from (25) have a crucial impact on the entrepreneurs’ net worth, which influences simultaneously both consumption and investment decisions described through Equations (22) and (23).
- (iii)
- Equations (23)–(25) can be interpreted as using past net worth, which is the basis to borrow money from intermediates with a given fraction in order to buy future capital.
- (iv)
- In detail, from Equations (22) and (24), we see that the current level of asset prices () has a positive relation with net worth; it has a positive impact on consumption, as well. Hence, the increase of the current level of asset prices will induce the increase of consumption. Conversely, the impact of the current level of asset prices on investment (Equations (23)–(25)) is ambiguous, because the positive effect of the current level of asset prices will be counteracted by the negative effect of leverage, which is considered as the cost of purchasing new capital. Expectations on future asset prices () positively impact investment (easy to see from Equations (23) and (25)), whereas the loan interest rate () negatively impacts both consumption and investment. Therefore, the increase of the loan rate will decrease net worth due to the increase of interest payments and the decrease of capital accumulation.
- (i)
- The loan supply schedule has a positive effect on the loan rate. The implication is that the increase of the lending amount will lead to a higher loan rate due to higher default risk.
- (ii)
- The multiplier of loan supply has a positive correlation for both the level of the bank’s target capital-to-asset ration (ν) and the cost for deviating from that target θ.
- (iii)
- From Equation (19), the level of bank capital has a positive effect on the loan supply, which depends positively on the bank’s profits. The capital will be accumulated through an increase in the bank’s profit; banks have numerous capital to lend, and this leads to the shift in the loan supply in the subsequent period. Moreover, the increase of bank profits will reduce the loan rate (in the subsequent period) for any given level of loans to the economy.
- (iv)
- In particular, the loan supply is inversely proportional to the level of the policy rate. Hence, whenever the central bank implements an easy policy, this will lead to the increase of loan supply. This feature is consistent with the existence of a bank-lending channel in the model.
5. Simulations
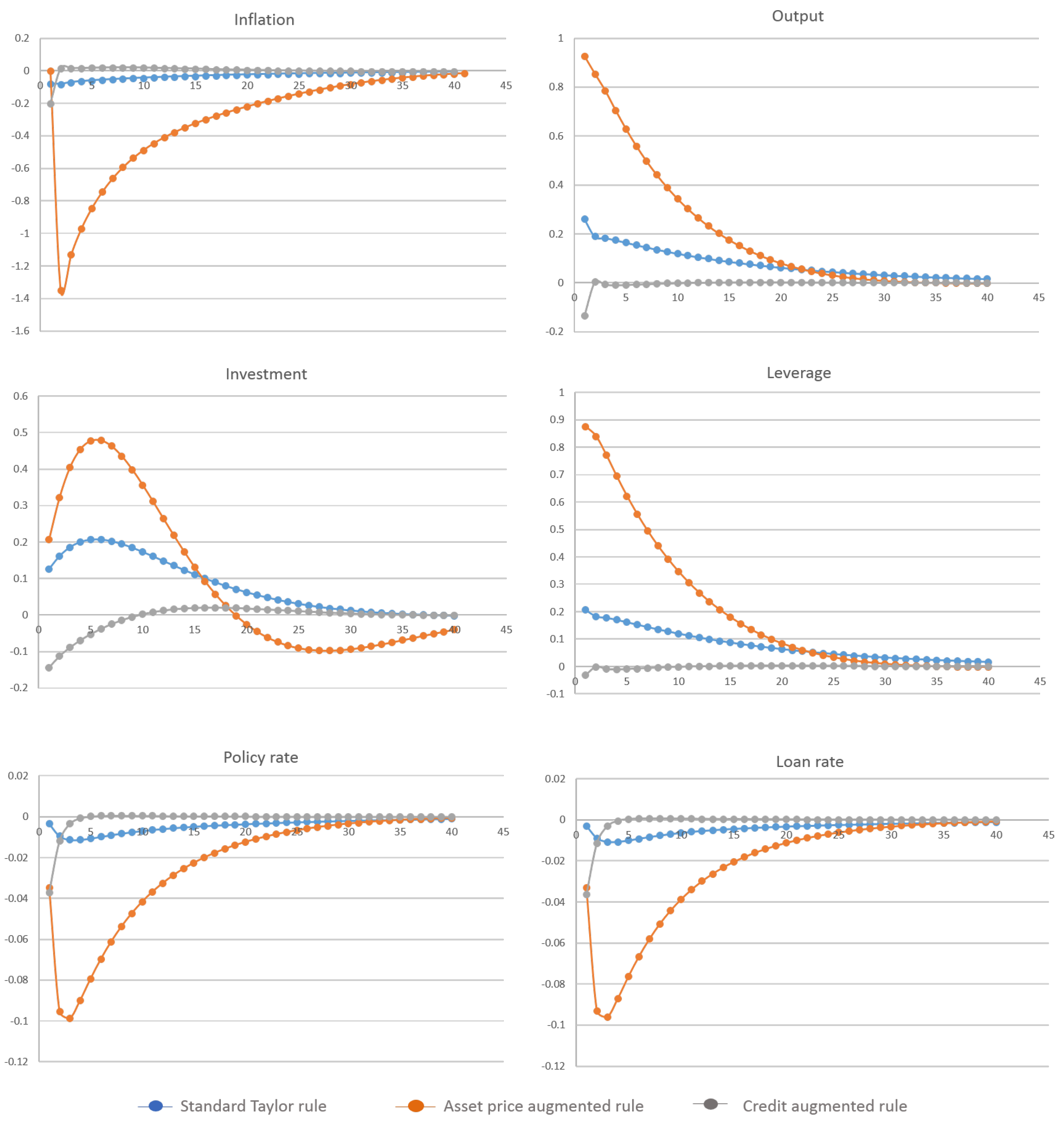
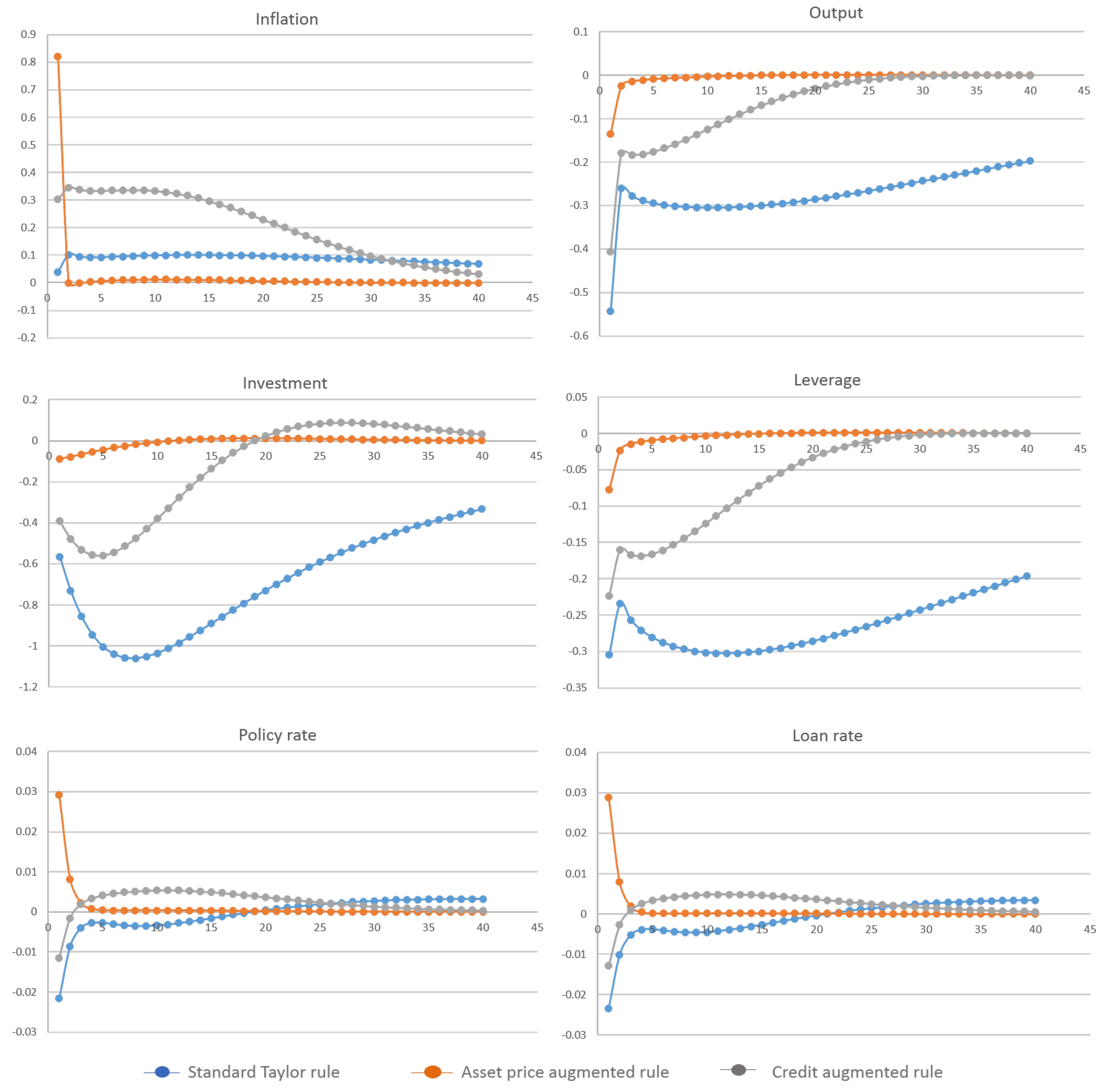
5.1. Monetary Policies
- (i)
- The standard Taylor rule:
- (ii)
- The Taylor rule augmented with asset prices:
- (iii)
- The Taylor rule augmented with credit:
5.2. Shocks
5.2.1. Technology Shock
5.2.2. Cost-Push Shock
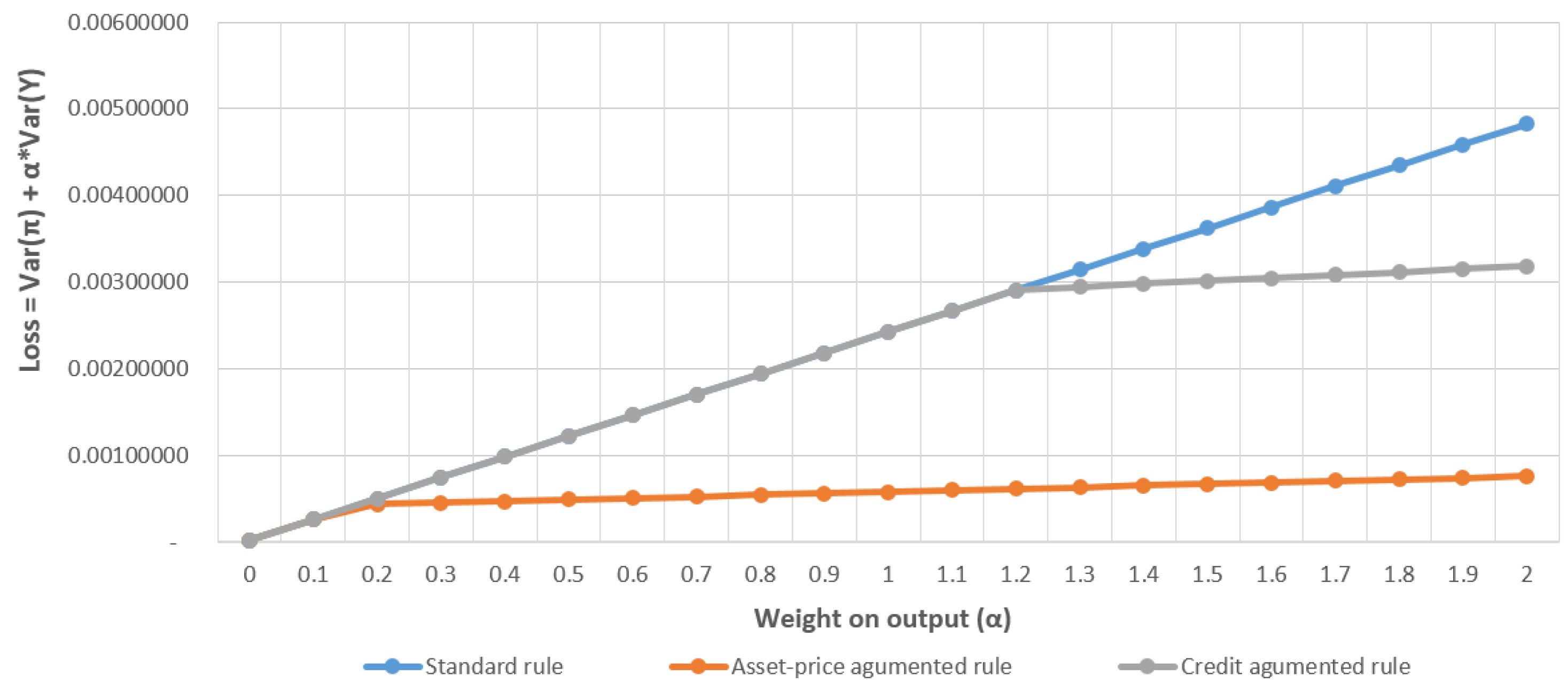
5.3. Loss Function
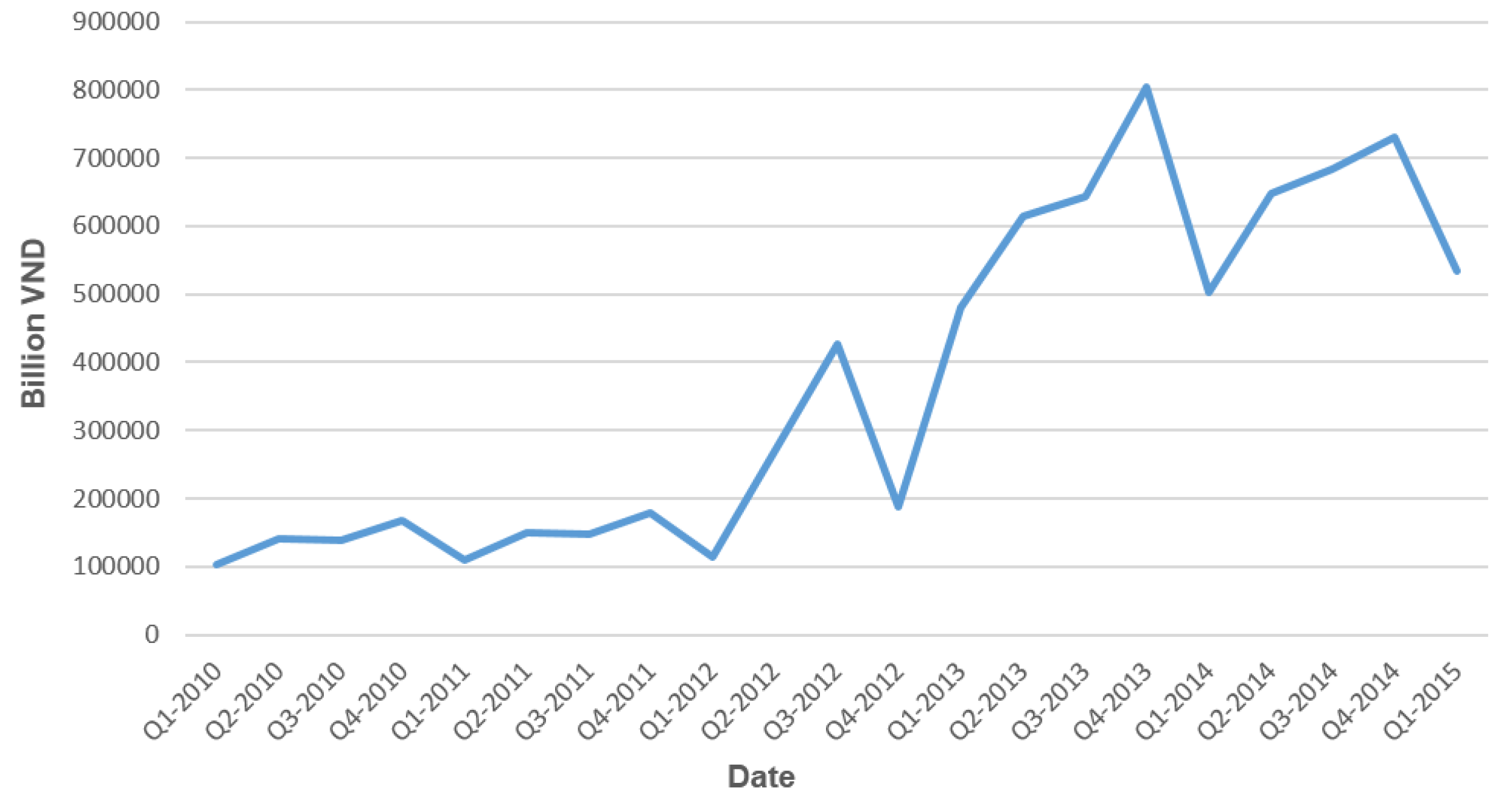
6. Calibration
7. Empirical Results
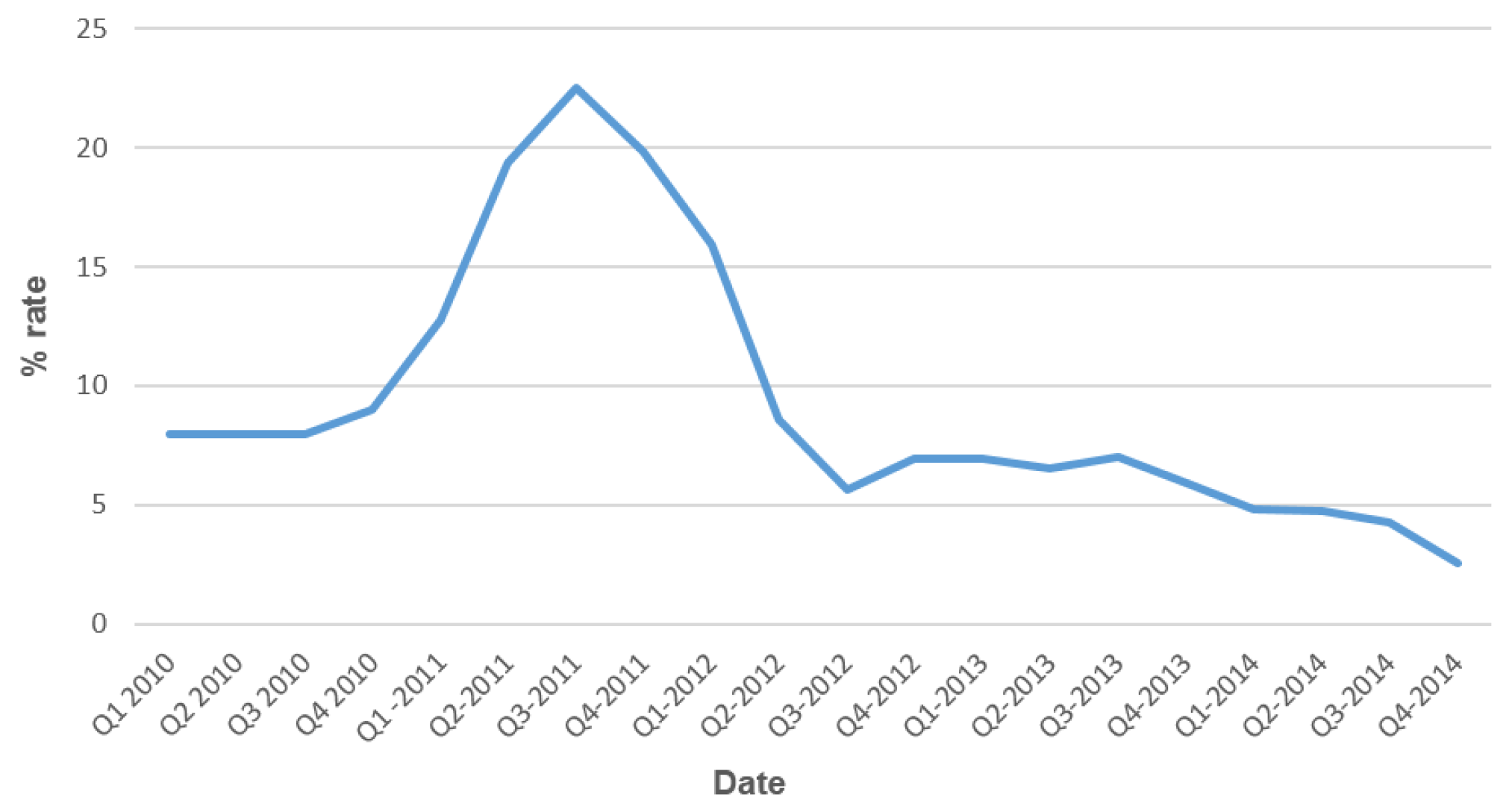
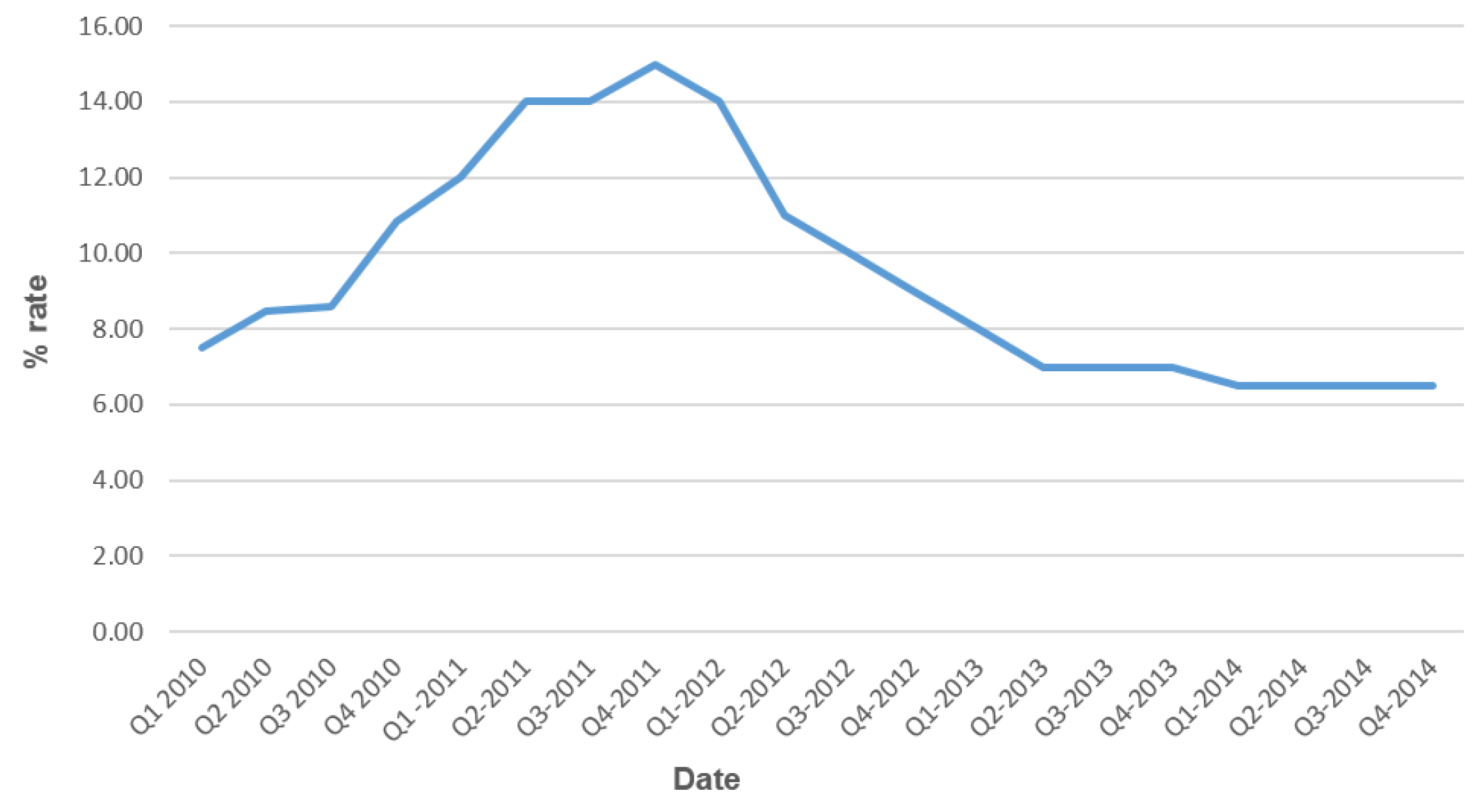
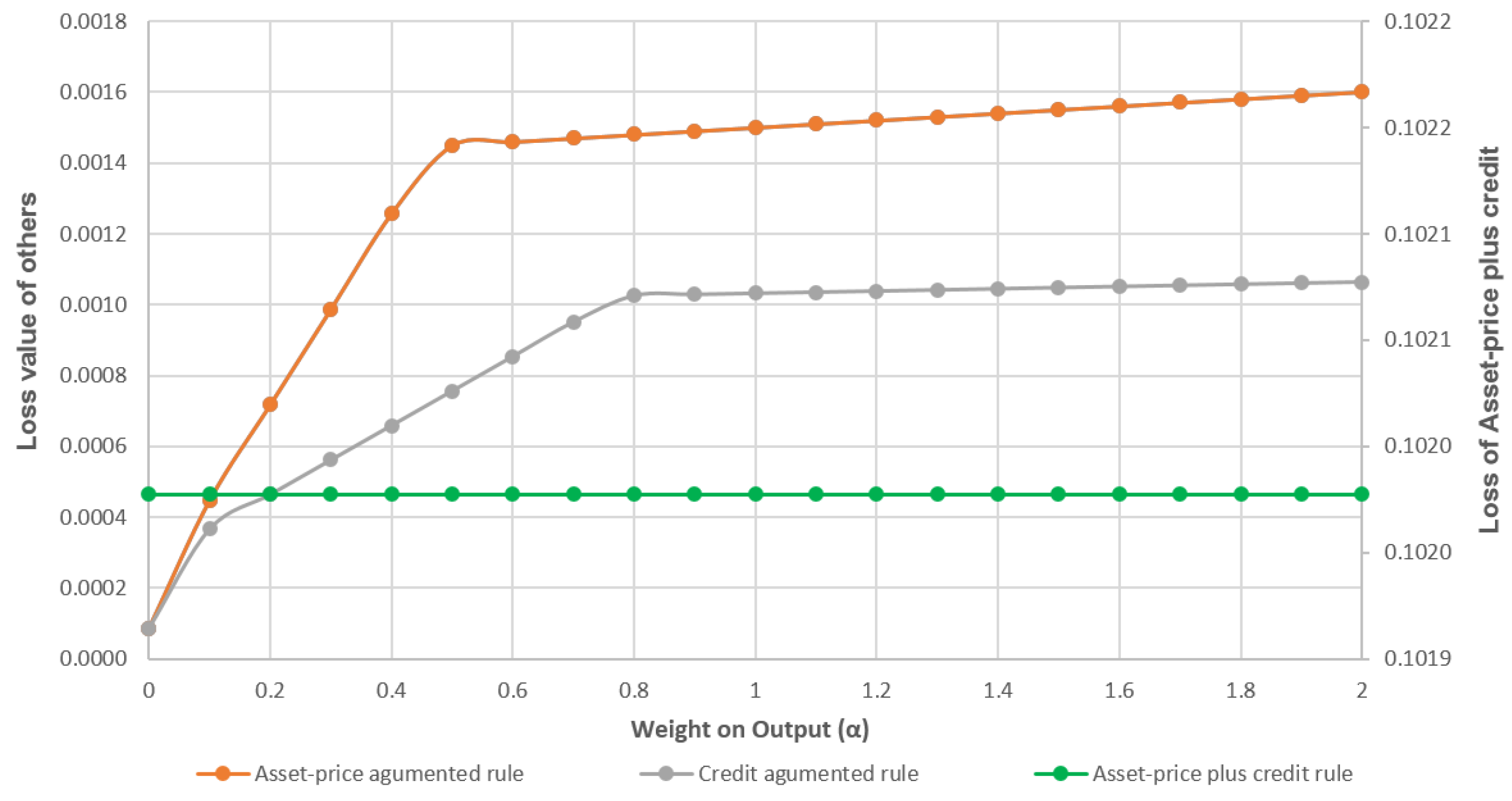
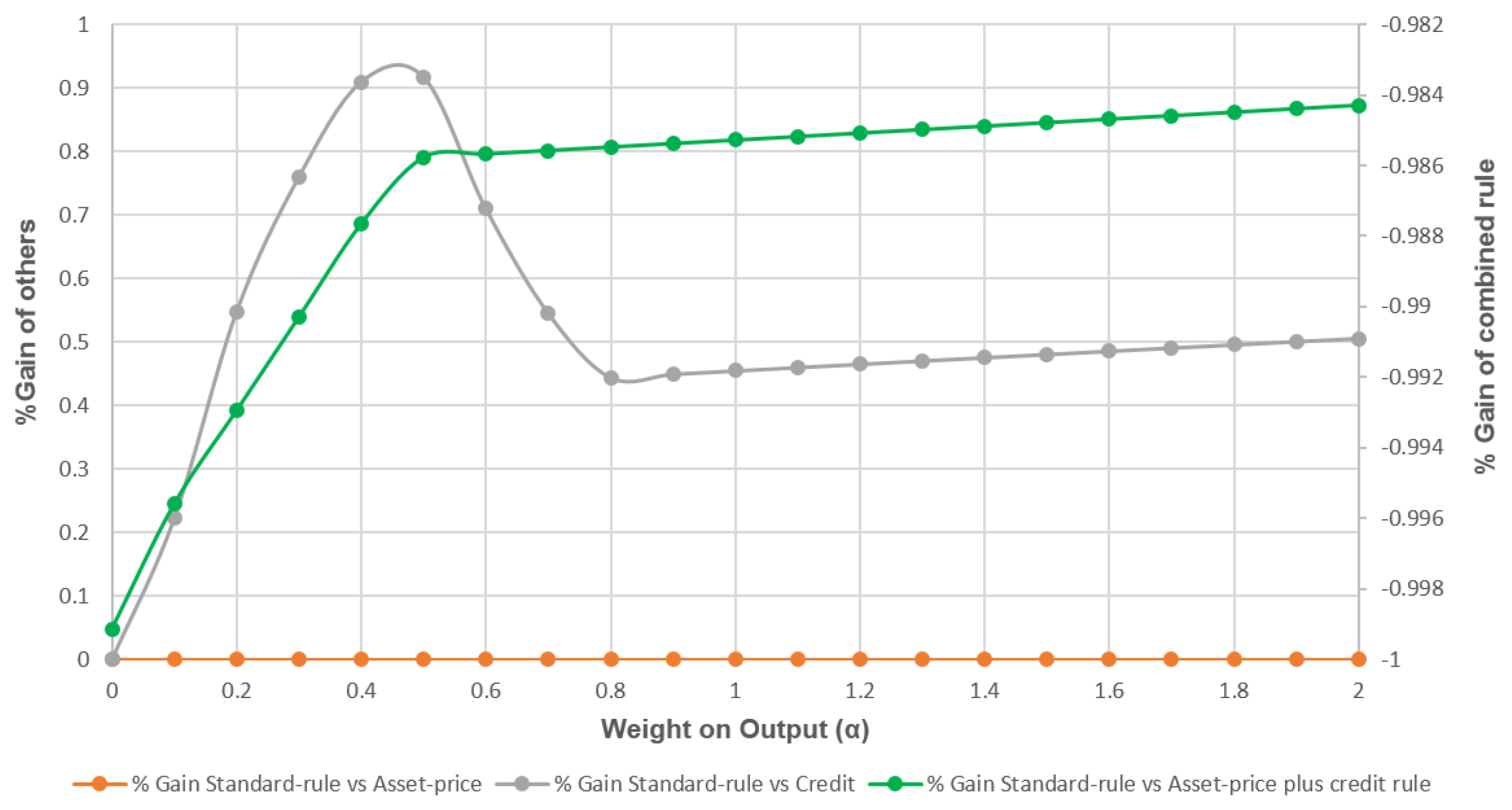
7.1. Scenario 1: Technology Shock
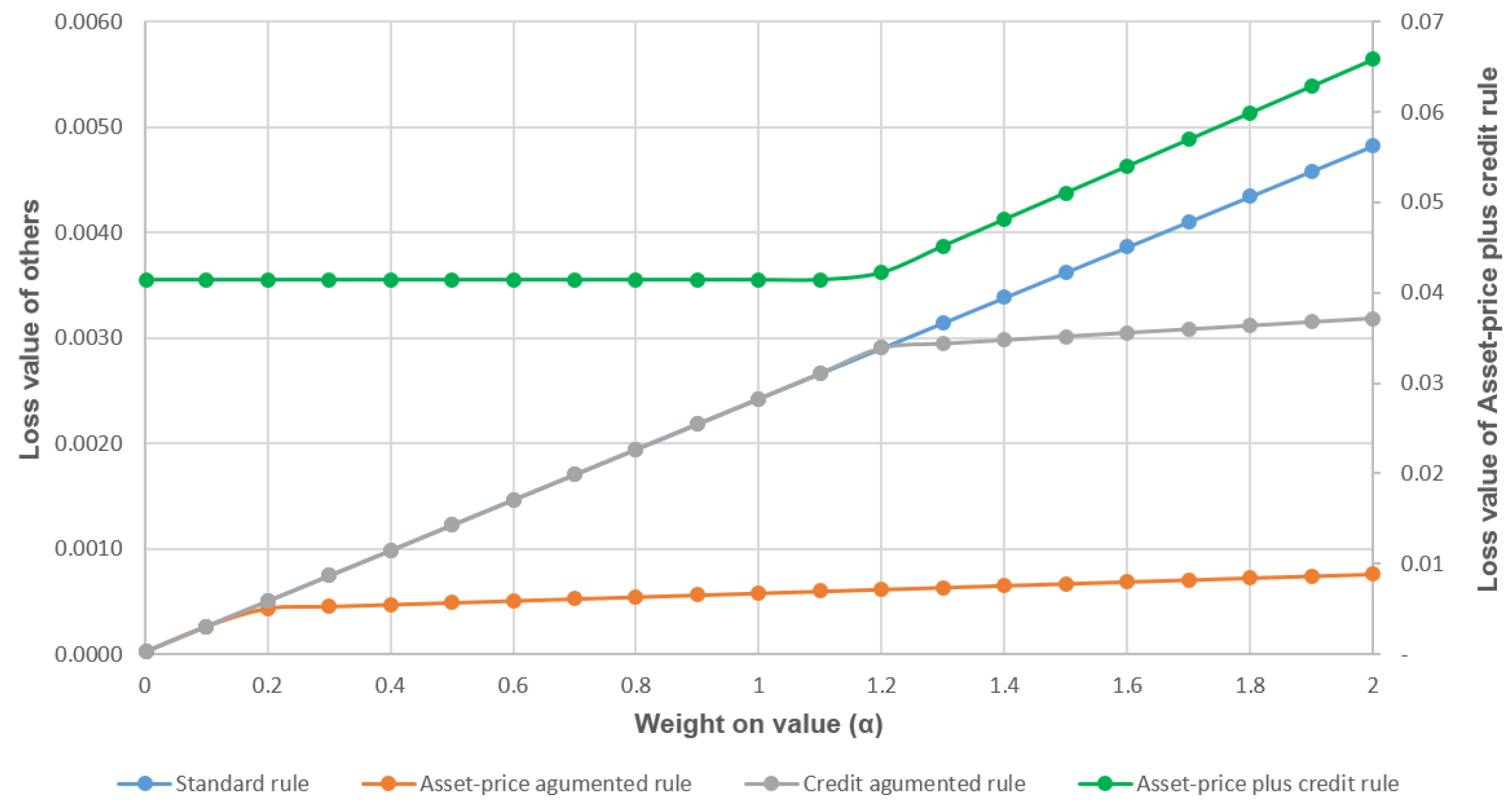
7.2. Scenario 2: Cost-Push Shock
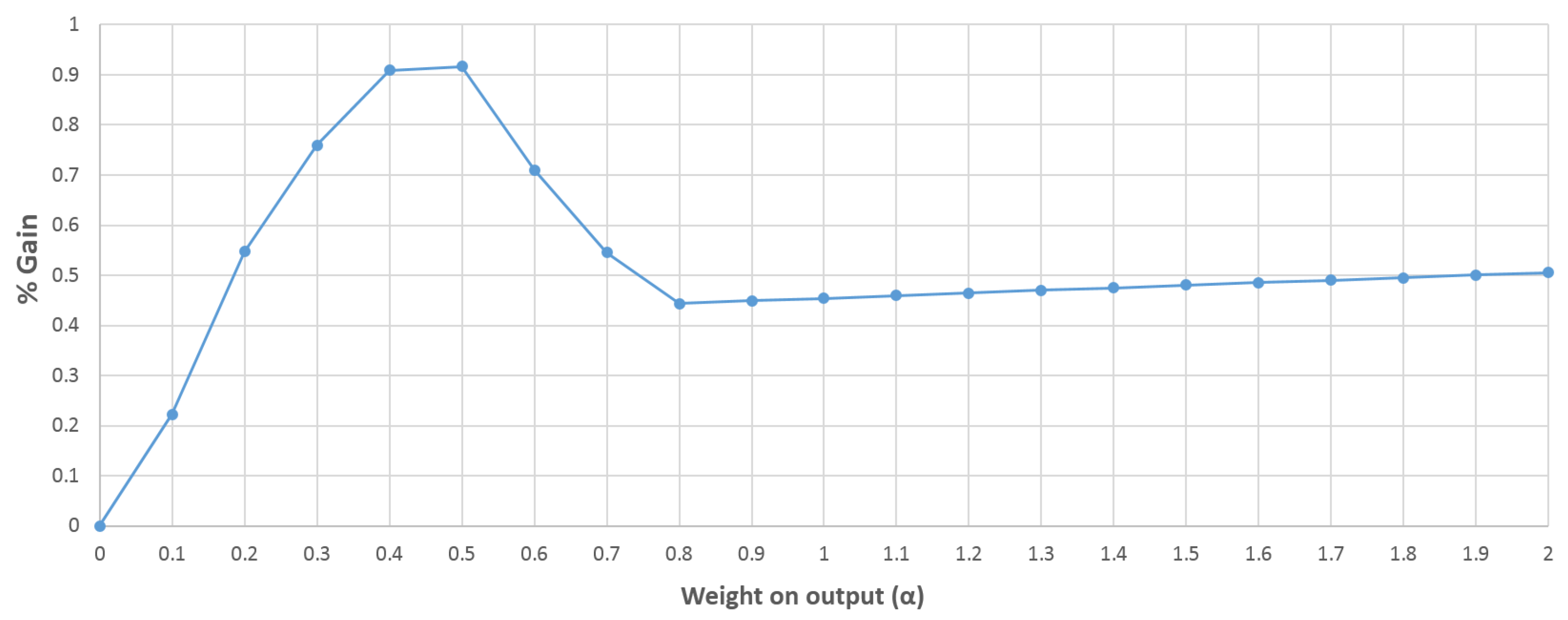
7.3. Combining Asset Price and Credit
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- D.N. Anh. “Non-Performing Loans—Case Study in Vietnam: Causes, Consequences, and Effects.” Bachelor’s Thesis, Uppsala University, Uppsala, Sweden, 2014. [Google Scholar]
- L. Gambbarcorta, and F.M. Signoretti. Should Monetary Policy Lean against the Wind? An Analysis Based on a DSGE Model with Banking. Economic Working Papers, Bank for International Settlements; Oslo, Norway: Norges Bank, 2013, Volume 418. [Google Scholar]
- L.E.O. Svensson. Why Leaning against the Wind Is the Wrong Monetary Policy for Sweden. Stockholm, Sweden: Stockholm School of Economics, Stockholm University, 2014. [Google Scholar]
- V. Fabio, and M.F. Manuel. “Martins and Ines Drumond.” In Financial Shocks and Optimal Monetary Policy Rules. Helsinki, Finland: Bank of Finland, 2014, Volume 418. [Google Scholar]
- L. Lambertini, C. Mendicino, and M.T. Punzi. “Leaning against boom–bust cycles in credit and housing prices.” J. Econ. Dyn. Control 37 (2013): 1500–1522. [Google Scholar] [CrossRef]
- L. Christiano, C. Ilut, R. Motto, and M. Rostagno. Monetary Policy and Stock Market Booms. Cambridge, MA, USA: National Bureau of Economic Research, 2010. [Google Scholar]
- A. Gerali, S. Neri, L. Sessa, and F.M. Signoretti. “Credit and Baking in a DSGE model of the Euro Area.” J. Money Credit Bank. 42 (2010): 44–70. [Google Scholar] [CrossRef]
- B.S. Bernanke, M. Gertler, and S. Gilchrist. “The Financial Accelerator in a Quantitative Business Cycle Framework.” In Handbook of Macroeconomics. Edited by J.B. Taylor and M. Woodford. Amsterdam, The Netherland: North-Holland, 1999, pp. 1341–1393. [Google Scholar]
- M. Iacoviello. “House Prices, Borrowing Constraints and Monetary Policy in the Business Cycle.” Am. Econ. Rev. 95 (2005): 739–764. [Google Scholar] [CrossRef]
- L. Christiano, M. Eichenbaum, and C. Evans. “Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy.” J. Political Econ. 113 (2005): 1–46. [Google Scholar] [CrossRef]
- F. Smets, and R. Wouters. “An Estimated Dynamic Stochastic General Equilibrium Model of the Euro Area.” J. Eur. Econ. Assoc. 1 (2013): 1123–1175. [Google Scholar] [CrossRef]
- V. Curdia, and M. Woodford. “Credit Spreads and Monetary Policy.” J. Money Credit Bank. 42 (2010): 3–35. [Google Scholar] [CrossRef]
- B. Bernanke, and M. Gertler. Monetary Policy and Asset Price Volatility. Cambridge, MA, USA: National Bureau of Economic Research, 2000. [Google Scholar]
- B.S. Bernanke, and M. Gertler. “Should Central Banks Respond to Movements in Asset Prices? ” Am. Econ. Rev. 91 (2001): 253–257. [Google Scholar] [CrossRef]
- S. Gilchrist, and J.V. Leahy. “Monetary Policy and Asset Prices.” J. Monet. Econ. 49 (2002): 75–97. [Google Scholar] [CrossRef]
- V. Cúrdia, and M. Woodford. Credit Frictions and Optimal Monetary Policy. Cambridge, MA, USA: National Bureau of Economic Research, 2015. [Google Scholar]
- J. Andrés, O. Arce, and C. Thomas. “Banking competition, collateral constraints, and optimal monetary policy.” J. Money Credit Bank. 45 (2013): 87–125. [Google Scholar] [CrossRef]
- J. Gali. Monetary Policy, Inflation, and the Business Cycle: An Introduction to the New Keynesian Framework. Princeton, NJ, USA: Princeton University Press, 2008. [Google Scholar]
- I. Christensen, P. Corrigan, C. Mendicino, and S. Nishiyama. An Estimated Open-Economy General Equilibrium Model with Housing Investment and Financial Frictions. Mimeo, Norway: Bank of Norway, 2007. [Google Scholar]
- 1.According to Basel 2regulations, referred to as the Capital Adequacy Ratio (CAR).
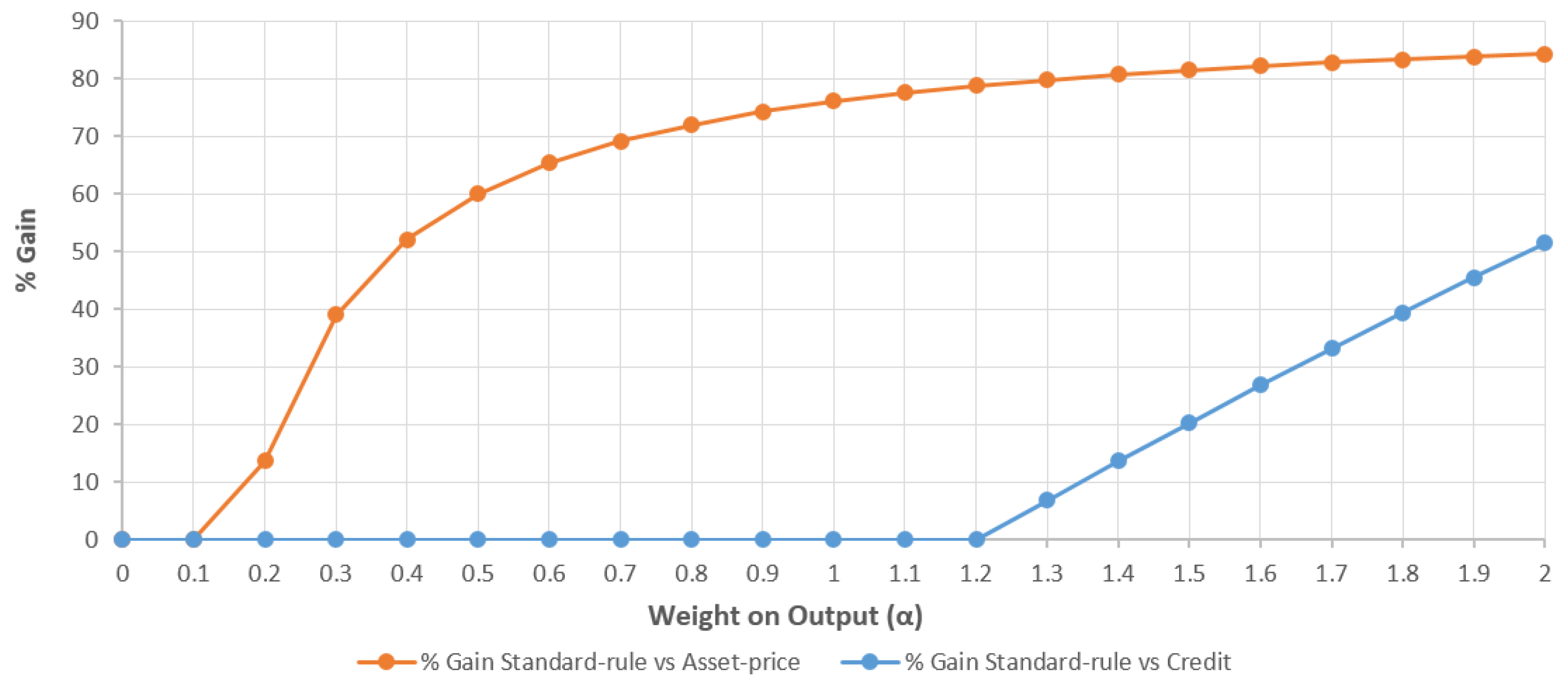
- 2.Gain is the percentage difference between the minimum loss under the standard Taylor rule and the augmented Taylor rule (100 × (Loss|STR − Loss|ATR) /Loss|STR). A positive number means that the augmented rule performs better than the standard one.
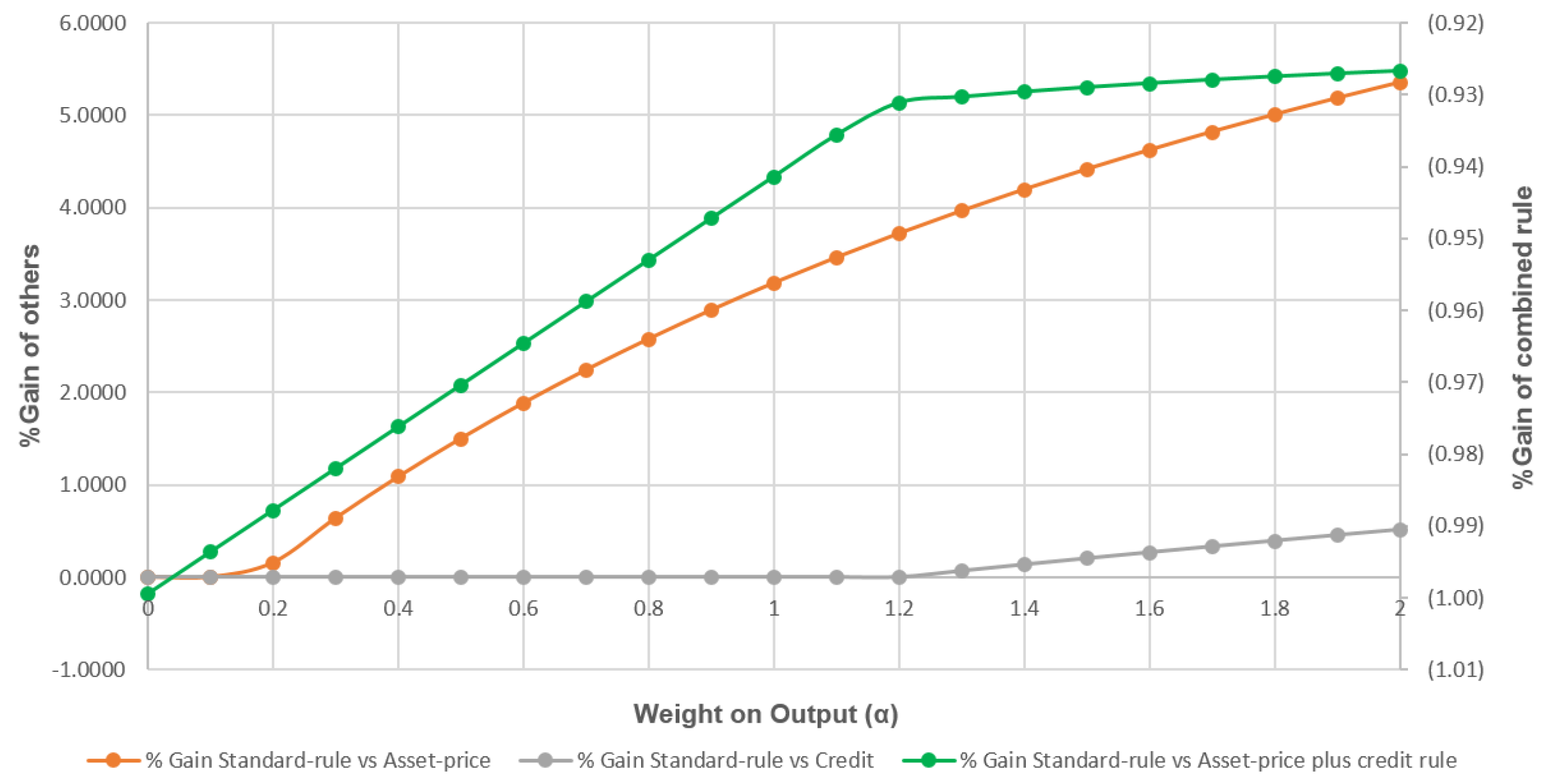
| Output Weight | Standard Taylor Rule | Asset-Price-Augmented Rule | ||||||||
| Loss | Loss | Gain | ||||||||
| 0 | 3 | 0 | 0.0008743 | 3 | 0 | 0 | 0.00008743 | 0 | ||
| 0.1 | 0.5 | 0 | 0.00044837 | 0.5 | 0 | 0 | 0.00044837 | 0 | ||
| 0.2 | 0.5 | 0 | 0.00071837 | 0.5 | 0 | 0 | 0.00071837 | 0 | ||
| 0.3 | 0.5 | 0 | 0.00098837 | 0.5 | 0 | 0 | 0.00098837 | 0 | ||
| 0.4 | 0.5 | 0 | 0.00125837 | 0.5 | 0 | 0 | 0.00125837 | 0 | ||
| 0.5 | 1.5 | 2 | 0.00145042 | 1.5 | 2 | 0 | 0.00145042 | 0 | ||
| 0.6 | 1.5 | 2 | 0.001460504 | 1.5 | 2 | 0 | 0.001460504 | 0 | ||
| 0.7 | 1.5 | 2 | 0.001470588 | 1.5 | 2 | 0 | 0.001470588 | 0 | ||
| 0.8 | 1.5 | 2 | 0.001480672 | 1.5 | 2 | 0 | 0.001480672 | 0 | ||
| 0.9 | 1.5 | 2 | 0.001490756 | 1.5 | 2 | 0 | 0.001490756 | 0 | ||
| 1.0 | 1.5 | 2 | 0.00150084 | 1.5 | 2 | 0 | 0.00150084 | 0 | ||
| 1.1 | 1.5 | 2 | 0.001510924 | 1.5 | 2 | 0 | 0.001510924 | 0 | ||
| 1.2 | 1.5 | 2 | 0.001521008 | 1.5 | 2 | 0 | 0.001521008 | 0 | ||
| 1.3 | 1.5 | 2 | 0.001531092 | 1.5 | 2 | 0 | 0.001531092 | 0 | ||
| 1.4 | 1.5 | 2 | 0.001541176 | 1.5 | 2 | 0 | 0.001541176 | 0 | ||
| 1.5 | 1.5 | 2 | 0.00155126 | 1.5 | 2 | 0 | 0.00155126 | 0 | ||
| 1.6 | 1.5 | 2 | 0.001561344 | 1.5 | 2 | 0 | 0.001561344 | 0 | ||
| 1.7 | 1.5 | 2 | 0.001571428 | 1.5 | 2 | 0 | 0.001571428 | 0 | ||
| 1.8 | 1.5 | 2 | 0.001581512 | 1.5 | 2 | 0 | 0.001581512 | 0 | ||
| 1.9 | 1.5 | 2 | 0.001591596 | 1.5 | 2 | 0 | 0.001591596 | 0 | ||
| 2.0 | 1.5 | 2 | 0.00160168 | 1.5 | 2 | 0 | 0.001591596 | 0 | ||
| Output Weight | Standard Taylor Rule | Credit-Augmented Rule | ||||||||
| Loss | Loss | Gain | ||||||||
| 0 | 3 | 0 | 0.0008743 | 3 | 0 | 0 | 0.00008743 | 0 | ||
| 0.1 | 0.5 | 0 | 0.00044837 | 3 | 0 | 2 | 0.000366897 | 18.17093026 | ||
| 0.2 | 0.5 | 0 | 0.00071837 | 3 | 0 | 2 | 0.000464364 | 35.35865919 | ||
| 0.3 | 0.5 | 0 | 0.00098837 | 3 | 0 | 2 | 0.000561831 | 43.15580198 | ||
| 0.4 | 0.5 | 0 | 0.00125837 | 3 | 0 | 2 | 0.000659298 | 47.60698364 | ||
| 0.5 | 1.5 | 2 | 0.00145042 | 3 | 0 | 2 | 0.000756765 | 47.82442327 | ||
| 0.6 | 1.5 | 2 | 0.001460504 | 3 | 0 | 2 | 0.000854232 | 41.51114958 | ||
| 0.7 | 1.5 | 2 | 0.001470588 | 3 | 0 | 2 | 0.000951699 | 35.28445765 | ||
| 0.8 | 1.5 | 2 | 0.001480672 | 3 | 2 | 1 | 0.001025644 | 30.73118152 | ||
| 0.9 | 1.5 | 2 | 0.001490756 | 3 | 2 | 1 | 0.00102885 | 30.98471514 | ||
| 1.0 | 1.5 | 2 | 0.00150084 | 3 | 2 | 1 | 0.001032055 | 31.23484182 | ||
| 1.1 | 1.5 | 2 | 0.001510924 | 3 | 2 | 1 | 0.001035261 | 31.48162978 | ||
| 1.2 | 1.5 | 2 | 0.001521008 | 3 | 2 | 1 | 0.001038466 | 31.72514543 | ||
| 1.3 | 1.5 | 2 | 0.001531092 | 3 | 2 | 1 | 0.001041672 | 31.96545341 | ||
| 1.4 | 1.5 | 2 | 0.001541176 | 3 | 2 | 1 | 0.001044877 | 32.2026167 | ||
| 1.5 | 1.5 | 2 | 0.00155126 | 1.5 | 2 | 0 | 0.001048083 | 32.43669662 | ||
| 1.6 | 1.5 | 2 | 0.001561344 | 3 | 2 | 1 | 0.001051288 | 32.66775291 | ||
| 1.7 | 1.5 | 2 | 0.001571428 | 3 | 2 | 1 | 0.001054494 | 32.89584378 | ||
| 1.8 | 1.5 | 2 | 0.001581512 | 3 | 2 | 1 | 0.001057699 | 33.12102595 | ||
| 1.9 | 1.5 | 2 | 0.001591596 | 3 | 2 | 1 | 0.001060905 | 33.34335472 | ||
| 2.0 | 1.5 | 2 | 0.00160168 | 3 | 2 | 1 | 0.00106411 | 33.56288397 | ||
| Output Weight | Standard Taylor Rule | Asset-Price-Augmented Rule | ||||||||
| Loss | Loss | Gain | ||||||||
| 0 | 1.5 | 0 | 0.00002388 | 1.5 | 0 | 0 | 0.00002388 | 0 | ||
| 0.1 | 3 | 0 | 0.000264782 | 3 | 0 | 0 | 0.000264782 | 0 | ||
| 0.2 | 3 | 0 | 0.000504782 | 3 | 0 | 1 | 0.000435828 | 13.66015428 | ||
| 0.3 | 3 | 0 | 0.000744782 | 3 | 0 | 1 | 0.000453812 | 39.06780776 | ||
| 0.4 | 3 | 0 | 0.000984782 | 3 | 0 | 1 | 0.000471796 | 52.0913258 | ||
| 0.5 | 3 | 0 | 0.001224782 | 3 | 0 | 1 | 0.00048978 | 60.01084275 | ||
| 0.6 | 3 | 0 | 0.001464782 | 3 | 0 | 1 | 0.000507764 | 65.33518298 | ||
| 0.7 | 3 | 0 | 0.001704782 | 3 | 0 | 1 | 0.000525748 | 69.16039705 | ||
| 0.8 | 3 | 0 | 0.001944782 | 3 | 0 | 1 | 0.000561716 | 72.0414936 | ||
| 0.9 | 3 | 0 | 0.002184782 | 3 | 0 | 1 | 0.00102885 | 74.28960876 | ||
| 1.0 | 3 | 0 | 0.002424782 | 3 | 0 | 1 | 0.0005797 | 76.09269617 | ||
| 1.1 | 3 | 0 | 0.002664782 | 3 | 0 | 1 | 0.000597684 | 77.5709983 | ||
| 1.2 | 3 | 0 | 0.002904782 | 3 | 0 | 1 | 0.000615668 | 78.80501876 | ||
| 1.3 | 3 | 0 | 0.003144782 | 3 | 0 | 1 | 0.000633652 | 79.85068599 | ||
| 1.4 | 3 | 0 | 0.003384782 | 3 | 0 | 1 | 0.000651636 | 80.7480659 | ||
| 1.5 | 3 | 0 | 0.003624782 | 1.5 | 2 | 1 | 0.00066962 | 81.52661319 | ||
| 1.6 | 3 | 0 | 0.003864782 | 3 | 0 | 1 | 0.000687604 | 82.20846609 | ||
| 1.7 | 3 | 0 | 0.004104782 | 3 | 0 | 1 | 0.000705588 | 82.81058531 | ||
| 1.8 | 3 | 0 | 0.004344782 | 3 | 0 | 1 | 0.000723572 | 83.346184 | ||
| 1.9 | 3 | 0 | 0.004584782 | 3 | 0 | 1 | 0.000741556 | 83.82570862 | ||
| 2.0 | 3 | 0 | 0.004824782 | 3 | 0 | 1 | 0.00075954 | 84.25752708 | ||
| Output Weight | Standard Taylor Rule | Credit-Augmented Rule | ||||||||
| Loss | Loss | Gain | ||||||||
| 0 | 1.5 | 0 | 0.00002388 | 1.5 | 0 | 0 | 0.00002388 | 0 | ||
| 0.1 | 3 | 0 | 0.000264782 | 3 | 0 | 0 | 0.000264782 | 0 | ||
| 0.2 | 3 | 0 | 0.000504782 | 3 | 0 | 0 | 0.000504782 | 0 | ||
| 0.3 | 3 | 0 | 0.000744782 | 3 | 0 | 0 | 0.000744782 | 0 | ||
| 0.4 | 3 | 0 | 0.000984782 | 3 | 0 | 0 | 0.000984782 | 0 | ||
| 0.5 | 3 | 0 | 0.001224782 | 3 | 0 | 0 | 0.001224782 | 0 | ||
| 0.6 | 3 | 0 | 0.001464782 | 3 | 0 | 0 | 0.001464782 | 0 | ||
| 0.7 | 3 | 0 | 0.001704782 | 3 | 0 | 0 | 0.001704782 | 0 | ||
| 0.8 | 3 | 0 | 0.001944782 | 3 | 0 | 0 | 0.001944782 | 0 | ||
| 0.9 | 3 | 0 | 0.002184782 | 3 | 0 | 0 | 0.002184782 | 0 | ||
| 1.0 | 3 | 0 | 0.002424782 | 3 | 0 | 0 | 0.002424782 | 0 | ||
| 1.1 | 3 | 0 | 0.002664782 | 3 | 0 | 0 | 0.002664782 | 0 | ||
| 1.2 | 3 | 0 | 0.002904782 | 0.5 | 0 | 2 | 0.000615668 | 0 | ||
| 1.3 | 3 | 0 | 0.003144782 | 0.5 | 0 | 2 | 0.002945406 | 6.769049836 | ||
| 1.4 | 3 | 0 | 0.003384782 | 0.5 | 0 | 2 | 0.002979668 | 13.59594425 | ||
| 1.5 | 3 | 0 | 0.003624782 | 0.5 | 0 | 2 | 0.00301393 | 20.267624 | ||
| 1.6 | 3 | 0 | 0.003864782 | 0.5 | 0 | 2 | 0.003082454 | 26.78932298 | ||
| 1.7 | 3 | 0 | 0.004104782 | 0.5 | 0 | 2 | 0.000705588 | 33.16604238 | ||
| 1.8 | 3 | 0 | 0.004344782 | 0.5 | 0 | 2 | 0.000723572 | 39.40256347 | ||
| 1.9 | 3 | 0 | 0.004584782 | 0.5 | 0 | 2 | 0.003150978 | 45.50345956 | ||
| 2.0 | 3 | 0 | 0.004824782 | 0.5 | 0 | 2 | 0.00318524 | 51.47310721 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huynh, P.; Nguyen, T.; Duong, T.; Pham, D. Leaning against the Wind Policies on Vietnam’s Economy with DSGE Model. Economies 2017, 5, 3. https://doi.org/10.3390/economies5010003
Huynh P, Nguyen T, Duong T, Pham D. Leaning against the Wind Policies on Vietnam’s Economy with DSGE Model. Economies. 2017; 5(1):3. https://doi.org/10.3390/economies5010003
Chicago/Turabian StyleHuynh, Phuc, Trang Nguyen, Thanh Duong, and Duc Pham. 2017. "Leaning against the Wind Policies on Vietnam’s Economy with DSGE Model" Economies 5, no. 1: 3. https://doi.org/10.3390/economies5010003
APA StyleHuynh, P., Nguyen, T., Duong, T., & Pham, D. (2017). Leaning against the Wind Policies on Vietnam’s Economy with DSGE Model. Economies, 5(1), 3. https://doi.org/10.3390/economies5010003





