Nonlinear Monetary Policy Rules: An Essay in the Comparative Study on Egyptian and Tunisian Central Banks
Abstract
:1. Introduction
2. Brief History of Monetary Policy
2.1. Tunisia
2.2. Egypt
3. Empirical Methodology
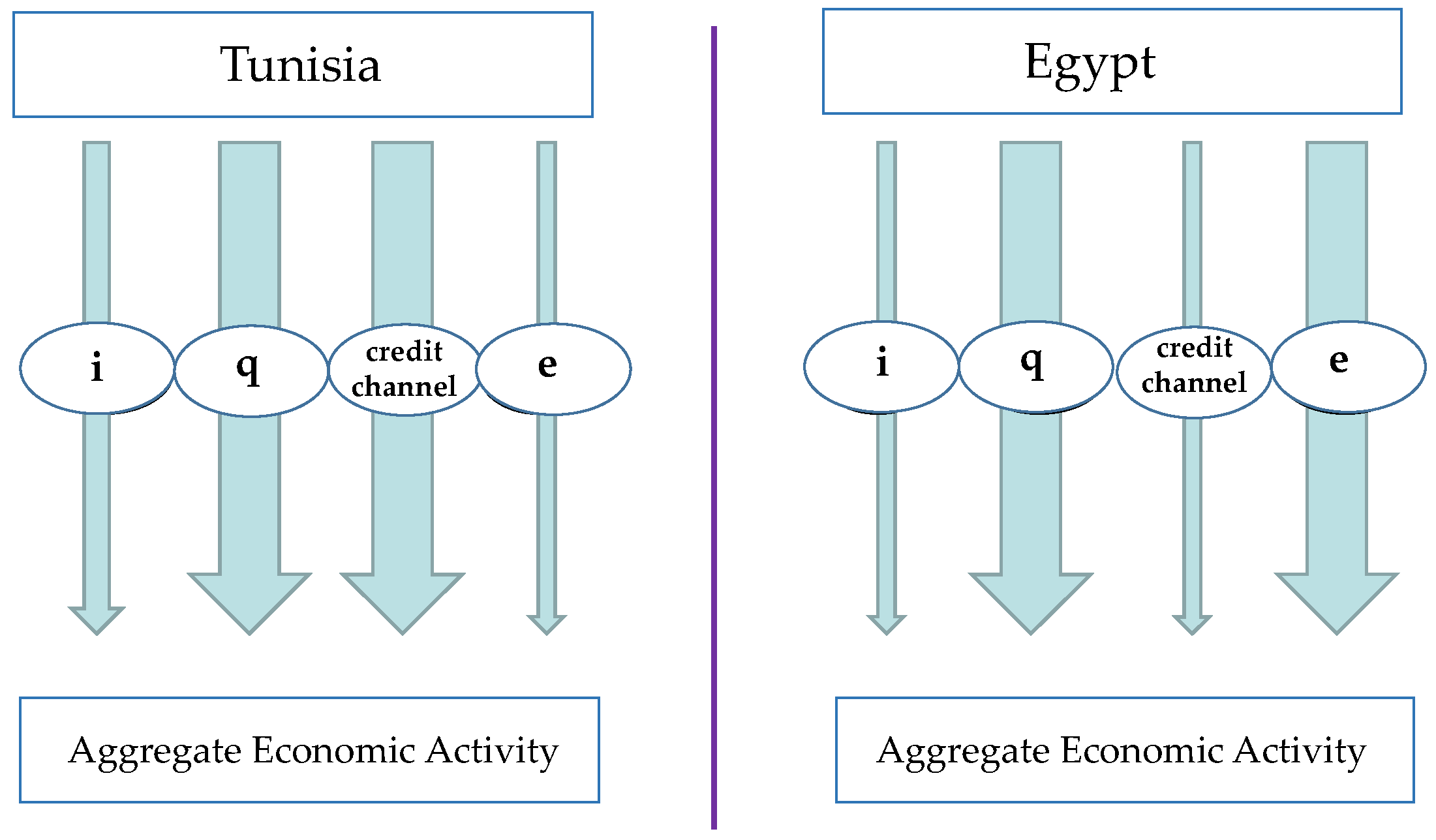
3.1. Transmission Channels of Monetary Policy
3.1.1. Interest Rate Channel
- Tunisia
- Egypt
3.1.2. Credit Channel
- Tunisia
- Egypt
3.1.3. Exchange Rate Channel
- Tunisia
- Egypt
3.1.4. Stock Price Channel
- Tunisia
- Egypt
3.2. Augmented Linear Taylor Rule
3.3. Nonlinear Taylor Rule
4. Data
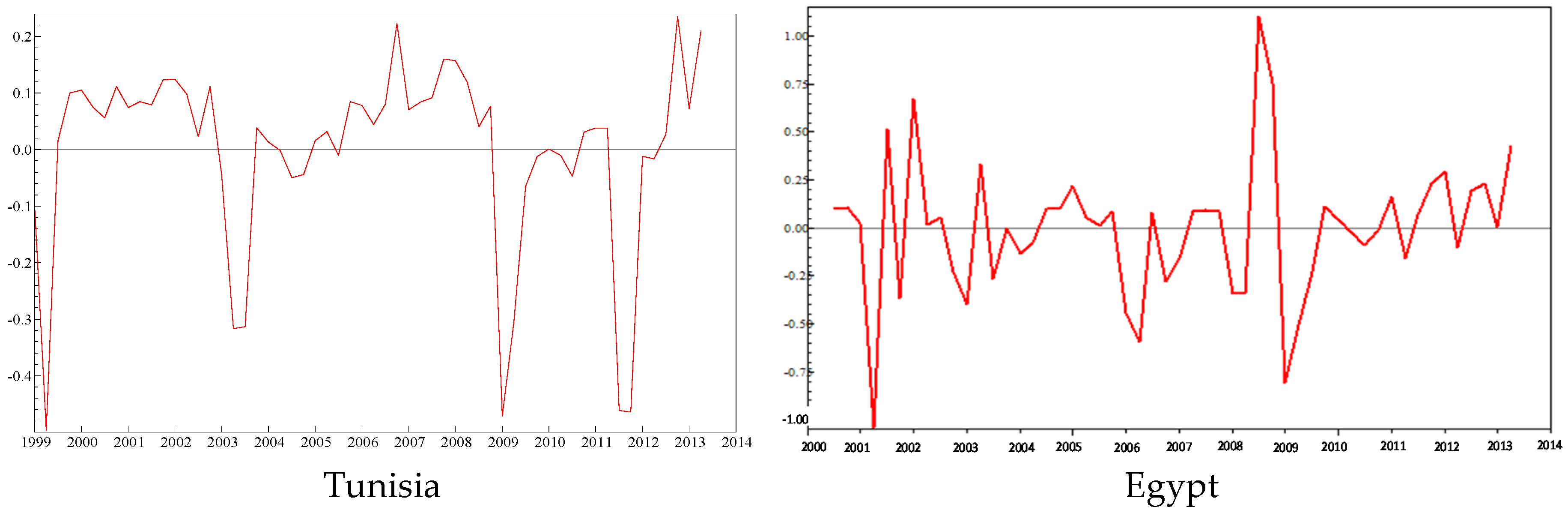
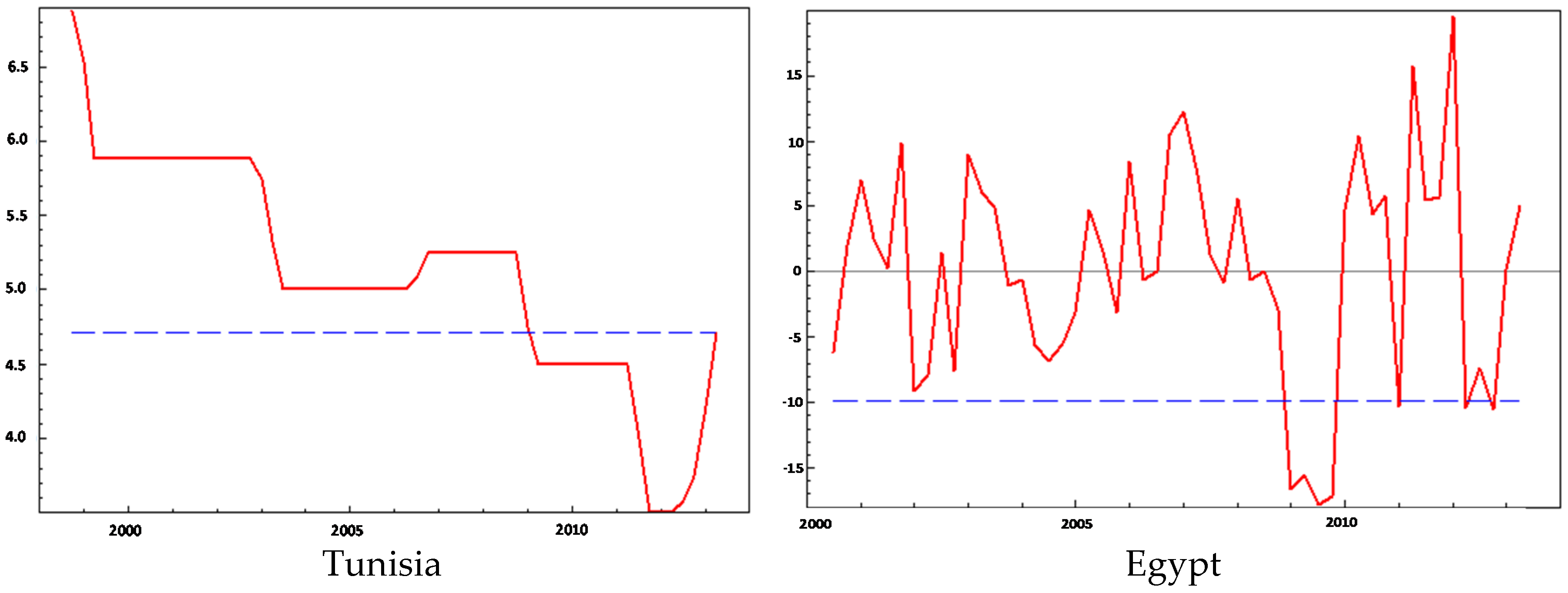
5. Results and Discussion
5.1. Linear Specification Results
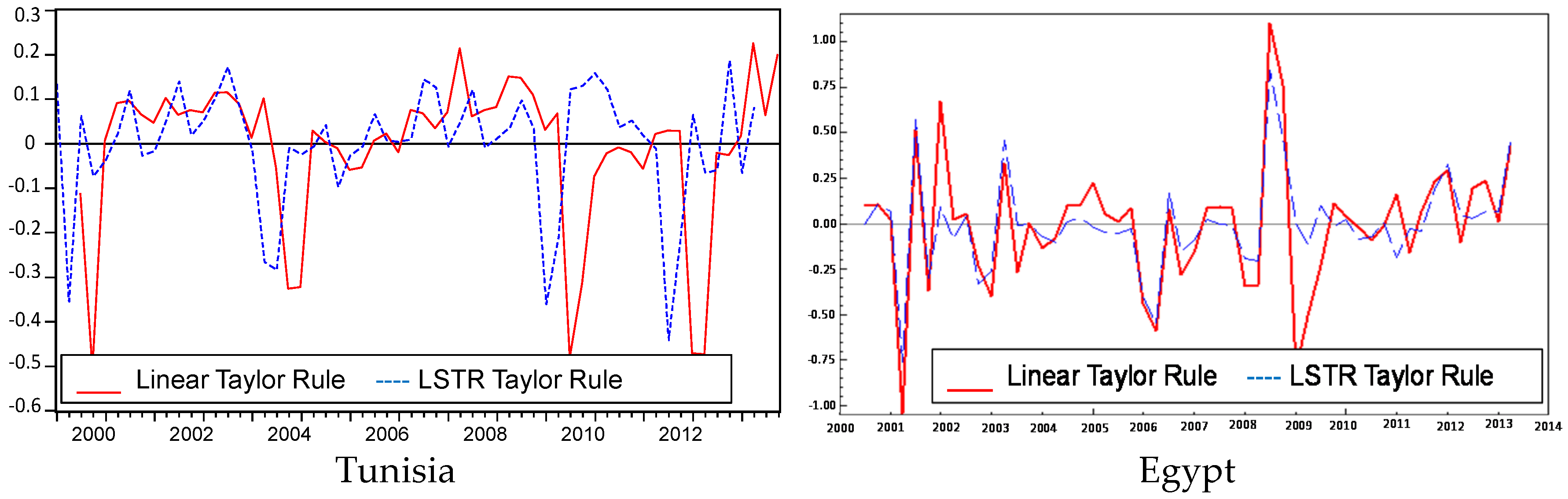
5.2. Nonlinear Specification Results
6. Conclusions
Author Contributions
Conflicts of Interest
References
- J.B. Taylor. “Discretion versus policy rules in practice.” Carnegie Rochester Conf. Ser. Public Policy 39 (1993): 195–214. [Google Scholar] [CrossRef]
- R. Clarida, J. Galí, and M. Gertler. “Monetary policy rules in practice: Some international evidence.” Eur. Rev. 4 (1998): 1033–1067. [Google Scholar]
- L.E.O. Svensson. “What is wrong with Taylor rules? Using judgment in monetary policy through targeting rules.” J. Econ. Lit. 42 (2003): 426–477. [Google Scholar] [CrossRef]
- N. Batini, R. Harrison, and S.P. Millard. “Monetary Policy Rules for an Open Economy.” Available online: http://www.frbsf.org/economic-research/files/0103conf2.pdf (accessed on 7 April 2016).
- R. Nobay, and D. Peel. “Optimal discretionary monetary policy in a model of asymmetric central bank preferences.” Econ. J. 113 (2003): 657–665. [Google Scholar] [CrossRef]
- J. Dolado, R. Dolores, and M. Naveira. “Are monetary policy reaction functions asymmetric? The role of nonlinearity in the Phillips Curve.” Eur. Econ. Rev. 49 (2005): 485–503. [Google Scholar] [CrossRef]
- O. Karagedikli, and K. Lees. “Asymmetric monetary policy in Australia.” Econ. Rec. 82 (2006): S85–S96. [Google Scholar]
- P. Surico. “The Fed’s monetary policy rule and US inflation: The case of asymmetric preferences.” J. Econ. Dyn. Control 31 (2007): 305–324. [Google Scholar] [CrossRef]
- A. Cukierman, and A. Muscatelli. “Nonlinear Taylor Rules and Asymmetric Preferences in Central Banking: Evidence from the United Kingdom and the United States.” B.E. J. Macroecon. 8 (2008): 7. [Google Scholar]
- E. Schaling. “The Nonlinear Phillips Curve and Inflation Forecast Targeting.” 1999. Available online: http://www.bankofengland.co.uk/archive/Documents/historicpubs/workingpapers/1999/wp98.pdf (accessed on 15 April 2015).
- R. Nobay, and D. Peel. “Optimal monetary policy with a nonlinear Phillips curve.” Econ. Lett. 67 (2000): 159–164. [Google Scholar] [CrossRef]
- F.S. Mishkin. “Monetary Policy Strategy Lessons from the Crisis.” NBER Working Paper No. 16755. February 2011. Available online: https://www.imf.org/external/np/seminars/eng/2011/res2/pdf/fm.pdf (accessed on 8 April 2016).
- C. Conrad, and T.A. Eife. “Explaining inflation gap persistence by a time-varying Taylor rule.” J. Macroecon. 74 (2012): 59–75. [Google Scholar] [CrossRef]
- D.J. Lee, and J.C. Son. “Nonlinearity and structural breaks in monetary policy rules with stock prices.” Econ. Model. 31 (2013): 1–11. [Google Scholar] [CrossRef]
- E. Olsen, W. Enders, and E. Vohar. “An empirical investigation of the Taylor curve.” J. Macroecon. 32 (2012): 392–404. [Google Scholar] [CrossRef]
- F. Kolman. “The asymmetric reaction of monetary policy to inflation and the output gap: Evidence from Canada.” Econ. Model. 30 (2013): 911–923. [Google Scholar]
- C.W.J. Granger, and T. Terasvirta. Modelling Nonlinear Economic Relationships. New York, NY, USA: Oxford University Press, 1993. [Google Scholar]
- R. Al-Mashat, and A. Billmeier. “The Monetary Transmission Mechanism in Egypt.” Working Paper WP/07/285. IMF, 2007. Avaiable online: https://www.imf.org/external/pubs/ft/wp/2007/wp07285.pdf (accessed on 8 April 2016).
- J.M. Fleming. “Domestic Financial Policies under Fixed and under Floating Exchange Rates.” Staff Papers, Int. Monet. Fund 9 (1962): 369–379. [Google Scholar] [CrossRef]
- R.A. Mundell. “The Significance of Capital Mobility for Stabilization Policy under Fixed and Flexible Exchange Rates.” Can. J. Econ. Polit. Sci. 29 (1963): 475–485. [Google Scholar] [CrossRef]
- A. Boughrara, M. Boughzala, and M. Moussa. Are the Conditions for the Adoption of Inflation Targeting Satisfied in Morocco. Giza, Egypt: The Economic Research Forum (ERF), 2008. [Google Scholar]
- G.D. Rudebusch. “Term Structure evidence on interest rate smoothing and monetary policy inertia.” J. Monet. Econ. 49 (2002): 1161–1187. [Google Scholar] [CrossRef]
- T. Teräsvirta. “Modelling economic relationships with smooth transition regressions.” In Smooth Transition Regression Modelling. Edited by H. Lutkepohl and M. Kratzig. Cambridge, UK: Cambridge University Press, 1998, pp. 222–242. [Google Scholar]
- D. Van Dijk, T. Teräsvirta, and P.H. Franses. “Smooth transition autoregressive models—A survey of recent developments.” Econ. Rev. 21 (2002): 1–47. [Google Scholar] [CrossRef]
- T. Teräsvirta. “Specification, estimation and evaluation of smooth transition autoregressive models.” J. Am. Stat. Assoc. 89 (1994): 208–218. [Google Scholar]
- R. Luukkonen, P. Saikkonen, and T. Teräsvirta. “Testing linearity against smooth transition autoregressive models.” Biometrika 75 (1988): 491–499. [Google Scholar] [CrossRef]
- T. Teräsvirta. “Smooth transition regression modelling.” In Applied Time Series Econometrics. Edited by H. Lutkepohl and M. Kratzig. Cambridge, UK: Cambridge University Press, 2004, pp. 222–242. [Google Scholar]
- Ø. Eitrheim, and T. Terasvirta. “Testing the adequacy of smooth transition autoregressive models.” J. Econ. 74 (1996): 59–75. [Google Scholar] [CrossRef]
- Y. Baaziz, M. Labidi, and A. Lahiani. “Does the South African Reserve Bank follow a nonlinear interest rate reaction function? ” Econ. Model. 35 (2013): 272–282. [Google Scholar] [CrossRef]
- Y. Baaziz, and M. Labidi. “What can nonlinear Taylor rule say about the Egyptian monetary policy conduct? ” Int. J. Innov. Appl. Stud. 9 (2014): 1245–1257. [Google Scholar]
- R. Bruggemann, and J. Riedel. “Nonlinear interest rate reaction functions for the UK.” Econ. Model. 28 (2011): 1174–1185. [Google Scholar] [CrossRef]
- C. Alcidi, A. Flamini, and A. Fracasso. “Policy regime changes, judgment and Taylor rules in the Greenspan Era.” Economica 78 (2011): 89–107. [Google Scholar] [CrossRef]
- V. Castro. “Can central banks’ monetary policy be described by a linear (augmented) Taylor rule or by a nonlinear rule? ” J. Financial Stab. 157 (2011): 228–246. [Google Scholar] [CrossRef]
- T. Teräsvirta, and H.M. Anderson. “Characterizing nonlinearities in business cycles using smooth transition autoregressive models.” In Nonlinear Dynamics, Chaos and Econometrics. Edited by M.H. Pesaran and S.M. Potter. Hoboken, NJ, USA: Wiley, 1992, pp. 111–128. [Google Scholar]
- 1The former Article 33 of May 2006, Central Bank law stated that “the ultimate objective of monetary policy is to safeguard the value of the currency by keeping inflation down to a rate close to the rate observed in partner and competitor countries”.
| Country | Obs | Sample Period |
|---|---|---|
| Tunisia | 64 | 1998 Q4→2013 Q4 |
| Egypt | 54 | 2000 Q1→2013 Q2 |
| Tunisia | |||||||
| ADF | −2.633 *** | −0.4959 | −4.66 *** | −3.702 *** | --- | −5.714 *** | --- |
| KPSS | 0.6537 *** | 0.948 | 0.0801 *** | 1.9421 | --- | 0.0312 *** | --- |
| ZA | −7.626 *** | −3.6865 | −5.3419*** | −6.3857 *** | --- | −7.368 *** | --- |
| Egypt | |||||||
| ADF | −0.8092 | −0.7317 | −3.587 *** | −0.7799 | −4.8753 *** | −5.766 *** | −2.754 *** |
| KPSS | 1.288 | 0.8652 | 0.046 *** | 0.4312 ** | 0.1358 *** | 0.0546 *** | 0.4413 ** |
| ZA | −2.546 | −1.362 | −6.204 *** | −3.105 | −5.387 | −8.452 | −6.539 |
| Tunisia | Egypt | |||
|---|---|---|---|---|
| Estimates | t-Statistics | Estimates | t-Statistics | |
| 0.207 | 0.066 | −0.006 | 0.366 | |
| 0.031 * | 0.1563 | 0.044 *** | 1.8633 | |
| −0.0045 *** | 3.215 | 0.013 *** | 3.166 | |
| 0.915 *** | 3.6612 | 0.337 *** | 3.4081 | |
| 0.0053 * | 2.136 | 0.018 ** | 1.182 | |
| AIC | −3.41 | −1.9772 | ||
| 0.945 | 0.3462 | |||
| ARCH (8) | 11.793 [0.1607] | 9.8408 [0.0017] | ||
| F | F2 | F3 | F4 | Selected Model | |
|---|---|---|---|---|---|
| Tunisia | |||||
| it−1 | 3.7702 × 10−4 | 3.637 × 10−1 | 7.873 × 10−3 | 2.383 × 10−3 | LSTR1 |
| yt | 8.792 × 10−2 | 8.959 × 10−2 | 2.303 × 10−1 | 2.32 × 10−1 | Linear |
| πt | 1.4092 × 10−1 | 1.179 × 10−1 | 6.602 × 10−1 | 1.1439 × 10−1 | Linear |
| qt | 3.2244 × 10−2 | 2.457 × 10−1 | 7.5092 × 10−2 | 7.9037 × 10−2 | LSTR2 |
| Egypt | |||||
| it−1 | 1.5013 × 10−3 | 1.0905 × 10−1 | 2.6572 × 10−2 | 6.9245 × 10−3 | LSTR1 |
| yt | 4.1783 × 10−4 | 8.9142 × 10−3 | 7.7167 × 10−2 | 8.9499 × 10−3 | LSTR1 |
| πt | 2.4598 × 10−2 | 9.741 × 10−2 | 3.5677 × 10−1 | 2.0537 × 10−2 | LSTR1 |
| qt | 2.4421 × 10−2 | 1.7443 × 10−1 | 1.0814 × 10−1 | 4.135 × 10−2 | LSTR1 |
| Tunisia | Egypt | |
|---|---|---|
| Linear part | ||
| Constant | 4.808 (40.763) | −1.469 (23.652) |
| 0.892 *** (1.814) | 0.972 *** (2.382) | |
| −0.007 *** (4.058) | −0.1049 ** (1.24) | |
| 0.077 (0.167) | 0.2237 ** (0.983) | |
| −0.046 (0.045) | −0.1967 ** (1.058) | |
| Nonlinear part | ||
| Constant | −3.655 (40.453) | 1.5539 (18.947) |
| −0.393 (0.709) | 0.592 ** (2.104) | |
| 0.019 *** (3.978) | 0.1039 (0.558) | |
| 0.068 (0.124) | −0.2141 *** (2.298) | |
| 0.061 (0.092) | 0.1039 (0.372) | |
| 3.455 ** (1.480) | 5.324 * (5.789) | |
| c | 4.708 *** (0.218) | −9.855 *** (5.465) |
| AIC | −3.622 | −2.135 |
| 0.965 | 0.5916 | |
| Jarque-Bera | 31.401 [0.000] | 51.7188 [0.000] |
| ARCH(8) | 3.3436 [0.911] | 2.6563 [0.954] |
| Parameter Constancy Test Results | ||||
| Transition Variable | Tunisia | Egypt | ||
| H1 | 1.8391 0.1015 | 2.1958 0.062 | ||
| H2 | 1.8854 0.0688 | 1.412 0.203 | ||
| H3 | 2.36 0.0275 | 4.3635 0.012 | ||
| No remaining nonlinearity test results | ||||
| Tunisia | ||||
| Transition Variable | F | F2 | F3 | F4 |
| 1.85 × 10−4 | 6.41 × 10−2 | 8.876 × 10−2 | 5.939 × 10−4 | |
| Egypt | ||||
| Transition Variable | F | F2 | F3 | F4 |
| Output gap | 7.035 × 10−1 | 5.85 × 10−1 | 3.226 × 10−1 | 8.6529 × 10−1 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baaziz, Y.; Labidi, M. Nonlinear Monetary Policy Rules: An Essay in the Comparative Study on Egyptian and Tunisian Central Banks. Economies 2016, 4, 6. https://doi.org/10.3390/economies4020006
Baaziz Y, Labidi M. Nonlinear Monetary Policy Rules: An Essay in the Comparative Study on Egyptian and Tunisian Central Banks. Economies. 2016; 4(2):6. https://doi.org/10.3390/economies4020006
Chicago/Turabian StyleBaaziz, Yosra, and Moez Labidi. 2016. "Nonlinear Monetary Policy Rules: An Essay in the Comparative Study on Egyptian and Tunisian Central Banks" Economies 4, no. 2: 6. https://doi.org/10.3390/economies4020006
APA StyleBaaziz, Y., & Labidi, M. (2016). Nonlinear Monetary Policy Rules: An Essay in the Comparative Study on Egyptian and Tunisian Central Banks. Economies, 4(2), 6. https://doi.org/10.3390/economies4020006





