The Impact of Geopolitical Risk on Portuguese Exports
Abstract
1. Introduction
2. Literature Review
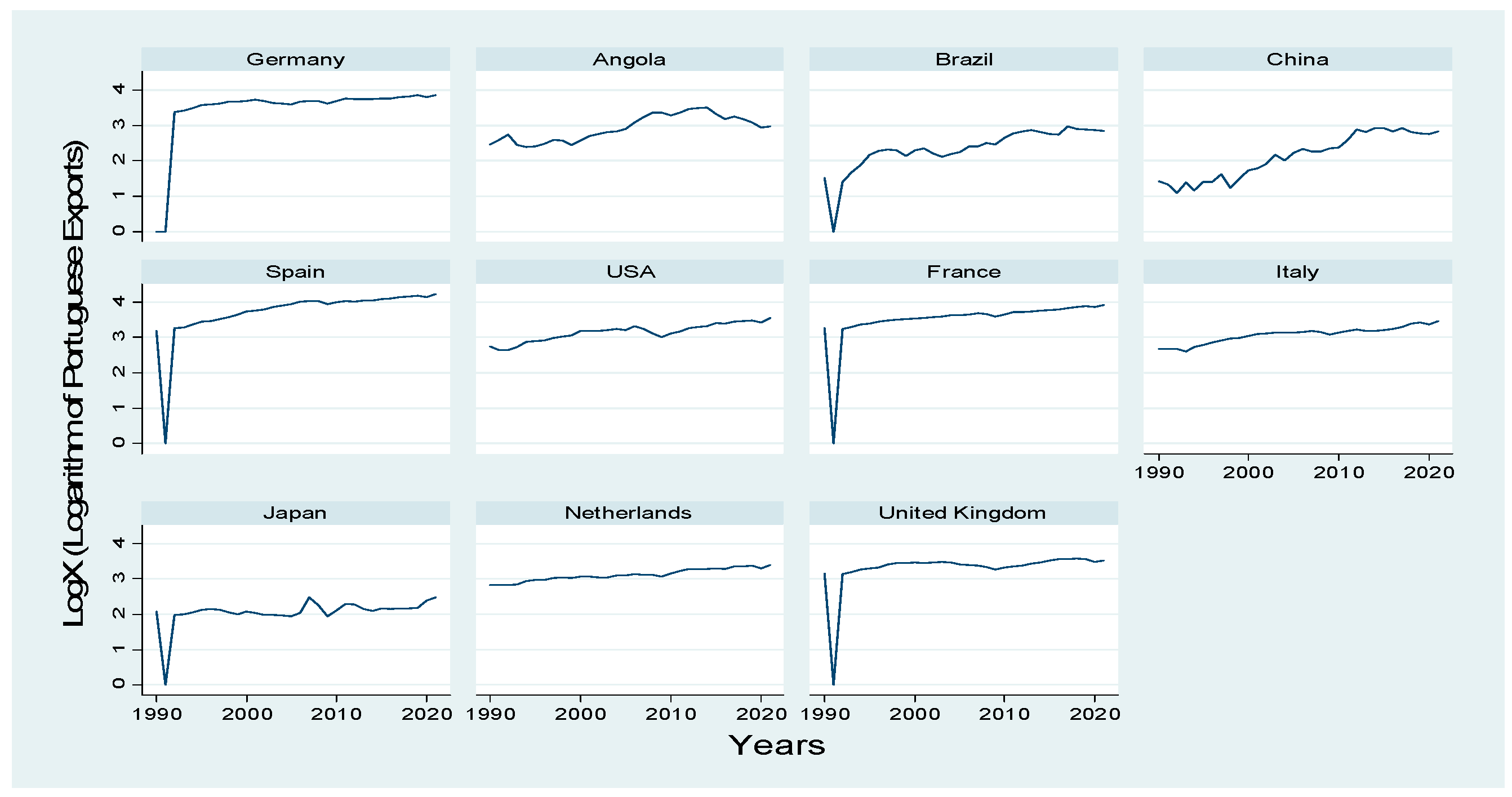
3. Econometric Strategy and Data
4. Empirical Results
5. Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Variables | Gamma |
|---|---|
| LogINC | 0.878 *** (0.000) |
| LogINCK | 0.525 *** (0.000) |
| Language | 0.181 *** (0.000) |
| LogDIST | −1.259 *** (0.000) |
| LogRISK | −1.261 *** (0.000) |
| Constant | 1.294 ** (0.011) |
| AIC | 0.778 |
| Obs | 352 |
References
- Abbas, Shujaat, and Sindhu Bhutto. 2022. Macroeconomic determinants and potential markets for Pakistani textile-clothing and apparel industries: Evidence from gravity model analysis. The Journal of The Textile Institute, 1–11. [Google Scholar] [CrossRef]
- Abdullah, Nazir Muhammad, Olufemi Adewale Aluko, and Xuexi Huo. 2021. Determinants, Efficiency and Potential of Agri-Food Exports from Nigeria to the EU: Evidence from the Stochastic Frontier Gravity Model. Agricultural Economics–Czech 67: 337–49. [Google Scholar] [CrossRef]
- Anderson, James, E. 1979. A Theoretical Foundation for the Gravity Equation. American Economic Review 69: 106–16. [Google Scholar]
- Anderson, James E., and Douglas Marcouiller. 2002. Insecurity and the Pattern of Trade: An Empirical Investigation. Review of Economics and Statistics 84: 342–52. [Google Scholar] [CrossRef]
- Anderson, James E., and Eric van Wincoop. 2003. Gravity with Gravitas: A Solution to the Border Puzzle. American Economic Review 93: 170–92. [Google Scholar] [CrossRef]
- Ayuda, María-Isabel, Hugo Ferrer-Pérez, and Vicente Pinilla. 2020. Explaining World Wine Exports in the First Wave of Globalization, 1848–938. Journal of Wine Economics 15: 263–83. [Google Scholar] [CrossRef]
- Baier, Scoot, and Samuel Standaert. 2020. Gravity Models and Empirical Trade. In Oxford Research Encyclopedia of Economics and Finance. Oxford: Oxford University Press. [Google Scholar] [CrossRef]
- Balogh, Jeremiás Máté, and Giovanna Maria Borges Aguiar. 2022. Determinants of Latin American and the Caribbean agricultural Trade: A Gravity Model Approach. Agricultural Economics–Czech 4: 127–36. [Google Scholar] [CrossRef]
- Balogh, Jeremiás Máté, and Nuno Carlos Leitão. 2019. A Gravity Approach of Agriculture Trade: The Nexus of EU and African, Caribbean and Pacific Countries. Agricultural Economics-Czech 65: 509–19. [Google Scholar] [CrossRef]
- CEPII (Centre d’Etudes Prospectives et d´Informations Internationales). 2023. Dataset for the Variables of Geographical Distance, and Common Language. Available online: http://www.cepii.fr/CEPII/en/bdd_modele/bdd_modele.asp (accessed on 30 August 2023).
- Chen, Natalie, and Dennis Novy. 2022. Gravity and Heterogeneous Trade Cost Elasticities. The Economic Journal 132: 1349–77. [Google Scholar] [CrossRef]
- Dadakas, Dimitrios, Salim Ghazvini Kor, and Scott Fargher. 2020. Examining the Trade Potential of the UAE using a Gravity model and a Poisson Pseudo Maximum Likelihood Estimator. The Journal of International Trade & Economic Development 29: 619–46. [Google Scholar]
- Dorakh, Alena. 2020. A Gravity Model Analysis of FDI across EU Member States. Journal of Economic Integration 35: 426–56. [Google Scholar] [CrossRef]
- Egger, Peter, H., and Kevin E. Staub. 2016. GLM Estimation of Trade Gravity Models with Fixed Effects. Empirical Economics 50: 137–75. [Google Scholar] [CrossRef]
- Eshetu, Fassil, and Degye Goshu. 2021. Determinants of Ethiopian Coffee Exports to Its Major Trade Partners: A Dynamic Gravity Model Approach. Foreign Trade Review 56: 185–96. [Google Scholar] [CrossRef]
- Faustino, Horácio C., and Nuno Carlos Leitão. 2011. Fragmentation in the Automobile Industry: Evidence from Portugal. Journal of Economic Studies 38: 287–300. [Google Scholar] [CrossRef]
- Fernandes, Ana, and Rosa Forte. 2022. The Impact of Economic Diplomacy on Exports: The Portuguese Case. International Journal 77: 216–47. [Google Scholar] [CrossRef]
- Ginsburgh, Victor, and Shlomo Weber. 2020. The Economics of Language. Journal of Economic Literature 58: 348–404. [Google Scholar] [CrossRef]
- Goswami, Gour Gobinda, and Nisit Panthamit. 2022. Does Political Risk Matter for China’s Trade with ASEAN and MENA Countries? A Belt Road Initiative Perspective. The Chinese Economy 55: 188–207. [Google Scholar] [CrossRef]
- Gouveia, Sofia, João Rebelo, and Lina Lourenço-Gomes. 2018. Port Wine Exports: A Gravity Model Approach. International Journal of Wine Business Research 30: 218–42. [Google Scholar] [CrossRef]
- Gouveia, Sofia, João Rebelo, Lina Lourenço-Gomes, and Alexandre Guedes. 2017. International Demand for the Douro (Portugal) River Cruises: A Gravity Model Approach. Tourism Economics 23: 1679–86. [Google Scholar]
- Grin, François. 2003. Language Planning and Economics. Current Issues in Language Planning 4: 1–66. [Google Scholar] [CrossRef]
- Gupta, Rangan, Giray Gozgor, Huseyin Kaya, and Ender Demir. 2019. Effects of Geopolitical Risks on Trade Flows: Evidence from the Gravity Model. Eurasian Economic Review 9: 515–30. [Google Scholar] [CrossRef]
- Hassan, Adewale Samuel. 2022. Does Country Risk Influence Foreign Direct Investment Inflows? A Case of the Visegrád Four. Economies 10: 221. [Google Scholar] [CrossRef]
- Helpman, Elhanam. 1987. Imperfect competition and international trade: Opening remarks. European Economic Review 31: 77–81. [Google Scholar] [CrossRef]
- Helpman, Elhanam, and Paul Krugman. 1985. Market Structure and Foreign Trade: Increasing Returns, Imperfect Competition, and the International Economy. Cambridge: MIT Press. [Google Scholar]
- Hummels, David, and James Levinsohn. 1995. Monopolistic Competition and International Trade: Reconsidering the Evidence. Quarterly Journal of Economics 110: 799–836. [Google Scholar] [CrossRef]
- Huseyni, Ibrahim, Ali Kemal Çelik, and Miraç Eren. 2019. Application of Panel Quantile Regression and Gravity Models in Exploring the Determinants of Turkish Automotive Export Industry. In Understanding the Role of Business Analytics. Edited by Hardeep Chahal, Jeevan Jyoti and Jochen Wirtz. Singapore: Springer, pp. 31–44. [Google Scholar]
- ICRG (International Country Risk Guide). 2023. Available online: https://www.prsgroup.com/explore-our-products/icrg/ (accessed on 29 September 2023).
- Im, Kyung So, M. Hashem Pesaran, and Yongcheol Shin. 2003. Testing for Unit Roots in Heterogeneous Panels. Journal of Econometrics 115: 53–74. [Google Scholar] [CrossRef]
- INE (National Institute of Statistics of the Portuguese Economy). 2023. Statistics on International Trade in Goods and by Main Trading Partners in Millions of Euros. Available online: http://www.pordata.pt (accessed on 29 September 2023).
- Isard, Walter, and Merton J. Peck. 1954. Location Theory and International and Interregional Trade Theory. The Quarterly Journal of Economics 68: 97–114. [Google Scholar] [CrossRef]
- Khan, Mohammad Azeem, Zeenat Fatima, and Sumbul Fatima. 2023. Revisiting the Gravity Model of Migration. Foreign Trade Review 58: 329–49. [Google Scholar] [CrossRef]
- Koenker, Roger, and Gilbert Bassett, Jr. 1978. Regression Quantiles. Econometrica 46: 33–50. [Google Scholar] [CrossRef]
- Krugman, Paul R. 1979. Increasing Returns, Monopolistic Competition, and International Trade. Journal of International Economics 9: 469–79. [Google Scholar] [CrossRef]
- Krugman, Paul. 1980. Scale Economies, Product Differentiation and the Pattern of Trade. American Economic Review 70: 950–59. [Google Scholar]
- Lancaster, Kelvin. 1980. Intra-Industry Trade under Perfect Monopolistic Competition. Journal of International Economics 10: 151–75. [Google Scholar] [CrossRef]
- Leitão, Nuno Carlos. 2023. A Gravity Model Analysis of Portuguese Foreign Direct Investment. Economies 11: 237. [Google Scholar] [CrossRef]
- Leitão, Nuno Carlos, and Horácio C. Faustino. 2013. Intra-industry trade in the medical and optical instruments industry: A panel data analysis. Economic Research- Ekonomska Istrazivanja 26: 129–40. [Google Scholar] [CrossRef]
- Leitão, Nuno Carlos, Horácio C. Faustino, and Yushi Yoshida. 2010. Fragmentation, Vertical Intra-Industry Trade, and Automobile components. Economics Bulletin 30: 1006–15. [Google Scholar]
- Levin, Andrew, Chien-Fu Lin, and Chia-Shang James Chu. 2002. Unit root tests in panel data: Asymptotic and finite-sample properties. Journal of Econometrics 108: 1–24. [Google Scholar] [CrossRef]
- Li, Enkang, Mengqiu Lu, and Yu Chen. 2020. Analysis of China’s Importance in “Belt and Road Initiative” Trade Based on a Gravity Model. Sustainability 12: 6808. [Google Scholar] [CrossRef]
- Linnemann, Hans. 1966. An Econometric Study of International Trade Flows. Amsterdam: North Holland Publishing Co. [Google Scholar]
- Macedo, Anthony, Sofia Gouveia, and João Rebelo. 2019. Horizontal Differentiation and Determinants of Wine Exports: Evidence from Portugal. Journal of Wine Economics 15: 163–80. [Google Scholar] [CrossRef]
- Maddala, G. S., and Shaowen Wu. 1999. A Comparative Study of Unit Root Tests with Panel Data and a New Simple Test. Oxford Bulletin of Economics and Statistics 61: 631–52. [Google Scholar] [CrossRef]
- Masood, Shah, Nabila Khurshid, Maqsood Haider, Jamila Khurshid, and Arif Masih Khokhar. 2023. Trade Potential of Pakistan with the South Asian Countries: A Gravity Model Approach. Asia Pacific Management Review 28: 45–51. [Google Scholar] [CrossRef]
- Moser, Christoph, Thorsten Nestmann, and Michael Wedow. 2008. Political Risk and Export Promotion: Evidence from Germany. The World Economy, 781–803. [Google Scholar] [CrossRef]
- Paas, Tiiu, Egle Tafenau, and Nancy J. Scannell. 2008. Gravity Equation Analysis in the Context of International Trade: Model Specification Implications in the Case of the European Union. Eastern European Economics 46: 92–113. [Google Scholar] [CrossRef]
- Pacheco, Luís Miguel, and André Pereira Matos. 2022. Foreign Presence and Export Performance: The Role of Portuguese Commercial Diplomacy. The International Trade Journal 36: 147–69. [Google Scholar] [CrossRef]
- Paz, Loureço S., Magnus dos Reis, and André Filipe Zago de Azevedo. 2023. New Evidence on WTO Membership After the Uruguay Round: An Analysis at the Sectoral Level. Open Economies Review. [Google Scholar] [CrossRef]
- Phillips, Peter C. B., and Hyungsik R. Moon. 1999. Linear Regression Limit Theory for Nonstationary Panel Data. Econometrica 67: 1057–11. [Google Scholar] [CrossRef]
- Pöyhönen, Pentti. 1963. A Tentative Model for the Volume of Trade between Countries. Weltwirtschaftliches Archiv 90: 93–100. [Google Scholar]
- Proença, Isabel, Enrique Martínez-Galán, and Maria Paula Fontoura. 2017. Trade Potential Revisited: A Panel Data Analysis for Zimbabwe. Applied Econometrics and International Development 17: 113–30. [Google Scholar]
- Proença, Isabel, Maria Paula Fontoura, and Enrique Martínez-Galán. 2008. Trade in the Enlarged European Union: A New Approach on Trade Potential. Portuguese Economic Journal 7: 205–24. [Google Scholar] [CrossRef][Green Version]
- Rajesh, Raj. 2018. Assessing the Impact of Great Recession on India’s Trade in Gravity Model Framework. Foreign Trade Review 53: 239–70. [Google Scholar] [CrossRef]
- Ramaswamy, Sunder, Abishek Choutagunta, and Santosh Kumar Sahu. 2021. Evaluating Asian Free Trade Agreements: What Does Gravity Model Tell Us? Foreign Trade Review 56: 60–70. [Google Scholar] [CrossRef]
- Santos Silva, J. M. C., and Silvana Tenreyro. 2006. The Log of Gravity. Review of Economics and Statistics 88: 641–58. [Google Scholar] [CrossRef]
- Santos Silva, J. M. C., and Silvana Tenreyro. 2022. The log of gravity at 15. Portuguese Economic Journal 21: 423–37. [Google Scholar] [CrossRef]
- Shahriar, Saleh, Sokvibol Kea, Nazir Muhammad Abdullahi, Redwanur Rahman, and Rajib Moshfequl Islam. 2021. Determinants of Bangladesh’s Leather Exports to Its Major Trade Partners: A Panel Gravity Model Approach. Global Business Review, 1–22. [Google Scholar] [CrossRef]
- Shi, Shuaiwei, Qingru Sun, Zenglei Xi, Meiyi Hou, and Jiaoyun Guo. 2022. The Impact of Country Risks on the Dependence Patterns of International Cobalt Trade: A Network Analysis Method. Frontiers in Energy Research 10: 951235. [Google Scholar] [CrossRef]
- Sun, Qingru, Meiyi Hou, Shuaiwei Shi, Liwei Cui, and Zenglei Xi. 2022. The Influence of Country Risks on the International Agricultural Trade Patterns Based on Network Analysis and Panel Data Method. Agriculture 12: 361. [Google Scholar] [CrossRef]
- Tavares, Jean Max, and Nuno Carlos Leitão. 2017. The Determinants of International Tourism Demand for Brazil. Tourism Economics 23: 834–45. [Google Scholar] [CrossRef]
- Tinbergen, Jan. 1962. Shaping the World Economy; Suggestions for an International Economic Policy. New York: Twentieth Century Fund. [Google Scholar]
- Wang, Zhengwen, Yunxiao Zong, Yuwan Dan, and Shi-Jie Jiang. 2021. Country Risk and International Trade: Evidence from the China-B&R countries. Applied Economics Letters 28: 1784–88. [Google Scholar]
- World Bank Indicators. 2023. Available online: https://data.worldbank.org/indicator (accessed on 30 August 2023).
- Yoshida, Yushi, Nuno Carlos Leitão, and Horácio Faustino. 2009. Vertical Intra-Industry Trade and Foreign Direct Investment between Japan and European Countries. Atlantic Economic Journal 37: 351–65. [Google Scholar] [CrossRef]
| Studies | Period | Methodology | Results |
|---|---|---|---|
| Ramaswamy et al. (2021) | 2007–2014 | OLS and PPML estimator | The gravity equation is valid in Asian countries. |
| Shahriar et al. (2021) | 1989–2015 | PPML estimator and Heckman models | The gravity equation is valid for Bangladesh’s experience. |
| Masood et al. (2023) | 2000–2019 | PPML estimator | The gravity equation is valid for OIC countries’ experience. |
| Ayuda et al. (2020) | 1848–1938 | PPML estimator | The World Wine Gravity equation is partially valid. |
| Abdullahi et al. (2021) | 1995–2019 | SFA estimator | The gravity equation is partially valid. |
| Balogh and Aguiar (2022) | 1995–2019 | PPML estimator | The Latin American and Caribbean agricultural trade gravity model is valid. |
| Abbas and Bhutto (2022) | 2003–2019 | Panel data | The Pakistan gravity model is valid. |
| Li et al. (2020) | 2000–2018 | OLS and Fixed Effects | The gravity equation is valid for BRI countries’ experience. |
| Rajesh (2018) | 2001–2013 | Pooled OLS estimator | The gravity equation is valid for the recession in India’s trade. |
| Dadakas et al. (2020) | 2002–2016 | PPML estimator | The gravity model is valid for UAE countries. |
| Balogh and Leitão (2019) | 1996–2017 | PPML estimator | The gravity model is valid for ACP countries. |
| Proença et al. (2017) | 2007–2011 | PPML estimator | Zimbabwe’s gravity model is partially valid. |
| Dependent Variable | Explanation | Source | |
|---|---|---|---|
| LogXit | Monetary values of exports | INE a (2023) | |
| Explanatory Variables | Explanation | Expected Signs | Source |
| LogINC | Portuguese GDP per capita | + | World Bank (2023) |
| LogINCK | GDP per capita of partners | + | World Bank (2023) |
| Language | Portuguese language | + | CEPII b (2023) |
| LogGDIST | Geographical Distance | − | CEPII b (2023) |
| LogRISK | Country Risk | − | ICRG c (2023) |
| Variables | Mean | Median | St. Dev. | Min. | Max. | Skewness | Kurtosis | Obs. |
|---|---|---|---|---|---|---|---|---|
| LogXit | 3.0335 | 3.179 | 0.649 | 1.097 | 4.231 | −0.699 | 2.991 | 352 |
| LogINC | 4.211 | 4.279 | 0.153 | 3.897 | 4.397 | −0.436 | 1.709 | 352 |
| LogINCK | 4.217 | 4.445 | 0.563 | 2.401 | 4.845 | −1.468 | 4.174 | 352 |
| LogDIST | 3.489 | 3.277 | 0.412 | 2.698 | 4.048 | −0.215 | 1.961 | 352 |
| Language | 0.182 | 0.000 | 0.386 | 0.000 | 1.000 | 1.650 | 3.722 | 352 |
| LogRISK | −0.154 | −0.104 | 0.137 | −0.515 | 0.000 | −0.959 | 2.657 | 352 |
| Variables | Levin, Lin & Chu | Im, P. Shin | ADF | PP |
|---|---|---|---|---|
| LogX | −3.625 *** (0.000) | −0.842 (0.199) | 25.849 (0.258) | 19.970 (0.585) |
| LogINC | −2.449 *** (0.007) | 0.351 (0.637) | 12.836 (0.937) | 21.334 (0.507) |
| LogINCK | −1.698 * (0.045) | 0.311 (0.622) | 17.539 (0.733) | 16.634 (0.783) |
| LogRISK | −0432 (0.333) | −0.937 (0.174) | 29.0134 (0.145) | 21.406 (0.496) |
| First Differences: Variables | ||||
| DLogX | −9.880 *** (0.000) | −10.104 *** (0.000) | 136.465 *** (0.000) | 201.902 *** (0.000) |
| DLogINC | −14.569 *** (0.000) | −13.286 *** (0.000) | 185.306 *** (0.000) | 165.851 *** (0.000) |
| DLogINCk | −8.167 *** (0.000) | −8.948 *** (0.000) | 118.749 *** (0.000) | 145.335 *** (0.000) |
| DLogRISK | 3.234 (0.999) | −5.487 *** (0.000) | 77.321 *** (0.000) | 101.958 *** (0.000) |
| Variables | VIF | 1/VIF |
|---|---|---|
| LogINC | 1.62 | 0.62 |
| LogINCK | 3.61 | 0.28 |
| Language | 2.69 | 0.37 |
| LogDIST | 1.27 | 0.79 |
| LogRISK | 4.67 | 0.214 |
| Mean VIF | 2.77 |
| Variables | OLS | Random Effects (RE) | PPML Estimator |
|---|---|---|---|
| LogINC | 0.924 *** (0.000) | 0.321 *** (0.000) | 0.260 *** (0.000) |
| LogINCK | 0.434 *** (0.000) | 0.949 *** (0.000) | 0.1995 *** (0.000) |
| Language | 0.233 *** (0.000) | 0.594 ** (0.047) | 0.127 *** (0.000) |
| LogDIST | −1.159 *** (0.000) | −1.025 *** (0.000) | −0.378 *** (0.000) |
| LogRISK | −0.693 *** (0.000) | −0.911 *** (0.000) | −0.268 *** (0.007) |
| Constant | 1.209 ** (0.013) | 1.004 (0.286) | 0.4108 ** (0.017) |
| Adj. R2 | 0.778 | 0.802 | 0.752 |
| Obs | 352 | 352 | 352 |
| Hausman test: Chi2 (4)= | 0.10 (0.998) |
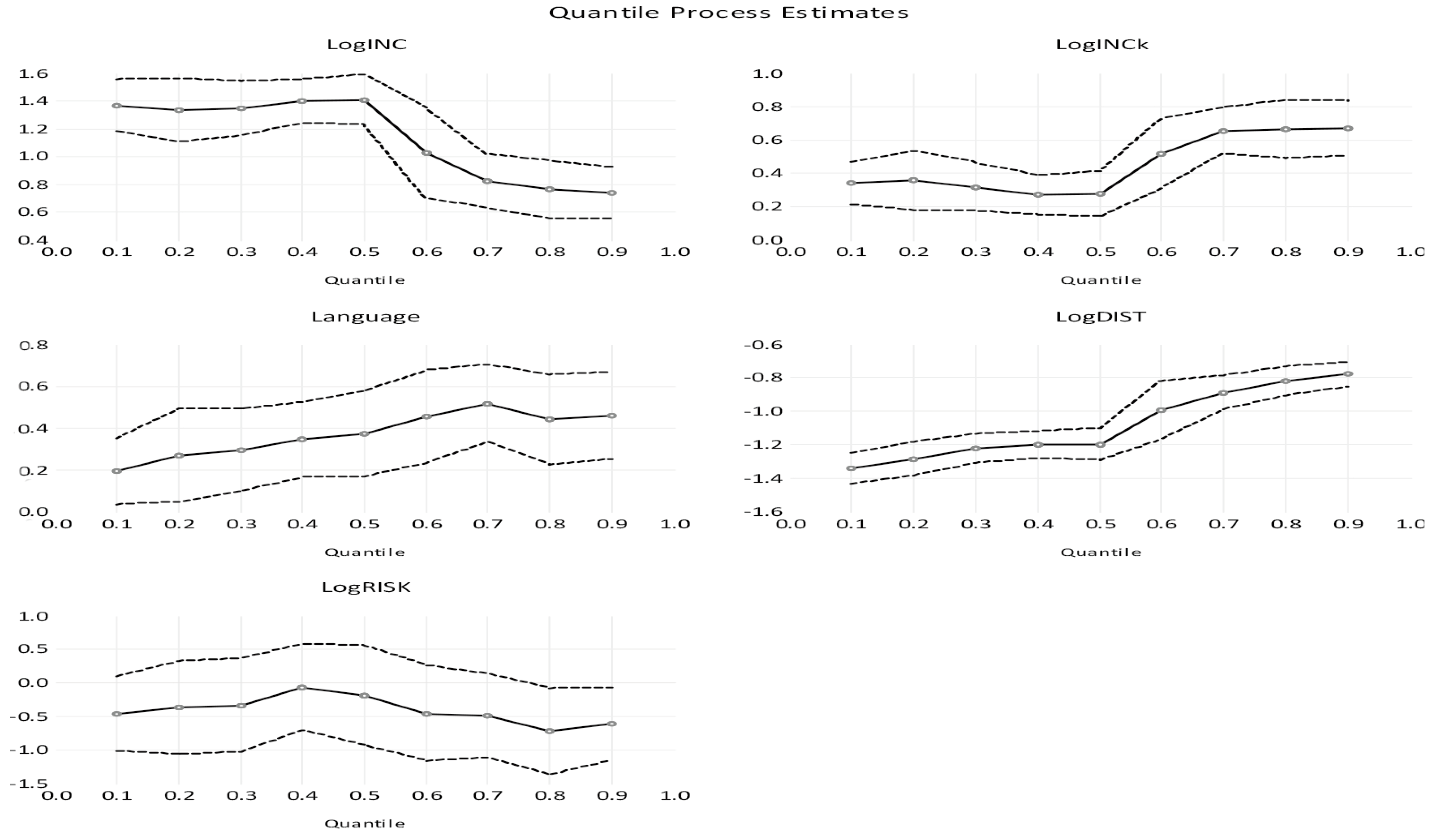
| Variables | (tau = 0.10) | (tau = 0.20) | (tau = 0.25) | Median (0.50) | (tau = 0.75) | (tau = 0.90) | (tau = 0.99) |
|---|---|---|---|---|---|---|---|
| LogINC | 1.104 *** | 1.009 *** | 0.971 *** | 1.140 *** | 0.711 *** | 0.618 *** | 0.122 |
| LogINCK | 0.393 ** | 0.356 *** | 0.333 *** | 0.239 *** | 0.682 *** | 0.647 *** | 0.564 *** |
| Language | 0.214 ** | 0.300 *** | 0.319 *** | 0.354 *** | 0.520 *** | 0.468 *** | 0.397 *** |
| LogDIST | −1.316 *** | −1.329 *** | −1.316 *** | −1.268 *** | −0.877 *** | −0.779 *** | −0.809 *** |
| LogRISK | −0.477 * | −0.273 | −0.350 | −0.206 | −0.592 * | −0.534 * | −0.382 * |
| C | 0.825 | 1.531 ** | 1.795 ** | 1.505 * | 0.305 | 0.621 | 3.347 *** |
| Pseudo R2 | 0.636 | 0.604 | 0.596 | 0.500 | 0.498 | 0.530 | 0.548 |
| Obs | 352 | 352 | 352 | 352 | 352 | 352 | 352 |
| Quantile | Coefficient | Std. Error | t-Statistic | p-Value | |
|---|---|---|---|---|---|
| C | 0.10 | 0.825 | 0.613 | 1.346 | (0.179) |
| 0.20 | 1.531 ** | 0.725 | 2.113 | (0.035) | |
| 0.30 | 1.647 ** | 0.737 | 2.235 | (0.026) | |
| 0.40 | 1.362 * | 0.787 | 1.730 | (0.085) | |
| 0.50 | 1.505 * | 0.800 | 1.881 | (0.061) | |
| 0.60 | 0.980 | 0.810 | 1.209 | (0.228) | |
| 0.70 | 0.271 | 0.562 | 0.483 | (0.629) | |
| 0.80 | 0.137 | 0.506 | 0.270 | (0.786) | |
| 0.90 | 0.622 | 0.501 | 1.241 | (0.215) | |
| LogINC | 0.10 | 1.104 *** | 0.211 | 5.233 | (0.000) |
| 0.20 | 1.009 *** | 0.218 | 4.6298 | (0.000) | |
| 0.30 | 1.040 *** | 0.181 | 5.729 | (0.000) | |
| 0.40 | 1.112 *** | 0.173 | 6.448 | (0.000) | |
| 0.50 | 1.140 *** | 0.176 | 6.492 | (0.000) | |
| 0.60 | 0.818 *** | 0.211 | 3.879 | (0.000) | |
| 0.70 | 0.753 *** | 0.1619 | 4.650 | (0.000) | |
| 0.80 | 0.734 *** | 0.154 | 4.753 | (0.000) | |
| 0.90 | 0.618 *** | 0.154 | 4.012 | (0.000) | |
| LogINCk | 0.10 | 0.393 *** | 0.071 | 5.571 | (0.000) |
| 0.20 | 0.356 *** | 0.085 | 4.170 | (0.000) | |
| 0.30 | 0.292 *** | 0.073 | 4.007 | (0.000) | |
| 0.40 | 0.275 *** | 0.059 | 4.623 | (0.000) | |
| 0.50 | 0.240 *** | 0.065 | 3.673 | (0.000) | |
| 0.60 | 0.510 *** | 0.124 | 4.113 | (0.000) | |
| 0.70 | 0.658 *** | 0.072 | 9.123 | (0.000) | |
| 0.80 | 0.663 *** | 0.090 | 7.384 | (0.000) | |
| 0.90 | 0.647 *** | 0.096 | 6.7510 | (0.000) | |
| Language | 0.10 | 0.214 ** | 0.083 | 2.579 | (0.010) |
| 0.20 | 0.300 *** | 0.099 | 3.013 | (0.003) | |
| 0.30 | 0.326 *** | 0.111 | 2.937 | (0.004) | |
| 0.40 | 0.354 *** | 0.099 | 3.546 | (0.000) | |
| 0.50 | 0.355 *** | 0.099 | 3.562 | (0.000) | |
| 0.60 | 0.402 *** | 0.136 | 2.962 | (0.003) | |
| 0.70 | 0.514 *** | 0.096 | 5.333 | (0.000) | |
| 0.80 | 0.435 *** | 0.112 | 3.888 | (0.000) | |
| 0.90 | 0.468 *** | 0.118 | 3.956 | (0.000) | |
| LogDIST | 0.10 | −1.316 *** | 0.045 | −29.129 | (0.000) |
| 0.20 | −1.330 *** | 0.047 | −28.528 | (0.000) | |
| 0.30 | −1.289 *** | 0.049 | −26.486 | (0.000) | |
| 0.40 | −1.259 *** | 0.052 | −24.033 | (0.000) | |
| 0.50 | −1.268 *** | 0.058 | −21.670 | (0.000) | |
| 0.60 | −1.019 *** | 0.1053 | −9.6738 | (0.000) | |
| 0.70 | −0.893 *** | 0.055 | −16.124 | (0.000) | |
| 0.80 | −0.826 *** | 0.047 | −17.672 | (0.000) | |
| 0.90 | −0.779 *** | 0.041 | −18.908 | (0.000) | |
| LogRISK | 0.10 | −0.477 * | 0.276 | −1.727 | (0.085) |
| 0.20 | −0.273 | 0.312 | −0.876 | (0.382) | |
| 0.30 | −0.218 | 0.318 | −0.685 | (0.494) | |
| 0.40 | −0.274 | 0.326 | −0.841 | (0.401) | |
| 0.50 | −0.206 | 0.343 | −0.601 | (0.548) | |
| 0.60 | −0.528 | 0.4108 | −1.287 | (0.199) | |
| 0.70 | −0.555 * | 0.335 | −1.655 | (0.098) | |
| 0.80 | −0.727 ** | 0.341 | −2.132 | (0.033) | |
| 0.90 | −0.534 * | 0.306 | −1.745 | (0.082) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leitão, N.C. The Impact of Geopolitical Risk on Portuguese Exports. Economies 2023, 11, 291. https://doi.org/10.3390/economies11120291
Leitão NC. The Impact of Geopolitical Risk on Portuguese Exports. Economies. 2023; 11(12):291. https://doi.org/10.3390/economies11120291
Chicago/Turabian StyleLeitão, Nuno Carlos. 2023. "The Impact of Geopolitical Risk on Portuguese Exports" Economies 11, no. 12: 291. https://doi.org/10.3390/economies11120291
APA StyleLeitão, N. C. (2023). The Impact of Geopolitical Risk on Portuguese Exports. Economies, 11(12), 291. https://doi.org/10.3390/economies11120291






