Economic Downturns, Urban Growth and Suburban Fertility in a Mediterranean Context
Abstract
:1. Introduction
2. Methodology
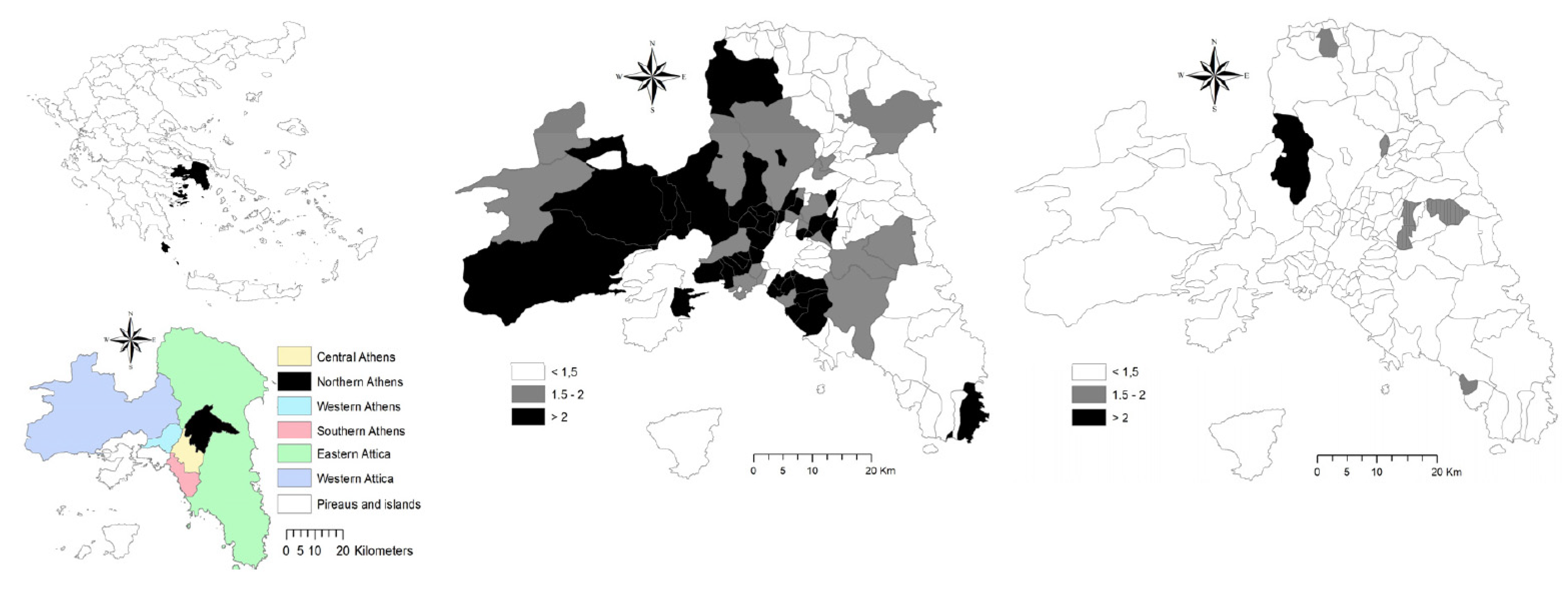
2.1. Study Area
2.2. Data and Variables
2.3. Data Analysis
2.3.1. Descriptive Statistics
2.3.2. Principal Component Analysis (PCA)
2.3.3. Global Econometric Models
2.3.4. Non-Metric Multidimensional Scaling (n-MDS)
2.3.5. Local Regressions
3. Results
3.1. Fertility Rates in Athens: A Descriptive Analysis
3.2. Exploratory Analysis of Fertility Rates (1956–2020)
3.3. Global Models Specifying Fertility Rates as a Function of the Distance from Downtown
3.4. Non-Metric Multidimensional Scaling Tracing the Evolution of Fertility Regimes
3.5. Local Regressions Estimating the Relationship between Fertility and the Metropolitan Gradient
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Adserà, Alicia. 2004. Changing fertility rates in developed countries. The impact of labor market institutions. Journal of Population Economics 17: 17–43. [Google Scholar] [CrossRef]
- Adserà, Alicia. 2006. An economic analysis of the gap between desired and actual fertility: The case of Spain. Review of Economics of the Household 4: 75–95. [Google Scholar] [CrossRef]
- Ali, Kamar, Mark D. Partridge, and M. Rose Olfert. 2007. Can geographically weighted regressions improve regional analysis and policy making? International Regional Science Review 30: 300–29. [Google Scholar] [CrossRef]
- Angel, Shlomo, Jason Parent, Daniel L. Civco, Alexander Blei, and David Potere. 2011. The dimensions of global urban expansion: Estimates and projections for all countries, 2000–2050. Progress in Planning 75: 53–107. [Google Scholar] [CrossRef]
- Arapoglou, Vasilis P., and John Sayas. 2009. New facets of urban segregation in southern Europe—gender, migration and social class change in Athens. European Urban and Regional Studies 16: 345–62. [Google Scholar] [CrossRef]
- Arpino, Bruno, and Lara Patrício Tavares. 2013. Fertility and values in Italy and Spain: A look at regional differences within the European context. Population Review 52: 62–86. [Google Scholar]
- Azarnert, Leonid V. 2010. Immigration, fertility, and human capital: A model of economic decline of the West. European Journal of Political Economy 26: 431–40. [Google Scholar] [CrossRef] [Green Version]
- Azarnert, Leonid V. 2014. Integrated public education, fertility and human capital. Education Economics 22: 166–80. [Google Scholar] [CrossRef] [Green Version]
- Azarnert, Leonid V. 2019. Migration, congestion and growth. Macroeconomic Dynamics 23: 3035–64. [Google Scholar] [CrossRef] [Green Version]
- Bagavos, Christos, Georgia Verropoulou, and Cleon Tsimbos. 2018. Assessing the contribution of foreign women to period fertility in Greece, 2004–2012. Population 73: 115–30. [Google Scholar]
- Balbo, Nicoletta, Francesco C. Billari, and Melinda Mills. 2013. Fertility in advanced societies: A review of research. European Journal of Population 29: 1–38. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bayona-Carrasco, Jordi, and Fernando Gil-Alonso. 2012. Suburbanisation and international immigration: The case of the Barcelona Metropolitan Region (1998–2009). Tijdschrift voor Economische en Sociale Geographie 103: 312–29. [Google Scholar] [CrossRef]
- Benassi, Federico, and Luca Salvati. 2019. Economic downturns and compositional effects in regional population structures by age: A multi-temporal analysis in Greek regions, 1981–2017. Quality & Quantity 53: 2611–33. [Google Scholar]
- Benassi, Federico, and Luca Salvati. 2020. Urban cycles and long-term population trends in a Southern European city: A demographic outlook. Applied Spatial Analysis and Policy 13: 777–803. [Google Scholar] [CrossRef]
- Benassi, Federico, Ricardo Iglesias-Pascual, and Luca Salvati. 2020. Residential segregation and social diversification: Exploring spatial settlement patterns of foreign population in Southern European cities. Habitat International 101: 102200. [Google Scholar] [CrossRef]
- Bernardi, Fabrizio. 2005. Public policies and low fertility: Rationales for public intervention and a diagnosis for the Spanish case. Journal of European Social Policy 15: 123–38. [Google Scholar] [CrossRef]
- Billari, Francesco C., Hans Peter Kohler, Gunnar Andersson, and Hans Lundström. 2007. Approaching the limit: Long-term trends in late and very late fertility. Population and Development Review 33: 149–70. [Google Scholar] [CrossRef]
- Billari, Francesco, and Hans Peter Kohler. 2004. Patterns of low and lowest-low fertility in Europe. Population Studies 58: 161–76. [Google Scholar] [CrossRef]
- Bocquier, Philippe, and Rafael Costa. 2015. Which transition comes first? Urban and demographic transitions in Belgium and Sweden. Demographic Research 33: 1297–332. [Google Scholar] [CrossRef] [Green Version]
- Bocquier, Philippe, and Sandra Bree. 2018. A regional perspective on the economic determinants of urban transition in 19th-century France. Demographic Research 38: 1535–76. [Google Scholar] [CrossRef] [Green Version]
- Bongaarts, John, and Susan Cotts Watkins. 1996. Social Interactions and Contemporary Fertility Transitions. Population and Development Review 22: 639–82. [Google Scholar] [CrossRef]
- Bongaarts, John. 2009. Human population growth and the demographic transition. Philosophical Transactions of the Royal Society B: Biological Sciences 364: 2985–90. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Borg, Ingwer, and Patrick J. Groenen. 2005. Modern Multidimensional Scaling: Theory and Applications. Berlin: Springer Science & Business Media. [Google Scholar]
- Boyle, Paul. 2003. Population geography: Does geography matter in fertility research? Progress in Human Geography 27: 615–26. [Google Scholar] [CrossRef]
- Buckley, Cynthia. 1998. Rural/urban differentials in demographic processes: The Central Asian states. Population Research and Policy Review 17: 71–89. [Google Scholar] [CrossRef]
- Burillo, Pilar, Luca Salvati, Stephen A. Matthews, and Federico Benassi. 2020. Local-Scale Fertility Variations in a Low-Fertility Country: Evidence from Spain (2002–2017). Canadian Studies in Population 47: 279–95. [Google Scholar] [CrossRef]
- Butler, Declan. 2004. The fertility riddle. Nature 432: 38–39. [Google Scholar] [CrossRef]
- Buzar, Stefan, Philip E. Ogden, and Ray Hall. 2005. Households matter: The quiet demography of urban transformation. Progress in Human Geography 29: 413–36. [Google Scholar] [CrossRef]
- Cabré, Anna. 2003. Facts and Factors on Low Fertility in Southern Europe. The Case of Spain. Journal of Population and Social Security (Population) 2003: 309–21. [Google Scholar]
- Caldwell, John C. 2006. Demographic Transition Theory. Berlin: Springer. [Google Scholar]
- Caldwell, John C., and Thomas Schindlmayr. 2003. Explanations of the fertility crisis in modern societies: A search for commonalities. Population Studies 57: 241–63. [Google Scholar] [CrossRef]
- Caltabiano, Marcantonio, Maria Castiglioni, and Alessandro Rosina. 2009. Lowest-low fertility: Signs of a recovery in Italy? Demographic Research 21: 681–718. [Google Scholar] [CrossRef] [Green Version]
- Caltabiano, Marcantonio. 2008. Has the fertility decline come to an end in the different regions of Italy? New insights from a cohort approach. Population 63: 157–72. [Google Scholar] [CrossRef]
- Campisi, Nicholas, Hill Kulu, Julia Mikolai, Sebastian Klüsener, and Mikko Myrskylä. 2020. Spatial variation in fertility across Europe: Patterns and determinants. Population, Space and Place 26: e2308. [Google Scholar] [CrossRef]
- Canning, David. 2011. The causes and consequences of demographic transition. Population Studies 65: 353–61. [Google Scholar] [CrossRef] [PubMed]
- Carbonaro, Gianni, Eugenio Leanza, Philip McCann, and Francesca Medda. 2018. Demographic decline, population aging, and modern financial approaches to urban policy. International Regional Science Review 41: 210–32. [Google Scholar] [CrossRef]
- Carlucci, Margherita, Efstathios Grigoriadis, Kostas Rontos, and Luca Salvati. 2017. Revisiting a hegemonic concept: Long-term ‘Mediterranean urbanization’in between city re-polarization and metropolitan decline. Applied Spatial Analysis and Policy 10: 347–62. [Google Scholar] [CrossRef]
- Carlucci, Margherita, Francesco M. Chelli, and Luca Salvati. 2018. Toward a new cycle: Short-term population dynamics, gentrification, and re-urbanization of Milan (Italy). Sustainability 10: 3014. [Google Scholar]
- Cecchini, Massimo, Ilaria Zambon, Antonella Pontrandolfi, Rosario Turco, Andrea Colantoni, Anastasios Mavrakis, and Luca Salvati. 2019. Urban sprawl and the ‘olive’ landscape: Sustainable land management for ‘crisis’ cities. GeoJournal 84: 237–55. [Google Scholar] [CrossRef]
- Cherlin, Andrew, Erin Cumberworth, S. Philip Morgan, and Christopher Wimer. 2013. The effects of the Great Recession on family structure and fertility. The Annals of the American Academy of Political and Social Science 650: 214–23. [Google Scholar] [CrossRef]
- Chi, Guangqing, and Jun Zhu. 2008. Spatial regression models for demographic analysis. Population Research and Policy Review 27: 17–42. [Google Scholar] [CrossRef]
- Chorianopoulos, Ioannis, Georgios Tsilimigkas, Sotirios Koukoulas, and Thomas Balatsos. 2014. The shift to competitiveness and a new phase of sprawl in the Mediterranean city: Enterprises guiding growth in Messoghia–Athens. Cities 39: 133–43. [Google Scholar] [CrossRef]
- Ciommi, Mariateresa, Francesco M. Chelli, and Luca Salvati. 2019. Integrating parametric and non-parametric multivariate analysis of urban growth and commuting patterns in a European metropolitan area. Quality and Quantity 53: 957–79. [Google Scholar] [CrossRef]
- Ciommi, Mariateresa, Francesco M. Chelli, Margherita Carlucci, and Luca Salvati. 2018. Urban growth and demographic dynamics in southern Europe: Toward a new statistical approach to regional science. Sustainability 10: 2765. [Google Scholar] [CrossRef] [Green Version]
- Coppola, Lucia, and Mariachiara Di Cesare. 2008. How fertility and union stability interact in shaping new family patterns in Italy and Spain. Demographic Research 18: 117–44. [Google Scholar] [CrossRef] [Green Version]
- De Beer, Joop, and Ingeborg Deerenberg. 2007. An explanatory model for projecting regional fertility differences in the Netherlands. Population Research and Policy Review 26: 511–28. [Google Scholar] [CrossRef] [Green Version]
- De Castro, Marcia Caldas. 2007. Spatial demography: An opportunity to improve policy making at diverse decision levels. Population Research and Policy Review 26: 477–509. [Google Scholar] [CrossRef]
- Di Feliciantonio, Cesare, and Luca Salvati. 2015. ‘Southern’ Alternatives of Urban Diffusion: Investigating Settlement Characteristics and Socio-Economic Patterns in Three Mediterranean Regions. Tijdschrift voor Economische en Sociale Geografie 106: 453–70. [Google Scholar] [CrossRef]
- Di Feliciantonio, Cesare, Luca Salvati, Efthymia Sarantakou, and Kostas Rontos. 2018. Class diversification, economic growth and urban sprawl: Evidences from a pre-crisis European city. Quality & Quantity 52: 1501–22. [Google Scholar]
- Dijkstra, Lewis, Enrique Garcilazo, and Philip McCann. 2015. The effects of the global financial crisis on European regions and cities. Journal of Economic Geography 15: 935–49. [Google Scholar] [CrossRef]
- Doignon, Yoann, Elena Ambrosetti, and Sara Miccoli. 2021. The spatial diffusion of fertility decline in Egypt (1950–2006). Genus 77: 1–30. [Google Scholar] [CrossRef]
- Duvernoy, Isabelle, Ilaria Zambon, Adele Sateriano, and Luca Salvati. 2018. Pictures from the other side of the fringe: Urban growth and peri-urban agriculture in a post-industrial city (Toulouse, France). Journal of Rural Studies 57: 25–35. [Google Scholar] [CrossRef]
- Dyson, Tim. 2011. The role of the demographic transition in the process of urbanization. Population and Development Review 37: 34–54. [Google Scholar] [CrossRef]
- Egidi, Gianluca, and Luca Salvati. 2021. Changes over time in the spatial structure of fertility rates as a dynamic indicator of urban transformations. Quality & Quantity 55: 151–72. [Google Scholar]
- Evans, Ann, and Edith Gray. 2018. Modelling Variation in Fertility Rates Using Geographically Weighted Regression. Spatial Demography 6: 121–40. [Google Scholar] [CrossRef] [Green Version]
- Feng, Wang. 2011. The future of a demographic overachiever: Long-term implications of the demographic transition in China. Population and Development Review 37: 173–90. [Google Scholar] [CrossRef] [PubMed]
- Fernandez, Raquel, and Alessandra Fogli. 2009. Culture: An empirical investigation of beliefs, work, and fertility. American Economic Journal: Macroeconomics 1: 146–77. [Google Scholar] [CrossRef] [Green Version]
- Ferrara, Agostino, Claire Kelly, Geoff A. Wilson, Angelo Nolè, Giuseppe Mancino, Sofia Bajocco, and Luca Salvati. 2016. Shaping the role of ‘fast’ and ‘slow’ drivers of change in forest-shrubland socio-ecological systems. Journal of Environmental Management 169: 155–66. [Google Scholar] [CrossRef] [Green Version]
- Fotheringham, Alexander S., Chris Brunsdon, and Martin Charlton. 2003. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships. London: Wiley. [Google Scholar]
- Frejka, Tomas, and Tomáš Sobotka. 2008. Fertility in Europe: Diverse, delayed and below replacement. Demographic Research 19: 15–46. [Google Scholar] [CrossRef]
- Galor, Oded. 2005. The demographic transition and the emergence of sustained economic growth. Journal of the European Economic Association 3: 494–504. [Google Scholar] [CrossRef]
- Garcia, Marisol. 2010. The breakdown of the Spanish urban growth model: Social and territorial effects of the global crisis. International Journal of Urban and Regional Research 34: 967–80. [Google Scholar] [CrossRef] [Green Version]
- Gavalas, Vasilis S., Kostas Rontos, and Luca Salvati. 2014. Who becomes an unwed mother in Greece? Socio-demographic and geographical aspects of an emerging phenomenon. Population, Space, and Place 20: 250–63. [Google Scholar] [CrossRef]
- Georgiadis, Katerina. 2011. Fertile debates: A comparative account of low fertility in the British and Greek national press. European Journal of Population 27: 243–62. [Google Scholar] [CrossRef] [Green Version]
- Gil-Alonso, Fernando, Jordi Bayona-i-Carrasco, and Isabel Pujadas-i-Rúbies. 2016. From boom to crash: Spanish urban areas in a decade of change (2001–2011). European Urban and Regional Studies 23: 198–216. [Google Scholar] [CrossRef]
- Gkartzios, Menelaos, and Karen Scott. 2015. A cultural panic in the province? Counterurban mobilities, creativity, and crisis in Greece. Population, Space and Place 21: 843–55. [Google Scholar] [CrossRef] [Green Version]
- Gkartzios, Menelaos. 2013. ‘Leaving Athens’: Narratives of counterurbanisation in times of crisis. Journal of Rural Studies 32: 158–67. [Google Scholar] [CrossRef]
- Goldstein, Joshua R., and Sebastian Klüsener. 2014. Spatial analysis of the causes of the fertility decline in Prussia. Population and Development Review 40: 497–525. [Google Scholar] [CrossRef]
- Goldstein, Joshua R., Tomáš Sobotka, and Aliva Jasilioniene. 2009. The end of lowest-low fertility? Population and Development Review 35: 663–700. [Google Scholar] [CrossRef]
- Goldstein, Joshua, Michaela Kreyenfeld, Aliva Jasilioniene, and Deniz Karaman Örsal. 2013. Fertility reactions to the “Great Recession” in Europe: Recent evidence from order-specific data. Demographic Research 29: 85–104. [Google Scholar] [CrossRef]
- Guilmoto, Christophe Z., and S. Irudaya Rajan. 2001. Spatial patterns of fertility transition in Indian districts. Population and Development Review 27: 713–38. [Google Scholar] [CrossRef]
- Haase, Annegret, Sigrun Kabisch, Annett Steinführer, Stefan Bouzarovski, Ray Hall, and Philip Ogden. 2010. Spaces of reurbanisation: Exploring the demographic dimension of inner-city residential change in a European setting. Population, Space and Place 16: 443–63. [Google Scholar] [CrossRef]
- Halbac-Cotoara-Zamfir, Rares, Gianluca Egidi, Rosanna Salvia, Luca Salvati, Adele Sateriano, and Antonio Gimenez-Morera. 2021. Recession, Local Fertility, and Urban Sustainability: Results of a Quasi-Experiment in Greece, 1991–2018. Sustainability 13: 1052. [Google Scholar] [CrossRef]
- Hank, Karsten. 2002. Regional social contexts and individual fertility decisions: A multilevel analysis of first and second births in western Germany. European Journal of Population 18: 281–99. [Google Scholar] [CrossRef]
- Hondroyiannis, George, and Evangelia Papapetrou. 2002. Demographic transition and economic growth: Empirical evidence from Greece. Journal of Population Economics 15: 221–42. [Google Scholar] [CrossRef]
- Işik, Oğuz, and M. Melih Pinarcioglu. 2006. Geographies of a silent transition: A geographically weighted regression approach to regional fertility differences in Turkey. European Journal of Population 22: 399–421. [Google Scholar] [CrossRef]
- Kabisch, Nadja, and Dagmar Haase. 2011. Diversifying European agglomerations: Evidence of urban population trends for the 21st century. Population, Space and Place 17: 236–53. [Google Scholar] [CrossRef]
- Kaika, Maria. 2012. The economic crisis seen from the everyday: Europe’s nouveau poor and the global affective implications of a ‘local’ debt crisis. City 16: 422–30. [Google Scholar] [CrossRef]
- Kalwij, Adriaan. 2010. The impact of family policy expenditure on fertility in Western Europe. Demography 47: 503–19. [Google Scholar] [CrossRef]
- Kohler, Hans Peter, Francesco C. Billari, and José Antonio Ortega. 2002. The emergence of lowest-low fertility in Europe during the 1990s. Population and Development Review 28: 641–80. [Google Scholar] [CrossRef]
- Kreyenfeld, Michaela, Gunnar Andersson, and Ariane Pailhé. 2012. Economic uncertainty and family dynamics in Europe: Introduction. Demographic Research 27: 835–52. [Google Scholar] [CrossRef] [Green Version]
- Kreyenfeld, Michaela. 2010. Uncertainties in female employment careers and the postponement of parenthood in Germany. European Sociological Review 26: 351–66. [Google Scholar] [CrossRef] [Green Version]
- Kroll, Franziska, and Nadja Kabisch. 2012. The relation of diverging urban growth processes and demographic change along an urban-rural gradient. Population, Space and Place 18: 260–76. [Google Scholar] [CrossRef]
- Kulu, Hill, and Andres Vikat. 2007. Fertility differences by housing type: The effect of housing conditions or of selective moves? Demographic Research 17: 775–802. [Google Scholar] [CrossRef] [Green Version]
- Kulu, Hill, and Paul J. Boyle. 2009. High fertility in city suburbs: Compositional or contextual effects? European Journal of Population 25: 157–74. [Google Scholar] [CrossRef] [Green Version]
- Kulu, Hill, Paul J. Boyle, and Gunnar Anderson. 2009. High suburban fertility: Evidence from four Northern European countries. Demographic Research 31: 915–44. [Google Scholar] [CrossRef] [Green Version]
- Kulu, Hill. 2013. Why do fertility levels vary between urban and rural areas? Regional Studies 47: 895–912. [Google Scholar] [CrossRef]
- Lamonica, Giuseppe Ricciardo, Gloria Polinesi, and Luca Salvati. 2022. Sprawl or Segregation? Local Fertility as a Proxy of Socio-spatial Disparities Under Sequential Economic Downturns. Social Indicators Research. [Google Scholar] [CrossRef]
- Lankford, Hamilton, and James Wyckoff. 2006. The effect of school choice and residential location on the racial segregation of students. In Advances in Applied Microeconomics. Edited by Timothy Gronberg and Dennis Jensen. Amsterdam: Emerald, vol. 14, pp. 185–239. [Google Scholar]
- Lauf, Steffen, Dagmar Haase, Ralf Seppelt, and Nina Schwarz. 2012. Simulating demography and housing demand in an urban region under scenarios of growth and shrinkage. Environment and Planning B: Planning and Design 39: 229–46. [Google Scholar] [CrossRef]
- Lee, Kwan Ok, and Gary Painter. 2013. What happens to household formation in a recession? Journal of Urban Economics 76: 93–109. [Google Scholar] [CrossRef] [Green Version]
- Lee, Ronald. 2003. The demographic transition: Three centuries of fundamental change. Journal of Economic Perspectives 17: 167–90. [Google Scholar] [CrossRef] [Green Version]
- Lerch, Mathias. 2013. Fertility decline during Albania’s societal crisis and its subsequent consolidation. European Journal of Population 29: 195–220. [Google Scholar] [CrossRef]
- Lerch, Mathias. 2014. The role of migration in the urban transition: A demonstration from Albania. Demography 51: 1527–50. [Google Scholar] [CrossRef] [Green Version]
- Lerch, Mathias. 2016. Internal and international migration across the urban hierarchy in Albania. Population Research and Policy Review 35: 851–76. [Google Scholar] [CrossRef] [Green Version]
- Lerch, Mathias. 2019. Regional variations in the rural-urban fertility gradients in global South. PLoS ONE 14: e0219624. [Google Scholar] [CrossRef] [Green Version]
- Lesthaeghe, Ron J., and Lisa Neidert. 2006. The second demographic transition in the United States: Exception or textbook example? Population and Development Review 32: 669–98. [Google Scholar] [CrossRef]
- Lesthaeghe, Ron, and Antonio Lopez-Gay. 2013. Spatial continuities and discontinuities in two successive demographic transitions: Spain and Belgium, 1880–2010. Demographic Research 28: 77–136. [Google Scholar] [CrossRef] [Green Version]
- Liu, Lee. 2005. Fertility trends in China’s more developed urban districts: The case of four cities. Population, Space and Place 11: 411–24. [Google Scholar] [CrossRef]
- López-Gay, Antonio, Andrea Andújar-Llosa, and Luca Salvati. 2020. Residential Mobility, Gentrification and Neighborhood Change in Spanish Cities: A Post-Crisis Perspective. Spatial Demography 8: 351–78. [Google Scholar] [CrossRef]
- Machado, J. Tenreiro, Gonçalo Monteiro Duarte, and Fernando B. Duarte. 2011. Identifying economic periods and crisis with the multidimensional scaling. Nonlinear Dynamics 63: 611–22. [Google Scholar] [CrossRef]
- Maloutas, Thomas, and Isabel Ramos Lobato. 2015. Education and social reproduction: Educational mechanisms and residential segregation in Athens and Dortmund. Local Economy 30: 800–17. [Google Scholar] [CrossRef]
- Maloutas, Thomas, Stavros Nikiforos Spyrellis, and Antoinetta Capella. 2019. Residential segregation and educational performance. The case of Athens. Urban Studies 56: 3143–61. [Google Scholar] [CrossRef]
- Maloutas, Thomas. 2007. Middle class education strategies and residential segregation in Athens. Journal of Education Policy 22: 49–68. [Google Scholar] [CrossRef]
- Michielin, Francesca. 2004. Lowest low fertility in an urban context: The role of migration in Turin, Italy. Population, Space and Place 10: 331–47. [Google Scholar] [CrossRef]
- Morelli, Vittorio Gargiulo, Kostas Rontos, and Luca Salvati. 2014. Between suburbanisation and re-urbanisation: Revisiting the urban life cycle in a Mediterranean compact city. Urban Research & Practice 7: 74–88. [Google Scholar]
- Morgan, S. Philip. 2003. Is low fertility a twenty-first-century demographic crisis? Demography 40: 589–603. [Google Scholar] [CrossRef] [PubMed]
- Muniz, Jeronimo O. 2009. Spatial dependence and heterogeneity in ten years of fertility decline in Brazil. Population Review 48: 32–65. [Google Scholar]
- Ogden, Philip E., and Ray Hall. 2000. Households, reurbanisation and the rise of living alone in the principal French cities 1975–90. Urban Studies 37: 367–90. [Google Scholar] [CrossRef]
- Oinonen, Eriikka. 2004. Starting the first family. Changes in patterns of family formation and demographic trends in Finland and Spain. European Societies 6: 319–46. [Google Scholar] [CrossRef]
- Oueslati, Walid, Seraphim Alvanides, and Guy Garrod. 2015. Determinants of urban sprawl in European cities. Urban Studies 52: 1594–614. [Google Scholar] [CrossRef] [Green Version]
- Panori, Anastasia, Yannis Psycharis, and Dimitris Ballas. 2019. Spatial segregation and migration in the city of Athens: Investigating the evolution of urban socio-spatial immigrant structures. Population Space and Place 25: e2209. [Google Scholar]
- Pérez, Jesús M. González. 2010. The real estate and economic crisis: An opportunity for urban return and rehabilitation policies in Spain. Sustainability 2: 1571–601. [Google Scholar] [CrossRef] [Green Version]
- Pili, Silvia, Efstathios Grigoriadis, Margherita Carlucci, Matteo Clemente, and Luca Salvati. 2017. Towards sustainable growth? A multi-criteria assessment of (changing) urban forms. Ecological Indicators 76: 71–80. [Google Scholar] [CrossRef]
- Pison, Gilles. 2011. Two children per woman in France in 2010: Is French fertility immune to economic crisis? Population & Societies 476: 1. [Google Scholar]
- Potter, Joseph E., Carl P. Schmertmann, Renato M. Assunção, and Suzana M. Cavenaghi. 2010. Mapping the timing, pace, and scale of the fertility transition in Brazil. Population and Development Review 36: 283–307. [Google Scholar] [CrossRef] [Green Version]
- Rees, Philip, Martin Bell, Marek Kupiszewski, Dorota Kupiszewska, Philipp Ueffing, Aude Bernard, Elin Charles Edwards, and John Stillwell. 2017. The impact of internal migration on population redistribution: An international comparison. Population, Space and Place 23: e2036. [Google Scholar] [CrossRef]
- Reher, David S. 2004. The demographic transition revisited as a global process. Population, Space and Place 10: 19–41. [Google Scholar] [CrossRef]
- Reher, David S. 2011. Economic and social implications of the demographic transition. Population and Development Review 37: 11–33. [Google Scholar] [CrossRef]
- Remoundou, Kyriaki, Menelaos Gkartzios, and Guy Garrod. 2016. Conceptualizing mobility in times of crisis: Towards crisis-led counterurbanization? Regional Studies 50: 1663–74. [Google Scholar] [CrossRef] [Green Version]
- Rodrigo-Comino, Jesús, Gianluca Egidi, Adele Sateriano, Stefano Poponi, Enrico Maria Mosconi, and Antonio Gimenez Morera. 2021. Suburban fertility and metropolitan cycles: Insights from European cities. Sustainability 13: 2181. [Google Scholar] [CrossRef]
- Rodriguez-Rodriguez, Vincente. 2000. The seven demographic Spains. Inter-municipal contrasts in age structure: Fertility and migration are the determining factors. Espace, Populations, Sociétés 18: 425–35. [Google Scholar]
- Rontos, Kostas, and Luca Salvati. 2020. Space Matters? Exploring Gender Differentials in the Age at Marriage, Greece (1980–2017). Social Sciences 9: 59. [Google Scholar] [CrossRef] [Green Version]
- Rontos, Kostas, Efstathios Grigoriadis, Adele Sateriano, Maria Syrmali, Ioannis Vavouras, and Luca Salvati. 2016. Lost in Protest, Found in Segregation: Divided Cities in the Light of the 2015 ‘Oki’ Referendum in Greece. City, Culture and Society 7: 139–48. [Google Scholar] [CrossRef]
- Sabater, Albert, and Elspeth Graham. 2019. International migration and fertility variation in Spain during the economic recession: A spatial Durbin approach. Applied Spatial Analysis and Policy 12: 515–46. [Google Scholar] [CrossRef] [Green Version]
- Salvati, Luca. 2019. Bridging the divide: Demographic dynamics and urban–rural polarities during economic expansion and recession in Greece. Population, Space and Place 25: e2267. [Google Scholar]
- Salvati, Luca, Agostino Ferrara, and Francesco M. Chelli. 2018. Long-term growth and metropolitan spatial structures: An analysis of factors influencing urban patch size under different economic cycles. Geografisk Tidsskrift-Danish Journal of Geography 118: 56–71. [Google Scholar] [CrossRef]
- Salvati, Luca, and Federico Benassi. 2021. Salvati, Luca, and Federico Benassi. 2021. Rise (and decline) of European migrants in Greece: Exploring spatial determinants of residential mobility (1988–2017), with special focus on older ages. Journal of International Migration and Integration 22: 599–613. [Google Scholar] [CrossRef]
- Salvati, Luca, and Ilaria Zambon. 2018. Does residential mobility anticipate urban growth? The importance of the local socioeconomic context in a European Metropolitan Region. Population Review 57: 23–46. [Google Scholar] [CrossRef]
- Salvati, Luca, and Margherita Carlucci. 2020. Shaping dimensions of urban complexity: The role of economic structure and socio-demographic local contexts. Social Indicators Research 147: 263–85. [Google Scholar] [CrossRef]
- Salvati, Luca, and Pere Serra. 2016. Estimating rapidity of change in complex urban systems: A multidimensional, local-scale approach. Geographical Analysis 48: 132–56. [Google Scholar] [CrossRef]
- Salvati, Luca, Federico Benassi, Sara Miccoli, Hamidreza Rabiei-Dastjerdi, and Stephen A. Matthews. 2020. Spatial variability of total fertility rate and crude birth rate in a low-fertility country: Patterns and trends in regional and local scale heterogeneity across Italy, 2002–2018. Applied Geography 124: 102321. [Google Scholar] [CrossRef]
- Salvati, Luca, Marco Zitti, and Adele Sateriano. 2013. Changes in city vertical profile as an indicator of sprawl: Evidence from a Mediterranean urban region. Habitat International 38: 119–25. [Google Scholar] [CrossRef]
- Salvati, Luca. 2016. The dark side of the crisis: Disparities in per-capita income (2000–2012) and the urban-rural gradient in Greece. Tijdschrift voor Economische en Sociale Geografie 107: 628–41. [Google Scholar] [CrossRef]
- Sato, Yasuhiro, and Kazuhiro Yamamoto. 2005. Population concentration, urbanization, and demographic transition. Journal of Urban Economics 58: 45–61. [Google Scholar] [CrossRef]
- Schneider, Daniel. 2015. The Great Recession, fertility, and uncertainty: Evidence from the United States. Journal of Marriage and Family 77: 1144–56. [Google Scholar] [CrossRef]
- Serra, Pere, Ana Vera, Antoni Francesc Tulla, and Luca Salvati. 2014. Beyond urban–rural dichotomy: Exploring socioeconomic and land-use processes of change in Spain (1991–2011). Applied Geography 55: 71–81. [Google Scholar] [CrossRef]
- Sobotka, Tomáš, Vegard Skirbekk, and Dimiter Philipov. 2011. Economic recession and fertility in the developed world. Population and Development Review 37: 267–306. [Google Scholar] [CrossRef] [PubMed]
- Sobotka, Tomáš. 2004. Postponement of childbearing and low fertility in Europe. Amsterdam: Dutch University Press. [Google Scholar]
- Stockdale, Aileen. 2016. Contemporary and ‘messy’ rural in-migration processes: Comparing counterurban and lateral rural migration. Population, Space and Place 22: 599–616. [Google Scholar] [CrossRef] [Green Version]
- Surkyn, Johan, and Ron Lesthaeghe. 2004. Value orientations and the second demographic transition (SDT) in Northern, Western and Southern Europe: An update. Demographic Research 3: 45–86. [Google Scholar] [CrossRef]
- Tenreiro Machado, J., Fernando B. Duarte, and Gonçalo Monteiro Duarte. 2011. Analysis of financial data series using fractional Fourier transform and multidimensional scaling. Nonlinear Dynamics 65: 235–45. [Google Scholar] [CrossRef] [Green Version]
- Thygesen, Lau Caspar, Lisbeth B. Knudsen, and Niels Keiding. 2005. Modelling regional variation of first-time births in Denmark 1980–1894 by an age-period-cohort model. Demographic Research 13: 573–90. [Google Scholar] [CrossRef]
- Toulemon, Laurent. 2004. Fertility among immigrant women: New data a new approach. Population and Societies 400: 1–4. [Google Scholar]
- Tragaki, Alexandra, and Christos Bagavos. 2014. Male fertility in Greece: Trends and differentials by educational level and employment status. Demographic Research 31: 137–60. [Google Scholar] [CrossRef] [Green Version]
- Tragaki, Alexandra, and Christos Bagavos. 2019. Fertility variations in the recession context: The case of Greece. Genus 75: 18. [Google Scholar] [CrossRef] [Green Version]
- Van de Kaa, Dirk J. 1987. Europe’s second demographic transition. Population Bulletin 42: 1–59. [Google Scholar]
- Vignoli, Daniele, Sven Drefahl, and Gustavo De Santis. 2012. Whose job instability affects the likelihood of becoming a parent in Italy? A tale of two partners. Demographic Research 26: 41–62. [Google Scholar] [CrossRef] [Green Version]
- Vitali, Agnese, and Francesco C. Billari. 2017. Changing determinants of low fertility and diffusion: A spatial analysis for Italy. Population, Space and Place 23: e1998. [Google Scholar] [CrossRef] [Green Version]
- Voss, Paul R. 2007. Demography as a spatial social science. Population Research and Policy Review 26: 457–76. [Google Scholar] [CrossRef]
- Wachter, Kenneth W. 2005. Spatial demography. Proceedings of the National Academy of Sciences 102: 15299–300. [Google Scholar] [CrossRef] [Green Version]
- Waldorf, Brigitte, and Rachel Franklin. 2002. Spatial dimensions of the Easterlin hypothesis: Fertility variations in Italy. Journal of Regional Science 42: 549–78. [Google Scholar] [CrossRef]
- Walford, Nigel, and Slavomir Kurek. 2016. Outworking of the Second Demographic Transition: National Trends and Regional Patterns of Fertility Change in Poland, and England and Wales, 2002–2012. Population, Space and Place 22: 508–25. [Google Scholar] [CrossRef] [Green Version]
- Wang, Donghui, and Guangqing Chi. 2017. Different Places, Different Stories: A Study of Spatial Heterogeneity of County-Level Fertility in China. Demographic Research 37: 493. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Williamson, Lee, and Paul Norman. 2011. Developing strategies for deriving small population fertility rates. Journal of Population Research 28: 129–48. [Google Scholar] [CrossRef] [Green Version]
- Wilson, Ben. 2019. The intergenerational assimilation of completed fertility: Comparing the convergence of different origin groups. International Migration Review 53: 429–57. [Google Scholar] [CrossRef]
- Zaidi, Batool, and Philip Morgan. 2017. The second demographic transition theory: A Review and Appraisal. Annual Review of Sociology 43: 473–92. [Google Scholar] [CrossRef] [Green Version]
- Zambon, Ilaria, and Luca Salvati. 2019. Metropolitan growth, urban cycles and housing in a Mediterranean country, 1910s–2010s. Cities 95: 102412. [Google Scholar] [CrossRef]
- Zambon, Ilaria, Andrea Colantoni, and Luca Salvati. 2019. Horizontal vs vertical growth: Understanding latent patterns of urban expansion in large metropolitan regions. Science of the Total Environment 654: 778–85. [Google Scholar] [CrossRef] [PubMed]
- Zambon, Ilaria, Anna Benedetti, Carlotta Ferrara, and Luca Salvati. 2018. Soil matters? A multivariate analysis of socioeconomic constraints to urban expansion in Mediterranean Europe. Ecological Economics 146: 173–83. [Google Scholar] [CrossRef]
- Zambon, Ilaria, Kostas Rontos, Cecilia Reynaud, and Luca Salvati. 2020. Toward an unwanted dividend? Fertility decline and the North–South divide in Italy, 1952–2018. Quality & Quantity 54: 169–87. [Google Scholar]





| Regional Unit | 1991–2000 | 2001–2010 | 2011–2020 |
|---|---|---|---|
| Central Athens * | 1.21 | 1.28 | 1.26 |
| Piraeus ** | 1.33 | 1.39 | 1.32 |
| Northern Athens *** | 1.39 | 1.47 | 1.42 |
| Western Athens *** | 1.55 | 1.54 | 1.34 |
| Southern Athens *** | 1.37 | 1.37 | 1.29 |
| Eastern Attica **** | 1.38 | 1.63 | 1.52 |
| Western Attica **** | 1.81 | 1.97 | 1.86 |
| Year | Linear | Quadratic | Gain | ||||||
|---|---|---|---|---|---|---|---|---|---|
| a0 | a1 | Adj-R2 | a0 | a1 | a2 | Adj-R2 | R2 | Max (km) | |
| 1860 | 0.028 | 0.348 * | 0.422 * | 0.740 | −0.321 | 0.136 | 0.466 * | 0.104 | - |
| 1884 | 0.408 * | 0.296 * | 0.401 * | −0.212 | 0.878 | −0.118 | 0.444 * | 0.107 | - |
| 1956 | 1.635 * | −0.480 ** | 0.286 ** | 0.542 | 0.445 | −0.181 | 0.305 ** | 0.066 | - |
| 1960 | 0.984 * | −0.283 * | 0.200 * | 0.186 | 0.393 | −0.132 | 0.220 * | 0.100 | - |
| 1970 | 0.983 * | −0.286 ** | 0.243 * | 0.357 | 0.244 | −0.103 | 0.258 * | 0.062 | - |
| 1980 | 1.072 ** | −0.339 ** | 0.321 ** | 0.887 | −0.183 | −0.030 | 0.322 ** | 0.003 | - |
| 1990 | 0.479 * | −0.233 * | 0.178 * | 0.058 | 0.124 | −0.070 | 0.186 * | 0.045 | - |
| 2000 | 0.525 * | −0.258 * | 0.263 * | −0.520 | 0.626 | −0.173 | 0.318 ** | 0.209 † | 6.6 |
| 2008 | 0.477 | −0.187 | 0.093 | −0.834 | 0.923 | −0.217 | 0.153 * | 0.645 † | 8.7 |
| 2016 | 0.380 | −0.216 | 0.104 | −1.981 | 1.782 | −0.390 | 0.264 * | 1.538 † | 10.4 |
| 2020 | 0.148 | −0.190 | 0.084 | −1.520 | 1.239 | −0.281 | 0.186 * | 1.214 † | 10.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nickayin, S.S.; Chelli, F.; Turco, R.; Nosova, B.; Vavoura, C.; Salvati, L. Economic Downturns, Urban Growth and Suburban Fertility in a Mediterranean Context. Economies 2022, 10, 252. https://doi.org/10.3390/economies10100252
Nickayin SS, Chelli F, Turco R, Nosova B, Vavoura C, Salvati L. Economic Downturns, Urban Growth and Suburban Fertility in a Mediterranean Context. Economies. 2022; 10(10):252. https://doi.org/10.3390/economies10100252
Chicago/Turabian StyleNickayin, Samaneh Sadat, Francesco Chelli, Rosario Turco, Bogdana Nosova, Chara Vavoura, and Luca Salvati. 2022. "Economic Downturns, Urban Growth and Suburban Fertility in a Mediterranean Context" Economies 10, no. 10: 252. https://doi.org/10.3390/economies10100252
APA StyleNickayin, S. S., Chelli, F., Turco, R., Nosova, B., Vavoura, C., & Salvati, L. (2022). Economic Downturns, Urban Growth and Suburban Fertility in a Mediterranean Context. Economies, 10(10), 252. https://doi.org/10.3390/economies10100252









