Monetary Transfers in the U.S.: How Efficient Are Tax Rebates?
Abstract
:1. Introduction
2. Literature Review
3. Theoretical Model
 ) and deposits to earn a return (
) and deposits to earn a return (  ) one period in advance, such that when agents want to alter their money holdings they will face an adjustment cost—the subscript t means the corresponding variable at time t. This implies that bank deposits would not change significantly following a monetary shock, generating a large and persistent liquidity effect. A monetary injection then increases the amount of funds available for lending, and the firm could take advantage of the lower interest rate.
) one period in advance, such that when agents want to alter their money holdings they will face an adjustment cost—the subscript t means the corresponding variable at time t. This implies that bank deposits would not change significantly following a monetary shock, generating a large and persistent liquidity effect. A monetary injection then increases the amount of funds available for lending, and the firm could take advantage of the lower interest rate.3.1. Structure of the Model
3.1.1. The Household



 ) brought forward from period t−1, but we also allow for the government to transfer money that can be used for current consumption:
) brought forward from period t−1, but we also allow for the government to transfer money that can be used for current consumption:


 , the amount of money kept as cash,
, the amount of money kept as cash,  , and the foreign asset position Bt+1. Household income is determined by the real wage wt and the profits (or dividends) received at the end of the period from the firm and the commercial bank,
, and the foreign asset position Bt+1. Household income is determined by the real wage wt and the profits (or dividends) received at the end of the period from the firm and the commercial bank,  and
and  , as well as interest on deposits and on foreign bonds. Foreign bonds yield a risk-free nominal interest rate
, as well as interest on deposits and on foreign bonds. Foreign bonds yield a risk-free nominal interest rate  .
. , subject to the cash-in-advance constraint (Equation (5)) and the budget constraint (Equation (6)). Here
, subject to the cash-in-advance constraint (Equation (5)) and the budget constraint (Equation (6)). Here  refers to the expected value of the term(s) in brackets conditional on information up to time t. Letting λt denote the Lagrangian multiplier associated with the budget constraint, the first order conditions for the household’s choice of consumption, labor, money deposits, money-cash holdings, and foreign assets provide the following relationships:
refers to the expected value of the term(s) in brackets conditional on information up to time t. Letting λt denote the Lagrangian multiplier associated with the budget constraint, the first order conditions for the household’s choice of consumption, labor, money deposits, money-cash holdings, and foreign assets provide the following relationships:




3.1.2. The Firm






3.1.3. The Monetary Authority
3.1.4. The Financial Intermediary


3.2. Closing the Model



 , and the technology shock denoted by:
, and the technology shock denoted by:

 . ρθ and ρz are the respective persistence parameters, while θ and z are the steady states of θ and z, respectively.
. ρθ and ρz are the respective persistence parameters, while θ and z are the steady states of θ and z, respectively.3.3. Calibration and Steady State Equilibrium
| α = 0.36 | ν = −0.0288 | ξ = 3 | σ = 1.05 | H = 0.2 |
| β = −0.988 | θ = 1.0083 | φ = 0.1 | τ = 0.0019 | δ = 0.025 |
| ρθ = 0.29 | σθ = 0.00194 | γ = 1.05 | ρz = 0.95 | σz = 0.00816 |
 ;
;  ;
;  ;
;  ;
;  . Obviously adjustment costs disappear in the steady state, and values do not need time subscripts. We look at a steady state in which the domestic and foreign inflation levels are the same, so purchasing power parity implies that the change in the nominal exchange rate is constant [30]. Consequently, the uncovered interest rate parity condition implies that the domestic interest rate and the interest rate on foreign bonds are equal (i = i*). The calculation of steady state equilibrium is straight forward, and a detailed explanation of its derivation is available in Vacaflores [27] under the section Appendix (B).
. Obviously adjustment costs disappear in the steady state, and values do not need time subscripts. We look at a steady state in which the domestic and foreign inflation levels are the same, so purchasing power parity implies that the change in the nominal exchange rate is constant [30]. Consequently, the uncovered interest rate parity condition implies that the domestic interest rate and the interest rate on foreign bonds are equal (i = i*). The calculation of steady state equilibrium is straight forward, and a detailed explanation of its derivation is available in Vacaflores [27] under the section Appendix (B).| 100% Injections towards Investment | Percent of Output | |
|---|---|---|
| Nominal Interest Rate | 0.0202 | - |
| Interest on Foreign Bonds | 0.0202 | - |
| Investment | 0.1685 | 0.23 |
| Physical Capital | 6.7402 | - |
| Output | 0.7095 | 1.00 |
| Hours Worked | 0.2 | - |
| Real Wages | 2.2705 | - |
| Consumption | 0.5615 | 0.79 |
| Real Money Balances | 0.7300 | - |
| Real Money Cash | 0.5660 | - |
| Real Money Deposits | 0.1640 | - |
| Inflation | 1.0080 | - |
| Foreign Bonds | 1.6825 | - |
| Trade Balance | −0.0204 | −0.028 |
4. Dynamic Response
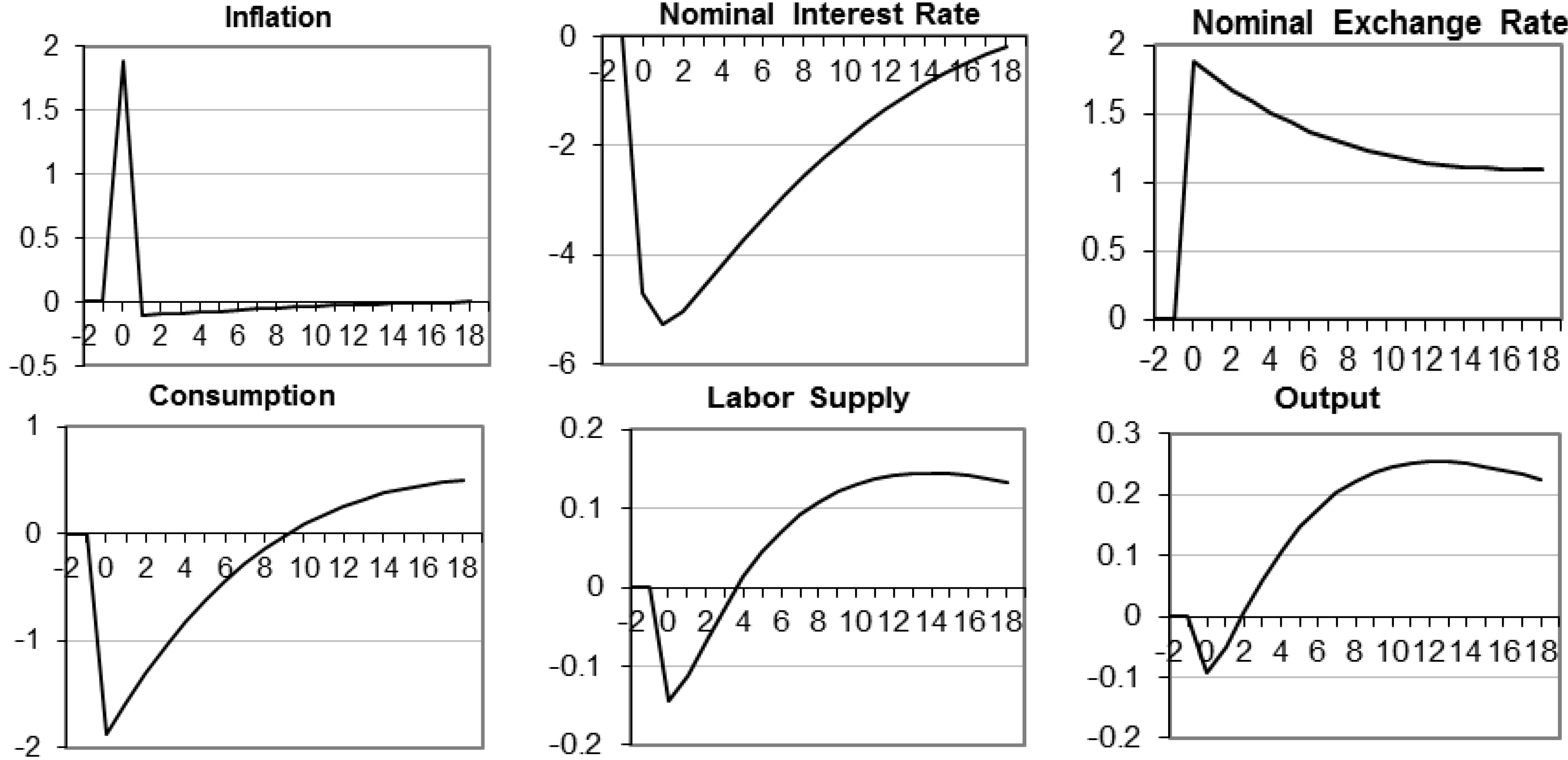
| Data | Standard Deviation | Relative Standard Deviation | Correlation with Output |
|---|---|---|---|
| Output | 0.5392 | 1.00 | 1.0000 |
| Investment | 2.9170 | 5.40 | 0.7385 |
| N. Interest Rate | 13.5008 | 25.03 | 0.2991 |
| Consumption | 0.4805 | 0.89 | 0.6262 |
| Inflation (CPI) | 0.4741 | 0.88 | −0.2247 |
| N. Exchange Rate | 2.2070 | 4.09 | −0.1567 |
| Model | |||
| Output | 0.0272 | 1.00 | 1.00 |
| Investment | 0.0619 | 2.27 | 0.95 |
| N. Interest Rate | 0.3093 | 11.37 | 0.70 |
| Consumption | 0.0483 | 1.77 | 0.85 |
| Inflation | 0.0322 | 1.18 | −0.17 |
| N. Exchange Rate | 0.0491 | 1.80 | −0.53 |
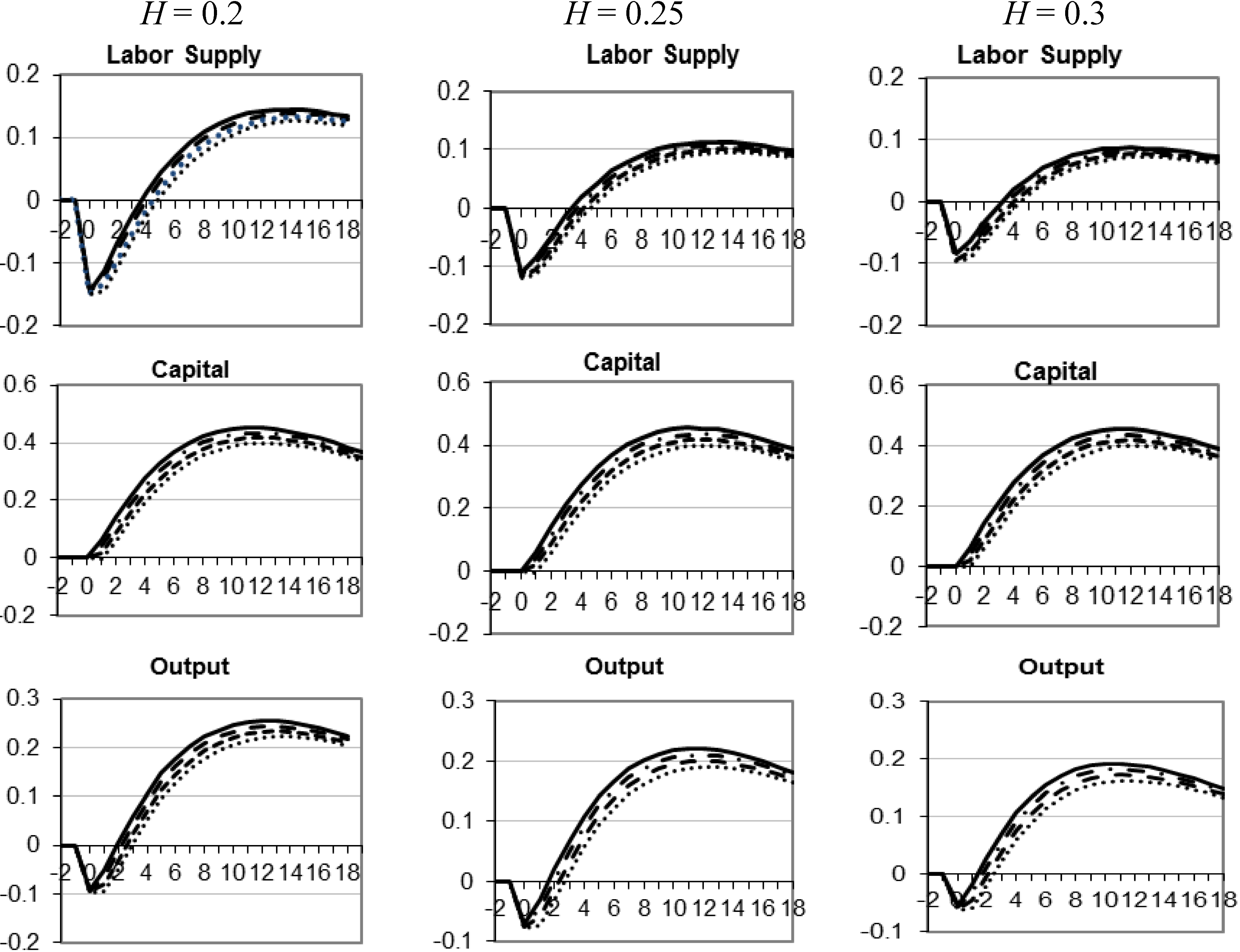
4.1. Alternative Distributions of Monetary Injections

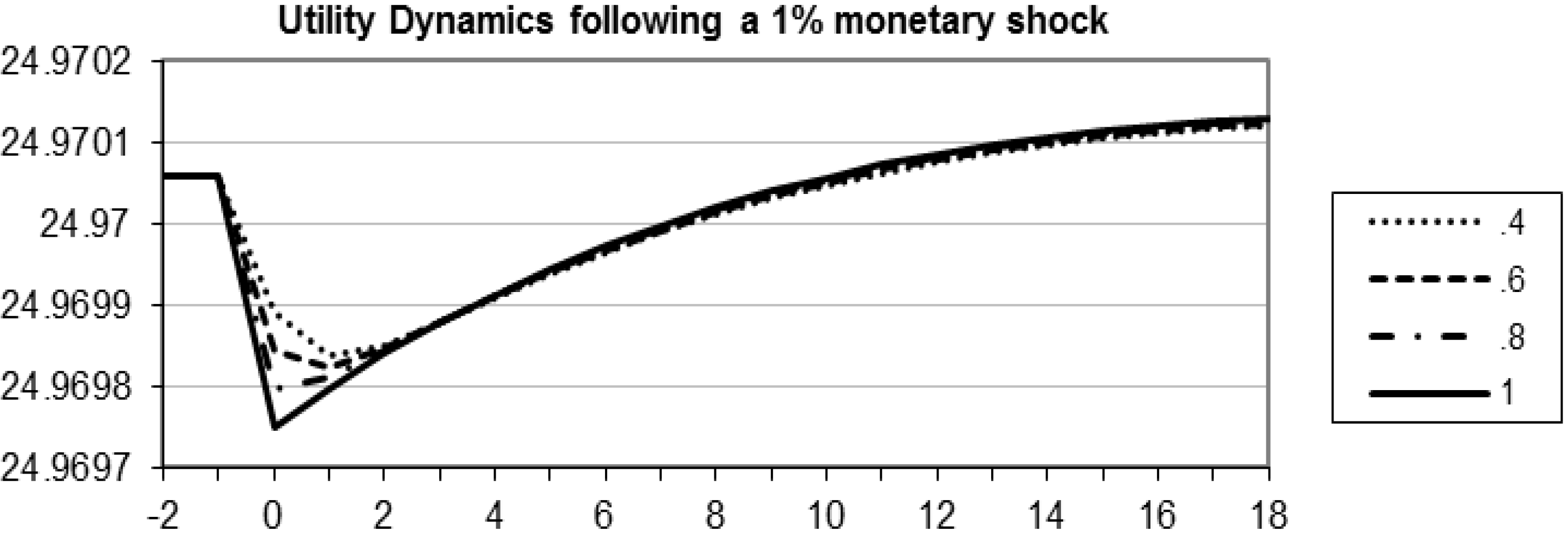
5. Robustness of the Differential Effect

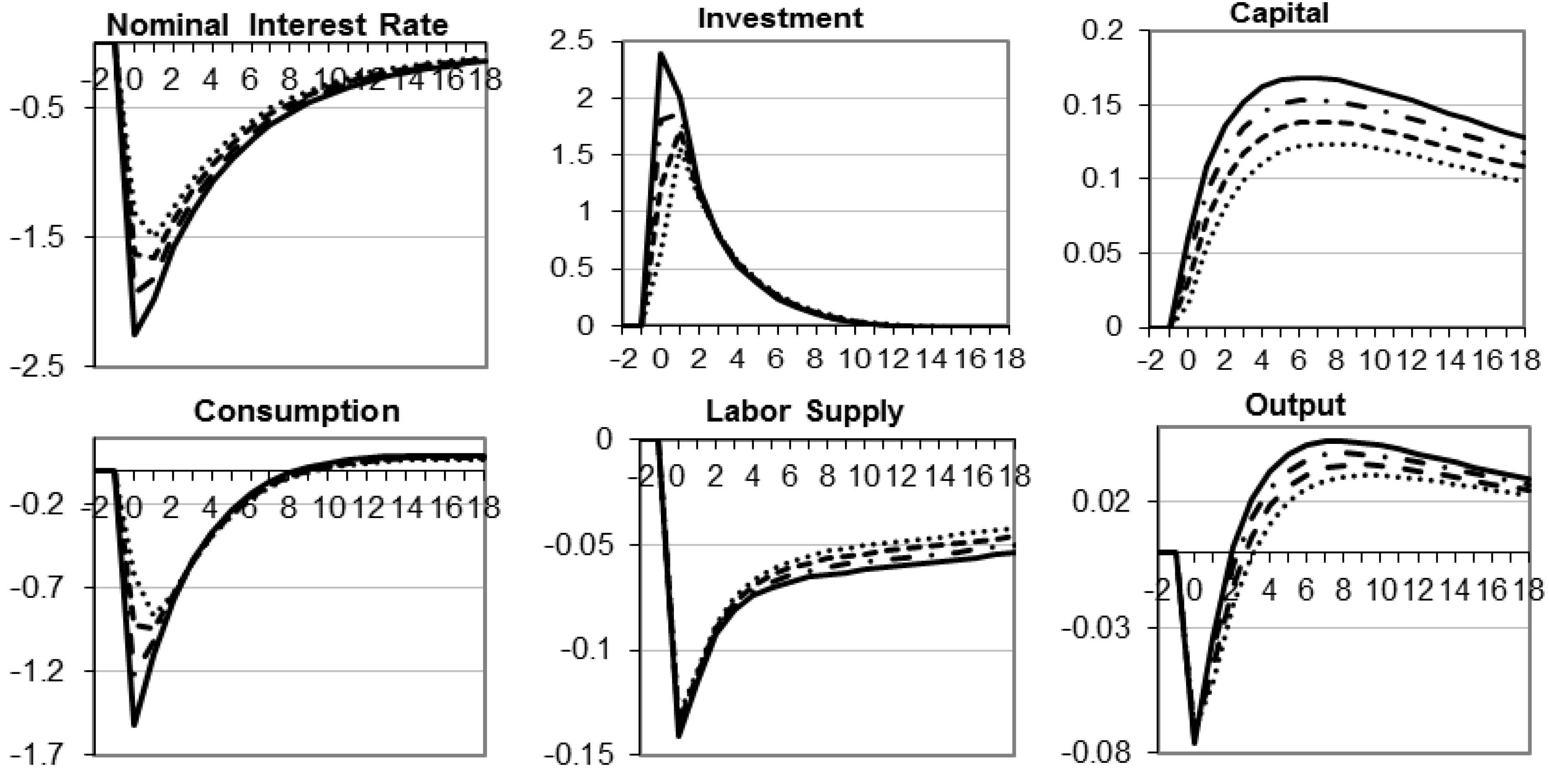
6. Conclusions
Conflicts of Interest
References and Notes
- M. Zandi. “Written Testimony before the House Committee on Small Business Hearing on “Economic Stimulus for Small Business: A Look Back and Assessing Need for Additional Relief”.” 24 July 2008. Available online: http://zh.scribd.com/doc/12002123/Written-Testimony-of-Mark-Zandi-Chief-Economist-and-CoFounder (accessed on 26 October 2013).
- C. Broda, and J. Parker. “The Impact of the 2008 Tax Rebates on Consumer Spending: A First Look at the Evidence.” Available online: http://insight.kellogg.northwestern.edu/article/the_impact_of_the_2008_tax_rebates_on_consumer_spending/ (accessed on 26 October 2013).
- D.S. Johnson, J.A. Parker, and N.S. Souleles. “Household expenditure and the income tax rebate of 2001.” Am. Econ. Rev. 96 (2006): 1589–1610. [Google Scholar] [CrossRef]
- S. Agarwal, C. Liu, and N.S. Souleles. “The reaction of consumer spending and debt to tax rebates—Evidence from consumer credit data.” J. Polit. Econ. 115 (2007): 986–1019. [Google Scholar] [CrossRef]
- J.A. Parker, N.S. Souleles, D.S. Johnson, and R. MacClelland. “Consumer Spending and the Economic Stimulus Payments of 2008.” Available online: https://www.kellogg.northwestern.edu/research/risk/projects/Parker%20PSJM%20Feb%2018%202010.pdf (accessed on 26 October 2013).
- D.W. Elmendorf, and D. Reifschneider. “Short run effects of fiscal policy with forward-looking financial markets.” Natl. Tax J. 55 (2002): 357–386. [Google Scholar]
- D.W. Elmendorf, and J. Furman. “If, When, How: A Primer on Fiscal Stimulus.” Available online: http://www.brookings.edu/~/media/research/files/papers/2008/1/10%20fiscal%20stimulus%20elmendorf%20furman/0110_fiscal_stimulus_elmendorf_furman (accessed on 26 October 2013).
- M. Eichenbaum. “Some thoughts on practical stabilization policy.” Am. Econ. Rev. 87 (1997): 236–239. [Google Scholar]
- M. Feldstein. “The Role for Discretionary Fiscal Policy in a Low Interest Rate Environment.” Available online: https://notendur.hi.is/bge1/EC542/Feldstein%202002.pdf (accessed on 26 October 2013).
- J.B. Taylor. “The State of the Economy and Principles for Fiscal Stimulus.” Available online: http://www.stanford.edu/~johntayl/Onlinepaperscombinedbyyear/2008/The_State_of_the_Economy_and_Principles_for_Fiscal_Stimulus_Senate_Budget_Committee-11-19-08.pdf (accessed on 26 October 2013).
- J.B. Taylor. “The Financial Crisis and the Policy Responses: An Empirical Analysis of What Went Wrong.” Available online: http://www.stanford.edu/~johntayl/FCPR.pdf (accessed on 26 October 2013).
- J.B. Taylor. “An empirical analysis of the revival of fiscal activism in the 2000s.” J. Econ. Lit. 49 (2011): 686–702. [Google Scholar] [CrossRef]
- M.W. Shapiro, and J.B. Slemrod. “Did the 2008 tax rebates stimulate spending? ” Am. Econ. Rev. 99 (2009): 374–379. [Google Scholar] [CrossRef]
- They assumed that households will spend 50% of the tax rebate.
- M.W. Shapiro, and J.B. Slemrod. “Consumer response to tax rebates.” Am. Econ. Rev. 93 (2003): 381–396. [Google Scholar] [CrossRef]
- Congressional Budget Office. “Did the 2008 Tax Rebates Stimulate Short-Term Growth? ” Available online: http://www.cbo.gov/sites/default/files/cbofiles/ftpdocs/96xx/doc9617/06-10-2008stimulus.pdf (accessed on 26 October 2013).
- They use weekly data provided by 34,000 participating households that scanned their purchases for ACNielsen’s Homescan.
- The Consumer Expenditure Survey is collected by the Bureau of Labor Statistics; it provides information on the buying habits of American consumers.
- R.J. Barro. “Government Spending Is Not Free Lunch.” Wall Street Journa, 22 January 2009, A17. [Google Scholar]
- J.A. Parker. “On measuring the effects of fiscal policy in recessions.” J. Econ. Lit. 49 (2011): 703–718. [Google Scholar] [CrossRef]
- D.E. Vacaflores. “Monetary stimulus: Through Wall Street or Main Street? ” Rev. Anal. 14 (2012): 9–40. [Google Scholar]
- J. Greenwood, Z. Hercowitz, and G.W. Huffman. “Investment, capacity utilization and the real business cycle.” Am. Econ. Rev. 78 (1988): 402–417. [Google Scholar]
- The parameter φ thus allows us to test the differential impact of a monetary injection by modeling a helicopter drop on households or on banks.
- Remember that Ben Bernanke actually said that the Fed could inject money into the system as a helicopter drop directly to the consumers if necessary (Bernanke [40]).
- When φ = 1 we have that all the monetary injection goes through the financial intermediaries.
- F. Karame, L. Patureau, and T. Sopraseuth. “Limited participation and exchange rate dynamics: Does theory meet the data? ” J. Econ. Dyn. Control 32 (2008): 1041–1087. [Google Scholar] [CrossRef]
- D.E. Vacaflores. “Technical Appendix (Monetary Transfers in the U.S.: How Efficient Are Tax Rebates?).” Available online: http://www.business.txstate.edu/users/dv13/research.htm (accessed on 26 October 2013).
- E. Nakamura, and J. Steinson. “Fiscal Stimulus in a Monetary Union: Evidence from U.S. Regions.” Available online: http://www.columbia.edu/~js3204/papers/fiscal.pdf (accessed on 26 October 2013).
- Note that M1 in 2008Q2 was $1399 billion, which at the average growth of money will become $1410 billion by 2008Q3, when tax rebates introduced an initial $78 billion that was followed by another $15 billion in 2008Q3.
- This assumption sets the steady-state nominal exchange rate to be constant instead of growing at a constant rate.
- Results for a 1% technology shock are standard, but since there are only used to establish the strength of the model they are presented in the Supplementary Materials.
- Note that the model assumes instant adjustment in prices, which can be oversimplifying the behavior of prices. Alternatively, one could introduce price rigidities to reduce these volatilities, but the gains are only marginal (see Patureau [33] for a model with these characteristics).
- L. Patureau. “Pricing-to-market, limited participation and exchange rate dynamics.” J. Econ. Dyn. Control 31 (2007): 3281–3320. [Google Scholar] [CrossRef]
- L.J. Christiano, and M. Eichenbaum. “Some Empirical Evidence on the Liquidity Effect.” In Political Economy, Growth and Business Cycle. Edited by Z. Cukierman, Z. Hercowitz and L. Leiderman. Cambridge, MA, USA: MIT Press, 1992. [Google Scholar]
- Again, this arises from flexibility of prices assumed in the model, but the main results from the alternative distribution of the injection should not depend on the modeling of sticky prices.
- Note that we can alternatively interpret this distribution of the injection as the actual use of the funds by the household between consumption and savings, responding to a given marginal propensity to consume.
- P. Krugman. “Stimulus Arithmetic (Wonkish but Important).” Available online: http://krugman.blogs.nytimes.com/2009/01/06/stimulus-arithmetic-wonkish-but-important/?_r = 0 (accessed on 28 October 2013).
- Parker et al. [5] reports that 130 million U.S. tax filers received the 2008 tax rebate (around 85% of eligible tax payers) and Shapiro and Slemrod [13] report that 8.4% of respondents stated that they will not receive the tax rebate. The total adult population is approximately 230 million.
- We had to set α, the parameter that determines the share of capital in production, to a higher level (0.46) to generate comparable responses to the results under the main specification.
- B.S. Bernanke. “Deflation: Making sure “it” doesn’t happen here. Remarks by Governor Ben S Bernanke before the National Economists Club, Washington, DC, USA.” 12 November 2002. [Google Scholar]
- O. Blanchard, G. Dell’Ariccia, and P. Mauro. “Rethinking macroeconomic policy.” J. Money Credit Bank. 42 (2010): 199–215. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Vacaflores, D.E. Monetary Transfers in the U.S.: How Efficient Are Tax Rebates? Economies 2013, 1, 26-48. https://doi.org/10.3390/economies1030026
Vacaflores DE. Monetary Transfers in the U.S.: How Efficient Are Tax Rebates? Economies. 2013; 1(3):26-48. https://doi.org/10.3390/economies1030026
Chicago/Turabian StyleVacaflores, Diego E. 2013. "Monetary Transfers in the U.S.: How Efficient Are Tax Rebates?" Economies 1, no. 3: 26-48. https://doi.org/10.3390/economies1030026
APA StyleVacaflores, D. E. (2013). Monetary Transfers in the U.S.: How Efficient Are Tax Rebates? Economies, 1(3), 26-48. https://doi.org/10.3390/economies1030026




