Enhancing Q-Factor in a Biquadratic Bandpass Filter Implemented with Opamps
Abstract
:1. Introduction
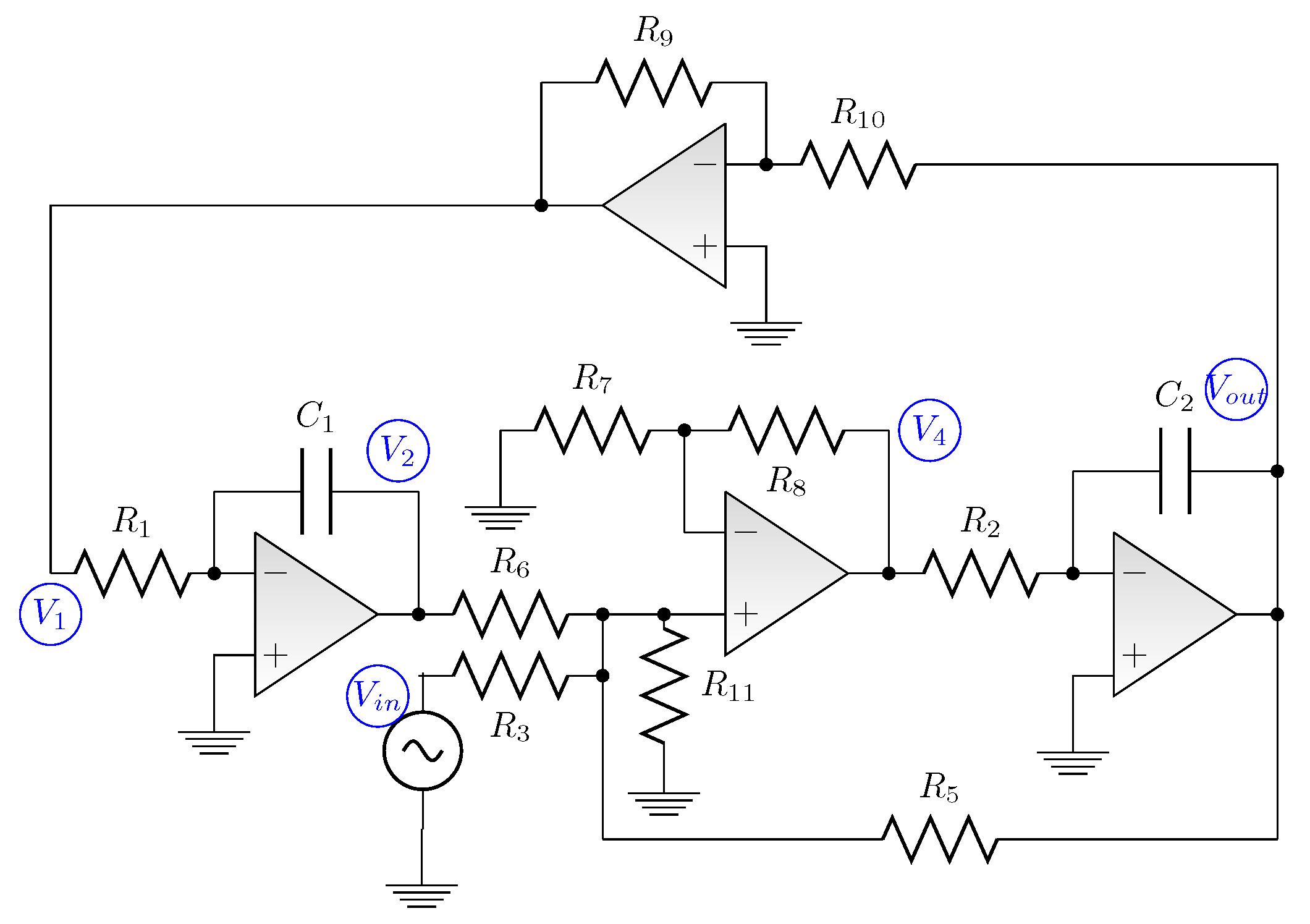
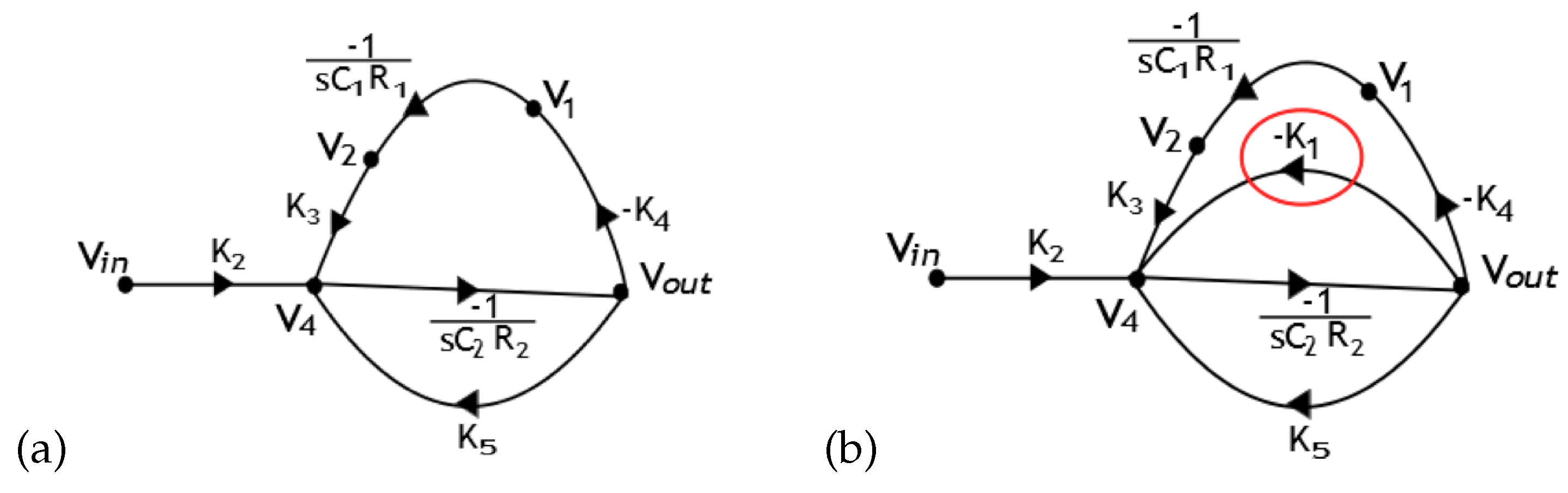
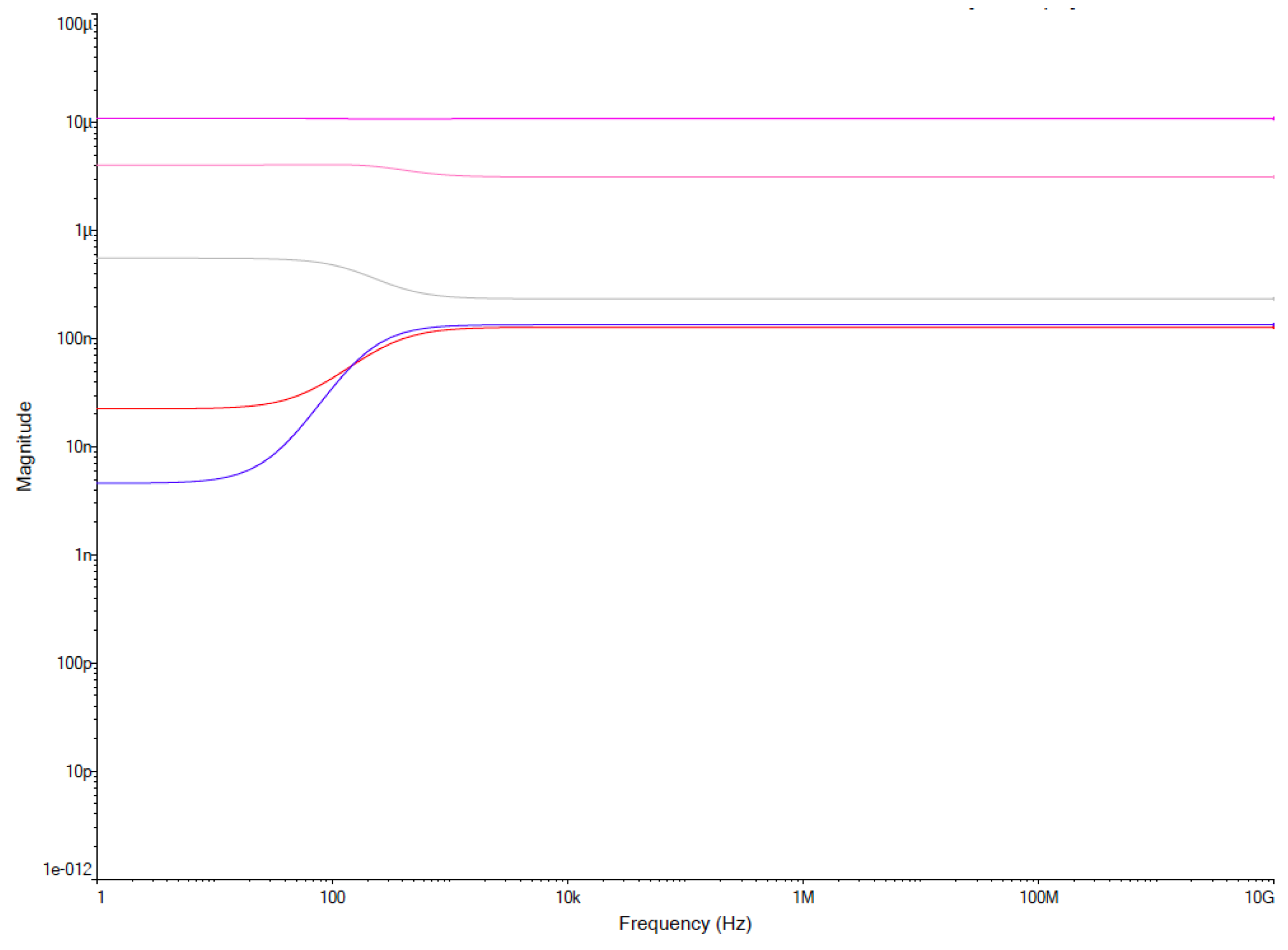
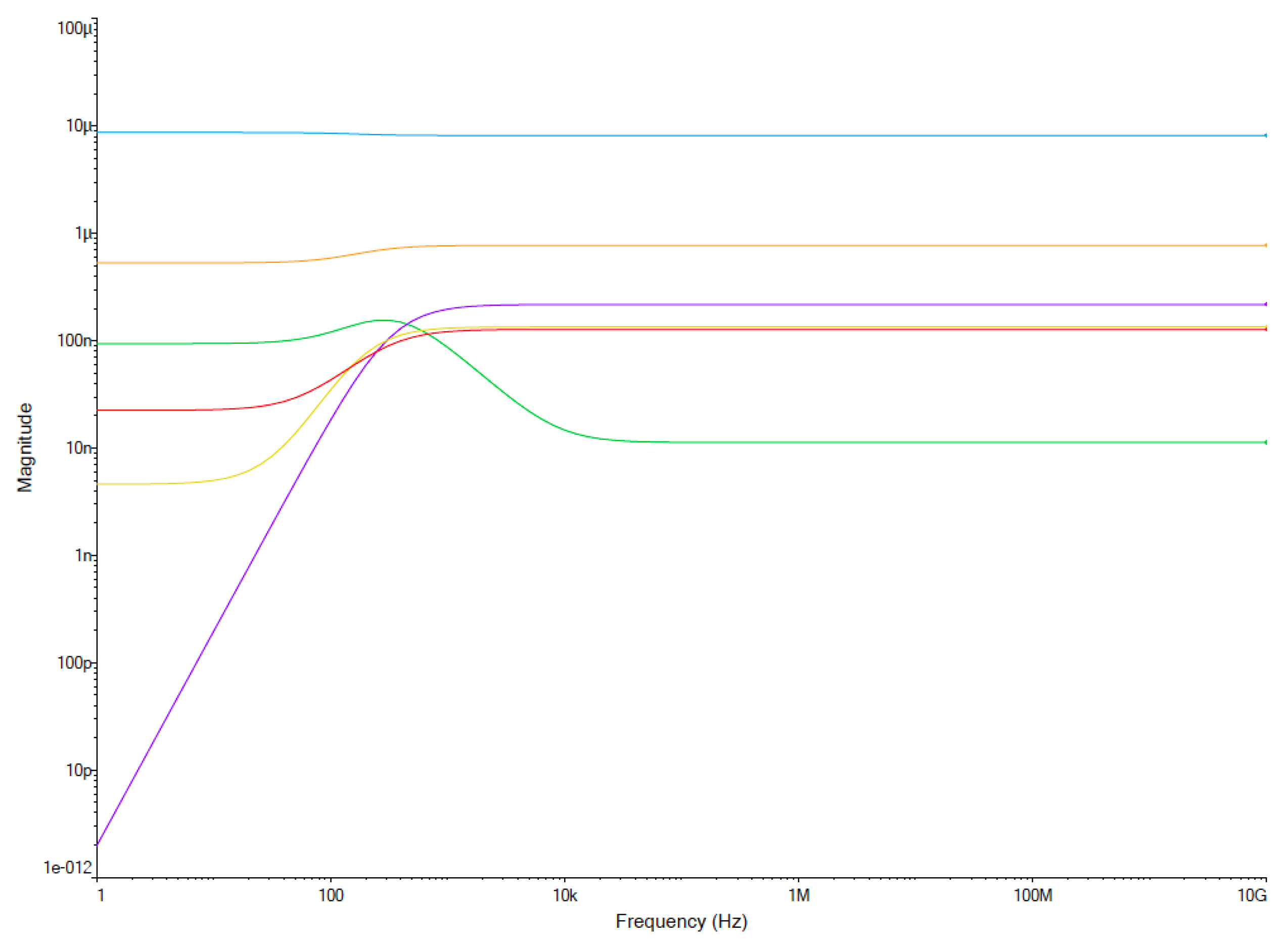
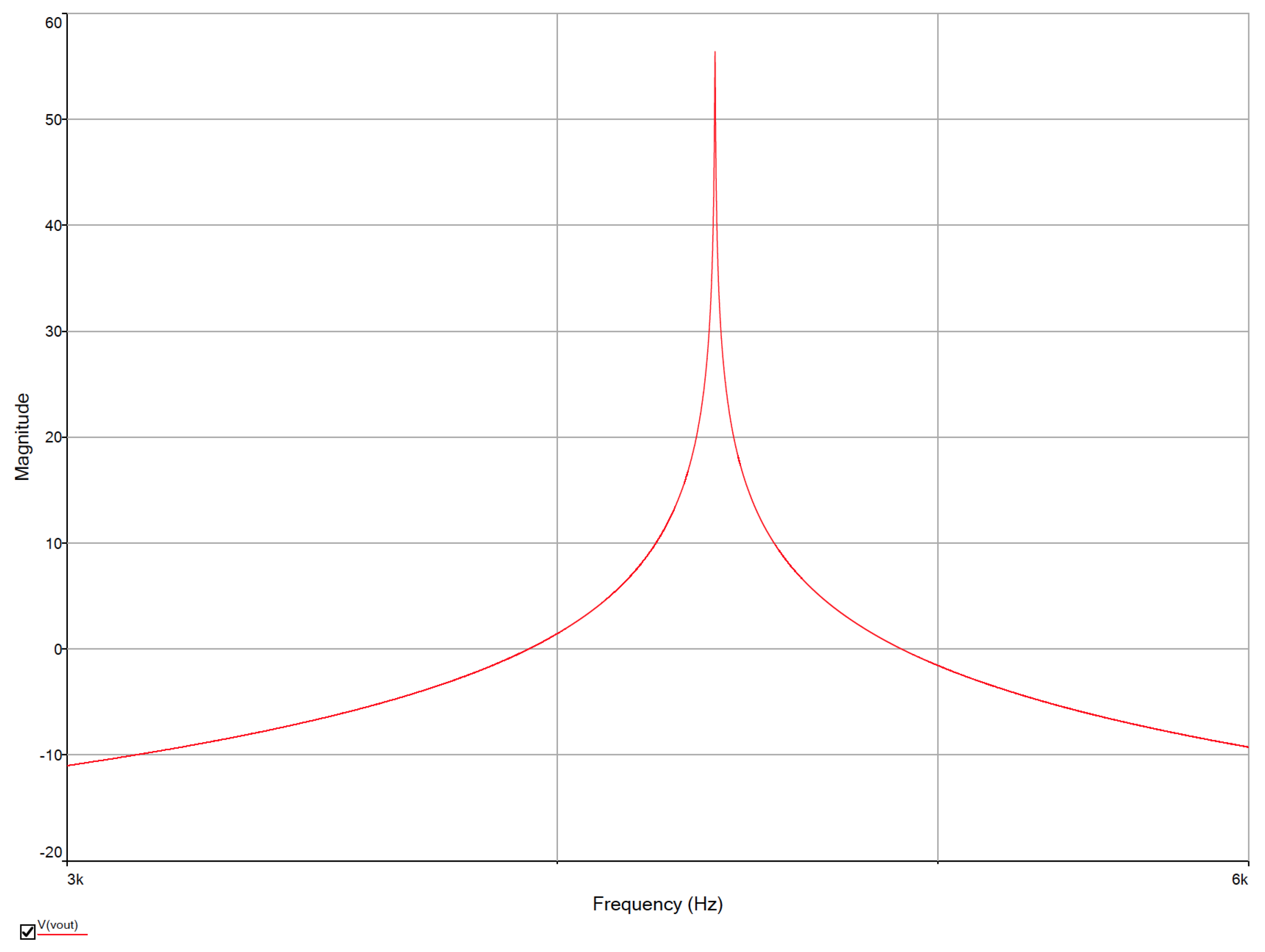
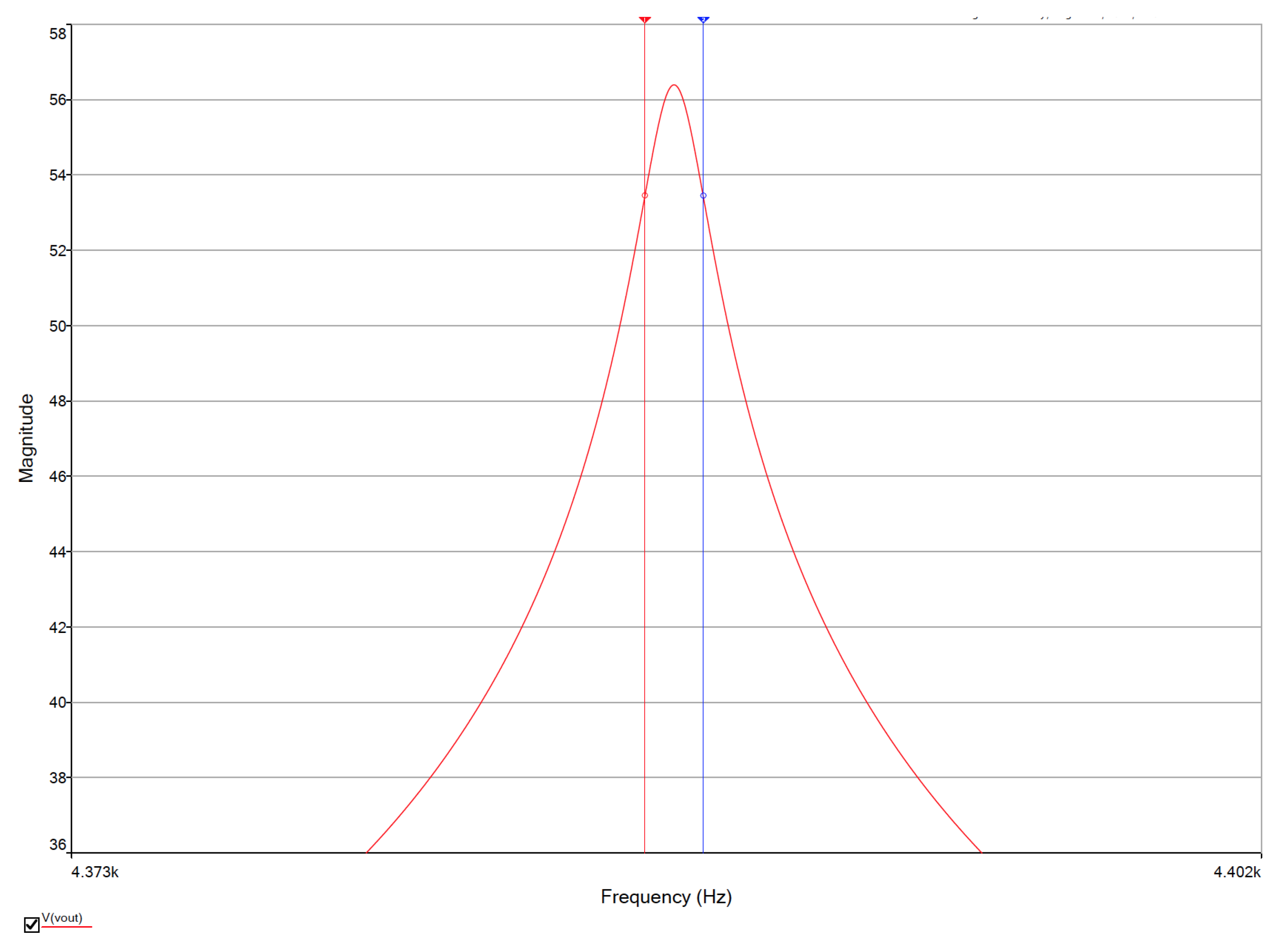
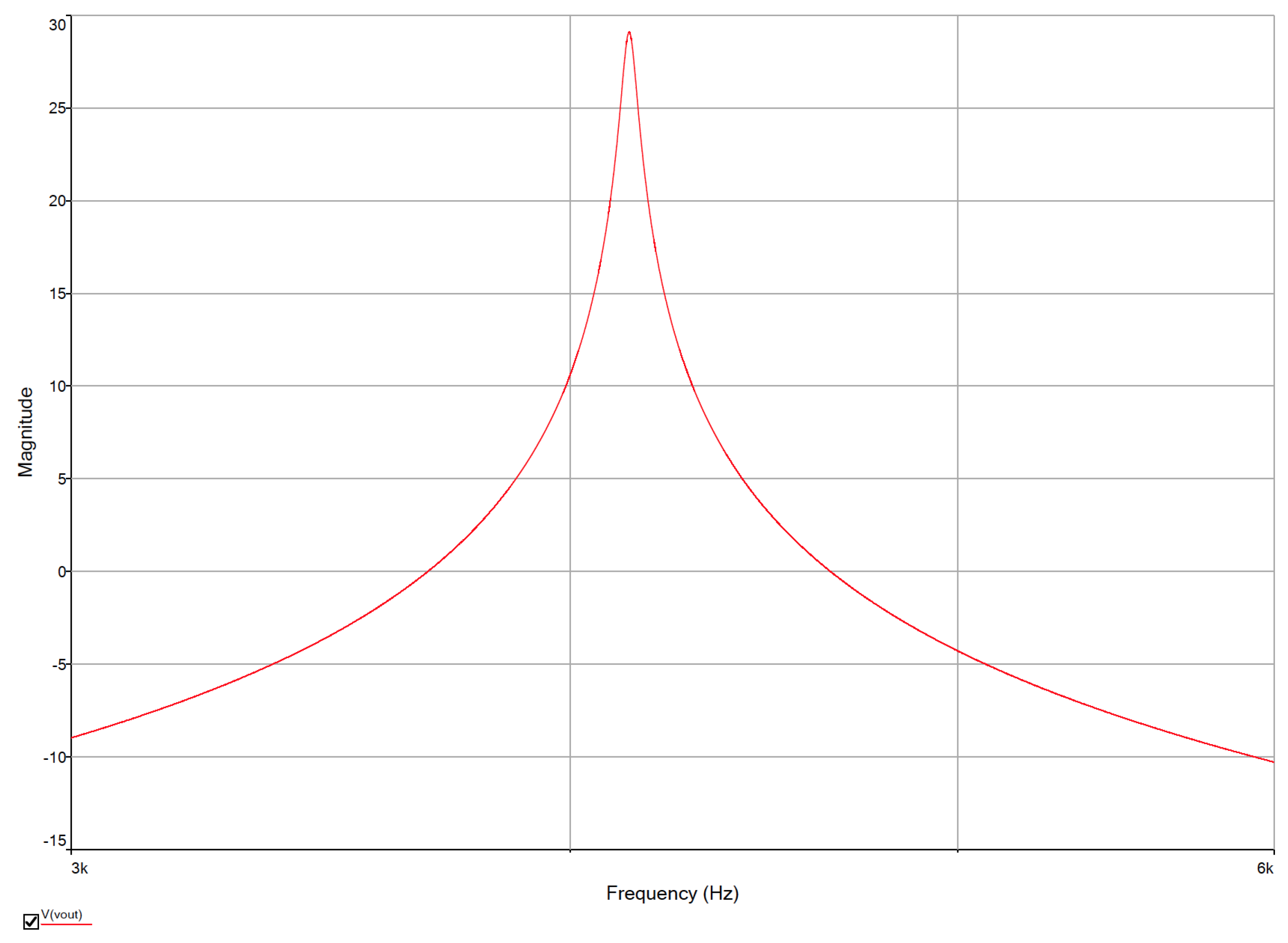
2. Simulation and Signal Flow Graph Analysis
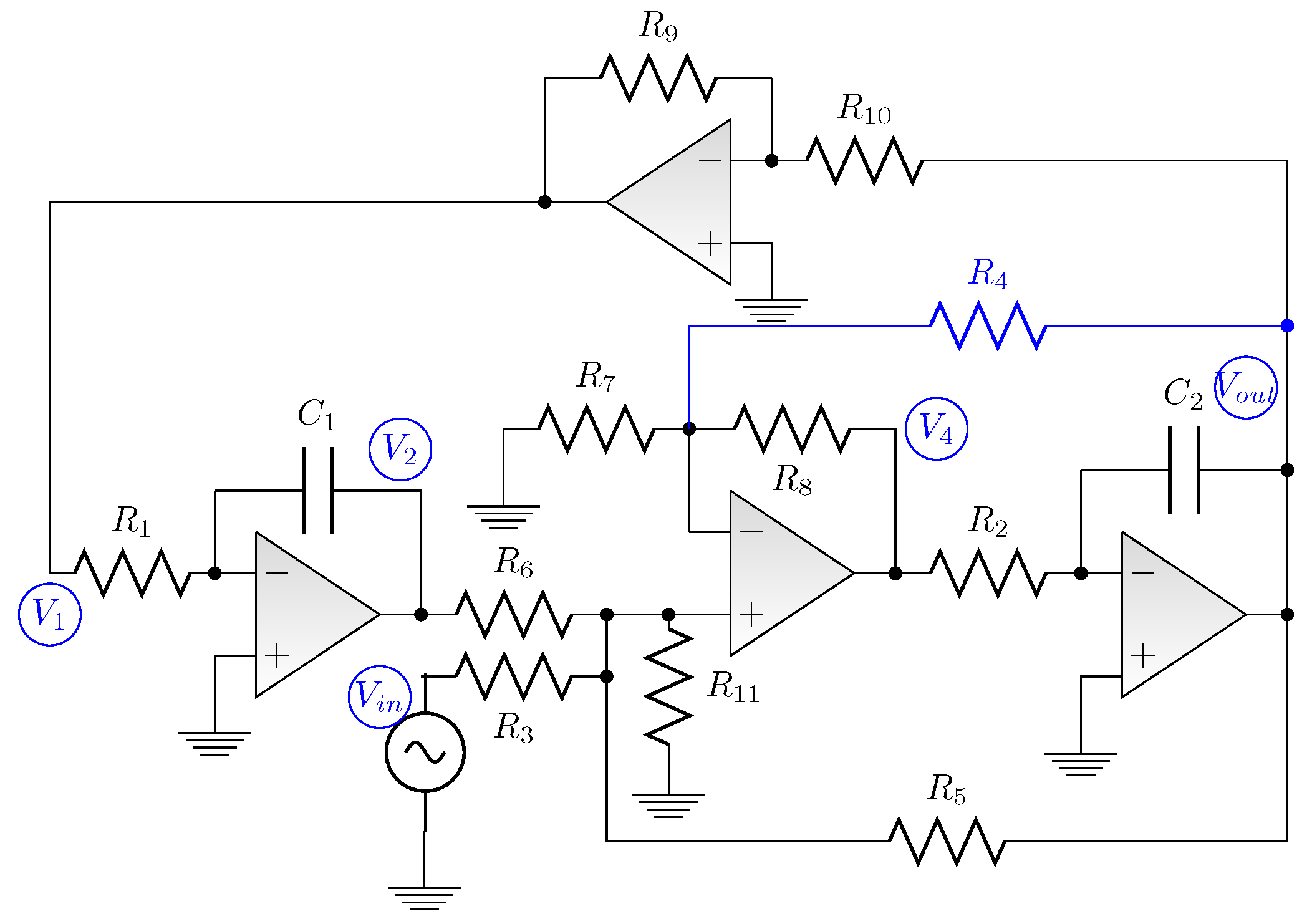
3. Sensitivity Analysis Performed in NI Multisim
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Allen, P.; Huelsman, L. Introduction to the Theory and Design of Active Filters; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Ganji, H.; Jannesari, A.; Sohrabi, Z. Charge-sharing bandpass filter with independent bandwidth and center frequency adjustment. Electron. Lett. 2019, 55, 638–640. [Google Scholar] [CrossRef]
- Shi, Y.; Li, R.; Teo, K. Design of a Band-Stop Filter for a Space Shuttle Vehicle. IEEE Trans. Circuits Syst. II Express Briefs 2015, 62, 1174–1178. [Google Scholar] [CrossRef]
- Sebastian, R.; Jos Prakash, A.V.; Jose, B.R.; Mathew, J. A re-configurable MASH 2-2 bandpass DQEFM for multi-standard applications. Int. J. Electron. 2019, 106, 1498–1513. [Google Scholar] [CrossRef]
- Wen, P.; Ma, Z.; Liu, H.; Zhu, S.; Ren, B.; Guan, X.; Ohira, M. Individually controllable dual-band bandpass filter with multiple transmission zeros and wide stopband. IEICE Electron. Express 2019, 16, 20190127. [Google Scholar] [CrossRef]
- Maragheh, S.S.; Dousti, M.; Dolatshahi, M.; Ghalamkari, B. A dual-mode tunable bandpass filter for GSM, UMTS, WiFi, and WiMAX standards applications. Int. J. Circuit Theory Appl. 2019, 47, 561–571. [Google Scholar] [CrossRef]
- Hsu, Y.P.; Liu, Z.; Hella, M.M. A 1.8 uW- 65 dB THD ECG Acquisition Front-End IC Using a Bandpass Instrumentation Amplifier With Class-AB Output Configuration. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 1859–1863. [Google Scholar] [CrossRef]
- Serra, H.; Oliveira, J.P.; Paulino, N. A 0.9-V Programmable Second-Order Bandpass Switched-Capacitor Filter for IoT Applications. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 1335–1339. [Google Scholar] [CrossRef]
- Zhang, M.; Cai, Q.; Yang, Z.; Jia, X.; Fan, X. A 1-MHz-Bandwidth Gm-C-Based Quadrature Bandpass Sigma-Delta Modulator Achieving- 153.7-dBFS/Hz NSD With Background Calibration. IEEE Trans. Circuits Syst. I Regular Pap. 2018, 66, 909–919. [Google Scholar] [CrossRef]
- Garcia-Ortega, J.M.; Tlelo-Cuautle, E.; Sanchez-Lopez, C. Design of current-mode gm-c filters from the transformation of opamp-rc filters. J. Appl. Sci. 2007, 7, 1321–1326. [Google Scholar]
- Kumngern, M.; Khateb, F. Current-mode universal filter and quadrature oscillator using current controlled current follower transconductance amplifiers. Analog Integr. Circ. Signal Process. 2019, 100, 235–248. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Zhu, B.; Hu, Z. Universal Current-Mode Filters Based on OTA and MO-CCCA. IETE J. Res. 2018, 64, 897–906. [Google Scholar] [CrossRef]
- Wang, S.F.; Chen, H.P.; Ku, Y.; Chen, P.Y. A CFOA-Based Voltage-Mode Multifunction Biquadratic Filter and a Quadrature Oscillator Using the CFOA-Based Biquadratic Filter. Appl. Sci. 2019, 9, 2304. [Google Scholar] [CrossRef]
- Wang, S.F.; Chen, H.P.; Ku, Y.; Lin, Y.C. Versatile Tunable Voltage-Mode Biquadratic Filter and Its Application in Quadrature Oscillator. Sensors 2019, 19, 2349. [Google Scholar] [CrossRef] [PubMed]
- Singh, V.S.; Shankar, C. A new Trans-Impedance Mode biquad filter employing single DVCCTA. J. Electron. Syst. 2019, 15, 249–263. [Google Scholar]
- Tangsrirat, W. Voltage Differencing Transconductance Amplifier-Based Quadrature Oscillator and Biquadratic Filter Realization with All Grounded Passive Elements. J. Commun. Technol. Electron. 2018, 63, 1418–1423. [Google Scholar] [CrossRef]
- Kumar, V.; Mehra, R.; Islam, A. Design and analysis of MISO bi-quad active filter. Int. J. Electron. 2019, 106, 287–304. [Google Scholar] [CrossRef]
- Dvorak, J.; Jerabek, J.; Polesakova, Z.; Kubanek, D.; Blazek, P. Multifunctional Electronically Reconfigurable and Tunable Fractional-Order Filter. Elektron. Elektrotech. 2019, 25, 26–30. [Google Scholar] [CrossRef]
- Baumgratz, F.D.; Ferreira, S.B.; Steyaert, M.S.; Bampi, S.; Tavernier, F. 40-nm CMOS Wideband High-IF Receiver Using a Modified Charge-Sharing Bandpass Filter to Boost Q-Factor. IEEE Trans. Circuits Syst. I Regular Pap. 2018, 65, 2581–2591. [Google Scholar] [CrossRef]
- Amin, F.; Raman, S.; Koh, K.J. Integrated Synthetic Fourth-Order Q-Enhanced Bandpass Filter With High Dynamic Range, Tunable Frequency, and Fractional Bandwidth Control. IEEE J. Solid-State Circuits 2019, 54, 768–784. [Google Scholar] [CrossRef]
- Shi, G.; Tan, S.X.D.; Tlelo-Cuautle, E. Advanced Symbolic Analysis for VLSI Systems; Springer: New York, NY, USA, 2014. [Google Scholar]
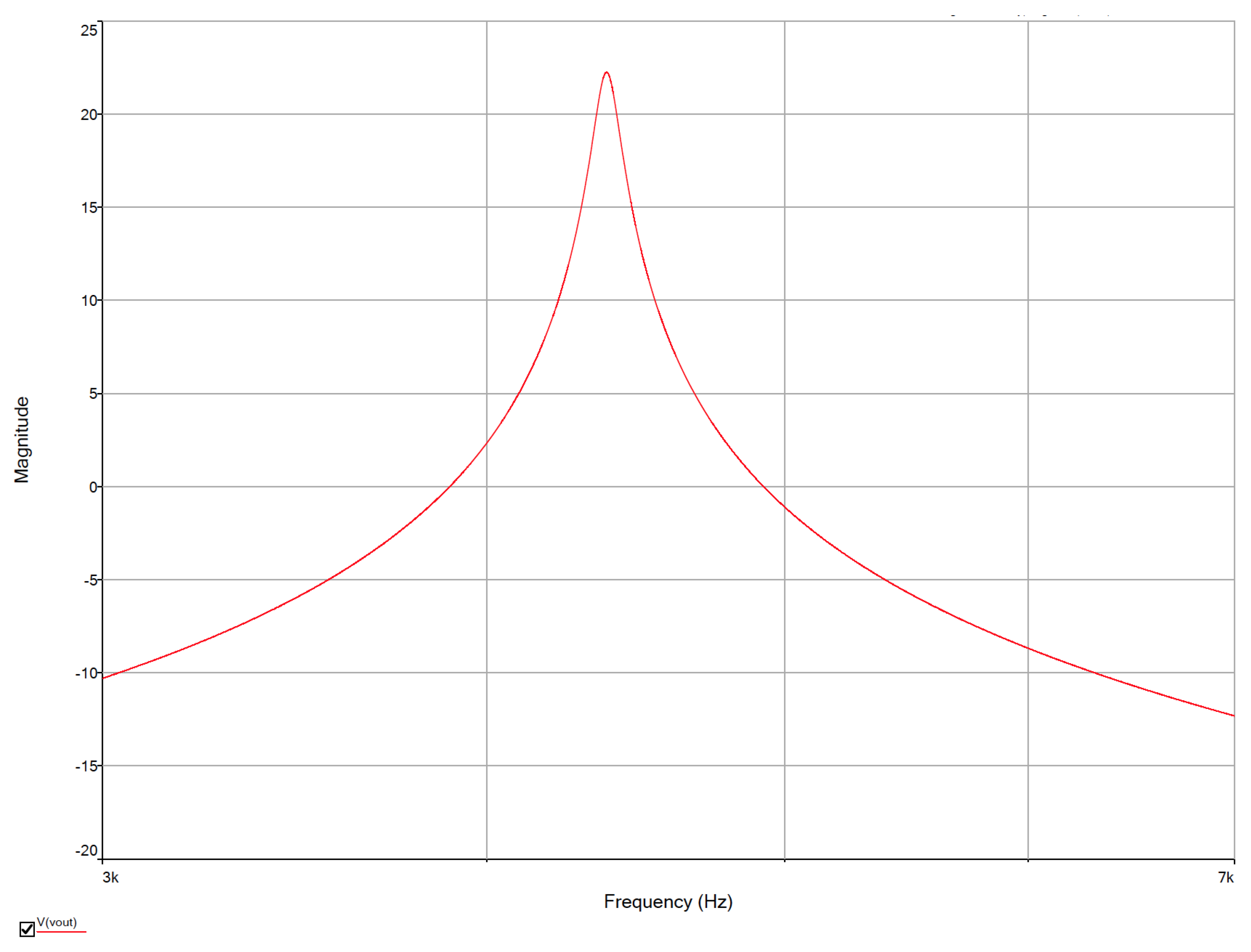
| Q Value | Pole 1 | Pole 2 |
|---|---|---|
| 22.697 | −3.2629 | −0.0023 |
| 2920.06 | −3.2734 | −0.0025 |
| 122.79 | −3.2742 | −0.0022 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tlelo-Coyotecatl, E.; Díaz-Sánchez, A.; Rocha-Pérez, J.M.; Vázquez-González, J.L.; Sánchez-Gaspariano, L.A.; Tlelo-Cuautle, E. Enhancing Q-Factor in a Biquadratic Bandpass Filter Implemented with Opamps. Technologies 2019, 7, 64. https://doi.org/10.3390/technologies7030064
Tlelo-Coyotecatl E, Díaz-Sánchez A, Rocha-Pérez JM, Vázquez-González JL, Sánchez-Gaspariano LA, Tlelo-Cuautle E. Enhancing Q-Factor in a Biquadratic Bandpass Filter Implemented with Opamps. Technologies. 2019; 7(3):64. https://doi.org/10.3390/technologies7030064
Chicago/Turabian StyleTlelo-Coyotecatl, Esteban, Alejandro Díaz-Sánchez, José Miguel Rocha-Pérez, Jose Luis Vázquez-González, Luis Abraham Sánchez-Gaspariano, and Esteban Tlelo-Cuautle. 2019. "Enhancing Q-Factor in a Biquadratic Bandpass Filter Implemented with Opamps" Technologies 7, no. 3: 64. https://doi.org/10.3390/technologies7030064
APA StyleTlelo-Coyotecatl, E., Díaz-Sánchez, A., Rocha-Pérez, J. M., Vázquez-González, J. L., Sánchez-Gaspariano, L. A., & Tlelo-Cuautle, E. (2019). Enhancing Q-Factor in a Biquadratic Bandpass Filter Implemented with Opamps. Technologies, 7(3), 64. https://doi.org/10.3390/technologies7030064






