Abstract
This review presents a synthesis of fuzzy logic-based (FL) controllers applied to photovoltaic (PV) systems over the last decade, with a specific focus on maximum power point tracking (MPPT) and power management. These subsystems are critical for improving the efficiency of PV energy conversion, as they directly address the nonlinear, time-varying, and uncertain behavior of solar generation under dynamic environmental conditions. FL-based control has proven to be a powerful and versatile tool for enhancing MPPT accuracy, inverter performance, and hybrid energy management strategies. The analysis concentrates on three main categories, namely, Mamdani, Takagi–Sugeno (T-S), and Type-2, highlighting their architectures, operational characteristics, and application domains. Mamdani controllers remain the most widely adopted due to their simplicity, interpretability, and effectiveness in scenarios with moderate response time requirements. T-S controllers excel in real-time high-frequency operations by eliminating the defuzzification stage and approximating system nonlinearities through local linear models, achieving rapid convergence to the maximum power point (MPP) and improved power quality in grid-connected PV systems. Type-2 fuzzy controllers represent the most advanced evolution, incorporating footprints of uncertainty (FOU) to handle high variability, sensor noise, and environmental disturbances, thereby strengthening MPPT accuracy under challenging conditions. This review also examines the integration of metaheuristic algorithms for automated tuning of membership functions and hybrid architectures that combine fuzzy control with artificial intelligence (AI) techniques. A bibliometric perspective reveals a growing research interest in T-S and Type-2 approaches. Quantitatively, Mamdani controllers account for 54.20% of publications, T-S controllers for 26.72%, and Type-2 fuzzy controllers for 19.08%, reflecting the balance between interpretability, computational performance, and robustness to uncertainty in PV-based MPPT and power management applications.
1. Introduction
The global transition towards renewable energy sources has intensified research efforts aimed at reducing dependence on hydrocarbons and mitigating climate change [1]. Among these alternatives, solar energy has emerged as one of the most promising options due to its abundance and scalability; however, its efficient exploitation remains a challenge because of the nonlinear, time-varying, and uncertain nature of photovoltaic (PV) energy conversion [2,3]. As such, while PV systems have gained popularity worldwide as a feasible solution for power generation and consumption, their performance remains strongly dependent on advanced control techniques that can maximize efficiency under dynamic environmental conditions [4,5]. As highlighted in [6,7,8], the efficiency of a PV panel is influenced not only by material selection but also by the implementation of MPPT strategies.
In this context, fuzzy logic controllers (FLCs) have been widely adopted as a relevant solution thanks to their robustness, flexibility, and ability to handle uncertainties without requiring precise mathematical models [9,10]. Recent contributions illustrate this trend; for instance, [11] proposed a hybrid approach integrating artificial neural networks (ANN), variable-step perturb and observe (P&O), and FLC observers to ensure fast MPPT convergence under partial shading. Similarly, [12] combined FLC with Gray Wolf optimization (GWO), achieving reduced iteration counts for membership function tuning, high reliability, shorter converter settling times, and stable operation under both uniform and partially shaded conditions.
Despite these advances, the literature presents fragmented perspectives. Several works compare FLC performance against classical or intelligent techniques, reporting strengths such as adaptability and simplicity but also highlighting limitations related to computational burden and rule complexity [13,14,15]. Moreover, while many studies focus on Type-1 fuzzy controllers, less attention has been paid to contrasting the distinct paradigms of Mamdani, T-S, and Type-2 fuzzy systems, particularly in the context of PV MPPT applications. This lack of unified perspective motivates the present review.
A critical factor in the performance of FLCs is the correct tuning of their membership functions and rule bases, since these parameters directly affect tracking speed, stability, and energy efficiency. Traditional trial-and-error approaches are being increasingly replaced by metaheuristic algorithms such as genetic algorithms (GAs), particle swarm optimization (PSO), and GWO, which provide automated and adaptive optimization of fuzzy parameters. This integration has enabled higher accuracy and faster convergence under rapidly changing environmental conditions, further justifying the need to assess recent advances in this field [16,17,18,19].
In this context, it is also necessary to delimit the scope of the present work. While PV systems comprise multiple components, including modules, converters, inverters, storage units, and grid interfaces, this review concentrates specifically on the application of FLCs to MPPT and power management [20]. These subsystems are the critical domains where fuzzy logic has demonstrated clear advantages in terms of adaptability, robustness, and energy efficiency. Consequently, rather than attempting a broad survey of all PV system elements, the contribution of this review lies in synthesizing and analyzing advances in fuzzy-based MPPT optimization and power quality enhancement.
Accordingly, the contributions of this review are summarized as follows:
- To conduct a systematic review of Mamdani, T-S, and Type-2 fuzzy controllers in PV systems, focusing on advanced MPPT techniques and hybrid architectures integrating AI.
- To examine and classify the main strategies reported in the literature while identifying the trends, strengths, and limitations of each paradigm.
- To highlight existing research gaps and propose recommendations for developing more robust and efficient control solutions.
- To suggest future directions, including adaptive control schemes, experimental validation in real-world environments, and deployment on high-performance embedded platforms.
- To provide a comprehensive reference for researchers and practitioners, thereby establishing a conceptual framework for optimizing the stability and efficiency of PV systems under dynamic operating conditions.
The rest of this manuscript is structured as follows: Section 2 outlines PV system fundamentals, followed by Section 3, which presents the bibliometric analysis and PRISMA-based methodology used to discriminate, select, and classify relevant studies on fuzzy controllers applied to PV systems; Section 4 describes Mamdani controllers, Section 5 covers T-S controllers, and Section 6 focuses on Type-2 controllers for high-uncertainty scenarios; Section 7 discusses findings, summarizes research areas, and shows publication trends; finally, Section 8 provides overall conclusions.
2. Theoretical Background
Currently, technological advancements have significantly benefited PV systems, enabling more efficient, accessible, and versatile sustainable energy generation. These technologies, which capture and directly convert solar radiation into electrical energy, have established themselves as a fundamental pillar in the development of renewable energy thanks to their positive impact on reducing energy costs, accelerating global growth, and ability to be integrated into various industrial, residential, and rural applications. PV systems are commonly classified into three broad groups according to their mode of operation: stand-alone (off-grid) systems, hybrid systems, and grid-connected (on-grid) systems [21].
Stand-alone systems are primarily implemented in remote, isolated, or rural areas where there is no access to the conventional electricity grid. They are composed of an array of solar panels, charge controllers, inverters, battery banks, and regulators, which collectively enable the storage and continuous delivery of energy even in conditions of low or no solar irradiation. In the telecommunications field, these systems are used in radio communication antennas located in rural areas, providing an independent energy source. Similarly, in the agricultural sector, their integration has facilitated the use of sustainable irrigation systems, autonomous lighting, and improvements in local productivity [22]. The presence of battery banks in these configurations is essential, as they ensure a stable and reliable electricity supply in the face of environmental variations or during periods of low demand, such as nighttime. Hybrid systems integrate photovoltaic generation with auxiliary energy sources, such as diesel generators, wind turbines, or microturbines, to ensure a continuous electricity supply in adverse environmental conditions or areas with limited infrastructure. These systems consist of a set of solar panels, charge controllers, inverters, battery banks, and a secondary energy source that serves as a backup. Their application has expanded to various environments, including rural housing, telecommunication systems, livestock stations, and rural electrification projects. They are especially useful in remote regions where standalone PV systems face low solar irradiance or electrical grid failures and instability, where they can allow for improved system reliability and energy autonomy [23]. On-grid systems, on the other hand, are designed to operate in synchrony with the distribution grid, allowing the energy generated by the PV system to be supplemented or exported to the public grid. These systems consist of an array of solar panels, controllers, grid-synchronized inverters, bidirectional meters, and in some cases battery banks that provide support during peak hours or brief power outages. Their main advantage is that they guarantee the continuity of the power supply even during periods of low solar irradiation or high demand. This type of configuration is widely adopted in urban homes, solar electric vehicles, smart buildings, and industrial facilities; the goal is to optimize energy efficiency and reduce dependence on conventional sources, thereby contributing to a smaller carbon footprint [24].
Although PV systems can operate in different modes, such as stand-alone, hybrid, or grid-connected, their definition in this review remains focused on configurations where solar generation is the primary source, supported by power conditioning units such as DC–DC converters, inverters, and in some cases storage or auxiliary backup. This perspective differs from that of a microgrid, which constitutes a broader and more complex architecture integrating multiple distributed generation sources under a coordinated control and management framework. While a PV system may form part of a microgrid, the scope of this review is restricted to FLCs applied to MPPT and power management within PV systems, rather than to the global coordination of heterogeneous microgrid resources.
Figure 1 presents a representative block diagram of a general PV system. It illustrates the basic operation of the system, starting with the solar panel or module, which is responsible for converting solar energy into electrical energy. The generated power directly depends on the number of connected panels and the rated power of each panel (in Watts), which determines the level of energy available to the system. The generated energy is then delivered to the DC–DC converter block, which regulates the output voltage to the load. This converter receives the current and voltage generated by the panel and adapts them in order to provide a constant predefined output voltage suitable for the load’s consumption [25,26]. To ensure optimal system performance in the face of variations in irradiance, temperature, or dynamic panel conditions, an FLC block is incorporated. This controller utilizes a fuzzy logic system (FLS) to intelligently adjust the duty cycle of the DC–DC converter. Its objective is to compensate for fluctuations in the solar panel input and maintain a stable output voltage.
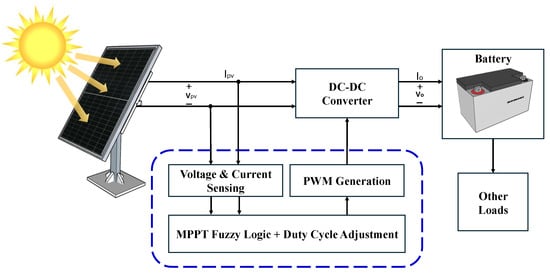
Figure 1.
Block diagram of a PV system with fuzzy logic-based MPPT and DC–DC conversion.
Additionally, the system includes a voltage and current sensing block which continuously monitors the panel’s output to provide the necessary input data for the FL MPPT controller. The controller output is processed by the PWM generation block, which produces the appropriate switching signals to drive the DC–DC converter. On the output side, the regulated energy can be directed to a battery storage unit, ensuring energy availability during low irradiance periods, as well as to other loads, which represent the actual consumption points of the system. This integration of sensing, control, and power management guarantees that the PV system maintains high efficiency, robust stability, and reliable energy supply under diverse operating conditions.
3. Materials and Methods
This review focuses on the analysis of FLCs and their most relevant contributions in recent years within the field of PV systems. The implementation of fuzzy control techniques in these systems has proven effective in mitigating the impact of external and internal variables that affect their performance, such as low solar irradiance, partial shading, temperature variations, and nonlinear system dynamics. Through the use of rules based on expert knowledge and adaptive schemes, FLCs have enhanced output stability and improved energy efficiency under varying environmental conditions. However, the challenge remains to develop strategies that achieve faster response times and more precise optimization of the energy extracted from the panel, thereby maintaining operation at the MPP and ensuring an efficient supply to the connected loads.
Within the reviews that were carried out, the FLC has managed to position itself as a key element in PV systems due to its rapid response to variations, its ability to manage energy due to changing weather conditions, and the improvement in the quality of the energy supplied. This has enabled advanced studies to be conducted in the design, analysis, performance, and development of techniques to optimize the energy of PV systems, making them adaptable without requiring a complex mathematical model [27,28].
Other studies have analyzed the impact of FLC using neuro-fuzzy systems, a modern technique that is adaptable to complex environments. The authors have applied these neurocontrollers to take advantage of their adaptability in learning automatically from analyzed data in real time, allowing for a reduced number of fuzzy rules and increased accuracy in nonlinear systems [29,30,31]. Some reviews have focused on Type-2 FLCs; these are an extension of Type-1 FLCs that have gained popularity in various areas, including PV systems, where they can provide more robust suppression of the uncertainty of input variables in systems with high-variability environments [32,33].
The bibliographic search for the information sources used in this review was carried out through the Scopus platform database [34]. Table 1 provides a detailed description of the search strategy employed in this review; the keywords were selected based on the key elements that comprise a PV system. The search focused on publications between 2015 and mid-2025, as fuzzy controllers have evolved significantly in recent years. This criterion was applied in order to obtain the most up-to-date information on fuzzy controllers and the techniques used in PV systems.

Table 1.
Search strategy, including search string, inclusion and exclusion criteria, and language.
The application of the search formula to the Scopus platform database generated 1422 publications, which were used to prepare the initial bibliometric analysis. For this purpose, VOSViewer 1.5.5 software was used, a computational tool for constructing and visualizing bibliometric networks [35]. Figure 2 displays a bibliometric density map, highlighting the areas of highest density and those of lower density, which correspond to the most frequent terms in the search results. The central section displays the most frequently used terms, including FL, fuzzy systems, MPPT, and PV. This is due to the significant evolution of fuzzy controllers in a short time and their potential for energy optimization in areas such as PV systems. The peripheral sections contain terms such as algorithms, energy, partial shading, power, and loads. These terms suggest that more specific applications are being developed to achieve maximum efficiency in delivering maximum power from a PV system. It can be seen that the most-researched areas focus on controlling MPPT by using fuzzy controllers to optimize the energy supplied from the solar panel to the loads. A number of research areas focus on improving the power quality of electrical power systems and energy optimization in PV systems through the use of fuzzy and AI techniques, as well as on the analysis and optimization of systems that manage energy transfer to battery banks or other loads. This allows for the observation that research is being focused on improving and optimizing power quality in renewable systems, particularly in the area of PV systems, which can help to reduce greenhouse gas emissions through alternative renewable sources.
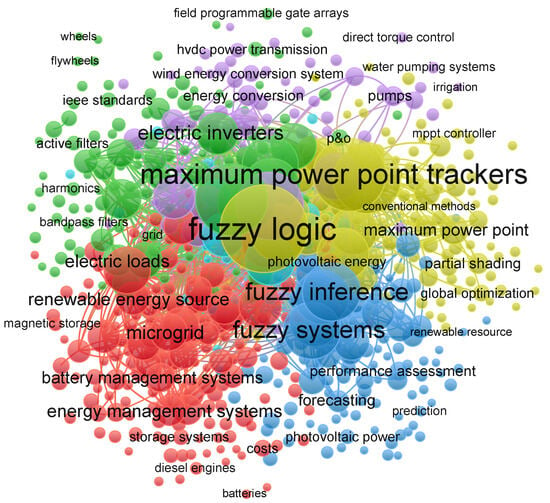
Figure 2.
Keyword co-occurrence network: blue (MPPT), green (fuzzy/optimization), red (microgrids/management), yellow (power quality/inverters), purple (other renewable energy applications).
Figure 2 presents the bibliometric density generated from the selected papers. This analysis covers articles published between 2015 and mid-2025, showing that research on energy optimization through fuzzy logic has consistently remained a central focus within PV systems. In recent years, however, there has been a noticeable shift towards topics such as energy systems management and battery bank optimization, power delivery from renewable sources, integration of proportional–integral–derivative (PID) and fuzzy controllers, development of advanced algorithms, improvements in energy conversion efficiency, and the application of emerging techniques to enhance FL performance.
Figure 3 illustrates the methodology employed, which followed the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) approach for identifying, evaluating, and selecting relevant publications. An initial search in the Scopus database yielded 1422 articles based on specific keywords related to FLCs and PV systems. In the first stage, we excluded articles without a digital object identifier (DOI), duplicates, and those not associated with the selected keywords, resulting in 1045 articles. In the second stage, a manual review of the titles of each publication was conducted in order to exclude articles that only mentioned FLCs without focusing on their application to photovoltaic systems as well as studies on other renewable energy sources, metaheuristic algorithms, or neural networks unrelated to fuzzy control in PV systems. Works addressing applications outside our scope, such as robotics, the Internet of Things, hybrid vehicles, or general power electronics, were excluded as well. This rigorous process eliminated 913 records, leaving a final set of 132 articles that specifically addressed the role of Type-1 and Type-2 fuzzy controllers in PV systems, which were considered eligible for review and analysis.
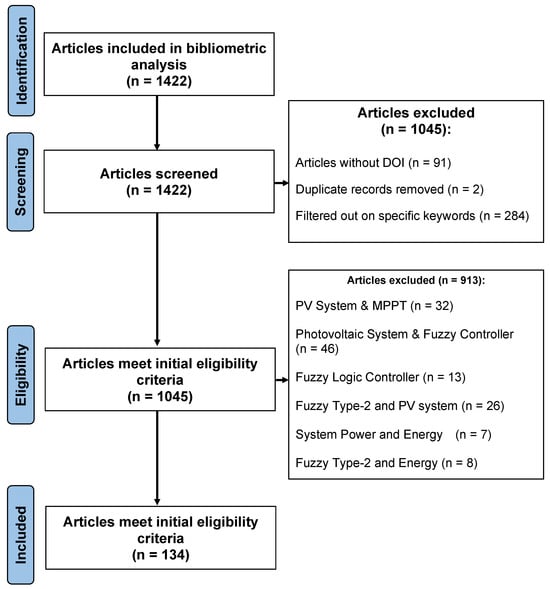
Figure 3.
PRISMA-based flowchart of the systematic selection of relevant studies.
4. Mamdani Fuzzy Control Systems
FLCs are notable for their ability to manage nonlinear systems within complex environments with a high degree of uncertainty in the input variables through the use of FL based on linguistic rules that emulate human reasoning. This feature enables them to reach adaptive decisions without requiring a precise mathematical model of the system. FLCs exhibit high efficiency, robustness, and adaptability to dynamic environments compared to classical control methods, making them a superior alternative for processes where conditions change constantly [36]. An FLC operates using linguistic rules, and is especially suitable for systems with a high degree of ambiguity or uncertainty.
A particular type of FLC, the Mamdani-type fuzzy controller (MFCL), stands out for its human-based approach, utilizing parameterizable membership functions that model variables using imprecise terms such as “low”, “medium”, and “high”. These functions can be triangular, trapezoidal, or bell-shaped, among others, and their shape can be tuned through parameters that control the slope, width, and center.
According to Zainuri [37], the optimal number of fuzzy sets per variable depends on the system’s complexity and the level of precision constraints; nevertheless, they recommend setting up between five and seven fuzzy sets for efficient performance. Unlike Sugeno- or Tsukamoto-type controllers, which prioritize numerical efficiency and require precise mathematical models, the Mamdani approach does not need an exact model, making it more flexible for applications with limited knowledge of the system to be controlled [38].
Figure 4 illustrates the block diagram of an MFLC with a standardized architecture. The structure presented here comprises four well-defined stages: fuzzification, rule base, inference engine, and defuzzification [39]. The fuzzification stage converts the input variables into membership degrees over a previously defined fuzzy set; designers usually use triangular membership functions with normalized values between 0 and 1; these must be properly tuned, as their shape directly influences the system’s performance.
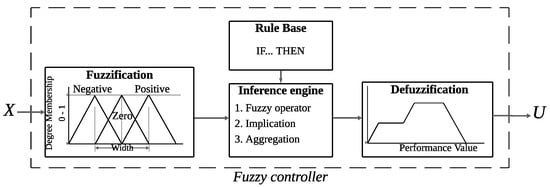
Figure 4.
Overview of a Mamdani fuzzy controller, showing the fuzzification, inference, and defuzzification stages for rule-based decision-making.
The rule base is composed of if-then statements that relate antecedents and consequents using fuzzy operators such as minimum (AND) and maximum (OR), or combinations of both. Subsequently, the inference engine evaluates the rule set and produces a fuzzy output by modifying the consequents according to the computed membership degrees. Finally, the defuzzifier translates the fuzzy output into a numerical value using methods such as centroid or average of maxima, allowing the controller to interact with the real environment.
Several authors who have developed general applications of the MFLC highlight its straightforward interpretation and tuning, especially in environments that integrate multiple renewable energy sources. For example, Bayu [40] conducted a study to manage intelligent systems under uncertain laboratory conditions by applying fuzzy linguistic rules, successfully implementing energy management strategies and optimizing energy distribution to battery banks and specific loads. Similarly, Jasmine [41] proposed a system synchronized with the electrical grid through a PI-controlled inverter; this was complemented with IoT tools to monitor PV parameters in real time, allowing for enhanced optimization and management of the supplied energy. In a different field, Min-Fan Ricky Lee [42] and Yi Yuan [43] improved MFLC performance by incorporating optimization techniques, demonstrating higher energy efficiency in mobile robotic platforms and medical instrumentation.
In addition, Eugenio Salgado-Plasencia [44] addressed accuracy improvement in MFLC and the optimal placement of critical components, which is essential in both industrial and energy processes. Among these domains, PV systems are particularly relevant, since their operation is subject to significant uncertainties, nonlinear behaviors, and dynamic environmental conditions. The performance of PV panels strongly depends on external factors such as solar irradiance, temperature, humidity, partial shading, dust, and dirt [45,46,47] in addition to panel type and orientation. In this context, MFLC plays a pivotal role in maximizing energy performance by controlling MPPT, ensuring maximum power extraction even under abrupt climatic variations.
In PV applications, the conversion of solar to electrical energy is especially sensitive to irradiance and temperature [48,49], both of which are highly nonlinear variables. MFLC contributes to optimizing MPPT by efficiently handling uncertainties in these inputs even when they change rapidly. Engineers can design fuzzy rules to adjust the MPPT operating point, combining expert knowledge with heuristic logic (e.g., “if irradiance is low and temperature is medium, then slightly increase the operating voltage”). This approach enables tracking of the maximum power point even under adverse conditions such as partial shading, where multiple peaks may arise [50]; moreover, MFLC achieves smooth adjustments of input variables (voltage, current, power) even when a precise mathematical model of the PV system is unavailable. Laagoubi [36] and Sutikno [51] confirmed these benefits, reporting significant improvements in the dynamic response of PV systems. Another typical fuzzy rule in MPPT is “if the error is large negative and the error change is small positive, then increase the duty cycle”.
Other studies have specifically advanced the role of MFLCs in PV-based MPPT. For instance, Chouksey [52] demonstrated that a two-input, two-output MFLC regulating both voltage reference and duty cycle could reduce oscillations and improve convergence to the MPP under abrupt irradiance and temperature variations, outperforming deterministic algorithms such as P&O and INC. Building on this line, Cheng [53] introduced a hybrid approach in which the fuzzy parameters were optimized using PSO, successfully overcoming the limitations of manual tuning and achieving faster convergence with reduced steady-state ripples. Complementarily, Shiau, Wei, and Lee [54] focused on hybrid PV–battery systems and highlighted how MFLCs provide smooth voltage regulation and seamless transitions between energy sources, which is particularly relevant for safety-critical or mobile applications such as UAVs.
On the other hand, DC–DC converters enable the efficient adjustment of voltage and output power generated by solar modules, thereby maximizing system efficiency and adapting to the levels required by battery banks or specific loads. In this regard, P. Kamalakar [55] and Tole Sutikno [56] evaluated the variable environmental conditions of the PV system and employed techniques that allowed them to locate and maintain the MPP. This reduces oscillations and regulates the output voltage, which is crucial for protecting loads that are sensitive to voltage variations. These converters can boost, reduce, or reverse the voltage polarity according to system needs, and their integration into PV systems is critical to ensure the stability and efficiency of both the power and the supplied voltage.
In residential environments, PV systems provide support for the energy supply in conjunction with microgrids, where the use of MFLC controllers enables efficient regulation of the energy delivered to the system. Tapia [57] and Huang [58] proposed a system with an MFLC to control electric heaters in residential areas in order to ensure that their operation does not contribute to excessive energy demand. For applications to energy storage, although PI controllers are commonly used to manage the charge of battery banks, their performance can be limited by the variations of the solar panel itself. Due to this situation, M.R. Khan [59] developed MFLC and PI controllers in conjunction to establish a constant voltage and meet the current demand; this increases system efficiency, reduces losses, and prevents premature battery deterioration. MFLCs have also been used to ensure a stable energy supply, reduce dependence on the electricity grid, or balance both systems, as in the case of hydroponic greenhouses. W. Ahmed [60] explored and designed a renewable system with MFLC, achieving greater energy efficiency, cost reduction, and lower environmental impact. In electric vehicle (EV) charging stations, S. Sarita [61] proposed the application of MFLC controllers that allow intelligent management of the power supplied while avoiding overloads and optimizing energy consumption, considering factors such as the vehicle’s charge level, priority of use, and grid status. In addition, process automation has driven the adoption of MFLCs in IoT environments due to its ability to manage the variations and noise inherent in controlled devices. Likewise, Peyghami [62] extended their work to the real-time monitoring of photovoltaic systems within industrial processes, facilitating optimized energy consumption and improved overall performance.
Table 2 presents a detailed selection of works that specifically focus on the application of MFLCs in PV systems. The contributions can be grouped into several categories. First, several studies have concentrated on improving MPPT tracking efficiency and reducing oscillations, such as the adaptive and modified MFLC-based P&O algorithms proposed by Zainuri [37], Krim [63], Slamet [64], and Verma [65], which resulted in fast responses, stable operation, and lower overshoots. Similar results were reported by Giurgi [66] and Bouarroudj [7], who integrated MFLC with PI controllers and optimized structures to enhance system stability further.
Second, the flexibility of MFLCs in handling diverse membership functions and simplified rule bases has been demonstrated. Farah [67] showed that stability can be achieved at high frequencies even with a reduced number of rules, while Sutikno [51] compared triangular, trapezoidal, Gaussian, and generalized bell (Gbell) membership functions, reporting higher precision and robustness with Gbell sets. El-Khatib [68] confirmed these findings by showing shorter rise times and better performance.
Third, efforts have been made in hardware integration of MFLC; Ilyas [69] proposed FPGA-based implementations that improved system efficiency, while Bouarroudj [70] validated their simulations experimentally, confirming stability under real operating conditions.
Fourth, several works focused on enhancing global maximum power point (GMPP) tracking and energy conversion. Nur [71] reported improved DC–AC conversion efficiency, while Naick [72] demonstrated high GMPP tracking performance in TCT-configured PV arrays. Mehmood [73] and Lagudu [74] optimized MPPT with MFLC by improving the dynamic response, reducing total harmonic distortion (THD), and ensuring steady-state stability.
Several advanced works have explored the integration of metaheuristic optimization with MFLC; among these, Jalali [75] applied cuckoo optimization to accelerate convergence and minimize ripples, Laxman [76] used GWO to improve tracking speed and reduce oscillations, and Attia [77] enhanced voltage stability by tuning 49 fuzzy rules with triangular membership functions. These approaches clearly show the synergy between fuzzy inference and bio-inspired algorithms in improving MPPT robustness and adaptability.

Table 2.
Applications of the Mamdani fuzzy controller in PV systems.
Table 2.
Applications of the Mamdani fuzzy controller in PV systems.
| Ref. | Fuzzy Rules | Membership Function | Simulation Platform | Main Contribution |
|---|---|---|---|---|
| [37] | 16, 25, 42 | Triangular | MatLab/Simulink | Adaptive MFLC P&O, fast response, stable, lower overshoot. |
| [63] | 25 | Triangular | MatLab/Simulink | Modified MFLC P&O variable pitch size, minimal oscillations, fast response. |
| [64] | 25 | Triangular | MatLab/Simulink | MFLC with PI control, oscillation reduction, minimal impulses. |
| [65] | 49 | Triangular | MatLab/Simulink | Asymmetric MFLC in GMPP, low energy losses stationary and dynamic. |
| [66] | 49 | Triangular | MatLab/Simulink | PI with MFLC, low energy losses, improved performance. |
| [67] | 8 | Triangular | MatLab/Simulink | Reduced MFLC in rules, stability at high frequencies. |
| [51] | 25 | Triangular Trapezoidal Gaussian Gbell | MatLab/Simulink | MFLC applying Gbell, high precision, stability at high frequencies. |
| [68] | 25 | Triangular | MatLab/Simulink | Better rise time, better performance. |
| [69] | 49 | Triangular Trapezoidal | MatLab/Simulink | MFLC and FPGA card, better efficiency in the PV system. |
| [70] | 5 | Triangular | Matlab/Simulink y Experimental | Improved efficiency, stable even with variations. |
| [71] | 25 | Triangular | MatLab/Simulink | Conversion efficiency DC–AC energy. |
| [7] | 25 | Triangular | MatLab/Simulink | Reduction of oscillations, system stability. |
| [72] | 25 | Triangular | MatLab/Simulink | Tracking efficiency GMPP, configuration TCT, maximum power. |
| [73] | 25, 49 | Triangular | MatLab/Simulink | Optimizes MPPT, improves dynamic response, reduces THD factor. |
| [74] | 25 | Triangular | MatLab/Simulink | MPPT tracking efficiency, lower oscillations |
| [75] | 25 | Triangular | MatLab/Simulink | Convergence speed, reduction in ripples, high efficiency. |
| [77] | 49 | Triangular | MatLab/Simulink | Voltage stability of the system, without oscillations in steady state. |
| [76] | 20 | Triangular | MatLab/Simulink | Improved MPPT tracking speed, reduced oscillations. |
5. Takagi–Sugeno Fuzzy Controllers in Photovoltaic Systems
The T-S FL approach, commonly known as the Sugeno or TSK model, is one of the most advanced and widely applied fuzzy inference mechanisms in modern control systems. Initially proposed by Takagi and Sugeno in 1985 [78], this model was designed to overcome certain inherent limitations of traditional fuzzy control approaches, including those found in Mamdani-type systems. The core concept of T-S fuzzy controllers lies in using a set of if–then rules with consequents that are mathematical functions—typically linear, affine, or constant—of the system inputs, in contrast to the fuzzy sets used in Mamdani inference systems [79].
In classical Mamdani fuzzy models, a defuzzification step is required to convert the fuzzy consequents into a crisp output. This process, although fundamental for obtaining actionable control signals, introduces additional computational overhead that can hinder the controller’s responsiveness, especially in real-time applications where low latency is critical. Furthermore, the complexity of the defuzzification procedure grows with the number of rules and the granularity of the membership functions, making the computational burden even more significant in large-scale systems. In contrast, T-S fuzzy controllers inherently produce crisp outputs without requiring an explicit defuzzification stage. This is achieved by combining the outputs of the individual fuzzy rules through a weighted average of the activated consequents, where the weights are determined by the degree of activation of each rule. As a result, T-S controllers offer higher computational efficiency [80]. They are particularly well-suited for real-time implementations, including in PV energy systems, where rapid adaptation to environmental changes such as fluctuations in solar irradiance or temperature is essential for maximizing energy conversion efficiency. A further significant advantage of T-S fuzzy systems lies in their ability to approximate nonlinear system dynamics through a structured set of local linear models. In this framework, each fuzzy rule represents a linearized model of the system’s behavior within a specific operating region, effectively capturing the local dynamics [81]. The overall control law is obtained by smoothly interpolating between these local models according to the degree of rule activation, resulting in a continuous and differentiable control surface. This property not only ensures smooth transitions between operating regions but also enables the application of rigorous stability and performance analysis techniques. In particular, methods such as Lyapunov stability theory and linear matrix inequalities (LMI) [82] can be systematically employed to design and verify T-S controllers, offering a solid theoretical foundation for guaranteeing robust performance in the presence of uncertainties and disturbances.
Equations (1) and (2) present the general form of a T-S fuzzy model, where each local rule defines its consequent as a linear combination of the input variables.
Each rule is activated to a certain degree according to the fuzzy premise conditions. The partial outputs are then combined in the Weighted Average block, which computes the global output as the weighted average of the local outputs, using the firing strengths as weights.
Figure 5 illustrates the structure of the T-S fuzzy controller, where the input vector is processed through M local rules. Each rule generates a partial output through a linear function of the inputs, and all partial outputs are aggregated in the weighted average block to produce the final system output.
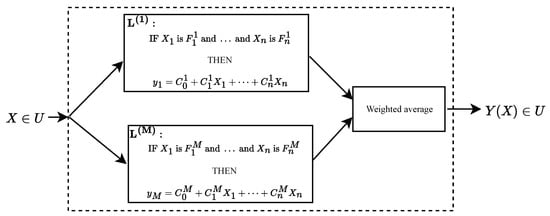
Figure 5.
Structure of a T-S fuzzy logic controller, consisting of M local linear rules and a weighted average block that produces the global output .
In the context of PV applications, T-S fuzzy controllers have gained significant attention due to their superior ability to handle the nonlinear and time-varying nature of solar energy conversion systems. PV arrays operate under highly dynamic environmental conditions, since solar irradiance and temperature can vary abruptly due to factors such as passing clouds, partial shading, or seasonal changes [83]. These fluctuations directly affect the PV output voltage and current, altering the operating point and making it challenging to maintain optimal performance. The inherent adaptability and fast response of T-S fuzzy logic provide a distinct advantage in such scenarios, enabling controllers to react swiftly to parameter changes while preserving stability and maximizing energy harvesting.
One of the most impactful applications of T-S fuzzy controllers in PV systems is within MPPT strategies. Efficient MPPT is essential to ensure that the PV array consistently operates at its MPP, thereby optimizing energy yield. Conventional MPPT algorithms such as P&O and Incremental Conductance (IncCond), while simple and widely adopted, suffer from inherent drawbacks such as oscillations around the MPP in steady-state, slow convergence under rapidly changing environmental conditions, and vulnerability to local maxima in the presence of partial shading [84]. These limitations can lead to noticeable energy losses, particularly in complex and unpredictable operational environments. T-S fuzzy MPPT controllers overcome these challenges by combining expert-defined fuzzy rules with local linear models to dynamically and adaptively adjust the duty cycle of the power converter. This hybrid approach leverages the interpretability of FL with the computational efficiency of linear modeling, enabling fast convergence towards the true MPP even under adverse conditions. Experimental and simulation-based studies confirm these benefits: Oubella [85] showed that a 25-rule T-S MPPT implemented on a cost-effective PIC microcontroller could achieve efficient tracking with reduced ripples, while Hadjidj [86] proved that even a compact four-rule T-S design was sufficient to achieve GMPP tracking under partial shading while delivering fast convergence with minimal overshoot. These results highlight both the scalability and robustness of T-S fuzzy MPPT controllers across different levels of hardware complexity and operating conditions.
In this context, the study by Palaniswamy and Srinivasan [87] demonstrated the capacity of a T–S fuzzy control approach for standalone PV systems to improve both tracking speed and stability under varying irradiance conditions. Their design, which defined rule consequents as linear equations, simplified the defuzzification process and improved computational efficiency compared to classical Mamdani-based controllers. Simulations confirmed that the proposed algorithm consistently outperformed incremental conductance by achieving faster convergence with minimal oscillations. At the same time, its implementation on a DC–DC boost converter highlighted the feasibility for embedded applications. Nevertheless, the accuracy of this approach depended strongly on the adequacy of the rule base and parameter tuning, which may limit its generalization across different PV modules and system configurations.
Building on this line of research, Kamal, Aitouche, and Ould Bouamama [88] introduced a robust T-S fuzzy framework that explicitly addressed parameter uncertainty through linear matrix inequalities. By integrating fuzzy reasoning with rigorous robust control theory, the authors ensured stability and resilience under temperature, irradiance, and electrical variations, outperforming both Mamdani FLCs and heuristic MPPT algorithms such as P&O in terms of convergence speed and reduced oscillations. While this integration offered clear theoretical and practical advantages, it also introduced higher design complexity and computational demands, potentially restricting implementation in low-cost microcontrollers. Despite these challenges, the study underscored the potential of robust fuzzy formulations to enhance both MPPT efficiency and long-term stability under uncertain real-world conditions.
Further refinements have been explored to strengthen the reliability of MPPT operation in highly dynamic environments. Aboulkassim [89] introduced an LMI-based state feedback strategy within the T-S framework, ensuring mathematical stability and minimizing ripples, while Ahmouda [90] integrated a variable step-size P&O approach to eliminate steady-state oscillations. Similarly, Chaibi [91] incorporated H-infinity robust control into a T-S fuzzy design, maintaining consistent MPPT performance under severe partial shading scenarios. Collectively, these works confirm that the adaptability of T-S fuzzy controllers extends beyond rapid convergence, providing systematic tools to guarantee stability, robustness, and resilience under fluctuating irradiance conditions.
In grid-connected PV systems, inverters must comply with stringent standards for voltage regulation, frequency stability, reactive power support, and low harmonic distortion, as mandated by IEEE 1547. T-S fuzzy inference has proven particularly effective in this domain. Asif [92] enhanced this line of research by applying ANFIS structures that allowed online adaptation of fuzzy parameters, resulting in robust performance under grid fluctuations. In parallel, Pidikiti [93] designed a single-stage grid-tied inverter with embedded T-S fuzzy MPPT, which maintained precise power tracking and stability even during voltage sags, swells, and frequency deviations. These findings reinforce that the integration of T-S fuzzy logic in inverter-based architectures is not only beneficial for MPPT accuracy but also crucial for guaranteeing grid code compliance and improving overall power quality.
In addition to conventional MPPT and inverter designs, T-S fuzzy controllers have also been applied to specialized PV-based systems. Ben Safia [94] proposed a decentralized T-S fuzzy framework that managed both MPPT and water pumping powered by PV arrays, demonstrating that such controllers can simultaneously balance energy extraction and load regulation under dynamically varying irradiance and demand. Basu [95] addressed the growing relevance of energy storage by implementing a gain-scheduled T-S fuzzy controller for bidirectional DC–DC converters. Validated on an OPAL-RT hardware-in-the-loop setup, their design enabled stable charging and discharging cycles, safeguarded battery health, and improved overall system reliability by reducing switching losses and preventing overcharging or deep discharging. Together, these contributions illustrate that the application of T-S fuzzy logic extends to diverse PV domains, from generation and grid integration to storage and load management, thereby consolidating its role as a comprehensive control strategy for next-generation PV energy systems.
On the other hand, recent research trends have sought to integrate T-S fuzzy controllers with AI and optimization techniques to further enhance adaptability and intelligence. Metaheuristic algorithms such as PSO, GWO, and the firefly algorithm (FA) [96] have been applied to automate the tuning of fuzzy membership functions and rule bases, reducing manual design effort and improving robustness against uncertainty. These hybrid approaches demonstrate the potential of combining T-S fuzzy logic with predictive control, reinforcement learning, and cloud-based optimization to create intelligent, resilient, and efficient PV systems capable of maintaining optimal performance under the most variable and uncertain operating conditions.
Table 3 summarizes recent studies on the application of T-S fuzzy controllers to PV systems. The table provides a structured state-of-the-art overview, highlighting the control objectives, system configurations, and main contributions. This compilation allows for a clear comparison of methodologies and outcomes, offering valuable insights into current trends and research gaps in TS-based PV control strategies.

Table 3.
Applications of Takagi–Sugeno fuzzy controllers in PV systems (2020–2025).
6. Type-2 Fuzzy Systems
Type-2 FL is an advanced extension of the Type-1 FL paradigm, which aims to more precisely manage the levels of uncertainty inherent in many real-world systems. Unlike Type-1 logic, which uses well-defined membership functions with numerical values between 0 and 1, Type-2 FL introduces an additional level of imprecision by allowing these membership degrees to be subject to uncertainty. In other words, instead of assigning a single membership value to an element within a fuzzy set, a fuzzy membership function is assigned to each value within the set. This enables the modeling of vagueness in the input variables and the degree of certainty associated with those assignments [97].
One of the main defining characteristics of Type-2 FL is the footprint of uncertainty (FOU), which represents the set of all possible membership values that a variable can take; as displayed in Figure 6, this introduces a tolerance region around each membership function.
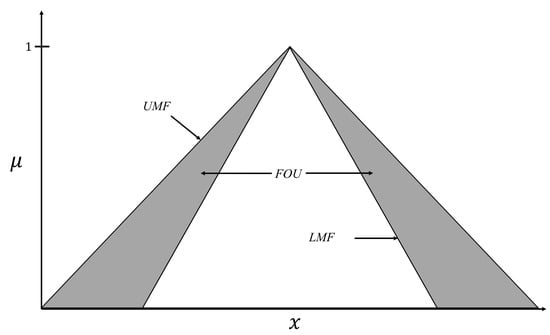
Figure 6.
Structure of a triangular Type-2 membership function.
This area captures the variability caused by measurement errors, environmental fluctuations, or incomplete information. Another relevant feature is the type reduction process, which transforms the Type-2 output into a Type-1 production to allow for the final defuzzification stage. Although this increases the computational complexity of the system, it provides significantly greater capability to represent and manage uncertainty compared to Type-1 systems. The architecture of a Type-2 FLS is presented in Figure 7, showing the five main components: fuzzification, rule base, inference engine, type reduction, and defuzzification. Among these, the type reduction stage is the most distinctive and computationally demanding feature of Type-2 systems [98]. It transforms the fuzzy output of the inference engine, which is still Type-2, into a Type-1 fuzzy set that can be defuzzified. Algorithms such as Karnik–Mendel (KM) and its extensions are commonly employed to perform this reduction by iteratively computing interval bounds for the output. This step is critical, as it preserves and conveys the embedded uncertainty of the system’s reasoning process into a usable output form. The precision and robustness achieved by a T2FLS, particularly in control and prediction tasks under uncertainty, depend primarily on the quality and efficiency of the applied type reduction method. Therefore, type reduction is not only a computational bridge but also the key enabler that distinguishes Type-2 fuzzy systems from their Type-1 counterparts in real-world decision-making contexts [99].
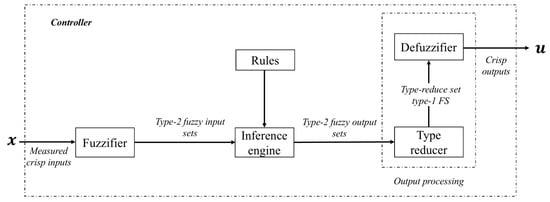
Figure 7.
Block diagram of the Type-2 FLC architecture.
This capability is particularly valuable in the context of PV systems, given the highly variable nature of operating conditions. Factors such as solar irradiance, ambient temperature, dust, partial shading, and the behavior of connected loads can introduce dynamic variations that affect system performance. Conventional methods such as deterministic algorithms or even Type-1 fuzzy controllers are often not flexible enough to accommodate these fluctuations in real time. One of the most notable applications of Type-2 FL in PV systems is MPPT. This procedure seeks to operate the solar panel at the optimal point where the generated power is at its maximum even when external conditions change rapidly [100,101]. The use of Type-2 controllers enables a more precise response to these variations, reducing the tracking error and enhancing overall system efficiency. T2FLC has also been used in inverter control to improve output signal quality, minimize THD, and manage hybrid systems that integrate multiple energy sources [102].
Recent advancements have expanded the role of Type-2 FL in PV systems by integrating it with robust and intelligent control strategies to enhance MPPT performance. Applications combining Type-2 fuzzy inference with super-twisting sliding mode control or ANNs have demonstrated improved tracking accuracy, reduced chattering, and increased system stability under rapidly changing irradiance conditions [103]. Additionally, Type-2 FL has proven effective in intelligent fault diagnosis, working in conjunction with machine learning methods to identify anomalies such as short circuits or partial shading. A further contribution involves its integration with quasi-Z-source converters, which enhances voltage boosting and continuity of input current in dynamic environments [104]. In such configurations, Type-2 fuzzy MPPT controllers have shown superior convergence to track the GMPP under partial shading, highlighting the growing trend of hybrid approaches that merge advanced power electronics with uncertainty-aware computational intelligence. Extending beyond MPPT, Type-2 FL has also been applied to the adaptive control of grid-connected inverters. For example, an adaptive interval Type-2 fuzzy approximation controller (AIT2FAC) has shown improved current regulation and disturbance rejection in three-phase PV inverters without requiring a precise system model, demonstrating the broader applicability of Type-2 logic in enhancing inverter stability and grid integration [105]. A study by Tsai and Huang [106] proposed an interval Type-2 fuzzy logic controller (IT2FLC) for MPPT in photovoltaic charging systems, emphasizing its capacity to manage the uncertainty and nonlinear dynamics of PV arrays more effectively than conventional Type-1 approaches. The IT2FLC was implemented to regulate the duty cycle of a DC–DC converter, enabling smoother convergence to the MPP under varying irradiance and load conditions. Simulation and experimental results demonstrated that the IT2FLC achieved faster response and reduced oscillations compared to perturb-and-observe methods while also improving voltage stability during charging cycles. A key contribution of this work lies in its demonstration of the practical feasibility of IT2FLCs, showing that uncertainty modeling through FOUs can enhance both robustness and reliability in real-world PV systems. However, the study also highlighted the increased computational requirements of the type reduction and defuzzification processes, which may pose a challenge to deployment on resource-constrained embedded platforms. Despite this limitation, the above work serves as an essential reference in the evolution of Type-2 fuzzy MPPT strategies, bridging the gap between theoretical robustness and experimental validation.
Further advancements have explored the integration of Type-2 fuzzy control systems with metaheuristic optimization algorithms to automatically tune the fuzzy membership functions and rule bases for MPPT applications [107]. Designing effective fuzzy controllers typically involves defining appropriate membership functions, linguistic rules, and inference strategies, which are traditionally handled through expert knowledge or trial-and-error procedures [108,109]. However, these manual approaches often fall short in dynamic environments such as PV systems, where optimal control parameters may vary significantly due to changes in irradiance, temperature, and load conditions. To address this, researchers have increasingly turned to metaheuristic algorithms as an automated and adaptive means of optimizing fuzzy systems. Metaheuristic techniques such as PSO, GA, artificial bee colony (ABC), and FA have been successfully applied to the tuning of interval Type-2 FL systems (IT2FLSs) for MPPT. These algorithms offer global search capabilities and flexibility in handling complex, nonlinear, and high-dimensional optimization landscapes [110,111]. By encoding fuzzy system parameters such as the shape, width, and position of the membership functions or the structure of the fuzzy rule base into candidate solutions, these methods evolve populations over successive generations toward optimal configurations that maximize control performance. The resulting systems are not only more accurate and responsive but also more robust to the inherent uncertainty and variability present in PV environments [112,113].
The study by Haraoubia, Hamzaoui, and Essounbouli [114] introduced an IT2FLC approach for MPPT in which the membership functions were tuned using a genetic algorithm (GA). This hybridization addresses one of the main challenges of IT2FLC design, namely, the complexity of determining suitable footprints of uncertainty and rule parameters. By leveraging GA optimization, the controller demonstrated improved convergence speed toward the MPP and reduced oscillations compared to conventional Type-1 FLCs and perturb-and-observe methods. Simulation results under dynamic irradiance confirmed the enhanced robustness of the IT2FLC in handling the nonlinearities and parameter uncertainties inherent in PV systems. However, the computational overhead introduced by both the interval type reduction process and GA-based tuning raises questions regarding scalability for real-time embedded applications. Despite these limitations, this contribution represents an important milestone in advancing Type-2 fuzzy MPPT strategies by showing the potential of combining intelligent optimization with fuzzy inference to improve adaptability and tracking precision. Kececioglu [115] proposed a hybrid MPPT strategy that integrates an interval Type-2 Takagi–Sugeno–Kang FLC (IT2-TSK-FLC) with the FA to optimize the performance of PV systems using a positive-output elementary super-lift Luo converter (POESLLC). While efficient and capable of high voltage gain, this converter is highly sensitive to control signal variations under dynamic conditions. To address this, the FA dynamically adjusts fuzzy scaling factors and rule parameters, enhancing tracking precision and reducing settling time by up to 90%. This approach demonstrated an improvement of over 10% in efficiency compared to non-optimized Type-2 controllers, with robust performance under variable irradiance and temperature. More broadly, the integration of IT2FLSs with bio-inspired metaheuristic algorithms can enable real-time adaptability, leading to improved convergence speed and increased resilience to uncertainty. These hybrid systems consistently outperform static fuzzy controllers, particularly under partial shading and noisy conditions, highlighting a growing trend toward intelligent and self-adaptive MPPT solutions in advanced PV architectures [116].
In addition to their direct application in MPPT and fault detection, IT2FLSs have demonstrated remarkable capabilities in modeling and forecasting solar radiation, a task that is inherently fraught with uncertainty due to meteorological variability. Accurate solar radiation prediction plays a vital role in the planning, control, and optimization of PV systems, particularly in energy management tasks such as dynamic load balancing, battery scheduling, and grid integration. Traditional forecasting methods often rely on statistical or numerical models that struggle to capture the nonlinear, nonstationary, and context-dependent nature of solar irradiance data [117]. In contrast, IT2FLSs provide a powerful alternative by explicitly accounting for the uncertainty and imprecision present in both the measurement data and the model structure. By introducing an FOU around the membership functions, IT2FLSs allow for more flexible representations of input–output relationships, leading to better generalization and robustness in the face of noisy or incomplete environmental data. Furthermore, these systems can be adapted to hybrid architectures that combine data-driven learning with expert knowledge, enabling them to operate effectively even in locations with limited historical data [118]. The ability of IT2FLSs to integrate human expertise, historical patterns, and real-time measurements within a unified framework makes them ideal candidates for next-generation solar forecasting engines. Their application is not limited to daily or hourly predictions; IT2FLSs have also shown promise in very short-term forecasting (e.g., minute-level resolution), which is critical for real-time power regulation and demand response scenarios [119]. As such, the role of interval Type-2 FL extends beyond control into the broader domain of intelligent solar energy management, serving as a bridge between prediction, decision-making, and autonomous control in uncertain and dynamically changing environments.
Recent developments in solar radiation forecasting have highlighted the effectiveness of IT2FLSs in modeling uncertainty while maintaining computational efficiency. Almaraashi [120] proposed a hybrid architecture combining Type-1 and Type-2 fuzzy components optimized via simulated annealing, which achieved notable improvements in prediction accuracy and reduced computational cost, building on the life-long learning framework with explainable AI features introduced in [121] to enable real-time adaptation to new data along with enhanced system transparency and autonomy. Complementarily, Jafarzadeh [122] demonstrated the superior performance of IT2-TSK models with Type-2 antecedents and crisp consequents (A2-C0) for solar power prediction. These models not only outperformed classical and Type-1 approaches in terms of root mean square error (RMSE) but also provided meaningful uncertainty bounds, making them valuable tools for energy forecasting in critical grid applications. On the other hand, Jain [123] extended the application of IT2FLSs beyond forecasting to real-time energy management, developing a power-sharing strategy for hybrid energy storage systems in solar-powered EV charging stations. Their fuzzy logic-based controller was able to effectively coordinate the energy flow between batteries and supercapacitors under fluctuating solar and load conditions, resulting in improved system responsiveness, energy efficiency, and battery longevity. This example reinforces the versatility of IT2FLSs across both the predictive and operational layers of solar energy systems.
The continuous evolution of PV systems has led to the exploration of advanced control and power conversion strategies capable of coping with nonlinear dynamics and operational uncertainty. In this context, the integration of high-gain DC–DC converters with interval Type-2 FLCs has become increasingly relevant due to their superior ability to manage imprecise inputs, adapt to changing environmental conditions, and ensure robust energy delivery. In addition to conventional MPPT, recent developments have expanded the use of T2FLCs to broader energy management roles in hybrid PV architectures. For example, Shaaban [124] implemented a T2FLC-based energy management system (EMS) in a PV–battery–grid setup, successfully mitigating voltage sags and achieving smoother transitions between power sources compared to traditional and Type-1 fuzzy approaches. Similarly, Kumar [125] introduced a novel BIFRED (Boost-Integrated Flyback–Forward) converter managed by a T2FLC MPPT controller tailored for EV charging applications. Their results revealed notable improvements in dynamic response and voltage regulation under fluctuating irradiance, with tracking efficiencies reaching up to 96.6%. Further advancing the field, Rinesh [126] proposed a hybrid system that integrates T2FLCs with GA and multilayer perceptrons (MLPs) for real-time optimization of solar panel orientation. Their approach maintained high power generation (94.5%) and tracking accuracy (96.5%) while keeping computational demands low (10.5%), demonstrating the effectiveness of combining T2FLCs with machine learning and evolutionary algorithms. Collectively, these contributions illustrate the growing potential of Type-2 FL as a core component in intelligent, high-efficiency, and adaptive solar energy systems. Table 4 summarizes the main characteristics and contributions of the articles presented in this section, highlighting how IT2FLSs have been applied across different PV domains from MPPT optimization and converter regulation to grid integration, energy storage, and sustainability assessment. The comparison emphasizes the versatility and robustness of IT2FLSs in addressing the nonlinearities, uncertainties, and dynamic conditions inherent to PV systems.

Table 4.
Applications of interval Type-2 fuzzy logic systems in PV systems.
7. Discussion
Figure 8 shows the results of the percentage distribution of the most relevant keywords in PV systems as determined using the Scopus platform. PV systems are highlighted as the central focus of our analysis, representing all the components such as converters, inverters, controllers, batteries, etc., that comprise them. The use of techniques such as MPPT and fuzzy control is an essential element in the optimization and development of more efficient and sustainable systems seeking to maximize the performance of PV systems by applying metaheuristic algorithms related to MPPT and proper energy management.
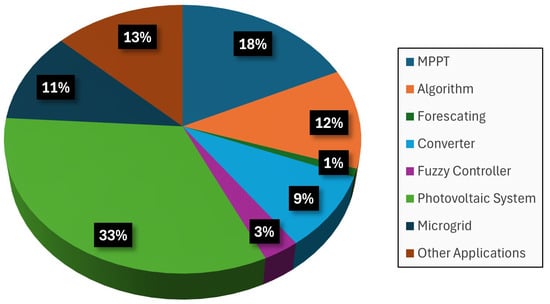
Figure 8.
Percentage chart illustrating the distribution of research areas related to PV systems.
Within the analysis of FLCs applied to PV systems, research has consistently shown that performance can be significantly enhanced by tailoring the system design to the specific process being controlled. MFLCs remain one of the most widely used approaches, especially in applications where interpretability and low computational demand are priorities. For instance, Zainuri [37] evaluated hybrid MPPT algorithms with 4, 5, and 7 membership functions, showing that the MFLC achieved reduced overshoot; however, an excessive number of functions (seven) compromised stability, with the best tradeoff obtained using five. Slamet [64] simplified the rule base to ten fuzzy rules with a single input variable, reducing computational load while maintaining acceptable performance. Verma [65] focused on partial shading conditions, applying asymmetric membership functions to improve GMPP tracking and minimize energy losses, while Mehmood [73] combined MFLC with 49 fuzzy rules and harmonic elimination in inverters, achieving reduced THD and superior efficiency in grid-connected systems. Collectively, these contributions demonstrate that MFLCs are versatile and robust for a wide range of PV applications. Nonetheless, their effectiveness is highly dependent on careful tuning of membership functions and rule bases as well as hybridization with complementary control methods.
In contrast, T-S FLCs excel in scenarios that require fast dynamic response and reduced computational burden. Features such as elimination of the defuzzification stage and reliance on linear consequents make them particularly suitable for real-time PV applications. Pidikiti [93] demonstrated this advantage by designing an inverter regulated with a T-S fuzzy model combined with a Kalman filter, achieving oscillations below 1% and lower THD under nonlinear loads. Basu [95] validated a gain-scheduled T-S controller in a PV-battery microgrid, showing that it reduced current oscillations and achieved millisecond-level responses compared to the slower performance of PI controllers. These studies underline that while T-S controllers can provide superior precision and speed, their effectiveness depends strongly on the availability of accurate models and careful parameter scheduling, which can limit their applicability in systems with high parameter uncertainty.
In addition to these approaches, IT2FLCs represent the most advanced evolution of fuzzy inference in PV systems, explicitly designed to handle high levels of uncertainty and sensor noise. Tsai [106] implemented a Type-2 controller with seven fuzzy sets and an FOU, resulting in improved energy extraction and minimized oscillations in noisy environments. Similarly, Makhloufi [129] optimized the interaction between PV arrays and inverters using five Type-2 fuzzy sets per input, showing that system performance could be enhanced without relying on detailed meteorological data. These studies highlight the potential of Type-2 controllers in adverse and unpredictable operating conditions; however, their higher computational cost remains a challenge for real-time embedded implementations, particularly in low-cost platforms.
Figure 9 complements this discussion by presenting the bibliometric distribution of fuzzy controllers in PV systems. MFLCs dominate the literature due to their simplicity and ease of implementation, especially in off-grid and resource-constrained environments. Nevertheless, an upward trend is evident in the use of T-S and Type-2 controllers. T-S approaches are increasingly favored in high-frequency real-time scenarios, while Type-2 controllers are gaining traction in applications where robustness against uncertainty and noise is critical. This evolution reflects a broader shift in PV research towards more adaptive and computationally sophisticated controllers that can address the limitations of classical FL while meeting the demands of modern renewable energy infrastructures.
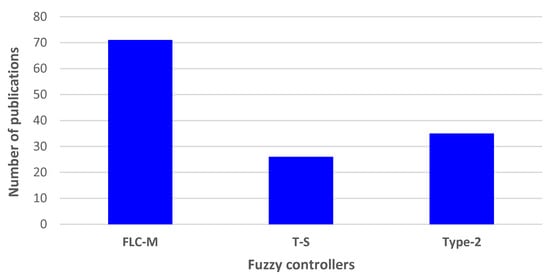
Figure 9.
Distribution of FL controllers by number of publications.
7.1. Critical Insights and Research Gaps
In addition to the outcomes of individual case studies, several broader patterns and gaps emerge. While Mamdani, T-S, and Type-2 controllers each offer clear advantages, most existing research remains confined to simulation or short-term laboratory experiments. The scarcity of long-term outdoor validations under absolute irradiance and grid disturbances limits the generalizability of current findings and raises questions about the scalability of these results to full-scale PV installations [3,136].
Another critical gap concerns the integration of fuzzy control with metaheuristic optimization and artificial intelligence. Although these hybrid approaches accelerate convergence and enhance robustness [137], they often entail significant computational costs and hardware demands. Few studies evaluate the feasibility of implementing such methods on embedded platforms with limited resources, leaving open the challenge of developing lightweight and hardware-friendly solutions that preserve adaptability without compromising efficiency [138].
Moreover, the field lacks standardized benchmarks for comparing fuzzy paradigms in terms of MPPT efficiency, implementation complexity, and execution time. Current studies report improvements in isolation, making it challenging to consistently assess tradeoffs across techniques. Establishing shared performance metrics and experimental protocols would provide a fairer comparison and guide the selection of controllers for real-time PV applications.
Finally, promising avenues remain underexplored, including hybrid frameworks that combine the interpretability of MFLCs, the computational efficiency of the T-S model, and the robustness of Type-2 controllers. Coupled with large-scale validation campaigns and standardization efforts, such integrated approaches could significantly advance the practical deployment of fuzzy control in next-generation PV systems [139,140].
7.2. Limitations of Fuzzy Controllers in PV Systems
Despite the robustness and adaptability of FLCs in PV systems, their implementation faces notable limitations when benchmarked against more advanced or computationally efficient strategies. One of the most recurrent challenges is execution time. The processes of fuzzification, rule evaluation, and defuzzification introduce a computational burden that can compromise real-time operation in embedded systems with limited resources. This drawback is obvious in MFLCs, where centroid-based defuzzification, although providing smooth and interpretable outputs, demands iterative numerical calculations that reduce efficiency when deployed in hardware-constrained devices. Consequently, MFLCs may struggle in scenarios requiring fast dynamic responses under abrupt irradiance changes. In contrast, T-S controllers alleviate part of this overhead by employing linear or constant consequents, eliminating the need for complex defuzzification and improving efficiency. However, their performance depends strongly on the accuracy of the rule base and the parameterization of the linear consequents. If these are not carefully designed to reflect nonlinear PV characteristics, the resulting control law can be suboptimal, even underperforming compared to heuristic or hybrid MPPT algorithms. Thus, while MFLCs excel in interpretability and T-S in computational speed, both exhibit tradeoffs that limit their scalability for next-generation PV converters.
A further limitation concerns accuracy and stability under dynamic operating conditions. Rapid variations in irradiance and temperature often lead MFLCs and T-S controllers to oscillate around the MPP, reducing energy yield, increasing switching losses, and stressing the converter. T2FLCs were introduced to mitigate this issue by explicitly modeling uncertainty within their membership functions through the footprint of uncertainty, resulting in improved resilience to sensor noise, parameter drift, and environmental variability. This enhanced robustness allows for smoother trajectories toward the MPP under fluctuating conditions, but comes at the expense of substantially higher computational complexity. The type reduction and defuzzification stages impose additional processing demands that often exceed the capabilities of the typically low-cost embedded hardware used in PV inverters. As a result, although T2FLCs can provide enhanced robustness, their efficiency in terms of execution time remains less competitive compared to MPC, ANNs, or bio-inspired hybrid algorithms (e.g., PSO-enhanced P&O or DE-based methods), which achieve faster convergence, reduced oscillations at steady state, and higher overall energy conversion efficiency. From a practical perspective, this comparison underscores the tradeoff between robustness and computational feasibility: T2FLCs offer clear advantages in their handling of uncertainty, but their applicability in real-world PV systems remains constrained unless lightweight type-reduction algorithms, hardware accelerators, or high-performance embedded platforms are employed. Table 5 presents a comparative analysis of fuzzy logic controllers applied to PV systems.

Table 5.
Comparative analysis of FLCs applied to MPPT in PV systems.
8. Conclusions
FL-based control has proven to be a powerful and versatile tool for enhancing the efficiency, stability, and adaptability of PV systems under dynamic environmental conditions. Mamdani controllers remain widely adopted due to their simplicity, interpretability, and effectiveness in scenarios with moderate response time requirements. In contrast, T-S controllers excel in real-time high-frequency applications, offering rapid convergence to the MPP and improved power quality in grid-connected systems. Type-2 fuzzy controllers represent the most advanced evolution, capable of managing high uncertainty and sensor noise while maintaining optimal energy extraction. The incorporation of metaheuristic optimization further enhances the adaptability and performance of all fuzzy controller types. Bibliometric analysis indicates a growing research focus on T-S and Type-2 controllers driven by the demand for robust high-performance control solutions in modern PV systems. Future developments are expected to integrate these controllers more deeply with AI, IoT-based monitoring, and advanced energy management strategies, paving the way for more resilient and efficient renewable energy infrastructures.
In the context of PV systems, MFLCs are widely applied in scenarios such as solar-powered irrigation systems in agriculture, autonomous lighting systems, and off-grid rural electrification, which require intuitive rule-based decision-making and robustness to environmental uncertainties. T-S controllers are often implemented in automotive solar auxiliary systems, real-time MPPT algorithms for grid-connected PV installations, and adaptive control of hybrid renewable energy plants thanks to their ability to provide smooth and computationally efficient control outputs. Meanwhile, Type-2 fuzzy controllers offer enhanced performance under high levels of uncertainty; this makes them particularly suitable for outdoor applications with rapidly changing irradiance and temperature, including large-scale PV farms, building-integrated PV systems, and mobile solar charging stations. These application domains demonstrate the flexibility and scalability of fuzzy control strategies for optimizing energy generation and system reliability under diverse operational conditions.
Despite these advances, several challenges and research gaps remain. First, there is a lack of standardized benchmarks that allow for fair comparison between different fuzzy-based MPPT strategies in terms of efficiency, transient response, computational complexity, and hardware feasibility. Second, while many studies have demonstrated effectiveness through simulation, experimental validations under real outdoor conditions remain limited, which restricts the generalization of results to large-scale PV deployments. Third, integration of fuzzy controllers with metaheuristic algorithms often improves performance but comes at the cost of increased computational demand, raising questions about suitability for low-cost or resource-constrained embedded platforms. Moreover, although Type-2 fuzzy controllers show great promise, their design and tuning remain complex, which hampers their widespread adoption in industrial settings. Finally, emerging challenges such as cyber–physical security, interoperability with smart grids, and long-term reliability under harsh environmental conditions require further exploration.
Overall, fuzzy logic controllers—whether Mamdani, T-S, or Type-2—constitute a robust framework for PV optimization; however, addressing the outlined challenges through standardized evaluation metrics, broader experimental testing, and integration with next-generation intelligent systems will be key to fully realizing their potential in advancing sustainable and resilient PV energy infrastructure.
Author Contributions
Conceptualization, R.V.-M. and J.R.G.-M.; methodology, R.V.-M., J.M.Á.-A. and J.R.G.-M.; software, J.M.Á.-A. and J.R.-R.; validation, J.R.G.-M., J.R.-R. and R.R.-G.; formal analysis, R.V.-M., R.R.-G. and J.R.G.-M.; investigation, R.V.-M. and J.R.G.-M.; resources, R.V.-M., R.R.-G. and J.R.G.-M.; data curation, J.M.Á.-A., J.R.G.-M., R.V.-M., R.R.-G., M.G.-L. and J.R.-R.; writing—original draft preparation, R.V.-M. and J.R.G.-M.; writing—review and editing, J.M.Á.-A., R.R.-G., M.G.-L. and J.R.-R.; visualization, J.M.Á.-A., J.R.G.-M., R.V.-M. and R.R.-G.; supervision, J.R.G.-M.; project administration, J.M.Á.-A., J.R.G.-M., R.V.-M., R.R.-G., M.G.-L. and J.R.-R.; funding acquisition, J.M.Á.-A., J.R.G.-M., R.V.-M., R.R.-G., M.G.-L. and J.R.-R. All authors have read and agreed to the published version of the manuscript.
Funding
“Secretaría de Ciencia, Humanidades, Tecnología e Innovación” (SECIHTI) for scholarship support with CVU: 2100052.
Data Availability Statement
Data sharing is not applicable.
Acknowledgments
The first author thanks the “Facultad de Ingeniería en Electrónica y Comunicaciones, Universidad Veracruzana, Región: Poza Rica—Tuxpan” for its support of this research. Grammarly was used to check the grammar in this manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ABC | Artificial Bee Colony algorithm |
| AI | Artificial Intelligence |
| AIT2FAC | Adaptive Internal Type-2 Fuzzy Adaptive Control |
| ANN | Artificial Neural Network |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| BIFRED | Boost-Integrated Flyback–Forward |
| DSP | Digital Signal Processors |
| DC–DC | Direct Current-to-Direct Current |
| DOI | Digital Object Identifier |
| EMS | Energy Management System |
| EV | Electric Vehicle |
| FA | Firefly Algorithm |
| FL | Fuzzy Logic |
| FLC | Fuzzy Logic Controller |
| FLS | Fuzzy Logic System |
| FOU | Footprint of Uncertainty |
| FPGA | Field-Programmable Gate Array |
| GA | Genetic Algorithm |
| GMPP | Global Maximum Power Point |
| GWO | Grey Wolf Optimization |
| HIL | Hardware-in-the-Loop |
| IEEE | Institute of Electrical and Electronics Engineers |
| INC | Incremental Conductance |
| IncCond | Incremental Conductance |
| IoT | Internet of Things |
| IT2FLS | Interval Type-2 Fuzzy Logic System |
| IT2-TKS-FLC | Interval Type-2 Takagi–Sugeno–Kang Fuzzy Logic Controller |
| KM | Karnik–Mendel algorithm |
| LMI | Linear Matrix Inequality |
| MFLC | Mamdani Fuzzy Logic Controller |
| MLP | Multilayer Perception |
| MPP | Maximum Power Point |
| MPPT | Maximum Power Point Tracking |
| MSE | Mean Squared Error |
| OPAL-RT | Trusted Real-Time Simulation Solutions |
| PI | Proportional–Integral |
| PIC | Peripheral Interface Controller |
| PID | Proportional–Integral–Derivative |
| P&O | Perturb-and-Observe |
| POESLLC | Positive-Output Elementary Super-Lift Luo Converter |
| PQ | Active Power and Reactive Power |
| PRISMA | Preferred Reporting Items for Systematic Reviews and Meta-Analyses |
| PSO | Particle Swarm Optimization |
| PV | Photovoltaic |
| PVA | Apparent Volt-Ampere Power |
| RMSE | Root Mean Square Error |
| T1FLC | Type-1 Fuzzy Logic Controller |
| T2FLC | Type-2 Fuzzy Logic Controller |
| TCT | Total Cross-Tied |
| THD | Total Harmonic Distortion |
| TS FLC | Takagi–Sugeno Fuzzy Logic Controller |
| T-S | Takagi–Sugeno |
References
- Pawar, B.; Batzelis, E.I.; Chakrabarti, S.; Pal, B.C. Grid-forming control for solar PV systems with power reserves. IEEE Trans. Sustain. Energy 2021, 12, 1947–1959. [Google Scholar] [CrossRef]
- Ali, A.I.M.; Mohamed, H.R.A. Improved P&O MPPT algorithm with efficient open-circuit voltage estimation for two-stage grid-integrated PV system under realistic solar radiation. Int. J. Electr. Power Energy Syst. 2022, 137, 107805. [Google Scholar]
- Hassan, A.; Bass, O.; Masoum, M.A.S. An improved genetic algorithm based fractional open circuit voltage MPPT for solar PV systems. Energy Rep. 2023, 9, 1535–1548. [Google Scholar] [CrossRef]
- Ketjoy, N.; Chamsa-ard, W.; Mensin, P. Analysis of factors affecting efficiency of inverters: Case study grid-connected PV systems in lower northern region of Thailand. Energy Rep. 2021, 7, 3857–3868. [Google Scholar] [CrossRef]
- Irshad, A.S.; Ludin, G.A.; Masrur, H.; Ahmadi, M.; Yona, A.; Mikhaylov, A.; Krishnan, N.; Senjyu, T. Optimization of grid-photovoltaic and battery hybrid system with most technically efficient PV technology after the performance analysis. Renew. Energy 2023, 207, 714–730. [Google Scholar] [CrossRef]
- Venkateswari, R.; Sreejith, S. Factors influencing the efficiency of photovoltaic system. Renew. Sustain. Energy Rev. 2019, 101, 376–394. [Google Scholar] [CrossRef]
- Bouarroudj, N.; Abdelkrim, T.; Farhat, M.; Feliu-Batlle, V.; Benlahbib, B.; Boukhetala, D.; Boudjema, F. Fuzzy Logic Controller Based Maximum Power Point Tracking and its Optimal Tuning in Photovoltaic Systems. Serbian J. Electr. Eng. 2021, 18, 351–384. [Google Scholar] [CrossRef]
- Ilyas, A.; Khan, M.R.; Ayyub, M. FPGA based real-time implementation of fuzzy logic controller for maximum power point tracking of solar photovoltaic system. Optik 2022, 213, 164668. [Google Scholar] [CrossRef]
- de Lima, T.M.; Oliveira, J.A.C.B. FPGA-based Fuzzy Logic Controllers Applied to the MPPT of PV Panels—A Systematic Review. IEEE Trans. Fuzzy Syst. 2024, in press. [CrossRef]
- Arcos-Aviles, D.; Pacheco, D.; Pereira, D.; Garcia-Gutierrez, G.; Carrera, E.V.; Ibarra, A.; Ayala, P.; Martínez, W.; Guinjoan, F. A comparison of fuzzy-based energy management systems adjusted by nature-inspired algorithms. Appl. Sci. 2021, 11, 1663. [Google Scholar] [CrossRef]
- Masry, M.Z.E.; Mohammed, A.; Amer, F.; Mubarak, R. New hybrid MPPT technique including artificial intelligence and traditional techniques for extracting the global maximum power from partially shaded PV systems. Sustainability 2023, 15, 10884. [Google Scholar] [CrossRef]
- Zafar, M.H.; Khan, N.M.; Mirza, A.F.; Mansoor, M.; Akhtar, N.; Qadir, M.U.; Khan, N.A.; Moosavi, S.K.R. A novel meta-heuristic optimization algorithm based MPPT control technique for PV systems under complex partial shading condition. Sustain. Energy Technol. Assessments 2021, 47, 101367. [Google Scholar] [CrossRef]
- Abidi, H.; Sidhom, L.; Chihi, I. Systematic literature review and benchmarking for photovoltaic MPPT techniques. Energies 2023, 16, 3509. [Google Scholar] [CrossRef]
- Devarakonda, A.K.; Karuppiah, N.; Selvaraj, T.; Balachandran, P.K.; Shanmugasundaram, R.; Senjyu, T. A comparative analysis of maximum power point techniques for solar photovoltaic systems. Energies 2022, 15, 8776. [Google Scholar] [CrossRef]
- Katche, M.L.; Makokha, A.B.; Zachary, S.O.; Adaramola, M.S. A comprehensive review of maximum power point tracking (MPPT) techniques used in solar PV systems. Energies 2023, 16, 2206. [Google Scholar] [CrossRef]
- Rodríguez-Abreo, O.; Rodríguez-Reséndiz, J.; García-Cerezo, A.; García-Martínez, J.R. Fuzzy logic controller for UAV with gains optimized via genetic algorithm. Heliyon 2024, 10, e26363. [Google Scholar] [CrossRef]
- Rojas-Galván, R.; García-Martínez, J.R.; Cruz-Miguel, E.E.; Barra-Vázquez, O.A.; Olmedo-García, L.F.; Rodríguez-Reséndiz, J. Hunting search algorithm-based adaptive fuzzy tracking controller for an aero-pendulum. Technologies 2024, 12, 63. [Google Scholar] [CrossRef]
- Vinitha, J.; Ramadas, G.; Rani, P.U. PSO based fuzzy logic controller for load frequency control in EV charging station. J. Electr. Eng. Technol. 2024, 19, 193–208. [Google Scholar] [CrossRef]
- Zehra, S.S.; Ahmed, S.H.; Ahmad, I.; Grimaccia, F.; Niccolai, A.; Mussetta, M. A Grey Wolf-Driven Refinement of Fuzzy-Based Controller for Enhanced DC Microgrid Operation. In Proceedings of the 2024 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Yokohama, Japan, 30 June–5 July 2024; pp. 1–8. [Google Scholar]
- Drir, N.; Barazane, L.; Loudini, M. Comparative study of maximum power point tracking methods of photovoltaic systems. In Proceedings of the CISTEM, Tunis, Tunisia, 3–6 November 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Rehman, T.u.; Qaisrani, M.A.; Shafiq, M.B.; Filali Baba, Y.; Aslfattahi, N.; Shahsavar, A.; Cheema, T.A.; Park, C.W. Global perspectives on advancing photovoltaic system performance—A state-of-the-art review. Renew. Sustain. Energy Rev. 2025, 207, 114889. [Google Scholar] [CrossRef]
- Hernández Mora, J.A.; Cortés Borray, A.F.; Balaguera Cañola, D.A.; Urueña Saavedra, M.A. Aplicación de los sistemas fotovoltaicos conectados a la red: Estado del arte. Tecnura 2014, 18, 157–172. [Google Scholar] [CrossRef]
- Roldán Rojas, J. Sistemas fotovoltaicos en Arquitectura y Urbanismo. Rev. Urban. 2005, 12, 45–61. [Google Scholar] [CrossRef]
- Carrera, L.A.I.; Molina-Santana, E.; Álvarez Alvarado, J.M.; García-Martínez, J.R.; Rodríguez-Reséndiz, J. Energy Efficiency Analysis of East-West Oriented Photovoltaic Systems for Buildings: A Technical-Economic-Environmental Approach. IEEE Access 2023, 11, 137660–137679. [Google Scholar] [CrossRef]
- Abou Jieb, Y.; Hossain, E. Photovoltaic Systems; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Ma, T.; Yang, H.; Lu, L. Solar photovoltaic system modeling and performance prediction. Renew. Sustain. Energy Rev. 2014, 36, 304–315. [Google Scholar] [CrossRef]
- Salman, U.H.; Nawaf, S.F.; Salih, M.O. Studying and analyzing the performance of photovoltaic system by using fuzzy logic controller. Bull. Electr. Eng. Inform. 2022, 11, 1687–1695. [Google Scholar] [CrossRef]
- Chekenbah, H.; El Abderrahmani, A.; Aghanim, A.; Maataoui, Y.; Lasri, R. Solving problem of partial shading condition in a photovoltaic system through a self-adaptive fuzzy logic controller. Int. J. Tech. Phys. Probl. Eng. 2021, 13, 130–137. [Google Scholar]
- Dawan, P.; Sriprapha, K.; Kittisontirak, S.; Boonraksa, T.; Junhuathon, N.; Titiroongruang, W.; Niemcharoen, S. Comparison of Power Output Forecasting on the Photovoltaic System Using Adaptive Neuro-Fuzzy Inference Systems and Particle Swarm Optimization-Artificial Neural Network Model. Energies 2020, 13, 351. [Google Scholar] [CrossRef]
- Mansouri, M.M.; Hadjeri, S.; Brahami, M. New Method of Detection, Identification, and Elimination of Photovoltaic System Faults in Real Time Based on the Adaptive Neuro-Fuzzy System. IEEE J. Photovoltaics 2021, 11, 798–806. [Google Scholar] [CrossRef]
- Salameh, T.; Farag, M.M.; Hamid, A.K.; Hussein, M. Adaptive Neuro-Fuzzy Inference System for Accurate Power Forecasting for On-Grid Photovoltaic Systems: A Case Study in Sharjah, UAE. Energy Convers. Manag. X 2025, 26, 100958. [Google Scholar] [CrossRef]
- Seshadri, G.; Marutheswar, G.V. A Novel Architecture for Series-Connected Photovoltaic Distributed System with Enhanced Power Quality Using Type-II Fuzzy Controller. Int. J. Intell. Eng. Syst. 2018, 11, 178–186. [Google Scholar] [CrossRef]
- Gani, A. Improving Dynamic Efficiency of Photovoltaic Generation Systems Using Adaptive Type-2 Fuzzy-Neural Network via EN 50530 Test Procedure. Int. J. Circuit Theory Appl. 2021, 49, 3922–3940. [Google Scholar] [CrossRef]
- Elsevier. Scopus—Abstract and Citation Database. Available online: https://www.scopus.com (accessed on 11 July 2025).
- van Eck, N.J.; Waltman, L. VOSviewer—Visualizing Scientific Landscapes. Available online: https://www.vosviewer.com (accessed on 11 July 2025).
- Laagoubi, T.; Bouzi, M.; Benchagra, M. MPPT & Power Factor Control for Grid Connected PV Systems with Fuzzy Logic Controllers. Int. J. Power Electron. Drive Syst. 2018, 9, 105–113. [Google Scholar] [CrossRef]
- Zainuri, M.A.A.M.; Azari, E.A.; Ibrahim, A.A.; Ayob, A.; Yusof, Y.; Radzi, M.A.M. Analysis of Adaptive Perturb and Observe-Fuzzy Logic Control Maximum Power Point Tracking for Photovoltaic Boost DC-DC Converter. Int. J. Adv. Trends Comput. Sci. Eng. 2019, 8, 201–210. [Google Scholar] [CrossRef]
- Samavat, T.; Nazari, M.; Ghalehnoie, M.; Azimi Nasab, M.; Zand, M.; Sanjeevikumar, P.; Khan, B. A Comparative Analysis of the Mamdani and Sugeno Fuzzy Inference Systems for MPPT of an Islanded PV System. Int. J. Energy Res. 2023, 2023, 7676113. [Google Scholar] [CrossRef]
- Mastacan, L.; Dosoftei, C.C. Temperature Fuzzy Control System with Mamdani Controller. In Proceedings of the 2018 International Conference on Electrical and Power Engineering (ICEPE), Brno, Czech Republic, 18–19 October 2018; pp. 352–356. [Google Scholar] [CrossRef]
- Prasetyo, B.; Aziz, F.S.; Handayani, A.N.; Priharta, A.; Bin Che Ani, A.I. Lux and current analysis on lab-scale smart grid system using Mamdani fuzzy logic controller. J. Mechatron. Electr. Power Veh. Technol. 2020, 11, 11–21. [Google Scholar] [CrossRef]
- Malar, A.J.G.; Kumar, C.A.; Saravanan, A.G. IoT based sustainable wind green energy for smart cities using fuzzy logic based fractional order darwinian particle swarm optimization. Measurement 2020, 166, 108208. [Google Scholar] [CrossRef]
- Lee, M.F.R.; Nugroho, A. Intelligent Energy Management System for Mobile Robot. Sustainability 2022, 14, 10056. [Google Scholar] [CrossRef]
- Yuan, Y.; Long, A.; Wu, Y.; Li, X. Closed-loop transcranial ultrasound stimulation with a fuzzy controller for modulation of motor response and neural activity of mice. J. Neural Eng. 2022, 19, 036046. [Google Scholar] [CrossRef] [PubMed]
- Salgado-Plasencia, E.; Carrillo-Serrano, R.V.; Rivas-Araiza, E.A.; Toledano-Ayala, M. SCADA-Based Heliostat Control System with a Fuzzy Logic Controller for the Heliostat Orientation. Appl. Sci. 2019, 9, 2966. [Google Scholar] [CrossRef]
- Aldosary, A.; Ali, Z.M.; Alhaider, M.M.; Ghahremani, M.; Dadfar, S.; Suzuki, K. A modified shuffled frog algorithm to improve MPPT controller in PV system with storage batteries under variable atmospheric conditions. Control Eng. Pract. 2021, 112, 104831. [Google Scholar] [CrossRef]
- Guo, S.; Abbassi, R.; Jerbi, H.; Rezvani, A.; Suzuki, K. Efficient maximum power point tracking for a photovoltaic using hybrid shuffled frog-leaping and pattern search algorithm under changing environmental conditions. J. Clean. Prod. 2021, 297, 126573. [Google Scholar] [CrossRef]
- Khan, M.; Raza, M.A.; Jumani, T.A.; Mirsaeidi, S.; Ali, A.; Abbas, G.; Touti, E.; Alshahir, A. Modeling of intelligent controllers for solar photovoltaic system under varying irradiation conditions. Front. Energy Res. 2023, 11, 1288486. [Google Scholar] [CrossRef]
- da Rocha, M.V.; Sampaio, L.P.; da Silva, S.A.O. Comparative analysis of MPPT algorithms based on Bat algorithm for PV systems under partial shading condition. Sustain. Energy Technol. Assessments 2020, 40, 100761. [Google Scholar] [CrossRef]
- Dehghani, M.; Taghipour, M.; Gharehpetian, G.B.; Abedi, M. Optimized Fuzzy Controller for MPPT of Grid-connected PV Systems in Rapidly Changing Atmospheric Conditions. J. Mod. Power Syst. Clean Energy 2021, 9, 376–387. [Google Scholar] [CrossRef]
- Sreedhar, R.; Karunanithi, K.; Ramesh, S. Design, implementation and empirical analysis of a cascaded hybrid MPPT controller for grid tied solar photovoltaic systems under partial shaded conditions. Meas. Sens. 2024, 31, 100961. [Google Scholar] [CrossRef]
- Sutikno, T.; Subrata, A.C.; Elkhateb, A. Evaluation of Fuzzy Membership Function Effects for Maximum Power Point Tracking Technique of Photovoltaic System. IEEE Access 2021, 9, 109157–109165. [Google Scholar] [CrossRef]
- Chouksey, L.; Pattanaik, P.A.; Saket, R. Maximum power point tracking of photovoltaic system using two input and two output fuzzy system. In Power Electronics and Renewable Energy Systems: Proceedings of ICPERES 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 245–253. [Google Scholar]
- Cheng, P.C.; Peng, B.R.; Liu, Y.H.; Cheng, Y.S.; Huang, J.W. Optimization of a fuzzy-logic-control-based MPPT algorithm using the particle swarm optimization technique. Energies 2015, 8, 5338–5360. [Google Scholar] [CrossRef]
- Shiau, J.K.; Wei, Y.C.; Lee, M.Y. Fuzzy controller for a voltage-regulated solar-powered MPPT system for hybrid power system applications. Energies 2015, 8, 3292–3312. [Google Scholar] [CrossRef]
- Kamalakar, P.; Kumar, B.S.; Upendar, J. Performance Enhancement of Hybrid-Type Full-Bridge DC/DC Converter with Fuzzy MPPT for Efficient Photovoltaic Power Extraction. SSRG Int. J. Electr. Electron. Eng. 2024, 11, 291–301. [Google Scholar]
- Sutikno, T.; Subrata, A.C.; Jusoh, A. A New FL-MPPT High Voltage DC-DC Converter for PV Solar Application. Distrib. Gener. Altern. Energy J. 2022, 37, 1527–1548. [Google Scholar] [CrossRef]
- Tapia, C.; Ulloa, D.; Pacheco-Cunduri, M.; Hernández-Ambato, J.; Rodríguez-Flores, J.; Herrera-Perez, V. Optimal Fuzzy-Based Energy Management Strategy to Maximize Self-Consumption of PV Systems in the Residential Sector in Ecuador. Energies 2022, 15, 5165. [Google Scholar] [CrossRef]
- Huang, T.; Sun, Y.; Li, B.; Hao, J. A Collaborative Fuzzy Control Strategy of Aggregated Regenerative Electric Heaters for Real-Time Energy Balance in Micro-Grid. IEEE Access 2019, 7, 79388–79399. [Google Scholar] [CrossRef]
- Khan, M.R.; Motakabber, S.M.A.; Alam, A.Z.; Wafa, S.A.F. Fuzzy Logic and PI Controller for Photovoltaic Panel Battery Charging System. IUM Eng. J. 2022, 23, 138–153. [Google Scholar] [CrossRef]
- Ahmed, W.; Sheikh, J.A.; Kouzani, A.Z.; Mahmud, M.A.P. The Role of Single End-Users and Producers on GHG Mitigation in Pakistan—A Case Study. Sustainability 2020, 12, 8351. [Google Scholar] [CrossRef]
- Sarita, S.; Reddy, S.S.; Sujatha, P. Control strategies for power quality enrichment in Distribution network using UPQC. Mater. Today Proc. 2023, 80, 2872–2882. [Google Scholar] [CrossRef]
- Peyghami, S.; Palensky, P.; Fotuhi-Firuzabad, M.; Blaabjerg, F. System-level design for reliability and maintenance scheduling in modern power electronic-based power systems. IEEE Open Access J. Power Energy 2020, 7, 414–429. [Google Scholar] [CrossRef]
- Krim, S.A.; Krim, F.; Afghoul, H.; Abdelmalek, F. An Improved Perturb and Observe MPPT for Photovoltaic Systems Using Fuzzy Step Size. WSEAS Trans. Power Syst. 2024, 19, 105–114. [Google Scholar] [CrossRef]
- Slamet; Rijanto, E.; Nugroho, A.; Ghani, R.A. A Robust Maximum Power Point Tracking Control for PV Panel using Adaptive PI Controller Based on Fuzzy Logic. TELKOMNIKA Telecommun. Comput. Electron. Control 2020, 18, 2999–3010. [Google Scholar] [CrossRef]
- Verma, P.; Garg, R.; Mahajan, P. Asymmetrical fuzzy logic control-based MPPT algorithm for stand-alone photovoltaic systems under partially shaded conditions. Sci. Iran. 2020, 27, 3162–3174. [Google Scholar] [CrossRef]
- Giurgi, G.I.; Szolga, L.A.; Giurgi, D.V. Benefits of Fuzzy Logic on MPPT and PI Controllers in the Chain of Photovoltaic Control Systems. Appl. Sci. 2022, 12, 2318. [Google Scholar] [CrossRef]
- Farah, L.; Haddouche, A.; Haddouche, A. Comparison between proposed fuzzy logic and ANFIS for MPPT control for photovoltaic system. Int. J. Power Electron. Drive Syst. 2020, 11, 1065–1073. [Google Scholar] [CrossRef]
- El-Khatib, M.F.; Sabry, M.N.; Abu El-Sebah, M.I.; Maged, S.A. Experimental Modeling of a New Multi-Degree-of-Freedom Fuzzy Controller Based Maximum Power Point Tracking from a Photovoltaic System. Appl. Syst. Innov. 2022, 5, 114. [Google Scholar] [CrossRef]
- Ilyas, A.; Ayyub, M.; Khan, M.R. Modelling and simulation of MPPT techniques for solar photovoltaic system using genetic algorithm optimised fuzzy logic controller. Int. J. Energy Technol. Policy 2020, 16, 174–195. [Google Scholar] [CrossRef]
- Bouarroudj, N.; Benlahbib, B.; Houam, Y.; Sedraoui, M.; Feliu-Batlle, V.; Abdelkrim, T.; Boukhetala, D.; Boudjema, F. Fuzzy based incremental conductance algorithm stabilized by an optimal integrator for a photovoltaic system under varying operating conditions. Energy Sources Part A Recover. Util. Environ. Eff. 2021, 47, 9682–9707. [Google Scholar] [CrossRef]
- Mohd Taib, N.S.; Mohammad Noor, S.Z.; Musa, S.; Abd Aziz, P.D. Fuzzy logic control based MPPT for standalone photovoltaic system with battery storage. Int. J. Power Electron. Drive Syst. 2023, 14, 2527–2536. [Google Scholar] [CrossRef]
- Naick, B.K.; Chatterjee, K.; Chatterjee, T.K. Fuzzy Logic Controller Based Maximum Power Point Tracking Technique for Different Configurations of Partially Shaded Photovoltaic System. Arch. Electr. Eng. 2018, 67, 307–320. [Google Scholar] [CrossRef]
- Mehmood, F.; Ashraf, N.; Alvarez, L.; Malik, T.N.; Qureshi, H.K.; Kamal, T. Grid integrated photovoltaic system with fuzzy based maximum power point tracking control along with harmonic elimination. Trans. Emerg. Telecommun. Technol. 2020, 31, e3856. [Google Scholar] [CrossRef]
- Lagudu, J.V.; Vulasala, G.; Narayana, S.S. Maximum Energy Harvesting in Solar Photovoltaic System using Fuzzy Logic Technique. Int. J. Ambient Energy 2018, 42, 131–139. [Google Scholar] [CrossRef]
- Zand, A.S.; Mobayen, S.; Zad, H.; Molashahi, H.; Nasiri, M.; Fekih, A. Optimized Fuzzy Controller Based on Cuckoo Optimization Algorithm for Maximum Power-Point Tracking of Photovoltaic Systems. IEEE Access 2022, 10, 71699–71716. [Google Scholar] [CrossRef]
- Bhukya, L.; Annamraju, A.; Srikanth, N.V. A grey wolf optimized fuzzy logic based MPPT for shaded solar photovoltaic systems in microgrids. Int. J. Hydrogen Energy 2021, 46, 10653–10665. [Google Scholar] [CrossRef]
- Attia, H.A.; del Ama, F.G. Stand-alone PV system with MPPT function based on fuzzy logic control for remote building applications. Int. J. Power Electron. Drive Syst. 2019, 10, 842–851. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- MathWorks. Mamdani and Sugeno Fuzzy Inference Systems. Fuzzy Logic Toolbox Documentation. 2022. Available online: https://www.mathworks.com/help/fuzzy/fuzzy-inference-systems.html (accessed on 15 June 2025).
- Precup, R.E.; Nguyen, A.T.; Blažič, S. A survey on fuzzy control for mechatronics applications. Int. J. Syst. Sci. 2024, 55, 771–813. [Google Scholar] [CrossRef]
- Dong, B.T.; Nguyen, T.V.A. Robust Fault-Tolerant Tracking Control for Nonlinear Systems Using a Takagi-Sugeno Fuzzy Model Based on a State and Fault Fuzzy Observer. Int. J. Robust Nonlinear Control 2025, 35, 6207–6229. [Google Scholar] [CrossRef]
- Wang, H.O.; Tanaka, K. An LMI-based approach to control of nonlinear systems via fuzzy model. IEEE Trans. Fuzzy Syst. 2001, 9, 601–615. [Google Scholar]
- Liu, F.; Li, R.; Li, Y.; Yan, R.; Saha, T. Takagi–Sugeno fuzzy model-based approach considering multiple weather factors for the photovoltaic power short-term forecasting. IET Renew. Power Gener. 2017, 11, 1281–1287. [Google Scholar] [CrossRef]
- Eltawil, M.A.; Zhao, Z. MPPT techniques for photovoltaic applications. Renew. Sustain. Energy Rev. 2013, 25, 793–813. [Google Scholar] [CrossRef]
- Oubella, M.; Ajaamoum, M.; Bouachrine, B. Low cost microcontroller implementation of Takagi–Sugeno fuzzy MPPT controller for photovoltaic systems. Int. J. Electr. Comput. Eng. Syst. 2022, 13, 971–981. [Google Scholar] [CrossRef]
- Hadjidj, N.; Benbrahim, M.; Ounnas, D.; Mouss, L.H. Global maximum power point tracking method for photovoltaic systems using Takagi–Sugeno fuzzy models and ANFIS approach. Electr. Eng. Electromechanics 2025, 1, 3–8. [Google Scholar] [CrossRef]
- Palaniswamy, A.M.; Srinivasan, K. Takagi-Sugeno fuzzy approach for power optimization in standalone photovoltaic systems. Sol. Energy 2016, 139, 213–220. [Google Scholar] [CrossRef]
- Kamal, E.; Aitouche, A.; Bouamama, B.O. Robust takagi-sugeno fuzzy control of pv system. In Proceedings of the 2016 International Conference on Control, Decision and Information Technologies (CoDIT), Saint Julian’s, Malta, 6–8 April 2016; pp. 52–58. [Google Scholar]
- Aboulkassim, A.; Kririm, S.; El Hanafi, A.; Ben Hmamou, D. New fuzzy control design for photovoltaic system using LMI technique. E3s Web Conf. 2023, 469, 00089. [Google Scholar] [CrossRef]
- Saidi, K.; Maamoun, M.; Bounekhla, M. A new high performance variable step size perturb-and-observe MPPT algorithm for photovoltaic system. Int. J. Power Electron. Drive Syst. 2019, 10, 1662. [Google Scholar] [CrossRef]
- Chaibi, R.; Bachtiri, R.E.; Hammoumi, K.E.; Yagoubi, M. Photovoltaic System’s MPPT Under Partial Shading Using T-S Fuzzy Robust Control. IFAC PapersOnLine 2022, 55, 214–221. [Google Scholar] [CrossRef]
- Asif.; Ahmad, W.; Qureshi, M.B.; Khan, M.M.; Fayyaz, M.A.B.; Nawaz, R. Optimizing Large-Scale PV Systems with Machine Learning: A Neuro-Fuzzy MPPT Control for PSCs with Uncertainties. Electronics 2023, 12, 1720. [Google Scholar] [CrossRef]
- Pidikiti, T.; Shreedevi.; Gireesha, B.; Subbarao, M.; Krishna, V.M. Design and control of Takagi-Sugeno-Kang fuzzy based inverter for power quality improvement in grid-tied PV systems. Meas. Sens. 2023, 25, 100638. [Google Scholar] [CrossRef]
- Ben Safia, Z.; Allouche, M.; Chaabane, M. Renewable energy management of a hybrid water pumping system (photovoltaic/wind/battery) based on Takagi–Sugeno fuzzy model. Optim. Control Appl. Methods 2023, 44, 373–390. [Google Scholar] [CrossRef]
- Basu, A.; Singh, M. Design and Real Time Digital Simulator Implementation of a Takagi–Sugeno Fuzzy Controller for Battery Management in Photovoltaic Energy System Application. Int. J. Eng. 2022, 35, 2275–2282. [Google Scholar] [CrossRef]
- Ozcan, O.F.; Kilic, H.; Ozguven, O.F. A unified robust hybrid optimized Takagi–Sugeno fuzzy control for hydrogen fuel cell-integrated microgrids. Int. J. Hydrogen Energy 2025, 143, 1279–1294. [Google Scholar] [CrossRef]
- Mittal, K.; Jain, A.; Vaisla, K.S.; Castillo, O.; Kacprzyk, J. A comprehensive review on type 2 fuzzy logic applications: Past, present and future. Eng. Appl. Artif. Intell. 2020, 95, 103916. [Google Scholar] [CrossRef]
- Guler, N.; Ismail, Z.; Hazem, Z.B.; Naik, N. Adaptive fuzzy logic controller-based intelligent energy management system scheme for hybrid electric vehicles. IEEE Access 2024, 12, 173441–173454. [Google Scholar] [CrossRef]
- Wang, C.; Ma, Y.; Shi, Y.; Chen, G. A Type-2 Fuzzy Review Topic-Based Model for Personalized Recommendation. Electron. Commer. Res. 2024. [Google Scholar] [CrossRef]
- Soltani, S.; Kouhanjani, M.J. Fuzzy logic type-2 controller design for MPPT in photovoltaic system. In Proceedings of the 2017 Conference on Electrical Power Distribution Networks (EPDC), Semnan, Iran, 19–20 April 2017; pp. 149–155. [Google Scholar]
- Gheibi, A.; Mohammadi, S.M.A.; Maghfoori, M. Maximum power point tracking of photovoltaic generation based on the type-2 fuzzy logic control method. Energy Procedia 2011, 12, 538–546. [Google Scholar] [CrossRef]
- Altin, N. The type-2 fuzzy logic controller-based maximum power point tracking algorithm and the quadratic boost converter for PV system. J. Electron. Mater. 2018, 47, 4475–4485. [Google Scholar] [CrossRef]
- Kayisli, K. Super twisting sliding mode-type 2 fuzzy MPPT control of solar PV system with parameter optimization under variable irradiance conditions. Ain Shams Eng. J. 2023, 14, 101950. [Google Scholar] [CrossRef]
- Pérez-Briceño, C.; Ponce, P.; Mei, Q.; Robinson, F.A. A Type-2 Fuzzy Logic Expert System for AI Selection in Solar Photovoltaic Applications Based on Data and Literature-Driven Decision Framework. Processes 2025, 13, 1524. [Google Scholar] [CrossRef]
- Shadoul, M.; Yousef, H.; Al Abri, R.; Al-Hinai, A. Adaptive interval type-2 fuzzy tracking control of PV grid-connected inverters. IEEE Access 2021, 9, 130853–130861. [Google Scholar] [CrossRef]
- Tsai, C.C.; Huang, C.C. Interval type-2 fuzzy maximum power point tracking for solar photovoltaic power charging systems. In Proceedings of the 2015 15th International Conference on Control, Automation and Systems (ICCAS), Busan, Republic of Korea, 13–16 October 2015; pp. 1353–1358. [Google Scholar]
- Farajdadian, S.; Hosseini, S.M.H. Optimization of fuzzy-based MPPT controller via metaheuristic techniques for stand-alone PV systems. Int. J. Hydrogen Energy 2019, 44, 25457–25472. [Google Scholar] [CrossRef]
- Sharma, A.K.; Pachauri, R.K.; Choudhury, S.; Minai, A.F.; Alotaibi, M.A.; Malik, H.; Márquez, F.P.G. Role of metaheuristic approaches for implementation of integrated MPPT-PV systems: A comprehensive study. Mathematics 2023, 11, 269. [Google Scholar] [CrossRef]
- Verma, P.; Alam, A.; Sarwar, A.; Tariq, M.; Vahedi, H.; Gupta, D.; Ahmad, S.; Mohamed, A.S.N. Meta-heuristic optimization techniques used for maximum power point tracking in solar PV system. Electronics 2021, 10, 2419. [Google Scholar] [CrossRef]
- Maroua, B.; Zarour, L.; Benbouhenni, H.; Elbarbary, Z.M.S.; Colak, I.; Alammer, M.M. Genetic algorithm type-2 fuzzy logic controller of microgrid system with a fractional-order technique. Sci. Rep. 2025, 15, 6318. [Google Scholar]
- Mishra, V.L.; Chauhan, Y.K.; Verma, K.S. A critical review on advanced reconfigured models and metaheuristics-based MPPT to address complex shadings of solar array. Energy Convers. Manag. 2022, 269, 116099. [Google Scholar] [CrossRef]
- Rezk, H.; Harrag, A. A robust type-2 fuzzy logic-based maximum power point tracking approach for thermoelectric generation systems. Int. J. Energy Res. 2021, 45, 18066–18080. [Google Scholar] [CrossRef]
- Mohamed, R.G. Optimal type-2 fuzzy logic control for sizing and control of grid-connected PV system with battery. In Proceedings of the 2023 24th International Middle East Power System Conference (MEPCON), Mansoura, Egypt, 19–21 December 2023; pp. 1–6. [Google Scholar]
- Amine, H.M.; Abdelaziz, H.; Najib, E. Maximum power point tracking using IT2FL Tuned with GA. Energy Procedia 2015, 83, 399–407. [Google Scholar] [CrossRef]
- Kececioglu, O.F. Design of type-2 fuzzy logic controller optimized with firefly algorithm for maximum power point tracking of photovoltaic system based on super lift Luo converter. Int. J. Numer. Model. Electron. Netw. Devices Fields 2022, 35, e2994. [Google Scholar] [CrossRef]
- Maroua, B.; Zarour, L.; Benbouhenni, H.; Mehazzem, F.; Debdouche, N.; Colak, I. Robust type-2 fuzzy logic control microgrid-connected photovoltaic system with battery energy storage through multi-functional voltage source inverter using direct power control. Energy Rep. 2024, 11, 3117–3134. [Google Scholar] [CrossRef]
- Rojas-Galván, R.; García-Martínez, J.R.; Cruz-Miguel, E.E.; Álvarez-Alvarado, J.M.; Rodríguez-Reséndiz, J. Performance comparison of bio-inspired algorithms for optimizing an ANN-based MPPT forecast for PV systems. Biomimetics 2024, 9, 649. [Google Scholar] [CrossRef]
- Li, J.; Liu, Q. Forecasting of short-term photovoltaic power generation using combined interval type-2 Takagi–Sugeno–Kang fuzzy systems. Int. J. Electr. Power Energy Syst. 2022, 140, 108002. [Google Scholar] [CrossRef]
- Ren, Y.; Wen, Y.; Liu, F.; Zhang, Y.; Zhang, Z. Deep convolution IT2 fuzzy system with adaptive variable selection method for ultra-short-term wind speed prediction. Energy Convers. Manag. 2024, 309, 118420. [Google Scholar] [CrossRef]
- Almaraashi, M.S. A practical design of interval type-2 fuzzy logic systems with application to solar radiation prediction. Cogent Eng. 2024, 11, 2395426. [Google Scholar] [CrossRef]
- Almaraashi, M.; Abdulrahim, M.; Hagras, H. A life-long learning XAI metaheuristic-based type-2 fuzzy system for solar radiation modeling. IEEE Trans. Fuzzy Syst. 2023, 32, 2102–2115. [Google Scholar] [CrossRef]
- Jafarzadeh, S.; Fadali, M.S.; Evrenosoglu, C.Y. Solar power prediction using interval type-2 TSK modeling. IEEE Trans. Sustain. Energy 2012, 4, 333–339. [Google Scholar] [CrossRef]
- Balasundar, C.; Sundarabalan, C.K.; Srinath, N.S.; Sharma, J.; Guerrero, J.M. Interval type-2 fuzzy logic-based power sharing strategy for hybrid energy storage system in solar powered charging station. IEEE Trans. Veh. Technol. 2021, 70, 12450–12461. [Google Scholar]
- Belhadj, S.M.; Meliani, B.; Benbouhenni, H.; Zaidi, S.; Elbarbary, Z.M.S.; Alammer, M.M. Control of multi-level quadratic DC-DC boost converter for photovoltaic systems using type-2 fuzzy logic technique-based MPPT approaches. Heliyon 2025, in press. [CrossRef]
- Kumar, R.T.; Rajan, C.C.A. Novel DC to DC boost integrated BIFRED converter for type-2 MPPT fuzzy-based PV/EV application. In Proceedings of the 2023 International Conference on Energy, Materials and Communication Engineering (ICEMCE), Madurai, India, 14–15 December 2023; pp. 1–6. [Google Scholar]
- Rinesh, S.; Arun, M.; Kumar, S.N.; Prajitha, C.; Kumar, A.P.S. Evaluating the type-2 fuzzy logic controller with multilayer perceptrons for optimal tracking of solar photovoltaic systems. Int. J. Low Carbon Technol. 2025, 20, 394–403. [Google Scholar] [CrossRef]
- Khavari, F.; Ghamari, S.M.; Abdollahzadeh, M.; Mollaee, H. Design of a novel robust type-2 fuzzy-based adaptive backstepping controller optimized with antlion algorithm for buck converter. IET Control Theory Appl. 2023, 17, 1132–1143. [Google Scholar] [CrossRef]
- Liang, Y.; Wang, H.; Hong, W.C. Sustainability evaluation of modern photovoltaic agriculture based on interval type-2 fuzzy AHP-TOPSIS and least squares support vector machine optimized by fireworks algorithm. Energy Eng. 2022, 119, 163. [Google Scholar] [CrossRef]
- Makhloufi, S.; Abdessemed, R. Type-2 fuzzy logic optimum PV/inverter sizing ratio for grid-connected PV systems: Application to selected Algerian locations. J. Electr. Eng. Technol. 2011, 6, 731–741. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Rathinasamy, S. Energy management in photovoltaic battery hybrid systems: A novel type-2 fuzzy control. Int. J. Hydrogen Energy 2020, 45, 20970–20982. [Google Scholar] [CrossRef]
- Altin, N. Single-phase grid interactive PV system with MPPT capability based on type-2 fuzzy logic systems. In Proceedings of the 2012 International Conference on Renewable Energy Research and Applications (ICRERA), Nagasaki, Japan, 11–14 November 2012; pp. 1–6. [Google Scholar]
- Gani, A.; Sekkeli, M. Experimental evaluation of type-2 fuzzy logic controller adapted to real environmental conditions for maximum power point tracking of solar energy systems. Int. J. Circuit Theory Appl. 2022, 50, 4131–4145. [Google Scholar] [CrossRef]
- Kumar, C.S.; Kamaraja, A.S.; Kumar, K.K.; Bhuvanesh, A. Performance evaluation of solar-combined boosting topology for EV battery charger using interval type-2 fuzzy controller. Electr. Eng. 2024, 106, 2325–2345. [Google Scholar] [CrossRef]
- Chuang, C.Y.; Chen, P.S.; Hsu, C.C.; Li, J.Y.; Chen, J.F.; Lin, C.L. Novel maximum power point tracker for PV systems using interval type-2 fuzzy logic controller. In Proceedings of the 2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia (IFEEC 2017–ECCE Asia), Kaohsiung, Taiwan, 3–7 June 2017; pp. 1505–1507. [Google Scholar]
- Prastyawan, A.B.; Efendi, M.Z.; Murdianto, F.D. MPPT full bridge converter using fuzzy type-2. J. Adv. Res. Electr. Eng. 2021, 5, 120–127. [Google Scholar] [CrossRef]
- Singh, P.; Mangu, B.; Saho, S. A new dragonfly optimized fuzzy logic-based MPPT technique for photovoltaic systems. Int. J. Electr. Electron. Res. 2023, 11, 1097–1102. [Google Scholar] [CrossRef]
- García-Gutiérrez, G.; Arcos-Aviles, D.; Carrera, E.V.; Guinjoan, F.; Ibarra, A.; Ayala, P. The Cuckoo Search algorithm applied to fuzzy logic control parameter optimization. In Applications of Cuckoo Search Algorithm and Its Variants; Springer: Berlin/Heidelberg, Germany, 2020; pp. 175–206. [Google Scholar]
- Berrazouane, S.; Mohammedi, K. Parameter optimization via cuckoo optimization algorithm of fuzzy controller for energy management of a hybrid power system. Energy Convers. Manag. 2014, 78, 652–660. [Google Scholar] [CrossRef]
- Boukezata, B.; Chaoui, A.; Gaubert, J.P.; Boutalbi, O. An enhanced control scheme for multifunctional grid connected PV system using fuzzy and predictive direct power control. Bull. Electr. Eng. Inform. 2024, 13, 853–864. [Google Scholar] [CrossRef]
- Zou, Y.; Yan, F.; Wang, X.; Zhang, J. An efficient fuzzy logic control algorithm for photovoltaic maximum power point tracking under partial shading condition. J. Frankl. Inst. 2019, 357, 3135–3149. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).