1. Introduction
The escalating demand for electricity, driven by global economic and demographic growth, has underscored the urgency to diversify energy sources, especially nuclear power [
1]. This change is required by the rapid depletion of non-renewable fossil fuels, contributing to an increasing energy crisis and exacerbating environmental issues such as global warming and air pollution [
2]. In response, a worldwide movement towards clean, efficient, and sustainable renewable energy solutions has gained momentum to support future economic development [
3]. Among these, nuclear energy emerges as a critical component due to its high energy yield, reliability, and wide accessibility [
4]. Its adoption has been widespread, with countries such as France leading in nuclear power facilities within the European Union, even as nations such as Germany move toward decommissioning their plants [
5].
Some methodologies have been developed to estimate the power generation of nuclear power plants (NPPs), which are crucial for decision-making processes. Recent studies have emphasized the importance of ensemble learning in this context [
6], highlighting its ability to improve accuracy and robustness by combining predictions from multiple models. Ensemble learning reduces bias and variance, thus enhancing the reliability and precision of forecasting models in critical structures such as nuclear power plants [
7]. This ensemble learning approach can be used in both homogeneous and heterogeneous forms, using different algorithms such as decision trees, support vector machines, or artificial neural networks trained on various subsets of data, which has been shown to significantly improve the forecasting of power generation [
8].
Accurate forecasting of nuclear power generation is a complex, yet vital issue. It plays a crucial role for energy planners and grid operators in managing the electricity grid efficiently. Accurate forecasts enable companies to incorporate nuclear power availability into their broader energy generation and delivery strategies, ensuring system reliability and reducing the risks of blackouts or shortages. In nuclear power plants, the careful handling of fuel sources, such as uranium, is paramount. Optimized fuel utilization is achievable through accurate forecasting, which helps plant operators plan fueling cycles and efficiently manage inventory. This optimization not only leads to cost savings but also improves plant productivity by facilitating informed decisions regarding the timing and quantity of fuel purchases [
9].
Accurate nuclear power generation forecasting is essential to the economic efficiency of nuclear power stations. By strategically scheduling maintenance activities during periods of lower demand, the need for expensive shutdowns during peak periods can be significantly reduced. This strategy not only ensures a continuous revenue stream but also minimizes operating costs, contributing to the overall sustainability and efficiency of nuclear power generation [
2]. It is essential too to ensure the safety and security of nuclear power plant operations, which are subject to strict safety standards. A reliable forecasting approach help operators organize and schedule maintenance, inspections, and other safety-related tasks. Additionally, they improve preparedness and planning for unexpected circumstances, such as extreme weather events or unexpected operational difficulties. The significance of nuclear power generation forecasting increases as renewable energy sources like solar and wind gain greater use. Predicting nuclear energy is important because while nuclear power provides a stable base load, it supports the integration of intermittent renewable sources by ensuring overall grid reliability. This stability allows more flexible energy sources to be used to compensate for the short-term variability inherent in renewable energy production.
The main contribution of this paper is the proposition of a novel ensemble learning model with a heterogeneous learning structure. Through a comparative evaluation with established forecasting models, the proposed ensemble learning model demonstrates significant performance improvements. It combines three distinct machine learning models, namely least-squares support vector regression (LSSVR), gated recurrent unit (GRU), and long-short-term memory (LTSM) models. Additionally, the forecasting model incorporates feature selection using the RreliefF (Robust relief Feature) algorithm to identify the most relevant features for prediction. The model’s hyperparameters are optimized using a tree-structured Parzen estimator.
The suggested ensemble learning model effectively leverages the strengths of each model while mitigating their limitations through the integration of diverse approaches, including feature selection and hyperparameters tuning. As a result, the model can comprehensively capture a wide range of patterns and generate more accurate predictions compared to conventional models. The heterogeneous structure of the ensemble learning model combines various learning algorithms, leading to improved prediction accuracy and generalization.
The research findings highlight the effectiveness of ensemble learning models with heterogeneous structures and establish their superiority over conventional models in different domains. The contributions of this research are:
The comparison of several machine learning and deep learning models under the scope of nuclear energy generation forecasting using performance metrics;
The implementation of feature selection to improve forecasting’s performance of the machine learning models for the French nuclear fleet dataset;
The creation of a stacking ensemble model, based on LSTM, GRU, and support vector regression (SVR) that outperforms the other models evaluated in this research in terms of performance criteria.
The remainder of the paper is organized as follows:
Section 2 provides a review of related works in this field.
Section 3 presents the proposed research development, including details of the methodology and algorithms employed. The results obtained and a discussion of the forecast performance of the models are presented in
Section 4. Finally,
Section 5 concludes the article with final remarks and suggestions for future research directions.
2. Related Works
Forecasting power generation, particularly nuclear power, has gained a lot of attention from researchers in recent times, especially since the events that took place in Europe in 2022 and the energy crisis in some countries, such as Germany. Within the scope addressed, 2018 was the year that presented the lowest number of publications, with 245 publications. In 2019, there was a growth in publications (292, 47 more than the previous year) that, despite representing a shy volume, presented a percentage of 16.1% more publications than the previous year. In 2020, the interest in the energy area continued to grow, with 373 publications (128 more than in 2018), representing an increase of 34.4% compared to 2018, and 21.8% compared to 2019.
However, it was in 2021 that the number of publications in the area of power generation forecasting reached its peak: 457 publications, representing an increase of 46.4%, which shows that interest in the area has remained on a growing curve. The year 2022 so far (month 9, September) has shown a volume of publications in the area of 320. Although this is lower than 2021, it may give a misleading idea of a loss of interest in the area. If you average the number of publications in 2021 by the number of months, you obtain 38.08 publications per month. Performing the same arithmetic operation with the 2022 data (320 publications divided by 9 months) gives an average of 35.55 publications per month. This monthly percentage difference (6.58%) is too small to say that researchers are losing interest in the area, but it shows that the volume of research may have reached a plateau.
In 2023, as shown in
Figure 1 the number of publications in nuclear power generation forecasting continued to grow, reaching 490 publications. This represents a 53.1% increase from 2018 and a 7.2% increase from 2021, indicating a sustained interest in the field [
10]. In 2024, preliminary data suggest that publications are likely to surpass 500, maintaining a robust trend in research output [
11]. This demonstrates a continuing and significant investment in research on nuclear power generation forecasting, likely driven by ongoing global energy challenges and the need for sustainable energy solutions.
To understand the most representative research in the field, several performance indicators were taken into consideration for the bibliometric analysis in this state-of-art research, including Total Papers (TP), which is the total number of publications from a specific source, Total Citations (TC), which is the total number of citations an article has received, Citations per Paper (CPP) which is the total number of citations divided by the total publications, a metric to assess the average impact for a journal or author, and Citation Median (CM), used to reduce the potential confounding effect of a few highly mentioned articles when the data are presented as means [
12].
The most productive authors were measured based on their number of publications. For those with the same number of publications, the rank was then measured by the number of citations. The list with the 10 most productive authors is presented in
Table 1. The author Mohammad Rizwan is the largest contributor to this analysis, with 10 publications and 141 citations.
Following Rizwan, there are Yuan-Kang Wu also with 10 publications. Yan Xu, Jian-Zhou Wang, and Stanislav A. Eroshenko continue the list, with nine publications each. Yang Du is the only one with eight publications, followed by Shu Li Wen, Xin Ma, Wenqing Wu, and Alexandra Khalyasmaa with seven publications each. However, being the author with the most papers does not mean being the most influential author. Among those who produced the most papers, the most influential authors were determined by the number of citations, as presented in
Table 2.
As indicated in
Table 2, the researchers were ranked according to the total number of citations they had in all of the publications to compile a list of the most significant authors. Rizwan, who was the author with the most productions, appeared in fifth place of most influential authors, as did Yuan-Kang Wu, who appeared in eighth place. However, Yan Xu who was third on the list of most productive authors, showed himself to be the most influential, with a substantially high number of citations compared to the other authors, having almost five times as many citations as the second-place author (Yang Du) and also holding the highest CPP (122.22).
As shown in
Table 2, Yan Xu, even with nine articles, had a total of 1100 citations. Authors usually work in cooperation with each other. By analyzing
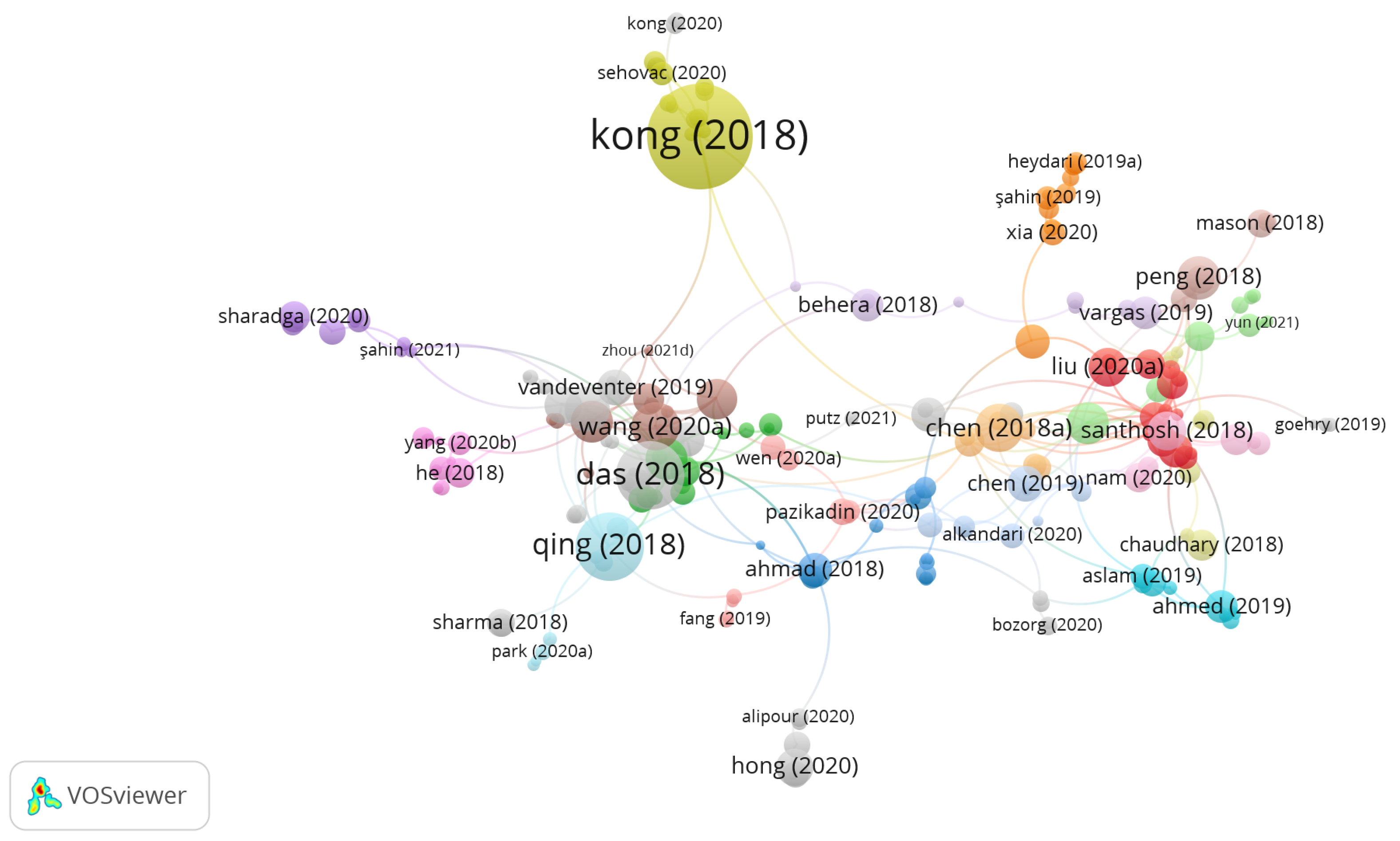
Figure 2, one can see that many of them are correlated, as shown in the clusters.
In
Figure 2 are considered 500 authors in the energy field between the years 2018 to 2024. Each cluster presents a group of authors who publish together, and the lines between the clusters represent the citations made between them. It is possible to see then that papers from certain clusters can come to influence other clusters by the relationship between the members of the clusters and the related citations. The first-place author Yan Xu (gray cluster) has correlations with the fourth-place author (Shu Li Wen), and both reference the same groups of authors in the energy field.
Finally, among the analyses performed in this related works section, the 40 most important articles that could influence this research were studied. Each of them is briefly explained in this section, and their study reflects where this article is placed in the literature and where its contributions occur, as presented in
Table 3. The most referenced paper, with 980 TC, is the work of [
13]. This paper deals with the application of RNN (recurrent neural network), more specifically, LSTM, for residential energy consumption. Although it is not energy generation forecasting but consumption forecasting, the techniques have a similar valid applicability.
Although the search strings did not consider any specific technique, many of the most cited papers had a combination of LSTM and photovoltaics or wind energy [
13,
14,
15,
16], for energy forecasting. Other techniques were also used in combination with these energy sources [
17,
18,
19,
20].
Among the most representative papers, several reviews used a large number of different techniques to benchmark [
21,
22,
23,
24]. These are important works to compare the best techniques. Finally, some research studies show a trend towards the use of optimization techniques and variations of existing techniques such as LSSVR [
25]. With a difference of more than twice as many citations compared to the second place, it can be seen in
Figure 3 that the work of (Kong, 2019) was the most referenced according to the state of the art. The second and third places in the number of citations had a similar number of references in terms of importance. The work of [
21] is a review of photovoltaic energy forecasting models, while the study of [
14] also presents a short-term forecast using LSTM for photovoltaic energy.
The fourth and fifth places are the works of [
15,
16]. Looking at
Figure 3, it is possible to see the correlation between these articles. The other papers presented have a representation of citations with small differences between them, as can be seen in the size of their clusters. These related works presented papers that were significant not only for the nuclear energy forecasting scenario but also for the field of energy research. Among all the articles analyzed and studied for this research, this article stands out for its use of LSTM in conjunction with GRU and SVR for nuclear energy power forecasting, for presenting results that combine the three algorithms, and for the application of feature selection using RreliefF, optimizing with tree-structured Parzen estimator.
3. Materials and Methods
The following subsections provide information about dataset description, time series forecasting models, and performance metrics.
3.1. Dataset
The primary source of data for this study was obtained from the Power Reactor Information System (PRIS) page. The dataset used includes the electricity production of nuclear power plants in France from 2009 to 2020. That dataset is comprehensive, comprising four separate files that contain information on yearly electricity delivered, operating factor, online time, and primary reactor data. These files are organized according to individual nuclear power plants.
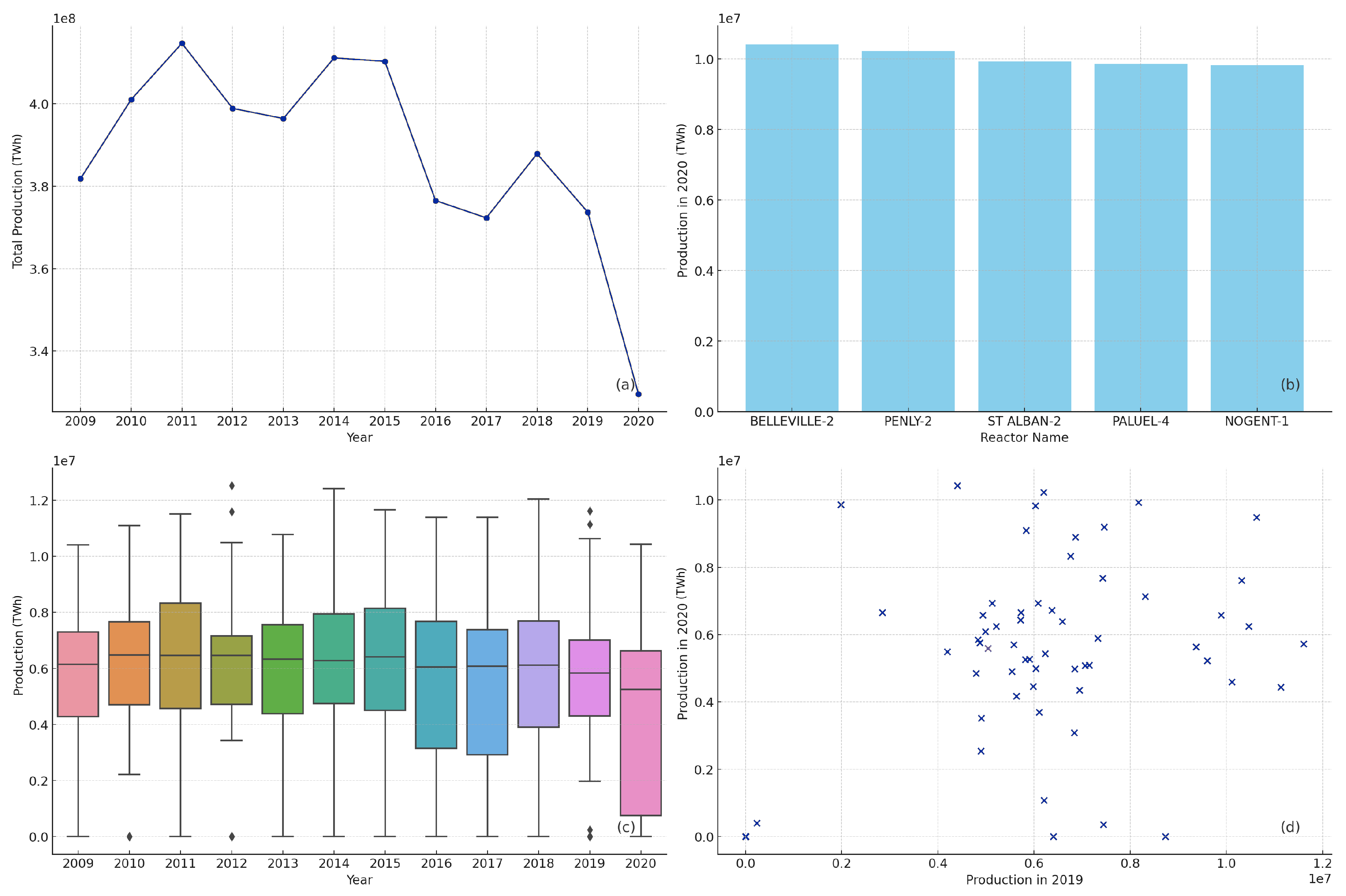
Figure 4 provides a detailed analysis of the French nuclear power generation from 2009 to 2020 through four distinct visualizations, offering a comprehensive analysis of trends and patterns in French nuclear power generation over the past decade, emphasizing both individual reactor performance and broader production trends:
Total production over the years: Line chart (a) illustrates the total annual production of all nuclear reactors from 2009 to 2020, measured in TWh. The data indicate fluctuations in production, with notable peaks in 2011 and 2014, and a marked decline in 2020. These trends suggest variability in nuclear power generation, which may be attributed to factors such as maintenance schedules, operational changes, or policy changes that affect nuclear energy.
Figure 4a captures the cyclic nature of power generation, highlighting recovery periods and subsequent drops, reflecting the dynamic nature of nuclear power production influenced by operational, regulatory, and external factors.
Production comparison of top 5 reactors in 2020: The bar chart (b) compares the production output of the top five reactors in 2020, measured in TWh. Belleville-2, Penly-2, St Alban-2, Paluel-4, and Nogent-1 are identified as the reactors with the highest production, each contributing significantly to the total output.
Yearly production distribution: The box plot (c) shows the distribution of production values for all reactors over the years, measured in TWh. This visualization provides insight into the central tendency and variability of the reactor output. There is considerable consistency in production levels with occasional outliers, indicating that most reactors operate within a similar range of output each year, with some exceptions.
Production in 2019 vs. 2020: The scatter plot (d) examines the relationship between the production of reactors in 2019 and their production in 2020, both measured in TWh. There is a general correlation visible, suggesting that reactors with higher production in 2019 tended to maintain higher production levels in 2020, despite the overall decline in total production, which suggests consistent performance levels across consecutive years for individual reactors.
The dataset
https://pris.iaea.org (accessed on 16 June 2024) includes various details related to each reactor, such as its name, model, status, owner, operator, reference unit power, net design capacity, gross electrical capacity, thermal capacity, construction start date, first critical date, first grid connection date, commercial operation date, lifetime electricity supplied, lifetime energy availability factor, lifetime operation factor, lifetime energy unavailability factor, and lifetime load factor. Electricity generation is expressed in (GW/h).
For this study, only two fields were considered: “Reactor Name” and “Electricity Provided for Ten Years”. The analysis focused on the dataset spanning from 2009 to 2019. In terms of forecast analysis, data for the year 2020 were used. The dataset was divided into training (70%), validation (15%), and testing (15%) subsets for the analysis.
In nuclear power forecasting, understanding both long-term trends and cyclicity is critical for accurate predictions. A comprehensive forecasting model should ideally account for seasonal patterns (such as routine maintenance schedules and weather-related efficiency changes) and cyclic factors (such as long-term economic trends or technological advances). Analyzing these patterns can help optimize nuclear plant operations and provide valuable insights for strategic planning in the nuclear power industry. The long-term trend and cyclicity observed in nuclear electricity generation can be attributed to a combination of operational, economic, and demand-related factors. As the energy landscape evolves with the integration of more renewable sources, the role and operation of nuclear reactors will also change, necessitating a deeper understanding of these patterns for effective energy management.
Additionally, the overall stability and slight increase in the baseline power generation across the years indicate an overall robust performance of the nuclear fleet, with each reactor contributing to a steady supply of power. However, the occasional extreme deviations, such as sharp drops or peaks in individual lines, might signify specific incidents or exceptional maintenance periods.
Figure 5 presents the cyclic trends in power generation for the French nuclear fleet from 2009 to 2020. The x-axis represents the years, while the y-axis indicates the total power generation in MWh. This graph showcases the overall performance and cyclic patterns in the nuclear power output, providing insights into the long-term trends and fluctuations in power generation. The power generation of the French nuclear fleet experienced significant variations over the 11 years. The total power generation peaked around 2010 and then exhibited a gradual decline. This decline was punctuated by periods of recovery and subsequent drops, indicating cyclic trends in power production. For example, there was a noticeable dip around 2012 followed by a brief recovery, and then another decline from 2015 onwards. The most significant drop occurred after 2018, with a steep decline continuing into 2020.
Several factors could contribute to the observed cyclic patterns in power generation. Maintenance schedules and reactor outages for refueling are routine operations that can temporarily reduce power output. In addition, regulatory changes, upgrades, and modernization efforts can also impact generation capacity. External factors such as variations in electricity demand, economic conditions, and policy shifts toward renewable energy sources could further influence these trends. The pronounced decline in recent years could be attributed to a combination of aging reactors requiring more frequent maintenance and a strategic shift in France’s energy policy to diversify its energy mix.
In general, the figure effectively captures the cyclic nature of power generation within the French nuclear fleet from 2009 to 2020. While the overall trend shows a decline, the cyclic patterns highlight periods of recovery and subsequent drops, reflecting the dynamic nature of nuclear power production influenced by operational, regulatory, and external factors. Understanding these trends is crucial for planning and optimizing the future energy strategy of the French nuclear fleet.
The data illustrated in these figures are ideal for forecasting because they demonstrate clear and consistent patterns in long-term trends and cyclicity, which are essential for reliable predictions. The graphs show regular, predictable fluctuations over the years, highlighting trends and periods of increase or decrease in nuclear power generation. This regularity makes it possible to anticipate changes in power generation needs based on historical patterns, such as increased demand during winter months. The cyclicity graph reveals longer-term trends and periodic fluctuations over multiple years, capturing broader economic and policy influences on power generation. By combining these insights, it is possible to develop a comprehensive understanding of both short-term and long-term variations in nuclear power output. This dual perspective enables more accurate and proactive planning, reduces the risk of unexpected supply shortages or overproduction, and ensures a stable and efficient power generation process. Consequently, the presence of these clear patterns makes the data highly reliable for forecasting purposes.
3.2. Feature Engineering
In signal processing, white noise is a random signal having equal intensity at different frequencies, giving it a constant power spectral density [
26]. In time series, white noise is defined by a zero mean, constant variance, and zero correlation [
27]. Considering this, the annual energy output of each reactor was normalized.
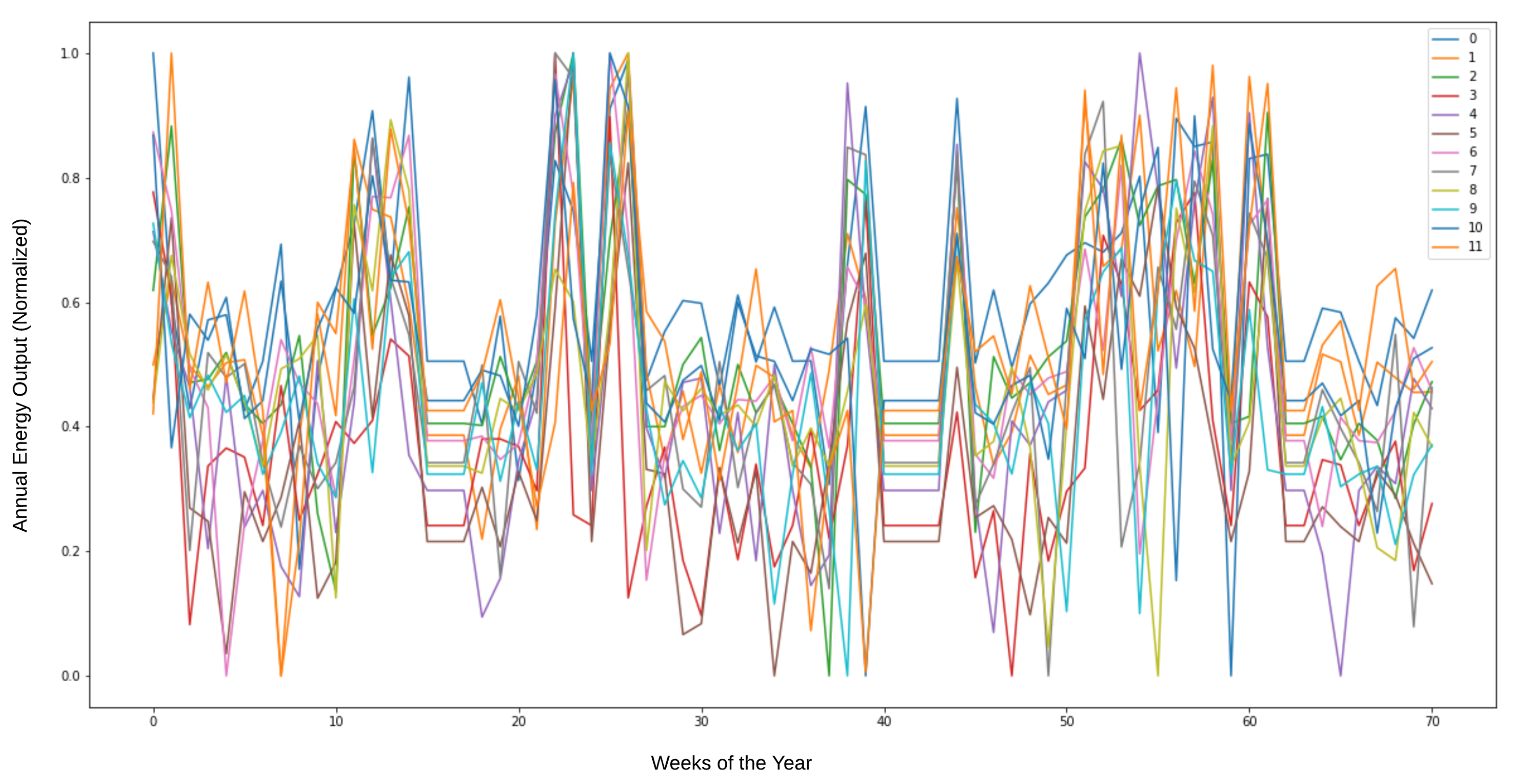
Figure 6 shows that the series is random, where the numbers 0 to 11 represent the 12 years used as the dataset (2009–2020) for each power generation sequence of each of the 58 reactors. This visualization helps to understand the variability and operational dynamics of each reactor in a standardized way. By normalizing the energy output, we can observe the relative performance and trends of each reactor over time on a comparable basis.
Figure 6 shows the normalized annual energy output for each of the 58 reactors over the twelve-year period from 2009 to 2020. Normalization allows for a comparison of the energy production across different reactors by scaling the data to a common range. This helps identify trends, consistency, and anomalies in reactor performance over time.
Skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined. For example, the skewness of a random variable X is the third standardized moment
, and it is defined as [
28]:
where
is the mean,
is the standard deviation, E is the expectation operator,
is the third central moment, and
is the
t-cumulant. The dataset used in this study presented a skewness of 0.05, very close to zero, indicating that the data were almost symmetric.
Kurtosis measures whether the data are heavy-tailed or light-tailed relative to a normal distribution, and datasets with high kurtosis tend to have heavy tails or outliers. Datasets with low kurtosis tend to have light tails or a lack of outliers. A uniform distribution would be the extreme case. The definition of the kurtosis formula for univariate data, as proposed by [
28], is:
where
is the mean,
s is the standard deviation, and
N is the number of data points [
29]. A 0.57 kurtosis value was calculated for this research dataset, indicating a low right tail (not too many outliers) after improvements using a power transformation function.
Figure 7 shows the distributions of the data for each of the twelve years from 2000 to 2019 for all reactors. The application of a power transformation helped stabilize variance, making the data more normally distributed.
This transformation also improved the validity of association measures, such as the Pearson correlation between variables. Additionally, a new family of distributions, similar to the Box-Cox power family [
30], can be used without restrictions and offers many of the same advantages. These transformations are defined by:
If
y is strictly positive, then the Yeo–Johnson transformation is the same as a Box–Cox power transformation of
If
y is strictly negative, then the Yeo–Johnson transformation is the Box–Cox power transformation of
but with a power of
. With negative and positive values, the transformation is a mixture of these two; then, different powers are used for positive and negative values [
31]. The Yeo–Johnson power transformation was the best option in this study because some negative values were present during the dataset preprocessing.
3.3. Feature Selection
ReliefF and its equivalent for handling regression data, i.e., RreliefF [
32], are the most widely used Relief-Based Algorithms (RBAs) [
33]. Similar to ReliefF, RreliefF penalizes predictors that give different values to neighbors with the same response values and rewards forecasters that give different values to neighbors with different response values when working with a continuous
y. Relief algorithms are successful, generalized attribute estimators, that can detect conditional connections between attributes and provide a unified perspective on the estimation of attributes in regression [
34]. However, RreliefF computes the final predictor weights using medium weights.
Given two nearest neighbors, then
is the weight of having different values for the response y;
is the weight of having different values for the predictor ;
is the weight of having different response values and different values for the predictor .
RreliefF first sets the weights , , , and equal to 0. Then, the algorithm iteratively selects a random observation , finds the k-nearest observations to , and updates, for each nearest neighbor , all intermediate weights as follows:
where the
i and
superscripts denote the iteration step number.
m is the number of iterations specified by “updates”.
is the difference in the value of the continuous response
y between observations
and
. Let
denote the value of the response for observation
, and let
denote the value of the response for observation
.
where the
and
functions are the same as for ReliefF, but RreliefF calculates the predictor weights
after fully updating all the intermediate weights.
3.4. Forecasting Models
In this research, three well-established machine learning algorithms for nuclear power generation forecasting were used: long-short-term memory neural network, gate recurrent unit, and least-square support vector regression (LSSVR).
Long-short-term memory neural network: LSTM neural networks are a type of recurrent neural network (RNN) capable of learning long-term dependencies, which makes them effective for time series prediction [
35].
Gate Recurrent Unit: GRUs are a simplified version of LSTM neural networks that also address the problem of vanishing gradients in RNNs. They have fewer parameters and can be more efficient for certain tasks [
36].
Least-Square Support Vector Regression: LSSVR is a variant of support vector regression that aims to find a linear or non-linear relationship between input variables and the target variable. It is particularly useful for regression problems involving time series data [
37].
These methods were chosen for their proven effectiveness in time series forecasting. This study combined these techniques into an ensemble model, leveraging their strengths to improve prediction accuracy for nuclear power generation. Although LSTM models are typically employed for datasets with extensive temporal data, the decision to include LSTM in the ensemble approach was based on its robustness and ability to capture complex patterns in time series data. Despite the relatively small dataset of 11 annual data points, the LSTM model contributed to the overall accuracy of the hybrid ensemble by leveraging its unique capabilities to identify underlying trends and dependencies. This approach ensures a comprehensive analysis and prepares our model for future scalability as more data become available.
3.5. Performance Criteria
Forecasting models can be analyzed using many types of performance measures. The selection of criteria is based on the details of the forecast issue and the analysis goals. In this study, three performance criteria were adopted, the coefficient of determination (
), the Mean Squared Error (MSE), and the Mean Absolute Error (MAE), presented in the following equations:
where
N is the number of samples,
is the prediction (estimated) value for the test sample
i,
is the true (measured) value of test sample
i, and
is the average value of true test samples. The coefficient of determination (
) is the ratio of the variance of the anticipated value to the variance of the actual value [
38]. A higher
value indicates a better fit, suggesting that the model captures a larger portion of the variance in the dependent variable. The MSE provides a quantitative measure of the model’s accuracy, with lower values indicating better performance [
39]. In addition, the MAE calculates the average magnitude of absolute differences between
n predicted vectors. If the MAE for a specific data point is significantly larger than the average MAE, it may indicate an anomaly.
3.6. Tree-Structured Parzen Estimator
Hyperparameters determine the model architecture and govern the learning process in machine learning, such as the number of hidden layers, activation function type, and learning rate. Automatic hyperparameter optimization is crucial to the development of machine learning models, such as current deep neural networks, e.g., LSTM, whose learning performance is highly dependent on the selection of multiple hyperparameters [
40]. Automatic hyperparameter optimization has several significant advantages, including: (1) a reduction in the human effort when deploying machine learning, which is essential in applications because different hyperparameter configurations are required for different datasets [
41] and (2) an improvement in the performance of machine learning models, by choosing the values of the most appropriate (according to specified objectives) hyperparameters for the target application [
42].
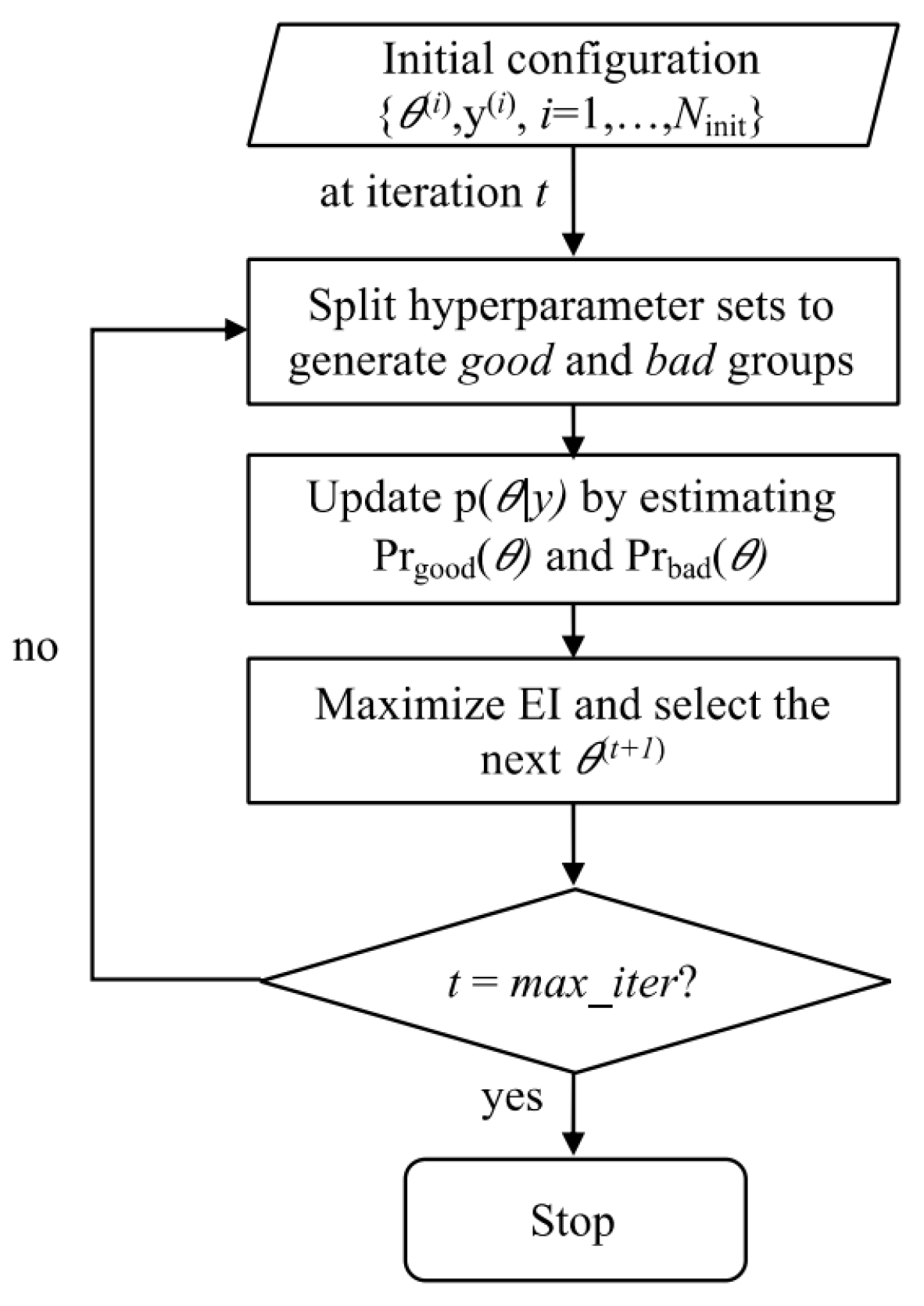
In this work, the hyperparameters of the proposed prediction model were automatically optimized using a form of Bayesian optimization (BO) known as tree-structured Parzen estimator (TPE). A common benefit of BO approaches is that they require fewer function evaluations than other classical optimization approaches, such as grid search or random search, because these approaches learn and select the optimal hyperparameter sets based on their distributions describing the fitness scores from previous iterations.
Thus, TPE has been widely used to tune machine learning models in various applications, such as image processing [
43,
44,
45], electricity price forecasting [
46], solar irradiance forecasting [
47], rail defect prediction [
48], occupational accident prediction [
49]. Parzen window density estimation, also known as kernel density estimation, is a non-parametric way to build a probability density function from empirical data. In the TPE algorithm, each sample from the empirical data defines a Gaussian distribution with a mean equal to the hyperparameter value and a specified standard deviation. At the start-up iterations, a random search is employed to initialize the distributions by sampling the response surface
, where
denotes the hyperparameter set,
y is the corresponding value on the response surface, i.e., the validation loss or the fitness value, and
is the number of start-up iterations. Then, the hyperparameter space is divided into two groups, namely good and bad samples, based on their fitness values and a predefined threshold value
(usually set to
), as follows:
where
and
are the probabilities that the hyperparameter set
is in the good and bad groups, respectively. The TPE initialization process for the hyperparameter distributions used
and
[
50].
The red points are the samples with the lowest fitness values after evaluation, thus being classified into the good group
, whereas the others form the bad group
. In this way, the selection of optimal hyperparameters relies on a set of best observations and their distributions. Then, the more iterations are used for initialization, the better the distribution we obtain at the beginning. An expected improvement (EI) is then calculated as follows:
The hyperparameter configuration
* that maximizes the expected improvement is chosen at each iteration.
Figure 8 shows the flowchart of the TPE optimization procedure.
3.7. Ensemble Learning
Stacked generalization, stacking-ensemble learning, or STACK for short, is one of the ensemble learning approaches cited in [
51]. In the STACK technique, which employs two or more levels or layers, different models are trained in the first layers, where the prediction of the response variable for each model is determined and utilized as input for the other ones. These predictions of the first layer models are known as weak or basic models.
For the next layer, the model, known as a robust or meta-model, is trained, and its prediction is the end outcome of the forecasting process. In addition, when there is variety amongst models of different levels, predicting results improve, mostly because models with distinct generalization principles tend to provide divergent outcomes. In other words, the total number of models in a level does not ensure model success; variety is crucial [
52]. This method has shown predicting enhancements in several sectors, including agrobusiness [
52], finance [
53], and epidemiology [
54].
3.8. Proposed Forecasting Approach
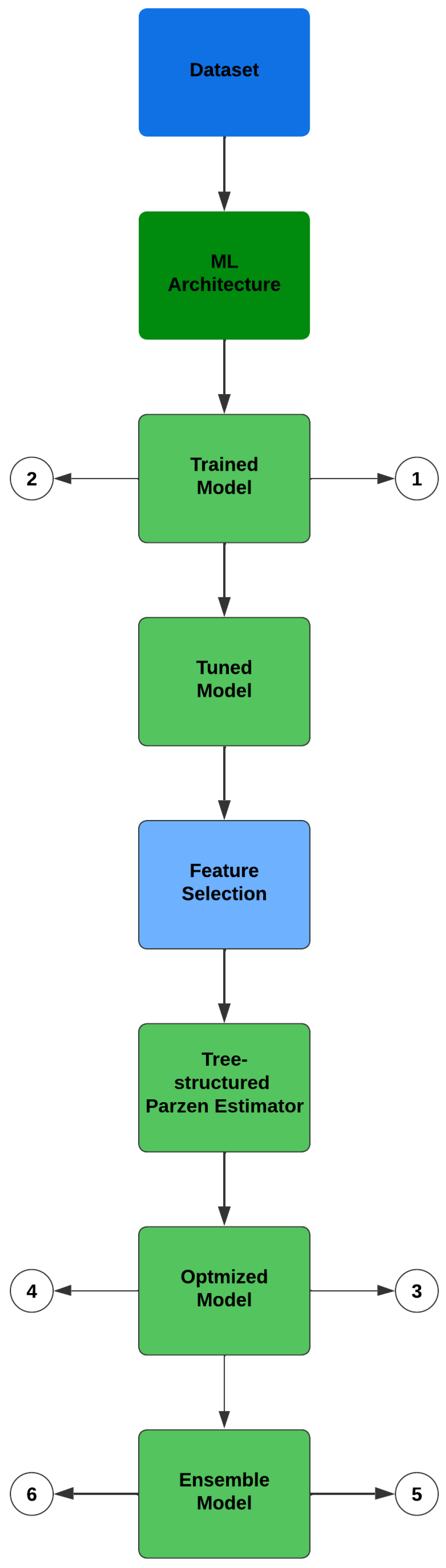
As shown in
Figure 9, three machine learning algorithms were individually applied to the dataset in the computational model proposed in this study. The process began with the model training using input data (step 1). Each algorithm, GRU, LSTM, and LSSVR, was individually trained, generating training output data (step 2) for each respective model.
The training process involved multiple steps to ensure the robustness and accuracy of the model. Initially, the dataset was preprocessed to handle missing or inconsistent data points. Each machine learning algorithm (GRU, LSTM, and LSSVR) was then applied to the preprocessed data, focusing on capturing different aspects of the time series patterns.
After training, the fitted models were subjected to RreliefF to select features, reduce dimensionality, and focus on the most relevant features. The feature selection process generated optimized models for each technique, which were then validated using the validation data (step 3), producing validation outputs (step 4). Subsequently, the tree-structured Parzen estimator (TPE) was used for hyperparameter optimization via the Optuna tool in Python. This Bayesian optimization technique iteratively refines the hyperparameters based on their performance, ultimately selecting the most effective configuration for each model.
The final stage involved combining the outputs from the three optimized models into an ensemble stack. The test data (step 5) were then submitted to the combined model, which generated the test output (step 6). This stacked-ensemble approach leveraged the strengths of each individual model, providing a more comprehensive and accurate prediction.
4. Results
The models were optimized, and their parameters discovered, whose best values are presented in
Table 4.
Once the optimized hyperparameters models were generated, they were passed through the ensemble stack. The ensemble model was then submitted to feature selection for dimensionality reduction with RreliefF, and compared to other models such as SVR, eXtreme gradient booting (XGBoost), adaptive boosting (AdaBoost), and Gradient Boost Regressor (GBR), as presented in
Table 4. Note that the best number of features indicated by RreliefF was fourteen. These models were not optimized with Optuna.
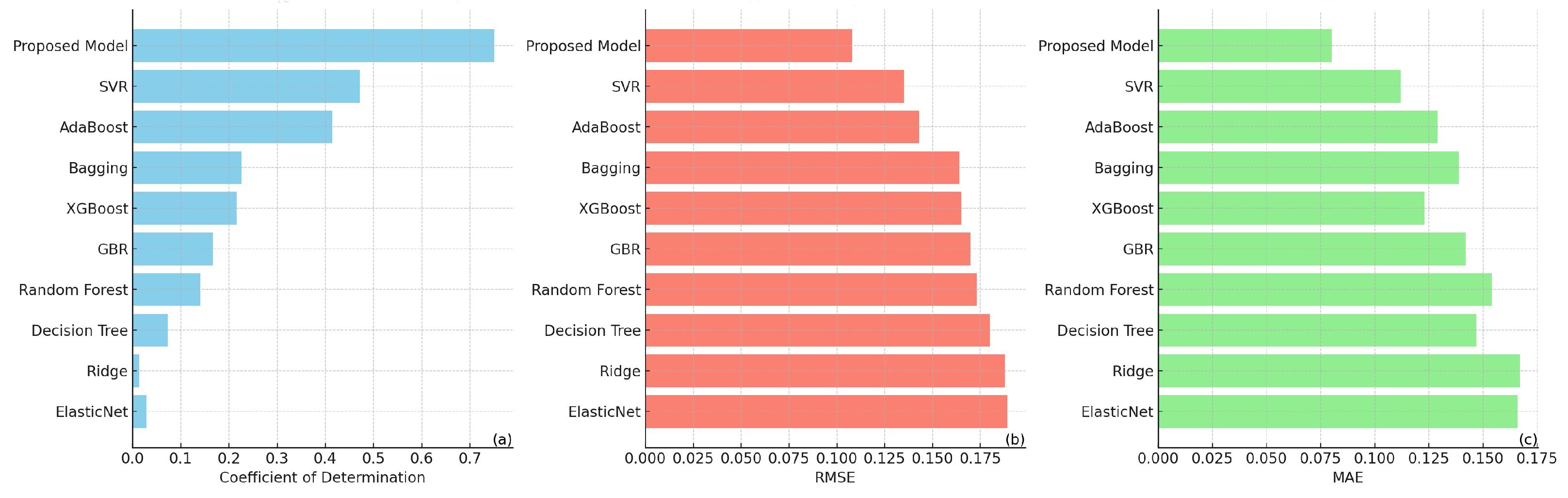
For the evaluation of various predictive models, including the proposed model, SVR, and a suite of ensemble models such as AdaBoost, Bagging, XGBoost, and Gradient Boosting Regressor (GBR), along with random forest, decision tree, ridge, and ElasticNet regression models, their performance was compared based on three key metrics: (coefficient of determination), RMSE (Root-Mean-Square Error), and MAE (Mean Absolute Error). These metrics served as critical indicators of the model’s capacity to explain variance, predict with accuracy, and minimize the average magnitude of prediction errors.
The proposed model emerged as the superior one, showcasing exemplary performance with an value of 0.751. This indicated a robust ability to account for variance within the dependent variable. In addition, it achieved the lowest RMSE and MAE values of 0.108 and 0.080, respectively, highlighting its superior predictive accuracy and consistency compared to its counterparts.
SVR exhibited moderate effectiveness, with an of 0.472, suggesting it as a viable though less capable alternative to the proposed model. Its RMSE and MAE values, although not as low as those of the proposed model, still indicated relatively high accuracy and lower prediction errors than the majority of other evaluated models.
Among the ensemble methods evaluated, AdaBoost and Bagging demonstrated moderate performance, with AdaBoost slightly outperforming Bagging in terms. XGBoost and GBR showed less capability in explaining variance. All ensemble models registered higher RMSE and MAE values compared to the proposed model and SVR, reflecting less accuracy in their predictions.
The random forest and decision tree models recorded lower values, indicating a diminished ability to capture variance in the dataset. This was further evidenced by their higher RMSE and MAE values, denoting a decline in predictive accuracy and consistency.
Ridge and ElasticNet regression models were the least effective, with notably low values and the highest RMSE and MAE scores among the compared models. This significant discrepancy between predicted and actual values highlighted their limitations in explaining variance and in predictive precision.
Figure 10 illustrates the performance comparison of various models based on three evaluation metrics: coefficient of determination (
R2), Root-Mean-Square Error (RMSE), and Mean Absolute Error (MAE). These metrics provide a comprehensive assessment of each model’s accuracy and predictive capability, crucial for evaluating their effectiveness in nuclear energy forecasting. The models compared included the proposed model, SVR, AdaBoost, Bagging, XGBoost, GBR, random forest, decision tree, ridge, and ElasticNet.
In the coefficient of determination chart, the proposed model exhibited a significantly higher R2 value of 0.751, indicating a better fit to the validation data compared to the other models. The next best model, SVR, achieved an R2 value of 0.472, which was substantially lower. This considerable difference highlighted the superior ability of the proposed model to explain the variance in the data, making it a more reliable predictor for the given forecasting task. Models like ridge and ElasticNet showed very low R2 values, suggesting poor performance in capturing the underlying patterns of the data.
The RMSE and MAE charts further emphasize the efficacy of the proposed model. With an RMSE of 0.108 and an MAE of 0.080, the proposed model outperformed all other models, which had higher error values in both metrics. Lower RMSE and MAE values indicate that the Proposed model not only had smaller prediction errors but also maintained consistency across different predictions. For instance, SVR, the second-best model in terms of R2, recorded an RMSE of 0.135 and an MAE of 0.112, both higher than those of the proposed model. This consistent performance across multiple error metrics confirmed the proposed model’s robustness and accuracy, making it the optimal choice for nuclear energy forecasting among the models evaluated.
The proposed model presented better results than the others evaluated in this study in terms of performance metrics.
Table 4 presents the values (not testing and training) using a validation dataset for each of the forecast algorithms evaluated. Once the model was created, the validation dataset was used to generate predictions, as shown in
Figure 11.
Analyzing
Figure 11, it is possible to make several observations regarding the performance of the model. The actual and predicted values are closely aligned for most of the data points, indicating that the model had a reasonable level of accuracy in its forecasts. The blue line representing the actual values and the red dashed line representing the predicted values show a similar trend, suggesting that the model captured the overall pattern of the data quite well.
However, there are noticeable discrepancies at certain points, reflected by the residuals (green bars). Some residuals are relatively large, indicating significant prediction errors at those points. For example, at data points where the residuals are most pronounced, such as those corresponding to large negative or positive bars, the model either significantly under-predicted or over-predicted the actual values. These instances of larger residuals suggest that while the model generally performed well, it occasionally failed to predict certain values accurately.
The LSSVR, LSTM, and GRU models individually presented lower results than the proposed model. However, once in the stacked ensemble, its results were superior to the other models tested in this research.
Table 4 presents the valid values (not testing and training) for each of the tested algorithms. Once the model was generated, the validation dataset was used to generate predictions, as shown in
Table 5.
Except for a few cases, the predicted values were very close to the current ones, with a shallow residual difference, which indicated the efficiency of the model of this study in predicting the results of nuclear energy generation. The residual difference was, in most predictions, less than 0.1, showing that the model could predict the power generation behavior of the reactors used in the dataset.
5. Conclusions and Future Research
This study presented the analysis of machine learning models using LSTM, GRU and LSSVR, optimized with the tree-structured Parzen estimator, and reducing dimensionality using short-term forecasting of nuclear energy from power plants in France. First, we conclude that the regression techniques based on deep learning and support vectors are more efficient when stacked together for this specific case. The dataset for training, in most models, was the one with the best response precisely because it had the most data (70% of the total), which means that for testing and validation, those that showed lower performance compared to training may have increased performance with a larger volume of data (up to a certain point). The tree-structured Parzen optimizer, through the Optuna framework, was efficient in improving the performance of all models. It means that in the case of the dataset of this research, using a vast number of features can cause overfitting. In conclusion, the use of LSTM, GRU, and LSSVR ensemble models was highly efficient for the analysis of nuclear energy prediction with this dataset, having a margin of mean error and quadratic error (except for outliers) of 15% to 20% on average, which could be significantly reduced with the use of the RreliefF algorithm. While the model demonstrated good predictive capabilities by following the actual data trends closely, the presence of notable residuals indicated room for improvement. The consistent patterns in residuals suggest that the model may benefit from further tuning or the inclusion of additional data features. In conclusion, the proposed model was the most effective and reliable for outcome prediction, as evidenced by its superior , RMSE, and MAE values. This analysis underscores the importance of model selection that is not only theoretically sound but also empirically effective in real-world data application.
To progress this research, some improvements can be considered:
Model accuracy and residuals: Despite the model’s overall accuracy, there were noticeable discrepancies in some predictions. The presence of significant residuals at certain data points indicated that the model occasionally failed to predict actual values accurately. This suggests that while the model generally performed well, it may benefit from further tuning or the inclusion of additional data features to improve its accuracy in all cases.
Overfitting concerns: The use of a vast number of features can cause overfitting, particularly when the model is trained on a dataset with a considerable quantity of data (70% of the total). Overfitting can lead to a decrease in model performance when applied to new, unseen data. This highlights the need for careful feature selection and possibly reducing the number of features used to mitigate this risk.
Dataset limitations: The dataset used for training and validation was limited to the electricity production data of nuclear power plants in France from 2009 to 2020. This may limit the generalizability of the model’s findings to other regions or different time periods. Expanding the dataset to include more diverse data could improve the robustness and applicability of the model.
Models’ improvements: Future research could focus on improving the model by evaluating it with enhancements based on stacking learning, adopting multi-objective optimization for hyperparameter tuning and feature selection, and using the tree-structured Parzen optimizer combined with optimization metaheuristics. The current model, while effective, has room for improvement through these advanced techniques
In conclusion, while the ensemble learning model shows strong predictive capabilities, the presence of notable residuals, overfitting concerns, and dataset limitations highlight areas for potential improvement. Future research should focus on further tuning the model, expanding the dataset, and exploring advanced optimization techniques to enhance the model’s performance and generalizability.