1. Introduction
The Emissions Trading System of the European Union (EU-ETS) is a cap-and-trade system, introduced to fight climate change and to accomplish the reduction targets of the Kyoto protocol. It sets a cap to the total amount of greenhouse gases (GHGs) that can be produced by the installations covered by the system, which is set to decrease over time to reduce the total amount of emissions. A market of allowances (EUA), representing a permit to emit a ton of CO
2, is established. Power producers can use the allowances they own either to sell them to other market participants or to cover the greenhouse gas emissions resulting from their power production. Allowances are, therefore, financial products, exchanged in financial markets (
Cludius and Betz 2020;
Daskalakis et al. 2009;
Graham et al. 2016;
Harasheh and Amaduzzi 2019). By using the allowances to produce electricity, one bares the opportunity cost of losing their financial value. Rationally, power producers should respond to an increase in costs due to a rise in the value of the allowances by adopting low-emitting technologies. This happens if the rise in costs is perceived as permanent and if prices cannot be raised to shift the burden of the allowances to the final consumers. As a consequence, whenever power producers perceive the cost of the allowances as a relevant component of their production costs and they are not able to rise their bids in the wholesale market, they should progressively respond to an increase in the allowance price by reducing the power production costs. They can do so by minimizing the extent to which they use less efficient (i.e., more emitting) power plants, or by adapting their production portfolio mix to increase the share of plants fueled by renewable energy sources (from now onward, RES-plants). These solutions should increase the share of RES energy in the energy system, lower the amount of emissions, and induce a decreasing wholesale (electricity) price. This is perfectly in line with the “polluters pay” principle when applied to greenhouse gas emission in the power production sector. However, the ability of the EU-ETS to effectively endogenize emissions’ cost relies on the impossibility to shift the burden of the policy to final consumers. The extent to which the CO
2 emission costs can be passed to the buyers through an increase in the electricity price is defined as the pass-through rate. It is therefore crucial to evaluate whether and to what extent emission costs of the EU-ETS can be shifted to final consumers. Many empirical studies have tackled such a research question. Most of these studies focus on the first two phases of the EU Emission Trading System (from 2005 to 2007, and from 2008 to 2012, respectively), finding a relevant and high pass-through rate of EUA costs into electricity prices, yet with a large range.
Sijm et al. (
2006) report a cost pass-through of about 60–117% for Germany, and of 64–81% for the Netherlands.
Sijm et al. (
2008) extend this analysis and find a positive but incomplete carbon cost pass-through in the Netherlands, Germany, France and Sweden, and a full pass-through in the U.K. market.
Fabra and Reguant (
2014) measure a pass-through rate for Spain that differs between peak and off-peak hours, and ranges from 70% to 140% for the former and from 28% to 97% for the latter, depending on the model used.
Honkatukia et al. (
2008) find a pass-through that ranges between 75% and 95% when analyzing the Finish Nord Pool electricity spot prices.
Hintermann (
2016) establishes a pass-through that ranges between 81% and 111% for the wholesale electricity price in Germany.
Jouvet and Solier (
2013) consider a set of European countries and, by analyzing both the first and (a part of) the second period of the EU-ETS, they show that the pass-through rates are less relevant during the second phase and even negative in some countries. Other scholars have also found limited pass-through rates.
Bariss et al. (
2016) find a 55% pass-through rate in the Nordic market and a 65% pass-through rate in Baltic countries.
Bunn and Fezzi (
2008) show that the pass-through rates can be as low as 42%. For
Ahamada and Kirat (
2015), the pass-through rates of the French and German electricity baseload prices during the second phase of the EU-ETS are even lower, roughly around 18%.
Ahamada and Kirat (
2018) further show that the pass-through rate is non-linear and dependent on the threshold levels of the allowances’ prices. Similarly, using futures on electricity, very low pass-through rates are obtained for Germany, France, Belgium and the Netherlands by
Lo Prete and Norman (
2013).
Chernyavs’ka and Gulli (
2008) follow a different approach and instead of relying on econometric analysis, they simulate the load duration curve and the merit order supply curve for two zones of the Italian market, showing that the pass-through depends on whether it refers to peak or off-peak hours and on the level of competition across producers.
In our paper, we aim at assessing the effectiveness of the EU-ETS in endogenizing emission costs and, therefore, in driving energy transition toward a less carbon-intensive power mix in Italy. To do so, by considering the most recent changes occurred in the third phase of the regulation, we test whether there is a relevant pass-through of the allowances price in the Italian electricity price, and whether there is a significant impact of EU-ETS costs in the final power price. A high pass-through rate would signal the relative ability of power producers to adapt to the EU-ETS regulation without the need for reducing their emissions in the attempt to decrease the allowances’ costs, and vice versa. By identifying the presence of cointegration between the allowances’ prices, gas prices and Italian electricity prices, we are able to analyze the long-run relationship between these variables. To see how such a relationship has changed over time, a dynamic analysis is set up, performing the cointegration analysis on two-year rolling windows for the whole period of observation (from the beginning of the third phase of the EU-ETS until the end of 2018). This provides a measure of how the pass-through of the EU-ETS costs has changed over time.
The European Emission Trading System is characterized by a total emission cap which is set to decrease over time: this translates into increasing costs for producers. For this reason, it is important to study the evolution of the regulatory framework in its most recent phase, using a dynamic approach, which is the major contribution of this study. Note, however, that the presence of cointegration is only a sufficient, not necessary, condition for a pass-through to happen. The correlation among electricity and allowances’ prices in the long run can, in fact, be determined by other factors, such as an increasing share of RES in the power production mix. If that were the case, the EU-ETS would be finally successful in reaching its reduction goals through a change in technologies caused by the “polluters pay” principle. To test for such a hypothesis, we finally study the impulse response functions, showing which variables adjust to bring the system back to the long-run equilibrium.
The paper is structured as follows. In
Section 2, the methodology is introduced.
Section 3 displays the results.
Section 4 discusses the policy implications. References follow.
Appendix A contains data summary statistics and graphical analyses, stationarity tests and impulse response functions for Models 2 and 3.
2. Materials and Methods
The Italian PUN (Prezzo Unico Nazionale), which is traded in the MGP, the Italian day-ahead market, is used as a proxy for the wholesale power price in Italy. Indeed, Italy is a zonal market in which the power selling price differs across zones while purchase offers are valued at the single weighted average of zonal prices. The electricity data are retrieved directly from the GME’s webpage, while the allowances’ prices are obtained from the European Climate Exchange (EEX), the most liquid platform for this type of product. In detail, we adopt the prices of the EEX futures contracts, which are expressed in euros per ton. Each contract represents 1000 emission allowances. In addition to the EUAs prices, our dataset includes Italian PSV (punto di scambio virtuale—virtual trading point) natural gas future prices.
Appendix A.1 provides summary statistics of all the variables and their graphical representation. All data were collected from January 2013 to December 2018.
Electricity hourly prices are transformed into daily prices, with the exclusion of weekends, through a weighted average, where the total volumes exchanged are used as weights. This allows us to compare the electricity prices with the daily CO2 prices, which we collected from the Refinitiv Eikon database. Moreover, by averaging daily prices, we control for intraday volatility and intraday price patterns: in this way, we can focus on the determinants of prices, which include emission costs. In addition, by excluding the weekends, we remove the most relevant component of the periodic evolution of electricity prices. Consequently, there is no need to introduce further seasonal adjustments on the electricity prices. Finally, as far as the analyses are concerned, we first consider the whole set of hourly prices, and we later distinguish between peak and off-peak prices. The latter distinction allows to take into consideration the differences in the marginal technology that occur between peak and off-peak hours.
In the preliminary analyses (see
Appendix A.2), we use the bound testing methodology, suggested by
Pesaran et al. (
2001), to identify the presence of cointegration in cases where statistical tests do not univocally indicate the stationarity properties of the series of interest. Having identified the existence of cointegration, we follow the Johansen approach (
Johansen 1991,
1988,
1995) and set the following vector error correction model (VECM):
where
is the vector including the log-prices of energy,
1 gas and allowances,
denotes first-order differencing, while
,
,
, …
are parameter matrices, and
is an innovation term which is assumed to be with a zero mean and with a covariance matrix equal to
. Notably, the VECM framework is flexible enough to allow for the presence of deterministic terms in both the cointegrating relations as well as in the dynamic evolution of the differenced variables. The trace and maximum eigenvalue tests of
Johansen (
1995) are used to identify the number of cointegration relations. The tests’ critical values depend on the presence of deterministic relations and on the lag order p. In our case, we specify the model with an intercept in both the cointegration relation and in the VECM, and we use 5 lags. The model estimation follows the Johansen approach (
Johansen 1995). We consider two possible cases: in the first one, we include in the model three variables (the overall wholesale electricity (PUN) price, the allowances price and the gas price); in the second case, we substitute the PUN price by its peak and off-peak components, respectively (PUNp and PUNop). Results are presented in
Table 1 and
Table 2 (* = statistically significant at 10% level).
In both cases, the tests are concordant and identify the presence of cointegration. While in the first case, a unique cointegrating relation is detected, in the second model, two relations are identified. This evidence is in line with the expectations. On the one hand, the role of allowances and gas in determining the energy price is associated with their role in the production process since they are both production costs. This justifies the long-run relationship with the electricity price. On the other hand, when peak and off-peak prices are separated, different levels of loads and prices are included in the model and, as a consequence, both prices can be related by a cointegration relation to gas and allowances.
Given the existence of cointegration, restrictions can be imposed on the structure of matrix
. Indeed, under cointegration, matrix
has a reduced rank, and its rank corresponds to the number of cointegrating relations that exist among the modeled variables. Matrix
can be, therefore, decomposed into the product of two matrices,
, including the cointegration vectors that contains the parameters linking the log-prices in equilibrium (or, equivalently, in the long-run), and
, the matrix of adjustment coefficients, capturing the speed of convergence toward the equilibrium of the variables in the model. The model specification we expect has thus the following structure, obtained by rearranging Equation (1):
where we set the lag order to 5, capturing up to a weekly lag. In this bivariate case, the term
becomes
where we point out that the first element of the vector
is normalized to 1. Differently, when we do have two cointegrating relations, we have
where the two long-run relations include just one price, which follows from traditional identification schemes adopted for VECM.
From the VECM model, one might also recover the impulse response functions (IRF), allowing to track the evolution of the target variable in response to a shock on a given variable. In our analyses, we recover the IRF from the VAR companion representation of the VECM, namely,
The IRF are evaluated after a unitary shock on the orthogonal residual such that . Note that the covariance matrix of the residuals is the identity matrix and the covariance matrix of satisfies .
3. Results
The estimates of the cointegrating equations are summarized in
Table 3. Note that since the model is run in logarithms, betas can be interpreted as elasticities. Consequently, the beta relative to the allowances’ price is our variable of interest, i.e., the pass-through rate. The table reports the estimate of the three variable specifications defined in Equation (3) for three different cases: Model 1 uses the PUN, Model 2 the peak prices, and Model 3 the off-peak prices. The last case, Model 4, refers to the specification that includes both peak and off-peak prices, defined in Equation (4).
Overall, the results confirm that the models fit well. All the betas are significant, at least at the 10% level. The results in Column 1 show that an increase in the natural gas price and in the price of the allowances is correlated with an increase in the Italian electricity price. Natural gas has a huge impact on the electricity price: a EUR 1 increase in the gas price produces, in the long-run, a 72-cent increase in the PUN. On the other hand, the impact of the allowances is more limited: a EUR 1 increase in the EUA is reflected in a modest 7-cent increase in the Italian electricity price. Results are confirmed in columns 2 and 3, which report the coefficients for the peak and off-peak prices, respectively. It can be noticed that the pass-through rates are almost equivalent, with a more moderate impact of the allowances during off-peak hours and a higher one for the peak prices. Similar figures are obtained for Model 4, the last two columns, which confirm that when we consider together the cointegrating relationships between natural gas and allowances prices with peak and off-peak electricity prices, there is a significant yet modest pass-through rate of the allowances’ prices into both peak and off-peak ones.
The limited pass-through rates of the allowances are in line with what is shown by
Jouvet and Solier (
2013) for the Italian markets. They show that, when considering only data of the first two phases of the EU-ETS, in Italy, it is possible to “[…] reasonably conclude that carbon costs were not yet passed through on spot markets over the second phase of the EU ETS.” (
Jouvet and Solier 2013, p. 1375). Note that a positive (although small) pass-through rate is not efficient since it allows polluters to partially shift the burden of their emissions to end consumers.
The significance of the electricity price in the α vector reported in the second part of the table indicates that the direction of the long-run adjustment goes from gas prices and allowances costs toward the PUN. More precisely, it indicates that when the average electricity price is too high, it slowly falls back toward the equilibrium. This is the case for the three single-price models (1, 2 and 3). In the four-variate model (4), interestingly enough, the evidence shows that off-peak prices react to both peak and off-peak prices, while the opposite is not true. This might signal a strategic behavior of power producers during off-peak hours, where they can bid considering both off-peak and peak prices.
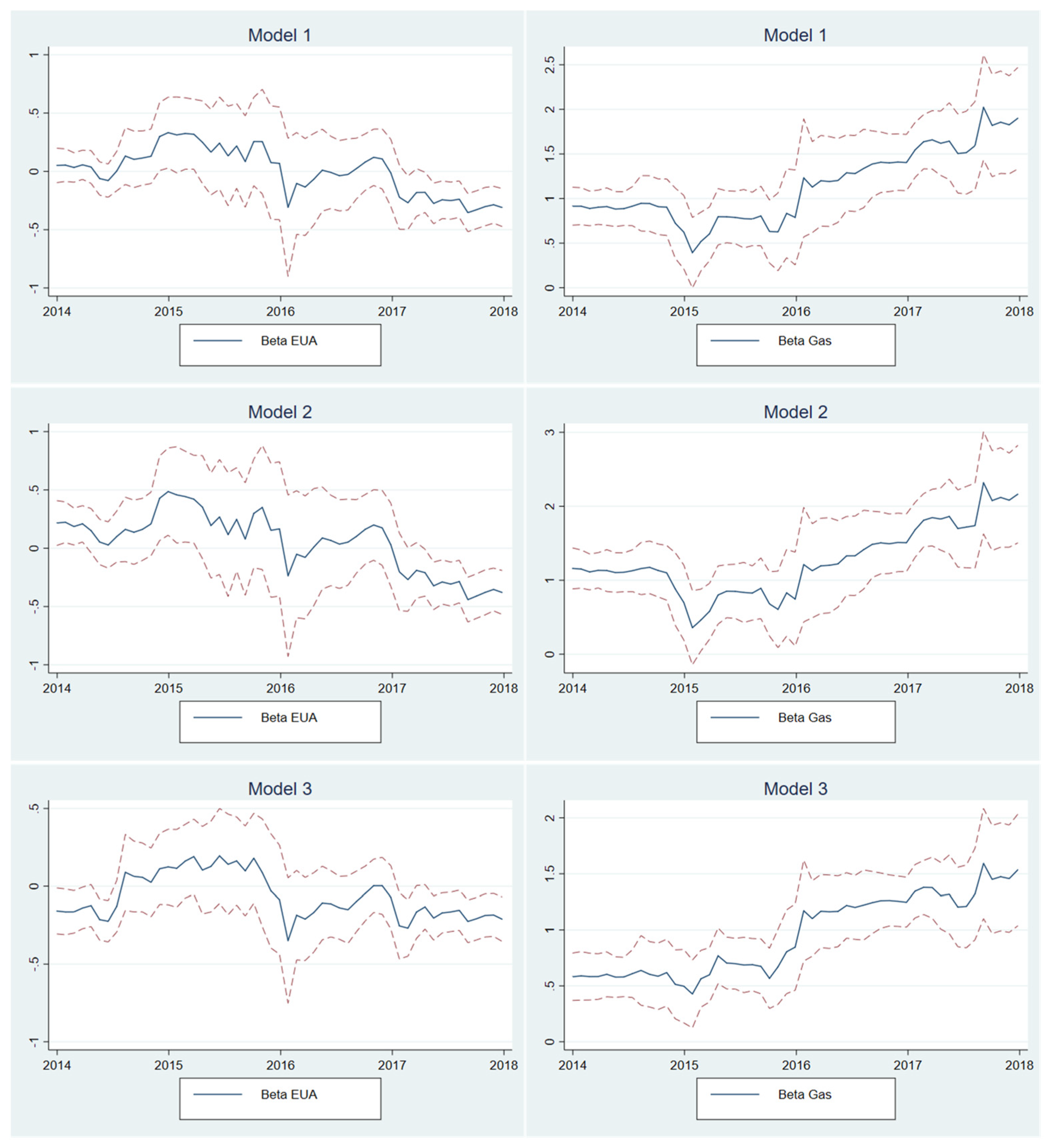
We then investigate the dynamic pass-through effect, calculating the pass-through for a window of two-years observations that is rolling every month throughout the sample period. For clarity of exposition, only Models 1, 2 and 3 are considered: the beta coefficients (and their confidence intervals) relative to both gas and allowances prices are plotted in
Figure 1.
It can be noted that the coefficients change significantly throughout the observation period. In particular, the pass-through rate of gas prices rises over time in all three model specifications. On the contrary, when considering the first model, the pass-through rates captured by the beta of the allowances (EUA) show an opposite trend (although less evident), going from a positive pass-through rate of almost 30% to a negative figure of roughly the same amount. This is even more striking when we look at the peak PUN (Model 2), for which the allowances pass-through rates go from a maximum of almost 50% to a minimum of 40% in the last rolling window. For the off-peak PUN, the dynamics have been equivalent, yet, with lower variations.
A drop in the pass-through rate suggests that, in the most recent years, the Italian electricity price tends to move less after a change in the allowances price. This could signal that the EU-ETS has been increasingly more effective in endogenizing emission costs for power producers, making them decrease the portion of production costs associated with their emissions. However, the mere (falling) correlation across these prices does not guarantee that a real interconnection among allowances and electricity prices exists also in the short run. To gain insight on the causality order and see whether, in the short run, a change in the allowances price (or natural gas one) impacts the electricity price or vice versa, or both, the impulse response functions of the models are evaluated. They are reported in
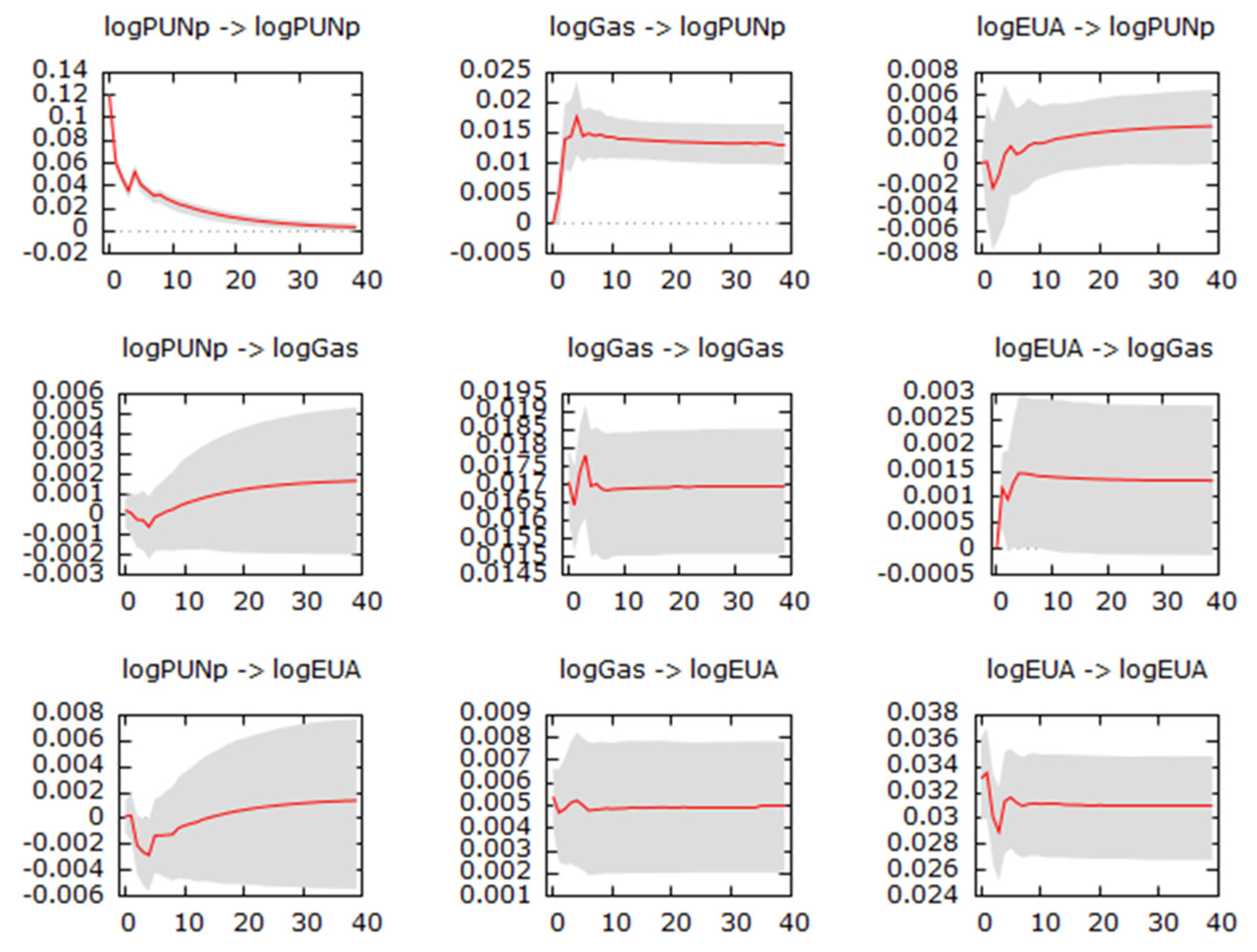
Figure 2 and
Figure 3.
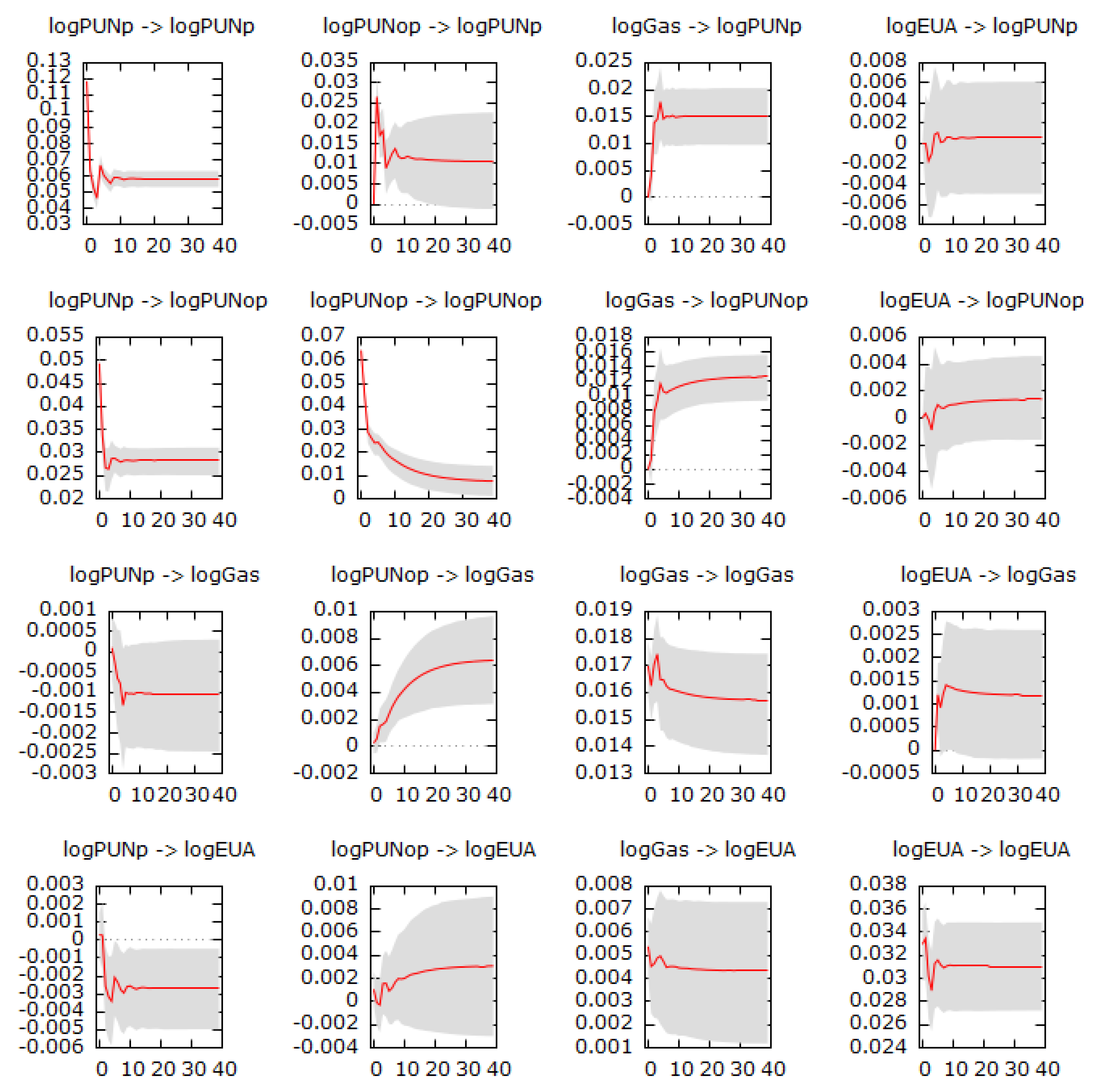
Figure 2 plots the impulse response functions of Model 1, i.e., the model that does not make any distinction between peak and off-peak prices, for up to 40 lags (8 weeks), and with a 90% confidence interval to evaluate their statistical significance (confidence intervals are obtained through bootstrap). Notably, the correlations among the VECM changes are very small, close to zero in most cases. The largest value is registered between allowances and gas changes, equal to 0.16. Consequently, unitary shocks on the orthogonalized residuals
ηt are almost equivalent to shocks on the correlated residuals
εt (see Equation (5)) and the IRFs are very close to those obtained after a one standard deviation shock on the VECM residuals. Given these strong similarities, the IRFs can be interpreted as if they were obtained with a one standard deviation shock on the correlated residuals (i.e., non-orthogonalized). In the tri-variate model, the standard deviations of the shocks are around 0.091 for the energy price, 0.017 for gas and 0.033 for allowances. Differently, in the four-variate model, 0.118 is for peak prices, 0.081 for off-peak prices, and for gas and allowances, they are comparable to the previous ones.
As expected, some of the IRFs converge to non-null values since non-stationary series are being considered. The diagonal elements of the IRF matrix are always statistically significant. It can be noted that shocks on the gas price transmit in large part to the energy price, with an IRF stabilizing with high significance around 0.0125 after a shock of 0.017. However, shocks on the allowances lead only to a marginally statistically significant impact on the energy prices after four weeks; the impact, in the long run, has a size comparable to that of the shock. Finally, across the remaining off-diagonal IRFs in
Figure 2, only in one other case there are statistically significant reactions: allowances react to a gas price shock, with reactions much smaller than the shock size.
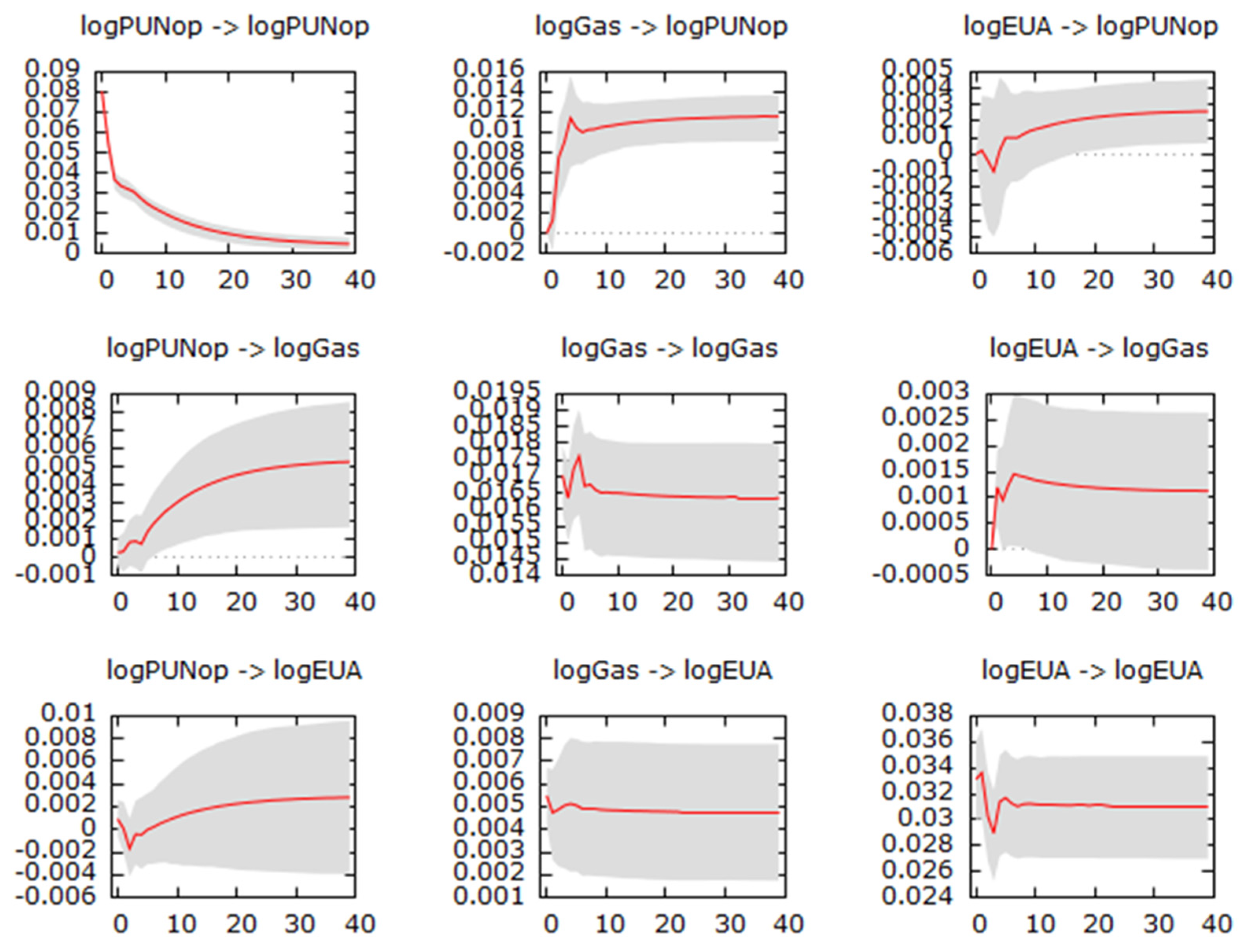
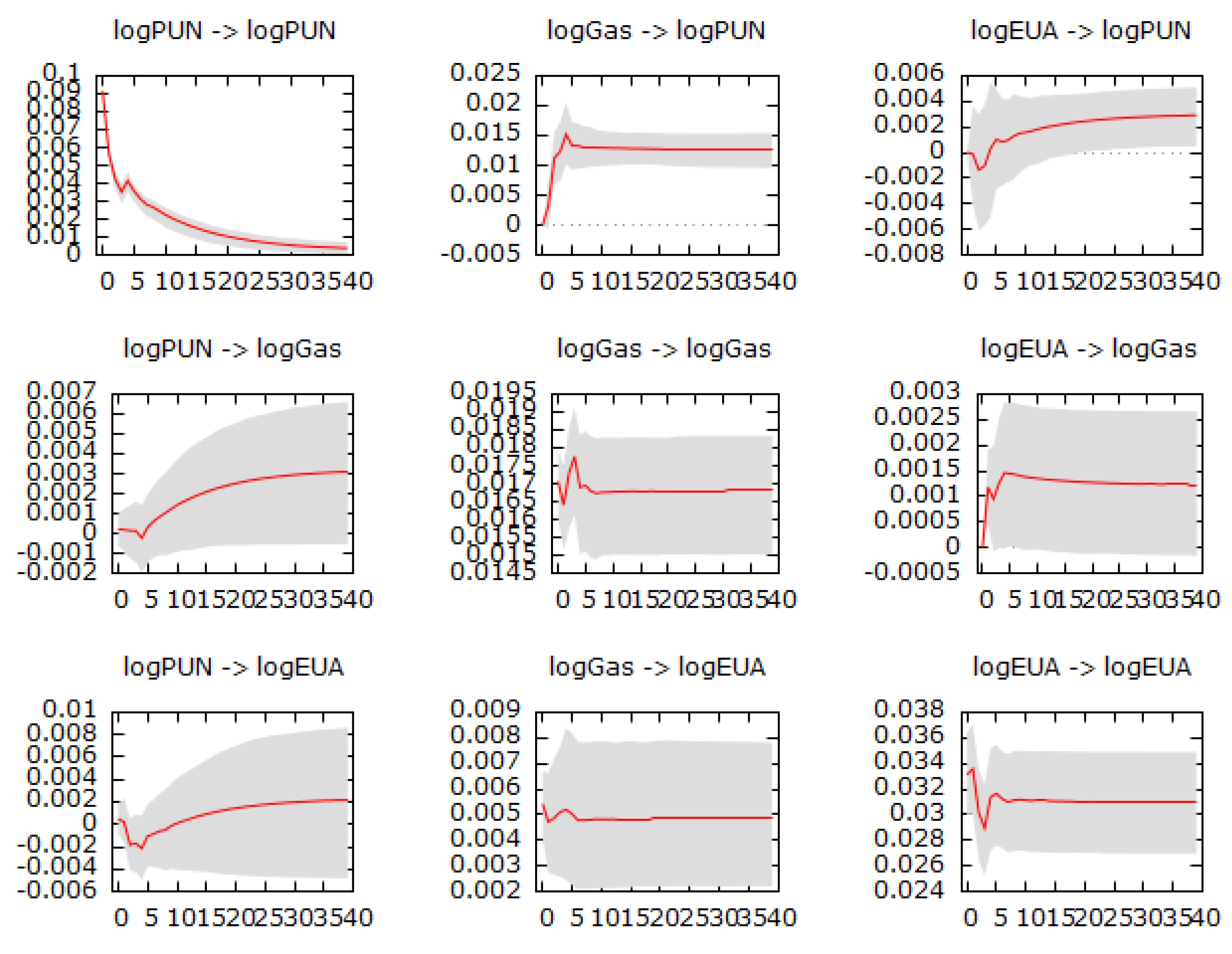
The IRF are evaluated also for Models 2 and 3, replacing the electricity price with either the peak or off-peak price, confirming the previous elements.
Appendix A.3 includes those figures.
Figure 3, that takes into consideration a four-variate model, confirms the relevant impact of gas price shocks on the energy prices. A shock, in the long run, is fully transmitted. Allowances do not impact the prices’ evolution. On the contrary, there is a significant, yet limited, negative impact going from the peak prices to the allowances. This seems to signal that, effectively, peak prices influence allowances’ prices and not vice versa. A possible explanation might depend on the dynamics of power markets and allowances market. A rise in peak price can be due to a shortage in supply. Given that the capacity installed is fixed, this can signal power outages from some power plants, that would not be demanding allowances in the market, as they would not need to cover their missed production. This reduction in demand can have a negative impact on the allowances’ price.
4. Conclusions
The EU Emission System, firstly introduced in 2005, is now at its third phase after a continuous process of refinement and improvement. One of its key elements is the emission permits, i.e., allowances, whose price is bound to increase over time as a consequence of the decreasing cap on the total emissions. Allowances are a component of the variable costs of (thermal) power production. Power producers can react to the increase in the price of the allowances by (partially) passing them on the final electricity price or, on the contrary, by reducing their emissions through a technological change. Our study analyzes the relationship between the price of the allowances and the electricity price in the Italian market, which is one of the biggest European markets in terms of size and electricity price level, focusing on the last phase of this regulatory framework (third phase of the EU-ETS). The analysis of the relationship among these prices can detect the presence of pass-through, which, if positive, would hinder the ability of the scheme to provide the correct incentive toward the decarbonization of the power sector.
Thanks to a dynamic approach, it is possible to see if the EU-ETS is effective in endogenizing emissions’ costs for thermal power production or if producers have adapted to it by passing through the cost of the allowances to end consumers. We show that there is a limited pass-through of emissions costs in the third phase: a EUR 1 rise in the allowances’ price is coupled with a 7-cent rise in the electricity price. Moreover, the pass-through rate has been falling significantly over time.
The falling pass-through rate can indicate a technology substitution effect induced by the allowances’ cost. In particular, if the rising price of the allowances is perceived as a permanent component of the production cost by thermal power producers, they can respond over time by changing technology, replacing net CO2 emitting technologies with less emitting technologies, or even carbon-neutral ones. However, this depends also on the degree of competitiveness of power markets. The more that players have market power, the less the system marginal price would reflect the cost structure of power generation of the marginal plants. Therefore, the substitution effect can take place only if the market is sufficiently competitive. At first sight, this is what has happened in the structure of the power production in Italy during the third phase of the EU-ETS, which experienced a large penetration of RES-fueled generation capacity that has replaced the share of large CO2 emitters (in particular, oil and coal plants). In particular, the share of power produced by RES in Italy increased from 33.9% in 2013 to 40.83% in 2018, with the final goal for renewables to surpass natural gas as the primary fuel for electric power generation by 2020. In the power market, the increase in electricity produced by RES-fueled plants lowers electricity prices since these plants produce at null or low marginal costs. This is what happened in Italy, which experienced a decrease in the average day-ahead price, which can hardly be explained by market power since the Italian wholesale market is quite competitive, at least in its biggest zone, North (note, however, that a precise assessment of the degree of competitiveness and its impact on the day-ahead price goes beyond the scope of the present paper). However, the reduction in electricity price, captured by a negative pass-through rate and an increasing price of the allowances, is not necessarily caused by a variation in the emissions cost component. The negative pass-through rates do not imply per se that the causality order necessarily goes from the allowances prices to the electricity ones through the technical substitution effect. Indeed, the rise in RES-plants production and in allowances’ prices might be induced by some policy-driven technological changes (such as incentive policies, regulatory changes in the electricity sector, more stringent environmental rules and similar).
The study of the impulse response functions of the VECM can shed a light on this issue by detecting the causality orders (if there are any) running across the variables of interest. The analysis shows that changes in the long-run equilibrium of the electricity price (be it the overall PUN or disentangled in peak and off-peak prices) are not caused by the allowances’ prices. In other words, data cannot support the claim that the long-run relationship (which is shown to exist) between electricity and allowances’ prices is affected by short-run changes in such a way that, when the allowances’ price rises, the electricity price adjusts accordingly, returning to the long-run equilibrium.
This casts some doubts on the impact that the EU-ETS mechanism has had in endogenizing emissions costs, implementing the “polluters pay” principle and inducing an increase in RES-plants penetration in the case of Italian power production. In other words, it seems that the allowances have not been able to finance the energy transition of the Italian power system (note, however, that most of the Italian thermal capacity participates also in the balancing market; the thermal power capacity can derive a relevant share of its profit from that market; and the analysis of the relationship between the ETS and the balancing price might shed further light on the pass-through rate, but this goes beyond the scope of the present paper). This does not mean that the system is inefficient as a whole.
2 The “trading” nature of the EU-ETS, in fact, makes the cut in emissions happen in those sectors where it is more efficient to do so, eventually reaching its primary goal of lowering the emission levels in Europe. As a consequence, regulators must put particular attention on those sectors where this does not happen, providing additional incentives when necessary, including proper tools to hedge climate-related sector-specific risks
3.