Country of Origin Effects on the Average Annual Values of NHL Player Contracts

Abstract

Using data from 2005 to 2016, this paper examines if players in the National Hockey League (NHL) are being paid a positive differential for their services due to the competition from the Kontinental Hockey League (KHL) and the Swedish Hockey League (SHL). In order to control for performance, we use two different large datasets, (N = 4046) and (N = 1717). In keeping with the existing literature, we use lagged performance statistics and dummy variables to control for the type of NHL contract. The first dataset contains lagged career performance statistics, while the performance statistics are based on the statistics generated during the years under the player’s previous contract. Fixed effects least squares (FELS) and quantile regression results suggest that player production statistics, contract status, and country of origin are significant determinants of NHL player salaries.

1. Introduction

The Kontinental Hockey League (KHL) was founded in 2008. It comprises of 27 teams based in Belarus, China, Finland, Kazakhstan, Latvia, Russia, and Slovakia. The Swedish Hockey League (SHL) was founded in 1975. It comprises of 14 teams that play their games in Sweden. The existence of these two leagues may provide an alternative to the National Hockey League (NHL) for players who want to play professional hockey. We examine if players that may play in these leagues because of their country of origin now command a higher salary in the NHL.

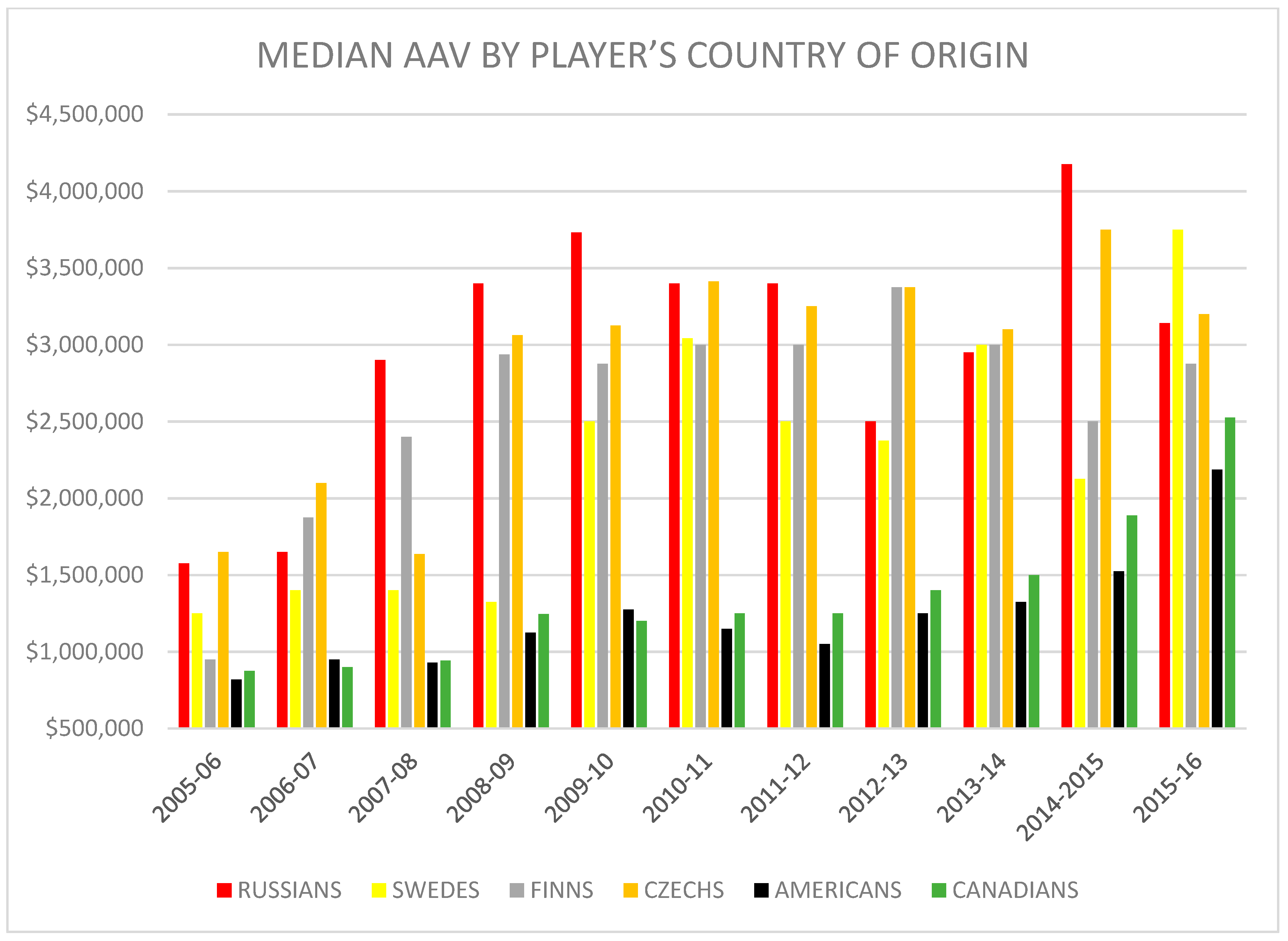
Figure 1 plots the annual average value (AAV) for players by their country of origin. AAV is the total salary over the term of a contract divided by the length of the contract in years plus annualized performance bonuses. The data are taken from https://www.capfriendly.com. In the 2015–2016 season, the NHL consisted of players from all over the globe, with players of Canadian descent dominating the league at 49%. Second on the list were players from the United States at 24.6%. Players of Swedish descent came third, making up 8.6% of the league, followed by Russians at 4.1%. Players from Czech Republic and Finland each represented 3.9% of the league. Looking at Figure 1, it is clear that median Russian, Swedish, Finnish, and Czech salaries exceed those of American and Canadians for every given year. Is this because Russian and European players are more talented than their American and Canadian counterparts? Or is it because Russian and European players have more leverage in NHL salary negotiations because of the demand from the KHL and the SHL for their services? We use salary and NHL statistics from the 2005–2016 seasons to explore these questions.

2. Literature Review

Salary discrimination and entry discrimination have both been studied extensively in North American professional sports (Kahn 1992; Holmes 2011; Yang and Lin 2012). Earlier studies focus on the discrimination against Francophones on Anglophone Canadian NHL teams (Lavoie et al. 1987; Jones and Walsh 1988). Previous studies on the NHL found salary discrimination against European players in the NHL (Bruggink and Williams 2009). Recently, Christie and Lavoie found discrimination against young Russian players in the NHL draft (Christie and Lavoie 2015).

There is also an established literature on salary and player performance in the NHL. There are many statistics that can determine what a player may be worth. The most common statistics used are points (for offensive production), penalty minutes (for defensive intensity), and a plus/minus statistic for a combination of both offensive and defensive skills (Idson and Kahane 2001). The impact of a player’s statistics on their salary can be challenging due to the fact that players are paid based on statistics of their play in previous years (Kahane 2001). Kahane uses lagged career statistics to account for this fact. Brander and Egan use on-ice statistics from the year immediately prior to the contract that determines the player’s salary in their dataset (Brander and Egan 2018). They also control for the type of player contract using dummy variables. We too use lagged on-ice statistics for the same reasons and dummy variables to control for the type of player contracts. Holmes studies the impact of performance on salary in Major League Baseball (Holmes 2011). He points out that ordinary least squares (OLS) models that employ a single dummy for ethnicity may fail to detect discrimination at various levels of the salary distribution. His approach is to use a quantile regression model, which detects the subtleties of discrimination at different quantiles. Vincent and Eastman also employ quantile regression to examine the impact of performance on salary at different quantiles of the NHL wage distribution (Vincent and Eastman 2009). They claim that the standard conditional expectations model employed by OLS misses some important subtleties of the earnings determination in the NHL, as opposing effects at different quantiles may cancel each other out in a single mean conditional expectations OLS model. We also present results from quantile regressions in addition to fixed effects ordinary least squares results (FELS).

3. Data

Two panel datasets, (N = 4046) and (N = 1717), are used in this study. The first dataset, called career lagged statistics data, uses player-years as the unit of observation. The second dataset, called previous contract statistics data, uses player contracts as the unit of observation. Both datasets include players that played in the NHL during the 2005–2006 to 2015–2016 seasons. Players must have played over 25 games in at least one season over the course of their career or their previous contract to be considered a full time player for the purposes of this study. Goalies are excluded because their statistics are quite different from other players. We also exclude any players that were traded during a season to another team. The original NHL statistical player data come from http://www.hockeyabstract.com and Rob Vollman, while the annual average value (AAV) data come from https://www.capfriendly.com.

The first panel dataset has player-years as the unit of observation. The nominal version of the dependent variable in this dataset is called the AAV. The AAV is the total salary over the term of a contract divided by the length of the contract in years plus annualized performance bonuses. We use AAV in part because it also factors in performance bonuses. This figure is used instead of total salary due to the variance in pay per season and the unavailability of total salary for some players. We obtain real AAV in year t by deflating nominal AAV in year t by the NHL salary cap in year t. AAV is expressed as a percentage of the NHL salary cap in a given year. Salary cap is used as the deflator instead of the consumer price index (CPI) because the salary cap rises faster than the CPI. We thank an anonymous referee for this helpful suggestion. As with Kahane, our first dataset uses lagged career statistics. In other words, player i’s AAV in year t is a function of his career statistics accumulated until year t − 1. The first dataset includes players on all types of contracts, including players on entry level contracts. We include a table of sample statistics by country of origin for this dataset in

Table 1. Sample statistics by country (career lagged dataset)

Averages with Standard Deviations Below
	AAV	Games Played	Goals per Game	Assists per Game	Plus-Minus	Penalty Minutes per Game	Shots per Game	Time on Ice per Game	Total Defensemen	Total Left Handed Players	N
Canadians	$2,358,205	315.11	0.14	0.22	2.23	0.46	1.54	14.97	675	1388	2231
	1,975,705	269.03	0.11	0.14	35.69	0.40	0.72	4.27
USA	$2,100,078	265.89	0.13	0.21	0.16	0.38	1.56	15.43	350	468	913
	1,713,163	235.43	0.10	0.12	24.65	0.29	0.68	3.87
Russians	$3,977,614	375.47	0.22	0.33	21.24	0.32	2.05	17	54	117	148
	2,619,935	298.29	0.18	0.18	54.33	0.16	1.11	3.77
Swedes	$2,662,338	282.59	0.13	0.24	23.55	0.26	1.64	17	103	185	226
	1,797,811	250.14	0.11	0.14	45.00	0.15	0.78	3.62
Finns	$3,119,577	414.64	0.17	0.29	9.05	0.32	1.76	16	25	87	101
	1,912,461	339.72	0.11	0.13	32.19	0.15	0.63	3.92
Czechs	$3,212,325	428.48	0.15	0.29	16.73	0.37	1.67	17.06	103	196	252
	1,820,973	280.99	0.10	0.13	50.47	0.27	0.58	3.85
OTHERS	$2,773,339	317.11	0.16	0.26	3.17	0.31	1.73	16	55	140	175
	2,101,381	259.39	0.13	0.13	27.53	0.23	0.63	3.59

AAV: annual average value.

. We thank an anonymous referee for suggesting this table.

The second panel dataset has contract-years as the unit of observation. The dependent variable in the second dataset (previous contract statistics) is the real AAV of a player in the first year of a new contract. Once again, we obtain real AAV in year t by deflating nominal AAV in year t by the NHL salary cap in year t. AAV is expressed as a percentage of the NHL salary cap in a given year for the reasons stated above. The player statistics in the second (contract lagged statistics) are the player’s statistics averaged over the years of their last contract. After excluding observations for missing data, this reduces the number of data points from 4046 to 1717. Both datasets contain dummy variables to control for the type of player contract. We thank an anonymous referee for this excellent suggestion. The previous contract dataset does not have players on entry level contracts; therefore, in keeping with Brander and Egan, restricted free agents (RFA) are the default comparison group. Both datasets also contain dummy variables for the player’s country of origin, team, and annual fixed effects. The second dataset does not have players on entry level contracts, as they have no previous NHL contract on-ice statistics. For the most part, academic researchers in the literature use lagged career statistics, while NHL executives tend to look at more recent measures of player performance, such as their statistics from their last few years. A notable exception is Brander and Egan, who use statistics from the year prior to the current contract. It is interesting to compare and contrast the results from the career lagged statistics dataset and the previous contract statistics dataset.

4. Empirical Model

The first empirical model, given by Equation (1), is applied to all players in both datasets. The second model, given by Equation (2), is estimated separately for defensemen and forwards in both datasets. We thank an anonymous referee for this suggestion. We employ dummy variables to capture the effects of nationality on salary. In addition, we also employ team specific and annual dummy variables to control for team and annual effects.

Real AAV = β₁ + β₂ Games played + β₃ Goals per game + β₄ Assists per game + β₅ Plus-minus + β₆ Penalty minutes per game + β₇ Shots per game + β₈ Time on ice per game + β₉ Defenseman Dummy + β₁₀ Defenseman Dummy X Time on ice per game + β₁₁ Left Handed Player Dummy + β₁₂ RFA Dummy + β₁₂ UFA Dummy + β₁₃ TFP35 Dummy + β₁₄ UFA Years Lost Dummy

(1)

Real AAV = β₁ + β₂ Games played + β₃ Goals per game + β₄ Assists per game + β₅ Plus-minus + β₆ Penalty minutes per game + β₇ Shots per game + β₈ Time on ice per game + β₉ Left Handed Player Dummy + β₁₀ RFA Dummy + β₁₁ UFA Dummy + β₁₂ TFP35 Dummy + β₁₃ UFA Years Lost Dummy

(2)

Real AAV is nominal AAV expressed as a percentage of the NHL salary cap in a given year. UFA stands for unrestricted free agents.

The on-ice variables are taken from (Kahane 2001). Games played is the total amount of games a player has played in during his career in t − 1 years or during his last contract, depending on the dataset. Each of the on-ice performance statistics is averaged over the entire course of the player’s previous years in the NHL for the lagged career statistics dataset and over the course of the years of his last contract for the previous contract statistics dataset. Goals per game is the amount of goals a player scored per game. Assists per game represents the amount of assists per game a player made divided by the number of games that he has played. Points are left out of the study because they are made up of goals and assists, both of which are already counted for. Plus-minus represents a player’s career plus/minus figure, a measurement describing the amount of times a player is on the ice for a goal or a goal against. If a player is out for a goal, then he gets a +1 rating, and if he is out for a goal against, he gets a −1 rating. Penalty minutes per game is the amount of penalty minutes taken per game during the time period in question. According to a referee, this is a good indicator of toughness for a player, and teams are willing to pay more for that player characteristic.

The literature finds that salary is influenced positively with goals and assists per game, plus-minus, and penalty minutes (Bruggink and Williams 2009). Shots per game is given by the total number of shots taken divided by the total number of games played. It is used as an indicator of offensive play other than goals and assists. Time on ice per game represents average time on ice per game for a player during his career. This indicates how much a player was on the ice for his team and usually shows if the player was used in special team situations.

In keeping with Coates (2017), we control for left handed players using the left handed player dummy that takes on a value of one if the player is left handed and zero otherwise. Coates finds that left handed players are paid a premium.

Defensemen play more minutes than forwards, thus we estimate the model separately for each group using Equation (2). The defenseman dummy takes on a value of one if the player is a defenseman and takes on a value of zero otherwise. At the suggestion of a referee, we account for the extra time played by defensemen by interacting the defensemen dummy with the time on ice variable when estimating (1) over both groups of players. This allows the slope of the time on ice variable to differ between defensemen and forwards. Our maintained hypothesis is that defensemen are usually paid less than other players but that they are paid more for their time on ice than forwards. We also include dummy variables to control for the player’s country of origin. We classify players into seven groups: Canadian, American, Russian, Swedish, Finnish, Czech, and Other. We include dummy variables for all groups except Canadians. Thus, all country dummies are in reference to the AAVs earned by Canadian players in the NHL.

Following Brander and Egan, we also include contract type dummies in both equations to control for the types of contracts and their impact on AAV. We thank an anonymous referee for this excellent suggestion. The reader is referred to Brander and Egan (page 86) for an excellent discussion of the different types of contracts and their impact on a player’s AAV. Most players start their careers on an entry level contract. This is the type of contract that we omit from the regression. Therefore, all contract dummy coefficients are to be interpreted relative to the impact of an entry level contract on player earnings. The RFA dummy takes on a value of one if the player is on a restricted free agent contract and zero otherwise. The UFA dummy takes on a value of one if the player is on an unrestricted free agent contract and zero otherwise. The TFP35 dummy takes on a value of one if the player is on a 35 plus TFP contract and zero otherwise. The UFA Years Lost variable is the number of years above the age of 27 that a player continues to play on as an RFA. According to Brander and Egan, UFAs have much more bargaining power than RFAs. TFP35s can also sell their services to the highest bidder but have some salary cap implications that reduce their bargaining power compared to UFAs. Brander and Egan find that players who play on beyond the age of 27 as RFAs receive a slight premium relative to other RFA players in order to do so. They capture this effect using the UFA years lost dummy variable.

5. Empirical Results

We employ fixed effects OLS estimators and quantile regression estimators for Equations (1) and (2) in both datasets.

Table 2. Fixed effects ordinary least squares (FELS) regression results.

Dependent Variable	Lagged Career Statistics			Previous Contract Statistics
Real AAV	All Players Column (1)	Defensemen Column (2)	Forwards Column (3)	All Players Column (4)	Defensemen Column (5)	Forwards Column (6)
Independent Variables	Coefficient (t-Statistic)	Coefficient (t-Statistic)	Coefficient (t-Statistic)	Coefficient (t-Statistic)	Coefficient (t-Statistic)	Coefficient (t-Statistic)
Games played	0.003	0.005	0.003	0.009	0.017	0.005
	(10.228) *	(8.560) *	(7.026) *	(3.588) *	(3.662) *	(2.189) **
Goals per game	3.982	3.016	2.840	4.669	4.815	3.802
	(3.906) *	(1.835) ***	(2.382) **	(3.478) *	(2.382) **	(2.346) **
Assists per game	5.230	3.853	6.581	5.240	2.949	6.489
	(7.734) *	(3.839) *	(8.070) *	(7.787) *	(2.723) *	(7.384) *
Plus-minus	0.007	0.007	0.007	0.040	0.043	0.033
	(4.458) *	(2.981) *	(3.395) *	(5.314) *	(3.829) *	(3.227) *
Penalty minutes per game	0.710	0.876	0.652	0.665	0.515	0.723
	(4.663) *	(2.877) *	(4.229) *	(6.540) *	(2.137) **	(6.108) *
Shots per game	0.680	0.425	0.918	0.747	0.431	0.976
	(5.047) *	(2.352) **	(5.603) *	(4.770) *	(1.579)	(5.675) *
Time on ice per game	0.146	0.225	0.110	0.157	0.282	0.125
	(5.597) *	(8.030) *	(3.532) *	(4.961) *	(7.823) *	(3.146) *
Defenseman	−0.795			−1.198
	(−1.92) ***			(−2.356) **
Defenseman X Time on ice	0.063			0.087
	(2.265) *			(2.373) *
Left Handed player	0.089	0.105	0.018	0.039	0.070	0.009
	(0.976)	(0.693)	(0.174)	(0.419)	(0.411)	(0.0826)
USA	−0.139	0.004	−0.203	−0.083	−0.146	−0.030
	(−1.374)	(0.022)	(−1.693) ***	(−0.766)	(−0.853)	(−0.232)
Russia	0.723	0.750	0.654	0.809	0.766	0.832
	(3.27) *	(2.296) **	(2.350) **	(3.057) *	(1.90) ***	(2.384) *
Sweden	0.129	0.457	−0.179	0.192	0.627	−0.163
	(0.787)	(1.775) ***	(−0.890)	(0.859)	(2.009) **	(−0.606)
Finland	0.298	0.079	0.374	−0.348	−0.188	−0.374
	(0.639)	(0.108)	(0.714)	(−0.984)	(−0.215)	(−0.919)
Czechoslovakia	0.214	0.407	0.071	0.370	0.629	0.209
	(1.103)	(1.349)	(0.356)	(1.601)	(1.72) ***	(0.772)
Other Country	0.188	−0.005	0.334	−0.121	−0.357	0.098
	(0.763)	(−0.012)	(1.186)	(−0.425)	(−0.803)	(0.301)
RFA Dummy	0.526	0.379	0.621
	(4.198) *	(1.953) ***	(3.925) *
UFA Dummy	0.464	0.417	0.513	0.280	0.446	0.146
	(2.986) *	(1.636)	(2.672) *	(3.161) *	(2.771) *	(1.397)
TFP35 Dummy	−2.126	−1.868	−2.333	−0.780	−0.618	−0.830
	(−8.967) *	(−5.599) *	(−7.646) *	(−3.805) *	(−1.626)	(−3.203) *
UFA Years Lost Dummy	0.046	−0.173	0.157	−0.109	−0.241	0.140
	(0.644)	(−1.440)	(2.196) **	(−0.635)	(−1.472)	(0.554)
Adjusted R2	0.69	0.65	0.72	0.70	0.64	0.74
F-stat	150.64	45.33	118.32	68.63	19.21	57.31
N	4046	1365	2681	1717	579	1138

* Significant at the 1% level, ** Significant at the 5% level, *** Significant at the 10% level. Newey-West robust standard errors are employed.

contains the FELS results for Equations (1) and (2) for all players. At the suggestion of an anonymous referee, we also estimate Equations (1) and (2) separately for forwards and for defensemen. Columns (1) to (3) are estimates of Equations (1) and (2) from the career lagged statistics dataset. Column (1) is the estimate of Equation (1), while columns (2) and (3) are the estimates of Equation (2) applied to defensemen and forwards, respectively, for the career statistics lagged dataset. Similarly, columns (4) to (6) contain the FELS estimates of Equations (1) and (2) estimated from the contract lagged dataset. We also employ Newey-West robust standard errors for the FELS models, because White and Breusch-Godfrey tests indicate the presence of both Heteroskedasticity and Serial Correlation, respectively. In keeping with Brander and Egan, we use a linear functional form instead of the semi-logarithmic functional form proposed by Mincer (1958).

The FELS results, columns (1) through (6), in Table 2 support all of the maintained hypotheses about player statistics and salary. All of the performance measure—games played, goals per game, assists per game, etc.—are statistically significant across both datasets, and the coefficients of the various performance statistics have the expected positive signs for all three groups of players (all players, defensemen, and forwards). A unit increase in a given continuous independent variable is interpreted as a percentage change of real AAV equal to the coefficient of the given variable. In column (1), an increase in one game played results in a 0.01 percent increase in a player’s salary, where salary is expressed as a percentage of the NHL salary cap, and so on. Penalty minutes per game are positive and significant in both datasets. The dummy variable for defenseman is negative and statistically significant in both datasets, indicating that defensemen get paid less than forwards. However, defensemen do play more minutes, and the positive and significant sign on the defensemen and time on ice interaction variable has a positive and significant sign. The dummy variable for left handed players is insignificant in both datasets. Both Russian and Swedish players command a higher salary over their Canadian counterparts (the omitted player category). The adjusted R-squares from both datasets are pretty close in magnitude. The difference in the magnitude of corresponding on-ice coefficients between both datasets is also quite small. Therefore, as a practical matter, the FELS results suggest that using one year lagged career statistics or statistics from the player’s last contract does not make much of a difference in the findings. The dummy variable for left handed players (Left Handed player) is insignificant across all three groups of players in both the career lagged and the contract lagged statistics datasets.

Country of origin effects are captured by the dummy variables named for the players’ countries of origin (USA, Russia, Sweden, Finland, Czechoslovakia, and Other). The comparison group is Canadian players. Players of Russian origin have positive and significant coefficients across all models in both datasets. This indicates that Russians are paid more than their Canadian counterparts. The dummy variable coefficient for Swedish defensemen is positive and significant in both the lagged career and the previous contract datasets (columns (2) and (4)), indicating that some Swedish players also command a premium. Czech defensemen command a higher AAV but only based on the previous contract dataset. Finally, USA forwards get paid less than their Canadian counterparts based on the career lagged dataset alone. The reader may refer back to Table 1 to compare and contrast sample statistics by player’s country of origin.

We include contract status dummy variables in all of our models, because a player’s contract status impacts their bargaining power and consequently their AAV. We are thankful to an anonymous referee for suggesting this improvement. Compared to entry level players, players who are restricted and unrestricted free agents command a premium. The contract status dummy variables, RFA, UFA, and TFP35, have the expected signs and are significant in most of the models. The comparison group in the career lagged statistics dataset is players on entry level contracts, while the comparison group in the previous contract dataset is restricted free agents. Both the RFA and the UFA dummies are positive and significant in the majority of the regression estimates. TFP35 players command a slightly lower premium than other UFAs because of certain salary cap rules. This is consistent with the negative sign on the TFP35 dummy. Finally, the UFA years lost dummy is positive and significant only for forwards in the career lagged dataset. Brander and Egan suggest that this is because RFAs that give up some years of unrestricted free agency are expected to receive slightly larger RFA contracts to compensate them for the delay to becoming unrestricted free agents.

We turn next to the quantile regressions estimates of Equation (1) from both the career lagged statistics dataset and the previous contract statistics dataset. We use Huber-White robust standard errors. As Vincent and Eastman point out, different variables have varying impacts at different quantiles of the wage distribution. Quantile regression estimates allow us to estimate these impacts at different quantiles of the wage distribution. The quantile regression results for the career lagged dataset are displayed in

Table 3. Quantile regression results based on lagged career statistics.

Dependent Variable	Real AAV
Regression Level	10th Quantile	25th Quantile	50th Quantile	75th Quantile	90th Quantile
Independent Variable	Coefficient	Coefficient	Coefficient	Coefficient	Coefficient
	t-Statistic	t-Statistic	t-Statistic	t-Statistic	t-Statistic
Games played	0.003	0.004	0.004	0.003	0.003
	(15.416) *	(19.826) *	(13.218) *	(10.377) *	(6.679) *
Goals per game	1.257	2.907	4.559	4.931	7.443
	(3.287) *	(4.106) *	(5.94) *	(5.768) *	(7.185) *
Assists per game	1.191	3.110	4.933	7.361	8.609
	(3.06) *	(6.72) *	(9.246) *	(13.895) *	(8.753) *
Plus-minus	0.010	0.012	0.009	0.006	0.003
	(6.11) *	(9.03) *	(7.016) *	(4.92) *	(0.921)
Penalty minutes per game	0.225	0.490	0.692	0.719	0.550
	(4.249) *	(5.614) *	(6.731) *	(6.26) *	(3.872) *
Shots per game	0.295	0.427	0.648	0.728	0.463
	(4.209) *	(4.143) *	(5.956) *	(7.137) *	(3.67) *
Time on ice per game (TOIPG)	0.036	0.077	0.107	0.102	0.104
	(2.323) **	(3.357) *	(5.569) *	(5.415) *	(4.05) *
Defenseman	−0.567	−0.689	−1.378	−1.116	−1.060
	(−1.119)	(−1.311)	(−3.593) *	(−3.884) *	(−3.253) *
Defenseman X TOIPG	0.040	0.052	0.104	0.108	0.123
	(1.252)	(1.489)	(4.33) *	(5.852) *	(5.551) *
Left Handed player	−0.023	0.046	−0.002	0.124	0.032
	(−0.55)	(0.79)	(−0.024)	(1.745)	(0.294)
USADUMMY	0.030	0.034	−0.180	−0.149	−0.126
	(0.624)	(0.565)	(−2.554) **	(−1.878) ***	(−0.967)
RUSDUMMY	0.441	0.827	0.902	0.753	0.418
	(2.088) **	(5.571) *	(3.566) *	(4.427) *	(1.782)
SWEDUMMY	0.316	0.300	0.136	0.087	0.088
	(3.048) *	(2.493) **	(0.905)	(0.631)	(0.374)
FINDUMMY	0.144	0.155	0.202	0.344	0.360
	(0.942)	(0.679)	(0.877)	(1.573)	(0.747)
CZEDUMMY	0.409	0.436	0.121	0.046	−0.120
	(3.348) *	(3.446) *	(0.904)	(0.288)	(−0.528)
OTHERDUMMY	−0.008	0.057	0.122	0.066	0.506
	(−0.072)	(0.364)	(0.624)	(0.378)	(1.237)
RFA Dummy	0.272	0.405	0.273	−0.034	−0.529
	(2.74) *	(3.699) *	(2.394) *	(−0.285)	(−2.726) *
UFA Dummy	−0.111	0.021	0.158	0.175	−0.142
	(−0.969)	(0.145)	(1.141)	(1.257)	(−0.612)
TFP35 Dummy	−1.737	−2.085	−1.837	−2.020	−1.837
	(−4.729) *	(−8.97) *	(−9.042) *	(−11.206) *	(−6.818) *
UFA Years lost	0.316	0.139	0.093135	−0.045358	−0.150418
	(2.805) *	(1.878) ***	(1.646) ***	(−0.754)	(−1.198)

* Significant at the 1% level, ** Significant at the 5% level, *** Significant at the 10% level. Robust standard errors are employed.

, while

Table 4. Quantile regression results based on previous contract statistics.

Dependent Variable	Real AAV
Regression Level	10th Quantile	25thQuantile	50th Quantile	75th Quantile	90th Quantile
Independent Variable	Coefficient	Coefficient	Coefficient	Coefficient	Coefficient
	t-Statistic	t-Statistic	t-Statistic	t-Statistic	t-Statistic
Games played	0.011	0.012	0.004	−0.004	−0.007
	(8.733) *	(7.203) *	(1.783) ***	(−1.071)	(−1.394)
Goals per game	1.244	4.005	6.344	6.417	9.556
	(2.539) **	(5.902) *	(6.076) *	(4.54) *	(4.03) *
Assists per game	0.894	2.693	5.127	7.804	8.740
	(2.42) **	(4.839) *	(7.122) *	(7.851) *	(8.147) *
Plus-minus	0.022	0.027	0.030	0.030	0.031
	(4.197) *	(4.115) *	(4.225) *	(3.318) *	(2.635) *
Penalty minutes per game	0.269	0.491	0.686	0.606	0.476
	(4.554) *	(6.902) *	(5.8) *	(3.846) *	(1.669)
Shots per game	0.202	0.482	0.592	0.733	0.630
	(2.553) **	(4.773) *	(3.981) *	(5.315) *	(2.444) **
Time on ice per game (TOIPG)	0.069	0.096	0.118	0.107	0.073
	(3.984) *	(4.574) *	(4.589) *	(4.085) *	(2.26) **
Defenseman	−0.209	−0.996	−2.332	−1.696	−2.043
	(−0.397)	(−1.16)	(−4.522) *	(−4.363) *	(−3.423) *
Defenseman X TOIPG	0.009	0.064	0.166	0.155	0.202
	(0.259)	(1.136)	(4.861) *	(5.885) *	(4.705) *
Left Handed player	−0.015	0.068	0.040	−0.076	0.043
	(−0.278)	(0.957)	(0.428)	(−0.733)	(0.314)
USADUMMY	−0.031	0.021	−0.004	−0.140	−0.051
	(−0.514)	(0.266)	(−0.035)	(−1.235)	(−0.269)
RUSDUMMY	0.454	0.592	0.671	0.839	0.517
	(1.982) **	(1.753) ***	(2.816) *	(2.254) **	(1.39)
SWEDUMMY	0.190	0.182	0.563	0.373	0.212
	(1.283)	(0.915)	(2.645) *	(1.564)	(0.748)
FINDUMMY	−0.019	−0.258	0.008	−0.082	0.420
	(−0.094)	(−0.799)	(0.023)	(−0.232)	(0.485)
CZEDUMMY	0.219	0.483	0.470	−0.076	−0.336
	(1.131)	(2.997) *	(2.544) **	(−0.366)	(−0.988)
OTHERDUMMY	−0.034	−0.154	−0.284	0.090	−0.212
	(−0.258)	(−0.79)	(−1.238)	(0.326)	(−0.505)
UFA Dummy	−0.052	0.110	0.335	0.460	0.452
	(−0.863)	(1.347)	(3.632) *	(4.423) *	(2.879) *
TFP35 Dummy	−0.053	−0.360	−0.605	−0.799	−0.752
	(−0.334)	(−1.68)	(−2.597) *	(−3.411) *	(−2.642) *
UFA Years lost	−0.165	0.003	−0.024	−0.040	−0.538
	(−1.132)	(0.043)	(−0.1)	(−0.141)	(−5.854) *

* Significant at the 1% level, ** Significant at the 5% level, *** Significant at the 10% level. Robust standard errors are employed.

gives the quantile regression results based on the player’s previous contract statistics. The career lagged dataset contains players on all types of contracts. The comparison group is players on entry level contracts. The previous contract dataset only contains players that are RFAs, UFAs, and TFP35s, thus the default comparison group in Table 4 is RFAs. We employ robust Huber-Sandwich standard errors and covariances for the quantile regressions. Once again, we do not report the annual and the team specific dummy variables for the sake of brevity.

The coefficient on games played is positive and significant across the 10th, the 25th, and the 50th quantiles in both datasets. Goals and assists per game are significant and positive across all quantiles in both datasets. The plus-minus variable is significant and positive up to the 75th quantile in the lagged career statistics dataset (Table 3) and across all quantiles in the previous contract dataset (Table 4). Penalty minutes per game is significant across all quantiles in the lagged career statistics dataset and is significant and positive up to the 75th quantile in the lagged contract statistics dataset (Table 4). Shots per game and time on ice per game are significant across all quantiles in both datasets.

Defensemen are paid less than forwards at the 50th, the 75th, and the 90th quantiles across both datasets. However, this effect is lessened when the defensemen time on ice interaction dummy has a positive and significant coefficient at the same quantiles in both datasets. The net effect of the defensemen dummy coefficient plus the defensemen time on ice interaction dummy coefficient is still negative at the 50th, the 75th, and the 90th quantiles. Once again, the dummy variable for left handed players is insignificant across all quantiles in both datasets.

The country of origin dummies show that Russian players are paid more than Canadian players at all quantiles except the 90th quantile in both datasets. Swedes and Finns are paid more at the 10th and the 25th quantiles according to the estimates from the lagged career statistics dataset. However, according to the regressions based on the contract lagged statistics dataset, they are paid more only at the median quantile. American players are underpaid relative to the Canadian group of players at the 50th quantile based on the lagged career dataset in Table 3.

The RFA contract status dummy is positive and significant in Table 3 up to the median quartile. Table 4 does not contain the RFA dummy because RFAs make up the comparison group in the contract lagged dataset. The UFA dummy is insignificant at all quantiles in the career lagged statistics dataset in Table 3. However, it is significant and positive at the 50th, the 75th, and the 90th quantiles in the contract lagged statistics dataset. This is in keeping with the logic that unrestricted free agents have more bargaining power and are likely to secure higher AAVs. The TFP35 dummy is negative and significant across all quantiles in the career lagged statistics dataset, while it is negatively significant at the 50th, the 75th, and the 90th quantiles in the contract lagged statistics dataset. This is in keeping with the reasoning that more restrictive salary cap rules make teams less likely to award high TFP35 contracts. The contract status dummies tend to perform better in the contract statistics lagged dataset than the career lagged statistics performance dataset. General managers are more likely to base their decisions on a player’s recent productivity from their last few years rather than on their career statistics. For older players, such as those in the TFP35 category, there could be a significant difference in those statistics.

6. Conclusions

The purpose of this paper is to examine if the country of origin influences a player’s average annual contract value in the NHL after controlling for on ice performance, contract status, and position. We use two different sets of on-ice statistics to control for on-ice performance. The first dataset contains players’ average annual values of their current contract in each year and a lagged career average of their various on ice statistics. This is the type of data used in most academic studies. The second dataset looks at player’s real average annual value in the first year of a new contract as a function of their average on-ice statistics during their last contract. This is the type of data that most NHL teams are likely to use when making contract offers.

The FELS results for on-ice production statistics are quite similar across both datasets. We find that players annual average values increase with their on-ice performance measured by games played, goals per game, assists per game, their plus-minus statistic, penalty minutes per game, shots per game, and their time on ice per game. However, the FELS results suggest that defensemen get paid less than forwards. The FELS results from both datasets do not support the idea that left handed players are paid more for being left handed. After controlling for on-ice productivity, contract status, and position, we find that Russian players are paid more than others in the NHL across the board in all FELS regressions based on both datasets. We also find that Swedish and Czech defensemen get paid more than their Canadian counterparts.

The quantile regression results are a little more nuanced and insightful. These results for both datasets show that on-ice productivity, for the most part, is related positively to NHL salaries. In general, goals per game, assists per game, plus-minus, penalty minutes, and shots per game are related positively and significantly to player salary. However, according to the estimates from the contract lagged statistics, games played is not significant in determining salary at the 75th and the 90th quantiles. This suggests that NHL general managers view the relationship between games played and higher end salaries differently than the results from academic studies, which find games played and salary to be related at all quantiles.

We find that defensemen are paid less than forwards at the 50th, the 75th, and the 90th quantiles in both datasets. However, when accounting for the time on ice played by defensemen, we find that defensemen are paid a little more than forwards for their time on ice. This allows us to understand why past FELS results in the literature found that defensemen get paid less than forwards. However, this slight increase is not enough to offset the negative differential in pay between forwards and defensemen, and defensemen still get paid less than forwards at the middle to upper quantiles of the distribution. These results are consistent with previous findings by Kahane (2001). However, unlike Coates (2017), we do not find any significant salary differential for left handed players.

The results from the contract lagged statistics dataset show that Russians get paid more at every quantile up to the 75th quantile. Players from other countries do not see additional compensation above the median quantile. There is also a country of origin effect on compensation for Swedish and Czech players from the lower to the middle quantiles, depending on the dataset used. Given that the KHL and the SHL cannot outbid NHL teams for the very top talent, it makes sense that country of origin dummies are insignificant beyond the median quantile (for the previous contract dataset). The only exception is Russia, which is significant at the 75th quantile. These country of origin effects are observed after controlling for on-ice performance, contract status, team effects, annual effects, and player position. Given that NHL teams are trying to win subject to a hard salary cap, the only plausible explanation is that some of these Russian, Swedish, and Czech players have leverage in negotiations due to the availability of options to play in other leagues such as the SHL and the KHL. According to the dataset based on lagged career statistics, Russians get paid more in the NHL at every quantile. However, NHL teams are more likely to award contracts based on recent performance as measured by the previous contract dataset.

In closing, this study suggests that, while the statistical significance of most on ice performance variables on AAV are very similar between career lagged statistics and previous contract lagged statistics datasets, there may be differences in the magnitude of the coefficients. Academics may be missing nuances of salary studies by just focusing on lagged career statistics instead of statistics generated during the player’s most recent contract. In addition, the use of quantile regression produces interesting results at different points of the wage distribution that are masked by the use of a simple ordinary least squares estimator.