Risk Management for the Optimal Order Quantity by Risk-Averse Suppliers of Food Raw Materials
Abstract
:1. Introduction
2. Literature
2.1. Food Safety
2.2. Food Supply Chain Management (FSCM) and Optimal Order Quantity
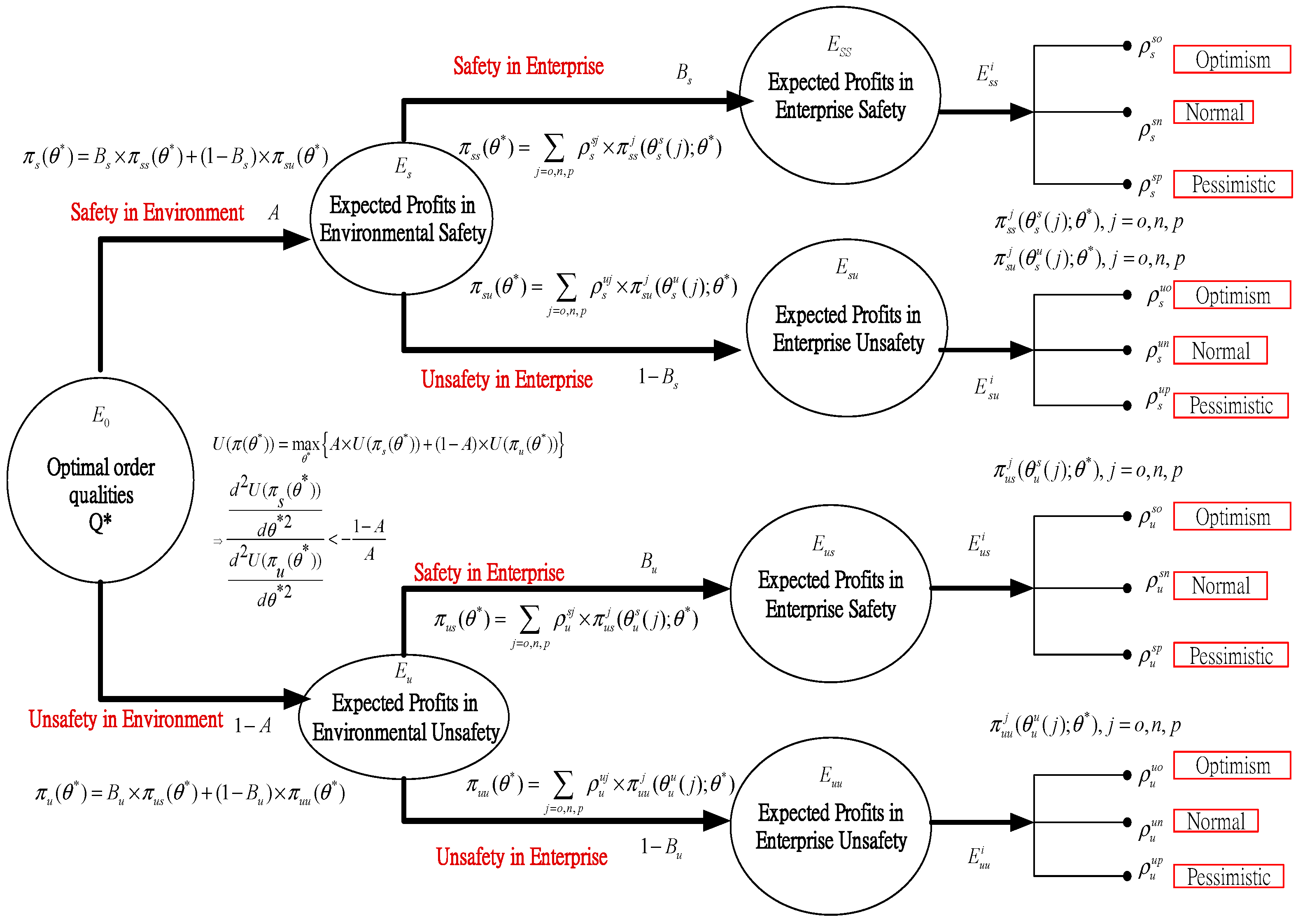
3. Method
3.1. Optimization Methods
- (1)
- The external environment and the individual FRM suppliers do not have food safety problems;
- (2)
- The individual FRM suppliers have an internal food safety problem and the external environment does not have a food safety problem;
- (3)
- The external environment has a food safety problem and the individual FRM suppliers do not have an internal food safety problem;
- (4)
- Both the external environment and the individual FRM suppliers have food safety problems.
3.2. Risk Aversion Concept
4. Numerical Example and Sensitivity Analysis
4.1. Numerical Example
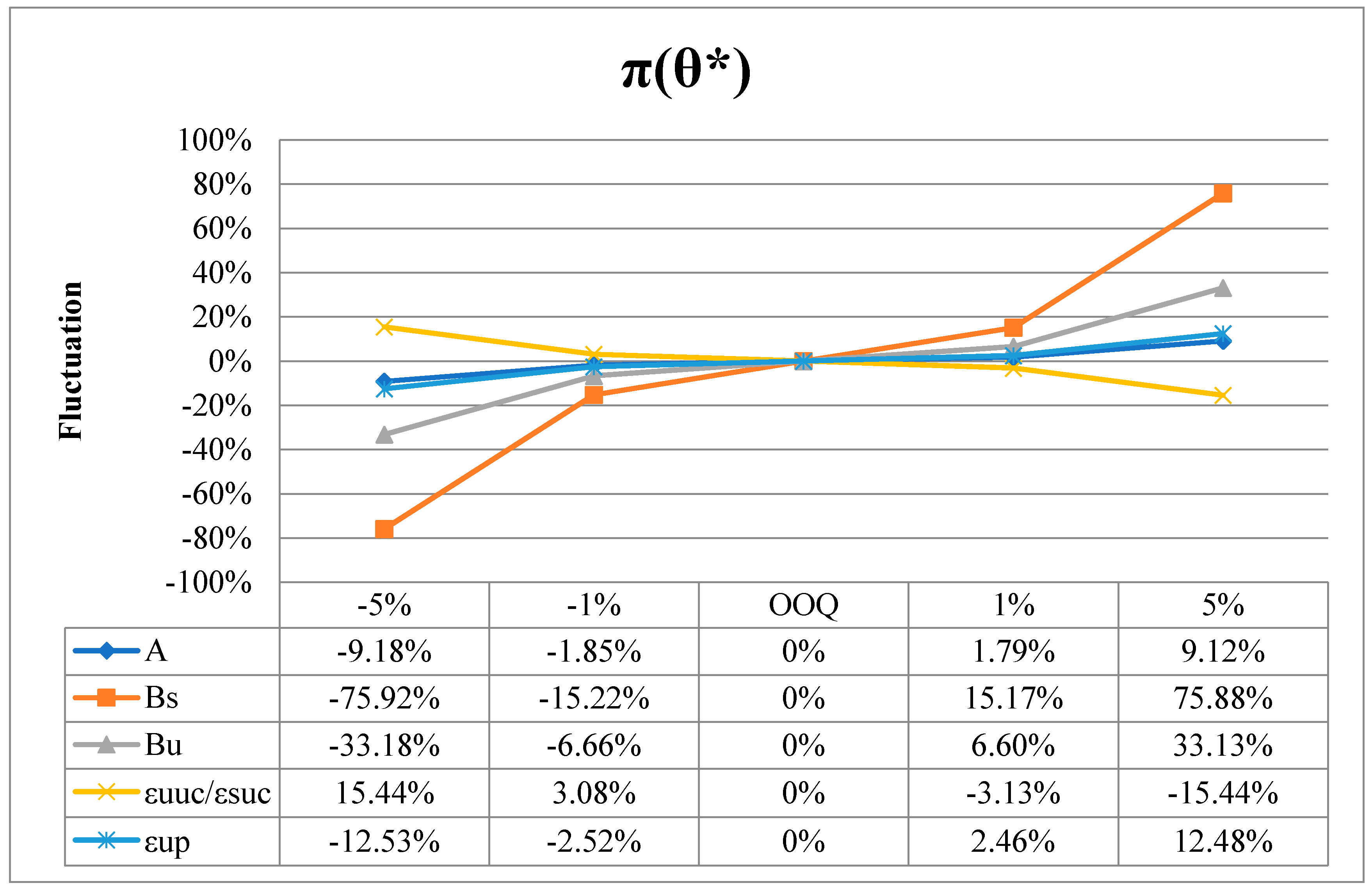
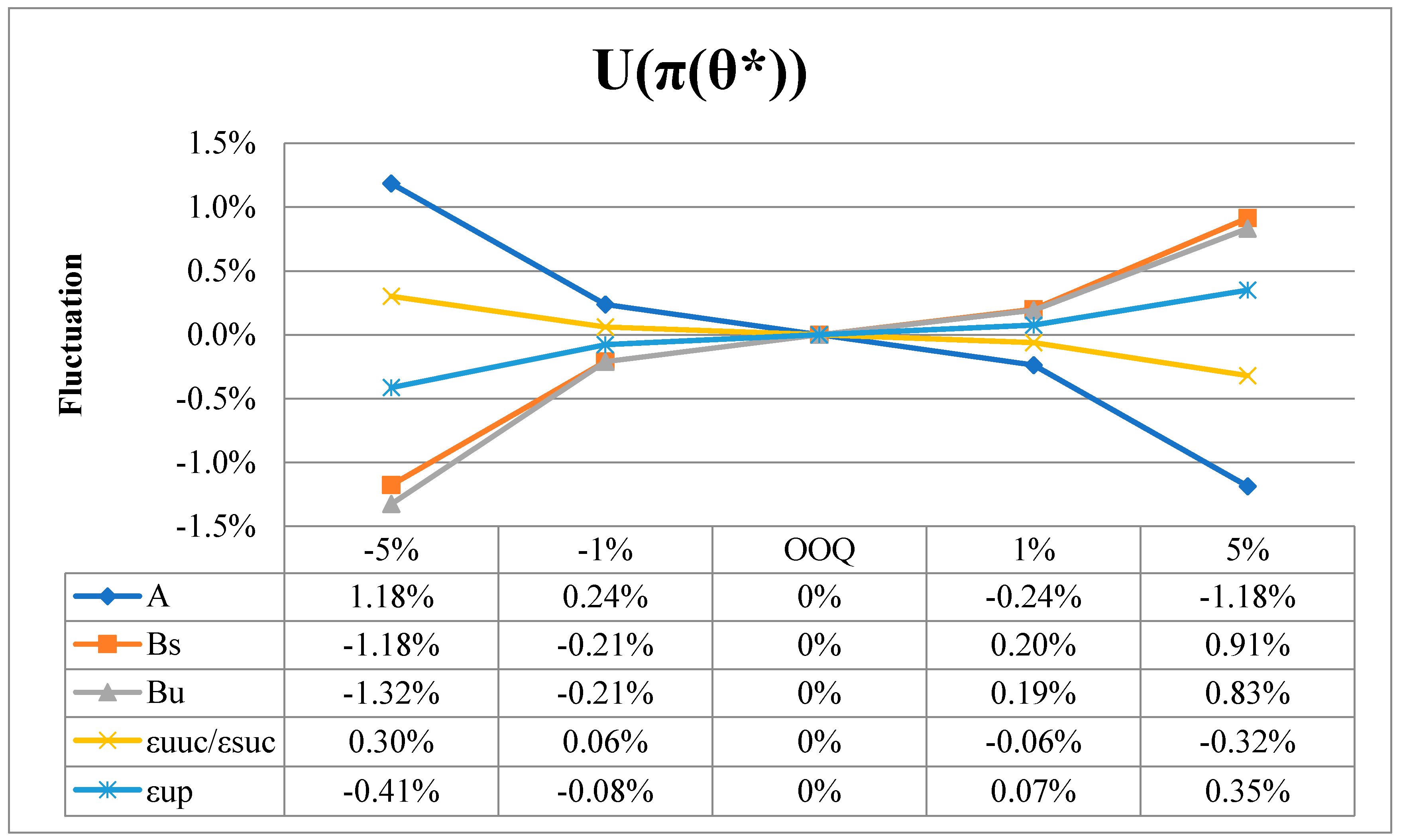
4.2. Sensitivity Analysis of the Model
5. Discussion and Conclusions
5.1. Discussion
5.2. Research Limitation
5.3. Conclusions
5.4. Implications for Practice
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Parameter | Definition |
|---|---|
| The probability of FRM with no safety problems in the external environment | |
| The probability that the imported FRM have no food safety problems when the external environment has no food safety problems | |
| The probability that the imported FRM have no food safety problems when the external environment has food safety problems | |
| The unit cost of imported FRM | |
| The unit sales price of imported FRM | |
| Three market reactions. Optimistic (o), normal (n), and pessimistic (p) | |
| The unit sales price of three market reactions when the external environment and imported FRM have no food safety problems | |
| The unit sales price of three market reactions (optimistic, normal, and pessimistic) when the external environment has no food safety problems, but the imported FRM has a food safety problem | |
| The unit sales price of three market reactions (optimistic, normal, and pessimistic) when the external environment has a food safety problem and the imported FRM has no food safety problem | |
| The unit sales price of three market reactions (optimistic, normal, and pessimistic) when the external environment and imported FRM have food safety problems | |
| The handling cost for each rise, when the external environment has no food safety problem, but the imported FRM has a food safety problem | |
| The unit of premium when the external environment has a food safety problem, but the imported FRM has no food safety problem | |
| The unit of disposal cost for each increase when the external environment and the imported FRM have food safety problems | |
| The probability of three market reactions (optimistic, normal, and pessimistic) when the external environment and imported FRM have no food safety problems | |
| The probability of three market reactions (optimistic, normal, and pessimistic) when the external environment has no food safety problem, but the imported FRM has a food safety problem | |
| The probability of three market reactions (optimistic, normal, and pessimistic) when the external environment has a food safety problem, but the imported FRM has no food safety problem | |
| The probability of three market reactions (optimistic, normal, and pessimistic) when the external environment and the imported FRM have food safety problems | |
| The multiple rewards for the suppliers of FRM in relation to the expectation of net income when the external environment has a food safety problem, as compared to the external environment with no food safety problem | |
| The parameter of the basic utility function, where the FRM supplier runs the business of imported FRM without considering profit and loss | |
| The discounted price when the external environment and the imported FRM have no food safety problems with three market reactions (optimistic, normal, and pessimistic) | |
| The discounted price when the external environment has no food safety problem, but the imported FRM has a food safety problem with three market reactions (optimistic, normal, and pessimistic) | |
| The discounted price when the external environment has a food safety problem, but the imported FRM has no food safety problem with three market reactions (optimistic, normal, and pessimistic) | |
| The discounted price when the external environment and the imported FRM have food safety problems with three market reactions (optimistic, normal, and pessimistic) | |
| The urgent order cost when the external environment and imported FRM have no food safety problems with three market reactions (optimistic, normal, and pessimistic) | |
| The urgent order cost when the external environment has no food safety problem, but the imported FRM has a food safety problem with three market reactions (optimistic, normal, and pessimistic) | |
| The urgent order cost when the external environment has a food safety problem, but the imported FRM has no food safety problem with three market reactions (optimistic, normal, and pessimistic) | |
| The urgent order cost when the external environment and the imported FRM have food safety problems with three market reactions (optimistic, normal, and pessimistic) | |
| The sales amount when the external environment and the imported FRM have no food safety problems with three market reactions (optimistic, normal, and pessimistic) | |
| The sales amount when the external environment has no food safety problem, but the imported FRM has a food safety problem with three market reactions (optimistic, normal, and pessimistic) | |
| The sales amount when the external environment has food safety problems, but the imported FRM has no food safety problem with three market reactions (optimistic, normal, and pessimistic) | |
| The sales amount when the external environment and the imported FRM have food safety problems with three market reactions (optimistic, normal, and pessimistic) | |
| The optimal order quantity | |
| Net profits of the three market statuses under the condition of the external environment having no food safety problem and the imported FRM having a food safety problem | |
| Net profits of the three market statuses under the condition of both the external environment and the imported FRM having no food safety problems | |
| Net profits of the three market statuses under the condition of the external environment having a food safety problem and the imported FRM having no food safety problems | |
| Net profits of the three market statuses under the condition of both the external environment and the imported FRM having food safety problems | |
| The expected revenue of the external environment having no food safety problems | |
| The expected revenue of the external environment having a food safety problem | |
| The maximum expected net profits |
References
- Adalja, Aaron, and Erik Lichtenberg. 2016. Food borne illness outbreaks, collective reputation, and voluntary adoption of industry-wide food safety protocols by fruit and vegetable growers. Paper presented at Agricultural and Applied Economics Association Annual Meeting, Boston, MA, USA, July 31–August 2. [Google Scholar]
- Agrawal, Vipul, and Sridhar Seshadri. 2000. Impact of uncertainty and risk aversion on price and order quantity in the newsvendor problem. Manufacturing & Service Operations Management 2: 410–23. [Google Scholar]
- Ahearn, Mary Clare, Walt Armbruster, and Robert Young. 2016. Big data’s potential to improve food supply chain environmental sustainability and food safety. International Food and Agribusiness Management Review 19: 155–71. [Google Scholar]
- Bassin, William M. 1990. A technique for applying EOQ models to retail cycle stock inventories. Journal of Small Business Management 28: 48–55. [Google Scholar]
- Buzby, Jean C. 2001. Effects of food-safety perceptions on food demand and global trade. In Changing Structure of Global Food Consumption and Trade. Edited by Regmi Anita. Collingdale: DIANE Publishing, pp. 55–66. [Google Scholar]
- Buzby, Jean C., and Lorraine Mitchell. 2003. Food safety and trade: Regulations, risks, and reconciliation. Amber Waves 1: 14–21. [Google Scholar]
- Calvin, Linda, William Foster, Luis Solorzano, J. Daniel Mooney, Luis Flores, and Veronica Barrios. 2002. Response to a food safety problem in produce. In Global Food Trade and Consumer Demand for Quality. Edited by Krissoff Barry, Mary Bohman and Julie A. Caswell. Boston: Springer. [Google Scholar]
- CDC (Center for Disease Control and Prevention). 2018. Foodborne Illnesses and Germs. Available online: https://www.cdc.gov/foodsafety/foodborne-germs.html (accessed on 31 October 2018).
- Chang, Horng-Jinh, and Wen-Feng Lin. 2011. A simple solution for the finite horizon EOQ model for deteriorating items with cost changes. Asia-Pacific Journal of Operational Research 28: 689–704. [Google Scholar] [CrossRef]
- Chang, Chun-Tao, Liang-Yuh Ouyang, and Jinn-Tsair Teng. 2003. An EOQ model for deteriorating items under supplier credits linked to ordering quantity. Applied Mathematical Modelling 27: 983–96. [Google Scholar] [CrossRef]
- Chang, Chun-Tao, Mei-Chuan Cheng, and Pao-Yi Soong. 2016. Impacts of inspection errors and trade credits on the economic order quantity model for items with imperfect quality. International Journal of Systems Science: Operations & Logistics 3: 34–48. [Google Scholar]
- Chen, Xin, Melvyn Sim, David Simchi-Levi, and Peng Sun. 2007. Risk aversion in inventory management. Operations Research 55: 828–42. [Google Scholar] [CrossRef]
- Chung, Kun-Jen, and Jui-Jung Liao. 2009. The optimal ordering policy of the EOQ model under trade credit depending on the ordering quantity from the DCF approach. European Journal of Operational Research 196: 563–68. [Google Scholar] [CrossRef]
- Chung, Kun-Jen, Suresh Kumar Goyal, and Yung-Fu Huang. 2005. The optimal inventory policies under permissible delay in payments depending on the ordering quantity. International Journal of Production Economics 95: 203–13. [Google Scholar] [CrossRef]
- Crandall, Phil, Ellen J. Van Loo, Corliss A. O’Bryan, Andy Mauromoustakos, Frank Yiannas, Natalie Dyenson, and Irina Berdnik. 2012. Companies’ opinions and acceptance of global food safety initiative benchmarks after implementation. Journal of Food Protection 75: 1660–72. [Google Scholar] [CrossRef] [PubMed]
- Dammon, Robert M., and Chester S. Spatt. 1996. The optimal trading and pricing of securities with asymmetric capital gains taxes and transaction costs. The Review of Financial Studies 9: 921–52. [Google Scholar] [CrossRef]
- Dobson, Gregory, Edieal J. Pinker, and Ozlem Yildiz. 2017. An EOQ model for perishable goods with age-dependent demand rate. European Journal of Operational Research 257: 84–88. [Google Scholar] [CrossRef]
- El-Kassar, Abdul-Nasser M. 2009. Optimal order quantity for imperfect quality items. Proceedings of the Academy of Information and Management Sciences 13: 24–30. [Google Scholar]
- Food and Agriculture Organization of the United Nations. 2011. Guidelines for Risk Categorization of Food and Food Establishments Applicable to ASEAN Countries. Bangkok. Available online: http://www.fao.org/3/contents/dad345b8-7166-5e96-b2ff-01de10f8675e/i2448e00.htm (accessed on 1 December 2016).
- Giri, B. C., and Shagun Sharma Sharma. 2016. Optimal ordering policy for an inventory system with linearly increasing demand and allowable shortages under two levels trade credit financing. Operational Research 16: 25–50. [Google Scholar] [CrossRef]
- Haushalter, G. David, Randall A. Heron, and Erik Lie. 2002. Price uncertainty and corporate value. Journal of Corporate Finance 8: 271–86. [Google Scholar] [CrossRef]
- He, Zhongyu, Guofang Zhai, and Takeshi Suzuki. 2014. The immediate influence of a food safety incident on Japanese consumers’ food choice decisions and willingness to pay for safer food. Human and Ecological Risk Assessment 20: 1099–112. [Google Scholar] [CrossRef]
- Heinonen, Justin A., John Spink, and Jeremy M. Wilson. 2017. When crime defies classification: The case of product counterfeiting as white-collar crime. Security Journal 30: 621–39. [Google Scholar] [CrossRef]
- Herrera, M., R. Anadón, Shahzad Zafar Iqbal, J. D. Bailly, and Agustin Ariño. 2016. Climate change and food safety. In Food Safety. Edited by Selamat Jinap and Iqbal Shahzad Zafar. Cham: Springer, pp. 149–60. [Google Scholar]
- Ho, Thomas, and Hans R. Stoll. 1981. Optimal dealer pricing under transactions and return uncertainty. Journal of Financial Economics 9: 47–73. [Google Scholar] [CrossRef]
- Hsu, Shu-Yen, Chiao-Chen Chang, and Tyrone T. Lin. 2016. An analysis of purchase intentions toward organic food on health consciousness and food safety with/under structural equation modeling. British Food Journal 118: 200–16. [Google Scholar] [CrossRef]
- Kazemi, Nima, Salwa Hanim Abdul-Rashid, Raja Ariffin Raja Ghazilla, Ehsan Shekarian, and Simone Zanoni. 2018. Economic order quantity models for items with imperfect quality and emission considerations. International Journal of Systems Science: Operations & Logistics 5: 99–115. [Google Scholar]
- Kotsanopoulos, Konstantinos V., and Ioannis S. Arvanitoyannis. 2017. The role of auditing, food safety, and food quality standards in the food industry: A review. Comprehensive Reviews in Food Science and Food Safety 16: 760–75. [Google Scholar] [CrossRef]
- Koutsoumanis, Konstantinos P., and Zafiro Aspridou. 2016. Moving towards a risk-based food safety management. Current Opinion in Food Science 12: 36–41. [Google Scholar] [CrossRef]
- Kunreuther, Howard, and Jean François Richard. 1971. Optimal pricing and inventory decisions for non-seasonal items. Econometrica: Journal of the Econometric Society 39: 173–75. [Google Scholar] [CrossRef]
- Lee, Chia-Chi, Shu-Yen Hsu, and Tyrone T. Lin. 2012. Analysis of business performance for the food ingredient supplier with the concepts of pricing, product strategy, and customer industry attribute. Industry and Management Forum 14: 50–74. [Google Scholar]
- Li, Ho Shui, and Sue Mei Wang. 2015. Almanac of Food Industry in the Republic of China on Taiwan; Shinchu: Food Industry Research and Development Institute.
- MacKay, Peter, and Sara B. Moeller. 2007. The value of corporate risk management. The Journal of Finance 62: 1379–419. [Google Scholar] [CrossRef]
- Manzini, Riccardo, Riccardo Accorsi, Ziad Ayyad, Alessandra Bendini, Marco Bortolini, Mauro Gamberi, Enrico Valli, and Tullia Gallina Toschi. 2014. Sustainability and quality in the food supply chain: A case study of shipment of edible oils. British Food Journal 116: 2069–90. [Google Scholar] [CrossRef]
- Moyer, Douglas C., Jonathan W. DeVries, and John Spink. 2017. The economics of a food fraud incident-case studies and examples including melamine in wheat gluten. Food Control 71: 358–64. [Google Scholar] [CrossRef]
- Ouyang, Liang-Yuh, Kun-Shan Wu, Chih-Te Yang, and Hsiu-Feng Yen. 2016. Optimal order policy in response to announced price increase for deteriorating items with limited special order quantity. International Journal of Systems Science 47: 718–29. [Google Scholar] [CrossRef]
- Pan, Fu-Bin. 2016. Perishable product inventory model based on the food supply chain. Journal of Interdisciplinary Mathematics 19: 111–27. [Google Scholar] [CrossRef]
- Polatoglu, L. Hakan. 1991. Optimal order quantity and pricing decisions in single-period inventory systems. International Journal of Production Economic 23: 175–85. [Google Scholar] [CrossRef]
- Pouliot, Sébastien, and Daniel A. Sumner. 2008. Traceability, liability, and incentives for food safety and quality. American Journal of Agricultural Economics 90: 15–27. [Google Scholar] [CrossRef]
- Rezaei, Jafar. 2016. Economic order quantity and sampling inspection plans for imperfect items. Computers & Industrial Engineering 96: 1–7. [Google Scholar]
- Salameh, M. K., and M. Y. Jaber. 2000. Economic production quantity model for items with imperfect quality. International Journal of Production Economics 64: 59–64. [Google Scholar] [CrossRef]
- Salin, Victoria. 2000. A Real Option Approach to Valuing Food Safety Risks. Chapter 11. In Economics of HACCP: Costs and Benefits. Edited by Laurian J. Unnevehr. St. Paul: Eagan Press, pp. 225–40. [Google Scholar]
- Septiani, Winnie, Marimin Yeni Herdiyeni, and Liesbetini Haditjaroko. 2016. Method and approach mapping for agri-food supply chain risk management: A literature review. International Journal of Supply Chain Management 5: 51–64. [Google Scholar]
- Shekarian, Ehsan, Mohamad Y. Jaber, Nima Kazemi, and Ehsan Ehsani. 2014. A fuzzified version of the economic production quantity (EPQ) model with backorders and rework for a single-stage system. European Journal of Industrial Engineering 8: 291–324. [Google Scholar] [CrossRef]
- Shu, Lei, Feng Wu, Jian Ni, and Lap Keung Chu. 2015. On the risk-averse procurement strategy under unreliable supply. Computers & Industrial Engineering 84: 113–21. [Google Scholar]
- Tirado, M. C., R. Clarke, L. A. Jaykus, A. McQuatters-Gollop, and J. M. Frank. 2010. Climate change and food safety: A review. Food Research International 43: 1745–65. [Google Scholar] [CrossRef]
- USP. 2014. The United States Pharmacopieial Convetion: Guidance on Food Fraud Mitigation. Available online: https://www.usp.org/foods/food-fraud-mitigation-guidance?language_content_entity=en (accessed on 1 December 2016).
- Van Asselt, Esther, H. J. van der Fels-Klerx, H. J. P. Marvin, H. van Bokhorst-van de Veen, and Masja Nierop Groot. 2017. Overview of food safety hazards in the European dairy supply chain. Comprehensive Reviews in Food Science and Food Safety 16: 59–75. [Google Scholar] [CrossRef]
| Parameters | C | P | |||||||
| Assigned Values | 0.7 | 0.8 | 0.7 | 400 | 500 | 0.2 | 0.3 | 0.3 | 0.2 |
| Parameters | |||||||||
| Assigned Values | 510 | 500 | 490 | 510 | 500 | 490 | 510 | 500 | 490 |
| Parameters | |||||||||
| Assigned Values | 530 | 510 | 500 | 0.6 | 0.3 | 0.3 | 0.4 | 0.2 | 0.5 |
| Parameters | |||||||||
| Assigned Values | 0.1 | 0.7 | 1.3 | 480 | 460 | 440 | 420 | 400 | 380 |
| Parameters | |||||||||
| Assigned Values | 490 | 470 | 450 | 420 | 400 | 380 | 490 | 480 | 470 |
| Parameters | |||||||||
| Assigned Values | 490 | 480 | 470 | 490 | 480 | 470 | 500 | 490 | 480 |
| Parameters | |||||||||
| Assigned Values | 60,000 | 50,000 | 40,000 | 30,000 | 20,000 | 65,000 | 55,000 | 45,000 | 40,000 |
| Parameters | |||||||||
| Assigned Values | 30,000 | 20,000 | 35,000 |
| Parameters | Numerical Values | Numerical Values | Numerical Values | Numerical Values | Numerical Values |
|---|---|---|---|---|---|
| 5.00 × 104 | 5.50 × 104 | 6.00 × 104 | 6.50 × 104 | 7.00 × 104 | |
| −4.02 × 105 | −2.41 × 105 | 1.79 × 105 | 4.49 × 105 | 9.25 × 105 | |
| 6.973095 | 7.275677 | 7.417735 | 7.345711 | 7.383716 |
| Variation | −5% | −1% | 1% | 5% | |
|---|---|---|---|---|---|
| Parameter | |||||
| 0.65 | 0.69 | 0.71 | 0.75 | ||
| 0.75 | 0.79 | 0.81 | 0.85 | ||
| 0.65 | 0.69 | 0.71 | 0.75 | ||
| 0.15 | 0.19 | 0.21 | 0.25 | ||
| 0.25 | 0.29 | 0.31 | 0.35 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, T.T.; Hsu, S.-Y. Risk Management for the Optimal Order Quantity by Risk-Averse Suppliers of Food Raw Materials. Int. J. Financial Stud. 2018, 6, 96. https://doi.org/10.3390/ijfs6040096
Lin TT, Hsu S-Y. Risk Management for the Optimal Order Quantity by Risk-Averse Suppliers of Food Raw Materials. International Journal of Financial Studies. 2018; 6(4):96. https://doi.org/10.3390/ijfs6040096
Chicago/Turabian StyleLin, Tyrone T., and Shu-Yen Hsu. 2018. "Risk Management for the Optimal Order Quantity by Risk-Averse Suppliers of Food Raw Materials" International Journal of Financial Studies 6, no. 4: 96. https://doi.org/10.3390/ijfs6040096
APA StyleLin, T. T., & Hsu, S.-Y. (2018). Risk Management for the Optimal Order Quantity by Risk-Averse Suppliers of Food Raw Materials. International Journal of Financial Studies, 6(4), 96. https://doi.org/10.3390/ijfs6040096






