Are These Shocks for Real? Sensitivity Analysis of the Significance of the Wavelet Response to Some CKLS Processes
Abstract
1. Introduction and Problem Statement
1.1. Introduction and Motivation
- is the long-term equilibrium value about which the process performs random excursions;
- represents the elastic spring constant that determines how fast random excursions will revert back to the central attractor (a). Large values for k imply a tightly bound process resulting in short excursions;
- is the (specific) volatility;
- measures the sensitivity of the volatility with respect to the current process value.
1.2. Problem Statement
1.3. Overview of the Methodology
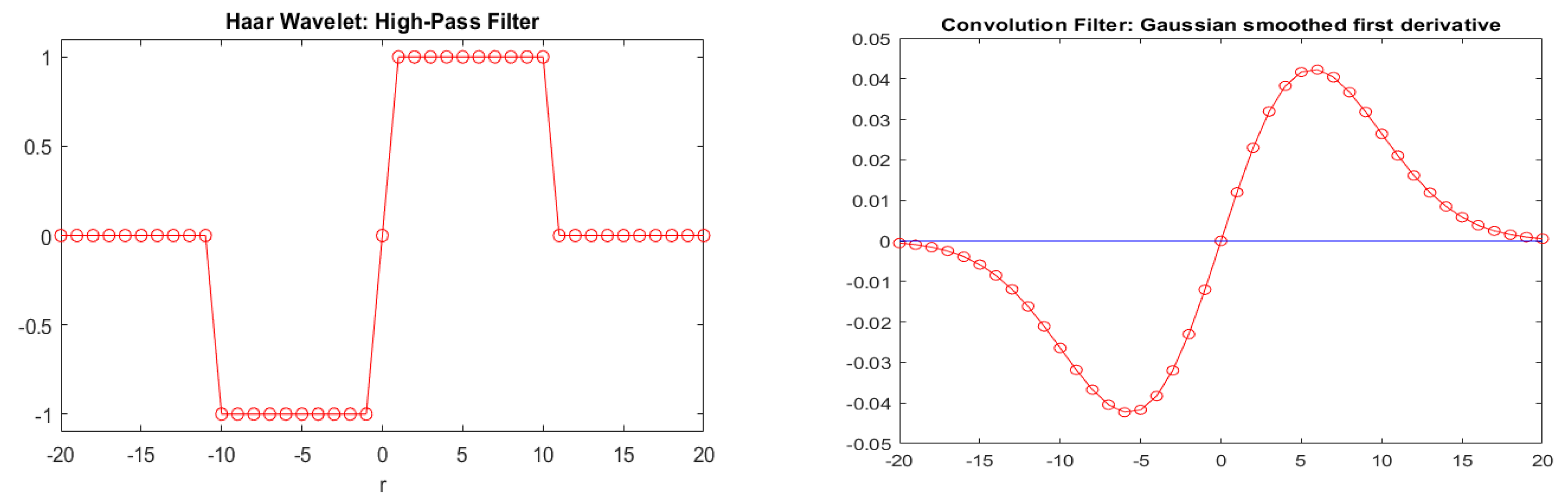
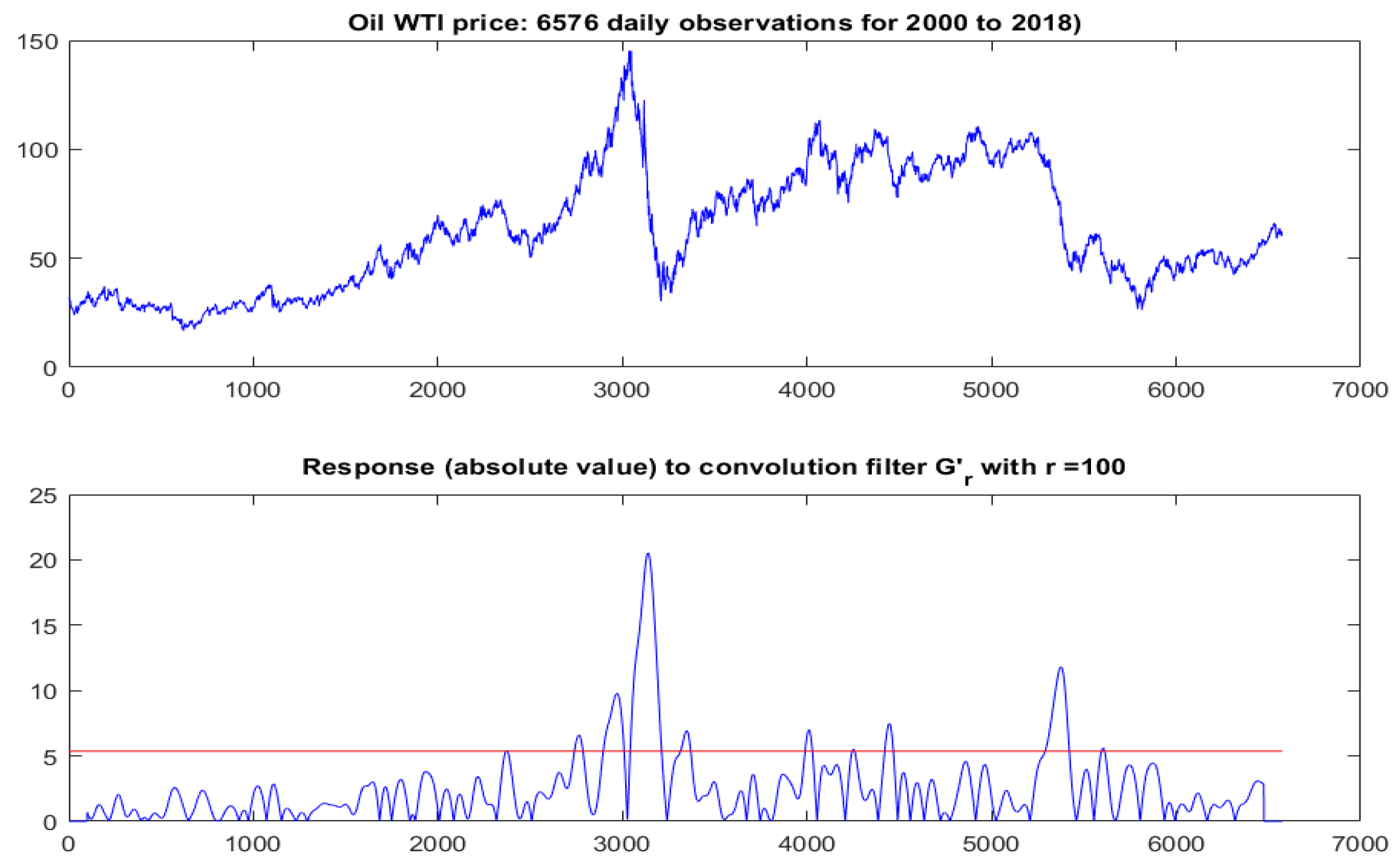
- We were interested in finding out whether the down-swing around observation 3000 (which corresponds to a period in 2008–2009) is unusual. Since this period comprises 100–200 daily observations, we picked a convolution filter () of size .
- The response (in absolute value) of the original data after convolution with is shown in the bottom panel of Figure 2 in Section 4.1.1. Clearly the most vigorous response occurred around location 3000. However, in and of itself this does not prove anything. The question is whether this response is unusually high.
- To proceed, we first defined a single number to express the size of the maximum response relative to a statistically stable response measure, e.g., the 90%-percentile of the response values (indicated by the red line in the bottom panel of Figure 2 in Section 4.1.1). We denoted the resulting value by , which, for the oil data, turns out to be 3.82.
- Next, we needed to decide whether this observed value for T is exceptional. We assumed that the dynamics underlying the observed time series were indeed governed by a CKLS process, estimated its parameters from the observed data sequence and used the results to generate a large number of simulated sample paths. For each of these simulated sample paths, we computed the corresponding T statistic. This allowed us to estimate the p-value of under the assumption of CKLS dynamics.
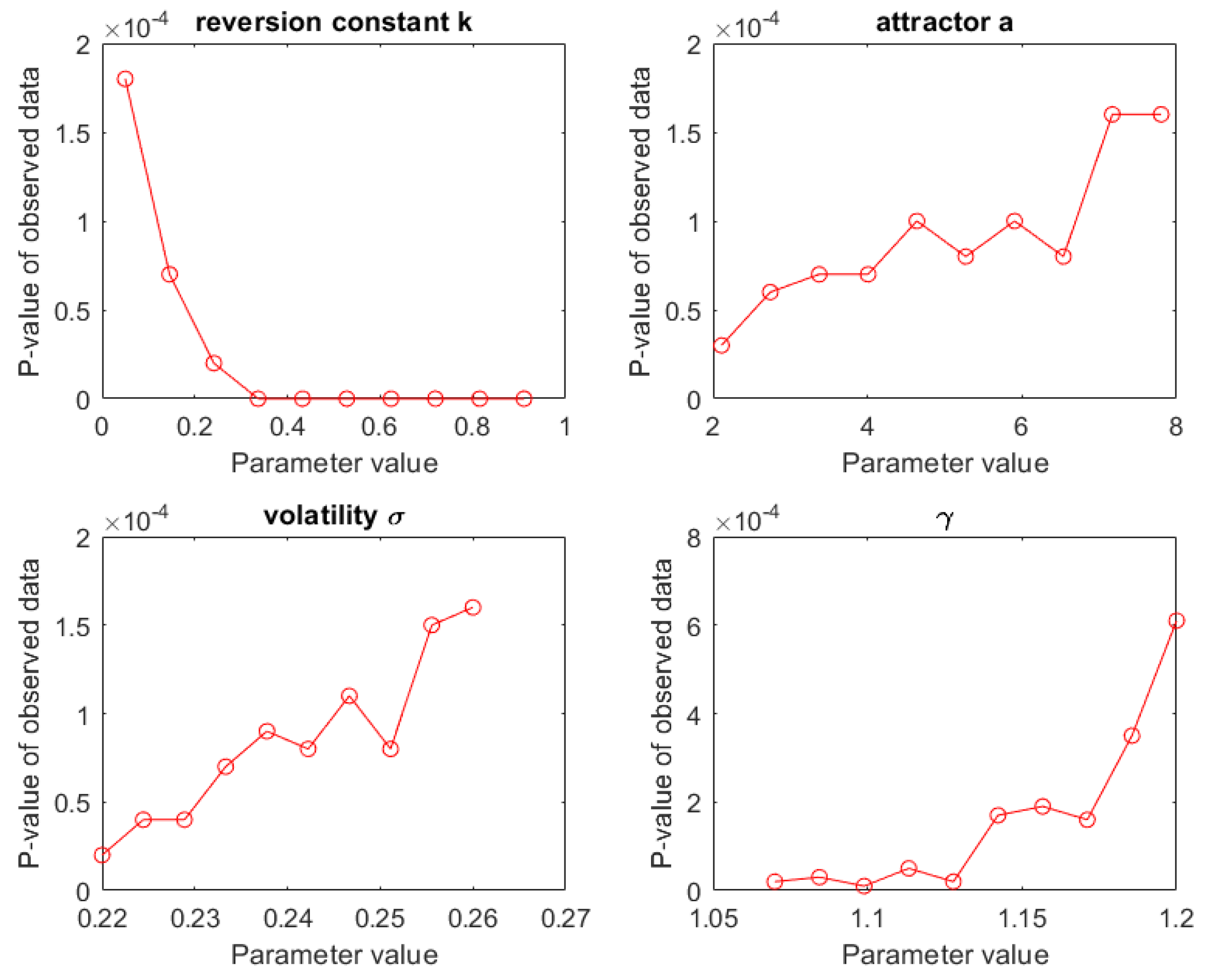
- Finally, since we know that the estimated CKLS parameters used to generate sample paths are subject to a considerable amount of uncertainty, we repeated the simulation experiments for a range of likely parameter values. This told us how sensitive our conclusions were to changes in the parameter values, and whether they would hold up if the parameters had slightly different values.
2. Data
- Oil Price (West Texas Intermediate) over the period 2000 to 2018 (see Figure 2, top panel in Section 4.1.1): This series comprises 6575 daily observations. The evolution of the oil price showed some sharp downward jumps. This begs the question: is this perceived discontinuity part of the natural evolution of an appropriate CKLS process or does it correspond to an (exogenous) shock?
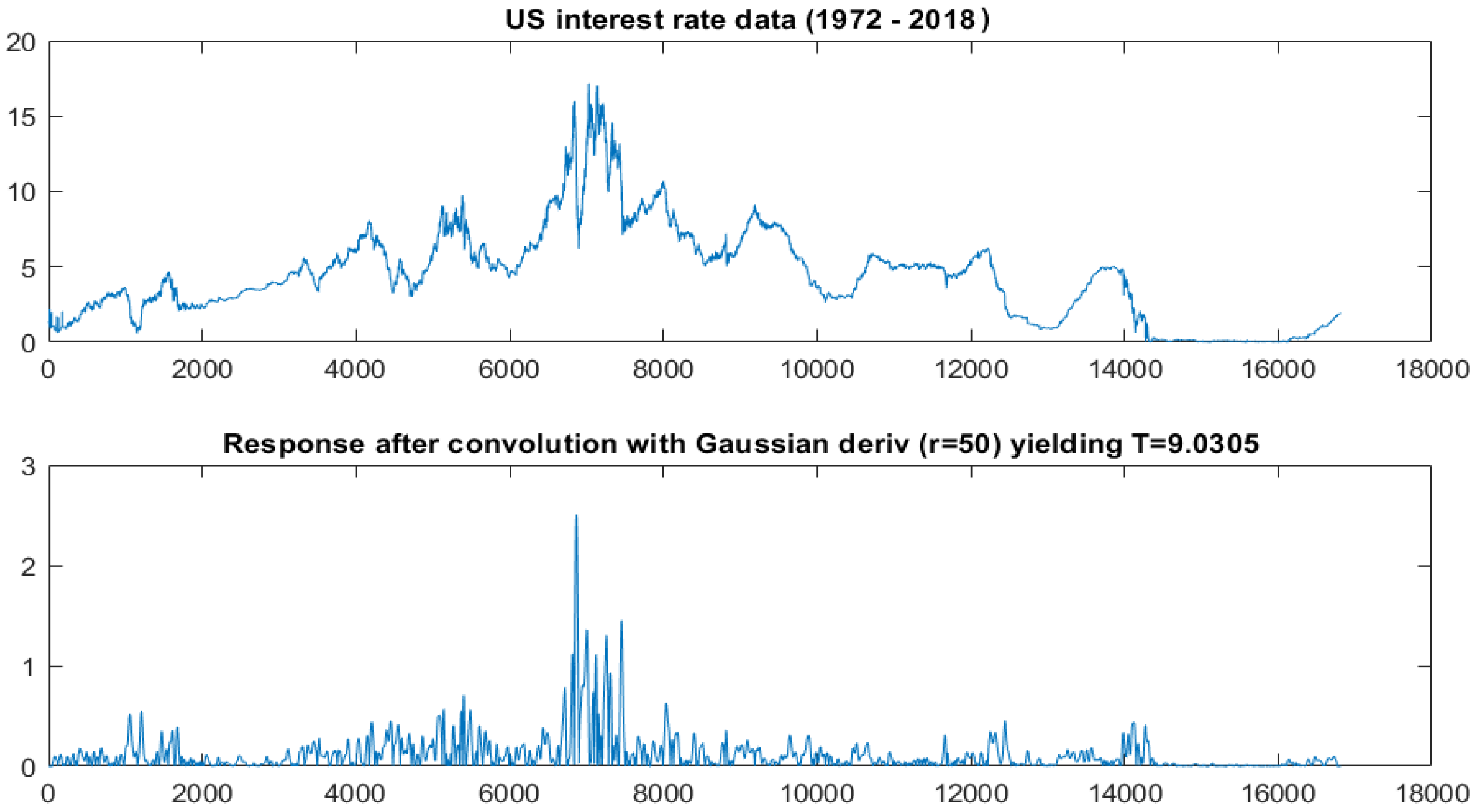
- US Interest Rate (see Figure 5, top panel in Section 4.2) over the period 1972 to 2018. This series comprises 16,816 daily observations and shows a conspicuous dip around observation 7000. Again, the question is whether this is unexpected given an appropriate CKLS model.
3. Related Work
4. Methodology and Results
4.1. Oil Price Data
4.1.1. Computing the Test Statistic
4.1.2. Using Monte Carlo to Compute the p-Value of the Test Statistic
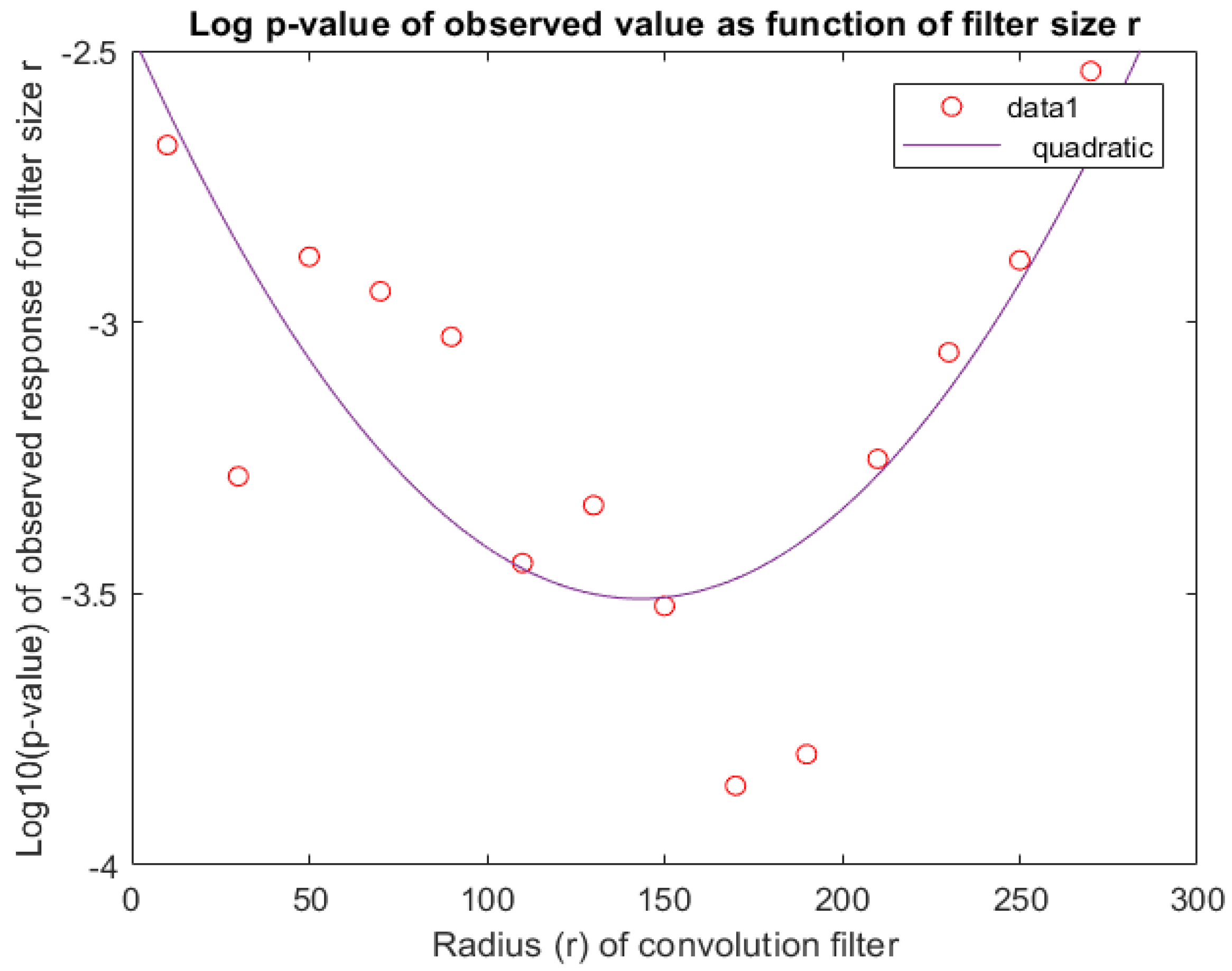
4.1.3. Sensitivity of the p-Value
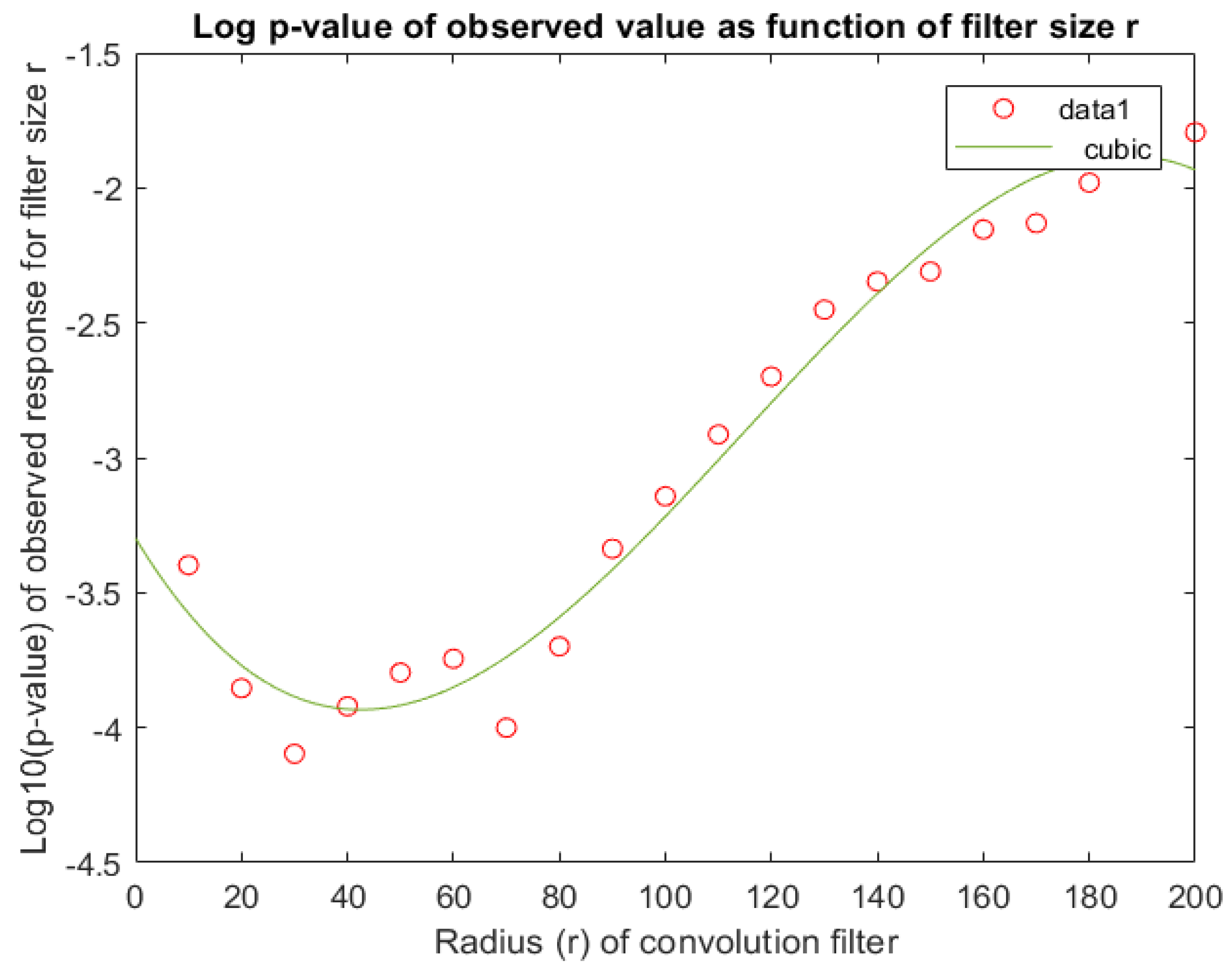
4.1.4. Corroborating the Choice of Filter Size (r)
4.2. US Interest Rate (1972–2018)
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BM | Brownian motion |
| CKLS | Chan, Karolyi, Longstaff, and Sanders (process) |
| GMM | Generalized Method of Moments |
| MC | Monte Carlo (estimation) |
| SDE | Stochastic Differential Equation |
References
- Aloui, Riadh, Rangan Gupta, and Stephen M. Miller. 2016. Uncertainty and crude oil returns. Energy Economics 55: 92–100. [Google Scholar] [CrossRef]
- Arora, Vipin, and Matthew Tanner. 2013. Do oil prices respond to real interest rates? Energy Economics 36: 546–55. [Google Scholar] [CrossRef]
- Bu, Ruijun, Ludovic Giet, Kaddour Hadri, and Michel Lubrano. 2010. Multivariate Interest Rates Using Time-Varying Copulas and Reducible Nonlinear Stochastic Differential Equations. Journal of Financial Econometrics 9: 198–236. [Google Scholar] [CrossRef]
- Chan, Ngai Hang, Song Xi Chen, Liang Peng, and Cindy L. Yu. 2009. Empirical likelihood methods based on characteristic functions with applications to Lévy processes. Journal of the American Statistical Association 104: 1621–30. [Google Scholar] [CrossRef]
- Chan, Kalok C., G. Andrew Karolyi, Francis A. Longstaff, and Anthony B. Sanders. 1992. An Empirical Comparison of Alternative Models of the Short-Term Interest Rate. The Journal of Finance 47: 1209–27. [Google Scholar] [CrossRef]
- Chatzikonstanti, Vasiliki. 2017. Breaks and outliers when modelling the volatility of the U.S. stock market. Applied Economics 49: 4704–16. [Google Scholar] [CrossRef]
- Chernozhukov, Victor, and Christian Hansen. 2008. Instrumental variable quantile regression: A robust inference approach. Journal of Econometrics 142: 379. [Google Scholar] [CrossRef]
- Croghan, Jakob, John Jackman, and K. Jo Min. 2017. Estimation of Geometric Brownian Motion Parameters for Oil Price Analysis. In IIE Annual Conference Proceedings. Peachtree Corners, GA, USA: Institute of Industrial and Systems Engineers, pp. 1858–63. Available online: https://search-proquest-com.eur.idm.oclc.org/docview/1951120561?accountid=13598 (accessed on 9 July 2018).
- Dell’Aquila, Rosario, Elvezio Ronchetti, and Fabio Trojani. 2003. Robust GMM analysis of models for the short rate process. Journal of Empirical Finance 10: 373–97. [Google Scholar] [CrossRef]
- Dewandaru, Ginanjar, Rumi Masih, and Mansur Masih. 2017. Regional spillovers across transitioning emerging and frontier equity markets: A multi-time scale wavelet analysis. Economic Modelling 65: 30–40. [Google Scholar] [CrossRef]
- Dutta, Anupam, Jussi Nikkinen, and Timo Rothovius. 2017. Impact of oil price uncertainty on Middle East and African stock markets. Energy 123: 189–97. [Google Scholar] [CrossRef]
- Ferrando, Laura, Román Ferrer, and Francisco Jareño. 2017. Interest Rate Sensitivity of Spanish Industries: A Quantile Regression Approach. The Manchester School 85: 212–42. [Google Scholar] [CrossRef]
- Gallant, A. Ronald, and George E. Tauchen. 1995. Specification Analysis of Continuous TimeModels in Finance. Electronic Journal, 297–321. [Google Scholar] [CrossRef]
- Grané, Aurea, and Helena Veiga. 2010. Wavelet based detection of outliers in financial time series. Computational Statistics and Data Analysis 54: 2580–93. [Google Scholar] [CrossRef]
- Hamilton, J.D. 2009. Causes and Consequences of the Oil Shock of 2007–2008. Brookings Papers on Economic Activity. vol. 40, pp. 215–83. [Google Scholar] [CrossRef]
- Hall, Alastair R., Sanggohn Han, and Otilia Boldea. 2012. Inference regarding multiple structural changes in linear models with endogenous regressors. Journal of Econometrics 170: 281–302. [Google Scholar] [CrossRef] [PubMed]
- Jain, Anshul, and P. C. Biswal. 2016. Dynamic linkages among oil price, gold price, exchange rate, and stock market in India. Resources Policy 49: 179–85. [Google Scholar] [CrossRef]
- Loisel, Sébastien, and Marina Takane. 2009. Fast indirect robust generalized method of moments. Computational Statistics Data Analysis 53: 3571–79. [Google Scholar] [CrossRef]
- MacKenzie, Donald. 2006. An Engine, Not a Camera: How Financial Models Shape Markets. Cambridge: MIT Press, p. 377. ISBN 0-262-13460-8. [Google Scholar]
- Martín-Barragán, Belén, Sofia B. Ramos, and Helena Veiga. 2015. Correlations between oil and stock markets: A wavelet-based approach. Economic Modelling 50: 212–27. [Google Scholar] [CrossRef]
- Monetary Policy Principles and Practice. Available online: https://www.federalreserve.gov/monetarypolicy/historical-approaches-to-monetary-policy.htm (accessed on 8 March 2018).
- Naccache, Théo. 2011. Oil price cycles and wavelets. Energy Economics 33: 338–52. [Google Scholar] [CrossRef]
- Ben Nowman, K., and Ghulam Sorwar. 2003. Implied option prices from the continuous time CKLS interest rate model: An application to the UK. Applied Finance and Economics 13: 191–97. [Google Scholar] [CrossRef]
- Petroleum and Other Liquids. Available online: https://www.eia.gov/dnav/pet/hist/LeafHandler.ashx?n=PET&s=RWTC&f=M (accessed on 15 August 2018).
- Salisu, Afees A., and Tirimisiyu F. Oloko. 2015. Modeling oil price—US stock nexus: A VARMA–BEKK–AGARCH approach. Energy Economics 50: 1–12. [Google Scholar] [CrossRef]
- Sorwar, Ghulam. 2011. Estimating single factor jump diffusion interest rate models. Applied Financial Economics 15: 1679–89. [Google Scholar] [CrossRef]
- Tang, Cheng Yong, and Song Xi Chen. 2009. Parameter estimation and bias correction for diffusion processes. Journal of Econometrics 149: 65–81. [Google Scholar] [CrossRef]
- Treepongkaruna, Sirimon, and Stephen Gray. 2003. On the robustness of short-term interest rate models. Accounting and Finance 43: 81–121. [Google Scholar] [CrossRef]
- Zhou, Zhongbao, Ling Lin, and Shuxian Li. 2018. International stock market contagion: A CEEMDAN wavelet analysis. Economic Modelling 72: 333–52. [Google Scholar] [CrossRef]

| Parameter | ||||
|---|---|---|---|---|
| value | 0.35 | 67.1 | 1.24 | 0.69 |
| Parameter | ||||
|---|---|---|---|---|
| value | 0.15 | 4.47 | 0.24 | 1.13 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kokabisaghi, S.; Pauwels, E.J.; Van Meulder, K.; Dorsman, A.B. Are These Shocks for Real? Sensitivity Analysis of the Significance of the Wavelet Response to Some CKLS Processes. Int. J. Financial Stud. 2018, 6, 76. https://doi.org/10.3390/ijfs6030076
Kokabisaghi S, Pauwels EJ, Van Meulder K, Dorsman AB. Are These Shocks for Real? Sensitivity Analysis of the Significance of the Wavelet Response to Some CKLS Processes. International Journal of Financial Studies. 2018; 6(3):76. https://doi.org/10.3390/ijfs6030076
Chicago/Turabian StyleKokabisaghi, Somayeh, Eric J. Pauwels, Katrien Van Meulder, and André B. Dorsman. 2018. "Are These Shocks for Real? Sensitivity Analysis of the Significance of the Wavelet Response to Some CKLS Processes" International Journal of Financial Studies 6, no. 3: 76. https://doi.org/10.3390/ijfs6030076
APA StyleKokabisaghi, S., Pauwels, E. J., Van Meulder, K., & Dorsman, A. B. (2018). Are These Shocks for Real? Sensitivity Analysis of the Significance of the Wavelet Response to Some CKLS Processes. International Journal of Financial Studies, 6(3), 76. https://doi.org/10.3390/ijfs6030076





