Does Gold Act as a Hedge and a Safe Haven for China’s Stock Market?
Abstract
:1. Introduction
2. Related Literature
3. Data, Definitions, Empirical Methodology
3.1. Data
3.2. Definitions of Bear and Nonbear Stock Markets in China
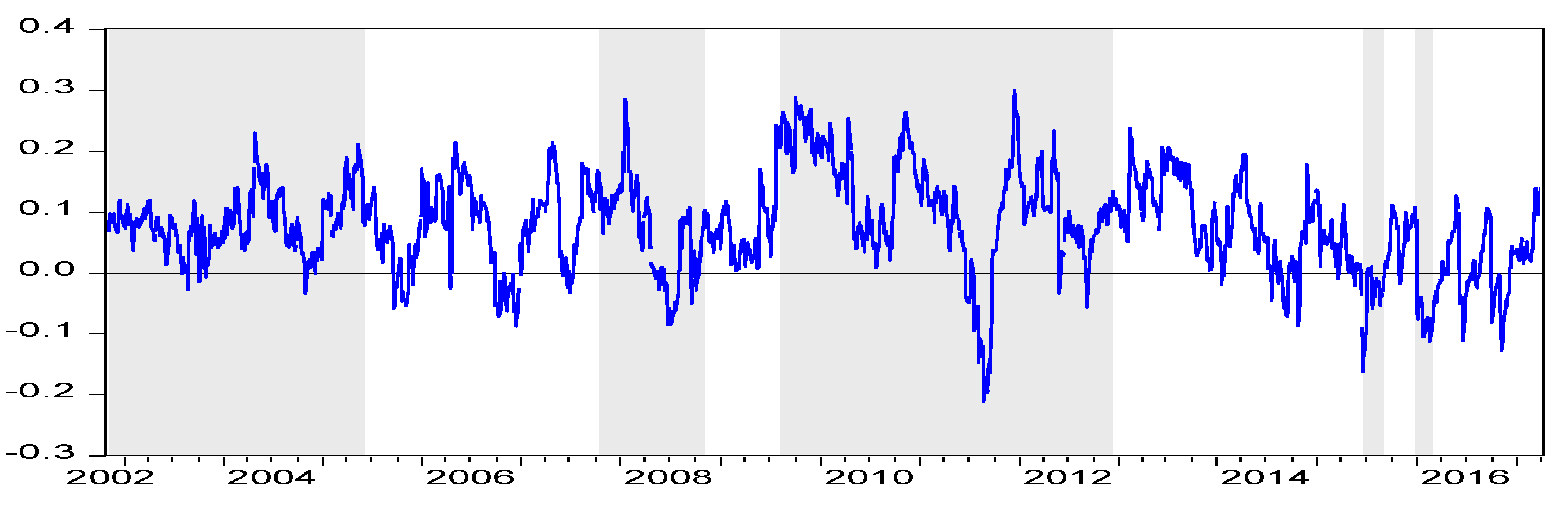
3.3. Methodology
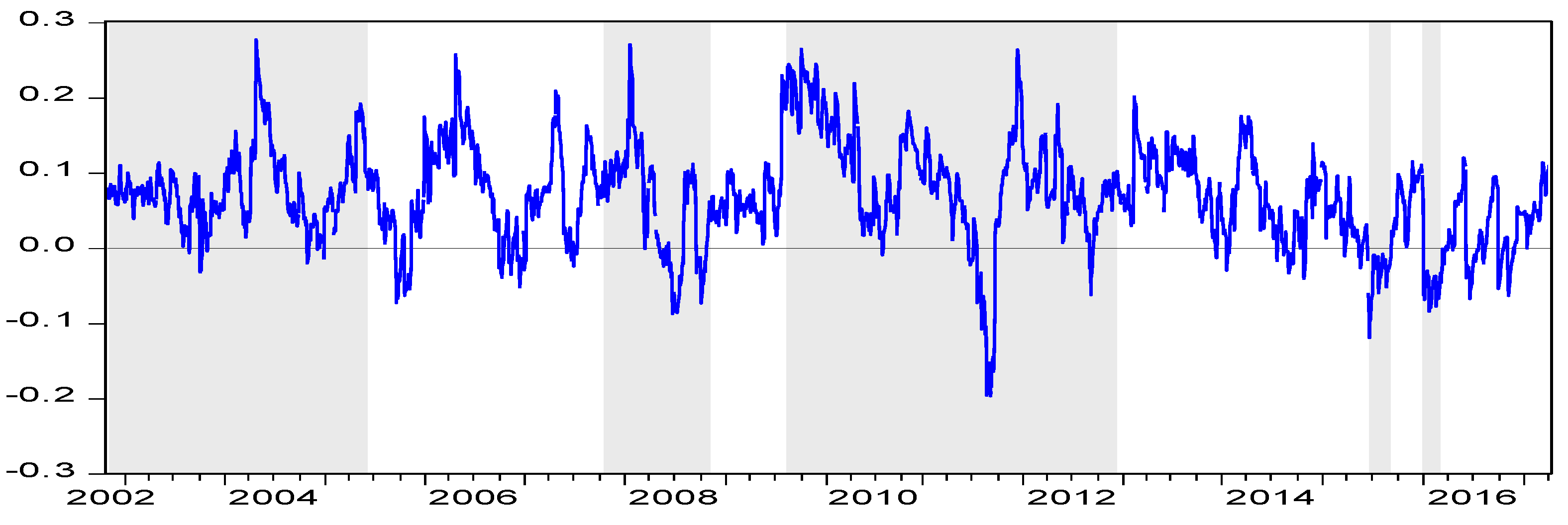
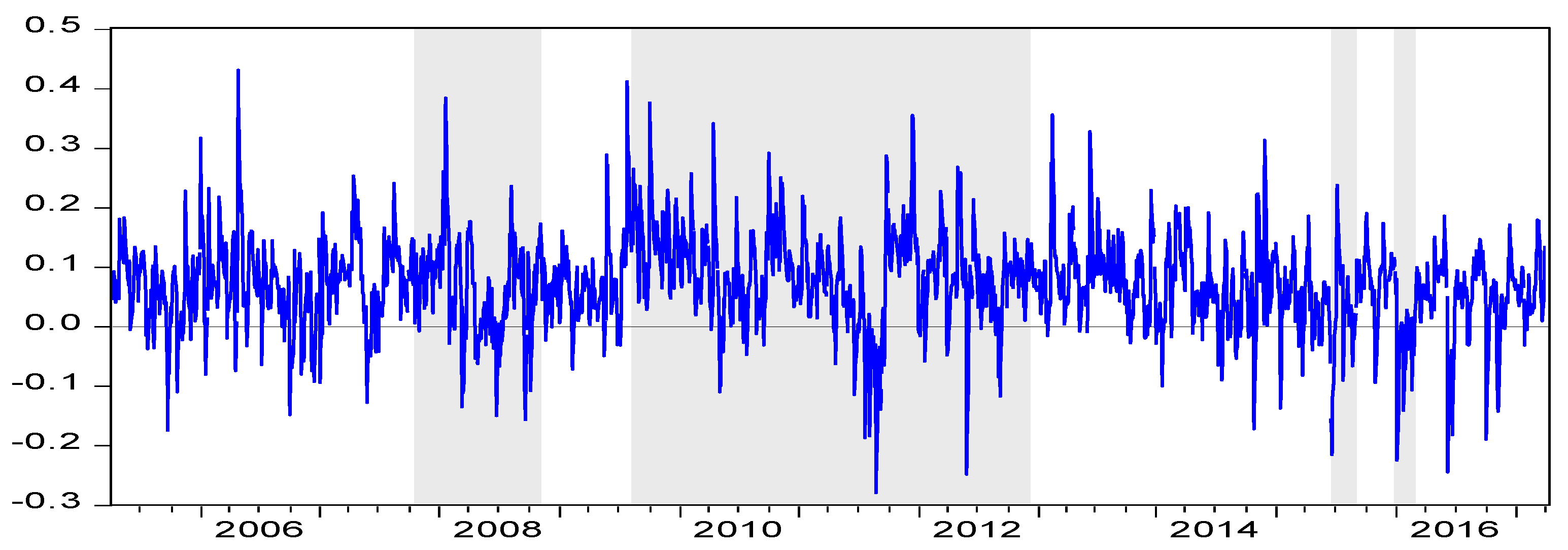
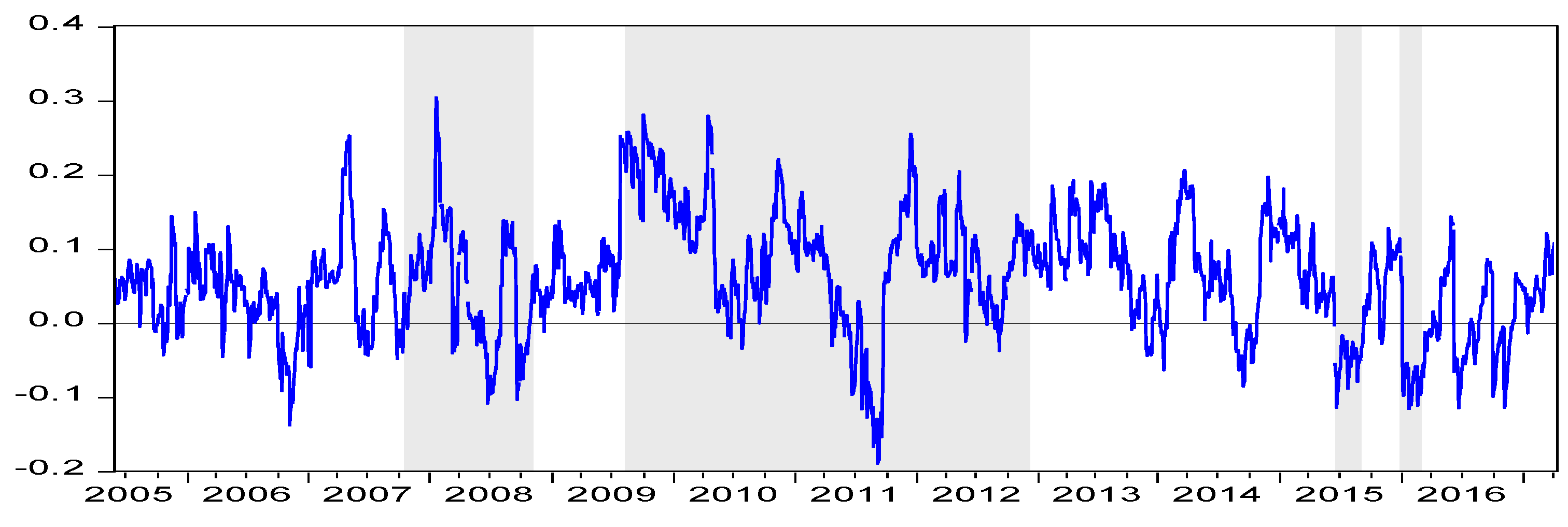
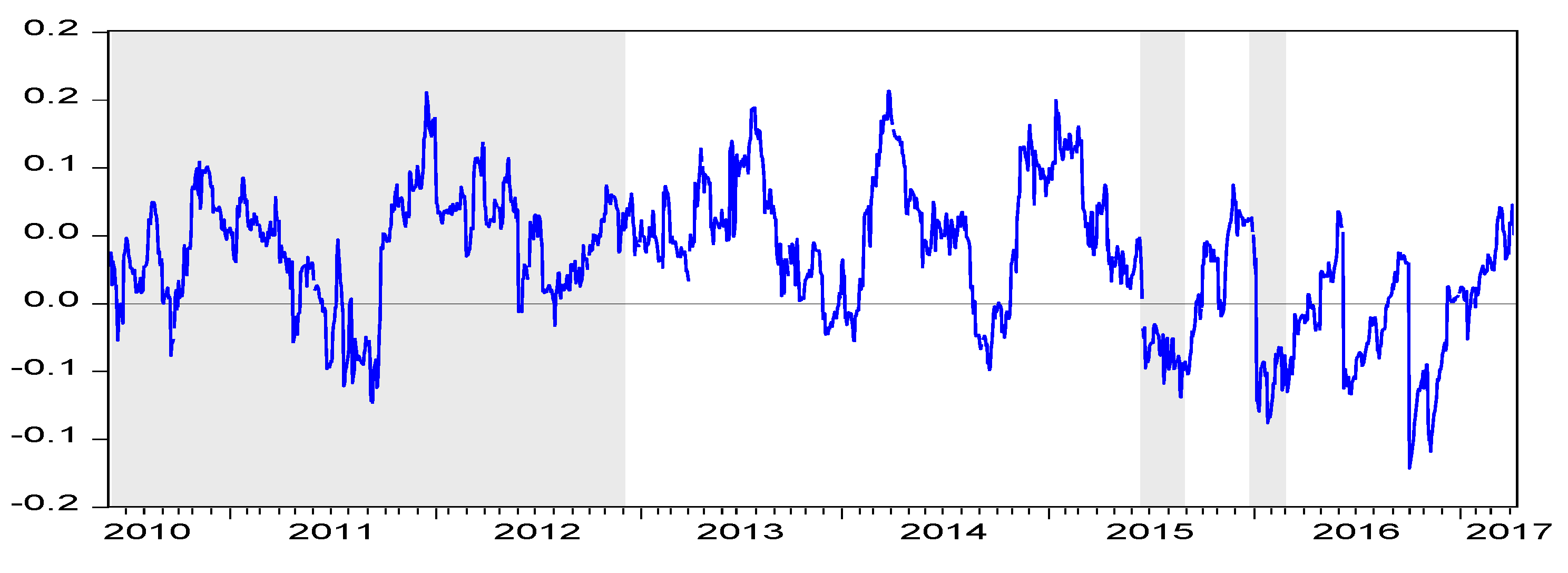
4. Empirical Results
5. Subsample Test
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Arouri, Mohamed El Hedi, Amine Lahiani, and Duc Khuong Nguyen. 2015. World Gold Prices and Stock Returns in China: Insights for Hedging and Diversification Strategies. Economic Modelling 44: 273–82. [Google Scholar] [CrossRef]
- Baruník, Jozef, Evžen Kočenda, and Lukáš Vácha. 2016. Gold, oil, and stocks: Dynamic correlations. International Review of Economics & Finance 42: 186–201. [Google Scholar]
- Basher, Syed Abul, and Perry Sadorsky. 2016. Hedging emerging market stock prices with oil, gold, VIX, and bonds: A comparison between DCC, ADCC and GO-GARCH. Energy Economics 54: 235–47. [Google Scholar] [CrossRef]
- Batten, Jonathan A., Cetin Ciner, and Brian M. Lucey. 2010. The macroeconomic determinants of volatility in precious metals markets. Resources Policy 35: 65–71. [Google Scholar] [CrossRef]
- Batten, Jonathan A., Cetin Ciner, and Brian M. Lucey. 2014. On the economic determinants of the gold-inflation relation. Resources Policy 41: 101–08. [Google Scholar] [CrossRef]
- Baur, Dirk G., and Brian M. Lucey. 2010. Is gold a hedge or a safe haven? An analysis of stocks, bonds and gold. Financial Review 45: 217–29. [Google Scholar] [CrossRef]
- Baur, Dirk G., and Thomas K. Mcdermott. 2010. Is gold a safe haven? International evidence. Journal of Banking & Finance 34: 1886–98. [Google Scholar]
- Beckmann, Joscha, Theo Berger, and Robert Czudaj. 2015. Does gold act as a hedge or a safe haven for stocks? A smooth transition approach. Economic Model 48: 16–24. [Google Scholar] [CrossRef]
- Bouri, Elie, Anshul Jain, P. C. Biswal, and David Roubaud. 2017. Cointegration and nonlinear causality amongst gold, oil, and the Indian stock market: Evidence from implied volatility indices. Resources Policy 52: 201–06. [Google Scholar] [CrossRef]
- Chen, An-Sing, and James Wuh Lin. 2014. The relation between gold and stocks: An analysis of severe bear markets. Applied Economics Letters 21: 158–70. [Google Scholar] [CrossRef]
- Choudhry, Taufiq, Syed S. Hassan, and Sarosh Shabi. 2015. Relationship between Gold and Stock Markets during the Global Financial Crisis: Evidence from Nonlinear Causality Tests. International Review of Financial Analysis 41: 247–56. [Google Scholar] [CrossRef]
- Ciner, Cetin, Constantin Gurdgiev, and Brian M. Lucey. 2013. Hedges and safe havens: An examination of stocks, bonds, gold, oil and exchange rates. International Review of Financial Analysis 29: 202–11. [Google Scholar] [CrossRef]
- Dee, Junpeng, Liuling Li, and Zhonghua Zheng. 2013. Is gold a hedge or a safe haven? Evidence from inflation and stock market. International Journal of Development and Sustainability 2: 1–16. [Google Scholar]
- Engle, Robert F. 1982. Autoregressive conditional heteroscedasticity with estimates of the variance of UK inflation. Econometrica 50: 987–1008. [Google Scholar] [CrossRef]
- Engle, Robert F. 2002. Dynamic conditional correlation: A simple class of multivariate GARCH models. Journal of Business and Economic Statistics 20: 339–50. [Google Scholar] [CrossRef]
- Frost, Alfred J., and Robert R. Prechter Jr. 2005. Elliott Wave Principle, 10th ed. Gainesville: New Classics Library, pp. 31, 78–85. [Google Scholar]
- Ghazali, Mohd Fahmi, Hooi Hooi Lean, and Zakaria Bahari. 2015. Sharia compliant gold investment in Malaysia: Hedge or safe haven? Pacific-Basin Finance Journal 34: 192–204. [Google Scholar] [CrossRef]
- Green, Timothy. 2007. The Ages of Gold. London: Gold Fields Minerals Services Ltd. [Google Scholar]
- Gürgün, Gözde, and Ibrahim Ünalmıs. 2014. Is gold a safe haven against equity market investment in emerging and developing countries? Finance Research Letters 11: 341–48. [Google Scholar] [CrossRef]
- Hamilton, James D. 1989. A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica 57: 357–84. [Google Scholar] [CrossRef]
- Huang, Shupei, Haizhong An, Xiangyun Gao, and Xuan Huang. 2016. Time–frequency featured co-movement between the stock and prices of crude oil and gold. Physica A: Statistical Mechanics and its Applications 444: 985–95. [Google Scholar] [CrossRef]
- Hoang, Thi-Hong-Van, Wing-Keung Wong, and Zhen Zhen Zhu. 2015. Is gold different for risk-averse and risk-seeking investors? An empirical analysis of the Shanghai Gold Exchange. Economic Modelling 50: 200–11. [Google Scholar] [CrossRef]
- Iqbal, Jav. 2017. Does gold hedge stock market, inflation and exchange rate risks? An econometric investigation. International Review of Economics & Finance 48: 1–17. [Google Scholar]
- Jain, Anshul, and P. C. Biswal. 2016. Dynamic linkages among oil price, gold price, exchange rate, and stock market in India. Resources Policy 49: 179–85. [Google Scholar] [CrossRef]
- Lu, Rong, and Longbing Xu. 2004. The asymmetry information effect on bull and bear stock markets. Economic Research 03: 65–72. [Google Scholar]
- Mensi, Walid, Shawkat Hammoudeh, Juan C. Reboredo, and Duc Kuong Nguyen. 2015. Are Sharia stocks, gold and US Treasury hedges and/or safe havens for the oil-based GCC markets? Emerging Markets Review 24: 101–21. [Google Scholar] [CrossRef]
- Mensi, Walid, Shawkat Hammoudeh, and Aviral Kumar Tiwari. 2016. New evidence on hedges and safe havens for Gulf stock markets using the wavelet-based quantile. Emerging Markets Review 28: 155–83. [Google Scholar] [CrossRef]
- Nguyen, Cuong, M. Ishaq Bhatti, Magda Komorníková, and Jozef Komorník. 2016. Gold price and stock markets nexus under mixed-copulas. Economic Modelling 58: 283–92. [Google Scholar] [CrossRef]
- O’Connor, Fergal A., Brian M. Lucey, Jonathan A. Batten, and Dirk G. Baur. 2015. The financial economics of gold-A survey. International Review of Financial Analysis 41: 186–205. [Google Scholar] [CrossRef]
- Smiech, Slawomir, and Monika Papiez. 2016. In search of hedges and safe havens: Revisiting the relations between gold and oil in the rolling regression framework. Finance Research Letters 20: 238–44. [Google Scholar] [CrossRef]
- Souček, Michael. 2013. Crude oil, equity and gold futures open interest co-movements. Energy Economics 40: 306–15. [Google Scholar] [CrossRef]
- Shahzad, Syed Jawad Hussain, Naveed Raza, Muhammad Shahbaza, and Azwadi Ali. 2017. Dependence of stock markets with gold and bonds under bullish and bearish market states. Resources Policy 52: 308–19. [Google Scholar] [CrossRef]
| 1 | From October 2007 to November 2008. |
| 2 | The SSE Composite Index is a stock market index of all stocks (A shares and B shares) that are traded at the Shanghai Stock Exchange. |
| 3 | The SZSE Component Index is an index of 500 stocks that are traded at the Shenzhen Stock Exchange (SZSE). It is the main stock market index of SZSE. |
| 4 | The CSI 300 is a capitalization-weighted stock market index designed to replicate the performance of 300 stocks traded in the Shanghai and Shenzhen stock exchanges. |
| 5 | SME Board is a supplement to the main board market, and it is a direct financing platform for small and medium enterprises. |
| 6 | GEM Index is a stock market index set up by Stock Exchange of Hong Kong for growth companies that do not fulfill the requirements of profitability or track record. |
| 7 | The conventional definition for a bear market which is usually defined as time periods when the stock market down more than 20% from its most recent highs to its corresponding relative minima (Chen and Lin 2014). |
| 8 | Evidence of conditional heteroscedasticity lends support to the use of ARCH-type models and, in particular, to the use of GARCH (1,1) models to capture the volatility behavior of the data series. |

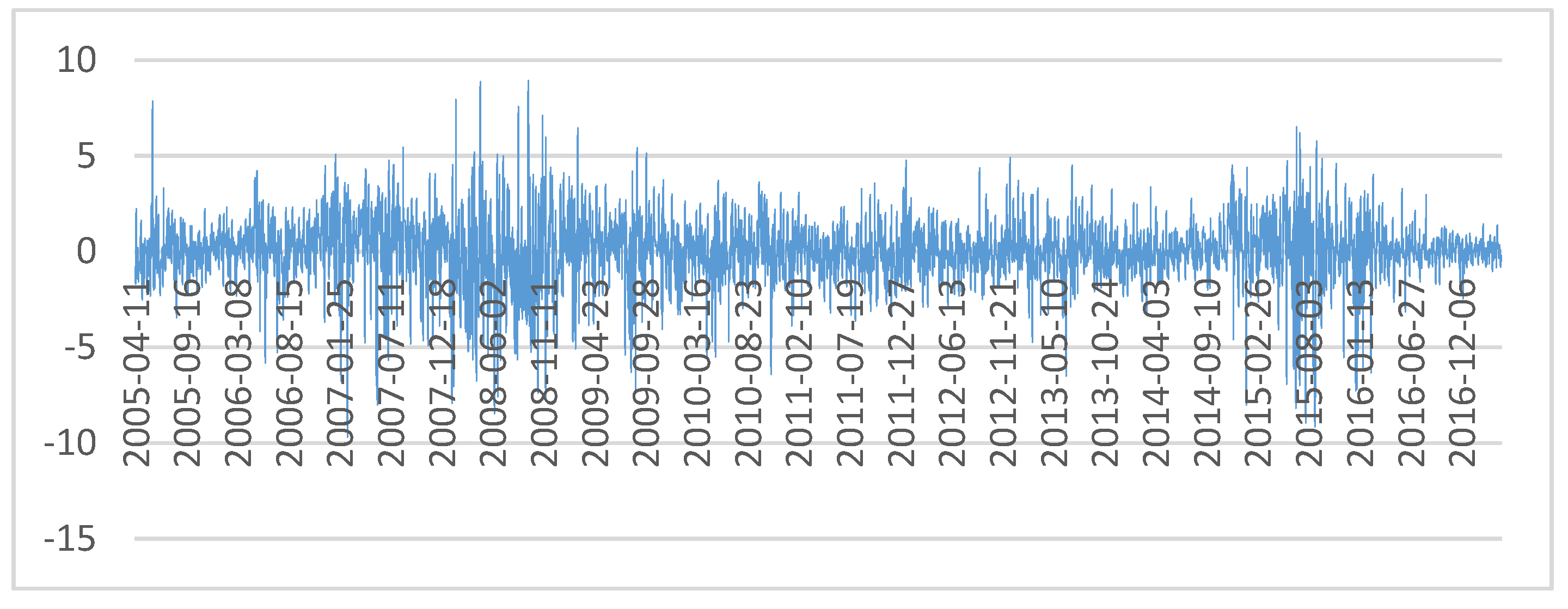
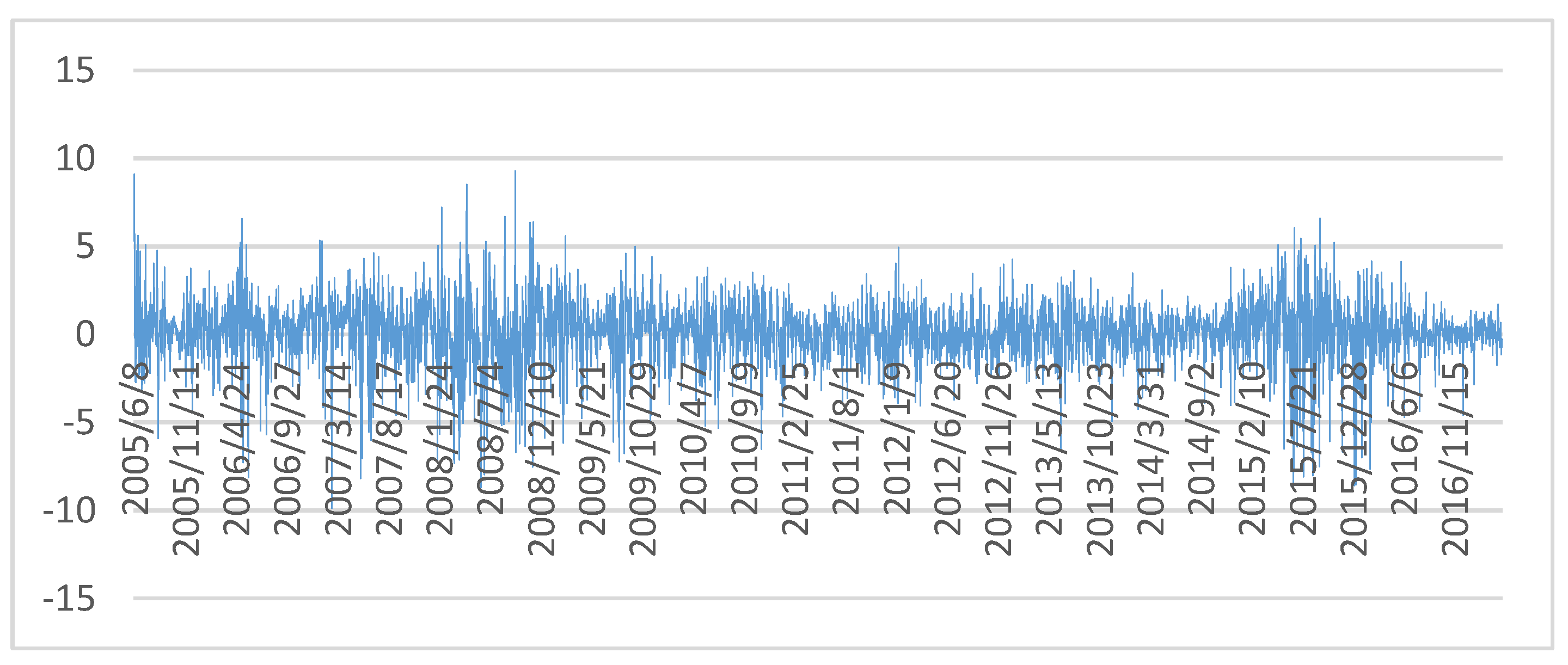
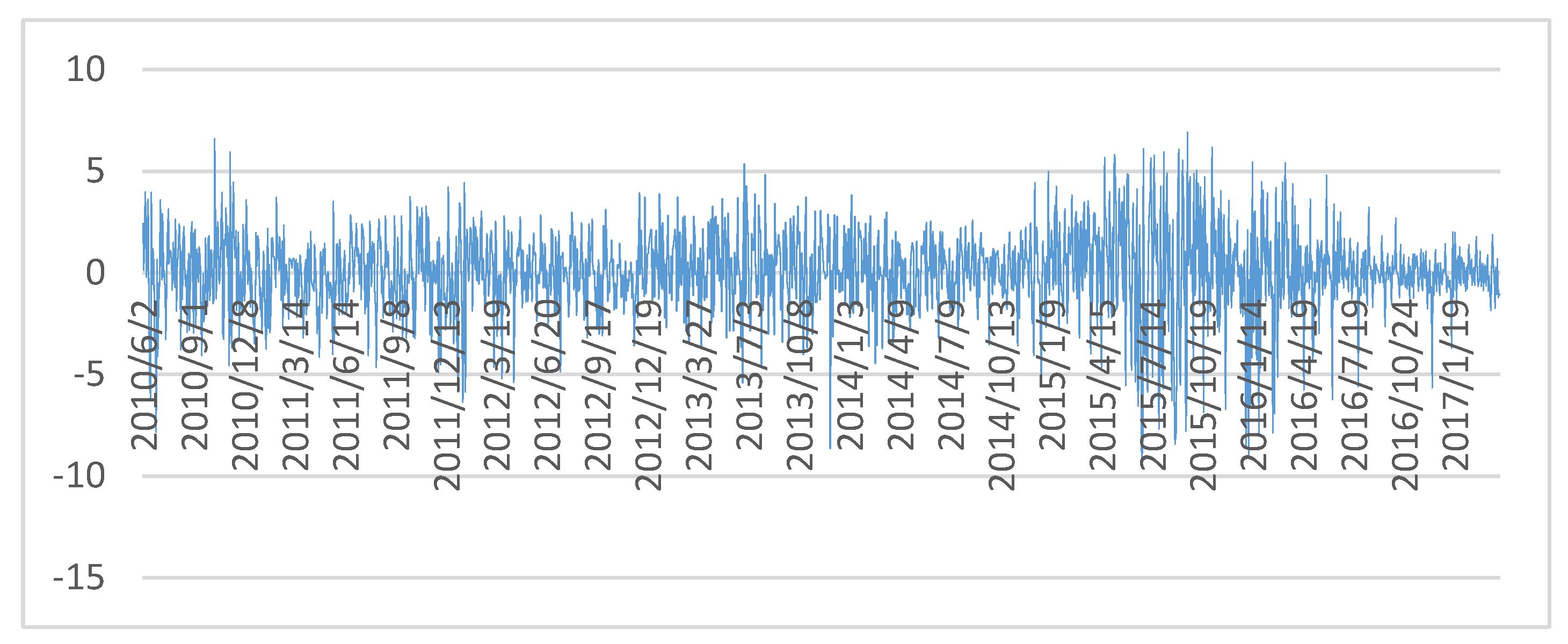

| Name | Data Sources | Sample Interval |
|---|---|---|
| Rgold | SGE | 31 October 2002–18 April 2017 |
| Rsse | Datastream | 31 October 2002–18 April 2017 |
| Rsz | Datastream | 31 October 2002–18 April 2017 |
| Rcsi | Datastream | 4 November 2005–18 April 2017 |
| Rsme | Datastream | 8 June 2005–18 April 2017 |
| Rgem | Datastream | 2 June 2010–18 April 2017 |
| Rsse | Rg(sse) | Rsz | Rg(sz) | Rsci | Rg(sci) | Rsme | Rg(sme) | Rgem | Rg(gem) | |
|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: Descriptive Statistics | ||||||||||
| Mean | 0.021 | 0.035 | 0.035 | 0.035 | 0.042 | 0.031 | 0.066 | 0.032 | 0.038 | 0.004 |
| Median | 0.068 | 0.06 | 0.06 | 0.06 | 0.102 | 0.052 | 0.192 | 0.052 | 0.108 | 0.009 |
| Max | 9.034 | 9.328 | 14.25 | 9.33 | 8.931 | 9.328 | 9.27 | 9.328 | 6.914 | 4.527 |
| Min | −9.256 | −9.474 | −9.75 | −9.47 | −9.695 | −9.474 | −9.87 | −9.474 | −9.332 | −9.474 |
| Std. Dev. | 1.656 | 1.102 | 1.876 | 1.095 | 1.834 | 1.155 | 1.995 | 1.161 | 2.128 | 1.014 |
| Skewness | −0.491 | −0.392 | −0.324 | −0.388 | −0.528 | −0.378 | −0.582 | −0.378 | −0.554 | −0.682 |
| Kurtosis | 7.13 | 10.069 | 6.757 | 10.11 | 6.456 | 9.769 | 5.58 | 9.682 | 4.873 | 11.582 |
| JB | 2637.04 *** | 7402.45 *** | 2120.62 *** | 7463.47 *** | 1589.86 *** | 5648.30 *** | 963.19 *** | 5435.87 *** | 329.39 *** | 5250.75 *** |
| Obs. | 3512 | 3512 | 3502 | 3502 | 2922 | 2922 | 2885 | 2885 | 1669 | 1669 |
| Panel B: Unit Root Test Statistics | ||||||||||
| DF | −57.938 *** | −62.295 *** | −56.115 *** | −62.172 *** | −52.426 *** | −56.584 *** | −50.653 *** | −56.248 *** | −37.577 *** | −43.123 *** |
| ADF | −57.939 *** | −62.323 *** | −56.120 *** | −62.198 *** | −52.441 *** | −56.609 *** | −50.687 *** | −56.278 *** | −37.566 *** | −43.110 *** |
| DF-GLS | −57.603 *** | −62.231 *** | −56.024 *** | −40.748 *** | −9.766 *** | −56.427 *** | −1.939 | −55.255 *** | −4.553 *** | −41.993 *** |
| PP | −57.998 *** | −62.252 *** | −56.229 *** | −62.122 *** | −52.499 *** | −56.582 *** | −50.636 *** | −56.199 *** | −37.501 *** | −43.085 *** |
| Q(10) | ARCH(1) | ARCH(5) | ARCH(10) | |
|---|---|---|---|---|
| Rsse | 37.954 (0.000) *** | 106.269 (0.000) *** | 295.041 (0.000) *** | 352.277 (0.000) *** |
| Rg(sse) | 29.23 (0.001) *** | 99.536 (0.000) *** | 170.455 (0.000) *** | 224.957 (0.000) *** |
| Rsz | 34.332 (0.000) *** | 71.440 (0.000) *** | 215.862 (0.000) *** | 313.094 (0.000) *** |
| Rg(sz) | 33.109 (0.000) *** | 90.553 (0.000) *** | 142.107 (0.000) *** | 178.969 (0.000) *** |
| Rsci | 36.5 (0.000) *** | 83.465 (0.000) *** | 233.190 (0.000) *** | 292.751 (0.000) *** |
| Rg(sci) | 24.404 (0.007) *** | 81.784 (0.000) *** | 137.488 (0.000) *** | 181.913 (0.000) *** |
| Rsme | 25.732 (0.004) *** | 78.634 (0.000) *** | 236.576 (0.000) *** | 278.628 (0.000) *** |
| Rg(sme) | 24.422 (0.007) *** | 78.974 (0.000) *** | 132.345 (0.000) *** | 175.468 (0.000) *** |
| Rgem | 27.884 (0.002) *** | 82.632 (0.000) *** | 205.258 (0.000) *** | 232.847 (0.000) *** |
| Rg(gem) | 9.5233 (0.483) | 74.896 (0.000) *** | 88.509 (0.000) *** | 93.421 (0.000) *** |
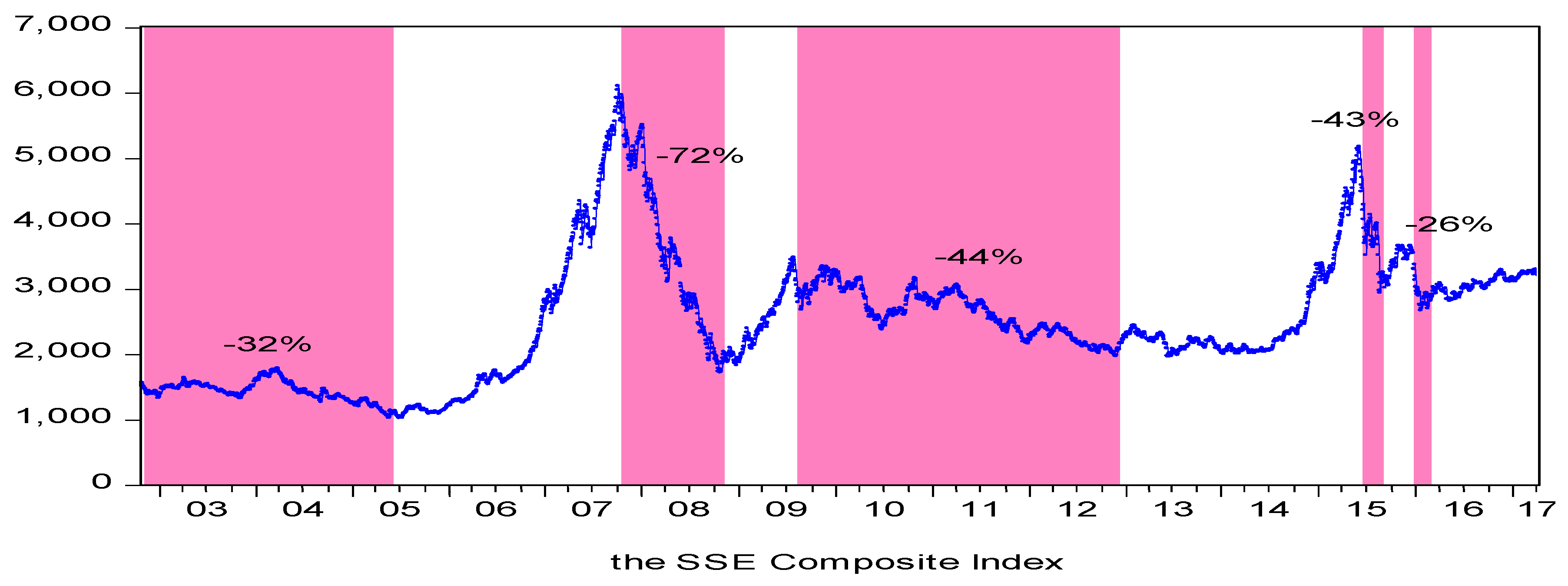
| Time Period | Maximum | Minimum | Drop | Origin | |
|---|---|---|---|---|---|
| Bear market I | 31 October 2002–7 June 2005 | 1507.50 | 1030.94 | 32% | Reduction of state-owned shares |
| Bear market II | 16 October 2007–4 November 2008 | 6092.06 | 1706.70 | 72% | The global financial crisis |
| Bear market III | 4 August 2009–3 December 2012 | 3471.44 | 1959.77 | 44% | Restarting IPO, tightening macro policies, the European debt crisis |
| Bear market IV | 12 June 2015–26 August 2015 | 5166.35 | 2927.29 | 43% | De-leveraging, checking OTC Future Financing by the CSRC (China Security Regulatory committee) |
| Bear market V | 22 December 2015–29 February 2016 | 3651.77 | 2687.98 | 26% | Implementing the fuse mechanism and the registration system, devaluation of RMB |
| Coefficient | Std. Error | z-Statistic | Prob. | ||
|---|---|---|---|---|---|
| Rsse | C | 0.014 *** | 0.005 | 2.774 | 0.006 |
| α | 0.058 *** | 0.008 | 7.541 | 0.000 | |
| β | 0.939 *** | 0.007 | 128.774 | 0.000 | |
| Rg(sse) | C | 0.017 *** | 0.004 | 3.794 | 0.000 |
| α | 0.068 *** | 0.009 | 7.264 | 0.000 | |
| β | 0.921 *** | 0.010 | 92.139 | 0.000 | |
| Rsz | C | 0.024 *** | 0.008 | 2.977 | 0.003 |
| α | 0.057 *** | 0.008 | 7.287 | 0.000 | |
| β | 0.938 *** | 0.008 | 119.071 | 0.000 | |
| Rg(sz) | C | 0.016 *** | 0.004 | 3.705 | 0.000 |
| α | 0.064 *** | 0.009 | 7.159 | 0.000 | |
| β | 0.925 *** | 0.010 | 96.013 | 0.000 | |
| Rsci | C | 0.009 * | 0.005 | 1.887 | 0.059 |
| α | 0.056 *** | 0.008 | 7.115 | 0.000 | |
| β | 0.945 *** | 0.007 | 135.173 | 0.000 | |
| Rg(sci) | C | 0.022 *** | 0.006 | 3.620 | 0.000 |
| α | 0.073 *** | 0.011 | 6.614 | 0.000 | |
| β | 0.914 *** | 0.012 | 76.444 | 0.000 | |
| Rsme | C | 0.041 *** | 0.013 | 3.104 | 0.002 |
| α | 0.078 *** | 0.011 | 7.052 | 0.000 | |
| β | 0.914 *** | 0.011 | 85.693 | 0.000 | |
| Rg(sme) | C | 0.024 *** | 0.007 | 3.665 | 0.000 |
| α | 0.071 *** | 0.011 | 6.445 | 0.000 | |
| β | 0.913 *** | 0.012 | 73.841 | 0.000 | |
| Rgem | C | 0.018 | 0.012 | 1.569 | 0.117 |
| α | 0.054 *** | 0.011 | 5.120 | 0.000 | |
| β | 0.943 *** | 0.010 | 94.613 | 0.000 | |
| Rg(gem) | C | 0.038 *** | 0.012 | 3.079 | 0.002 |
| α | 0.074 *** | 0.016 | 4.541 | 0.000 | |
| β | 0.888 *** | 0.023 | 38.610 | 0.000 |
| Coef. | S.E | Z | Prob | ||
|---|---|---|---|---|---|
| SSE-Gold | 0.017 *** | 0.006 | 2.944 | 0.003 | |
| 0.957 *** | 0.016 | 60.510 | 0.000 | ||
| SZ-Gold | 0.016 *** | 0.006 | 2.623 | 0.009 | |
| 0.953 *** | 0.019 | 50.333 | 0.000 | ||
| CSI-Gold | 0.045 | 0.028 | 1.599 | 0.110 | |
| 0.770 *** | 0.218 | 3.533 | 0.000 | ||
| SME-Gold | 0.021 ** | 0.009 | 2.252 | 0.024 | |
| 0.947 *** | 0.030 | 31.468 | 0.000 | ||
| GEM-Gold | 0.012 | 0.007 | 1.558 | 0.119 | |
| 0.960 *** | 0.025 | 38.843 | 0.000 |
| Bear Markets | Non-Bear Market | |||||
|---|---|---|---|---|---|---|
| I | II | III | IV | V | ||
| SSE-Gold | 0.0808 | 0.0667 | 0.1151 | −0.0410 | −0.0770 | 0.0639 |
| SZ-Gold | 0.0772 | 0.0561 | 0.0926 | −0.0345 | −0.0137 | 0.0612 |
| CSI-Gold | \ | 0.0623 | 0.0870 | 0.0182 | −0.0101 | 0.0669 |
| SME-Gold | \ | 0.0457 | 0.0920 | −0.0424 | −0.0337 | 0.0519 |
| GEM-Gold | \ | \ | 0.0405 | −0.0285 | −0.0278 | 0.0344 |
| Step One | Step Two | The Mean of Dynamic Conditional Correlations | ||||
|---|---|---|---|---|---|---|
| c | α | β | ||||
| Subsample 1: 31 October 2002–7 June 2005 | ||||||
| SSE | 0.115 (0.074) * | 0.065 (0.003) *** | 0.863 (0.000) *** | −0.026 (0.246) | 0.859 (0.000) *** | 0.0941 |
| GOLD | 0.015 (0.001) *** | 0.056 (0.000) *** | 0.921 (0.000) *** | |||
| Subsample 2: 16 October 2007–4 November 2008 | ||||||
| SSE | 0.079 (0.133) | −0.041 (0.011) ** | 1.035 (0.000) *** | 0.023 (0.318) | 0.958 (0.000) *** | 0.0074 |
| GOLD | 0.068 (0.193) | 0.065 (0.051) * | 0.921 (0.000) *** | |||
| Subsample 3: 4 August 2009–3 December 2012 | ||||||
| SSE | 0.017 (0.012) ** | 0.014 (0.003) *** | 0.974 (0.000) *** | 0.102 (0.107) | 0.694 (0.002) *** | 0.1714 |
| GOLD | 0.020 (0.000) *** | 0.064 (0.000) *** | 0.921 (0.000) *** | |||
| Subsample 4: 12 June 2015–26 August 2015 | ||||||
| SSE | 4.222 (0.849) | −0.039 (0.838) | 0.729 (0.641) | 0.151408 (0.388) | −0.213287 (0.804) | −0.0755 |
| GOLD | 0.082 (0.214) | −0.18245 (0.010) *** | 1.148 (0.000) *** | |||
| Subsample 5: 22 December 2015–29 February 2016 | ||||||
| SSE | 7.035 (0.399) | −0.182 (0.127) | 0.120 (0.919) | −0.065 (0.628) | 0.762 (0.105) | −0.2423 |
| GOLD | 0.259 (0.465) | −0.070 (0.239) | 0.785 (0.014) ** | |||
| Subsample 6: non-bear market | ||||||
| SSE | 0.007 (0.026) ** | 0.059 (0.000) *** | 0.940 (0.000) *** | 0.030 (0.206) | 0.653 (0.007) *** | 0.0701 |
| GOLD | 0.038 (0.000) *** | 0.085 (0.000) *** | 0.884 (0.000) *** | |||
| Step One | Step Two | The Mean of Dynamic Conditional Correlations | ||||
|---|---|---|---|---|---|---|
| c | α | β | ||||
| Subsample 1: 31 October 2002–7 June 2005 | ||||||
| SZ | 0.207 (0.103) | 0.069 (0.019) ** | 0.814 (0.000) *** | 0.005 (0.697) | 0.961 (0.000) *** | 0.1065 |
| GOLD | 0.015 (0.001) *** | 0.056 (0.000) *** | 0.921 (0.000) *** | |||
| Subsample 2: 16 October 2007–4 Novemver 2008 | ||||||
| SZ | 0.115 (0.065) * | −0.046 (0.011) ** | 1.037 (0.000) *** | 0.057 (0.236) | 0.849 (0.000) *** | −0.0111 |
| GOLD | 0.050 (0.237) | 0.046 (0.052) * | 0.944 (0.000) *** | |||
| Subsample 3: 4 August 2009–3 December 2012 | ||||||
| SZ | 0.043 (0.043) ** | 0.011 (0.006) *** | 0.972 (0.000) *** | 0.119 (0.033) ** | 0.591 (0.009) *** | 0.1461 |
| GOLD | 0.020 (0.001) *** | 0.063 (0.000) *** | 0.922 (0.000) *** | |||
| Subsample 4: 12 June 2015–26 August 2015 | ||||||
| SZ | 4.555 (0.869) | −0.049 (0.847) | 0.736 (0.685) | −0.192 (/) | 0.976 (/) | −0.0874 |
| GOLD | 0.096 (0.003) *** | −0.214 (0.003) *** | 1.163 (0.000) *** | |||
| Subsample 5: 22 December 2015–29 February 2016 | ||||||
| SZ | 10.267 (0.401) | −0.174 (0.199) | 0.096 (0.936) | −0.210 (/) | 1.051 (/) | −0.4322 |
| GOLD | 0.283 (0.469) | −0.068 (0.257) | 0.757 (0.030) ** | |||
| Subsample 6: non-bear market | ||||||
| SZ | 0.022 (0.000) *** | 0.053 (0.000) *** | 0.940 (0.000) *** | 0.002 (0.912) | 0.716 (0.417) | 0.0682 |
| GOLD | 0.038 (0.000) *** | 0.085 (0.000) *** | 0.884 (0.000) *** | |||
| Step One | Step Two | The Mean of Dynamic Conditional Correlations | ||||
|---|---|---|---|---|---|---|
| c | α | β | ||||
| Subsample 1: 16 October 2007–4 November 2008 | ||||||
| CSI | −0.004 (0.979) | −0.035 (0.113) | 1.036 (0.000) *** | 0.049 (0.324) | 0.822 (0.000) *** | −0.0021 |
| GOLD | 0.068 (0.192) | 0.065 (0.051) * | 0.921 (0.000) *** | |||
| Subsample 2: 4 August 2009–3 December 2012 | ||||||
| CSI | 0.028 (0.035) ** | 0.017 (0.004) *** | 0.967 (0.000) *** | 0.136 (0.021) | 0.499 (0.039) | 0.1669 |
| GOLD | 0.020 (0.000) *** | 0.064 (0.000) *** | 0.921 (0.000) *** | |||
| Subsample 3: 12 June 2015–26 August 2015 | ||||||
| CSI | 4.111 (0.863) | 0.029 (0.889) | 0.692 (0.687) | 0.171 (0.355) | 0.209 (0.826) | −0.0973 |
| GOLD | 0.096 (0.003) *** | -0.214 (0.003) *** | 1.163 (0.000) *** | |||
| Subsample 4: 22 December 2015–29 February 2016 | ||||||
| CSI | 5.669 (0.275) | −0.168 (0.127) | 0.206 (0.804) | 0.509 (0.170) | −0.157 (0.283) | −0.2234 |
| GOLD | 0.283 (0.469) | -0.068 (0.257) | 0.757 (0.030) ** | |||
| Subsample 5: non-bear market | ||||||
| CSI | 0.005 (0.107) | 0.055 (0.000) *** | 0.945 (0.000) *** | 0.019 (0.403) | 0.624 (0.039) ** | 0.0663 |
| GOLD | 0.030 (0.000) *** | 0.079 (0.000) *** | 0.895 (0.000) *** | |||
| Step One | Step Two | The Mean of Dynamic Conditional Correlations | ||||
|---|---|---|---|---|---|---|
| c | α | β | ||||
| Subsample 1: 16 October 2007–4 November 2008 | ||||||
| SME | −0.014 (0.928) | −0.030 (0.085) * | 1.032 (0.000) *** | 0.048 (0.322) | 0.722 (0.006) *** | 0.0043 |
| GOLD | 0.068 (0.193) | 0.065 (0.051) * | 0.921 (0.000) *** | |||
| Subsample 2: 4 August 2009–3 December 2012 | ||||||
| SME | 0.092 (0.047) ** | 0.053 (0.001) *** | 0.910 (0.000) *** | 0.027 (0.110) | 0.941 (0.000) *** | 0.1451 |
| GOLD | 0.020 (0.001) *** | 0.064 (0.000) *** | 0.921 (0.000) *** | |||
| Subsample 3: 12 June 2015–26 August 2015 | ||||||
| SME | 4.263 (0.874) | −0.048 (0.864) | 0.760 (0.656) | −0.033 (/) | 1.037 (/) | −0.1767 |
| GOLD | 0.096 (0.003) *** | -0.214 (0.003) *** | 1.163 (0.000) *** | |||
| Subsample 4: 22 December 2015–29 February 2016 | ||||||
| SME | 9.928 (0.375) | −0.169 (0.205) | 0.098 (0.931) | −0.216 (/) | 1.047 (/) | −0.4166 |
| GOLD | 0.259 (0.465) | −0.070 (0.239) | 0.785 (0.014) ** | |||
| Subsample 5: non-bear market | ||||||
| SME | 0.042 (0.000) *** | 0.065 (0.000) *** | 0.922 (0.000) *** | 0.014 (0.423) | 0.845 (0.000) *** | 0.0585 |
| GOLD | 0.038 (0.000) *** | 0.085 (0.000) *** | 0.884 (0.000) *** | |||
| Step One | Step Two | The Mean of Dynamic Conditional Correlations | ||||
|---|---|---|---|---|---|---|
| c | α | β | ||||
| Subsample 1: 4 August 2009–3 December 2012 | ||||||
| GEM | 0.091 (0.139) | 0.038 (0.008) *** | 0.933 (0.000) *** | 0.052 (0.369) | −0.155 (0.769) | 0.0686 |
| GOLD | 0.016 (0.009) *** | 0.068 (0.000) *** | 0.920 (0.000) *** | |||
| Subsample 2: 12 June 2015–26 August 2015 | ||||||
| GEM | 2.950 (0.128) | −0.318 (0.108) | 1.181 (0.000) *** | −0.131 (0.360) | 0.930 (0.000) *** | −0.1414 |
| GOLD | 0.096 (0.003) *** | −0.214 (0.003) *** | 1.163 (0.000) *** | |||
| Subsample 3: 22 December 2015–29 February 2016 | ||||||
| GEM | 8.104 (0.017) ** | −0.210 (0.056) * | 0.466 (0.165) | −0.117 (/) | 1.014 (/) | −0.1418 |
| GOLD | 0.259 (0.465) | −0.070 (0.239) | 0.785 (0.014) ** | |||
| Subsample 4: non-bear market | ||||||
| GEM | 0.018 (0.007) *** | 0.038 (0.000) *** | 0.956 (0.000) *** | −0.013 (/) | −0.001 (/) | 0.0594 |
| GOLD | 0.108 (0.000) *** | 0.122 (0.000) *** | 0.760 (0.000) *** | |||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.; Wang, M. Does Gold Act as a Hedge and a Safe Haven for China’s Stock Market? Int. J. Financial Stud. 2017, 5, 18. https://doi.org/10.3390/ijfs5030018
Chen K, Wang M. Does Gold Act as a Hedge and a Safe Haven for China’s Stock Market? International Journal of Financial Studies. 2017; 5(3):18. https://doi.org/10.3390/ijfs5030018
Chicago/Turabian StyleChen, Ke, and Meng Wang. 2017. "Does Gold Act as a Hedge and a Safe Haven for China’s Stock Market?" International Journal of Financial Studies 5, no. 3: 18. https://doi.org/10.3390/ijfs5030018
APA StyleChen, K., & Wang, M. (2017). Does Gold Act as a Hedge and a Safe Haven for China’s Stock Market? International Journal of Financial Studies, 5(3), 18. https://doi.org/10.3390/ijfs5030018






