1. Introduction
In recent years, principal component analysis (PCA) has been widely applied to the study of financial markets. PCA (
Jolliffe 1986) is a standard method in statistics for extracting an ordered set of uncorrelated sources of variation in a multivariate system, and is widely used as a dimension reduction method. The correlation matrix is computed from a finite sample, and it is well-understood that small sample effects increase the observed correlations. Thus, a PCA can be used to clean a correlation matrix by removing potentially spurious correlations which are only a consequence of sampling. PCA is an attractive method to apply, given that financial markets are typically characterised by a high degree of multicollinearity—implying that there are only a few independent sources of information in a market.
Using random matrix theory (or, more specifically, the spectral decomposition theorem—see
Jolliffe 1986, p. 13), many authorities have divided the eigenvectors into three distinct groups based on their eigenvalues. For example,
Kim and Jeong (
2005) decomposed a correlation matrix of 135 stocks which traded on the New York Stock Exchange (NYSE) into three parts:
The first principal component (PC1) with the largest eigenvalue which they asserted represents a market-wide effect that influences all stocks.
A variable number of principal components (PCs) following the market component which represent synchronized fluctuations affecting groups of stocks.
The remaining PCs indicate randomness in the price fluctuations.
Authorities such as
Driesson et al. (
2003),
Kim and Jeong (
2005),
Pérignon et al. (
2007),
Kritzman et al. (
2011),
Billio et al. (
2012), and
Zheng et al. (
2012) all assumed without any real question that the PCs of interest were PC1 and—depending on the author’s purposes—some or all of the PCs in group (2) above. The PCs in group (3) above have the smallest eigenvalues, and hence the smallest amount of information; it is very likely that they only contain noise. As a consequence of this well-understood fact, it is likely that if a PCA of a stock market correlation matrix is carried out, the analyst or researcher will not bother to examine the high-numbered components because she or he believes that they contain nothing of interest.
In this paper we show that the highest-numbered PCs may contain useful financial insights, while at the same time they may contain little or no information in the sense that that word is used in information science. We explain below how this apparent paradox arises—that a high-numbered PC can have little or no information yet there may still be useful financial insights to be gleaned from it.
While relatively unknown (and hence unexploited in the finance literature), it is widely understood in the both the statistical and econometric literatures that within group (3) (the random or noise PCs), there may be two more sub-categories of PC—both of which may be of interest to a stock (or other financial) market analyst. The first is the detection of outlier variables (rather than outlier observations). It is well understood that the presence of an outlier in a sample may dramatically affect an analysis of that sample. In the context of a stock market, an outlier stock would be one which behaves in a manner unlike any other individual stock or group of stocks in that market. The identification of such a stock or stocks would potentially be of considerable interest. However, in the analysis of our data below, we did not find any PCs of this type, so we are unable to give any further guidance on how to interpret the presence of such a stock, should one or more be found. Consequently, will not pursue this further, but see
Jolliffe (
1986, chp. 10) for details on this type of PC and
Hawkins (
1980),
Barnett and Lewis (
1994), or
Aggarwal (
2013) for further discussion on outlier detection and analysis.
The other type of PC is near-constant relationships between variables described in
Jolliffe (
1986, sct. 3.4). It is somewhat counter-intuitive that a high-numbered PC—which by definition contains very little explanatory power—can identify a grouping of stocks or other financial assets which are of interest to a financial analyst or portfolio manager. To see how these are detected, consider two stocks which are highly correlated with each other. We will consider the final (
) PC from the PCA, although as will be seen below, in our sample the last PC was not the only PC which detected stocks with a near-constant relationship. Assume the eigenvalue of the final principal component, PC
n, is small and close to zero. This assumption can be justified on the basis that the final PC explains the least amount of variation within the sample and thus will be the PC with the eigenvalue closest to zero. The actual amount of variation explained by any given principal component is given by
where
The eigenvector of each principal component is a linear combination of all variables (
Jolliffe 1986), which can be written as
where
is the eigenvector of component
n, and
is the coefficient (or loading) of variable
i (in our case stock
i) in component
k. For each principal component (for example, component
n),
If variables
and
are the two highly correlated variables (stocks) being detected in component
n, these two variables will have large coefficients while the remainder of the variables will have near-zero coefficients (note that the variation associated with each of the highly correlated variables and other variables in the data set will be captured in other principal components). Equation (
3) can then be written
but where
so that
As a consequence, the closer
and
are in magnitude, the more correlated are the
and
variables (stocks). To see why such a principal component explains so little variation (and hence contains so little information in the technical sense), it is clear from Equation (
5) that the contribution of variables 3 through
n are negligible because their coefficients (loadings) are near zero. If
and
are highly positively correlated, then
and
in Equation (
6) will have opposite signs so that variation in variable (stock) 1 is largely cancelled by variation in variable (stock) 2. If
and
are negatively correlated, the
and
will have the same sign. Again, however, the variation in
will be cancelled by variation in
. Thus, the manner in which the information has been eliminated from the PC to yield a small eigenvalue is of financial interest to us because it allows us to identify stocks with near-linear relationships, should such stocks exist.
In this illustration, we have used two stocks; however, associations of larger groups may be found and in the results below, where we report larger associations. In these cases, Equations (
4) and (
6) need to be modified to increase the number of stocks with significant loadings.
In any given market, such highly correlated assets may or may not exist. We argue that if a financial analyst or portfolio manager undertakes a PCA of a stock or other financial market as part of their routine analysis, then they should examine the last few components for the presence of highly correlated stocks. If they do exist, finding them is straight-forward, as we will show below and the implications for stock selection and portfolio management are easily understood. Using the information available in the PCA may mean the analyst could avoid using a separate clustering analysis (e.g.,
K-means) to identify these stocks (
Ding and He 2004). However, there is no point in undertaking a PCA if the only goal is to identify highly correlated stocks, because there are much more computationally efficient methods of finding them.
It is possible to automate this process of identifying highly correlated stocks in the process of portfolio selection and management; we gave details of this in an earlier paper (
Yang et al. 2016).
The remainder of this paper is structured as follows:
Section 2 describes the data and methods,
Section 3 presents our results, and
Section 4 concludes.
3. Results
In this section, we present some details on the eigenvalues of the last six PCs: , their values and variance explained in
Table 1, scatter plots of their loadings in
Figure 1,
Figure 2 and
Figure 3, which successfully picked up groups of stocks with highly correlated returns, together with time series plots of their adjusted price in
Figure 4,
Figure 5,
Figure 6,
Figure 7 and
Figure 8. As noted in Equation (
6), the
values (loadings) of the highly correlated stocks will dominate the principal component and this can be visualised with a scatter plot.
For our own reference, we made more scatter plots than are reported here. For the purpose of reporting, only the pairs which showed the behaviour of interest are reported. We start with principal components 151 and 152, which picked up three pairs of near-linear relationships and then discuss the “big four” banks and two mining firms. Each eigenvector is presented only once, as the vectors are dominated by just a handful of stocks.
These six low-variance principal components detected stocks with high correlations. In some applications, the eigenvalues associated with the last few principal components are very close to zero. In our case, the eigenvalues of the last few principal components were small but clearly different from zero. Nevertheless, they still picked up near-linear relationships between some stocks—see
Table 1 for a list of their eigenvalues and percentage of variance explained.
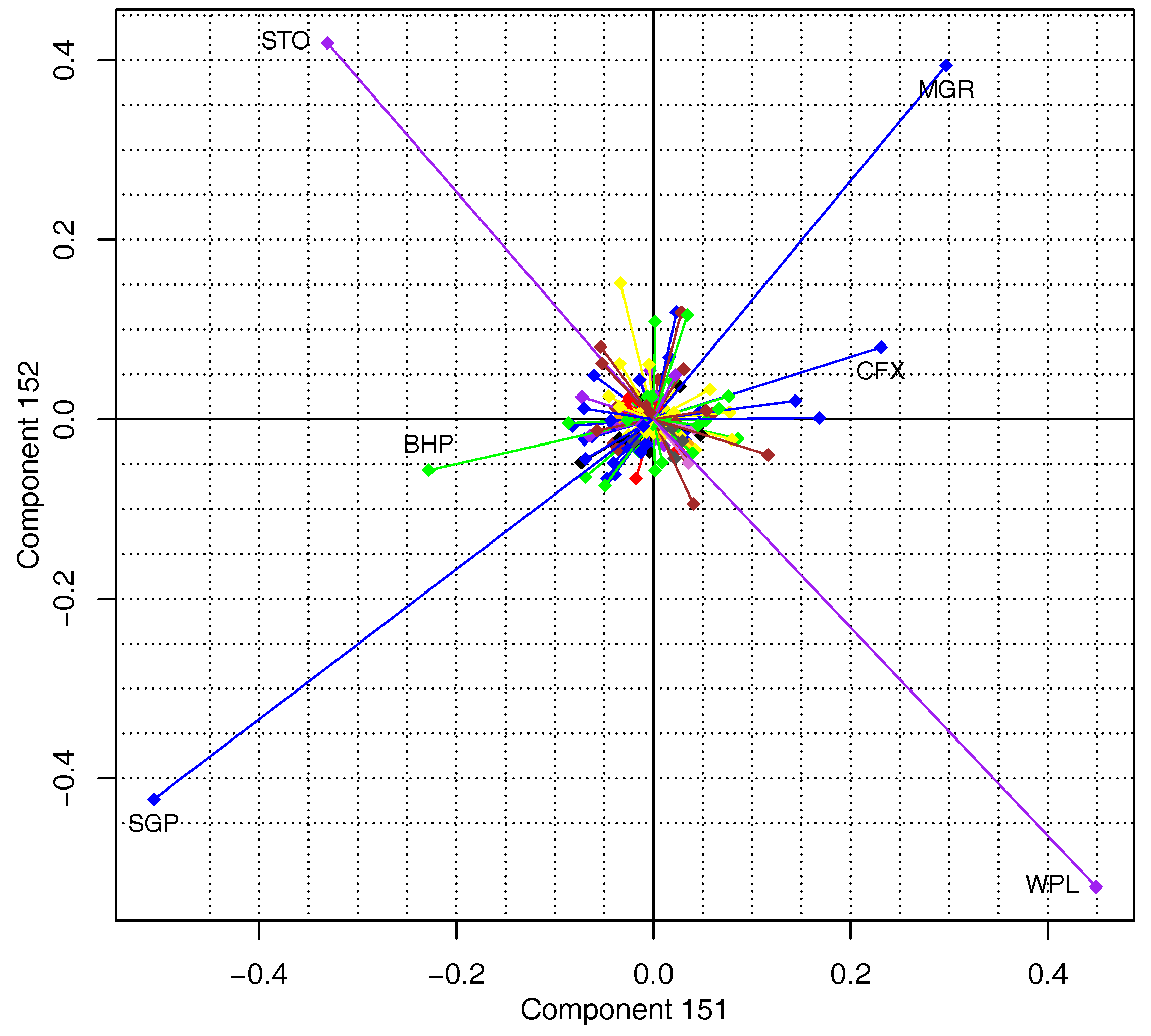
In
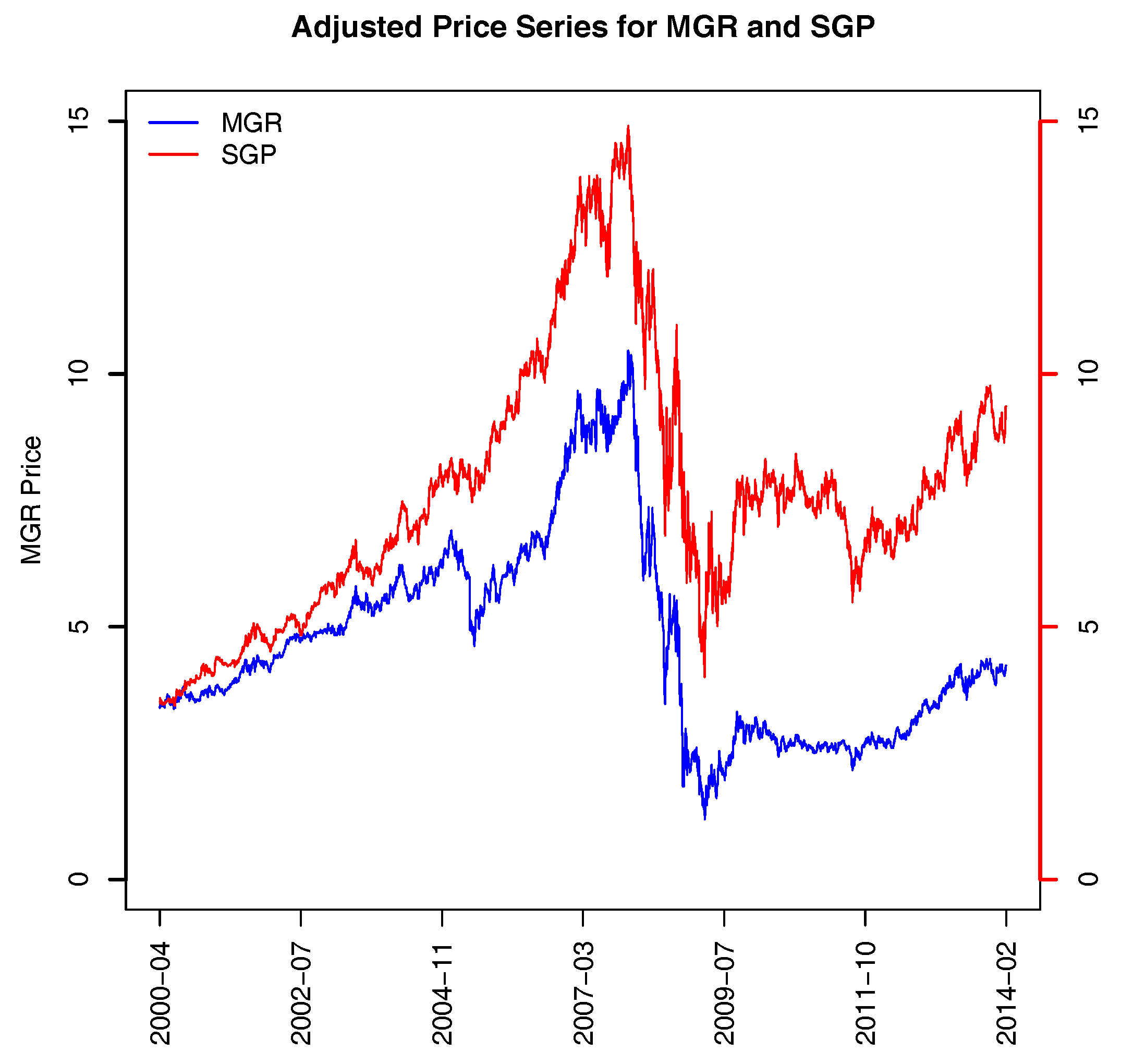
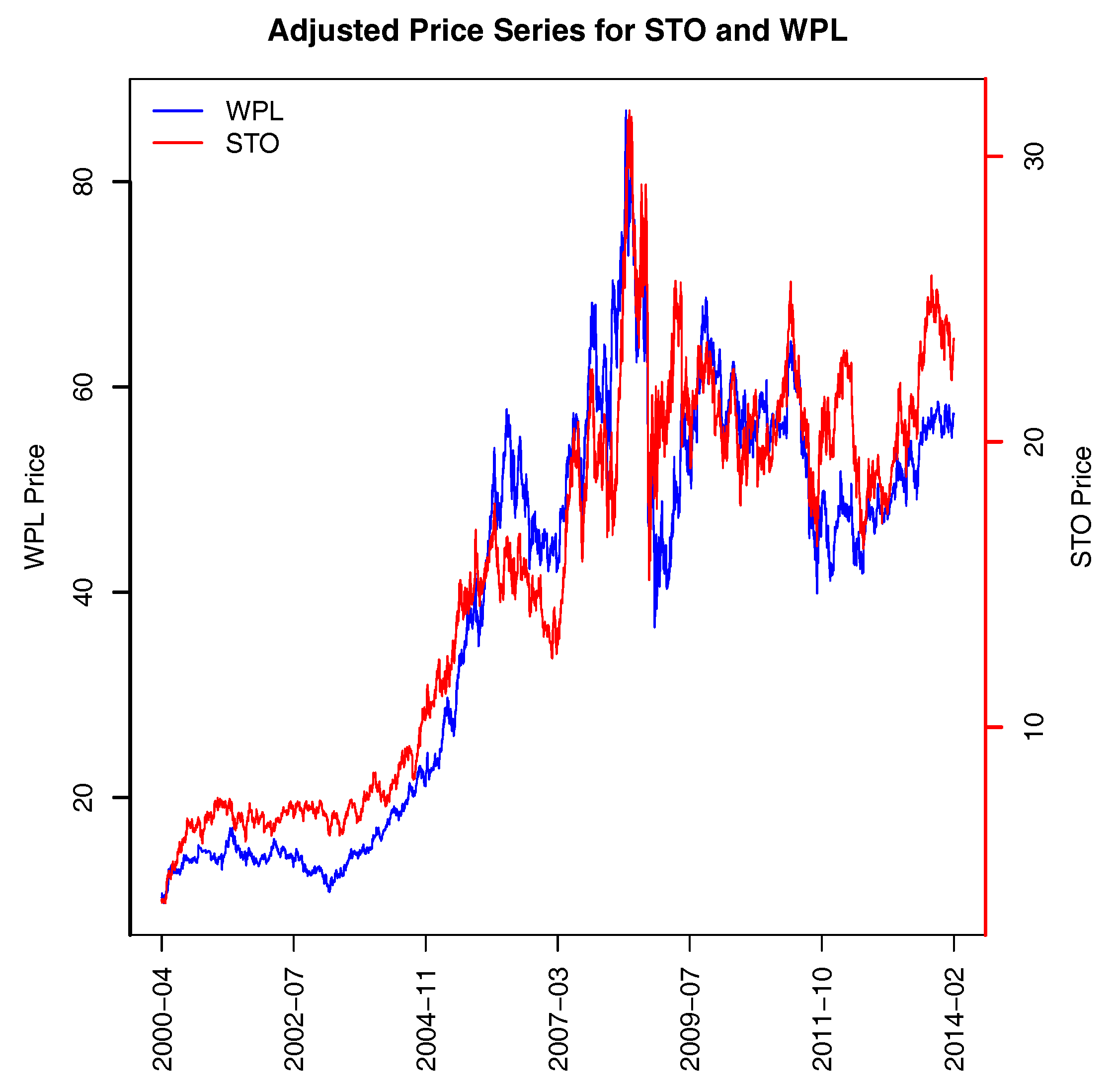
Figure 1, we present scatter plots of PCs 151 and 152. BHP Billiton (BHP) and CFS Retail Property Trust Group (CFX) in the real estate industry (CFX changed its name to Novion Property Group after the close of the study period and now has the ticker symbol NVN) clearly form a pair, they have high loadings of opposite signs on PC151 but low loadings on PC152. Mirvac Group (MGR), Stockland (SGP), Santos Limited (STO) and Woodside Petroleum Limited (WPL) form a group of four and have high loadings on both PC151 and PC152. This group of four can be broken into two pairs based on the signs of their loadings in PC151 and PC152 : STO with WPL, and MGR with SGP. Both pairs of stocks are positively correlated (see
Table 2), accounting for the loading having opposite signs in these PCs.
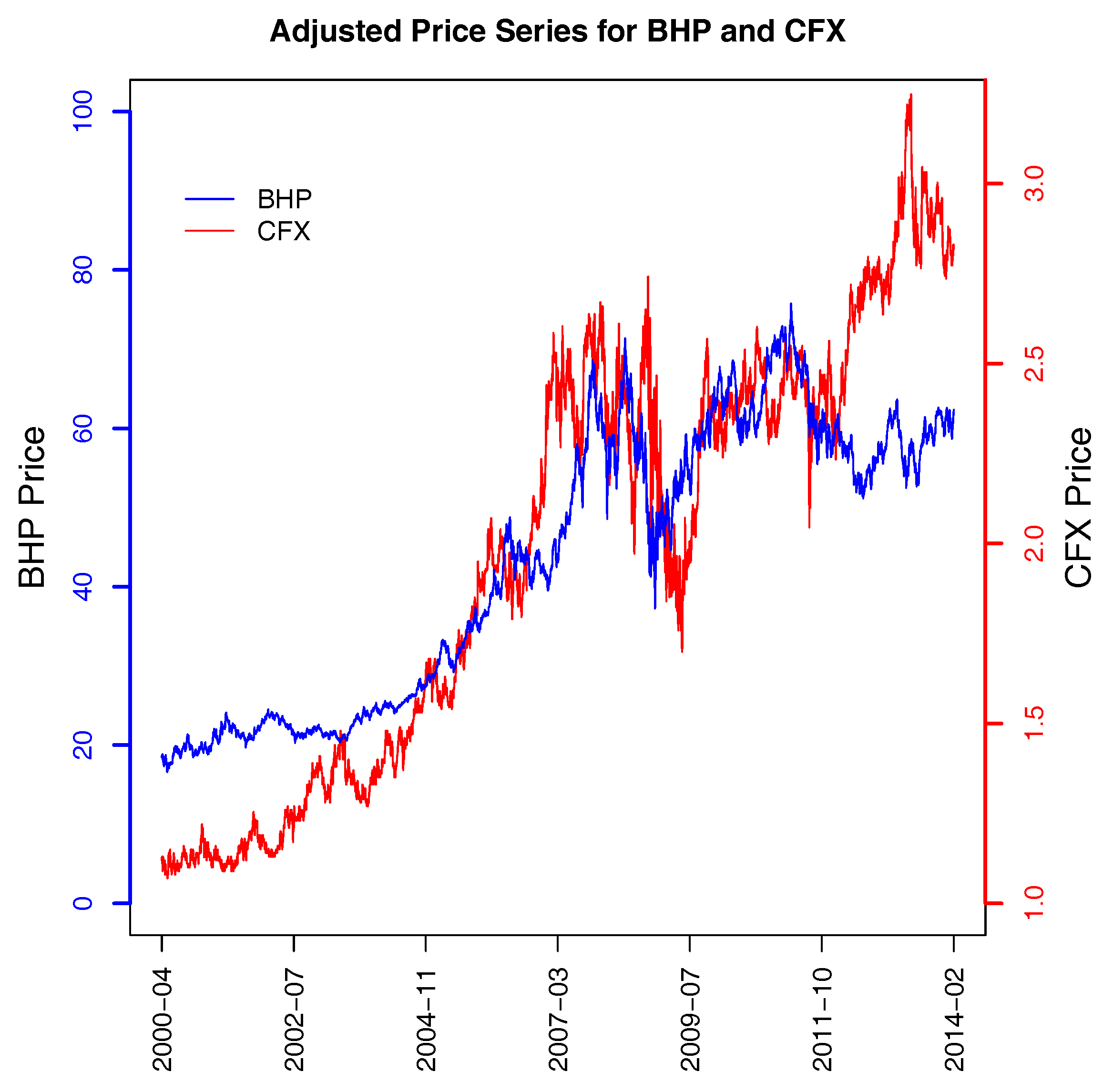
Curiously, the first pair of stocks are not in the same industry. BHP is in Basic Materials and CFX in the real estate industry. They tended to move in the same direction from the start of the study period until 2011. Their price trajectories then began to move in different directions after this time, as can be seen in
Figure 4.
The second pair—MGR and SGP—are both large diversified real estate groups. They had nearly the same stock price level in the beginning of 2000, and have diverged since then. The similarity in their price movements can be easily seen over short time frames, but over the longer term, their price level has diverged, as can be seen in
Figure 5.
The third pair of stocks are STO and WPL, which are in the Oil & Gas industry. Both companies explore for and produce oil and gas from onshore and offshore wells. The high correlations in their price movements over both the short- and long-term are clearly evident, as can be seen in
Figure 6.
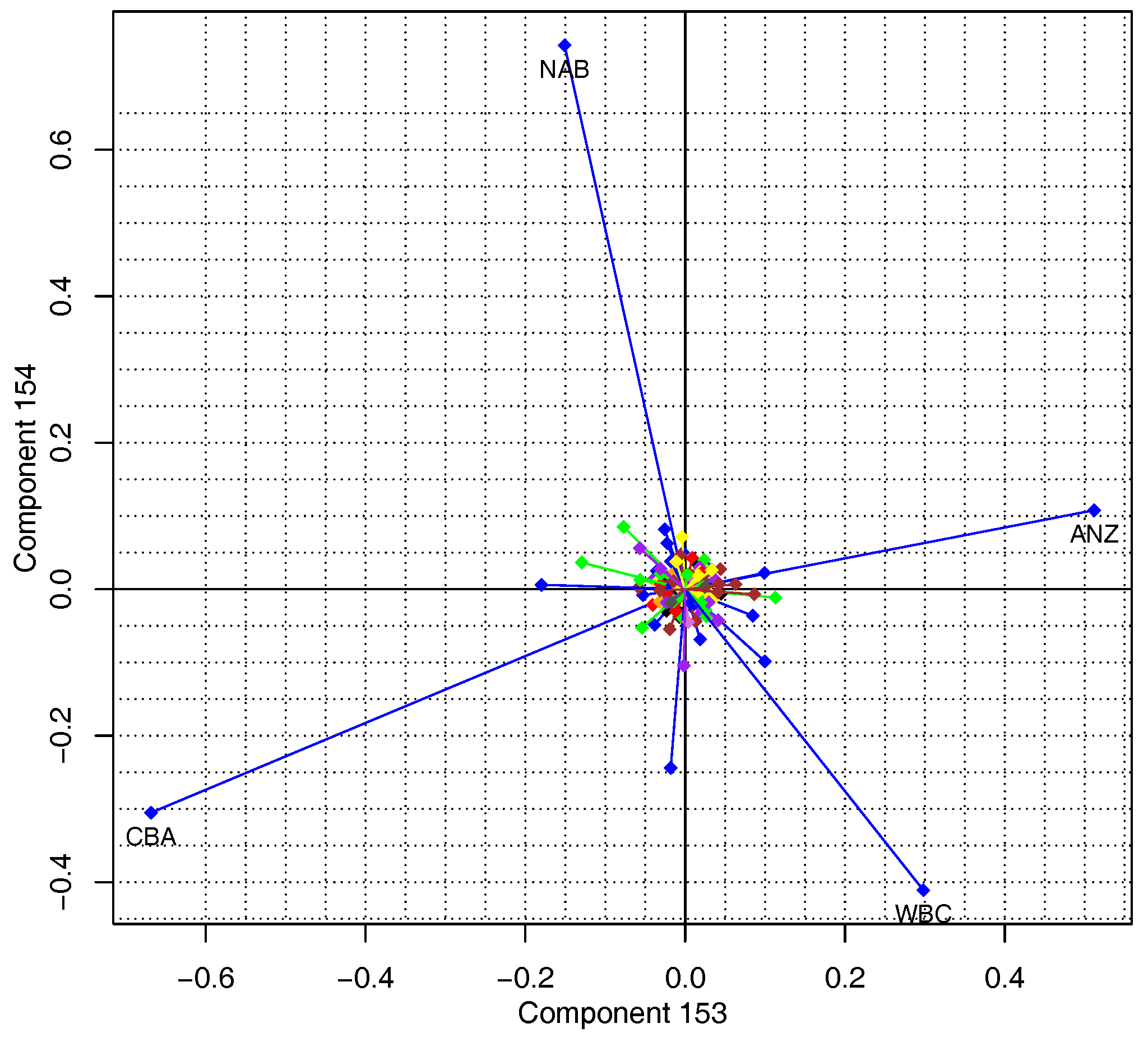
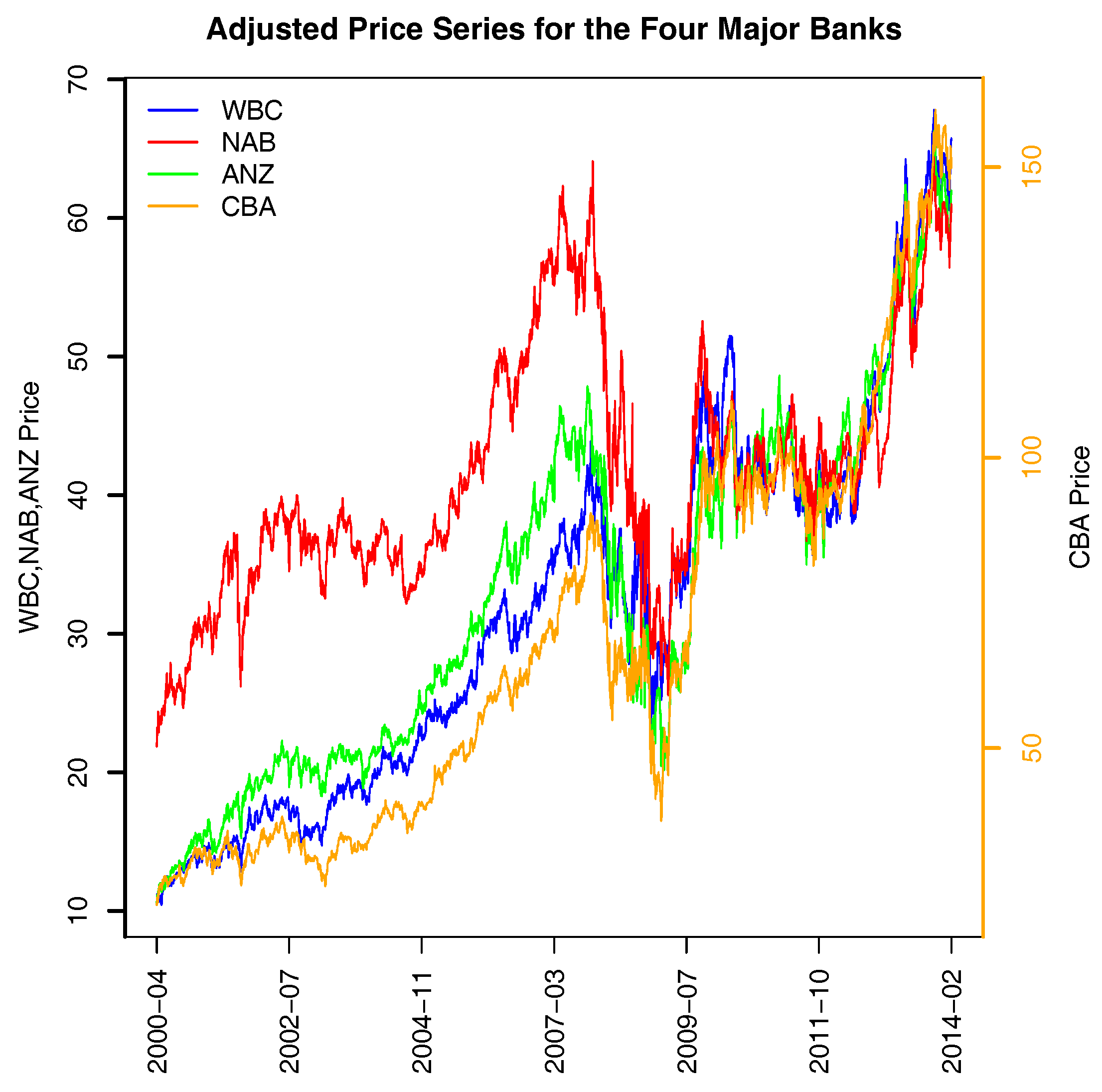
The last four components (PC 153–156,
Figure 2 and
Figure 3) all picked up the four largest banks in Australia, often referred to as the “four pillars”; their ticker symbols are ANZ, CBA, NAB, and WBC. The strong relationships in price (and consequently returns) are easily seen in
Figure 7; their correlations are reported in
Table 3. To help in visualizing the price co-movement of the four largest banks, we used a different scale for CBA. Its dividend-adjusted price changed from
$20 in the beginning of our study period to approximately
$150 at the end of study period, while the other three banks had price levels that ranged from
$10 to
$70. Obviously, NAB was least correlated with others among the four banks. However, after the 2008 financial crisis, all four banks converged to move very similarly.
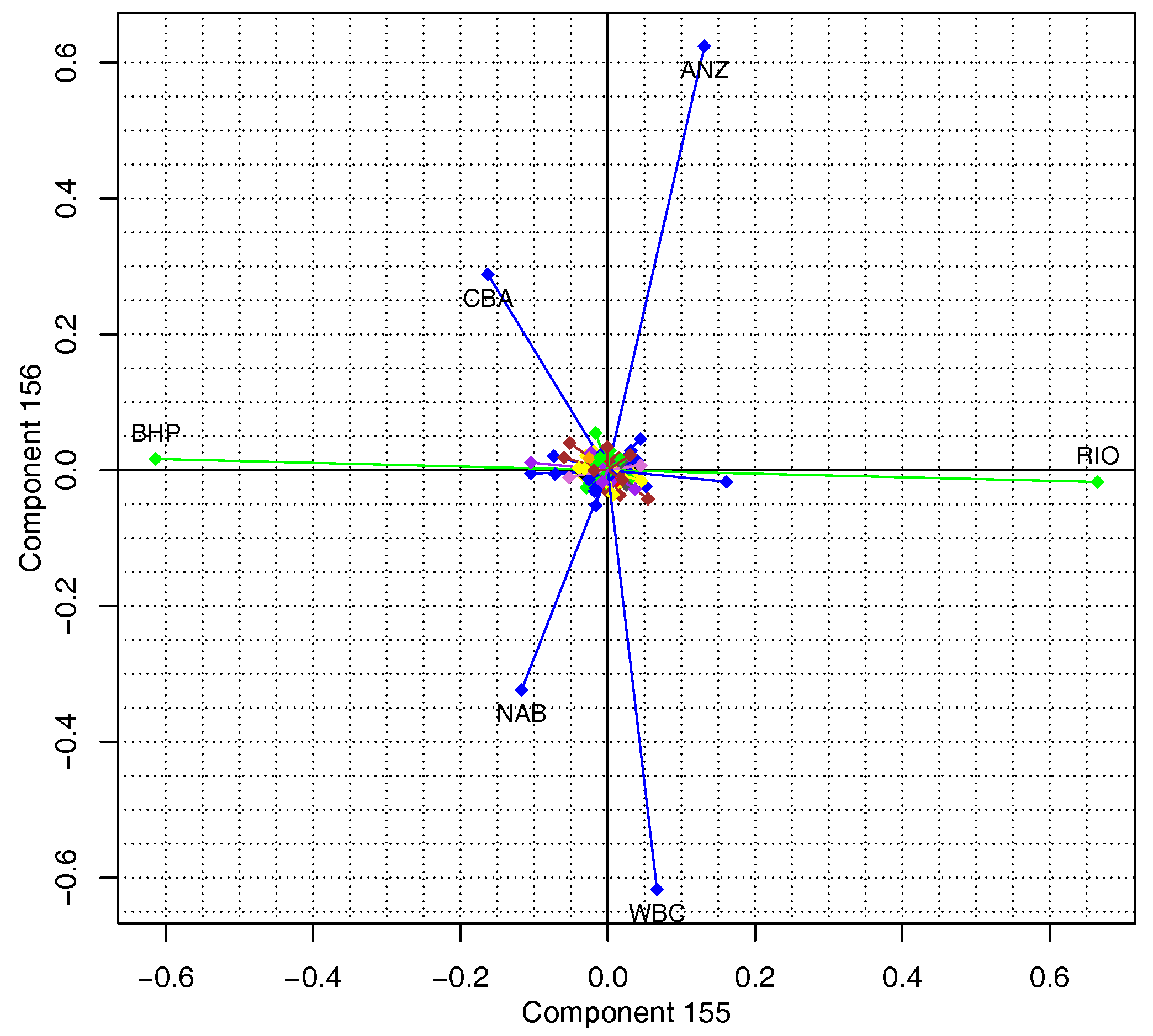
In the scatter plot of PC155 and PC156 (
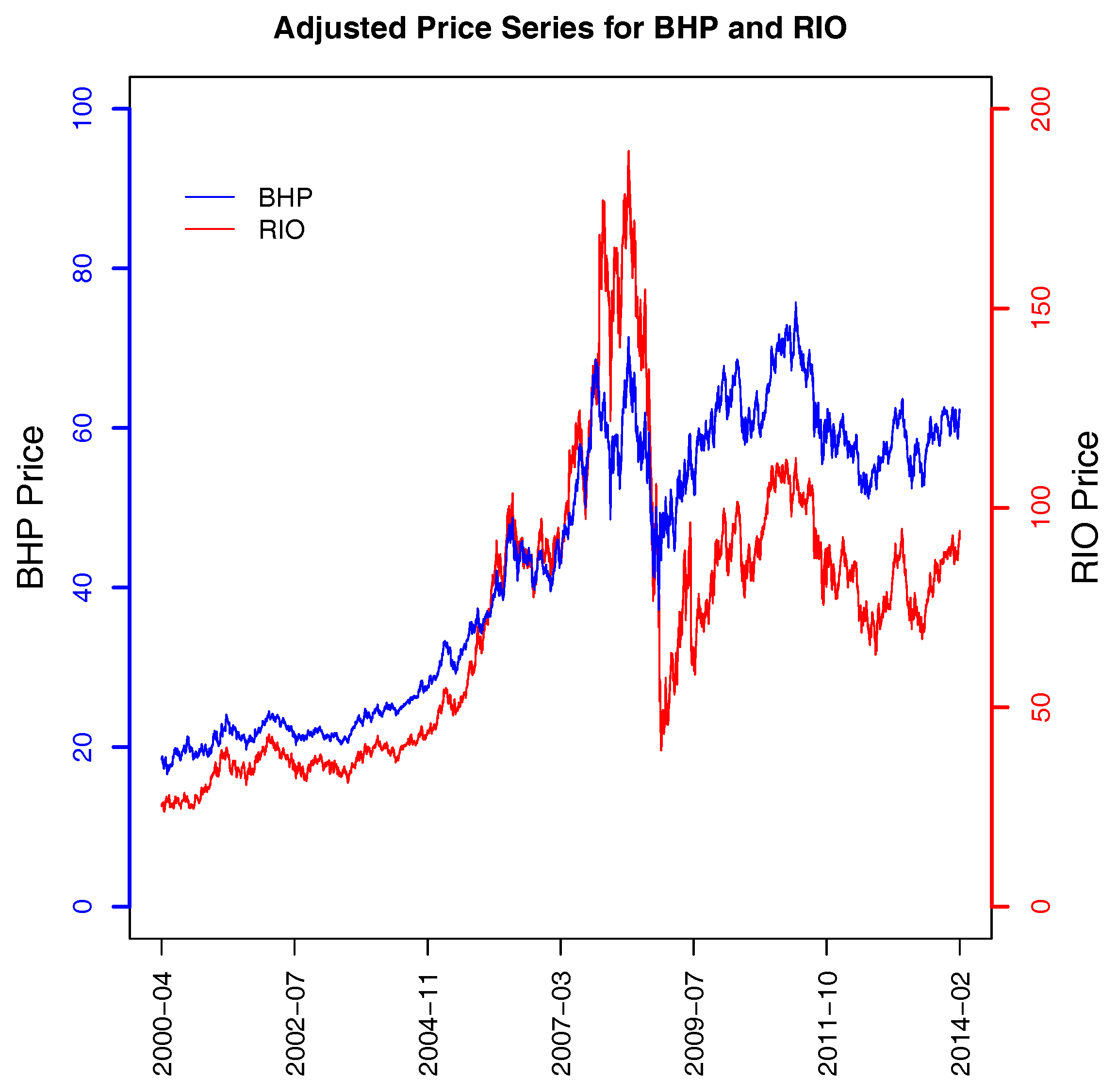
Figure 3), Australia’s two biggest mining firms were also picked up, BHP and Rio Tinto Ltd (RIO). They have a correlation of 0.77 over the sample period (see
Table 2). However, they are clearly different from the four banks because they have high loadings of opposite signs in PC155 and near-zero loadings in PC156. A plot of their price trajectories is presented in
Figure 8.
In
Figure 3 we have the best illustration of Equation (
6), because in PC155, BHP and RIO both have loadings whose absolute values are greater than 0.6. Combined, they account for somewhat over 72 percent of the variation, and (as discussed in
Section 1) because they are highly positively correlated (see
Table 2) their loadings have opposite signs, resulting in a component with only a small amount of variation.
At the beginning of our study period, the price of RIO was approximately 1.4 times that of BHP. Before the price collapsed in 2008, both stocks increased significantly; however, RIO increased more than BHP so that at the end of 2007, the price of RIO was about 2.5 times that of BHP. However, during the 2008 financial crisis, RIO also declined more than BHP. At the end of our study period, the price of RIO was about 1.5 times that of BHP, which is almost the same as it was at the beginning of our study period.
4. Conclusions
As indicated above, our argument is that if a financial analyst undertakes a PCA of a stock or other financial markets as part of their analysis, then they should examine the last few PCs, beginning with the final PC, because they may provide financially useful insights. In this sense, our results above differ from that of other authorities such as
Kim and Jeong (
2005), who reported that only the market component (PC1) and the subsequent group PCs contained useful information about the financial market analysed. Our results illustrate that further financially useful insights may be contained in the last few principal components because these may identify stocks with near-linear correlations. In the data we examined, the final six components were of this type. The potential existence of such components seems to have been overlooked in the finance literature, despite it being well known in the statistics and econometrics literatures.
The identification of highly correlated stocks (or other assets) can aid in the task of portfolio selection and management because it identifies pairs or groups of stocks which provide little benefit for diversification; holding one of the pair or group will provide most of the benefits of diversification while freeing funds to be invested in other assets. In the data analysed above, holding all four major banking stocks provides very little diversification to a portfolio because their prices all move in a nearly identical manner. It is not a given that such associations exist in any particular market. However, if they do exist, they can be easily detected and that information can be fed into the fund manager’s or other investor’s task of managing their portfolio well.
Even if, for example, a pair of highly correlated stocks are identified, there may be considerations other than diversification which mean that an investor may hold both.
Figure 4,
Figure 5, and
Figure 7 show that high correlations in price movements do not necessarily indicate that the returns over the longer term will be similar. Thus, depending on how much short-fall risk an investor is willing to take on, he or she may decide to hold more than one of the stocks identified in each of these groups.
In our analysis of the Australian Stock Market, we did not find any PCs which indicated the existence of outlier stocks in that market. However, it is possible that other markets may contain such stocks, so a market analyst should examine the PCs to see if evidence of such outliers can be found.
We applied the PCA to the full sample period to illustrate the value of the method. In practical applications, a fund manager would apply the PCA on a rolling window basis to a much shorter period of data. However, our results show that highly correlated stocks tend to remain highly correlated over long periods of time. Nevertheless, these correlations may break down, as is evident in
Figure 4. It is clear that the strong correlation between them evident in the first 11 years of the sample ceased to hold in about 2011.
While the method presented here was applied to a stock market, it is general and can be applied to any set of assets for which a correlation matrix can be generated.