Abstract
In this paper, a new form of weather derivative contract, namely the climatic zone-based growth degree-day (GDD) contract, is introduced. The objective is to increase the risk management efficiency in the agricultural sector of China and to reduce the model dimension of multi-regional temperature-based weather derivatives pricing. Since the proposed contract serves as a risk management tool for all of the cities in the same climatic zone, we compare the risk hedging power between the climatic zone-based and the city-based GDD contracts. As a result, we find that the differences between the two types of temperature-based weather contracts are maintained within a certain range.
JEL Classification:
C32, C61, G12, Q14
1. Introduction
Among all of the economic sectors that are influenced by weather uncertainties, agriculture is always the priority to be considered when it comes to managing weather risks in China (Turvey and Kong, 2010 [1], Heimfarth and Musshoff, 2011 [2], Ender and Zhang, 2015 [3]). The importance of the agriculture industry is recognized for three reasons. First, agriculture is one of the key sectors in terms of the contribution of the GDP in China. Second, 70% of the population of China live on farms (Heimfarth and Musshoff, 2011 [2]). Finally, agriculture in China is more sensitive to weather risks than in developed countries due to its extremely large rural population and underdevelopment.
Second to the USA, China has grown into one of the largest markets for agricultural insurance with its great potential demand (Mahul and Stutley, 2010 [4]). Among all of the agricultural risk hedging instruments discussed so far, weather insurance and derivatives are the most widely studied in the literature. Despite that weather derivatives have not been traded in China so far, the majority of the studies indicates that weather derivatives can reduce agricultural risks, especially those associated with yield variations (Sun et al., 2014 [5], Pelka et al., 2014 [6], Ender and Zhang, 2015 [3]).
Typically, the prices of weather derivative contracts are derived from the weather processes, which are highly localized. As a result, the prices should theoretically vary from place to place with the same contract specifications. According to the Chinese Government Network (2014) [7], there are 655 cities in mainland China, which makes it fairly time consuming to implement the contract valuation city by city. Further, increased transaction costs, low liquidity and inaccessible temperature data are attributed to the major disadvantage of the conventional city-based temperature contract. Göncü and Zong (2013) [8] propose to reduce the model dimension of cross-regional contract pricing in China with a basket option covering multiple cities.
This paper explores the practical value of temperature-based weather derivatives as a risk hedging tool in the agricultural sector of China. The motivation is to increase the risk hedging power of temperature-based derivative contracts by introducing new forms of temperature indices. Two new types of temperature-based weather derivative contracts, i.e., the average climatic zone-based (ACZB) growth-degree day (GDD) contract and the weighted climatic zone-based (WCZB) growth-degree day (GDD) contract, are introduced to address the problem of model dimension reduction. The advantages that come along with climatic zone-based GDD contracts are mainly demonstrated by cost reduction. To be specific, it is rather straightforward to determine the payoff of a contract written on GDD indices, which cuts the administration cost. Additionally, the underlying GDD index enables a unique way of modeling contract prices for all types of crops, which indicates a reduction in computational costs. Further, a lower level of the transaction cost is produced, as the climatic zone-based contract hedges yield risks for all of the regions in the same climatic zone with a single contract. Consequentially, such a contract is beneficial for a variety of sectors that are exposed to weather risks, such as agriculture-related industries, the banking sector, insurance companies, reinsurance, government, agricultural insurance schemes, etc.
Two main objectives are contained in this study. In the first place, we aim to reduce the model dimensions of cross-regional contract pricing by designing climatic zone-based GDD contracts with an identical price for all cities covered in one climatic zone. Model dimension reduction has four major advantages. First, it is time-saving for issuers as only one price is needed for climatic zone-based contracts for all cities in one climatic zone. Second, in addition to big cities, climatic zone-based contracts also cover rural regions where temperature data are not available. In this case, geographical basis risks that arise due to purchasing derivative contracts written on temperature indices of other locations can be reduced. Third, from the issuers’ point of view, with more regions covered by one contract, climatic zone-based contracts have lower transaction costs and higher profits, as less different contracts, but with a higher volume, exist. Last, replacing individual local weather contracts with climatic zone-based contracts increases the liquidity of the market. The second objective of the paper is to investigate the hedging efficiency of the climatic zone-based GDD contracts in comparison to the city-based ones, in terms of reducing yield-variation risks.
There are three key contributions of this study. First, we define two new contracts for spatial aggregation, namely the ACZB GDD contracts and the WCZB GDD contracts. Second, we provide a complete pricing scheme to evaluate the GDD contract, which takes into account the calculation of the contract tick size. Third, we analyze the hedging efficiency of those new contracts by applying aggregated contract prices and local yields. To the best of our knowledge, this paper is the first to introduce climatic zone-based GDD contracts and that applies them to real temperature and yield data of Chinese cities. The results provide evidence that climatic zone-based GDD contracts are capable of replacing city-based GDD contracts, as their risk-reducing performance is similar or even better.
The remaining part of the paper is organized as follows. In the next section, the data used for the empirical study are presented. In the third section, we explain the models and introduce the two new climatic zone-based GDD contracts. Section 4 gives and discusses the modeling results and the findings of the efficiency tests applied to eleven Chinese cities. The last section concludes the paper.
2. Data Overview
In this study, we apply the Standard of Climatic Zone Partition of China, which is a typical partition method used by Chinese architects for the purpose of distinguishing construction standards among regions with different climate characteristics.
As is displayed in Figure 1, the standard divides the mainland of China into seven climatic zones according to the climatic patterns of different regions. We are more interested in the three coastal Climatic Zones I, II and III, as they constitute the eastern part of China, which is more economically developed and having a higher chance of issuing weather derivative contracts.
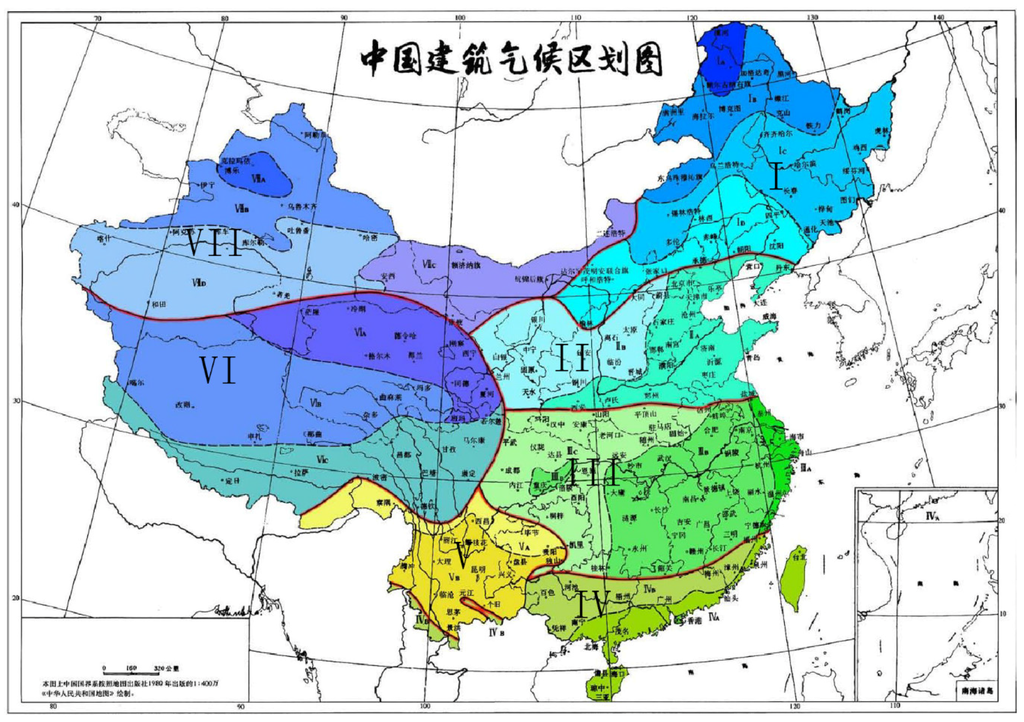
Figure 1.
Standard of Climatic Zone Partition of China (resource: www.baidu.com).
Eleven representative cities are selected, which cover Harbin and Changchun from Climatic Zone I; Beijing, Shijiazhuang, Ji’nan and Zhengzhou from Climatic Zone II; Nanjing, Hefei, Wuhan, Hangzhou and Nanchang from Climatic Zone III. Apart from the national capital Beijing, the rest of the representative cities in this study are chosen as they are the capital cities of the ten most agricultural productive provinces. This approach ensures that the locations of representative cities are distributed evenly and that the results are relevant for the highest possible number of inhabitants.
In order to calculate GDD indices and option prices, thirty years (from January 1984 to December 2013) of daily average temperature data collected from the China Meteorological Data Sharing Service System are used. Additionally, twenty-four years (from January 1984 to December 2007) of annual yield data collected from the China Agricultural Data Sharing System are used to conduct the efficiency tests. Note that we apply the yield data rather than the production data, as production also depends on the crop acreage, which changes from year to year.
3. Methodology
In order to test the efficiency of climatic zone-based GDD contracts for Chinese farmers, two questions need to be answered beforehand. First, a modeling method must be selected to evaluate temperature index contracts. The second question is whether climatic zone-based contracts are theoretically and practically appropriate. This section aims to give answers to both questions. Further, we provide a brief review of the continuous-autoregressive (CAR) model (Benth et al., 2007 [9]) and present a method to determine the optimal tick size for temperature-based contracts. Finally, we explain the three test criteria of the efficiency tests.
3.1. Temperature Modeling and Derivative Pricing
There is a broad range of studies that is dedicated to researching an accurate approach for modeling temperature-based derivatives. One of the earliest methods is the burn analysis, which calculates the price relying on historical payoff data. Dornier and Queruel (2000) [10] used for the first time a continuous-time Ornstein-Uhlenbeck (OU) process to model the temperature evolution. The OU process allows the simulation of the mean reverting random walk of the temperature dynamics. The first application of a stochastic model to real temperature data was presented by Alaton et al. (2002) [11]. In order to calibrate the model to daily temperature, Alaton et al. (2002) [11] included a sine function in the OU process. The temperature volatility is assumed to be monthly constant. Based on Alaton et al.’s study (2002) [11], Benth et al. (2007) [9] employed a continuous-autoregressive (CAR) process to fit the temperature evolution. Further, Benth et al. (2007) [9] modeled the temperature volatility with truncated Fourier series, which enables functional modeling of the volatility process. In addition to stochastic temperature models, Schiller et al. (2012) [12] introduced a spline model and applied it to daily temperature data of the USA.
In this study, the CAR model (Benth et al., 2007 [9]) is applied to fit the temperature oscillations, as it is shown to be more suitable to model Chinese temperature data, in comparison with other existing temperature models (Zong and Ender, 2014 [13], and Zong and Ender, 2016 [14]). To give details, the CAR model models the temperature dynamics as the summation of a seasonal function and a CAR process. To be specific, temperature on day can be expressed as:
is the function that captures the seasonal trend of the temperature process. It follows:
where denotes the starting value of the sine function, denotes the rate of global warming and and are respectively the scale parameter and the translation parameter of the sine function.
According to Benth et al. (2007) [9], expresses the coordinate of the vector , which is a vectorial OU process. Thus, the explicit solution of in for follows:
where and , is the unit vector in and denotes the Brownian motion. The parameter A is the mean-reverting matrix given by:
where are assumed to be constants. According to Benth et al. (2007) [9], the optimal order of the CAR process equals three.
Further, Benth et al. (2007) [9] modeled the volatility with a truncated Fourier series, which is expressed as:
where are the parameters of the fourth ordered truncated Fourier series.
In order to estimate the model parameters, namely, in Equation (2), in Equation (4) and in Equation (5), we implement the regression using the ordinary least square method.
Hence, given the threshold temperature and contract period , the price of a GDD future contract at time approximately follows (Benth et al., 2007 [9]):
where:
Note that is the cumulative distribution function of a standard normal distribution.
Consequently, the price of a GDD option contract with strike price K can be obtained from the following formula:
3.2. Climatic Zone-Based GDD Contracts
Weather derivatives can eliminate adverse selection and moral hazard as the valuation of their payoffs is based on an objective weather-index, which is impossible to manipulate. However, there is another type of risk that is inherent in weather derivatives: geographical basis risk should be considered with care. Practically, it is unlikely and extremely costly to cover all regions when weather derivatives are issued. In reality, weather contracts are written on weather indices of one specific location where the transaction takes place. Therefore, for those investors who are away from the trading spot, it is inevitable to be exposed to basis risk if they simply purchase weather contracts from the trading spot. According to the literature, there are at least two solutions for this problem. The first approach is to hedge basis risk via basis derivatives (Brockett et al., 2007 [15]). This means that the investor buys a second option based on the observed differences of the weather index between the location of interest and the trading spot. However, from the buyers’ point of view, transaction costs might be high to purchase a second derivative when the market is already illiquid. The second approach is to add risk premiums that reflect geographical basis risk. This approach is proposed by Härdle and Osipenko (2012) [16], who conducted an empirical analysis of temperature and price data from nine European cities. However, this method cannot be adopted for China as there are no real market data that allow the computation of the market price of risk. Woodard and Garcia (2008) [17] compared the basis risk of weather contracts on the individual level and on the spatially-aggregated level, using the root mean squared loss (RMSL) and the expected shortfall (ES). Further, Okhrin et al. (2013) [18] investigated the risk pooling efficiency of GDD contracts with buffer loads. Both studies indicated that spatial aggregation can reduce basis risk embedded in weather derivative contracts. Therefore, climatic zone-based contracts should theoretically prevail over city-based contracts in terms of basis risk, because it involves a greater level of aggregation. Albeit that mixed-indices contracts are suggested in the literature (Vedenov and Barnett, 2004 [19]), the hedging power of such contracts is revealed to be lower in comparison to combinations of several simple index contracts (Pelka and Musshoff, 2013 [20]).
Different from Woodard and Garcia (2008) [17] and Okhrin et al. (2013) [18], we compare climatic zone-based GDD contracts with city-based GDD contracts in terms of risk hedging efficiency. To begin with, we select a certain number of representative cities that are distributed evenly in the climatic zone. We assume that given the optimal growing temperature of a crop, , the temperature deviations above and below have the same effects on crop growth. Therefore, given the contract period [], the GDD index of representative city i and crop j is expressed as:
where is the daily observed temperatureand denotes the optimal growing temperature of crop j. Note that in our empirical tests, we proposed a so-called correlation-adjusted GDD index, which considered three different forms of deviations from the optimal growth temperature, namely the absolute value, the positive skewness and the negative skewness. The GDD of a given city was defined by the type of deviation that maximized the correlation between the corresponding index and the city’s crop yield. Efficiency tests were conducted based on the correlation-adjusted GDD. We found that it hardly provided a higher level of risk-reducing efficiency when the positive and negative skewness were considered. Therefore, we employed the absolute value of the deviations from the optimal growth temperature as the underlying GDD index in this paper.
Let the average climatic zone-based (ACZB) GDD index be equal to the average value of the GDD indices of the representative cities in one climatic zone. Thus, the ACZB GDD of crop j is given by:
Different from the averaged GDD, the weighted climatic zone-based (WCZB) GDD weights the individual GDD indices of the representative cities by their crop yields, which follows:
where is the proportion of the crop yield of representative city i over the total yield of all of the representative cities in the climatic zone. Hence, we have:
where denotes the yield of crop j in city i during the contract period. The other two methods of calculating weights, respectively obtained from crop acreage and the maximized correlation between the climatic zone-based index and the total crop yield, were applied and tested empirically. From the results, we found that both of them failed to provide better results in terms of efficiency and stability, compared to the way we defined weights in this paper.
3.3. GDD Contract Optimization
In this part, we propose a method to determine the optimal tick size for GDD contracts under the framework of Vedenov and Barnett’s work (2004) [19]. An optimized tick size is a crucial factor in terms of contract design and contributes directly to the risk hedging power of the contract. The overall idea of the optimization is to find a coefficient that minimizes the aggregated semi-variance of the loss (Markowitz, 1991 [21]; Vedenov and Barnett, 2004 [19]).
By first assuming that the annual yield series attains an exponential growth, the annual yield can be written as:
where is the white noise; and is the linear time trending the logarithm of the annual yield , which is given by:
Thus, the annual time-detrended yield can be obtained by:
where denotes the initial time.
Therefore, the optimal tick size of a GDD contract can be solved by minimizing the aggregated semi-variance of the loss:
where is the option price under the CAR model (Benth et al., 2007) [9], is the corresponding payoff and denotes the long-term average yield of a crop.
3.4. Efficiency Comparison
In order to compare the efficiency of city-based and the climatic zone-based GDD contracts in terms of risk reduction for farm households, we analyze the annual revenues of a certain crop with and without the considered GDD contracts. In the case of city-based contracts, we consider two scenarios. The first one (Case 1) is an ideal situation where weather contract transactions take place in all of the representative cities, while the second situation (Case 2) is more practical, which allows only one trading spot in each climatic zone. In Case 2, the trading spots are Changchun (Climatic Zone I), Shijiazhuang (Climatic Zone II) and Hefei (Climatic Zone III). The trading spots are selected, because they are located in the center of the other representative cities in their climatic zone.
Note that in this study, only European option contracts are considered. According to Vedenov and Barnett (2004) [19], the revenue without the GDD contract equals the gross income of selling the commodity, which follows:
while the revenue with the GDD contract is given by:
where p is the commodity price of the corresponding crop and is the time-detrended yield. The reason why is applied to calculate the revenue is that it eliminates any time-related trends in the time series of yield data; thus ideally, weather is the only factor that causes yield changes.
We start off with comparing revenue distributions with and without GDD contracts. Histograms, quantile-quantile (Q-Q) plots and Kolmogorov-Smirnov tests are employed in our study to analyze the revenue distributions. Note that in the case of climatic zone-based contracts, the yield in Equations (20) and (21) stays at the city level, as the objective is to compare the hedging power towards local weather risks.
Next, we apply three test criteria used by Vedenov and Barnett (2004) [19] in order to gain implications on the efficiency of weather contracts. Let denote the distribution of the revenue. The definitions and the mathematical expressions of the test criteria are given below:
- The mean root square loss (MRSL):
- The value-at-risk (VaR):
- The certainty-equivalent revenues (CERs):
The first criterion, the MRSL, measures the semi-variance of the revenue distribution. A smaller MRSL indicates a lower level of revenue variation, thus less pronounced yield risks. The VaR is an inverse function of the cumulative density function of the return distribution, which measures the value of return at a given risk level and over a defined time horizon. By computing the VaR for different confidence levels , one can gain a general understanding of the return distribution. Last, the CERs compute expected revenues with a given level of risk aversion. Both the VaR and the CERs assess the risk hedging power of a weather contract in a different way than MRSL. For VaR and CERs a smaller value refers to a lower degree of risk exposure.
Note that in the case of CERs, we estimate the risk aversion level (Babcock et al., 1993 [22]) by the following equation:
We compute the value of in Equation (24) with different risk premiums , i.e., 0%, 5% and 10%. However, we find that for yield data of Chinese cities, the results across cities and risk premiums exclusively tend to 1. This result indicates an extremely high level of risk aversion of Chinese farm households, which agrees with the literature. Under this condition, the values of the CERs of a given city should be proportional to the corresponding values of the risk premiums.
4. Results and Discussion
4.1. Climatic Zone-Based Contracts Pricing
The three climatic zones covered in the study, i.e., Climatic Zones I, II and III, comprise the eastern half of China from the north to the south. Consequently, Climatic Zone I has colder winters than Climatic Zones II and III, while Climatic Zone III has warmer summers. Table 1 gives the contract specifications of the European call options that are applied in this study. As was described in Section 3, the threshold temperature is selected to be the optimal growth temperature of the crops, and the contract period is the growing phase. Since there is no existing transaction history of weather derivatives in China, the strike levels are approximated and specified by the authors in Table 1.

Table 1.
Growth degree-day (GDD) call option contract specifications (year: 2007).
The call option prices using both the ACZB GDD and WCZB GDD are presented in Table 2. As the benchmark for the comparison, we provide the option prices of the city-based contracts for each city with the same contract specifications. As stated in Table 1, the crops for the GDD indices are respectively corn (Climatic Zone I), wheat (Climatic Zone II) and rice (Climatic Zone III). We choose these three crops, because they are the most productive crops locally.

Table 2.
GDD call option prices of city-based contracts, average climatic zone-based (ACZB) contracts and weighted climatic zone-based (WCZB) contracts (year: 2007; unit: RMB).
Table 2 lists the estimated GDD option prices using the CAR model (Benth et al., 2007 [9]). For climatic zone-based contracts, unique prices are computed for all cities in the same climatic zone with respect to the definition in Equations (13) and (14). The observations from Table 3 are discussed in the following.

Table 3.
Estimated tick sizes of city-based contracts, ACZB contracts and WCZB contracts (year: 2007).
First, the ACZB and the WCZB methods generate similar option prices for the climatic zone-based contracts. This finding indicates a similarity between the distributions of the average GDD and the weighted GDD indices.
Second, as is shown in Table 2, the largest price difference between the ACZB contracts and the WCZB contracts (19.06 RMB) takes place in Climatic Zone III, in which the GDDs of five representative cities are included. By contrast, in Climatic Zones I (two representative cities) and II (four representative cities), the price differences between the ACZB contracts and the WCZB contracts are respectively 7.35 RMB and 0.02 RMB. Therefore, we infer that the similarity between the distributions of the average GDDs and the weighted GDDs cannot be enhanced by simply increasing the number of representative cities included in climatic zone-based contracts.
Last, the price of a climatic zone-based contract can possibly stay outside the interval of the contract prices of its representative cities. For example, both the ACZB and the WCZB contract prices of Climatic Zone II are below 461.55 RMB, which is the lowest city-based contract price in the climatic zone. We infer that this is caused by the change of the GDD distribution.
With the determined contract prices from the CAR model (Benth et al., 2007 [9]), Table 3 gives the estimated optimal tick sizes according to Equation (19). We notice that in the same climatic zone, tick sizes can vary drastically from city to city. However, for different types of contracts for the same city, the tick sizes stay comparatively close to each other. Especially for the ACZB and WCZB contracts, the differences of the tick sizes are very small.
4.2. Efficiency Comparison: Climatic Zone-Based Contracts and City-Based Contracts
4.2.1. Revenue Distributions
Based on the Mann-Whitney U-test, Table 4 gives a comparison between the revenue distributions without the GDD contract and with different types of GDD contracts for each city. The objective is to examine the impact of GDD contracts on changing the revenue distributions. According to Table 4, the null hypothesis that the revenues without and with GDD contracts follow the same distribution is rejected at the significance level of 5% for all contracts and all locations.

Table 4.
Comparison of revenue distributions based on the Mann-Whitney U-test at the significance level of 5%.
We further compare the revenue distributions with and without GDD contracts using histograms and Q-Q plots. Figure 2 gives the histograms of the revenue distributions. Only one city from each climatic zone is selected to be shown in Figure 2, because the remaining cities show similar histograms. Based on Figure 2, we compare the annual revenue distributions without a GDD contract with respectively those with a city-based contract (multiple trading spots in one climatic zone (Case 1) and identical trading spot in one climatic zone (Case 2)), with an ACZB contract and with a WCZB contract.
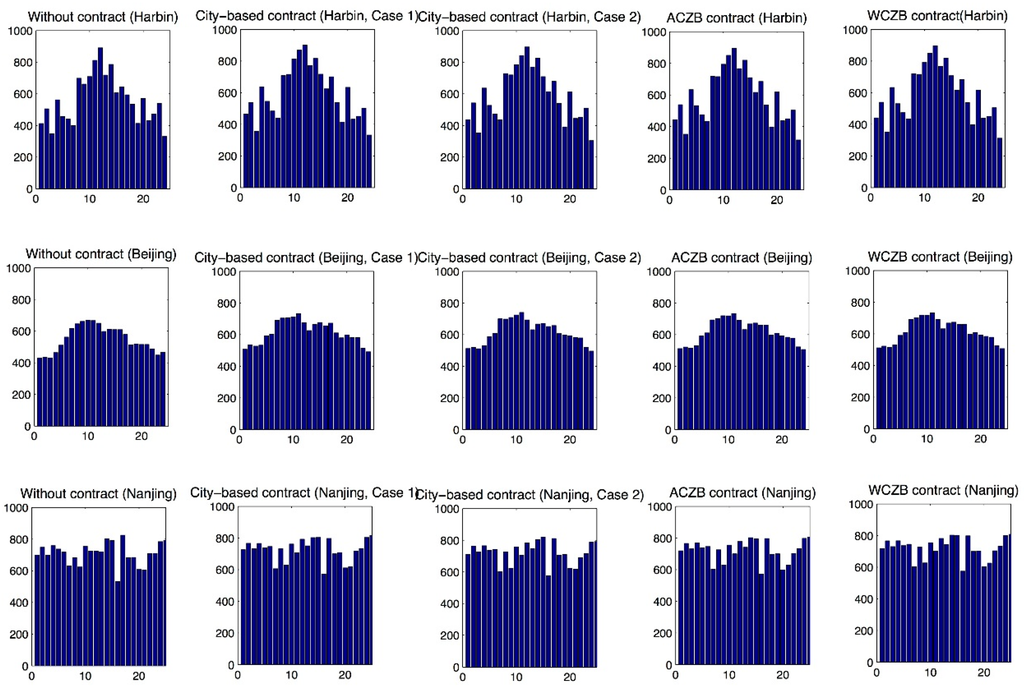
Figure 2.
Histograms: revenue distributions without GDD contracts, with the city-based contracts, with the ACZB contracts and with the WCZB contracts.
From Figure 2, we see that the revenue distributions of Harbin and Beijing are generally symmetric, while the distributions of Nanjing are more uniformly distributed. The effects of holding the GDD contract on the revenue distributions are observable in the histograms. This is especially the case for Harbin and Beijing, where the revenue distributions including GDD contracts have a smaller kurtosis, which is indicated by a flatter peak. As the distributions with city-based contracts and climatic zone-based contracts have similar shapes, we infer that their risk reducing performances are comparable.
In Figure 3, we present the Q-Q plots of the revenue distributions. The X-axis gives the quantiles of the revenue distribution without GDD contracts, while the Y-axis gives the revenue distribution quantiles with GDD contracts.
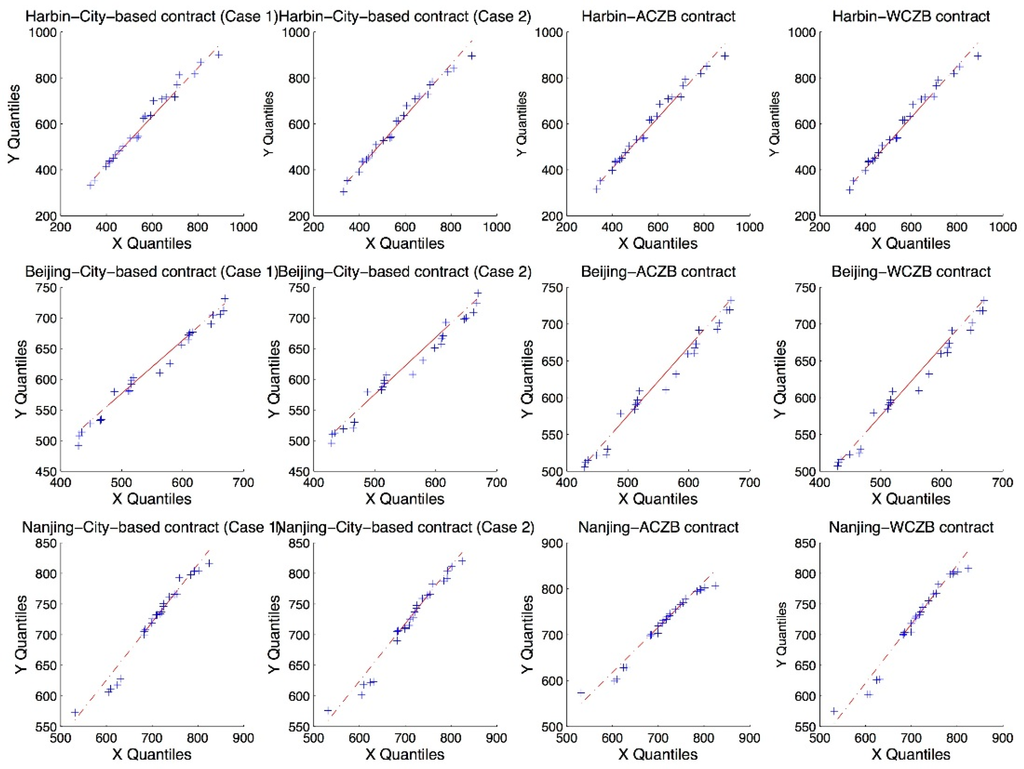
Figure 3.
Q-Q plots: revenue distributions without GDD contracts, with the city-based contracts, with the ACZB contracts and with the WCZB contracts.
From the Q-Q plots, we conclude that the revenue distributions of Harbin and Nanjing are more right-skewed with GDD contracts while the revenue distributions of Beijing are more likely to be left-skewed with GDD contracts.
Although we cannot assess the hedging efficiency directly from the distribution diagrams, the meaning behind them is of great importance, as one of our objectives is to compare the impacts of city-based contracts and of climatic zone-based contracts on changing the revenue distributions. According to the histograms and Q-Q plots, the differences between city-based contracts and climatic zone-based contracts are minor.
Thus, we infer that climatic zone-based contracts are as appropriate as city-based contracts for Chinese cities.
4.2.2. The MRSLs
Table 5 gives a comparison between the MRSL changes without any GDD contract and with respectively the city-based GDD contracts (Cases 1 and 2), the ACZB contracts and the WCZB contracts. As MRSL measures the semi-variance of the loss distribution, a smaller MRSL indicates a less risky setting. Three observations are made from Table 5.

Table 5.
Efficiency comparison among city-based GDD contracts, ACZB contracts and WCZB contracts: mean root square loss (MRSL).
First, GDD contracts can be considered as an effective risk management tool with the aim of hedging yield variation risks for Chinese farm households. As is shown in Table 5, MRSLs are exclusively reduced by holding a GDD contract in all of the cities considered. This observation agrees with the results of Ender and Zhang’s study (2015) [3] of wheat and rice GDD contracts in Beijing and Shanghai, as well as the results of Sun et al.’s study (2014) [5] of weather derivatives in northwestern China. Second, the climatic zone-based contracts outperform the city-based contracts when there is only one trading spot in each climatic zone. This indicates a promising reduction of geographical basis risk provided by climatic zone-based contracts. Further, in Case 2 when all of the representative cities have the authority to issue weather contracts, climatic zone-based GDD contracts are still more effective than city-based GDD contracts in some regions. For instance, in Nanchang, with a climatic zone-based contract, the MRSLs are reduced by respectively 5% (ACZB contracts) and 6% (WCZB contracts) on the basis of the MRSL from the city-based contract. In fact, seven out of the eleven cities display a smaller MRSL with the climatic zone-based contract. Third, weather contracts written on weighted GDD indices and on averaged GDD indices show very similar performances in smoothing return fluctuations.
4.2.3. The VaRs
Figure 4 shows the values of VaRs under five situations, respectively without contract, with city-based contract (Case 1), with city-based contract (Case 2), with ACZB contract and WCZB contract (left to right), for each city.
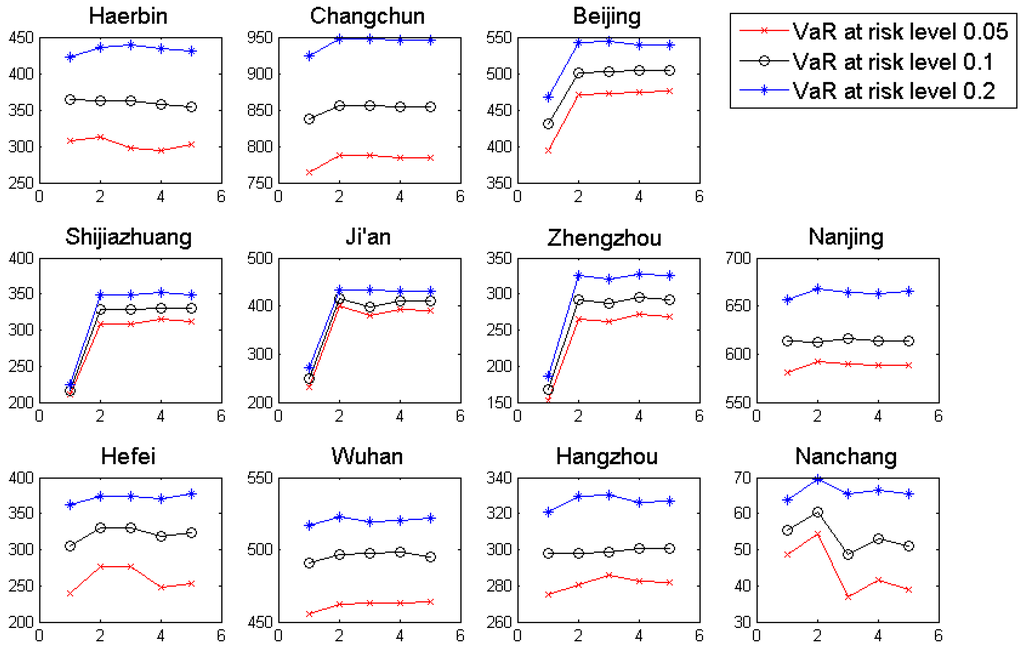
Figure 4.
Comparison of VaRs that are without contract, with city-based contract (Case 1), with city-based contract (Case 5), with ACZB contract and with WCZB contract (left to right).
According to Figure 4, apart from the city Harbin at risk level 10%, there always exists at least one GDD contract that can show a VaR with a larger value than the VaR without any GDD contract. This observation acknowledges the risk hedging power of GDD contracts. Similar to the results of the MRSL, city-based contracts generally perform better when there are multiple trading spots in the climatic zone. In Case 1 of city-based contracts, there are only two cities showing negative impacts on the VaRs at risk level 10%, while in Case 2, the number of cities is three.
Further, different from the overwhelming superiority shown in the MRSL measure, climatic zone-based contracts show a slightly larger chance of failing in increasing the VaR compared with city-based contracts in Case 1. For city-based contracts in Case 2, three cities show negative impacts both at risk levels of 5% and 10% when climatic zone-based contracts are applied.
Moreover, at the risk level of 5%, the number of cities for which climatic zone-based contracts produce higher VaRs than city-based contracts is five (in both Cases 1 and 2). At the risk level of 10%, the number increases to six (both Cases 1 and 2). From these results, the better contract specification cannot be uniquely determined. Generally, the performances of GDD contracts are highly related to the risk-aversion level. No further outstanding difference between the ACZB contracts and the WCZB contracts for the VaR measure can be observed.
4.2.4. The CERs
In Table 6, the CERs with the risk premium of 5% are given.

Table 6.
Efficiency comparison among city-based GDD contracts, ACZB contracts and WCZB contracts: certainty-equivalent revenue (CER).
The results of the CER measure support the results in the previous sections. By holding city-based contracts and climatic zone-based contracts, the revenue distributions tend to obtain a higher level of CER. Similar observations are made in Ender and Zhang’s study (2015) [3]. The percentage of changes varies from 1% to 72%. Further, climatic zone-based contracts show better performances on increasing CERs than city-based contracts. To be specific, in Case 1 of city-based contracts, which allows all of the representative cities to have weather contract transactions, eight out of eleven cites have higher or equal CERs when climatic zone-based contracts are applied. While in Case 2, which assumes that there is only one contract trading spot in each climatic zone, the number of cities with higher or equal CERs from climatic zone-based contracts increases to nine. Again, the behaviors of ACZB contracts and WCZB contracts continue to show great similarities for CERs.
5. Conclusions
In this paper, we introduce two climatic zone-based indices for temperature-based derivative contracts, i.e., the ACZB GDD and the WCZB GDD contracts. The objectives are to reduce the model dimension of temperature-based derivative pricing in China and to analyze the risk hedging power of climatic zone-based contracts for Chinese farm households.
In addition to Ender and Zhang’s (2015) [3] and Sun et al.’s (2014) [5] studies, which both confirm that city-based temperature indices are efficient hedging tools against yield-variation risks, we conclude that both climatic zone-based GDD contracts and city-based GDD contracts manage to reduce risks related to crop productivity in this study. In terms of cross-regional temperature-based derivatives modeling, this study suggests the possibility of contract spatial aggregation without influencing its risk hedging power, which is basically in line with Göncü and Zong’s study (2013) [8]. With respect to the results, changes of the GDD distributions are observed after transforming city-based GDD indices into climatic zone-based GDD indices. Regarding the results of efficiency tests, we infer that climatic zone-based GDD contracts have the same power to reduce fluctuations of the farmers’ income as city-based contracts. In some cases as for MRSLs and CERs, climatic zone-based GDD contracts even dominate. For the VaRs, the performances of climatic zone-based and city-based contracts are alike, with half of the cities having higher VaRs in each case. Furthermore, the average GDD and the weighted GDD generate similar contract prices on climatic zone levels, which leads to similar effects on risk reduction.
In the practical application, our study suggests that deliberately-used climatic zone-based GDD contracts can be a more efficient instrument for agricultural risk management due to the feature of cost reduction. Specifically, the ACZB GDD index is recommended as more suitable for agricultural risk management in China. By launching derivative contracts written on the ACZB GDD index, cities in the same climatic zone can use a common contract, which shares a unique price, to achieve the purpose of hedging weather risks. Such a means of transaction increases the efficiency, both in terms of modeling and market management. Additionally, no crop yield data are required to calculate ACZB indices, which is different from WCZB indices. Thus, the pricing procedure is simplified.
For future research, we intend to perform a study focused on GDD distributions. As the CAR model (Benth et al., 2007) [9] prices temperature-based derivatives with the assumption that the underlying indices are normally distributed, we assume that with a deeper understanding of the GDD distributions, more precise models for Chinese climatic zone-based GDD contracts can be derived. Additionally, a weather-yield regression model is recommended to be deduced and applied in order to conduct out-of-sample efficiency tests.
Author Contributions
Lu Zong and Manuela Ender conceived of and designed the experiments. Lu Zong performed the experiments and analyzed the data. Lu Zong and Manuela Ender wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- C.G. Turvey, and R. Kong. “Weather Risk and the Viability of Weather Insurance in China’s Gansu, Shaanxi, and Henan Provinces.” China Agric. Econ. Rev. 1 (2010): 5–24. [Google Scholar] [CrossRef]
- L. Heimfarth, and O. Musshoff. “Weather index-based Insurances for Farmers in the North China Plain: An Analysis of Risk Reduction Potential and basis Risk.” Agric. Finance Rev. 71 (2011): 218–239. [Google Scholar] [CrossRef]
- M. Ender, and R.Y. Zhang. “Efficiency of Weather Derivatives for Chinese Agriculture Industry.” Chin. Agric. Econ. Rev. 7 (2015): 102–121. [Google Scholar] [CrossRef]
- O. Mahul, and C.J. Stutley. Government Support to Agricultural Insurance: Challenges and Options for Developing Countries. Washington, DC, USA: The World Bank Publications, 2010. [Google Scholar]
- B. Sun, C. Guo, and G.C. van Kooten. “Hedging Weather Risk for Corn Production in Northestern China.” Agric. Finance Rev. 74 (2014): 555–572. [Google Scholar] [CrossRef]
- N. Pelka, O. Musshoff, and R. Finger. “Hedging Effectiveness of Weather Index-based Insurance in China.” China Agric. Econ. Rev. 6 (2014): 212–228. [Google Scholar] [CrossRef]
- Chinese Government Network (2014). “Administrative Area of the People’s Republic of China. ” Available online: http://www.gov.cn/test/2009-04/17/content_1288060.htm (accessed on 12 May 2014).
- A. Göncü, and L. Zong. “Pricing Futures and Options on a Basket of Temperature Indices.” Rev. Futures Mark. 21 (2013): 151–171. [Google Scholar]
- F.E. Benth, J. SaltyteBenth, and S. Koekebakker. “Putting a Price on Temperature.” Scand. J. Stat. 34 (2007): 746–767. [Google Scholar] [CrossRef]
- F. Dornier, and M. Queruel. “Caution to the Wind.” In Energy and Power Risk Management. London, UK: Palgrave Macmillan, 2000, pp. 30–32. [Google Scholar]
- P. Alaton, B. Djehiche, and D. Stillberger. “On Modeling and Pricing Weather Derivatives.” Appl. Math. Finance. 9 (2002): 1–20. [Google Scholar] [CrossRef]
- F. Schiller, G. Seidler, and M. Wimmer. “Temperature Models for Pricing Weather Derivatives.” Quant. Finance 12 (2012): 489–500. [Google Scholar] [CrossRef]
- L. Zong, and M. Ender. “Model Comparison for Temperature-based Weather Derivatives in Mainland China.” Emerg. Mark. Financ. Trade 50 (2014): 68–86. [Google Scholar]
- L. Zong, and M. Ender. “Comparison of Stochastic and Spline Models for Temperature-based Derivatives in China.” Pac. Econ. Rev., 2016. [Google Scholar] [CrossRef]
- P.L. Brockett, L.L. Golden, C.C. Yang, and H. Zou. “Addressing Credit and Basis Risk Arising From Hedging Weather-related Risk with Weather Derivatives.” Available online: http://citeseerx.ist.psu.edu/viewdoc/citations;jsessionid=E6E8418AE855562ABF0066485D9A95C4?doi=10.1.1.514.1179 (accessed on 5 May 2014).
- W.K. Härdle, and M. Osipenko. “Spatial Risk Premium on Weather Derivatives and Hedging Weather Exposure in Electricity.” Energy J. 33 (2012). [Google Scholar] [CrossRef]
- J.D. Woodard, and P. Garcia. “Basis Risk and Weather Hedging Effectiveness.” Agric. Financ. Rev. 68 (2008): 99–117. [Google Scholar] [CrossRef]
- O. Okhrin, M. Odening, and X. Wei. “Systematic Weather Risk and Crop Insurance: The Case of China.” J. Risk Insur. 80 (2013): 351–372. [Google Scholar] [CrossRef]
- D.V. Vedenov, and B.J. Barnett. “Efficiency of Weather Derivatives as PrimaryCrop Insurance Instruments.” J. Agric. Resour. Econ. 29 (2004): 387–403. [Google Scholar]
- N. Pelka, and O. Musshoff. “Hedging Effectiveness of Weather Derivatives in Arable Farming—Is There a Need for Mixed Indices? ” Agric. Finance Rev. 73 (2013): 358–372. [Google Scholar] [CrossRef]
- H.M. Markowitz. Portfolio Selection: Efficiency Diversification of Investments, 2nd ed. Cambridge, MA, USA: Basil Blackwell, 1991. [Google Scholar]
- B.A. Babcock, E.K. Choi, and E. Feinerman. “Risk and Probability Premiums for CARA Utility Functions.” J. Agric. Resour. Econ. 18 (1993): 17–24. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).